Advantages and pitfalls in the application of mixed model association methods

Abstract

Mixed linear models are emerging as a method of choice for conducting genetic association studies in humans and other organisms. The advantages of mixed linear model association (MLMA) include preventing false-positive associations due to population or relatedness structure, and increasing power by applying a correction that is specific to this structure. An underappreciated point is that MLMA can also increase power in studies without sample structure, by implicitly conditioning on associated loci other than the candidate locus. Numerous variations on the standard MLMA approach have recently been published, with a focus on reducing computational cost. These advances provide researchers applying MLMA methods with many options to choose from, but we caution that MLMA methods are still subject to potential pitfalls. Here, we describe and quantify the advantages and pitfalls of MLMA methods as a function of study design, and provide recommendations for the application of these methods in practical settings.

Mixed model association methods prevent false-positive associations and increase power

Mixed linear models are an emerging method of choice when conducting association mapping in the presence of sample structure, including geographic population structure, family relatedness and/or cryptic relatedness^1–12. The basic approach is to build a genetic relationship matrix (GRM) modeling genome-wide sample structure, estimate its contribution to phenotypic variance using a random-effects model (with or without additional fixed effects), and compute association statistics that account for this component of phenotypic variance (Online Methods). We note that mixed linear models can also be used to estimate components of heritability explained by genotyped markers^13–14, and to predict complex traits using genetic data^15–16.

Mixed linear model association (MLMA) methods are effective in preventing false-positive associations due to sample structure in studies of humans and model organisms^1–6. In particular, simulations show that the correction for confounding is nearly perfect for common variants even when geographic population structure, which is a fixed effect, is modeled as a random effect based on overall covariance^6,17–19 (however, rare variants pose a greater challenge for all methods, due to differential confounding of rare and common variants²⁰). MLMA methods also provide an increase in power, by applying a correction that is specific to sample structure^1–6. In the case of geographic population structure, markers with large allele frequency differences between populations will receive a larger correction. In the case of relatedness structure, the contribution of related individuals to test statistics will be reduced, preventing overweighting of redundant information due to correlation structure.

An underappreciated point is that MLMA can also increase power in studies without sample structure, by implicitly conditioning on associated loci other than the candidate locus that are not genome-wide significant in the data being analyzed⁸. For example, a GRM computed from all markers can be used to approximate the set of causal markers (implicitly assuming that all markers are causal), but this approximation can be generalized. The increase in power scales with the ratio N/M of the number of samples (N) to the effective number of independent markers (M), since the information about unknown associated loci depends on the number of samples. In simulations of a quantitative trait with no sample structure and no LD between markers (Online Methods), application of MLMA instead of linear regression increased average −log₁₀P-values at causal markers from 2.89 to 2.94 (1.8% increase) when N=10,000 and M=100,000, and from 2.92 to 3.46 (18% increase) when N=10,000 and M=10,000. We note that this improvement is contingent on the exclusion of the candidate marker from the GRM (see below).

Reducing the computational cost of mixed model association analysis

In initial implementations of MLMA, the component of phenotypic variance explained by the GRM was estimated separately when testing for the association of each candidate marker. This accounts for the fact that the total variance explained by all markers except the candidate marker may vary across candidate markers, in the case of markers of large effect^1–3. Even for efficient implementations³, this is computationally demanding, with computation time O(MN³) where M is the number of markers and N is the number of samples, because the variance component estimation is repeated for each candidate marker.

Several computational speedups have subsequently been developed. First, two independent studies observed that if markers have small effects, variance components can be approximated by estimating them only once using all markers (as previously proposed in family-based tests²¹), making MLMA feasible on large datasets^4–5. Two subsequent studies developed computationally efficient exact methods^7,11, which do not require variance components to be the same for all candidate markers. Each of these methods enables exact MLMA analysis in computation time O(MN² + N³). The difference between approximate and exact methods was reported to be large in a mouse dataset with pervasive relatedness and large effect sizes, but negligible in a human dataset¹¹. Another fast approximate method has recently been described¹². Several of these methods use a single eigendecomposition of the GRM to rotate the data, removing its structure^7,11–12.

The computation time of each method can be broken down into three steps: (1) building the GRM, (2) estimating variance components, and (3) computing association statistics for each SNP. In Table 1, we list the computational cost of each of these steps for the EMMAX⁴, FaST-LMM⁷, GEMMA¹¹ and GRAMMAR-Gamma¹² implementations, as well as our GCTA implementation (Online Methods and Web Resources). GRAMMAR-Gamma has the advantage that the cost of step (3) is reduced from O(MN²) to O(MN), greatly reducing the cost of analyzing a large number of phenotypes. To quantify the computational cost in datasets of realistic size, we benchmarked the running time and memory usage of GCTA using simulations of a quantitative trait without sample structure (Supplementary Note, Supplementary Table 1).

Table 1. Computational cost of EMMAX, FaST-LMM, GEMMA, GRAMMAR-Gamma and GCTA.

For each method we list the computational cost of each step (see main text).

	Building GRM	Variance components	Association statistics
EMMAX	O(MN2)	O(N3)	O(MN2)
FaST-LMM*	O(MN2)	O(N3)	O(MN2)
GEMMA	O(MN2)	O(N3)	O(MN2)
GRAMMAR-Gamma	O(MN2)	O(N3)	O(MN)
GCTA	O(MN2)	O(N3)	O(MN2)

^*If M<N, the computational cost of FaST-LMM can be reduced to O(M²N).

Pitfall: loss in power when candidate marker is included in GRM

Recent work has shown that inclusion of the candidate marker in the GRM can lead to a loss in power^7–8,22. This is due to double-fitting the candidate marker in the model, both as a fixed effect tested for association and as a random effect as part of the GRM. Listgarten et al.⁸, who referred to this phenomenon as “proximal contamination”, demonstrated that MLM with candidate marker excluded (MLMe) is the mathematically correct approach, and provided an elegant and efficient algorithm for MLMe analysis (implemented in FaST-LMM software). However, due to computation time or memory constraints (and complexities of LD), MLM with candidate marker included (MLMi) is more commonly applied in practice²². It is of interest to quantify the power loss of MLMi vs. MLMe, in order to help guide this choice. In this section, we provide new analytical derivations, validated by simulations, to quantify the reduction in test statistics when MLMi is applied.

Analytical derivations of mean association statistics (λ_mean)

We assume a set of unrelated samples without population structure or other artifacts. Let N denote the number of samples, M denote number of markers, and h_g² denote the heritability explained by genotyped and/or imputed markers¹³. We assume markers are unlinked, but the same derivations apply to linked markers if M denotes the effective number of independent markers, which for humans is approximately 60,000 (ref. ²³; Supplementary Note). We emphasize that it is the effective number of independent markers (not the total number of markers) that matters. Details of each derivation below are provided in the Supplementary Note.

For linear regression (LR), the expected mean of χ² association statistics (λ_mean) is

$${\lambda }_{\text{mean}}(\text{LR})=1+{{Nh}_g}^2/M$$ [1]

regardless of the genetic architecture of the trait²³.

For MLMi, λ_mean at markers used to construct the GRM is

$${\lambda }_{\text{mean}}(\text{MLMi})=1.$$ [2]

This highlights the dangers of using λ_mean (or λ_median) to assess the presence of population stratification or other artifacts. A researcher who observes lower λ_mean (or λ_median) for MLMi than for LR might conclude that this is due to correction for confounding, but in fact this result is expected even in the absence of any confounding.

Finally, for MLMe,

$${\lambda }_{\text{mean}}(\text{MLMe})=1+\frac{{Nh}_{\mathrm{g}}^2/M}{1-r^2{h}_{\mathrm{g}}^2}$$ [3]

where $r^2\approx {Nh}_g^2/M$ when M > N. The ratio of λ_mean between MLMe and MLMi is also $1+\frac{{Nh}_{\mathrm{g}}^2/M}{1-r^2{h}_{\mathrm{g}}^2}$, which is consistent for causal, null and all markers (Supplementary Table 2). If M ≫ N (i.e. r² is small), this is only slightly larger than $1+{Nh}_{\mathrm{g}}^2/M$. The difference between MLMe and MLMi is that MLMe is testing the null hypothesis that the candidate marker has no effect, whereas MLMi is testing the null hypothesis that the candidate marker has an effect size drawn from a normal distribution N(0, h_g²/M).

Simulations

We compared results of LR, MLMi and MLMe in simulations of a quantitative trait without sample structure, for various values of N and M (Online Methods). Our results show that MLMe increased power relative to LR but MLMi reduced power (Table 2, Supplementary Figure 1). The magnitude of these effects was proportional to N/M, consistent with our derivations (Table 2, Supplementary Table 3); the power differences are small at N=10,000 and M=100,000, but it is increasingly common for GWAS to be performed at sample sizes considerably larger than N=10,000. In all simulations, LR and MLMe had λ_mean at null markers equal to 1.00, but MLMi had λ_mean at all markers equal to 1.00 so that MLMi had λ_mean for null markers less than 1.

Table 2. MLMe increases power but MLMi decreases power vs. linear regression.

In scenario I, we report average χ² association statistics (± standard errors) at 500 candidate causal markers for linear regression, MLMi and MLMe, averaged across 100 simulations based on simulated genotypes. In scenario II, we report average χ² association statistics (± standard errors) at 200 causal markers for simulations based on ref. ²⁴ genotype data with simulated phenotypes. In both scenarios, expected values based on theoretical derivations are given in parentheses. More details including simulations at other values of N and M, results for all markers, power to detect significant associations at different P-value thresholds, and the equations to calculate the expected values are provided in Supplementary Table 3.

# samples (N)	#markers (M)	Linear regression (Expected value)	MLMi (Expected value)	MLMe & (Expected value)
Scenario I: Simulated unlinked markers
10,000	10,000	10.93 ± 0.03 (11.00)	9.81 ± 0.01 (10.05*)	13.27 ± 0.03 (13.36)
10,000	100,000	11.20 ± 0.03 (11.00)	10.97 ± 0.02 (10.09*)	11.40 ± 0.03 (11.25)
Scenario II: Simulations based on real genotype data24
10,000	133,036	26.99 ± 0.10 (26.00)	21.44 ± 0.05 (19.85)	28.42 ± 0.10 (29.08)

^*For MLMi, the $h_g^2$ of markers included in the GRM is 100%, and the derivation is much less accurate. However, the derivation is much more accurate at lower values of $h_g^2$ (Supplementary Table 3a).

^&The 500 candidate causal markers were always excluded from calculating the GRM in scenario I and the MLMe analysis was performed using GCTA-LOCO in scenario II.

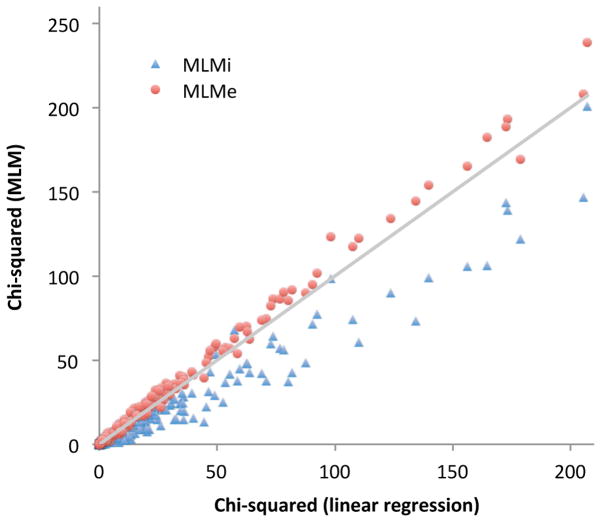
We also conducted simulations based on real genotypes of 133,036 SNPs on chromosomes 1, 2 and 3 in 10,000 unrelated individuals from data analyzed in ref. ²⁴ (Online Methods). For simplicity, when running MLMe we excluded from the GRM all the SNPs on a chromosome where the candidate SNP was located. Results again show that MLMe increases power relative to LR but MLMi reduces power (Figure 1, Table 2, Supplementary Table 3), consistent with our derivations. The effects are magnified because only a subset of the genome was analyzed, but analogous effects in proportion to N/M are expected at other values of N and M.

1. MLMe increases power but MLMi reduces power vs. linear regression.

We report χ² association statistics at 500 causal markers for MLMi vs. linear regression and MLMe vs. linear regression for one simulation with genotypes from ref. ²⁴ data and simulated phenotypes for N=10,000 samples. For MLMe, the 500 causal markers were always excluded from computing the GRM.

In summary, we recommend the use of MLMe in preference to MLMi. An efficient implementation of MLMe via a leave-one-chromosome-out analysis is provided in the GCTA software (GCTA-LOCO; Online Methods). An efficient implementation is also provided in the FaST-LMM software^7–8.

Pitfall: using a small subset of markers in GRM can compromise correction for stratification

Three recent papers have advocated choosing a subset of markers to include in the GRM when employing MLMA methods^7–8,25. FaST-LMM⁷ uses an equally spaced subset of M_R=4,000 (or 8,000) markers in the GRM, motivated by a computational speedup that reduces computational cost to O(M_R²N) when M_R<N. FaST-LMM-Select^8,25 uses the M_T markers with most significant linear regression P-values in the GRM, where M_T is chosen based on either the first local minimum of the genomic control factor λ_median⁸ or the global maximum of out-of-sample prediction accuracy using the resulting GRM²⁵. The latter approach allows for the possibility of including all markers in the GRM (M_T=M), but is computationally intensive (with a running time >10 times larger than MLMA using all markers) due to the high cost of computing out-of-sample prediction accuracy using all markers; an alternative (described on p.10 of the FaST-LMM version 2.05 user manual) is to choose M_T based on the first local maximum of out-of-sample prediction accuracy. These approaches have made the valuable observation that a substantial increase in power can be attained by implicitly conditioning only on loci that are relatively likely to be truly associated, motivating a thorough investigation of the impact on correcting for stratification. Below, we evaluate the impact of these choices on both false-positive associations and power. In all of these simulations, we excluded the candidate marker from the GRM (MLMe), consistent with ref. ^7–8,25.

To investigate the number of random markers needed to correct for stratification, we conducted simulations of a quantitative trait with population stratification (Online Methods). Our results indicate that when there is subtle population stratification, a few thousand random markers are not sufficient to provide a thorough correction for stratification (Figure 2, Supplementary Table 4, Supplementary Note), consistent with previous studies^11,26.

Figure 2. Effectiveness of MLM using M_R random or M_T top associated markers in correcting for stratification.

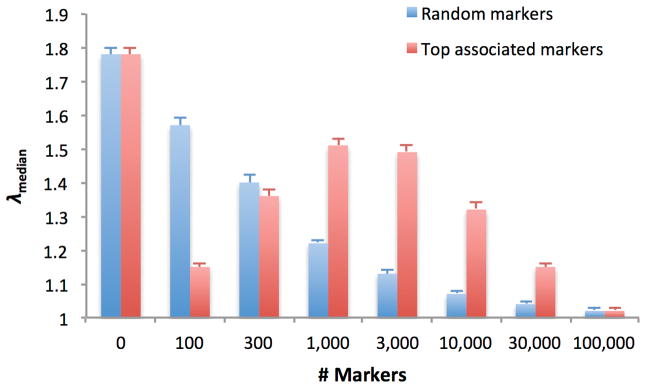
We report the average λ_median (± standard error) in 100 simulations with population stratification based on N=10,000 samples, M=100,000 markers, two discrete subpopulations with F_ST=0.005, and a mean trait difference of 0.25 standard deviations between subpopulations. Calibration of small P-values is reported in Supplementary Table 4.

We also investigated the use of the top M_T associated markers to correct for stratification. Our results indicate that using the top M_T associated markers based on the first local minimum of the genomic control factor λ_median⁸ may not be effective in correcting for stratification, and can lead to a local minimum in λ_median that is different from the global minimum²⁵ (Figure 2, Supplementary Note). On the other hand, the ref. ²⁵ approach of using the M_T top associated markers based on the global maximum of out-of-sample prediction accuracy selected M_T=M and thus provided an effective correction for stratification in these simulations (but see below).

We now turn to the question of power. We generalized our simulations without sample structure, with fraction p=0.05 or p=0.005 of causal markers, to consider the impact of using the top M_T associated markers in the GRM, for various values of M_T (Figure 3). When p=0.05, there are a large number of causal markers with small effect sizes, so that the top M_T associated markers do not correspond to the true set of causal markers, and including all markers in the GRM (M_T = M) performed best. When p=0.005, there are a smaller number of causal markers with larger effect sizes, so that the top M_T associated markers more closely reflect the true set of causal markers, and including only a small subset of top markers in the GRM performed best. Results at other parameter settings show that the optimal strategy depends on both the sample size and the genetic architecture of the trait (Supplementary Table 5, Supplementary Note). The ref. ²⁵ approach of using the M_T top associated markers based on the global maximum of out-of-sample prediction accuracy selected the value of M_T that maximized power in each of these simulations, achieving the optimal strategy.

Figure 3. Effectiveness of MLM using M_T top associated markers in increasing study power.

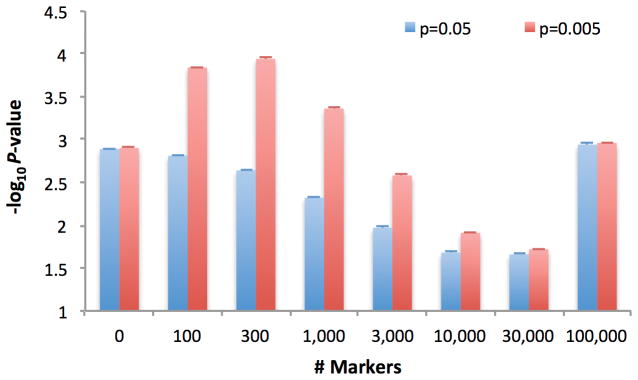
We report average −log₁₀P-values (± standard error) at causal markers in 100 simulations based on N=10,000 samples, M=100,000 markers, and fraction p=0.05 or p=0.005 of causal markers. Power to detect significant associations at different P-value thresholds is reported in Supplementary Table 5.

Finally, we explored using the top M_T associated markers in simulations with both stratification and causal markers. Results on stratification correction were similar to our simulations without causal markers (Supplementary Table 6), and results on power were similar to our simulations with no sample structure (Supplementary Table 7). The ref. ²⁵ approach of using the M_T top associated markers based on the global maximum of out-of-sample prediction accuracy again selected the value of M_T that maximized power in these simulations, often at the cost of effective stratification correction. For example, for N=10,000, M=100,000, p=0.005, this approach selected M_T=300, leading to a λ_median of 1.26 (vs. a λ_median of 1.00 if including all markers in the GRM). This highlights the challenge that efforts to maximize power can compromise effective stratification correction.

In summary, based on methods published to date, we recommend that studies of randomly ascertained quantitative traits in which population stratification is a key concern should generally include all markers (except for the candidate marker and markers in LD with the candidate marker) in the GRM. On the hand, the approach of ref. ²⁵ is expected to perform well when maximizing power and correcting for cryptic relatedness are the primary goals, and may also prove useful in the case of differential confounding of rare variants due to spatially localized stratification²⁷.

Pitfall: loss in power in ascertained case-control studies

All methods for mixed model association analysis published to date assume that study samples are randomly ascertained with respect to the phenotype of interest. While this is usually true for quantitative phenotypes, it is not true for case-control studies, which generally oversample disease cases to increase study power. Recent work has highlighted the loss in power that occurs in ascertained case-control studies when genetic or clinical covariates are modeled as fixed effects without accounting for ascertainment, and a subset of these studies have developed new methods to address this problem^28–32. However, the issue of power loss due to ascertainment has not previously been investigated for MLMA, which models both known and unknown associated markers as random effects.

We conducted simulations to investigate the use of existing MLMA methods in ascertained case-control studies. We extended our simulations without sample structure to simulate different values of disease prevalence f via the liability threshold model³³ (Online Methods). Results for MLMe vs. linear regression show that, for large N/M and small f, MLMe can suffer a substantial loss in power (Table 3). Similar results were obtained for different values of p (the fraction of non-candidate markers that are causal) and the proportion of variance explained by each candidate marker (Supplementary Table 8). We further note that, for large N/M and small f, the heritability explained by genotyped markers (h_g²) is mis-estimated by MLMe, even after accounting for observed vs. liability scale with correction for case-control ascertainment³⁴. However, using the correct value of h_g² does not ameliorate the loss in power (Supplementary Note and Supplementary Table 9).

Table 3. MLMe decreases power vs. linear regression under case-control ascertainment.

We report average −log₁₀P-values (± standard error) at causal markers for linear regression and MLMe, averaged across 100 simulations with p=0.05 and each candidate marker explaining 10/N of observed-scale variance. Results for different values of N, M, p and the proportion of variance explained by each candidate marker are reported in Supplementary Table 8, which also reports the power to detect significant associations at different P-value thresholds.

# samples (N)	#markers (M)	Disease prevalence (f)	Linear regression	MLMe
10,000	10,000	0.001	3.06 ± 0.15	2.22 ± 0.12
10,000	10,000	0.01	3.04 ± 0.16	2.64 ± 0.14
10,000	10,000	0.1	3.04 ± 0.17	3.06 ± 0.17
10,000	100,000	0.001	2.96 ± 0.16	2.78 ± 0.16
10,000	100,000	0.01	2.66 ± 0.14	2.54 ± 0.13
10,000	100,000	0.1	3.24 ± 0.16	3.26 ± 0.16

In summary, MLMA can suffer a severe loss in power due to case-control ascertainment, motivating further research on MLMA methods in case-control samples. The choice of whether to apply MLMA or other methods should be a function of sample size and severity of case-control ascertainment.

Advantages and pitfalls of MLMA in two empirical case-control studies

We investigated the advantages and pitfalls of MLMA in two recent GWAS of multiple sclerosis (MS) and ulcerative colitis (UC) involving over 20,000 samples^22,35. We chose these studies for several reasons. First, the MS study was the first large GWAS conducted using MLMA methods. Second, the authors of that study recognized that inclusion of candidate markers in the GRM (MLMi) was a potential pitfall, although analyses were conducted using MLMi based on available methods and software. Third, due to the large sample sizes, these were ideal datasets for exploring the issues highlighted by our simulations.

We analyzed data from 10,204 MS cases and 5,429 controls genotyped on Illumina arrays²² (Online Methods). This subset of cases and controls were not matched for ancestry (in contrast to ref. ²²), and exhibit substantial population stratification. We retained unmatched samples to maximize the sample size, which we believe is appropriate for these analyses. We also analyzed data from 2,697 UC cases and 5,652 controls genotyped on Affymetrix arrays³⁵ (Online Methods).

We compared seven methods of computing association statistics: linear regression (LR), LR with 5 PC covariates²⁶ (PCA), MLMi, MLMe, FaST-LMM using M_R=4,000 random markers⁷ (FaST-4K), FaST-LMM-Select using top M_T markers based on first local minimum of λ_median⁸ (FaST-Top), and FaST-LMM-Select using top M_T markers based on the first local maximum of out-of-sample prediction accuracy using the resulting GRM (FaST-TopX). For each method, we computed average χ² association statistics at all markers and at 75 and 24 known associated markers for MS and UC respectively (Online Methods).

We first consider genome-wide average χ² values (Table 4 and Supplementary Table 10). For MS, the genome-wide value of 0.994 for MLMi is consistent with our derivations and simulations (Table 2), as is the value of 1.232 for MLMe if the effective number of markers is M=60,000 and the heritability explained by genotyped markers is h_g²=0.266 on the liability scale (0.757 on the observed scale³⁴, assuming disease prevalence 0.1%), which is a plausible value given the liability-scale h_g²=0.30 ± 0.03 estimated in ref. ³⁶ using independent data. For UC, we observed a genome-wide value of 0.998 for MLMi and 1.100 for MLMe, consistent with h_g²=0.244 on the liability scale (0.695 on the observed scale) given the lower sample size. The average χ² for PCA was similar to that of MLMe for both traits. Thus, for both MLMe and PCA, the observed inflation in test statistics is consistent with polygenic effects according to our derivations, simulations, and independently obtained estimates of h_g². A higher value for PCA than for MLMi does not necessarily imply that PCA fails to correct for population structure (as suggested by ref. ²²), because our derivations and simulations show that correctly calibrated test statistics are expected to have a higher average χ² than MLMi under a polygenic model. On the other hand, FaST-4K, FaST-Top and FaST-TopX generally exhibit average χ² values that are higher than PCA and MLMe, consistent with an incomplete correction for stratification (Figure 2, Supplementary Tables 4 and 6). Although it is theoretically possible that the higher average χ² for these methods could be entirely due to higher average χ² at causal markers, this is unlikely given that the methods attain relatively similar average χ² at known associated markers (see below).

Table 4. Empirical results in MS and UC datasets.

We report average χ² association statistics for all markers (λ_median in parentheses) and for published associated markers, for each method (see main text). The FaST-Top method selected M_T=2,000 top markers for MS and M_T=400 top markers for UC, and the FaST-TopX method selected M_T=2,800 top markers for MS and M_T=3 top markers for UC.

	LR	PCA	MLMi	MLMe&	FaST-4K	FaST-Top	FaST-TopX
MS, 360,557 SNPs (λmedian)	3.95 (3.86)	1.25 (1.23)	0.99 (0.97)	1.23 (1.20)	1.86 (1.80)	1.42 (1.39)	1.41 (1.39)
MS, 75 published SNPs	18.50	10.20	8.90	11.30	13.98	10.99	10.56
UC, 458,560 SNPs (λmedian)	1.16 (1.16)	1.11 (1.10)	1.00 (0.99)	1.10 (1.09)	1.14 (1.13)	1.08 (1.09)	1.16 (1.15)
UC, 24 published SNPs	14.06	13.63	12.11	13.43	13.99	10.75	14.09

^&The MLMe analysis was performed using GCTA-LOCO.

We also tried running FaST-LMM-Select using top M_T markers based on the global maximum of out-of-sample prediction accuracy²⁵. Our runs failed to complete, because the 96GB memory limit was exceeded. The authors of ref. ²⁵ have reported that running this approach to completion on the same data results in every marker being selected for both MS and UC, and obtains results identical to MLMe (D. Heckerman and O. Weissbrod, personal communication).

We next consider χ² values at known associated markers (Table 4 and Supplementary Table 11). Among methods attaining a complete correction for stratification, MLMe consistently produced higher χ² values than MLMi for both MS (70 of 75 markers; P=1×10⁻¹⁵) and UC (24 of 24 markers; P=1×10⁻⁷), consistent with simulations (Figure 1). MLMe also produced higher χ² values than FaST-Top for UC (18 of 24 markers; P=0.02), the only instance in which FaST-4K, FaST-Top or FaST-TopX attained a complete correction for stratification. However, the comparison between MLMe and PCA was inconclusive, with MLMe producing higher values for MS (43 of 75 markers; P=0.25) and PCA producing higher values for UC (13 of 24 markers; P=0.84). Due to the lower correlation between these methods, these comparisons are noisy, and analyses of additional datasets will be needed to conclusively distinguish the performance of MLMe vs. PCA in empirical data. We note that the much lower χ² values for MLMi vs. PCA at known associated markers are consistent with ref. ²², who attributed this to structure that is not captured by PCA. However, the pitfalls of MLMi (Figure 1) provide an alternative explanation.

Recommendations and future directions

MLMA methods can prevent false-positive associations and increase power, at reasonable computational cost. However, our theoretical derivations, simulations and application to empirical data show that potential pitfalls include including the candidate marker in the GRM, using a small subset of markers in the GRM, and effects of case-control ascertainment.

We recommend excluding candidate markers from the GRM (MLMe) in preference to including them (MLMi). This can be efficiently implemented via a leave-one-chromosome-out analysis⁷, implemented in the GCTA software (GCTA-LOCO; Online Methods). An efficient implementation is also provided in the FaST-LMM software^7–8. Our analytical derivations demonstrate the advantages of MLMe over MLMi, and also quantify the expected inflation in MLMe test statistics in the absence of confounding, potentially ameliorating the need to apply an additional round of Genomic Control³⁷ correction as in many recent studies³⁸. However, distinguishing between polygenic effects and incomplete correction for stratification is an important direction of future research (B. Bulik-Sullivan, N. Patterson, A.L.P., M. Daly, B. Neale, unpublished data).

We recommend that studies of randomly ascertained quantitative traits should generally include all markers (except for the candidate marker and markers in LD with the candidate marker) in the GRM, except as follows. First, the set of markers included in the GRM can be LD-pruned to reduce running time (with association statistics still computed for all markers). Second, genome-wide significant markers of large effect should be conditioned out as fixed effects^4,9. Third, when population stratification is less of a concern, we recommend the ref. ²⁵ approach of using the M_T top associated markers based on the global maximum of out-of-sample prediction accuracy. (This approach may choose either a subset of markers (M_T<M) or all markers (M_T=M), but computational constraints may preclude the latter choice.) Finally, a potentially appealing way to capture the power advantages of selecting a subset of SNPs to include in the GRM while addressing concerns about stratification is to employ FaST-LMM-Select + PCs (G. Tucker, A.L.P., B. Berger, unpublished data and D. Heckerman, C. Lippert, J. Listgarten and O. Weissbrod, personal communication).

Ascertained case-control studies present a special challenge due to the potential loss in power of standard MLMA methods. When sample size is small or disease prevalence is high, standard MLMA methods can be used (Table 3). Otherwise, in datasets with no relatedness structure, PCA can be used²⁶. (In this case, conditioning on genome-wide significant markers or other covariates of large effect can be either omitted³¹, or retained using methods that explicitly model case-control ascertainment to increase power^28–30,32.) In ascertained case-control datasets with relatedness structure, we know of no good alternative to MLMA.

We conclude by highlighting three areas in mixed model association analysis in which there is a pressing need for development of new methods. First, there is a need for MLMA methods for ascertained control-traits that do not suffer a loss in power. Second, there is a need for MLMA methods that use mixture distributions of prior effect sizes to increase their power, mirroring advances in phenotypic prediction of livestock and human traits using Bayesian methods^39–41. Third, further work is needed to develop and assess methods for rare variants, which pose a greater challenge for all methods^20,27.

Online Methods

GCTA implementation of MLMi (GCTA-MLMi)

The phenotype y is modeled as

$$\mathbf{y}=\mathbf{Kc}+\mathbf{g}+\mathbf{e}$$ [Model 1]

where c is a vector of fixed covariates (including the affine term) with corresponding coefficient matrix K; g is a vector of genetic effects with g ~ N(0, Aσ_g²); A is the GRM defined by $A_{jk}=\frac{1}{M}{\displaystyle \sum _{i=1}^M}\frac{(x_{ij}-2p_i)(x_{ik}-2p_i)}{2p_i(1-p_i)}$, where x_ij = 0, 1 or 2 and M is the total number of autosomal markers; and e is a vector of non-genetic effects with e ~ N(0, Iσ_e²). We note that this is the same GRM used in previous work on principal components analysis²⁶. The variance explained by the GRM (σ_g²), the noise variance (σ_ε²) and the heritability explained by genotyped markers (h_g² = σ_g²/(σ_g² + σ_e²)) can be estimated via restricted maximum likelihood (REML)^13,42. Association statistics are computed by comparing the causal model with an effect at the candidate marker to the null model with no effect at the candidate marker, for example via a generalized least squares (GLS) F-test or χ² score test⁴.

We then test the effect of SNP i based on the model

$$\mathbf{y}=\mathbf{Kc}+{\mathbf{w}}_{\mathit{i}}{b}_i+\mathbf{g}+\mathbf{e}$$ [Model 2]

where w_i is a vector of mean-adjusted genotypes, i.e. w_ij = x_ij − 2p_i. The fixed effects, including both the effects of the covariates and the effect of SNP i, are estimated by GLS, i.e. q̂ = (Q^TV⁻¹Q)⁻¹Q^TV⁻¹ y with var(q̂) = (Q^TV⁻¹Q)⁻¹, where q = [c^T ⋮ b_i]^T, Q = [K ⋮ w_i] and $\mathbf{V}=\mathbf{A}{\sigma }_{\mathrm{g}}^2+\mathbf{I}{\sigma }_{\mathrm{e}}^2$. The test-statistic is calculated as ${\chi }^2={\widehat{b}}_i^2/var({\widehat{b}}_i)$, where var(b̂_i) the last diagonal entry of (Q^TV⁻¹Q)⁻¹. Assuming that the proportion of variance explained by a single SNP is small, the estimates of ${\sigma }_{\mathrm{g}}^2$ and ${\sigma }_{\mathrm{e}}^2$ from [Model 1] will be very similar to those from [Model 2]. To decrease the computational burden, we estimate ${\sigma }_{\mathrm{g}}^2$ and ${\sigma }_{\mathrm{e}}^2$ once based on [Model 1], without any SNPs included in the fixed effect vector c, and use them for effect size estimation and significance testing of each SNP based on [Model 2]; this is an approximate approach similar to that implemented in EMMAX⁴. If there are no covariates, the vector c will become a scalar (i.e. the affine term). In this case, for ease of computation, we can adjust the phenotype as y* = y − 1ĉ with ĉ = (1^T V⁻¹1)⁻¹1^T y and simplify the estimation of SNP effect as ${\widehat{b}}_i={\mathbf{w}}_i^T{\mathbf{V}}^{-1}{\mathbf{y}}^{\ast }/({\mathbf{w}}_i^T{\mathbf{V}}^{-1}{\mathbf{w}}_i)$ with $var({\widehat{b}}_i)=1/({\mathbf{w}}_i^T{\mathbf{V}}^{-1}{\mathbf{w}}_i)$. However, when there are covariates fitted in the models, we estimate the effects of the covariates and the SNP jointly rather than using the simplified approach. This is because if the covariates and the SNP genotype are correlated and the phenotype is pre-adjusted by the covariates, the power of detecting the SNP effect can be reduced. To improve computational efficiency, the efficient computational libraries EIGEN, BLAS and LAPACK are used for linear algebra calculation, and the parallel computing technique OpenMP is used for multi-thread computing.

GCTA implementation of MLMe via LOCO analysis (GCTA-LOCO)

This implementation is identical to GCTA-MLMi, except that markers on a given autosome are evaluated using a GRM constructed from the remaining autosomes, via pre-computing and storing the GRM constructed from all autosomes. GCTA-LOCO attains running time and memory usage only 2–3× higher than GCTA-MLMi (Supplementary Table 1).

Simulations of a quantitative trait with no sample structure

We simulated phenotypes for N samples using M non-candidate markers plus 500 candidate markers. All simulations used N=10,000 and M=100,000 unless otherwise specified. (We also included simulations at smaller values of N and M, in order to understand how the relative performance of different methods varies with N and M.) Allele frequencies were uniformly distributed on [0.1,0.9]. The M non-candidate markers included Mp causal markers (p=0.05 unless otherwise specified) explaining 50% of the variance of the trait, with normalized effect sizes ~ N(0,0.5/Mp). The 500 candidate markers explained an additional 50% of the variance of the trait, with normalized effect sizes ~ N(0,0.5/500). We ran MLMe by including the M non-candidate markers in the GRM and testing only the 500 candidate markers. We ran MLMi by the including the M non-candidate markers plus the 500 candidate markers in the GRM. Thus, the heritability explained by markers included in the GRM was 50% for MLMe and 100% for MLMi.

Yang et al. 2011 data and simulated phenotypes

We analyzed data from 14,347 individuals from the ARIC, HPFS and NHS cohorts that were genotyped using Affymetrix 6.0 arrays at 565,040 autosomal markers after quality control, as described previously²⁴. Informed consent was obtained from all subjects. We excluded one of each pair of individuals with genetic relatedness >0.025 in the GRM, leaving 11,586 unrelated individuals. We selected a random subset of 10,000 unrelated individuals. We restricted to 45,772 markers on chr1, 47,596 markers on chr2 and 39,668 markers on chr3, for a total of M=133,036 markers. We randomly selected 200 causal markers (100 each on chr1 and chr2) explaining 50% of the variance of the trait, with normalized effect sizes ~ N(0,0.5/200). We ran MLMi by including all markers in the GRM (GCTA-MLMi), and ran MLMe using a GRM estimated from the remaining chromosomes (GCTA-LOCO). We included causal markers on two different chromosomes in order to assess the benefit of running MLMe using a GRM containing causal markers on a different chromosome, and included a third chromosome with no causal markers in order to assess association statistics at markers that are not causal and not in LD with a causal marker.

Simulations of a quantitative trait with population stratification

We simulated phenotypes for N/2 samples from each of two discrete subpopulations, based on a mean trait difference of 0.25 standard deviations between subpopulations with no causal marker effects. We simulated M markers for the GRM plus 500 additional candidate markers, based on F_ST=0.005 or F_ST=0.0025 between subpopulations. Ancestral allele frequencies x were uniformly distributed on [0.1,0.9], and subpopulation allele frequencies were sampled from a beta distribution with parameters x(1− F_ST)/F_ST and (1−x)(1− F_ST)/F_ST, which has mean x and variance F_ST x(1−x). Causal markers in simulations with both stratification and causal markers were simulated in the same way as in simulations with no sample structure (see above).

Simulations of ascertained case-control traits

We simulated normally distributed liabilities, transformed liabilities to case-control status by defining individuals with liability >T to be cases and others to be controls (where the liability threshold T is chosen to achieve a specified disease prevalence f), and continued in this fashion until N/2 cases and N/2 controls were generated. Liabilities were simulated as in the simulations of a quantitative trait with no sample structure, except that liability-scale effect sizes of the 5 candidate markers were chosen so that each candidate marker explains the proportion 10/N of observed-scale variance, after accounting for the transformation between variance explained on the liability scale vs. the observed scale with correction for case-control ascertainment³⁴. We used only 5 candidate markers so as to limit the liability-scale variance explained by the candidate markers, which exceeds observed-scale variance when prevalence is low. We also included M non-candidate markers, of which the proportion p were causal (p=0.05 or p=0.005) and explained 50% of the liability-scale variance. To examine results for candidate markers of larger effect, we repeated all simulations with each candidate marker explaining the proportion 20/N of observed-scale variance.

MS and UC datasets

We analyzed data from 10,204 MS cases and 5,429 controls (from NBS and 1958BC) genotyped on Illumina arrays made available to researchers via WTCCC2 (see Web Resources). Although ref. ²² analyzed UK and non-UK samples separately followed by meta-analysis in most of their analyses, the data made available to researchers includes both UK and non-UK cases but only UK controls. We retained all samples in order to maximize sample size. We considered markers that were present in each of MS, NBS and 1958 BC datasets and removed markers with >0.5% missing data, P<0.01 for allele frequency difference between NBS and 1958BC, P<0.05 for deviation from Hardy-Weinberg equilibrium, P<0.05 for differential missingness between cases and controls, or MAF<0.1% in any dataset, leaving 360,557 markers. We employed filters more stringent than in a standard GWAS so as to minimize the impact of assay artifacts on our results³⁴. The 75 known associated markers were defined by including, for each MS-associated marker listed in the NHGRI GWAS catalogue (see Web Resources), a single best tag at r²>0.4 from the set of 360,557 markers if available.

We also analyzed data from 2,697 UC cases and 5,652 controls (from NBS and 1958BC) genotyped on Affymetrix arrays³⁵ and made available to researchers via WTCCC2. The MS and UC datasets contain overlapping control samples. We employed stringent QC filters as described above, leaving 458,560 markers. The 24 known associated markers were defined by, for each UC-associated marker listed in the NHGRI GWAS catalogue, a single best tag at r²>0.4 from the set of 458,560 if available.

PCA refers to PC correction using 5 PCs. Correction using 10 PCs (PCA10) or 20 PCs (PCA20) was also evaluated (Supplementary Table 10). FaST-4K was run by including M_R=4,000 random markers in the GRM. FaST-Top was run by including the top M_T markers based on first local minimum of λ_median⁸, using a grid search from 100 to 3,000 with a step size of 100. FaST-TopX was run using the command “fastlmmc -autoSelect <outfile> -randomSeed 1 -autoSelectFolds 10 -bfilesim <indata> -pheno <inpheno> -mpheno 1 -autoSelectSearchValues ASvalues.txt -topKbyLinReg 10000 -memoryFraction 0.2”, as described on p.10 of the FaST-LMM version 2.05 user manual. (The -topKbyLinReg 10000 option was not used in our simulations, which selected the global optimum of M_T.) FaST-Top selected M_T=2,000 top markers for MS and M_T=400 top markers for UC, and FaST-TopX selected M_T=2,800 top markers for MS and M_T=3 top markers for UC.