Non-invasive temperature mapping using temperature-responsive water saturation shift referencing (T-WASSR) MRI

Abstract

We present a non-invasive MRI approach for assessing the water proton resonance frequency (PRF) shifts associated with changes in temperature. This method is based on Water Saturation Shift Referencing (WASSR), a method first developed for assessing B₀ field inhomogeneity. Temperature-induced water PRF shifts were determined by estimating the frequency of the minimum intensity of the water direct saturation spectrum at each temperature using Lorentzian line-shape fitting. The change in temperature was then calculated from the difference in water PRF shifts between temperatures. Optimal acquisition parameters were first estimated using simulations and later confirmed experimentally. Results in vitro and in vivo showed that the temperature changes measured using the temperature-responsive WASSR (T-WASSR) were in good agreement with those obtained with MR spectroscopy or phase mapping-based water PRF measurement methods,. In addition, the feasibility of temperature mapping in fat-containing tissue is demonstrated in vitro. In conclusion, the T-WASSR approach provides an alternative for non-invasive temperature mapping by MRI, especially suitable for temperature measurements in fat-containing tissues.

Introduction

It is of great clinical interest to measure the temperature changes of deep-seated tissues non-invasively during the course of cancer thermotherapy (hyperthermia or high-temperature thermal ablation) (1-3), hypothermia treatment of acute ischemic stroke (4-6), and during triggered drug release from temperature-sensitive drug delivery systems (7-9). In addition to using temperature-sensitive MRI contrast agents (9-11), a number of noninvasive MRI techniques have been suggested for assessing temperature. These employ monitoring of a particular MRI property that is responsive to temperature changes, including proton density (12), diffusion constants (13), T1(14) and T2 (15) relaxation times, magnetization transfer ratio (16), intermolecular zero-quantum coherences (iZQCs) (17), and, the most widely used, the water proton resonance frequency (PRF) (3,18-21). Water PRF shifts are sensitive to temperature because temperature strongly affects the chemical shift of water protons by altering their hydrogen bonding state (22). Water PRF-based temperature measurement is widely used because of its relatively high sensitivity (−0.01 ppm/°C) over a wide temperature range (−15 to 100 °C), which can be approximated independent on tissue type for most tissues (23-26). Water PRF methods have employed two techniques, namely MR spectroscopic (MRS) imaging (18,27) and gradient-echo based phase mapping (19,28). Proton MRS directly determines the chemical shift of water protons by assessing the ¹H NMR spectrum of the region of interest. Using non-temperature-responsive methyl and methylene protons (e.g. from N-acetyl-aspartate (NAA) or lipid) as reference, the absolute temperature can be determined after calibration. However, this technique is often limited by a low spatial or temporal resolution, and as such, not suitable for real-time monitoring. Alternatively, a high-resolution temperature change map can be obtained by assessing the MR phase difference between two temperatures. To date, it is the most widely used non-invasive MRI method for temperature mapping in clinical and preclinical studies, with a capability of monitoring temperature change in real-time (29). However, the accuracy of measurement may be complicated when magnetic background gradient effects (e.g. due to changing shims) cannot be neglected (28) or a significant portion of fat is present in the tissue (30,31).

Recently, the so-called Water Saturation Shift Referencing (WASSR) method (32) was proposed to determine B₀ shifts by assessing the minimum of the water direct saturation (DS) spectrum (33) acquired using weak radiofrequency saturation. In this approach, the B₀ shift of each voxel is simply determined from a DS spectrum by finding the frequency that corresponds to the maximum saturation (or the minimum water signal intensity), using either a non-model-based maximal symmetry algorithm (32) or a model-based Lorentzian line shape algorithm (34). The latter is possible because the steady-state direct saturation spectrum can be described exactly by a Lorentzian line shape (35). We hypothesized that such an approach could also be used to map temperature changes if the temperature is the dominating factor causing the shift in B₀. We describe here a WASSR-based temperature mapping MRI method, namely Temperature-responsive Water Saturation Shift Referencing (T-WASSR), which has at least two desirable features. First, it can directly determine the chemical shift of water protons, similar to an MRS method, but with a higher temporal and spatial resolution. Second, in the T-WASSR spectrum, the water peak is inherently separated from that of lipid protons if the field inhomogeneity across the image volume is not too severe, allowing an unbiased assessment of water PRF in the presence of lipid protons without the need of a priori knowledge of fat composition and additional data processing steps.

Theory

MRI temperature measurement based on water PRF

At a given temperature (T), the apparent temperature-dependent water proton chemical shift δ (T) is determined by

$$\delta \left(T\right)={\delta }_0+{\delta }_T\left(T\right)$$ [1]

where δ₀ is the sum of temperature-independent contributions, including the inherent chemical shift and the shift that arises from local B₀ field inhomogeneity, and δ_T(T) is the temperature-dependent shift contribution, which changes linearly with respect to the change in temperature, i.e., Δδ_T(T) = αΔT, where the temperature coefficient α (= dδ/dT) is approximately −0.01 ppm/°C for most tissues except fat (23-25).

In MRI measurements, δ(T) is determined by measuring the local magnetic field, B_loc , with the relationship (28)

$$B_{loc}\left(T\right)=(1+\delta \left(T\right)-\frac{2}{3}\chi \left(T\right))B_0$$ [2]

where B₀ is the magnetic field strength and χ(T) is the temperature-dependent tissue susceptibility, which is dependent on the sample geometry and orientation (36). The temperature-dependent susceptibility constant, however, is much smaller than the constant of temperature-dependent PRF shift for pure water and tissues with high water content such as muscle, making the contribution of the temperature-dependent susceptibility effect to the local magnetic field less 10% than that of water PRF (28). Thus it is generally assumed that the temperature-dependent susceptibility can be neglected in most applications (24).

In the case of phase mapping (19,20), the image phase Φ(T) is determined by the water PRF δ(T), assuming there is a negligible temperature-dependent tissue susceptibility change and a perfect scanner offset frequency:

$$\Phi \left(T\right)=\gamma T_E(B_{loc}-B_0)=\gamma T_E\delta \left(T\right)B_0$$ [3]

where γ is the gyromagnetic ratio of water protons (42.58 ×10⁶ Hz/Tesla) and T_E is the echo time used in a gradient echo pulse sequence. To eliminate the contribution of the temperature-independent term δ₀ from δ(T), image phases at two temperatures, the temperature to be measured (T_measure) and a reference temperature (T_ref), are compared to calculate the temperature change (ΔT) between them:

$$\Delta T=T_{measure}-T_{ref}=[\Phi \left(T_{measure}\right)-\Phi \left(T_{ref}\right)]∕\alpha \gamma T_E{B}_0$$ [4]

Water Direct Saturation

Derived from Bloch equations of a single water pool model (37), the analytical solution of the observed water longitudinal magnetization at the steady state ($M_Z^{SS}$), in the presence of a saturation pulse with a B₁ field strength of ω₁ (in the unit of radian), at a particular offset (Δω= ω₀- ω_RF), is given by

$$M_Z^{SS}=\frac{M_Z^0}{1+{\left(\frac{{\omega }_1}{{\omega }_0-{\omega }_{RF}}\right)}^2\left(\frac{T_1}{T_2}\right)}$$ [5]

where ω₀ and ω_RF are the resonant frequency of water protons and the off-resonance irradiation frequency of the applied RF pulse, respectively, M_z⁰ is the longitudinal magnetization without saturation, and T₁ and T₂ are the spin-lattice and spin-spin relaxation times of water, respectively. Eq. [5] thus provides a mathematical model of the frequency dependence of the water DS spectrum described by a Lorentzian line shape (37). The maximum saturation occurs when the RF pulse is applied at offset ω₀= ω_RF, which provides a practical way to measure ω₀ by sweeping ω_RF (32,34). When discrete and noise-carrying experimental data are used, however, data fitting has to be performed using a non-model based (32) or model-based (34) algorithm. It should also be noted that the presence of Magnetization Transfer (MT) and/or Chemical Exchange Saturation Transfer (CEST) may compromise the single-pool assumption, especially when applied to in vivo measurements. Fortunately, as shown previously (32), implementation with a weak RF saturation pulse may effectively minimize the impact of MT and CEST. It should also be noted that, although a change in temperature can also changes in T1, T2 and M ⁰_z, leading to a change in the lineshape of WASSR spectrum, the ω₀ is only determined by the position where maximal saturation occurs in a WASSR spectrum and therefore is not susceptible to the changes in these temperature-dependent parameters.

Similarly to Eq. [4], and illustrated in Figure 1a, temperature changes can be determined by comparing the water PRF (ω₀) determined for each pixel in the B₀ shift map at two temperatures:

$$T_{measure}=T_{ref}+\Delta T=T_{ref}+({\omega }_0\left(T_{measure}\right)-{\omega }_0\left(T_{ref}\right))∕2\pi \cdot \alpha \gamma B_0$$ [6]

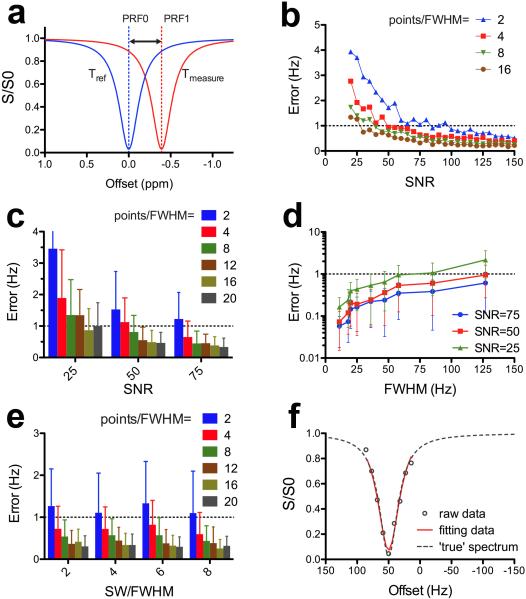
Figure 1.

Simulations showing the T-WASSR measurement of a water PRF shift. a) Illustration of measuring temperature-induced water PRF shifts using T-WASSR. b) Measurement error (Hz) as a function of SNR level at spectral resolutions ranging from 2 to 20 points per FWHM. c) Measurement error (Hz) as a function of resolution (points per FWHM) at SNR levels of 25, 50, and 75, respectively. d) Measurement error (Hz) as a function of line width (FWHM) at SNR levels of 25, 50, and 75, respectively. e) Measurement error (Hz) as a function of resolution (points per FWHM) for the sweep width ranging from 2 to 8 times FWHM. Dashed thresholds in b, c d and e correspond to 1 Hz error. The error bars shown in c, d and e indicate the standard deviations of the fitting errors of 30 repeated simulations. f) The fitting of the water DS spectra and the corresponding “true” DS spectra. The data set of discretely-sampled and noise-superimposed spectral data was simulated from the ‘true’ data using an SNR level of 50, a spectral resolution of 4 points per FWHM and a sweep width of SW/FWHM = 2.

Experimental

Simulations

All simulations were performed using MATLAB (Mathworks, Natick, MA). The saturation parameters used for all simulations were a continuous wave (CW) pulse with a duration of 0.5 seconds and a B₁ field strength of ω₁/2π = 21.3 Hz. The simulated raw data to be used for testing the proposed Lorentzian fitting algorithm was produced in two steps. First, saturation frequency-dependent DS spectral data sets were created using the steady-state analytical solution described by Mulkern et al. (37) with the frequency range from -500 Hz to 500 Hz. A fixed T1 relaxation time of 1.2 s (adapted from literature for muscle at 9.4T(38)) was used, whereas T2 relaxation times were varied from 5 to 500 ms to produce DS spectra with different linewidth. The full width at half maximum (FWHM) of each spectrum was experimentally measured based on the DS spectrum. All spectra were shifted by 50 Hz to resemble a water PRF shift (or B_{0, true}) of 50 Hz. The second step was to create ‘real’ data that are discretely sampled and contain noise. First, the ‘true’ data sets produced in the first step were asymmetrically segmented into new data sets from −450 to +550 Hz, with their spectral resolution ranging from 2 to 20 sampling points per FWHM to resemble discrete data sampling. Subsequently, zero-mean Gaussian white noise, at a signal-to-noise ratio (SNR) level ranging from 20:1 to 150:1, was produced and superimposed on each “discretely sampled” and “B₀-shifted” data set. To be specific, the SNR is defined based on the M0 image of a WASSR spectrum. Finally, the data sets were segmented symmetrically around the resonance offset with a sweep width (SW) varying from 2 times to 8 times the FWHM. These final data sets were then fitted to Eq. [5] to estimate the B₀ shift of the spectrum, i.e., B_0,estimated. The error of fitting was calculated by |B_0,estimated- B_{0, true}|, where B_{0, true} = 50 Hz in our simulations. Considering that the noise was randomly produced for each given SNR level and spectral resolution, we calculated the mean measurement error of thirty data sets that were produced in the second step separately. Finally, the mean and standard deviation of fitting errors were plotted with respect to SNR, spectral resolution (points per FWHM) and sweep width (SW/FWHM).

In vitro phantom studies

Three phantoms were prepared for in vitro temperature measurements. The first two phantoms were uniform samples containing either gelatin gel, to represent non-fat-containing tissues, or 25% (v/v) peanut-oil-in-gelatin gel, to mimic fat-containing tissues, prepared in cylindrical plastic tubes (OD= 15mm) according to the literature (31). To measure the absolute temperatures inside the phantom, three capillaries (OD=1mm) containing ethylene glycol (Sigma, St Louis, USA) were inserted into each phantom. Ethylene glycol has well documented temperature dependent chemical shift differences, i.e. T (K) = 466.5 - 102.0× Δδ between 273 and 416 K(39), and has been widely used as a means to calibrate temperature settings in NMR studies. The third phantom was prepared, to resemble irregularly shaped fat containing tissues, by immersing a piece of cheese (8.9 % fat, Saputo Cheese, USA Inc., Lincolnshire, IL) in 2% agarose gel in a cylindrical plastic tube (OD= 15mm).

The in vitro MRI acquisition was performed on a vertical bore 11.7 Tesla Bruker Avance system equipped with a 15 mm birdcage RF coil. A NMR thermocouple was used to control the temperature by blowing heating gas to the samples. For the phantoms containing gelatin gel, the intra-bore temperature was adjusted from 294K to 324K (51°C) at 10K increments. For the phantom that mimicked fat-containing tissues, the intra-bore temperatures were set to 302K, 310K, and 313K in addition to the initial room temperature (without heating, measured as 297K). There was always a 30-minute interval between each measurement after the thermocouple was set to the next temperature. The T-WASSR images at each temperature were acquired using a modified Rapid Acquisition with Relaxation Enhancement (RARE) sequence (RARE factor =16, slice thickness= 1 mm, TR = 1.5 s, TE = 5 ms, acquisition matrix size = 128×128, which corresponds to 80 phase encoding steps when a 1.6 partial Fourier transform (FT) acceleration was used; spatial resolution = 80×80 μm, and one average (NA = 1). The saturation of water or lipid protons was implemented using a single continuous wave (CW) RF pulse (t_sat = 500 ms, B₁ = 0.5 μT (ω₁/π = 21.3 Hz)), with saturation offsets swept from −0.5 ppm to + 0.5 ppm with respect to the water resonant frequency at a resolution of 0.1 ppm. To acquire the direct saturation spectrum of lipid protons, the saturation offset was swept from −3 ppm to −4 ppm with respect to the water resonance frequency, with the same increment of 0.1 ppm. The total acquisition time for each water (or fat) DS spectrum acquisition was two minutes. To study the potential influence of WASSR acquisition parameters on the accuracy of temperature measurement, we also acquired WASSR spectra using a) a fixed saturation B1= 0.5 μT and varied saturation durations ranging from 250 to 1300 ms; and b) a fixed saturation duration of 500 ms and varied saturation B1 ranging from 0.3 to 1.2 μT.

A phase map at each temperature was acquired using a multiple gradient echo method (40), implemented with a Fast Low Angle SHot (FLASH) sequence (flip angle= 30°, TR= 200ms, 128 phase encoding steps and NA = 4, spatial resolution = 80×80 μm). Five TE times (2.5ms, 5ms, 7.5ms, 10ms, and 12.5 ms) were used to calculate phase maps using a temporal phase unwrapping algorithm. The total acquisition time was 1.8 minutes (NA = 4). The reason for using NA=4 in phase imaging while using NA=1 in T-WASSR is to provide comaprable SNRs between the two studies. When applied to fat containing phantom, a fat suppression module (hermite pulses, bandwidth = 1600 Hz) was used. ¹H NMR spectra of the regions of interest were acquired using a point-resolved spectroscopy (PRESS) sequence (TR/TE = 3000/21 ms, spectrum acquisition size= 2048 points, sweep width = 6.0 kHz, and NA = 32). The acquisition time was 1.52 minutes. ¹H NMR spectra were processed using 1D FT with a line-broadening factor of 2, followed by phase and baseline correction using the Topspin software package (Bruker Biopsin Co., Billerica, MA).

In vivo animal studies

All animal experiments were approved by our institutional animal care and use committee (IACUC). Eight-week old female C57BL/6.SJL mice were purchased from Jackson Labs (Bar Harbor, Maine). The right leg of the mouse was wrapped with a heating pad with circulating water. Insulation material was placed between the left leg and the heating pad. After appropriately positioning the mouse in the scanner, the lower limbs of the mouse were assessed using both T-WASSR and phase mapping. Three measurements were performed: at room temperature (T(0) = 24°C) where the water circulation pump was not turned on, and during hyperthermia where the temperature of circulating water was maintained at T(1) = 45 °C and T(2) = 55°C using a thermostat. There was always 30 minutes waiting period each time after the thermostat was set at a new temperature.

In vivo images were collected on a 9.4 T Bruker scanner using a 25 mm sawtooth resonator. The same imaging scheme as that for in vitro imaging was used, except the RARE factor was reduced to 8 and a frequency-selective fat suppression pulse was used (hermite pulse, pulse length = 3.4 ms and offset = -3.5 ppm). The saturation offsets were swept from −2 ppm to +2 ppm with 0.1 ppm steps. We employed a keyhole approach (41,42) to reduce the acquisition matrix from 128x128 to 128x64 (spatial resolution = 250×172 μm), which resulted in a 12-s acquisition time per image or a total acquisition per WASSR spectrum of approximately eight minutes. The same phase-mapping procedure as that described above was also conducted immediately after each T-WASSR acquisition.

Data processing

All data were processed using custom-written MATLAB scripts. Images were first filtered by a SNR threshold (e.g. 40 for in vitro and 15 for in vivo respectively) to remove low SNR pixels, with the noise estimated by the standard deviation of an ROI containing pure noise (often the black regions at the upper right corners) of the S₀ image. For the T-WASSR approach, the B₀ maps at each temperature were first calculated by fitting the T-WASSR spectrum to Eq. [5]. Subsequently, the temperature change map was calculated by converting the B₀ difference (Hz), pixel-wise, between two temperatures, to temperature (K) using Eq. [6]. When a keyhole approach was used, the skipped 64 high spatial-frequency k-space lines in the raw data of each WASSR spectral image were substituted by the corresponding lines in a reference image that was acquired with the full sampling size (i.e., 128 phase-encoding steps). The raw data were then reconstructed and processed using the procedure described above. For phase mapping, temperature change maps were produced by directly comparing phase images at the two temperatures according to Eq. [4].

Statistics

Nonparametric Spearman correlation analysis was performed on the measured temperatures of the same subject between the proposed T-WASSR method and phase-mapping or localized MRS measurement of ethylene glycol using Graphpad Prism (GraphPad Software, San Diego, CA). In addition, Bland-Altman analysis (43) was also performed to assess the agreement between these methods, with a criteria of 95% of the standard deviation of the differences between the two methods. A pixel-by-pixel Student's t-test (two-tailed, unpaired) was performed to compare two specific ROIs of the in vivo temperature maps obtained by T-WASSR and phase imaging, respectively.

Results

Simulations

To examine whether the proposed Lorentzian fitting algorithm could provide an accurate estimation of water PRF, we first performed the fitting on the simulated data with full width half maximum (FWHM) of 127 Hz (T2 = 5 ms). Figure 1b shows that either increasing the SNR or increasing the sampling size improves the accuracy of estimating water PRFs, however, at the expense of an increased acquisition time. To estimate the minimal sampling size for a reliable fitting (i.e., error < 1 Hz or relative error < 2 %), we investigated the mean measurement error as a function of points per FWHM at three SNR levels (i.e., 75, 50 and 25, Figure 1c). The result clearly shows that the choice of spectral resolution greatly relies on the SNR. In particular, at least 2 points per FWHM should be used for scenario of high SNR (> 75), 4 points per FWHM for moderate SNR (~50), and 8 points per FWHM for low SNR (~25).

Next, we examined the influence of line width, which affects the choice of sweep width. As expected, the results (Figure 1d) show that the mean measurement error increases non-linearly with line width, indicating a larger sampling size should be used for in vivo applications where the spectral linewidth is generally broad. In general, a sufficiently broad sweep width (SW) should always be used in order to cover the complete range of B₀ inhomogeneity over the image slice. However, in the case that only some regions are of interest and their B₀ shifts are known, reducing the SW could be considered to accelerate the acquisition. This strategy is particularly useful for monitoring the temperature changes of a particular tissue during hyperthermia where the B₀ shifts before the procedure are known and the subsequent changes are within a range <1 ppm (~0.01 ppm per °C). Figure 1e shows that no significant reduction of measurement accuracy is found when the sweep width was decreased from 8 to 2 times of FWHM, indicating that a SW of two times of the FWHM is proper.

Collectively, the minimal sampling sizes for acquiring a T-WASSR data set are 2, 4 or 8 points per FWHM for high, moderate, or low SNR respectively. The SW generally should be large enough to cover the entire B₀ range, however, could be reduced to up to SW/ FWHM=2 for the cases that only the temperature changes of particular regions with known B₀ shifts are under monitoring. Figure 1f presents an example of the fitting of the simulated data (T2 = 50 ms, FWHM = 36 Hz) using a SNR of 50 and a spectral resolution of 4 points per FWHM. The systematic error between the estimated water PRF and the ‘true’ value was less than 1 Hz, corresponding to a 0.8°C error in temperature at 3T (128 MHz) or 0.25°C or less at a field strength higher than 9.4T (400 MHz).

The purpose of this simulation is to provide a guideline for designing a T-WASSR study with such a sampling strategy that warrants an efficient while accurate measurement. In practice, however, many factors can potentially affect the WASSR model and consequently change FWHM, which would affect the decision of sampling (the size of offset step in Hz) and scan time. It should be noted that the FWHM of a region of interest can be empirically estimated by the water peak in a ¹H spectrum acquired using a localized method, such as PRESS and STEAM.

Phantom study

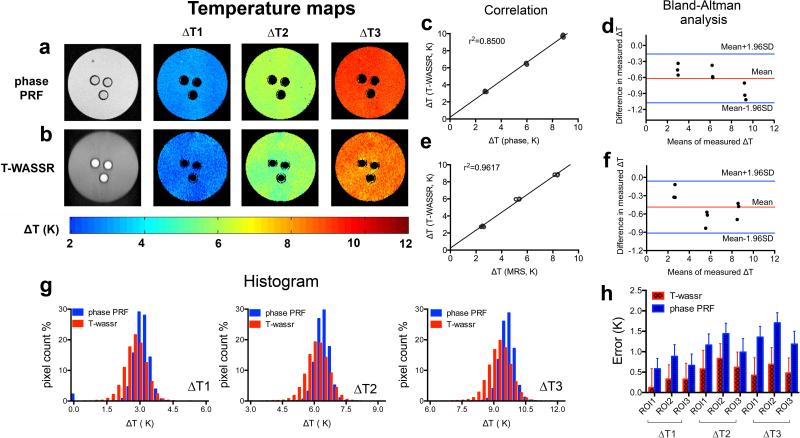
The T-WASSR method was first compared to the conventional phase mapping based PRF method using a gelatin gel phantom. Figures 2a,b show that both T-WASSR and phase PRF imaging could map temperature changes at a high spatial resolution (i.e. 80×80 μm in the present study). Similar to phase mapping, T-WASSR can report on only the relative changes in temperature (ΔT) and not the absolute temperature except when an internal reference is available. A quantitative comparison between the two methods was performed using the mean ΔTs of three ROIs that were manually drawn near the three tubes containing ethylene glycol. In addition to a relatively good linear correlation (r²=0.8500, Figure 2c), there is good agreement between the two methods according the Bland-Altman plot (Figure 2d). It is evident that, at each temperature, the difference between the two measurements falls into the region within 95% of the standard deviation of the differences between the two methods. In addition, the measured ΔTs of the three ROIs were consistent with those determined using single-voxel MRS of ethylene glycol, as shown again in both correlation analysis (r²=0.9617, Figure 2e) and Bland-Altman analysis (Figure 2f). While the mean ROI ΔT values were found well correlated between the two methods, the histogram analysis (Figure 2g) showed that the ΔTs measured by T-WASSR had a slightly broader distribution, indicating a larger pixel-by-pixel variation compared to those of phase PRF method. Despite this larger pixel-by-pixel variation, as revealed by Figure 2h, the relative error (calculated using the temperatures measured by the ethylene glycol chemical shift method as the standard) of a T-WASSR was shown to be smaller than that of phase PRF imaging, indicating T-WASSR may provide higher accuracy than the traditional phase PRF method.

Figure 2.

Measuring temperature change (ΔT) in a gelatin gel phantom using both phase PRF and T-WASSR. a, b) Temperature change maps measured by phase imaging and T-WASSR at three incremented temperatures. c, d) Linear regression plot and Bland-Altman plot of mean ΔTs of three ROIs near the ethylene-glycol- contained capillaries measured by T-WASSR and phase imaging respectively. e, f) Linear regression plot and Bland-Altman plot of mean ROI ΔTs measured by T-WASSR and ΔTs in capillaries determined by the chemical shift differences of ethylene glycol using single-voxel MRS. g) Histogram analysis showing the measured ΔT values for all the included pixels in the phantom using both methods. h) The errors in measuring temperature changes for all three ROIs of both T-WASSR and phase PRF methods. The errors were calculated by comparing the measured temperatures changes using either T-WASSR or phase PRF and that determined by MRS method using the chemical shift differences of ethylene glycol.

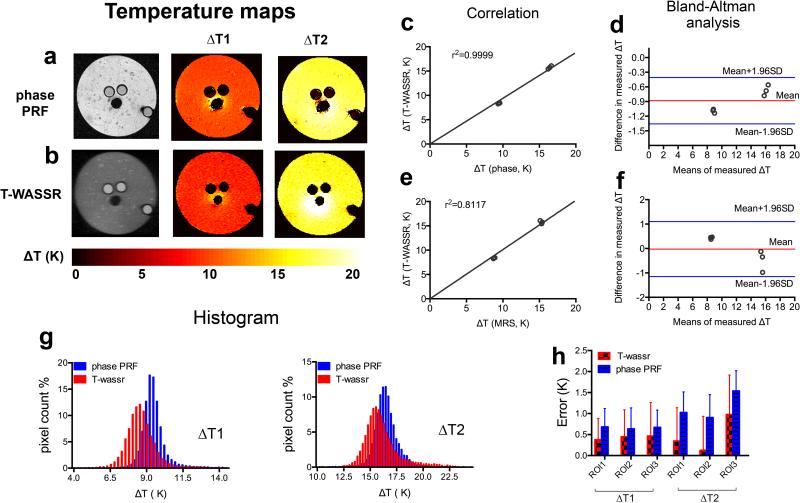
Similarly, a study was also conducted to compare the ΔTs measured by T-WASSR and phase PRF (with fat suppression) on a phantom composed of 25% oil-in-water gelatin gel (Figure 3a, b). As shown in Figures 3c-f, the temperature measured by T-WASSR correlated well with those of phase PRF (r²=0.9999, Figure 3c) and also those calculated by the chemical shift differences of ethylene glycol (r²=0.8117, Figure 3e), which is consistent with previous findings on water only gelatin phantom. A clear discrepancy in the measured ΔTs, however, was shown in the histogram (Figure 3g). Figure 3h showed that the temperatures obtained using T-WASSR are closer to those calculated using a chemical shift method than a fat suppressed phase PRF method, indicating that the T-WASSR method has higher applicability in monitoring the temperature of fat-containing tissues.

Figure 3.

Measuring temperature change (ΔT) in a gelatin gel phantom containing 25% peanut oil using both phase PRF and T-WASSR. a, b) Temperature change maps measured by phase imaging and T-WASSR at two incremented temperatures. c, d) Linear regression plot and Bland-Altman plot of mean ΔTs of three ROIs near the ethyleneglycol- contained capillaries measured by T-WASSR and phase imaging respectively. e, f) Linear regression plot and Bland-Altman plot of mean ROI ΔTs measured by T-WASSR and ΔTs in capillaries determined by the chemical shift differences of ethylene glycol using single-voxel MRS. g) Histogram analysis showing the measured ΔT values for all the included pixels in the phantom using both methods. h) The errors in measuring temperature changes for all three ROIs of both T-WASSR and phase PRF methods. The errors were calculated by comparing the measured temperatures changes using either T-WASSR or phase PRF and that determined by MRS method using the chemical shift differences of ethylene glycol.

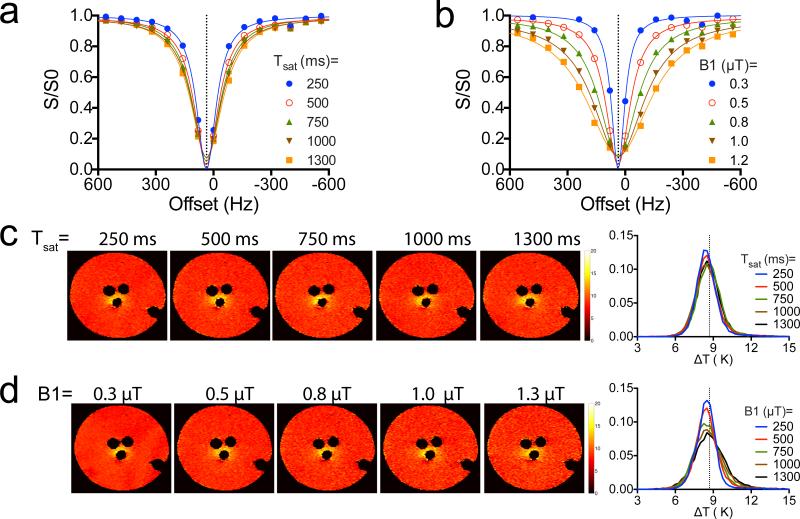
Using the same phantom, we also investigated the potential influence of WASSR acquisition parameters on the accuracy of temperature measurement. As shown in the Figures 4a and 4b, both saturation duration and saturation field strength (B1) could affect the shape of WASSR spectrum, but are not likely to significantly influence the B₀ measurement because the B₀ is determined solely by the offset where maximal saturation occurs. Consequently, as shown in Figures 4c and 4d, the measured temperatures were independent of saturation parameters that were used (as long as a strong saturation can be achieved). However, as shown in the right panel of Figure 4d, stronger B1 tends to increase the measurement variation potentially, therefore should be avoided.

Figure 4.

The effect of WASSR acquisition parameters on the accuracy of temperature measurement. a) The WASSR spectra acquired using a fixed saturation B1= 0.5 μT and varied saturation durations ranging from 250 to 1300 ms. b) The WASSR spectra acquired using a fixed saturation duration of 500 ms and varied saturation B1 ranging from 0.3 to 1.2 μT. c and d) On the left, the measured temperature maps using different parameters as shown on the top of each image. On the right, the histogram analysis of each temperature maps shown on the left.

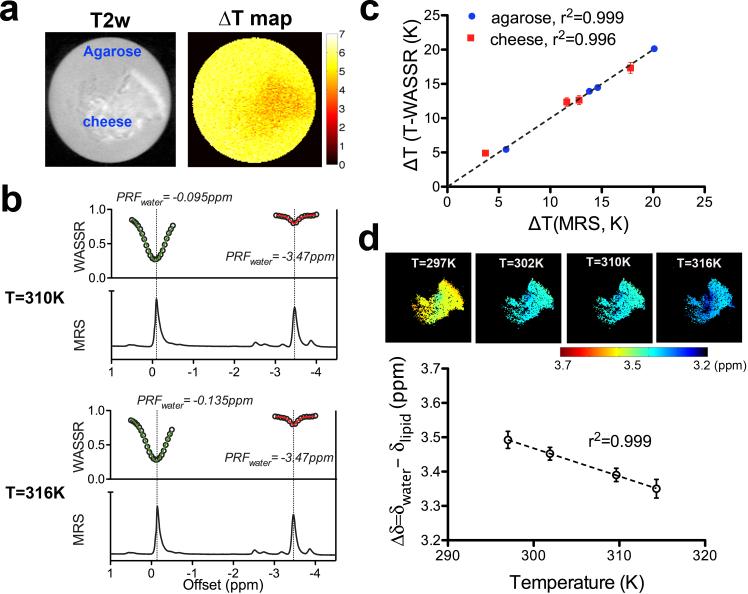
To further exam the capability of temperature measurement in tissues containing fat, we also applied the T-WASSR method on a cheese phantom composed of both water and fat (8.9% w/w) (30). As shown in Figure 5a, when the sample was heated from 310K (37°C) to 316K (43°C) using a thermostat, T-WASSR provided steady temperature mapping, of both regions containing water only and regions containing both a mixture of water and fat, with a mean ΔT of 5.7K and 4.6K for the agarose and cheese ROI, respectively. These results are consistent with the ΔT calculated using the water PRF shifts determined by the single-voxel MRS method (5.6 K and 5.0 K for the voxel containing agarose and that containing cheese, respectively, Figure 3b). In contrast, the phase mapping provided a clearly deviating mean ΔT for the cheese ROI (3.4K) because no fat correction was used, but a consistent measurement for the agarose ROI (5.3K). Good correlation (r²>0.996) was revealed between ΔT measured by T-WASSR and MRS for both the agarose and the cheese regions over a temperature range from 297K to 316K (Figure 5c).

Figure 5.

Measurement of temperature change (ΔT) in a phantom containing both fat and water using T-WASSR. a) T2-w image of the phantom and the ΔT map obtained by T-WASSR for a temperature change from 310K to 316K. b) Comparison between ¹H NMR spectra measured using a single-voxel localized MRS (PRESS) method and the T-WASSR spectra (both around the water proton resonance and fat proton resonance) of an ROI containing only cheese. c) Comparison between the measured mean ΔT of both agarose ROI (blue) and cheese ROI (red) obtained by T-WASSR and MRS, respectively. The temperature was increased from 297K to 316K using a thermostate. d) For the cheese region containing both fat and water, maps of the chemical shift difference (Δδ) between water PRF and lipid PRF (top panel) were calculated at each temperature. The mean ROI Δδ with respect to the absolute temperature (NMR thermocouple readings) is displayed in the bottom panel. The error bars indicate the standard deviation of the calculated Δδ for the ROI.

A lipid proton saturation spectrum was obtained by applying the saturation pulse around the lipid proton resonance (approximately −3.5 ppm with respect to the water proton resonance). Figure 5b shows that the extended T-WASSR spectra of both water PRF and lipid PRF exhibited consistent peak positions with ¹H NMR spectra at each temperature. Both the T-WASSR spectra and the ¹H NMR spectra show that the lipid PRF is insensitive to temperature changes, allowing a determination of absolute temperature using the lipid PRF as an internal reference. Similar to water PRF mapping, fitting the fat saturation spectral images pixel-by-pixel allows mapping the lipid PRF at high spatial resolution. In Figure 5d, the water-lipid PRF difference maps were calculated at four temperatures using the measured water and lipid PRF maps at the same temperature. Quantitatively analyzed on a manually drawn ROI, the mean water-lipid PRF differences exhibited a clear linear dependence (r²>0.999) on absolute temperature, i.e., Δδ_water-lipid = 5.92 - 0.0082×T (K) or 3.67 - 0.0082×T (°C). This result is close to that reported for ex vivo liver samples in the literature (44), where Δδ_water-lipid = 3.83 - 0.0135×T (°C). These results thus indicate it is possible to use the T-WASSR method to directly assess absolute temperature for tissues containing both water and fat with a validated calibration curve.

To test whether the acquisition speed of T-WASSR can be further increased, we also performed Lorentzian fitting on data sets with reduced points. The SNR of these in vitro measurements were estimated as 64 and 89 for ROI1 (agarose) and ROI2 (cheese) respectively. As can be seen in Table 1, fitting with a reduced number of points when the spectral resolution was reduced 3 times (i.e. from 25 Hz to 75 Hz) only produces ~4.1% relative deviation. The FWHM of ROI2 is almost twice that of ROI1, which allows reducing the number of data points by a factor of 3 without a significant impact on the result (relative deviation=1%). Using the criterion for the minimal spectral resolution found in the simulations, we expect to save at least half of the acquisition time for ROI2 by reducing the spectral resolution from 10 to 5 points per FWHM. For ROI1, conversely, the acceleration can be achieved through reducing the SW/FWHM, e.g. from 3.4 to 2, if only the temperature change within ROI1 is of interest.

Table 1.

The accuracy of Lorentzian fitting of the data sets truncated from the in vitro data using different spectral resolutions.

Spectral resolution (Hz)	ROI1			ROI2
	Points/FHWM	Estimated B0 (Hz)	Relative deviation%	Points/FHWM	Estimated B0 (Hz)	Relative deviation%
25	5.8	−41.4		9.8	−58.9
50	2.9	−40.4	2.5	4.9	−58.8	0.2
75	1.9	−43.1	4.1	3.3	−58.3	1.0
150	1.0	−43.5	5.0	1.6	−54.0	8.3

^a FWHM for ROI1 and ROI2 were measured as 145 and 245 Hz respectively

^b SNR for ROI1 and ROI2 were measured as 64 and 89 respectively

^c Sweep width was 500 Hz for all the measurements (−250 Hz to +250 Hz)

^d Relative deviation% was calculated as by |(B_0,Res - B_0,25Hz)/B_0,25Hz|%, where the B_0,Res is the estimated B0 at different spectral resolutions.

Temperature measurements in vivo

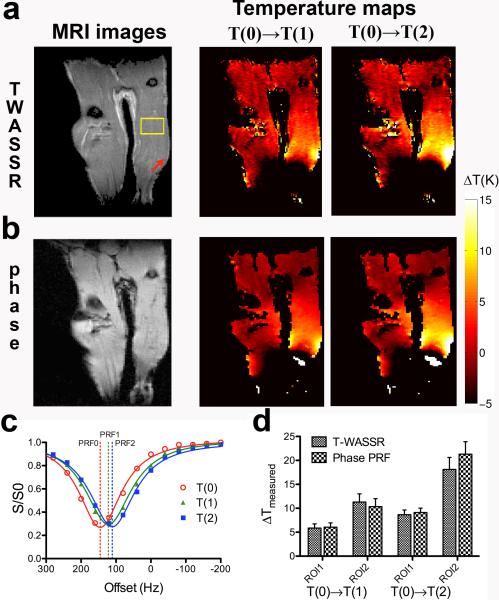
Finally, the feasibility of the in vivo application of the T-WASSR method was demonstrated in an animal model of local hyperthermia in the lower limbs at 9.4 Tesla. Due to the presence of a high B₀ inhomogeneity across the image (i.e., −500 Hz to +300 Hz for majoriry of regions as measured using PRESS method), we acquired T-WASSR spectra over a large frequency range (−800 to +800 Hz) at a spectral resolution of 40 Hz (approximately 4 points per FWHM). It should be noted that, due to the large FOV containing both lower limbs, even a sweep width of ± 2ppm could not fully cover the B₀ shifts according to the acquired B₀ maps at the initial temperature. Figures 6a and 6b show that, for heating at T(1) = 45 °C or T(2) = 55 °C , the ΔT maps obtained by T-WASSR are consistent with those obtained by phase mapping, except for several regions. One noticeable discrepancy was observed in the region around the left knee, which showed as bright strips in the temperature maps calculated by T-WASSR but totally dark in that of the phase PRF method. It is speculated due to a fitting error of the WASSR spectra of the region containing a relative high fat content and a relative low water content (appears as high signal intensity regions on the RARE T2w image in Figure 6a and dark region on the FLASH T1w image in Figure 6b). Another discrepancy was found on the lower part of the right leg, where the temperature maps acquired by phase PRF showed a small disrcete region with high ΔT vlaues while T-WASSR didn't. It is likely due to incorrect phase unwrapping in the phase PRF method. Nevertheless, the majority of temperature maps was found to be well correlated between the two methods. As evident by the spectra of a selected ROI (ROI1) at different temperatures (Figure 6c), the experimental spectral data could be well-fitted to a Lorentzian line shape for estimating water PRF shifts. As the temperature change was calculated by comparing the water PRF shift at each temperature during hyperthemia with that at T(0) (i.e., PRF₁-PRF₀ or PRF₂-PRF₀), the contibutions to water PRF shift by other temperature-independent factors, such as B₀ field inhomogeneity, were separated from that of temperature. The quantitative comparison was performed between the measured ΔT using T-WASSR and that of phase mapping for the same ROI as above and a secondary ROI corresponding to a small region close to the right knee, where a markedly high temperaure increase was found (Figure 6a). For the four groups shown in Figure 6d, the measured ΔTs were not statistically different (i.e., P< 0.05, Student's t-test), except for ROI 2 at T(2).

Figure 6.

In vivo temperature mapping of hyperthermia using the T-WASSR method. a) A RARE T2w image (left) and temperature maps measured using T-WASSR (right) , 30 minutes after the temperature of circulating water was set to 318K (45°C, T1) and 328K (55°C, T2), respectively. b) A FLASH T1w image and the corresponding temperature maps measured using phase PRF method. c) The WASSR spectra of a muscle ROI of the right leg of a mouse (yellow box in the T2-w image in a) before heating (T(0), red) and after heating to temperature T(1) (green) and temperature T(2) (blue). Solid lines show the Lorentzian fitting; dashed lines show the fitted water PRF for each temperature. d) Quantitative comparison of the measured temperature changes using two methods. ROI 1 is the same ROI used in c) and ROI 2 is a small region indicated by the red arrow on the T2-w image, where a very high temperature increase was observed.

Similar to the in vitro study, we also listed the estimated water PRF shifts for both ROI1 and ROI2 at temperature T(0) using reduced data points in Table 2. The results show that, because the SNR of in vivo measurement is only moderate (<50) and the spectral resolution is approximately 4 points per FWHM (40 Hz), the ability to improve the temporal resolution through reducing data points is limited. However, it should be noted that the long acquisition time of the study was mainly a result of the use of a very broad sweepwidth (1600 Hz) to compensate the large B₀ inhomogeneity. For example, for ROI1 where the FWHM is estimated as 157 Hz, the SW/FHWM is approximately equal to 10, which indicates that the acquisition time could be markedly shortened using a reduced sweepwidth for monitoring the temperature changes of a particular region.

Table 2.

The accuracy of Lorentzian fitting of the data sets truncated from the in vivo data using different spectral resolutions.

Spectral resolution (Hz)	ROI1			ROI2
	Points/FHWM	Estimated B0 (Hz)	Relative deviation%	Points/FHWM	Estimated B0 (Hz)	Relative deviation%
40	3.9	145.3		4.3	313.3
80	2.0	147.7	1.7	2.2	311.7	0.5
120	1.3	142.7	1.8	1.4	321.3	2.6
160	1.0	150.9	3.9	1.1	324.0	3.4

^a FWHM for ROI1 and ROI2 was measured as 157 and 172 Hz respectively.

^b SNR for ROI1 and ROI2 were measured as 42 and 39 respectively.

^c Sweep width was 1600 Hz for all the measurements (−800 Hz to +800 Hz).

^d Relative deviation% was calculated as by |(B_0,Res - B_0,40Hz)/B_0,40Hz|%, where the B_0,Res is the estimated B0 at different spectral resolutions.

Discussion

We demonstrated a water direct-saturation-based approach for temperature mapping, adding additional methodology to the arsenal of non-invasive, high-resolution MRI thermometry. This approach, namely Water Saturation Shift Referencing (WASSR), was originally developed to determine B₀ inhomogeneities in the study of chemical exchange saturation transfer (CEST) imaging (32). Here, we adapted the same strategy to estimate the temperature-induced water PRF shift and demonstrated its ability to assess temperature changes, both in vitro and in vivo. To implement the T-WASSR method with a minimal acquisition time without significantly comprising the measurement accuracy, we provided technical guidelines based on the theoretical simulations, which were subsequently verified in phantom and animal studies. Because brief low-power saturation pulses were used, the resultant DS spectra have negligible contamination from CEST and MTC effects, allowing accurate measurements of B₀ shifts to be attained, similar to previous studies either on human scanners (32) or high field preclinical scanners (45,46).

Our results demonstrate that the T-WASSR can perform robust high-resolution temperature mapping in fat-containing tissues. As evident from our phantom study, the water DS spectrum is inherently separated from that of fat, eliminating the need for a priori knowledge of fat content and further data processing (30,31,47). The capability of measuring intra-voxel lipid PRF endows T-WASSR with additional advantages. First, monitoring the change of temperature-independent lipid PRF can be used to correct unwanted magnetic field drift when calculating temperatures. In our study, we observed a drift of 6 Hz in lipid PRF after six hours. More importantly, simultaneous measurement of both water and lipid PRF within the same imaging scheme (at a cost of doubled acquisition time) enables high-resolution mapping of absolute temperature for tissues or regions containing both fat and water, if a pre-determined temperature-chemical shift difference calibration curve is available, as exemplified in Figure 5d. These features make the T-WASSR method ideally suited for measuring temperatures in fat-containing tissues, such as the breast (31) and the liver (44). In addition, the proposed T-WASSR method employs magnitude images, allowing a retrospective correction of motion artifacts in the post-processing step easily. Moreover, unlike a phase imaging method, no phase wrapping will be used in the T-WASSR method, which enables its application in tissues with severe B0 inhomogeneity.

Compared to MRS based temperature mapping methods, the present T-WASSR possesses several advantages. First, although fast chemical shift imaging has been recently developed (18,44,48) with high temporal resolution and sufficient spatial resolution, the T-WASSR is an imaging-based method with inherent high spatial resolution (e.g. 80×80 μm and 25×172 μm for in vitro and in vivo respectively in the present study). As discussed early, potential motion artifacts are correctable due to the fact that magnitude images are used in T-WASSR. Finally, no spatially restricted shimming procedure is required in a T-WASSR measurement.

Evidenced by the first WASSR study that was conducted on a 3T clinical scanner (32), the present T-WASSR is expected to be easily translatable to low field clinical scanners (i.e. 1.5 T and 3T). The quality of a T-WASSR measurement at low field may be affected by three major factors: lower SNR (↓), a reduced frequency shift in Hz per ppm, and reduced T1 (49). A shortened T1 is favorable for acquisition speed, because a shorter TR can be used. The decreased Hz /ppm leads to smaller PRF shifts in Hz but equivalent shifts in ppm. However, since our guidelines are based on ppm, the accuracy of measurement won't be affected if the same point/FWHM guidelines are followed. While lower SNR is a disadvantage, the advantages in hardware on modern clinical scanners (i.e. phased-array receiver RF coils with up to 32 channels) may overcome this in part. Finally, as many CEST studies have shown (32,50,51), the specific absorption rate (SAR) is not a limiting factor for clinical translation of methods employing saturation pulses, especially T-WASSR, where only brief low-power saturation pulses are used.

Several technical hurdles, however, have to be circumvented before the T-WASSR can be readily used in the clinic. First, in order to make it applicable for real-time temperature monitoring, the temporal resolution should be improved. In this study, acquisition took approximately two minutes for in vitro and eight minutes for in vivo imaging, using a fast spin echo RARE imaging sequence. Similar to CEST MRI (52), the acquisition speed of T-WASSR could be improved significantly by employing fast imaging sequences, such as EPI (53), FLASH (54), FISP (55), and GRASE (50). For example, in the original WASSR study, we demonstrated a total acquisition time of 1-2 minutes on a human scanner using two-shot TSE sequence (TSE factor = 34, SENSE factor = 2). In another study, Shah et al. showed that the acquisition time could be reduced to 20.5 s for a full set of CEST spectral images (14 offsets, 5 s pre-saturation pulse duration) using CEST-FISP method (55), indicating the temporal resolution of a T-WASSR can be reduced to tens of seconds. Finally, 3D CEST imaging approaches were developed recently for clinical application (50,56) indicating that 3D T-WASSR-based volumetric temperature mapping with a reasonable temporal resolution should also be feasible. With all these technique hurdles circumvented, together with future optimization of pulse sequences, we anticipate that the future version of T-WASSR will provide a fast temperature measurement with 3D imaging coverage, and ultimately with an accuracy of 0.2 °C.

Conclusion

We presented a temperature-responsive water saturation shift referencing (T-WASSR) method to measure the water proton resonance frequency (PRF) shift due to temperature change. By fitting the water direct saturation spectrum to a Lorentzian line shape, the water PRF could be accurately determined, providing an alternative means for non-invasive mapping of temperature changes in tissues. As demonstrated both in vitro and in vivo, the proposed T-WASSR method provides results consistent with other MRI methods but is more robust for temperature measurements in fat-containing tissues.

Abbreviations

PRF

proton resonance frequency

WASSR

Water Saturation Shift Referencing

DS

direct saturation

MT

Magnetization Transfer

CEST

Chemical Exchange Saturation Transfer

FWHM

full width half maximum

SW

Sweepwidth

CW

continuous wave

SNR

signal-to-noise ratio

RARE

Rapid Acquisition with Relaxation Enhancement

FLASH

Fast Low Angle SHot Magnetic Resonance Imaging

PRESS

point-resolved spectroscopy

NA

the number of averages