Reliability adjustment: A necessity for trauma center ranking and benchmarking

Abstract

Introduction

Currently trauma center quality benchmarking is based on risk adjusted observed:expected (O:E) mortality ratios. However, failure to account for number of patients has been recently shown to produce unreliable mortality estimates, especially for low volume centers. This study explores the effect of reliability adjustment (RA), a statistical technique developed to eliminate bias introduced by low volume, on risk-adjusted trauma center benchmarking.

Methods

Analysis of the NTDB 2010 was performed. Patients ≥16 years of age with blunt or penetrating trauma and an Injury Severity Score (ISS) ≥ 9 were included. Based on the statistically accepted standards of the Trauma Quality Improvement Program (TQIP) methodology, risk-adjusted mortality rates were generated for each center and used to rank them accordingly. Hierarchical logistic regression modeling was then performed to adjust these rates for reliability employing an empiric Bayes approach. The impact of RA was examined by 1) Recalculating inter facility variations in adjusted mortality rates and 2) comparing adjusted hospital mortality quintile rankings before and after RA.

Results

557 facilities (with 278,558 patients) included. RA significantly reduced the variation in risk-adjusted mortality rates between centers from 14 fold (0.7%–9.8%) to only 2 fold (4.4%–9.6%) after RA. This reduction in variation was most profound for smaller centers. A total of 68 "best" hospitals and 18 "worst" hospitals based on current risk adjustment methods were reclassified after performing RA.

DISCUSSION

“Reliability adjustment” dramatically reduces variations in risk adjusted mortality arising from statistical noise, especially for lower volume centers. Moreover, the absence of RA had a profound impact on hospital performance assessment, suggesting that nearly one of every six hospitals in NTDB would have been inappropriately placed amongst the very best or very worst quintile of rankings. RA should be considered while benchmarking trauma centers based on mortality.

Introduction

Trauma is the leading cause of death in United States between ages 1–44 (1). Each year an estimated 2.8 million Americans are hospitalized with injuries, with more than 180,000 mortalities from this group. Nationally $406 billion are needed to cover the annual costs associated with trauma (2). Hence, improving trauma outcomes and reducing costs has become a priority for health scientists and policy makers.

The recent seminal reports from The Institute of Medicine (To Err is Human-Building a Safer Health System; Crossing the Quality Chiasm: A New Health System for the 21st century) suggest a "systems approach" to health quality improvement (3,4). The initiative is based on the three key aspects of health quality: outcome, process and structure, described by Avedis Donabedian in 1966 (5). A well known and extremely successful implementation of the "systems approach" is the National Surgical Quality Improvement Program (NSQIP),which, since its inception in 1994, has reduced the 30-day post-operative morbidity and mortality after major surgery by 45% and 27%, respectively (6). Striving to replicate the success achieved by the NSQIP, the American College of Surgeons (ACS) Committee on Trauma established the Trauma Quality Improvement Program (TQIP) in 2008 (7).

External benchmarking, which allows direct inter-hospital performance comparisons, has been the cornerstone of both the NSQIP and TQIP. These comparisons exploit inter-hospital variation in risk-adjusted outcomes estimates to identify centers performing significantly better or worse than their peers. External benchmarking of trauma center performance has now become a vital component of trauma quality improvement initiatives. The established method to rank trauma centers on mortality compares the center's observed or actual mortality with its "expected," mortality given its patient case-mix. The “expected” mortality is computed by risk adjusting for patient demographic and injury severity characteristics and then is used to compute an observed-to-expected (O/E) mortality ratio (with 95% confidence interval; CI). The O/E ratio for each facility is then plotted on a graph for comparison with other centers. This information can then be used to provide feedback to individual centers and to assist them with developing targeted and informed quality improvement initiatives (7).

Low-volume hospitals, where one death in their trauma population could statistically impact mortality rates, are excluded from the risk adjusted O/E rankings and therefore, represent one limitation of external benchmarking. The exclusion of small samples lends statistical credence to hospital rankings, but it also deprives low-volume hospitals of critical quality improvement information. This limitation is not exclusive to trauma center benchmarking and is equally applicable to other areas of health care research.

In recent years, a novel statistical technique addressing the exclusion of small sample sizes has been developed and successfully implemented in the non-trauma literature. Reliability adjustment (RA), an application of hierarchical modeling employing the empirical Bayes approach, has been shown as an effective means to quantify and eliminate bias associated with small samples sizes. This technique has found widespread application in the healthcare literature, from improving patient satisfaction measures included in the Hospital Consumer Assessment of Health Plans (8), to accurately performing benchmarking of hospitals on outcomes following select surgical procedures (9–12). Although this technique is becoming the standard methodology for generating performance based rankings, the impact of RA on trauma center external benchmarking has not yet been explored.

The overwhelming advantage of this technique is in its ability to accurately report mortality estimates from previously excluded low volume hospitals. In addition, RA offers a unique statistical methodology to adjust for center volume. The objective of this study is to explore the effect of RA on risk-adjusted trauma center benchmarking in a large trauma data set.

Methods

We used data from National Trauma Data Bank (NTDB) 2010 to explore the effect of RA on trauma center benchmarking. The NTDB comprises data on approximately 2.5 million patients contributed by more than 900 trauma centers across the United States, offering a wide variation in mortality outcomes and hospital volumes (13). All patients aged ≥16 years, with blunt/penetrating injury and an Injury Severity Score (ISS)≥9 were included while patients who were dead on arrival and suffered burns and non-specified mechanism injuries were excluded. Hospitals missing ≥20% of the selected covariate data for risk adjustment for mortality were excluded.

We used the standard ACS-TQIP methodology for estimating risk-adjusted mortality for each facility (7). The TQIP, now entering its third year, provides quarterly estimates of robust risk-adjusted inter-hospital comparisons for more than 120 participating centers. Hence we used these standardized methods to perform risk-adjustment and calculate O/E mortality ratios for individual hospitals in this study. A standard logistic regression analysis was performed adjusting for age, gender, mechanism of injury, transfer status, physiology at initial presentation to the emergency department (pulse, systolic blood pressure and Glasgow Coma Scale (GCS) motor score) and anatomic injury severity (ISS and Head and Abdomen Abbreviated Injury Scale (AIS)). Subsequently, individual patient probabilities of mortality were generated using post-estimation commands and summed for each facility to yield the "expected" number of deaths. The observed number of deaths was then divided by the expected number to generate an O/E ratio for each facility. This ratio was then multiplied by the overall average to determine a risk-adjusted mortality rate for each hospital. To overcome the issue of missing data in the NTDB, we performed multiple imputation (MI) for all covariates used in the multivariate model. MI has previously been demonstrated as a superior method to account for missing data in the NTDB compared to complete-case analyses, both for patient as well as hospital level outcomes (14,15).

We employed the empiric Bayes approach to adjust the mortality rates for reliability (9,10,16). This technique allows for shrinking the observed mortality rate towards the overall average proportional to the reliability of the measure, a function of the sample size (i.e. hospital volume per year). Hence smaller the hospital volume, the less reliable is the observed mortality rate and the more it is shrunk towards the overall average. We used hierarchical logistic regression model to calculate the reliability-adjusted mortality rate as it is widely accepted that hierarchical modeling yields more stable estimates of coefficients and standard errors by accounting for variation at different levels of health care (i.e. patients, providers, hospitals). We used a two-level model with the patient as the first-level and the hospital as the second-level. A particular problem with hierarchical modeling is the likelihood of non-convergence especially with the inclusion of multiple covariates. To overcome this, we combined all patient-level covariates into a single patient risk-score. To generate this risk-score, we ran a standard logistic regression model (adjusting for all the covariates described above) and performed postestimation to predict the log(odds) of mortality for each patient. A sensitivity analysis using area under the receiver operating characteristics curve demonstrated complete agreement between using individual covariates versus the combined risk score to predict mortality. Hierarchical logistic regression, with mortality as the outcome, was then performed with this risk score as the only patient level covariate and hospital identification number as the only hospital level covariate. We then generated the empiric Bayes estimates of each hospital's random effect, in log(odds), using postestimation commands. This random effect represents the risk and reliability adjusted signal, which was then added to the average patient risk score, before performing an inverse logit to calculate the reliability adjusted mortality rate for each hospital.

We evaluated the effect of RA on mortality outcomes using several different methods. Firstly, we estimated the reliability of risk adjusted mortality for each hospital on a scale from 0 to 1, where 0 represented no reliability (i.e. 100% of the mortality estimate was due to statistical noise or erroneous) and 1 represented perfect reliability (i.e. 0% of the mortality estimate was due to statistical noise) (17). This reliability was estimated for hospitals of varying volume to explore the relationship between hospital case-load and reliability of risk-adjusted mortality.

Secondly, we explored the reduction in variation of hospital risk adjusted mortality brought about by performing RA. The impact of RA on individual hospital's risk-adjusted mortality was visually assessed by plotting mortality rates of 35 randomly selected hospitals before and after RA. To explore this reduction in variation at all hospitals, we placed hospitals into 5 equal-sized groups (quintiles) and calculated the risk-adjusted mortality rate before and after RA.

Lastly, we compared hospital quintile rankings before and after RA and estimated the proportion of hospitals that remained in the top 20% ("best hospitals") and in the bottom 20% ("worst hospitals"). A hospital was considered to be misclassified if there was a change in its quintile of risk-adjusted mortality after performing RA.

All analyses were performed using Stata12/MP statistical software package (StataCorp, College Station, TX).

Results

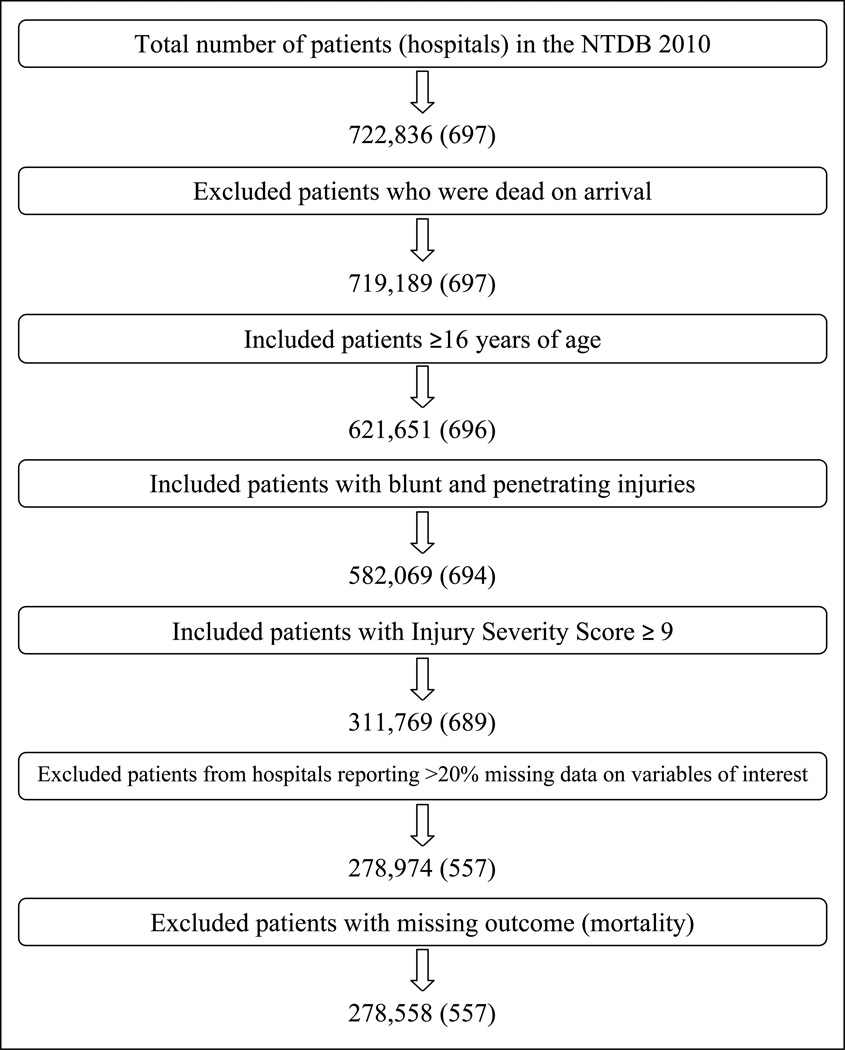
The NTDB 2010 dataset included 722,836 patients from 697 hospitals. After excluding patients and facilities as described in the methods above, a total of 278,558 patients from 557 hospitals were available for analysis (Figure 1).Table 1 describes patient demographic and injury severity characteristics. The unadjusted and adjusted mortality rates were 6.4% and 5.6%, respectively. Annual hospital volumes ranged from 1 to 3251 with a median of 374 cases [inter-quartile range: 101–760].

Figure 1.

Patient selection

Table 1.

Baseline demographic and injury severity characteristics (n=278,558)

	Number of patients	Percentage of total sample
Age in years
16–65	189,108	67.9
>65	77,366	27.8
Missing	12,084	4.3
Gender
Female	103,876	37.3
Male	174,635	62.7
Missing	47	0.0
Mechanism of injury
Firearm	15,359	5.5
All other mechanisms	263,199	94.5
Pulse
0–40	3,086	1.1
>40	271,954	97.6
Missing	3,518	1.3
Systolic Blood Pressure
0	2,327	0.8
1–90	10,140	3.6
>90	262,356	94.2
Missing	3,735	1.3
Glasgow Coma Scale–motor score
1	23,065	8.3
2–5	14,911	5.4
6	230,638	82.8
Missing	9,944	3.6
Injury Severity Score
9–24	235,722	84.6
>24	40,666	14.6
Missing	2,170	0.8
Head injury severity (AIS)*
0	151,747	54.5
1–2	32,714	11.7
3–4	76,039	27.3
5–6	13,671	4.9
Missing	4,387	1.6
Abdomen injury Severity (AIS)*
0	229,234	82.3
1–2	26,499	9.5
3–4	17,509	6.3
5–6	1,912	0.7
Missing	3,404	1.2
Transfer status
Transferred from an outside center	77,526	27.8
Transported from the field	201,015	72.2
Missing	17	0.0

Table 2 describes the relationship between hospital volume and reliability of risk-adjusted mortality. Hospital volumes were found to be proportional to the reliability of the risk-adjusted mortality estimate i.e. mortality estimates from higher volume hospitals were more reliable. For hospitals with ≤100 patients each year, nearly 1/3rd of the variation in risk-adjusted mortality rates was due to statistical noise i.e. it was erroneous and was not reflective of true patient mortality.

Table 2.

Relationship between hospital volume and reliability of hospital risk adjusted mortality

	Hospital Risk Adjusted Mortality
Hospital Volume (cases per year)	Percentage attributable to statistical noise*	Reliability**
≤50	88%	0.12
>50 to ≤100	32%	0.68
>100 to ≤150	9%	0.91
>150 to ≤200	3%	0.97
>200	3%	0.97

^*Defined as the proportion of error in the estimation of risk adjusted mortality (100% statistical noise means that the risk adjusted mortality estimate is completely erroneous).

^**Reliability is measured on a scale of 0 to 1 where 0 represents 100% statistical noise and 1 represents no statistical noise i.e. the estimation of risk adjusted mortality is accurate.

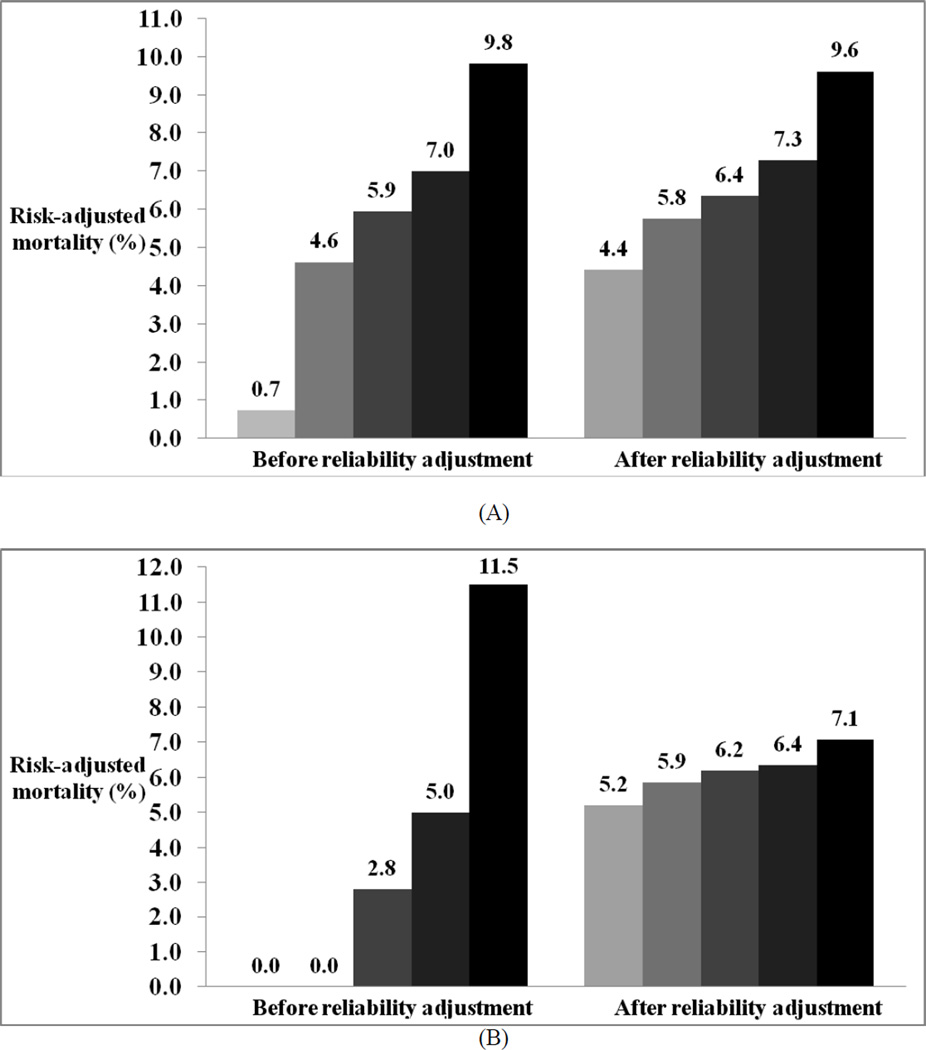
RA greatly reduced the variation in hospital risk-adjusted mortality both at individual hospitals as well as across hospital quintiles.Figure 2 demonstrates the dramatic shrinkage of risk-adjusted mortality, following RA, towards the overall average for 35 randomly selected hospitals. Across hospital quintiles, RA significantly reduced the variation in risk-adjusted mortality from almost 14 fold (0.7%–9.8%) to 2 fold (4.4%–9.6%). This reduction was much more profound at low volume hospitals (≤ 100 patients per year) with mortality rates ranging from 0%–11.5% before RA to 5.2%–7.1% after RA (Figure 3).

Figure 2.

Risk adjusted mortality rates for a random sample of 35 hospitals before and after adjusting for reliability.

Figure 3.

Risk adjusted mortality rates across hospital quintiles before and after reliability adjustment: A, All hospitals; B, Hospitals with ≤100 patients per year

Table 3 shows the effect of RA on risk-adjusted hospital mortality rankings. RA identified that an alarming 61% (68/112) of the "best" hospitals (top 20%) were being potentially misclassified using standard techniques alone. A smaller proportion, 16% (18/111), were being misclassified as the "worst" hospitals. Overall, 1 out of every 6 hospitals was being inappropriately placed amongst either the very best or the very worst quintile of risk-adjusted mortality.

Table 3.

Change in hospital classification status across quintiles of risk adjusted hospital mortality rankings after reliability adjustment (IQR=interquartile range).

			Quintiles of Reliability Adjusted Mortality Rankings
Quintiles of Risk Adjusted Mortality Rankings	Number of hospitals	Median Yearly Hospital Volume Median (IQR)	Hospitals correctly classified*	Hospitals potentially misclassified
1 "Best hospitals"	112	24 (9–121)	44 (39.3%)	68 (60.7%)
2	111	405 (135–794)	44 (39.6%)	67 (60.4%)
3	112	566 (259–883)	63 (56.3%)	48 (43.7%)
4	111	576 (375–869)	88 (79.3%)	23 (20.7%)
5 "Worst hospitals"	111	421 (207–796)	93 (83.8%)	18 (16.2%)

^*Hospitals correctly classified defined as hospitals undergoing no change in their quintile of risk-adjusted mortality ranking before and after reliability adjustment

Discussion

This study explores the potential for misclassifying trauma centers on risk-adjusted mortality due to low hospital volumes. Using reliability adjustment, a novel statistical technique, we were able to quantify and eliminate the bias associated with small samples sizes when performing external benchmarking of trauma center performance. At low volume hospitals, nearly 1/3rd of the variation in risk-adjusted mortality was attributable to statistical noise. Reliability adjustment dramatically reduced variation in risk-adjusted mortality at all hospitals, proportional to the reliability of their mortality estimate. Without reliability adjustment, nearly 1 out of every 6 hospitals may have been inappropriately classified among the very best or the very worst of hospital quintile rankings. These results demonstrate the inadequacy of current methods to externally benchmark trauma centers, and the potential use of reliability adjustment, as an effective means to reduce the apparent variation in risk-adjusted mortality rates introduced by low hospital volumes. We therefore recommend that reliability adjustment be considered while trauma center profiling.

Reliability adjustment (RA) has found an extensive and ever increasing application in non-trauma health care literature. The use of this technique was originally described in a landmark paper by Hofer et al. where they explored the "unreliability" of physician report-cards for diabetes care. They found that due to low patient volumes, the reliability of risk-adjusted outcomes estimates were unacceptably low (reliability of only 0.40) and that an alarming potential for artificially improving physician performance profiles, or "gaming outcomes," by simply deselecting a few patients with poor outcomes existed (16). Similar concerns regarding the inaccuracy of mortality estimates due to low hospital volumes were raised by Shahian et al. in their evaluation of cardiac surgery report-cards (18). Since then, RA has become an established statistical technique to overcome challenges associated with low hospital volumes when generating performance-based profiles. The Center for Medicare and Medicaid Services now uses this technique for its Hospital Compare website to report mortality and readmission rates for a range of medical conditions (19). In a recent series of papers, Dimick et.al have explored the impact of RA to rank hospitals on morbidity and mortality following select surgical procedures. Using the national Medicare data [for coronary artery bypass grafting (CABG), abdominal aortic aneurysm (AAA) and pancreatic resection] and the NSQIP data [for colon resection and vascular surgery procedures], they demonstrated the ability to reduce the apparent variation in risk adjusted morbidity and mortality rates across hospitals and use these adjusted rates to accurately forecast future mortality (9–12). These studies provide sufficient evidence that RA is practical and yields more accurate outcomes estimation for various surgical procedures than that achieved using standard techniques alone.

Biased risk-adjusted surgical mortality estimation threatens hospitals with low admission volumes and equally applies to trauma mortality rankings (20). The standard trauma mortality ranking methodology has several limitations dealing with low-volume bias. Firstly, low volume hospitals (i.e. centers with <100 patients per year) are excluded from the rankings. This deprives these hospitals from becoming involved in an outcomes-driven performance improvement and is quintessentially counterproductive. Secondly, despite the growing evidence that low hospital volumes are associated with adverse trauma outcomes, current methods do not perform volume adjustment (21–23). Lastly, the current methods report a risk-adjusted mortality estimate for each hospital along with a 95% confidence interval or a p-value to compare one hospital's performance to another or to the overall average. Outcomes are defined as significantly different if the confidence interval does not overlap or if the p-value is greater than 0.05. However, consumers of such comparative quality information often misinterpret these statistics and there is always a risk of misclassification of hospitals as better or worse than expected (24,25).

In contrast, RA offers a unique statistical approach to overcome each of these limitations. Using empirical Bayes estimations, it essentially "shrinks" the risk adjusted mortality rate towards the overall average, proportional to how reliably the outcome is measured (9,10). Reliability here is largely a function of the yearly hospital volume. Hence, at high volume hospitals, where mortality estimates are more reliable, this shrinkage is less than that at low volume hospitals, where one or two deaths can drastically change mortality rates. This in effect gives these low volume hospitals the benefit-of-the-doubt, labeling them as average performers until there is better evidence to suggest otherwise. Since RA quantifies and eliminates statistical noise from risk adjusted mortality estimates, even low volume hospitals can be benchmarked. Secondly by generating a measure of reliability proportional to each hospital's yearly volume, this method essentially adjusts for the volume associated variation in mortality estimation. In doing so, the reported risk adjusted mortality rates are far more robust and less uncertain than those without RA. Hence, these rates and subsequent rankings are easier to understand and interpret, reducing the risk of misclassifying hospitals during performance comparisons.

We acknowledge several important limitations to our work, including those inherent to all RA analyses. There is an ongoing debate that by shrinking estimates towards the overall average, RA itself introduces a bias (26). This is true when applied to low volume hospitals with worse outcomes as there is sufficient evidence to suggest that low volume hospitals have high trauma mortality (21–23). One way to overcome this problem is to shrink the estimates of these low volume hospitals towards the average mortality rate for their volume group instead of the overall average. Thus these hospitals are ascribed an average mortality rate as expected of their volume group (i.e. higher mortality) and are not inappropriately assumed to be performing at the national average. Such composite measures (combination of risk and hospital volume adjustment) have been described and validated using the national Medicare data (27,28). Additional limitations arise from the use of data from NTDB. Due to voluntary data submission, the NTDB is a convenience sample and hence not nationally representative of trauma outcomes (13). Additionally it contains a disproportionate share of high volume trauma centers even though in the current sample we did find hundreds of lower-volume trauma centers as well. Some other important limitations of the NTDB include: 1)lack of information about patients who die at the scene or are discharged from the ER without hospital admission, 2)potential for residual and/or unknown confounding arising from inconsistent charting and abstraction or lack of important clinical information (e.g. amount of blood products transfused is unknown) and 3)potential under-reporting of data on medical interventions, comorbidities and in-hospital complications. While acknowledging these limitations associated with all NTDB-based analyses, we have tried, as much as possible to replicate the standard patient selection and risk-adjustment techniques used by the ACS-TQIP to benchmark trauma centers (7).

The application of RA to rank hospitals on trauma mortality has great future implications for the ACS-TQIP. The use of this technique will become increasingly essential as progress is made towards reporting hospital outcomes for smaller, more specific trauma sub-populations. These sub-populations can be as diverse as 1)patients with specific types/mechanisms of injury e.g. traumatic brain injury, gunshot injuries, 2)patients undergoing specific procedures following trauma e.g. splenectomy or 3)patients with specific demographic characteristics e.g. elderly, uninsured or racial minority patients. In all these situations, the anticipated yearly hospital volume will be low and hence analyses performed without RA will yield unstable, inaccurate estimates.

Reliability adjustment is a robust, practical and increasingly cited methodology to eliminate statistical noise from outcomes-based hospital rankings. Using data from the NTDB, we have shown that volume-associated uncertainty in risk adjusted mortality rates can adequately be quantified and adjusted for, yielding much more accurate estimates without the need to exclude low volume hospitals. Therefore, this technique should strongly be considered when creating performance-based trauma center rankings.