Towards simultaneous measurements of electronic and structural properties in ultra-fast x-ray free electron laser absorption spectroscopy experiments

Abstract

The rapidly growing ultrafast science with X-ray lasers unveils atomic scale processes with unprecedented time resolution bringing the so called “molecular movie” within reach. X-ray absorption spectroscopy is one of the most powerful x-ray techniques providing both local atomic order and electronic structure when coupled with ad-hoc theory. Collecting absorption spectra within few x-ray pulses is possible only in a dispersive setup. We demonstrate ultrafast time-resolved measurements of the LIII-edge x-ray absorption near-edge spectra of irreversibly laser excited Molybdenum using an average of only few x-ray pulses with a signal to noise ratio limited only by the saturation level of the detector. The simplicity of the experimental set-up makes this technique versatile and applicable for a wide range of pump-probe experiments, particularly in the case of non-reversible processes.

X-ray absorption fine structure, XAFS, which includes x-ray near-edge spectroscopy, XANES, and extended x-ray absorption fine structure, EXAFS, has been proven to be one of the best tool to investigate the interplay between local atomic order and electronic structure. The advent of ultrashort x-ray light sources enabled experiments in the sub-ps time-scale in an increasing number of scientific fields like chemistry¹, solid state magnetism² and plasma physics³. While x-ray free electron lasers (XFEL) delivering intense femtosecond pulses with tunable photon energy would be a natural choice for time-resolved XAFS experiments, a number of drawbacks impedes their use. One way to perform XAFS is to select the incoming radiation wavelength using a crystal monochromator and scan wavelength⁴. Each energy point of the XAFS spectrum is obtained by averaging a number of pulses (120 or 240 in ref. 4) to achieve significant statistical accuracy. In a time-resolved experiment thus scanning of time delay and photon energy is required. Such a procedure is time consuming and requires a large number of x-ray pulses. For a (elaborated) solid state sample, which has to be renewed after each pulse, this technique is often not possible due to limitations by sample consumption. Reduced repetition rates, as a consequence of detector frame rate or sample refreshment, may further limit such experiments. We therefore apply dispersive XAFS, making use of the full pulse spectral bandwidth and of the high photon number per pulse (up to 10¹²). Dispersive XAFS, in the specific case of XANES, in principle allows measuring full spectra in a single pulse. The technical challenge using dispersive XANES at XFEL sources arises from the fluctuation of the incident spectrum due to the self-amplified spontaneous emission (SASE) process. The stochastic nature of SASE XFEL radiation produces single pulse spectra made of spikes⁵,⁶ with almost 100% intensity modulation. These spectra fluctuate from pulse to pulse. The obvious solution is to measure for each x-ray pulse the incident spectrum and simultaneously the XANES spectrum after transmission through the sample. The measurement of the incident spectra can be achieved using an x-ray beamsplitter. Using this scheme provides a XANES spectrum requiring few hundreds of pulses for a static measurement, as done in ref. 7. This solution requires an invasive set-up involving dispersive and focusing x-ray optics which of course complicates the experiment alignment procedure. In this contribution we present a method using the detection of dispersive XANES spectra requiring 20 x-ray pulses per measurement. This method is based on a very simple experimental set-up requiring a single bent crystal. As an example we show measurements at the LIII edge of Molybdenum (2.520 keV) which shows an enhanced absorption feature, known as a white line, due to its half-filled 4 d band. This choice was further motivated by a recent theoretical investigation highlighting the role of d band electrons in possible lattice strengthening under non-equilibrium conditions (electron temperature > lattice temperature)⁸. A comprehensive description of the dispersive XANES data treatment is provided as well as an analysis of the noise. The latter enables the evaluation of the error margins of the measured spectra. Using this analysis, we demonstrate sub-picosecond time-resolved XANES following the dynamics of the LIII edge of an ultra-short optical laser-heated Mo sample.

Results

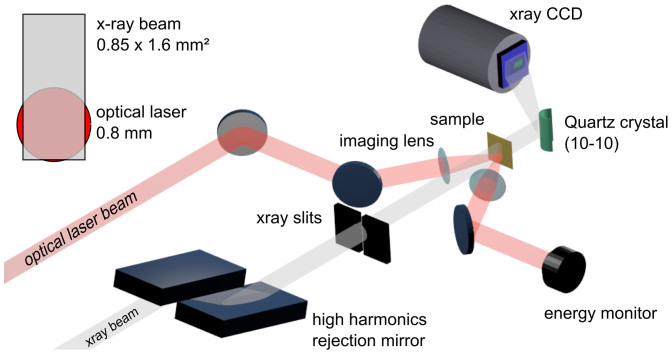
The experiment was performed at the MEC station of the Linac Coherent Light Source⁹ (LCLS). The sample was made of 100 nm of Mo deposited on a 100 μm thick polypropylene foil. The Mo layer was covered by a 8 nm layer of amorphous Carbon (a-C). The aim of the a-C layer was twofold: first to prevent formation of an oxide layer prior to the experiment and second to act as a tamper during the irradiation confining the hydrodynamic expansion of the heated Mo layer, i.e. insuring a homogenous Mo density along the beam direction during the first few ps. The thicknesses of both layers, deposited by magnetron sputtering, were carefully checked by x-ray reflectometry¹⁰. The optical pump delivered 300 fs full width half maximum (FWHM) pulses at 800 nm. A 15 mm diameter diaphragm located up-stream in the optical beamline was imaged at the surface of the sample using a 500 mm lens. The aperturing of the beam allowed us to obtain a nearly flat top profile, with sharp edges. The energy per pulse was set to reach 8 J/cm² on the sample. The unfocused x-ray beam passed through a pair of high harmonic rejection mirrors (single Si crystal mirror, 0.27 incidence angle) and was slit down in the horizontal direction resulting in a nearly rectangular 0.8 × 1.6 mm² spot at the sample. The bottom half of the x-ray spot was spatially overlapped with the optical beam while the top part of the x-ray beam probed the unheated sample as depicted in the figure 1. The temporal overlap of x-ray and optical laser pulses was established using the plasma switch method¹¹.

Figure 1. Schematic view of the experimental set-up.

The 800 nm optical pulse (in red) is imaged on the sample to provide 8 J/cm² fluence. The unfocused 2.520 keV beam is spatially overlapped with the optical laser beam. The recording sequence of n = 20 × 3 pulses (0,1,3) was fully automated.

The observed time arrival jitter between x-ray and optical pulses was in the 400 fs range. The spectrum was dispersed in the horizontal direction by using a convex quartz crystal (10-10) with a 100 mm radius of curvature. The Bragg angle at the LIII edge of Mo (2.520 keV) is 35.311°. The setup was designed to disperse the full XFEL spectrum on a CCD detector (2048 × 2048 pixels) and taking into account the available space in the experimental chamber. As a result the CCD detector was located 250 mm from the crystal and parallel to the x-ray beam axis. The energy resolution was determined from the width of narrowest SASE spike in the measured spectrum to 0.35 eV, equivalent to 4 pixels on the CCD. In this configuration the image recorded by the CCD provides the spectral information in the horizontal direction, while the vertical direction provides spatial information, which distinguishes between the cold and heated areas of the sample. The measured spectral bandwidth was 0.63% FWHM, i.e 16 eV at the LIII Mo edge corresponding to a smaller (270 μm) horizontal zone on the sample than the x-ray beam dimension.

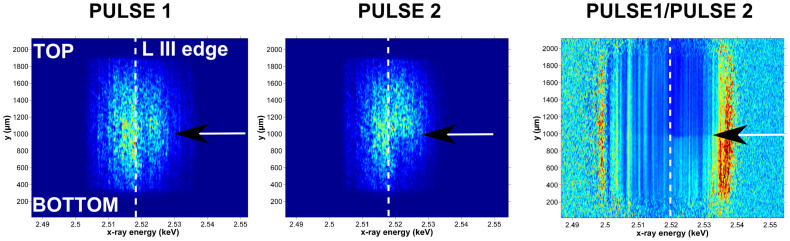
The question is now: how to extract the XANES spectrum given the XFEL radiation properties? Before detailing the exact formalism of the method (in the methods section), we first provide the qualitative description of the procedure. As discussed before, the main problem is the normalization of the measured spectrum. In practice two sources of noise have to be removed: the first one is due to the intrinsic structure in the SASE spectrum, the second one is due to the distortion of the x-ray wavefront during the propagation along the beamline¹². This later one leads to a non-trivial, but reproducible, spatial intensity distribution shown in the figure 2. The normalization was achieved through the following procedure: 3 x-ray pulses (noted pulse 0, 1 and 2) were measured consecutively at each location of the sample. For this basic sequence the full repetition rate of the machine could be used, taking into account the readout time of the detector, as the sample did not have to be refreshed. This sequence was repeated n times. The pulse 0 corresponds to a cold sample (the optical laser is blocked); pulse 1 corresponds to a warm sample heated by the laser and the pulse 2 corresponds to the Mo which has been ablated. The pulse 2 will be used as reference to remove the spatial distortion. As the x-ray spot is larger than the optical one, for each pulse two zones are measured: one where both beam overlap (bottom part) and one where only x-rays are impinging (top part). As a consequence one sequence results in the measurements of six different zones, which are summarized in the table 1.

Figure 2. Measured CCD images for n = 20 sequences.

Pulse 1 corresponds to x-ray + optical laser and pulse 2 corresponds to x-ray only at the same sample location. The bottom zone is ablated in this case. The third right image is the ratio of these two measurements where the two zones can clearly be distinguished. The vertical lines are the spikes due to the SASE process.

Table 1. Summary of the 6 different probed states with the pulse 0,1,3 sequence for the top and bottom part.

	Pulse 0 XFEL pulse	Pulse 1 XFEL + optical laser	Pulse 2 XFEL pulse
Top (spectral reference)	Cold Mo	Cold Mo	Cold Mo
Bottom	Cold Mo	Warm Mo	No Mo

The first step is to remove the non-homogeneous spatial intensity distribution. As this contribution is stable, dividing the measurement of pulse 1 (left image in the figure 2) by the one obtained for pulse 2 (center image in the figure 2) results in a normalization of the spatial inhomogeneity's, what will be denoted from now on as the primary normalization. If the SASE beam was free of spectral structures one would obtain directly the warm absorption spectrum in the bottom part of the sample. The result is the right image in the figure 2 which displays obvious vertical lines. These lines can be attributed to the spikes induced by the SASE process. As a result, a secondary normalization step is needed to get rid of these structures. We use the fact that these structures are spatially steady in the vertical direction. Having a cold (top) and a warm (bottom) part enables to divide the transmitted intensity through these two zones, hence removing the spectral variations. The same procedure was used with the pulse 0 measurement. This provides a cold XANES spectrum, prior to the warm one, at the same sample location. This ensures that no debris, contaminant on the surface or defect in the sample perturbed the measurement. Finally our procedure provides a measurement of a cold and warm spectrum, free of spectral SASE fluctuations.

Time resolved-experiment

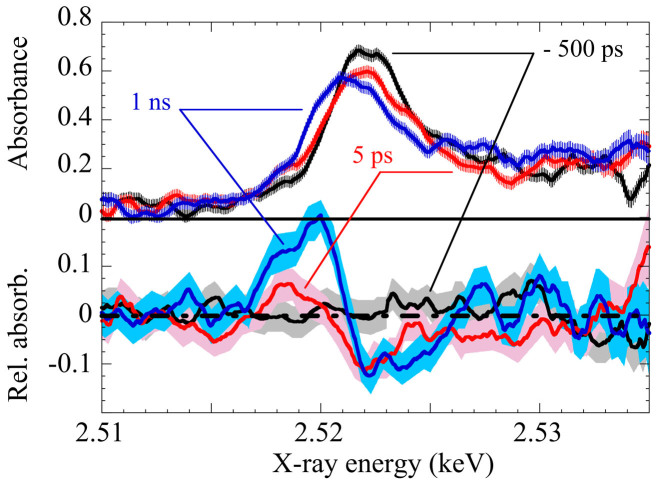
We performed a time resolved experiment taking n = 20 pulses, corresponding to a full acquisition time of 15 min. This time can be further reduced by reducing the read-out time of the CCD, which was not possible at the time of the experiment. The absorbance spectra were measured for several delays of which −550 ps, + 5 ps and +1 ns are shown in the figure 3. The error bar displayed for each point corresponds to the estimation provided by the analysis (Er, defined in the methods section). The results clearly show that over 32 eV, i.e. two times the FWHM spectral bandwidth; our secondary analysis provides a low noise XANES spectrum. In figure 3, the relative absorbance defined as the difference between the warm spectrum and the cold one (measured with the pulse 0) at the same location, are also displayed. For the −500 ps delay the relative absorbance is, within the error bar, equal to 0, as expected, while for positive delays a non-zero relative absorbance is obtained. For both positive delays, a decrease of the white line intensity is noticeable, as well as a shift of the L III edge. This shift is clearly evidenced by the positive relative absorbance at lower photon energies. This is a clear signature of a temporal evolution of the spectrum, demonstrating the feasibility of time-resolved XANES studies with hard x-ray FELs in the most demanding case, i.e. a solid sample with irreversible dynamics. The physical origins of the dynamics, requiring XANES modeling in non-equilibrium conditions, is underway, but beyond the scope of the present contribution.

Figure 3. Absorbance (top) and relative absorbance (bottom) obtained at 3 different delays: −500 ps (x-ray arriving before optical pulse), +5 ps and +1 ns.

The error bars (vertical lines and shaded areas) are evaluated from the described analysis.

Discussion

We performed a time-resolved dispersive XANES experiment using an original technique. The spectrum measured clearly show a ps dynamics on Molybdenum excited by an optical femtosecond laser. The time-resolution was in our case limited by the jittering between optical and x-ray laser. Using a time-sorting technique can improve the resolution down to 10 fs¹³. This can be easily implemented, as our technique relies on a very simple set-up. It provides results within the constraints of a typical XFEL beamtime even in the case of a sample ablated by the pump pulse. This method is versatile and usable for a wide range of experiments. The only requirement is the spatial separation of a warm and cold sample, which is in principle feasible for every kind of sample: gas, liquid or solid.

A single-pulse measurement is not feasible because of the nearly 100% variations within the SASE spectrum. In a single pulse there will always be spectral regions, even within the FWHM spectral bandwidth, where the measured signal will be nearly zero. Nevertheless, considering the low number of pulses required measuring a high quality spectrum, this technique opens up the prospective for time resolved dispersive XANES enabling detailed systematic studies.

Methods

Formal XANES extraction procedure

In order to quantify the efficiency of this procedure in terms of signal to noise ratio, a more formal approach is developed. Let's first express the incident intensity I_inc (photons.cm⁻².eV ⁻¹ per pulse) at the sample in the following manner:

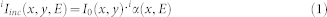Where I_o(x, y) is the spatial profile of the x-ray beam, ⁱα(x, E) is the pulse-to-pulse spectral variation which we assume to be independent of the vertical coordinate, i.e. y, and the index i denotes the pulse number: 0, 1 or 2. The transmitted intensity behind the sample is then given by:

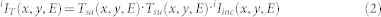Where T_sa(x, y, E) is the transmission of the sample of interest, the Mo in our case (the 8 nm a-C does not have a significant absorption at 2.5 keV), and T_su(x, y, E) is the transmission of the polypropylene substrate. This latter one is nearly flat over the explored spectral range. In both cases we assume the spatial uniformity of the materials leading to T_sa(x, y, E) = T_sa(E) and similarly for T_su(x, y, E) = T_su(E). In the case of the measurement with pulse 2, one can simplify the expression of ²I_T(x, y, E) = T_su(E)·²I_inc(x, y, E) because the Mo layer has been completely removed by the optical laser of pulse 1. As a result, the measured transmission T_mes is:

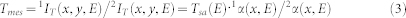In principle, averaging on a sufficient n number of pulses allows smoothing out the pulse-to-pulse spectral fluctuations, i.e. the averaged ratio¹α(x, E)/¹α(x, E) → 1. From a practical point of view, the value of n should be minimized as much as possible. In order to evaluate the noise of this basic analysis procedure, we performed a specific test in which the optical laser was switched off for pulse 1. In this case equation (2) simplify in:

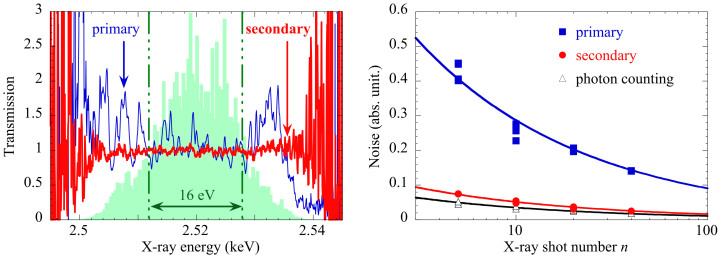
Between pulse 1 and pulse 2 the sample has not been modified as a result the ratio of the transmission should be equal to 1 over the whole spectrum. The result of this test, shown in the figure 4, clearly displays remaining noise.

Figure 4. Left: measured transmission in the case of the primary (blue curve) and secondary (red curve) analysis for n = 20 pulses.

The expected value is T_mes = 1. The green shaded area represents the corresponding to the same sequence than the x-ray spectrum. Right: Noise obtained for the primary, secondary procedure, and the corresponding photon counting statistics.

The S/N ratio can then be evaluated by computing the standard deviation σ(T_mes) on the pixels corresponding to the 16 eV FWHM bandwidth of the XFEL spectra. This provides a measurement of the absolute noise induced by the pulse-to-pulse spectral variation of the XFEL radiation. The values of σ(T_mes), as a function of n acquisitions, are shown in the figure 4. For n = 100, σ(T_mes) = 9% and decreases to 3.6% for n = 620 pulses. This results compare with the obtained using the beamsplitting technique⁷. This evidences that single step normalization for both spectral and spatial defects, requires an unaffordable high value of n. Hence the necessity of a secondary normalization, using the two zones top and bottom. We denote by the index “t” (for top) and “b” (for bottom) the different intensity related to these different zones, shown in the figure 2. The transmission for each part is then:

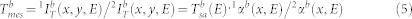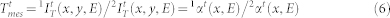In fact, in the top part for pulse 1 and 2, the beam is transmitted through a cold layer of Mo and contains the spectral information that is needed for the normalization. Finally:

In order to quantify the improvement obtained by applying this advanced analysis, we performed the same test previously described, i.e. switching off the laser during pulse 1, providing a measurement of σ(T_mes). The results are shown in the figure 4; a clear improvement is obtained compared with the primary analysis procedure. In this case, over the 16 eV FWHM of the spectrum, σ(T_mes) = 3.6% is reached after only n = 20. This number of acquisitions is sufficiently low to enable a time-resolved experiment involving irreversible dynamics. We also estimated the number of photon measured per pulse taking into account CCD characteristics and gain (the average number is around 300 photons/pixels). Summing over n images of single shot results in the counting of N photons. The probability to detect a photon is driven by Poisson statistics, which leads to a standard deviation of √N. This corresponds to the “photon counting” curves in the figure 4, and this is the lowest level of noise achievable. The figure 4 shows the results of σ(T_mes) for the primary and the secondary procedures. For n = 20, σ(T_mes) is nearly equal to the photon statistical noise, underlying the efficiency of our method. It should also be underlined that in case of FEL radiation, lowering the statistical noise is limited by saturation level of the detector and not by the number of photon per pulse.

The value of σ(T_mes) can be assumed to be constant during the experiment in the spectral region defined by the FWHM of the measured spectrum (shaded area in the figure 4). This can be considered as an assessment of the error. For higher and lower photon energy, the noise is mainly due to the photon counting statistics and can be estimated for every measured points of the spectrum by the quadratic sum of the two contributions: .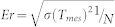

Author Contributions

J.G. and F.D. wrote the main manuscript text and prepared figures 1–4. J.G., F.B. and P.A.H. conceived the experiment. M.S. prepared and characterized the samples. J.G., C.F., B.I.C., K.E., E.G., M.H., P.M.L., H.J.L., B.N., M.N., C.O., S.T0., Th.T., P.A.H. and F.D. performed the experiment at SLAC. All the authors reviewed the manuscript.