Recalcitrant bubbles

Abstract

We demonstrate that thermocapillary forces may drive bubbles against liquid flow in ‘anomalous' mixtures. Unlike ‘ordinary' liquids, in which bubbles migrate towards higher temperatures, we have observed vapour bubbles migrating towards lower temperatures, therefore against the flow. This unusual behaviour may be explained by the temperature dependence of surface tension of these binary mixtures. Bubbles migrating towards their equilibrium position follow an exponential trend. They finally settle in a stationary position just ‘downstream' of the minimum in surface tension. The exponential trend for bubbles in ‘anomalous' mixtures and the linear trend in pure liquids can be explained by a simple model. For larger bubbles, oscillations were observed. These oscillations can be reasonably explained by including an inertial term in the equation of motion (neglected for smaller bubbles).

Bubble flow is of considerable use in the chemical, petrochemical, biochemical and metallurgical industries in applications such as bubble column reactors¹,². The technique of ‘bubble continuous positive airway pressure' (bubble CPAP), used in infantile respiratory care, relies on bubble flow³. Conversely, in decompression sickness, the appearance and flow of bubbles in the cardiovascular system is a bane to divers and airmen alike⁴.

Not only does bubble flow have important applications in chemical engineering, at a macroscopic scale, but also the behaviour and control of the motion of liquid drops and bubbles is becoming increasingly important in microfluidics, a subject in rapid expansion and with potential applications ranging from chemical analysis to information technology. In the seminal paper by Young et al.⁵, it was demonstrated that the flow of bubbles within a bulk liquid can be instigated by a temperature gradient. In fact, their elegant and simple system basically pitted the net, so-called, thermocapillary force of the bubble against buoyancy, by using a negative, vertical, temperature gradient, thus leading to stationary bubbles. Many authors have since contributed to the study of this fascinating and still incompletely understood phenomenon, using different experimental set-ups and contributing both experimental and theoretical refinements, of which good examples may be found in⁶,⁷,⁸,⁹,¹⁰,¹¹,¹². We consider here the effect of a variation of temperature, T, in a liquid, along the axis, x, of interest: dT/dx = α where α is assumed constant. This leads to a variation of liquid surface tension (or liquid/vapour tension at the bubble/bulk interface), γ, along the axis given by dγ/dx. The coefficient, dγ/dT = −β, is generally negative (and often fairly constant over small temperature ranges). Integration around the bubble, invoking the difference in γ between its two poles, leads to a resulting net force which, for a normal liquid, directs the bubble to the hotter region of the liquid, i.e. towards higher x. If, as in our experimental system, buoyancy in the direction of motion (along x) is eliminated (by using a horizontal channel containing the liquid and a horizontal temperature gradient), and neglecting minor inertial corrections, the thermocapillary force is balanced by liquid viscosity, leading to migration at essentially constant speed of the bubble towards the hotter region. We have observed this expected behaviour for (pure) butanol and water (see below).

However, if the variation of surface tension with temperature, dγ/dT, is not constant and γ presents a minimum¹³, rather different behaviour may be observed. The bubble may actually migrate against the imposed fluid flow. This is the principal theme of the present contribution.

Results

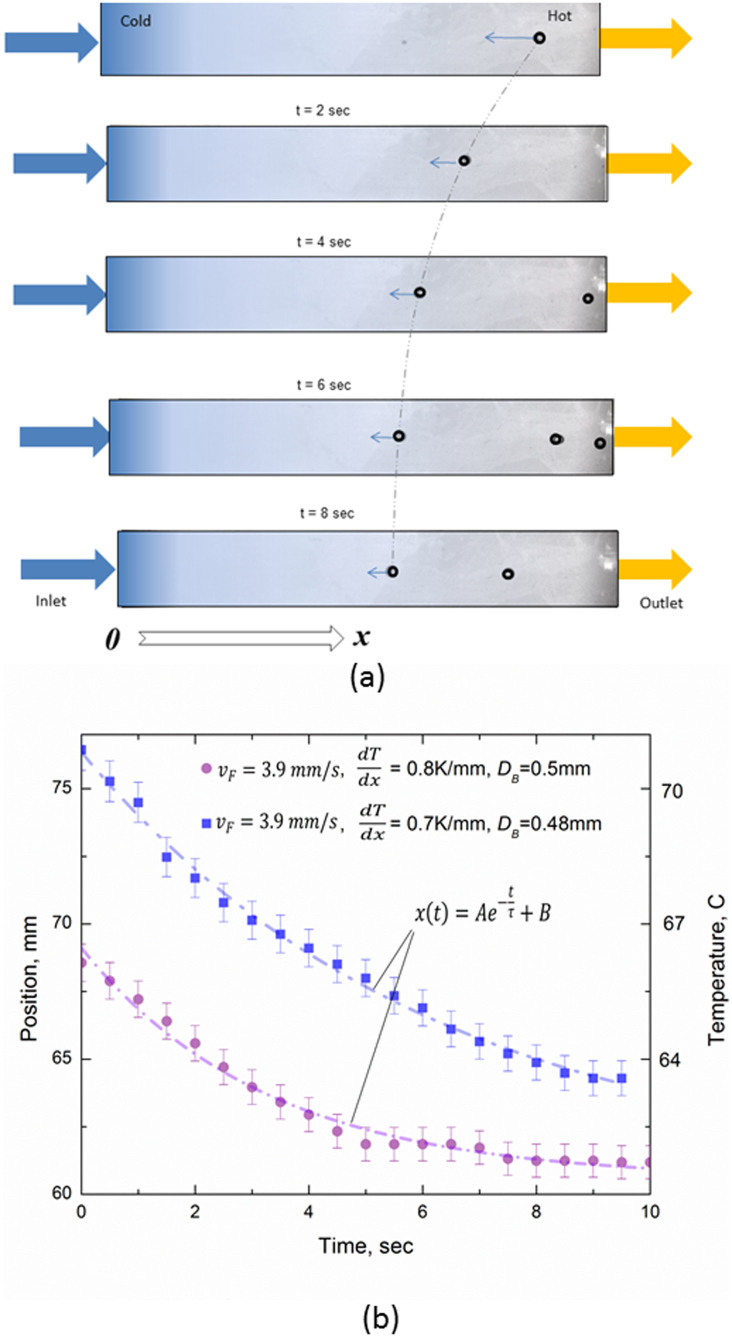
In Fig. 1(a), we present photographs of a (horizontal) heated micro-channel containing 5% butanol/water mixture, flowing from left to right and with temperature increasing in the same direction. A bubble has spontaneously formed near the outlet, due to high temperature, and in subsequent images can be seen migrating towards the left. This unexpected behaviour is shown graphically in Fig. 1(b), as position from the inlet, x, versus time after first observation, t. The bubble is actually propelled towards the region of lower temperature due to the unusual nature of the γ vs T curve. As discussed below, this curve has a minimum of surface tension in the neighbourhood of 70°C and, after asymptotic approach, the bubble comes to an equilibrium position, x_e, near, but not at, the value of x corresponding to this temperature.

Figure 1.

(a) Photographs of a bubble, of diameter, D_B ca. 0.7 mm, in a 5% mixture (by weight) of butanol in (distilled) water in a horizontal flow channel, with liquid flowing from left to right at an average speed, 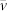, of 3.9 mm s⁻¹(flow rate of 1.5 ml min⁻¹). Resistance heating of the channel corresponds to a temperature gradient of 0.7°C mm⁻¹ from left to right, the two extremities being at ca. 35 and 90°C. The bubble of interest is that shown at the right of the top image, created spontaneously in the liquid where the temperature is sufficiently high. It migrates to the left as time passes (0 to 8 seconds) in the subsequent images, and can be seen to be arriving asymptotically at an equilibrium position at 8 seconds. Note that this motion is upstream, i.e. against the flow current. The bubble(s) to be seen on the right of the 3 lower images are later bubble creations, also showing similar recalcitrant behaviour, but not so clearly. This behaviour is in sharp contrast to that expected, in which the bubble should migrate to the right at a speed, in the observer's reference frame, given by the flow speed of the liquid added to the thermocapillary speed found by equating driving force to viscous drag. (b) Behaviour as shown in Fig. 1(a) portrayed as distance, x, from liquid inlet on left of channel vs time, t.

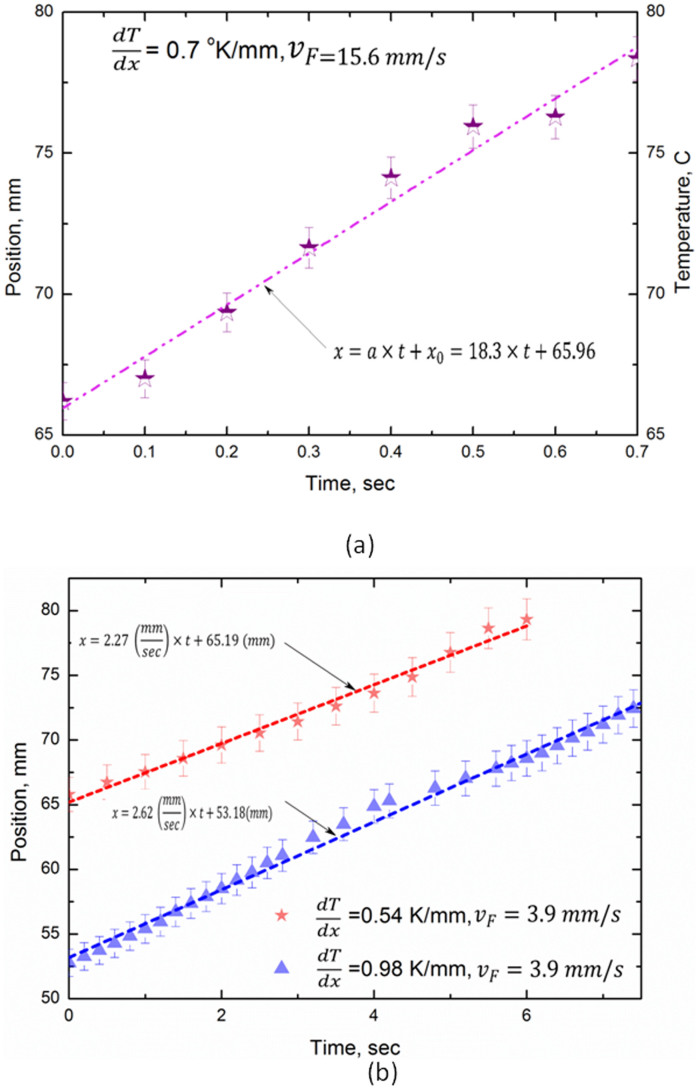
Although the behaviour of bubbles in the 5% butanol mixture is quite reproducible, it was considered judicious to consider behaviour in similar conditions but using the pure liquids constituting the mixture, viz. n-butanol and distilled water. The results of position along micro-channel, x, versus time are given in Fig. 2. The data show convincingly that no ‘upstream' migration occurs, although some quantitative evaluation and comments on these are necessary, and will be given below. Notwithstanding, from the point of view of the basic physics, it is quite clear that there is considerable difference between the behaviour of bubbles created in the 5% butanol mixture and that in the pure liquids. We present below an interpretation of the observed results.

Figure 2.

(a) Examples of position, x, along channel of bubble in pure water. (b) Examples of position, x, along channel of bubble in butanol vs time after ‘creation'. Coordinates are as in Figure 1(b).

Theoretical explanation

We propose a simple model to explain this strange behaviour, which successfully captures the basic physics of the observations. The starting point is to consider a spherical bubble of radius r, and surface tension γ (variable with temperature), in motion in a liquid under a constant temperature gradient (both spatially and temporally), assuming the bubble to be sufficiently small for us to neglect effects of gravity and inertia. As above, distance x is measured along the channel, following the temperature, T, gradient, with the origin at the cold end. The bubble driving term is due to the surface tension gradient, dγ/dx, at the bubble/liquid interface, caused in turn by the thermal gradient within the bulk liquid, dT/dx = α. (We here neglect effects of heat transfer across the bubble/liquid interface, which should be reasonable for small bubbles.) Two cases are of interest: (a) that of a ‘normal' liquid, for which we assume a linear temperature dependence of surface tension, dγ/dT = −β, leading to 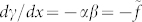, and (b) the ‘anomalous' case, in which a minimum of surface tension versus temperature is known to exist¹³,¹⁴,¹⁵,¹⁶. We assume parabolic temperature dependence (as a first approximation). With γ(T) = A(T − T_min)² + γ_min, where A is a constant and T_min is the temperature corresponding to minimal surface tension, γ_min, we find dγ/dx = 2Aα²(x − x_c) = 2f(x − x_c), where x_c is the position corresponding to T_min. This is shown schematically in Fig. 3. We note, in passing, that 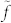has units of pressure and f those of a body force. Since γ varies over a range of 2r along x within the bubble, we may calculate the overall driving force, F_D, from: 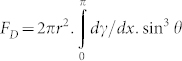, where θ is the azimuth, taking the x axis as the pole. It is found that for a ‘normal' liquid, 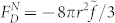and that for the ‘anomalous' case, 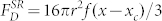. In the latter expression, x now represents the position of the centre of the bubble. For a spherical bubble in a liquid of infinite extent, viscous drag on the bubble, F_V, is given by (a modified form of) Stokes' law¹⁷: F_V = 4πrηv, where η is liquid viscosity and v is bubble speed along x, with respect to the liquid. However, as stated, this relation for F_V assumes a bubble in an effectively infinite liquid, whereas in our case, although the bubbles are essentially spherical (diameter < capillary length, ca. 1.5 mm), they are of dimensions comparable to the channel depth. Thus, drag will be greater than that expected, due to the proximity of the channel wall(s). We therefore, for commodity and without pretence at rigour, take into account this effect by a prefix k₁ for η, in order to obtain F_V = 4πrk₁ηv, where k₁ is unknown, but certainly k₁ > 1. The liquid is flowing along direction x with an average speed 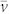, in the reference frame of the channel, the temperature gradient and therefore the observer. Again we have a problem due to the restricted dimensions of the channel used. Essentially 2D Poiseuille flow will be present within the channel and therefore, 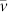will not be entirely representative of the flow speed ‘felt' by the bubble (although of similar order of magnitude). Instead, we adopt an effective value of (local) flow speed, v_F, and now we may write F_V = 4πrkη(dx/dt − v_F). Equating F_D and F_V, in what amounts to a simplified Navier-Stokes equation, we obtain respectively for, (a) the ‘normal' liquid and, (b) the ‘anomalous' liquid:

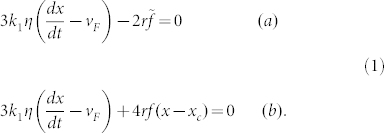Equations (1) have simple solutions giving bubble position, x, as a function of time, t, in the two cases, using as the initial condition the position of the bubble at its ‘creation' as x_o:

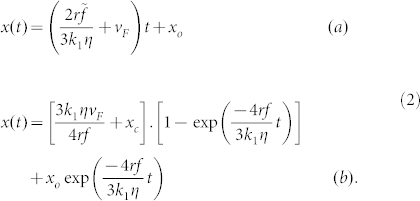We note from equations (1(a)) and (2(a)) that in a ‘normal' liquid, bubble motion is expected to be linear with respect to the observer and in the positive x direction. At first sight, this appears indeed to be the case for the results of bubble motion in both pure water and butanol, shown in Fig. 2(a) and Fig. 2(b). Nevertheless, closer examination indicates that, although progression is linear and from left to right in the micro-channel, the actual speed is less than that of the average liquid flow rate in the case of butanol. The exact explanation of this anomaly is not, as yet, clear, but we should remember that the micro-channel has one lateral dimension comparable to bubble diameter. Within the micro-channel, essentially 2D Poiseuille flow should pertain, which means that speed tends to zero near the walls. We therefore surmise that the average liquid flow speed is not the value pertinent to drag acting on the bubble (as noted above). In addition, for water, bubbles tended to adhere to the upper wall, necessitating a higher flow rate for bubble motion to occur.

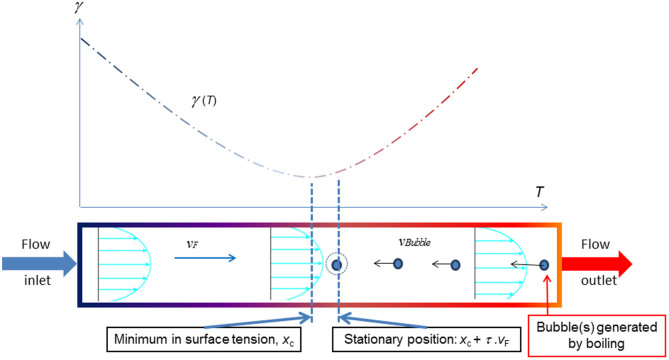
Figure 3. Schematic representations of curve of γ vs T (above), and bubble migrating against the flow, in the case of an anomalous mixture.

The temperature axis above corresponds with the distance below. Thus, at the equilibrium position, x_e, the bubble is downstream of that of the minimum of surface tension, x_c, by τ.v_F, due to liquid flow.

From equations (1(b)) and (2(b)), exponential behaviour is expected for an anomalous liquid. The direction of motion depends on several factors, notably (local) flow speed, v_F, and the position of ‘creation' of the bubble, x_o. Clearly v_F must not be too high and the bubble must initially appear downstream of its equilibrium position (see below) to be able to travel backwards against the current. As t → ∞, the bubble centre asymptotically approaches a value of x of 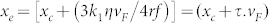, where τ is the characteristic time constant of the motion and x_e may be considered to be the equilibrium position of the bubble. The minimum of surface tension is centred on x_c, but the equilibrium position is offset by 3k₁ηv_F/4rf = τ.v_F to higher x because of the liquid flow, or drift, speed, as shown in Fig. 3.

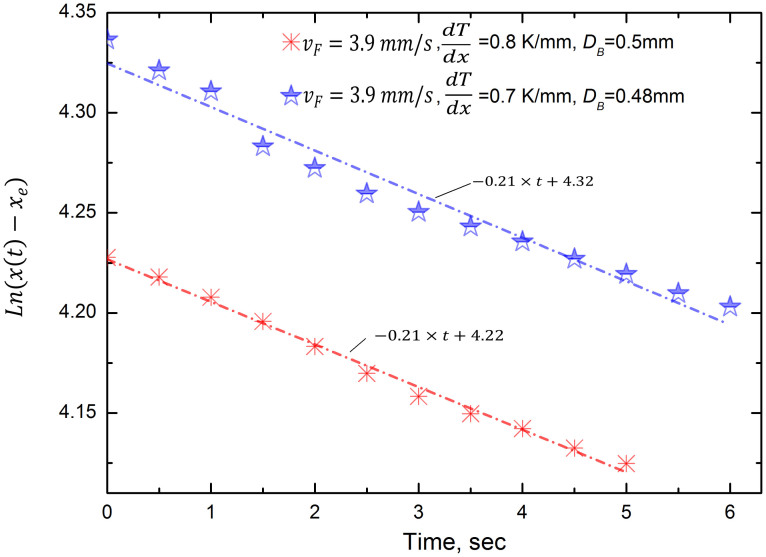
The general features of Fig. 1(b) and 2 are to be seen in equation (2), but we may improve on this by simple error analysis. Equation 2(b) can be simply rearranged to give:

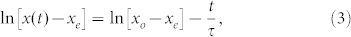or y = b + at, where y = ln[x(t) − x_e], a = −1/τ, and b = ln[x_o − x_e]. Equation (3) can be treated by simple regression analysis. Thus, with knowledge of b, the position of ‘creation' of the bubble, x_o, may be estimated. Of more interest is a = −1/τ since, in principal, all of the terms r, f and η are known, yet with varying degrees of precision. Fig. 4 gives two examples of application of equation (3) where it can be seen that the agreement is acceptably good, despite the simplifications used.

Figure 4. Logarithmic plot of data presented in Fig. 1(b), corresponding to equation (2b), or 3, with corresponding regression lines.

(The constants for the linear fits refer x in mm and t in s.).

The calculation above assumed a spherical bubble, radius r, which is probably reasonable since gravitational flattening is small in the range considered (capillary length of ca.1.5 mm). However, as noted, although viscosity, η, presents no problem per se, the proximity of the channel wall to the bubbles will perturb the viscous drag term.

Dancing bubbles

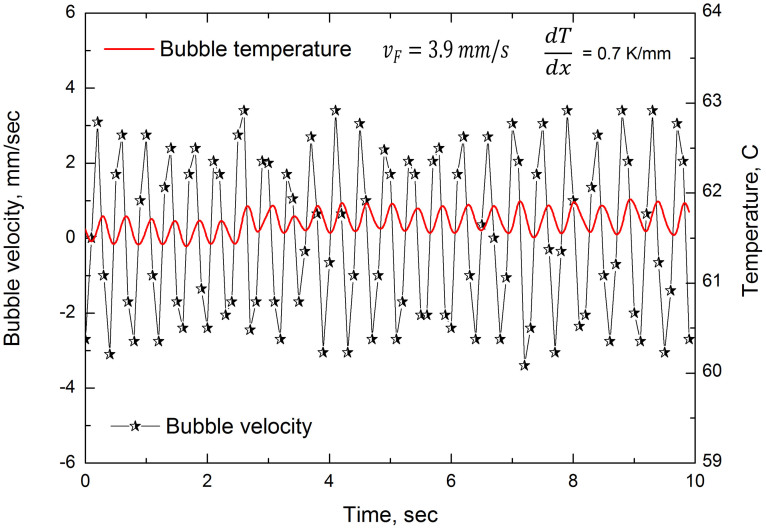
Up until here, we have considered bubbles of diameter, 2r, below or equal to ca. 0.7 mm. We have observed an interesting phenomenon with somewhat larger bubbles. As an example, in Fig. 5 are presented bubble speed (and temperature) vs time, of a bubble of diameter ca. 2.2 mm, the time being counted from arrival at the (approximately) equilibrium position. (In other words, the exponential-type behaviour seen in Fig. 1 and 2, although present, has been excluded for concision.) There are striking oscillations of position (and average temperature) which perpetuate, and which were undetected for the smaller bubbles. Unfortunately, with the present set-up, (most of) these larger bubbles were more disc-like than spherical, due to the constraint of channel depth, 0.8 mm, thus rendering them less amenable to quantitative treatment. Nevertheless, we tentatively present a simple yet plausible explanation.

Figure 5. Speed, dx/dt, of disc-shaped bubble of radius ca. 1.1 mm in 5% butanol mixture vs time after reaching ‘equilibrium' (left hand ordinate and large oscillations).

Temperature variations of bubble with time as obtained from IR camera (right hand ordinate and small oscillations). The bubble is disc-shaped due to the constraint of the larger channel walls being separated by 0.8 mm.

The simple theory presented above for smaller bubbles neglects two contributions which may be more important for larger bubbles: (i) inertia and (ii) heat transfer between liquid and vapour across the bubble interface. We may allow for the inertial term, assuming laminar flow, by introducing the ‘added mass', corresponding to displacement of liquid in the vicinity of the bubble¹⁸. In the case of a spherical bubble of radius, r, in a liquid of density, ρ, the added mass term is given by 1/2*4πρr³/3, i.e. half of the mass of the spherical bubble if it were liquid rather than gas¹⁹. As a result, equation (1(b)) may be rewritten as:

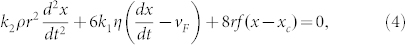where k₂ is a constant to allow for the fact that the bubble is not necessarily spherical, depending on the case. (In this simple approximation, k₂ = 1 for a sphere, but k₂ < 1 for the flattened shape, since 2r corresponds to the observed, circular diameter, which is larger than the channel wall separation, 0.8 mm.) (Clearly, the second and third terms of equation (4) should be modified too, in a rigorous approach, since their use also assumes a spherical bubble.) The solutions to this classic differential equation, found (in slightly simpler form, without the additive constants involving v_F and x_c) in standard texts on simple harmonic motion (SHM) involve exponentials with either real or imaginary arguments, the former corresponding to decaying (or amplifying) exponential behaviour and the latter to damped sinusoidal or oscillatory behaviour. We define r_o as:

If r < r_o, an exponentially decaying solution is appropriate, but for r > r_o, oscillatory behaviour is to be expected. We cannot evaluate r_o with any accuracy, given the simplicity of the model. However, experimental observations indicate that r_o ≈ 2 mm. The observed oscillations for large bubbles and the lack there of for smaller ones is a corroboration of the predictions in the present analysis. The angular frequency associated with equation (4) is given by 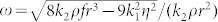. Appropriate values are ρ ≈ 1000 kg m⁻³, η ≈ 10⁻³ Pa.s and f is estimated at ca. 5 Nm⁻³. Taking both k₁ and k₂ to be approximately unity, in the absence of more precise values, for the bubbles of diameter 2.2 mm, we find frequency, v ≈ ω/2π, to be ca.0.9 s⁻¹, which, given the simplifications of this treatment, compares favourably with the value of ca. 2.5 s⁻¹ which is apparent in Fig. 5.

Equation (4) (with r > r_o) corresponds to damped SHM, but our observations suggest sustained SHM (or at least, slowly decaying). Close inspection of Fig. 5 shows the temperature to be out of phase with the position by ca.π/2, presumably due to (relatively) slow heat transfer. Although the problem is intrinsically rather complicated, this effectively means that the last (force) term of equation (4) may be written approximately as a truncated Taylor series: 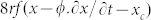, where ϕ is a time lag. Thus, under appropriate circumstances, the two terms in speed (dx/dt or ∂x/∂t) may (approximately) cancel, leaving more or less the equation for undamped or lightly damped SHM. It is the transfer of heat energy from the liquid source which sustains the SHM by cancelling out the effects of the expected viscous damping. Clearly, at this stage, this amounts to conjecture but it does plausibly explain the observed physics.

Discussion

In summary, by using a 5% mixture (by weight) of butanol in (distilled) water as the bulk liquid in a heated micro-channel, Fig. 6, we have observed some very unusual behaviour. Instead of migration towards the warmer zone (downstream), bubbles actually move towards the colder region (upstream) with a basically exponentially decaying motion, until equilibrium is reached. Fig. 1 clearly shows an example of this behaviour, which is quite reproducible. The system shown in Fig. 6, described in the Methods and Experiments section, corresponds to a channel in which the bulk liquid mixture is pumped from left to right. Using resistive wall heating, the liquid is maintained with a constant temperature gradient in the reference frame of the channel, with T increasing from x = 0. Towards the higher values of x, and therefore, T, bubbles are created spontaneously and, under normal circumstances, would be expected to move to the right since two motions are superimposed in the observer's frame of reference (that of the fixed channel): the liquid flow and that due to thermocapillarity, for reasons invoked above. Therefore, the fact that the bubble moves upstream is doubly surprising, since clearly both tendencies for the bubble to move to the right are being overcome. The quantitative behaviour corresponding to Fig. 1(a) is portrayed in Fig. 1(b), as position along the channel, x, and equivalently temperature, T, vs time, t. The exponential-type decay to the equilibrium position is clear. To check that this effect is not due to some experimental artefact, the results obtained in pure water and butanol were treated as those of our mixture and examples are given in Fig. 2 for comparison.

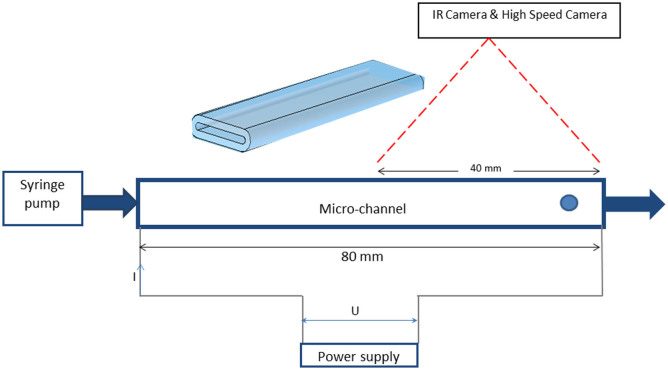
Figure 6. Schematic representation of micro-channel experimental set-up.

The programmable syringe pump delivers a constant flow through the channel. The nucleation site of bubble is downstream, at the exit of the microchannel.

Thermocapillarity, or decrease of surface tension with increasing temperature, leads to bubble motion⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹,¹². A bubble in a temperature gradient generally experiences a net capillary force causing its motion towards the hotter region (unless compensated by gravity⁵,⁶,⁹ or a flow field). However, some liquids show a minimum in surface tension vs temperature¹³. We show that this can cause bubble migration away from the hotter zone, until equilibrium is attained. This may be of use in, for example, reactors to prolong contact time.

The fact that ‘recalcitrant' bubbles are created and move upstream in a 5% butanol mixture is due to this unusual property of the liquid. Petré et al.¹³,¹⁴,¹⁵ discovered that various mixtures of water and n-paraffins had strange properties and, in particular, possessed a minimum of surface tension, say at T = T_min, thus dγ/dT is negative for T < T_min, but positive for T > T_min. T_min is ca. 70°C for the present mixture¹⁶. These liquids have been referred to as ‘anomalous'¹⁶. With this knowledge, we may interpret our observations. Furthermore, the proposed models allow for two solutions, either exponential decay towards the equilibrium position or oscillations around this latter depending on the size of the bubbles, as well as other parameters such as temperature gradient and physical properties. Although oscillations have been experimentally observed for larger bubble, it is fair to state that these oscillations might have more than one mechanism driving them. Further investigation of bubble oscillations for thermocapillary migration of bubbles in anomalous fluids is worthwhile. Unfortunately, with the present set-up, (most of) these larger bubbles were more disc-like than spherical, due to the constraint of channel depth, 0.8 mm, thus rendering them less amenable to quantitative treatment. Nevertheless, we tentatively present a simple yet plausible explanation.

Vapour or gas bubbles are known to be entrained by liquid flow if not constrained by a supplementary force (e.g. by adhesion to a solid surface). This is intuitive and also an observation dating back to recorded history. It is only in the last 60 years⁵ that scientists have realised that bubbles can be moved by another force than flow i.e. surface tension. The work of Young et al.⁵ demonstrated that bubbles can be driven by surface tension gradients in stationary liquids. The direction of motion has been established as being from the cold side towards the hot region. Numerous studies⁶,⁷,⁸,⁹,¹⁰,¹¹ have extended the work of Young et al.⁵ to confirm and further quantify thermocapillary motion of bubbles, yet without offering any fundamental difference in expected trends⁶,⁹,¹⁰,¹¹.

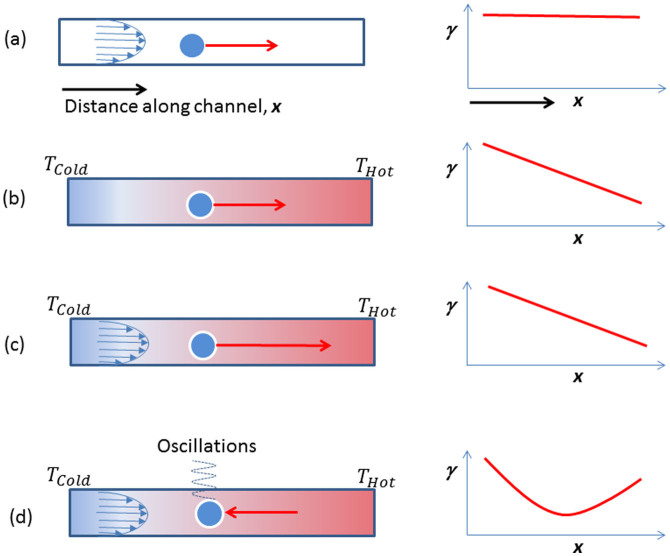
However, the findings presented in the present article bring to light a new phenomenon, previously unreported, in which bubbles drift against the liquid flow and from the hot region to the cold one. These observations reveal a new type of behaviour, contradictory to experimental observations reported up to present, for ‘ordinary' liquids. The newly observed behaviour clearly corresponds to an unusual phenomenon and differs from the trend reported by the plethora of studies in the literature on thermocapillary flow. Four possible scenarios, depending on intrinsic liquid flow, temperature gradient and temperature dependent liquid surface tension are depicted in Fig. 7. The first three are well known; the fourth corresponds schematically to findings presented here.

Figure 7. Schematic representation of four scenarios.

(a) For constant liquid temperature (and therefore surface tension, γ) along the channel, direction x, progression of the bubble towards the right depends uniquely on liquid flow (shown as a parabolic front). (b) In the absence of liquid flow, but the presence of a temperature gradient from cold, on the left, to hot, on the right, the classic thermocapillary effect causes bubble migration, also towards the right, due to decreasing γ. (c) With both a temperature gradient and flow, in a normal liquid, bubble motion is quicker. (d) For an anomalous liquid, showing a minimum in γ, reversal of motion may occur, with the bubble actually moving upstream. Oscillations may ensue after migration.

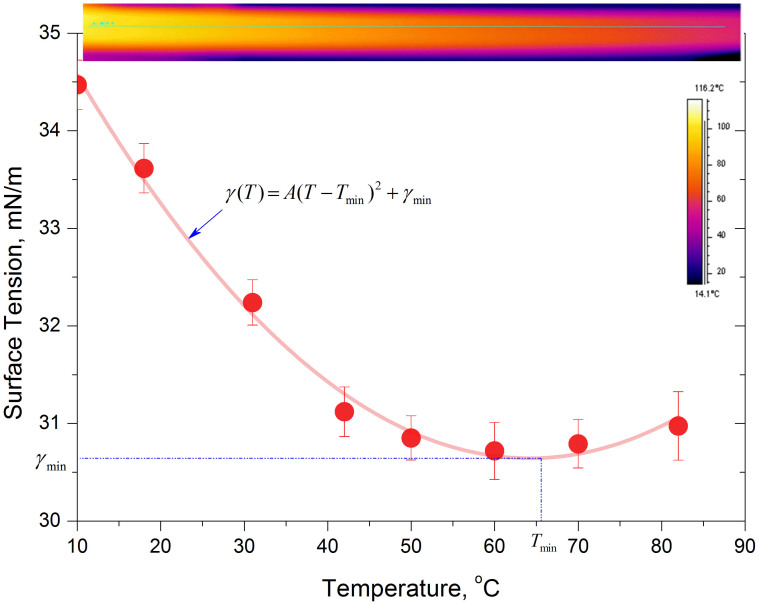
The conclusions from this work may be readily extended to other mixtures exhibiting similar properties concerning surface tension dependence on temperature. Based on surface tension measurements and values given in the literature, and our own measurements, Fig. 8, the minimum in surface tension is observed around a concentration of 5% butanol in water. Higher or lower concentrations of butanol will lead to a deviation from a minimum in surface tension. The further we deviate from this specific concentration, the more we tend to a monotonic decrease of surface tension with temperature. The effect is also observed for higher carbon alcohols at different concentrations e.g. 0.1% heptanol in water¹⁶.

Figure 8. Surface tension as a function of temperature for 5% butanol in water.

Measurements were performed using a pendent drop technique and show the minimum in surface tension near 67°C.

Methods

A heated, high aspect ratio channel, 8 mm wide, 0.8 mm deep and 80 mm long was used, through which the requisite liquid was pumped and in which bubbles were created spontaneously at high enough temperature (towards the hot end of the channel). To be able to visualise inside the micro-channel at the same time as applying a heat flux, a transparent, conductive, metallic deposit of tantalum was applied to the exterior of the microchannels. The thickness of the deposit required for suitable heating was of the order of tens of nanometres, which is negligible in comparison to the glass thickness (micrometers). The deposit was uniform both across and along the microchannel. The channel was connected by its ends to a power supply, enabling heating of the channel by passing a current through the resistive coating, thus controlling wall temperature.

The injection system used a syringe pump to produce the required constant liquid mass flow rate through the system.

Liquid was injected through the micro-channel where it was subjected to heating/boiling and collected at the exit of the micro-channel in a glass tank. A National Instruments® system was used for data acquisition, connected to a computer and a Labview® user interface. Inlet and outlet temperature and pressure were monitored using thermocouples and pressure sensors connected to the data acquisition board on the PC. A high speed camera was set-up to visualise the flow at frame rates up to 1500 fps. A cold light source was used in conjunction with the high speed camera, providing back lighting of the micro-channel. The high-speed camera employed was a NanoSense® MK II (IDT), with interchangeable macro and micro lenses, used as appropriate. The resolution of the camera allowed for either the entire heated micro-channel length to be captured or for just a particular section of interest to be focussed upon. An FLIR Systems® ThermaCam SC3000 infrared camera was used to visualise and record the temperature profile at the micro-channel exterior wall. The IR camera used here was a multi-detector model, with a spatial resolution of the order of 10 μm. It has a thermal sensitivity of 20 mK at 30°C, an accuracy of ±1°C for temperatures up to 150°C, a resolution of 320 × 240 pixels, and is Stirling cooled. The camera operates at 50 Hz, therefore 50 frames per second are recorded. The system provides for automatic transmission correction of temperature, based on atmospheric temperature, relative humidity, input distance from the object and emissivity of the object. The IR camera was used with an appropriate lens and a dedicated PC for acquisition, with specialised software (ThermaCAM Researcher Professional®) for image analysis. An FTA200 drop shape analysis instrument was used to measure surface tension of the 5% butanol/water mixture. A minimum in surface tension as a function of temperature was measured at ca. 67°C.

Author Contributions

K.S. conceived the original idea, designed and supervised the experiments. M.E.R.S. formulated the physical model and drafted the paper. Both authors reviewed the manuscript.