Abstract
Interstitial cells of Cajal (ICC) act as pacemaker cells in the gastrointestinal tract by generating electrical slow waves to regulate rhythmic smooth muscle contractions. Intrinsic Ca2+ oscillations in ICC appear to produce the slow waves by activating pacemaker currents, currently thought to be carried by the Ca2+-activated Cl− channel anoctamin 1 (Ano1). In this article we present a novel model of small intestinal ICC pacemaker activity that incorporates store-operated Ca2+ entry and a new model of Ano1 current. A series of simulations were carried out with the ICC model to investigate current controversies about the reversal potential of the Ano1 Cl− current in ICC and to predict the characteristics of the other ion channels that are necessary to generate slow waves. The model results show that Ano1 is a plausible pacemaker channel when coupled to a store-operated Ca2+ channel but suggest that small cyclical depolarizations may still occur in ICC in Ano1 knockout mice. The results predict that voltage-dependent Ca2+ current is likely to be negligible during the slow wave plateau phase. The model shows that the Cl− equilibrium potential is an important modulator of slow wave morphology, highlighting the need for a better understanding of Cl− dynamics in ICC.
Keywords: interstitial cells of Cajal, mathematical model, anoctamin 1, store-operated calcium entry
smooth muscle contractions in the gastrointestinal tract are partly controlled by spontaneous electrical events called slow waves, which originate in pacemaker cells known as interstitial cells of Cajal (ICC). In the stomach and small intestine of mice and guinea pigs, slow waves are generated by ICC located in the region of the myenteric plexus between the circular and longitudinal muscle layers (ICC-MY), while in the colon the primary pacemaker ICC are in the region of the submuscular plexus (ICC-SMP). Other classes of ICC regenerate slow waves within the smooth muscle layers and mediate neural signals (15, 33). Slow waves recorded from ICC-MY are often called pacemaker potentials to differentiate them from the smaller amplitude slow waves recorded from smooth muscle. In this article we refer to the electrical events in both ICC and smooth muscle cells (SMC) as slow waves, reflecting the origin of all slow wave activity in ICC (52).
Slow waves recorded from ICC-MY in the stomach and small intestine have a characteristic morphology: a rapid upstroke phase, in which the cell depolarizes from a resting membrane potential between −80 and −50 mV to a peak potential between −25 and 0 mV (33, 52); a plateau phase, in which the membrane potential is maintained close to the peak potential; and a repolarization phase, in which the cell returns to the resting membrane potential.
Cyclical changes in intracellular Ca2+ underlie the slow wave activity in ICC (51, 64). The Ca2+ cycle involves Ca2+ release from and uptake into inositol 1,4,5-trisphosphate (IP3)-mediated stores in the endoplasmic reticulum (ER). Ca2+ oscillations occur at the same frequency as slow waves, but to our knowledge intracellular Ca2+ concentration ([Ca2+]i) has not been quantitatively measured in ICC. However, the amplitude of global Ca2+ transients in ICC is likely to be similar to that seen in other cell types, such as cardiac myocytes, in which [Ca2+]i typically increases from a resting level ∼100 nM to a peak ∼1 μM (54).
IP3 receptors (IP3Rs) are known to contribute to the pacemaker mechanism, because slow waves are absent in gastric smooth muscle tissue from mice lacking type 1 IP3R (59), and pacemaker activity is inhibited when phospholipase C blockers are used to inhibit IP3 production (38, 40). In previous pacemaker hypotheses, IP3-mediated ER Ca2+ release was proposed to initiate the pacemaker cycle, either by Ca2+-dependent activation of pacemaker channels (33) or by stimulating mitochondrial Ca2+ uptake to relieve Ca2+-dependent inhibition of pacemaker channels (52).
Another possible pacemaker mechanism involves activation of pacemaker channels by store-operated Ca2+ entry (SOCE) (36, 64). In brief, SOCE is the activation of Ca2+-permeable ion channels, called store-operated Ca2+ (SOC) channels, in the plasma membrane in response to depletion of Ca2+ stores in the ER. SOCE is initiated when stromal interaction molecule (STIM) proteins in the ER membrane sense a depletion of ER Ca2+ stores and respond by translocating to sections of ER close to the cell membrane (35, 74). SOC channels are formed by the oligomerization of STIM with pore-forming proteins in the cell membrane. STIM can interact either with pore-forming proteins called Orai to form Ca2+ release-activated Ca2+ (CRAC) channels that are highly selective for Ca2+ or with canonical transient receptor potential (TRPC) channel proteins to form nonselective cation channels (17, 45, 46) (see refs. Refs. 56, 58 for further details).
Evidence for the importance of SOCE in ICC comes from the inhibitory effects of 2-aminoethoxydiphenyl borate (2-APB) on pacemaker activity (36, 38), although it should be noted that 2-APB has complex effects on Ca2+ influx and release. 2-APB has varying effects on Orai, but in general >10 μM 2-APB inhibits CRAC channels, while low micromolar concentrations of 2-APB potentiate CRAC channels (50, 56). At similar concentrations, 2-APB inhibits a variety of TRPC and TRPM channels (26, 71). 2-APB inhibits IP3Rs with an IC50 of 42 μM to 1 mM, depending on the IP3 concentration (5, 41). The effects of 2-APB on ICC must be interpreted with caution, but 2-APB appears to be a more consistent and potent inhibitor of SOC channels than IP3Rs, suggesting a role for SOCE in ICC pacemaking.
The exact mechanism of interaction between the intracellular Ca2+ dynamics and the ion currents contributing to the slow wave potential is a matter of ongoing discussion. Recent reviews have described the possible roles of ion channels that have been identified in ICC (2, 33). A crucial step in understanding pacemaker activity is identifying the pacemaker channel that initiates slow waves. Proposed candidates for the pacemaker channel include Ca2+-activated Cl− channels (69); Ca2+-inhibited nonselective cation channels (30); Ca2+-activated nonselective cation channels (21); or TRPM7 nonselective cation channels (26). A likely candidate is anoctamin 1 (Ano1, previously called TMEM16A), which has been identified as a Ca2+-activated Cl− channel (8, 53, 72). Ano1 is highly expressed in all classes of ICC in the human and murine gastrointestinal tracts (20) and appears to be essential for the electrical pacemaker activity of ICC, because Ano1 knockout mice do not exhibit slow waves (23).
Ano1 channels have a complex dependence on Ca2+ and voltage. They are slowly activating and outwardly rectifying at low [Ca2+]i, but at high [Ca2+]i they activate rapidly and have a linear voltage-current relationship (70). Ca2+-activated Cl− currents were studied extensively before the discovery that the anoctamin family of proteins, particularly Ano1, is a major component of Ca2+-activated Cl− channels (7, 62). Mathematical models of these Ca2+-activated Cl− currents were developed (7, 32), but we cannot ascertain whether the experimental recordings on which these models were based were exclusively carried by Ano1 or whether other Ca2+-activated Cl− channels were involved, requiring us to develop a novel Ano1 channel model.
Furthermore, it is important to understand how the Ano1 channel fits into a model of pacemaker activity. The existing biophysically based models of ICC slow wave activity were completed before the discovery of Ano1 in ICC, so none of these models incorporated the Ano1 channel (10, 16, 73). In addition, SOCE was not represented in the existing ICC models. Both the Faville small intestine ICC model (16) and the Corrias and Buist gastric ICC model (10) implemented a Ca2+-inhibited nonselective cation channel as the pacemaker channel, based on a pacemaker hypothesis that has since been called into question (23, 33).
Therefore, we have developed a novel ICC model that includes our Ano1 model as the pacemaker channel and incorporates SOCE as a key component of the Ca2+ dynamics. We chose to represent the pacemaker activity of ICC-MY from murine small intestine with this model, because mice are a common animal model for studying ICC electrophysiology. Slow waves in the murine small intestine typically occur at 16–30 min−1 (21, 29), but frequencies of 10–50 min−1 have been observed (61). The overall morphology of a slow wave, rapid upstroke, plateau phase, and repolarization, is determined by the summation of the individual ion currents active during the slow wave.
The primary aim of the modeling work presented here is to elucidate how Ano1 Ca2+-activated Cl− channels contribute as pacemaker channels in ICC. The precise function of Ano1 current in ICC depends on the Cl− equilibrium potential (ECl). Measurements of intracellular Cl− concentration ([Cl−]i) indicate that ECl in murine ICC-MY is 40 to −50 mV (76), but microelectrode techniques used to record slow waves may lead to Cl− loading (4), and previous studies have suggested that Cl− currents reverse positive to the slow wave plateau (29). Therefore, we also aimed to test the effect of varying ECl on slow waves in ICC-MY.
In addition, the identity of the ion channels active during the plateau phase remains unclear. We also aimed to predict the characteristics of the ion channels that are required to reproduce the expected slow wave morphology. Specifically, suitable ion channel candidates may be activated by voltage or Ca2+, remain active for the duration of the plateau phase, and carry an inward current at the plateau.
We present first the development of the ICC and Ano1 models, followed by verification that the Ano1 model exhibits the expected Ca2+ and voltage-dependent behavior of Ano1 channels. We then report the results of simulations testing the impact of altering ECl, showing that the ability to reproduce the characteristic slow wave morphology is highly dependent on ECl. Finally, we report the results of varying the ion currents in the model and show that the properties of Ca2+ transients and slow waves are particularly sensitive to the properties of Ca2+ currents included in the model.
METHODS
Overview of Baseline Cell Model
The baseline cell model presented in this study represents the pacemaker activity of ICC-MY from murine small intestine. Our model is predicated on the fundamental hypothesis that Ano1 channels activated by SOCE initiate slow waves in ICC-MY. A baseline model of this pacemaker hypothesis was developed and is adapted to investigate the effects of varying the ion currents and ECl in the model. Several key assumptions were made in the development of the baseline model, and the experimental evidence supporting each assumption is outlined below, followed by a summary of the pacemaker hypothesis.
The first assumption is that cyclical oscillations of Ca2+ in the ER and cytosol are an essential component of the ICC pacemaker mechanism. The importance of intracellular Ca2+ dynamics in ICC pacemaker activity is well established. Pacemaker activity is inhibited when Ca2+ uptake via the sarco-endoplasmic reticulum ATPase (SERCA) is blocked (40, 66). IP3Rs and ongoing IP3 generation are essential for pacemaker activity in ICC (38, 40, 59). Mitochondrial Ca2+ handling has also been proposed to play a role in slow wave generation (66), but more recent evidence from ICC in situ indicates that mitochondria may not be essential for Ca2+ cycling (38), so they were not included in our model.
The second assumption is that SOCE is a key part of ICC pacemaker activity. The occurrence of SOCE following Ca2+ store depletion was demonstrated in ICC by inhibiting SERCA pumps with thapsigargin (64). Furthermore, inhibition of Ca2+ oscillations by Ca2+-free external solution and the SOC channel inhibitors SK&F96365 and 2-APB also demonstrated the importance of SOCE (36, 64).
The third assumption is that Ano1 Ca2+-activated Cl− currents are crucial for the initiation of slow waves (23).
The fourth assumption is that Ano1 channels in ICC are colocalized with SOC channels, such that Ca2+ release from the ER causes SOCE, resulting in Ca2+-dependent activation of nearby Ano1 channels. Ano1 gating occurs in a complex Ca2+ and voltage-dependent manner. The literature is not consistent, but in general the EC50 for Ca2+ decreases from 5.9 ± 25 μM at +100 mV to 0.4 ± 01 μM at +100 mV (70). Global Ca2+ transients in ICC are likely to be similar in magnitude to those in other cell types, which typically peak around 1 μM (54), but at this level of Ca2+ the Ano1 channel variant we modeled is <10% activated at resting membrane potential (see Fig. 2). Ano1 channels can be exposed to sufficiently high Ca2+ concentrations by being in close proximity to a Ca2+ source. For example, Ca2+-activated Cl− channels are activated by SOC channels in vascular SMC (1) and Xenopus oocytes (31, 32), and Ano1 channels were recently shown to be coupled to IP3Rs in nociceptive sensory neurons (24). We assume that Ano1 channels are colocalized with SOC channels in ICC because of the evidence detailed above about the importance of SOCE.
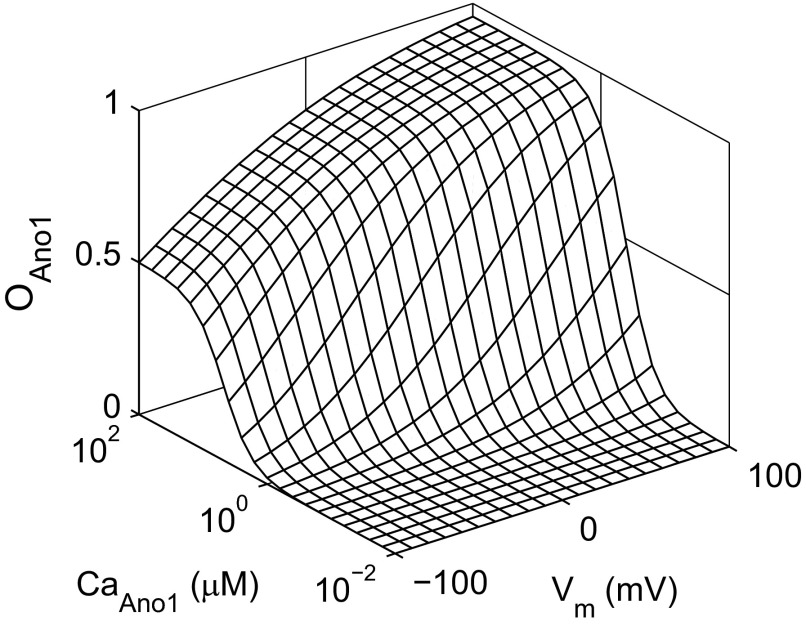
Fig. 2.
Steady-state open probability of the Ano1 (OAno1) model as a function of membrane potential (Vm) and the intracellular Ca2+ concentration ([Ca2+]i) seen by the Ano1 channel (CaAno1). Maximal open probability is achieved with simultaneously high Ca2+ concentration and positive membrane potential.
The final assumption is that T-type Ca2+ channels contribute to the upstroke phase of slow waves in ICC. A number of voltage-dependent ion channels have been identified in ICC-MY, and the role of these ion channels remains a matter of ongoing discussion (2, 33), but experimental evidence shows that T-type Ca2+ currents are important for the upstroke phase (19, 29). In addition, Ca2+ influx through T-type Ca2+ channels can modulate the intrinsic Ca2+ cycle by activating quiescent IP3Rs, enabling voltage-dependent coordination and propagation of slow waves (52).
In summary, the proposed pacemaker cycle we model begins when IP3-mediated Ca2+ release from the ER leads to depletion of the ER Ca2+ stores, activating SOCE via SOC channels. Ano1 channels colocalized with SOC channels are activated by the local rise in Ca2+ in microdomains surrounding the open SOC channels, causing depolarization of the ICC. The depolarization initiates a slow wave by activating voltage-dependent ion channels. The morphology of the slow wave, including the plateau phase and repolarization, is determined by the balance of voltage- and Ca2+-dependent ion currents. The pacemaker cycle concludes when Ca2+ influx via SOC channels and uptake via SERCA pumps is sufficient to refill the ER stores, resulting in deactivation of the SOC channels and Ano1 channels.
This pacemaker hypothesis shares similarities with previous pacemaker hypotheses (33, 52), notably the importance of ER Ca2+ handling, Ca2+ microdomains, and the role of T-type Ca2+ channels.
The key components of this pacemaker hypothesis are incorporated in the baseline cell model, as illustrated in the schematic diagram of an ICC in Fig. 1. Each component is described in more detail below. The model supports the pacemaker hypothesis if it can quantitatively and qualitatively reproduce experimentally observed results. If the model cannot adequately simulate slow waves, then the pacemaker hypothesis needs to be revised accordingly.
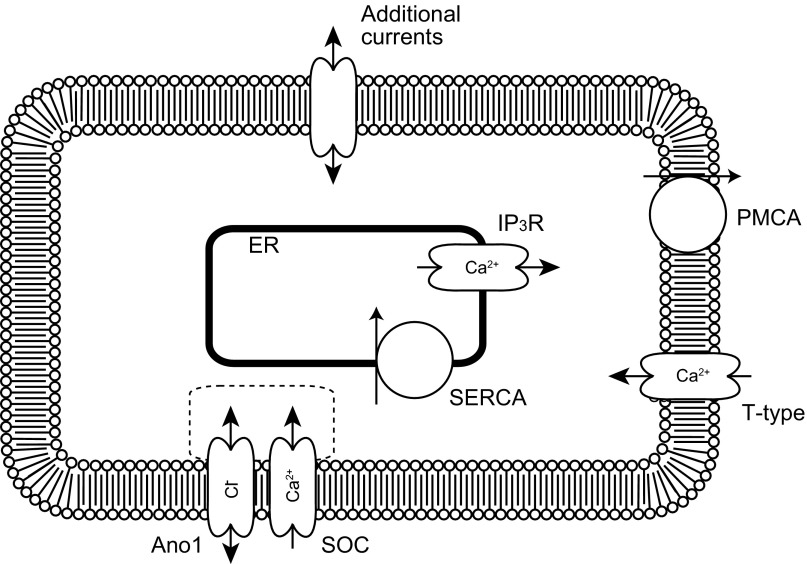
Fig. 1.
Schematic diagram of the cell, including ion channels and transporters in the plasma membrane and endoplasmic reticulum (ER). The cell is divided into two compartments: the bulk cytosol and the ER. Ca2+ changes in the bulk cytosol are determined by the Ca2+ flux through the inositol 1,4,5-trisphosphate (IP3) receptors (IP3R) and sarco-endoplasmic reticulum ATPase (SERCA) pumps in the ER, and the T-type and store-operated Ca2+ (SOC) channels and plasma membrane Ca2+ ATPase (PMCA) in the cell membrane. The Ca2+ microdomain around the colocalized Ano1 and SOC channels is indicated by a dotted line. The microdomain is not modeled as a separate compartment but rather is directly dependent on the Ca2+ flux through the SOC channel. The membrane potential across the plasma membrane is governed by ion currents through the Ano1, SOC, and T-type Ca2+ channels along with additional inward and outward currents passed by other channels as specified later.
The baseline ICC model is a compartmental model in which the membrane potential within the cell and the ion concentrations within each subcellular compartment are homogeneous. The model was implemented using a Hodgkin-Huxley type formulation, in which the cell membrane lipid bilayer is represented as a capacitance (Cm), and the ion channels in the membrane are represented as conductances. The change in the transmembrane potential (Vm) over time depends on the total ionic current:
| (1) |
where Iion is the sum of the individual ion currents through each class of ion channel in the cell. Cm was set to 25 pF, which is a representative value for a murine small intestinal ICC (21, 27).
Each class of ion channel is represented as a variable conductor, where the conductance depends on the channel open probability as a function of voltage or [Ca2+]i. The whole cell current through each class of ion channel is proportional to the difference between Vm and the reversal potential of the channel. For an ion channel selective for a single ion, the reversal potential is equal to the Nernst or equilibrium potential of that ion. The equations for the open probability of each channel are given in the appendix. The model equations were solved in MATLAB (R2012a).
Calcium Model
Two intracellular Ca2+ compartments were included in the model: bulk cytosol Ca2+ ([Ca2+]i) and an endoplasmic reticulum Ca2+ store ([Ca2+]ER), as shown in Fig. 1. To model Ca2+ flux into and out of the ER, a simple model of intracellular Ca2+ dynamics was adapted from the oscillatory Ca2+ model developed by Wang et al. (65) for airway SMC. The specific components used were a sigmoidal model of the SERCA pump and an IP3R model based on the De Young and Keizer model (12). The ryanodine receptor was excluded because it appears to be less important for ICC pacemaker activity (40). The equations describing the IP3R and SERCA Ca2+ flux were unchanged from the model presented by Wang et al. (65) with parameter values modified to adjust the frequency of Ca2+ oscillations to an appropriate value for murine small intestine (see appendix for details).
SOC Channel Model
The type of SOC channel that might be present in ICC is unknown. Activation of SOC channels occurs when STIM1 senses depletion of the [Ca2+]ER. The [Ca2+]ER at which STIM1 activates is around 200–250 μM (6, 57). Measured Hill coefficients for activation of the STIM1-Orai1 complex by ER depletion range from 4 to 8 (6, 39). Therefore, a Hill function with a coefficient of 8 and Kd of 200 μM was used to model SOC channel open probability as a function of [Ca2+]ER.
When STIM1 is activated it can oligomerize with either Orai or TRPC proteins to form CRAC channels or nonselective cation channels, respectively (45, 46). CRAC channels are highly selective for Ca2+, and native CRAC currents are very small (56). In this model the Ca2+ influx via the SOC channel was important for activating Ano1, but the SOC channel itself was expected to make a negligible contribution to depolarizing the membrane potential, as evidenced by the lack of slow waves in smooth muscle tissue from Ano1 knockout mice (23). Therefore, the SOC channel was implemented as a highly Ca2+-selective CRAC channel with a small conductance of 0.1 nS. The mechanism by which Ca2+ flux through the SOC channel acts on Ano1 is described below.
Ano1 Ca2+-Activated Cl− Channel Model
The voltage- and Ca2+-dependent behavior of mouse Ano1 channels heterologously expressed in HEK 293 cells was recently characterized. Equations were reported for both the steady-state Ca2+-dependent activation as a function of voltage and voltage-dependent activation as a function of [Ca2+]i. The time constants of activation and deactivation were also quantified (70).
Using this data we developed a novel Hodgkin-Huxley type model of coupled voltage- and Ca2+-dependent Ano1 activation. The steady-state activation for an ion channel is given by G/Gmax (or I/Imax), whereas the previously published equations scaled G to the maximal conductance recorded at a set value of [Ca2+]i or Vm; Gmax,Ca or Gmax,V, respectively (70). Thus, we model the steady-state open probability (OAno1) by scaling G/Gmax,V by the G/Gmax,Ca at a very high [Ca2+]i, giving OAno1 as the product of a Boltzmann function for voltage-dependent activation and a Hill equation for Ca2+ binding:
| (2) |
where Vh is the half-activation potential at high [Ca2+], kv is the slope factor associated with the gating charge of the channel, EC50 is a voltage-dependent expression for the half-concentration of Ca2+-dependent activation, and CaAno1 is the [Ca2+]i in the vicinity of the Ano1 channel. The steady-state open probability of the Ano1 channel model is shown in Fig. 2.
Calcium Microdomain Calculation
Ano1 channels are likely to be located within a Ca2+ microdomain near a Ca2+ channel. In previous models of ICC, microdomains were represented using a small compartment with separate differential equations for the microdomain Ca2+ concentration and the bulk cytosol [Ca2+]i (10, 16) or using a spatial representation of Ca2+ concentration throughout the microdomain and bulk cytosol (44).
The compartmental method does not have a heavy computational load, although computational efficiency decreases as the number of microdomains represented increases (10, 16). However, the Ca2+ concentration calculated within the microdomain compartment is unlikely to be realistic. On the other hand, the spatial method provides greater accuracy in estimating Ca2+ concentration but is computationally expensive (44).
In the present study the [Ca2+]i seen by the Ano1 channel due to SOC channel Ca2+ influx is represented using the analytical formulation for the steady-state solution to the rapid buffering approximation of [Ca2+]i near the entrance of a point source (55). This enables colocalized channels to be modeled without the additional computational expense or uncertainties introduced by spatial or compartmental methods.
The [Ca2+] seen by Ano1 (CaAno1) was calculated using the solution for the [Ca2+] near a channel mouth with one mobile buffer in the cytosol (55). The solution depends on the bulk Ca2+ concentration far away from the point source, i.e., [Ca2+]i (Cai); the [Ca2+] at the mouth of the SOC channel (CaSOC); and the distance from the SOC channel to the Ano1 channel, which was set to 50 nm to provide sufficiently high CaAno1. To ensure CaAno1 represented the [Ca2+] seen by an individual Ano1 channel, CaSOC was calculated by dividing the total flux of Ca2+ into the cell through SOC channels by an estimate of the number of SOC channels or channel clusters in the cell, which was estimated to be 50 channel clusters, based on the estimation that there are approximately 50 separate Ca2+ microdomains in an ICC (16).
Voltage-Gated Calcium Channel Model
The final component implemented in the baseline model was a voltage-dependent T-type Ca2+ channel. This channel was modeled using the voltage-dependent dihydropyridine-resistant (VDDR) Ca2+ channel model from the Corrias and Buist ICC model (10), except where otherwise stated.
Total Calcium Fluxes in the Cytosol
Cytosolic Ca2+ in the model was determined by the Ca2+ fluxes across the ER and plasma membranes, and cytosolic Ca2+ buffers were assumed to be fast and linear. Thus the total change in [Ca2+]i for each of the model variations presented below, except where otherwise stated, was given by
| (3) |
where bc is the buffering constant in the cytosol, JIPR is the flux out of the ER through the IP3R, JSERCA is the uptake into the ER, JSOC is the total flux through the SOC channels, JCaT is the total flux through the voltage-gated T-type Ca2+ channels, and JPMCA is the rate of extrusion of Ca2+ out of the cell via the plasma membrane Ca2+ ATPase (PMCA) pump.
Model Variations
The baseline cell model was used to develop six model variations to investigate the currents active during the plateau phase and the effects of changing ECl. ECl in ICC-MY is reported to be around −40 to −50 mV (76). However, previous estimates of ECl were often higher than this (63) and depolarizing Ca2+-activated Cl− currents were suggested to produce the plateau phase (29). In contrast, Cl− loading during microelectrode recordings may raise [Cl−]i and ECl above endogenous levels, as discussed later (4). Therefore, we test two different levels of ECl: one in which ECl is close to the plateau potential; and one in which ECl is at the reported value of −50 mV (76).
Ano1 Cl− currents can initiate the slow wave and T-type Ca2+ channels contribute to the upstroke, but the identity of the ion channels active during the plateau phase remains undetermined, so four hypothetical plateau currents are considered. These currents encompass a range of ion channel properties that could theoretically maintain a depolarizing current at the peak potential of a slow wave, including currents that have thus far not been identified in ICC. The four scenarios considered are as follows: 1) plateau current is carried by voltage-dependent Na+ channels; 2) plateau current is carried by voltage-dependent nonselective channels; 3) plateau current is carried by Ca2+-dependent nonselective channels that are activated by a voltage-dependent Ca2+ influx; or 4) plateau current is carried by voltage-dependent Ca2+ channels.
No long-lasting Na+ channels have been identified in ICC to date, but this type of channel is theoretically capable of generating the plateau phase. A candidate Ca2+ channel that may stay open long enough to generate the plateau current is the L-type Ca2+ channel (27). The voltage- and Ca2+-dependent nonselective channels may be either nonselective cation channels of maxi channels, both of which pass currents that reverse close to 0 mV. Nonselective cation channels in ICC are likely to be Ca2+ dependent (60). Maxi channels observed in ICC in situ are permeable to both Cl− and Na+ ions and display voltage-dependent activation and inactivation (49).
Originally, a Cl− current generated by the Ano1 channel was also considered as a fifth plateau current candidate. However, we found that a Cl− current could not maintain the plateau in our model unless the conductance was unrealistically large and ECl was unphysiologically positive, so this possibility was not considered plausible.
The six model variations have different hypotheses regarding the ion currents involved in generating slow waves, such that the “additional currents” mentioned in Fig. 1 differ in each variation. The model variations are grouped into two categories based on [Cl−]i and the resultant ECl.
High-Cl.
ECl is close to the peak of the slow wave at −20 mV. Ano1 current is responsible for initiating the slow wave, but an additional plateau current is included to maintain depolarization through the peak and plateau. There were four variations to the High-Cl hypothesis:
1) A voltage-dependent Na+ current (INaV) acts to maintain depolarization through the peak and plateau.
2) A voltage-dependent nonselective cation or maxi current (INSV) with a reversal potential of 0 mV maintains depolarization through the peak and plateau.
3) The voltage-dependent T-type Ca2+ current, activated by the initial depolarization caused by Ano1, contributes to the upstroke and produces a larger increase in [Ca2+]i than that due to Ca2+ influx through SOC channels alone. The Ca2+ transient activates a Ca2+-dependent nonselective cation or maxi current (INSCa) with a reversal potential of 0 mV to maintain depolarization through the peak and plateau.
4) A long-lasting voltage-dependent Ca2+ current (ICaV) acts to maintain depolarization through the peak and plateau.
Low-Cl.
ECl is −50 mV, as measured in ICC in situ (76). Depolarization to the peak potential and during the plateau phase is due to either a voltage-gated current or a Ca2+-activated current. Based on the High-Cl simulation results, there was little value in testing ICaV at the lower ECl. The similarities between the High-Cl results with INaV and INSV and the effect of ECl on the simulation results, as discussed later, meant that a single voltage-gated current could be tested in the Low-Cl hypotheses without affecting the conclusions of the study. Therefore, the candidate plateau currents tested were as follows:
1) A voltage-activated Na+ current, as in High-Cl(NaV), or
2) A Ca2+-activated nonselective current that is activated by transient voltage-gated Ca2+ current, as in High-Cl(NSCa).
Repolarization at the end of the plateau phase may be initiated by a combination of a delayed activation or increased amplitude of a K+ current or Ano1 current, and a voltage-, Ca2+-, or time-dependent inactivation of the inward plateau current.
The full complement of ion currents included in each model variation is detailed in results. The equations and parameters for each of these ion channels are given in the appendix.
RESULTS
Ano1 Model
The first step was to verify our novel Ano1 model against published data at various Ca2+ and voltage levels. The steady-state open probability of the Ano1 channel model in Fig. 2 shows that open probability is increased by both CaAno1 and membrane potential, resulting in strong outward rectification of steady-state Ano1 current at lower Ca2+ concentrations, as expected. The kinetics of the Ano1 model (Fig. 3) were compared with published voltage-clamp and fast Ca2+ perfusion experiments (see Figs. 1 and 3 in Ref. 70). For these simulations Ano1 currents were calculated by setting a reversal potential of 0 mV and a maximal conductance of 0.5 nS.
Fig. 3.
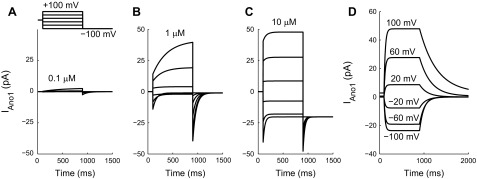
A–C: simulated voltage-clamp experiments to test the response of the Ano1 model to the voltage protocol used by Xiao et al. (see Fig. 1, A–E, in Ref. 70). From a holding potential of 0 mV, the Ano1 model was stepped for 800 ms to a Vm between −100 and +100 mV in 40-mV increments, followed by a hyperpolarizing step to −100 mV, as shown in the inset. Depolarizing steps activate Ano1 currents more strongly and rapidly at higher Ca2+ concentrations, as expected. However, above 1 μM Ca2+ the decay of the simulated tail currents following a hyperpolarizing step occurs more rapidly than expected based on experimental observations. D: simulated rapid Ca2+ perfusion experiments, to compare the response of the Ano1 model to published rapid perfusion experiments (see Fig. 3, A and B, in Ref. 70). Vm in the Ano1 model was set at a fixed holding potential ranging from −100 to +100 mV and CaAno1 was stepped from 0.1 to 20 μM for 800 ms. Ano1 activation upon application of 20 μM Ca2+ occurs quickly and the rate of activation is only weakly voltage-dependent, while deactivation upon removal of 20 μM Ca2+ is slow and the deactivation rate is strongly voltage dependent.
In the voltage-clamp simulations the voltage protocol stepped the Ano1 model from a holding potential of 0 mV to a Vm between −100 and +100 mV in 40-mV increments for 800 ms, followed by a hyperpolarizing step to −100 mV (Fig. 3A, inset). Voltage clamp simulations were carried out at three different values of fixed [Ca2+]: 0.1 μM (Fig. 3A), 1 μM (Fig. 3B), and 10 μM (Fig. 3C). The simulated voltage-dependent activation qualitatively matches the experimentally observed behavior, with higher Ca2+ concentrations producing larger and more rapid activation. However, at higher Ca2+ concentrations the decay of the tail currents following a hyperpolarizing step occurs much more rapidly in the simulations than in published data (see Fig. 1, A–E, in Ref. 70), indicating that the model does not fully capture the time dependence of voltage-dependent deactivation (Fig. 3C).
Rapid perfusion experiments were performed in which [Ca2+] was changed within several milliseconds (70). These experiments were reproduced using the Ano1 model by setting Vm at a fixed holding potential (ranging from −100 to +100 mV in 40-mV increments) and applying a step change in CaAno1 from 0.1 μM to 20 μM for 800 ms. The Ano1 model produces fast Ca2+-dependent activation at all voltages and slower deactivation upon Ca2+ removal with a strongly voltage-dependent deactivation rate (Fig. 3D), in qualitative agreement with published data (see Fig. 3, A and B, in Ref. 70).
ICC Model: Impact of Altering ECl
Following validation of the Ano1 channel model we tested the impact of varying ECl and the plateau current on the ICC model. Two values of ECl were tested: −20 and −50 mV, referred to as High-Cl and Low-Cl model variations, respectively. The results of each model variation are presented below.
Simulations were carried out using both the normal (“wild-type”) cell model and an “Ano1 knockout” scenario in which the maximal whole cell conductance of Ano1 (gAno1) is set to 0 nS to verify that Ano1 channels are essential for initiating the slow wave in each model variation.
The resting membrane potential, amplitude, frequency, and half-width (duration at half-maximal amplitude) were quantified, as summarized in Table 1. All the simulated slow waves have similar resting membrane potentials and amplitudes, and these values are within the expected range for ICC. The greatest variations in the quantified model results are in the frequency and half-width values, indicating that these temporal characteristics of the slow wave are more dependent than the membrane potential on the changes to ECl and the ion currents in the model.
Table 1.
Quantitative characteristics of slow waves simulated by the six model variations
| RMP, mV |
Amplitude, mV | Half-Width, s | Frequency, min−1 |
|||
|---|---|---|---|---|---|---|
| Variation | Wild Type | Knockout | Wild Type | Wild Type | Wild Type | Knockout |
| High-Cl | ||||||
| NaV | −66.4 | −67.2 | 44.4 | 1.2 | 18.8 | 17.7 |
| NSV | −64.6 | −65.1 | 44.4 | 1.5 | 19.2 | 17.8 |
| NSCa | −65.3 | −65.1 | 41.9 | 1.1 | 15.7 | 19.1 |
| CaV | −65.1 | −63.2 | 48.8 | 0.6 | 9.6 | — |
| Low-Cl | ||||||
| NaV | −66.7 | −66.0 | 42.9 | 0.8 | 18.3 | 17.8 |
| NSCa | −67.2 | −65.0 | 47.6 | 0.8 | 14.9 | 21.3 |
RMP is the resting membrane potential; amplitude is the difference between resting membrane potential and peak slow wave potential; half-width is the duration of slow wave as measured at half of the amplitude; wild-type denotes the simulations using normal model variations; knockout denotes anoctamin 1 (Ano1) knockout simulations; V is voltage; NS is nonselective.
High-Cl simulations.
The four High-Cl model variations (Fig. 4) set ECl at −20 mV, close to the peak potential of a slow wave. In addition to the three ion channels described in the baseline model, SOC channels (ISOC), Ano1 channels (IAno1), and T-type Ca2+ channels (ICaT), each High-Cl model variation incorporates a voltage-activated inward current to enable the plateau phase to be generated, as detailed below. Two “background” or “leak” channels are also included, a background K+ current (IKb) and a background Na+ current (INab). IKb acts to maintain the resting membrane potential and to repolarize the cell following a slow wave, while INab also contributes to maintenance of the resting membrane potential.
Fig. 4.
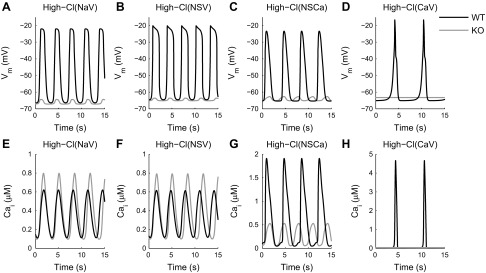
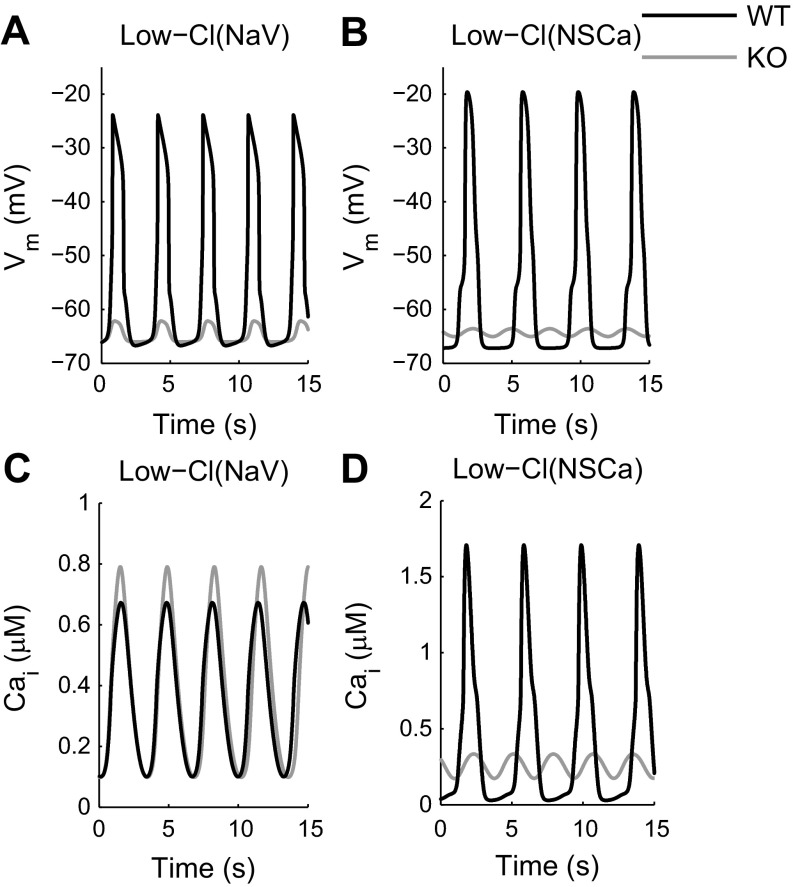
Membrane potential and Ca2+ oscillations produced from High-Cl model simulations with Cl− equilibrium potential (ECl) set to −20 mV. The plateau current is generated by a voltage-activated Na+ channel (A and E), a voltage-activated nonselective channel (B and F), a Ca2+-activated nonselective channel (C and G), or a voltage-activated Ca2+ channel (D and H). A–D: membrane potentials simulated using the wild-type (WT) and Ano1 knockout (KO) scenarios (black and gray lines, respectively). E–H: oscillations in [Ca2+]i simulated using the WT and Ano1 KO scenarios (black and gray lines, respectively).
Each of the High-Cl model variations were tested in both the wild-type scenario, with normal Ano1 current, and in the Ano1 knockout scenario, in which Ano1 conductance is set to zero (Fig. 4, A–D, black and gray lines, respectively). The background Na+ current plays an important role in inhibiting membrane potential oscillations in the Ano1 knockout simulations. When gAno1 is set to zero in test simulations without the background Na+ current, the depolarizations generated by the SOC current are tens of millivolts in amplitude (not shown), which runs counter to the key assumption that loss of Ano1 blocks slow waves.
As well as the Na+ background channel, the efficacy of two other channels at inhibiting membrane potential oscillations in Ano1 knockout simulations was trialed. A voltage-activated K+ channel with strong voltage dependence at resting membrane potential and a Ca2+- activated K+ channel colocalized with the SOC channel both act to reduce membrane potential oscillations in the Ano1 knockout scenario, but these channels are less effective than the Na+ leak channel (not shown).
Slow wave-like potentials are successfully produced by the High-Cl(NaV) model variation, which incorporates a voltage-activated Na+ channel (Fig. 4A). Qualitatively similar results are obtained using a voltage-activated nonselective channel [High-Cl(NSV), see Fig. 4B] or a Ca2+-activated nonselective channel in conjunction with a transient voltage-activated Ca2+ channel [High-Cl(NSCa), see Fig. 4C] but not with a longer lasting voltage-activated Ca2+ channel [High-Cl(CaV), see Fig. 4D], as described below.
HIGH-CL(NAV): SODIUM CHANNEL.
For the High-Cl(NaV) variation, a hypothetical voltage-activated, noninactivating Na+ current (INaV) is added to the model, so the total ionic current across the membrane is
| (4) |
The model produces slow wave-like depolarizations that peak 2.0 mV negative to ECl (Fig. 4A; Table 1). Simulating Ano1 knockout results in a loss of slow waves, with residual oscillations <3 mV in amplitude (Fig. 4A, gray line) and little change in the resting membrane potential or frequency (Table 1).
Cytosolic Ca2+ oscillations occur at the same frequency as slow waves and persist in Ano1 knockout simulations (Fig. 4E). In the wild-type simulation, the bulk cytosolic Ca2+ concentration (Cai) peaks at 0.6 μM, whereas the [Ca2+] in the microdomain near the SOC channel mouth is ∼14 times greater than this (not shown), enabling a much higher level of Ano1 activation than would occur if Ano1 channels were not localized near SOC channels.
HIGH-CL(NSV): VOLTAGE-ACTIVATED NONSELECTIVE CHANNEL.
Currents with reversal potentials close to 0 mV have been observed in ICC, either carried by nonselective cation channels (21, 30) or maxi channels permeable to Cl− and Na+ (49). Maxi channels in particular display activation and inactivation in response to voltage changes (49). Thus the High-Cl(NSV) model variation incorporates a voltage-dependent nonselective current (INSV) that reverses at 0 mV and displays voltage-dependent activation and partial inactivation. The total ionic current is
| (5) |
The quantitative and qualitative characteristics of the membrane depolarizations generated by this model variation are comparable to those of slow waves generated by murine small intestine ICC. Membrane potential oscillations are reduced to 1.5 mV in amplitude in Ano1 knockout simulations, with little change in resting membrane potential or frequency (Fig. 4B, gray line; Table 1). Ca2+ oscillations occur at the same frequency as the slow waves, and are maintained in the Ano1 knockout simulation (Fig. 4F).
HIGH-CL(NSCA): CA2+-ACTIVATED NONSELECTIVE CHANNEL.
Ca2+ dependence has been identified in nonselective cation channels (30, 60). The Ca2+ dependence of the maxi channel identified in situ is unknown, although the maxi Cl− channel observed in cultured ICC is Ca2+ dependent (69). The High-Cl(NSCa) model variation includes a Ca2+-activated nonselective channel 6 (INSCa) and the total ionic current is
| (6) |
The parameters for ICaT in this model variation are modified to generate a larger voltage-dependent Ca2+ influx, and the Kd for the INSCa current is set higher than the peak voltage-independent Ca2+ amplitude. The resultant Ca2+-activated nonselective channel is activated by voltage-dependent Ca2+ influx in the wild-type scenario, generating slow waves that peak at −23.4 mV (Fig. 4C, black line; Table 1). However, the channel remains relatively inactive during Ano1 knockout simulations in which the voltage-dependent Ca2+ influx is negligible, so the amplitude of the residual membrane potential oscillations during Ano1 knockout simulations is reduced to 2.5 mV (Fig. 4C, gray line).
HIGH-CL(CAV): CALCIUM CHANNEL.
The reversal potentials of both Na+ and Ca2+-selective currents are much more positive than the peak potential of a slow wave, suggesting that a long-lasting voltage-activated Ca2+ current could be just as effective at generating the slow wave plateau phase as the voltage-activated Na+ current used in High-Cl(NaV). The High-Cl(CaV) model variation incorporates a long-lasting voltage-gated Ca2+ channel (ICaV), so the total ionic current across the membrane is
| (7) |
Correspondingly, the change in cytosolic [Ca2+]i is
| (8) |
The peak potential of depolarizations generated by this model variation is within the expected range for an ICC-MY, and oscillations are abolished by Ano1 knockout (Fig. 4D). However, the model exhibits a much faster initial repolarization than that of a normal slow wave because of the impact of the long-lasting Ca2+ influx on the intrinsic Ca2+ dynamics (Fig. 4H). Consequently, the results of the High-Cl(CaV) model variation differ from those of the other High-Cl models and will be considered in more detail in ICC Model: Impact of Varying Ca2+ Currents.
In summary, the High-Cl model variations generate membrane potentials with amplitudes comparable to slow waves from the mouse small intestine, and this activity is inhibited when simulating Ano1 knockout (Fig. 4, A–D). Membrane potential oscillations occur at the same frequency as Ca2+ oscillations (Fig. 4, E–H). The Ano1 channel contributes negligible current at the slow wave peak in these model variations because the peak potential is close to ECl. The plateau phase is generated by a current with a more positive reversal potential, such as a nonselective or Na+ current.
Low-Cl simulations.
In the High-Cl model variation ECl is set at −20 mV, but this is higher than the ECl measured in ICC from the mouse small intestine (76). Furthermore, none of the model variations presented so far are able to depolarize the cell past ECl while retaining the characteristic plateau phase of the slow wave. The delayed repolarization in the High-Cl model variations is facilitated by deactivation of the Ano1 current at the end of the Ca2+ transient. The Low-Cl model variations set ECl at −50 mV, as measured in ICC-MY in situ (76). The slow wave depolarizes the ICC membrane potential past ECl, so a combination of time-, voltage-, and Ca2+-dependent currents is necessary to reproduce the plateau phase and initiate the repolarization phase.
When developing the Low-Cl model variations, many different combinations of inward and outward currents were tested in an effort to reproduce ICC slow wave activity. The model variations described below represent two of the most successful attempts. Both produce cyclical depolarizations with an amplitude and frequency comparable to those of slow waves recorded from murine small intestine ICC-MY and similar to the simulated slow waves in the High-Cl model variations. However, the morphology of the depolarizations produced by the Low-Cl model variations do not match the expected slow wave morphology (Fig. 5).
Fig. 5.
Membrane depolarizations and Ca2+ oscillations produced from model simulations with ECl set to −50 mV. The plateau current is carried by either a voltage-activated Na+ channel (A and C), or a Ca2+-activated nonselective channel (B and D). A and B: membrane potentials simulated using the WT and Ano1 KO scenarios (black and gray lines, respectively). C and D: oscillations in [Ca2+]i simulated using the WT and Ano1 KO scenarios (black and gray lines, respectively).
LOW-CL(NAV): SODIUM CHANNEL.
The Low-Cl(NaV) model variation uses a voltage-dependent Na+ channel (INaV) to generate depolarization during the plateau phase, similar to High-Cl(NaV). In addition, two voltage-gated K+ currents are introduced, a transient K+ current (IKt), and an ERG-like K+ current (IKERG) that activates upon repolarization (2). The total ion current is
| (9) |
This model produces slow wave-like depolarizations with a similar resting membrane potential, amplitude, and frequency to the previous model variations (Table 1). However, the “plateau” phase is steeper than expected for an ICC, and the slow wave duration at half amplitude is 27–47% shorter than the High-Cl(NaV), High-Cl(NSV), and High-Cl(NSCa) model variations. In addition, repolarization slows down when the cell repolarizes past −50 mV as Ano1 current becomes inward again (Fig. 5A).
In the Ano1 knockout simulations, the membrane potential oscillations are reduced to 3.9 mV in amplitude, with little change in the resting membrane potential and frequency, while Ca2+ oscillations are retained (Fig. 5, A and C; Table 1).
LOW-CL(NSCA): CA2+-ACTIVATED NONSELECTIVE CHANNEL.
The final model variation tested is a Low- Cl variation in which a Ca2+-dependent nonselective channel is used to maintain depolarization during the plateau in response to a larger voltage-dependent Ca2+ influx, similar to High-Cl(NSCa).
Thus, the Low-Cl(NSCa) model variation incorporates a Ca2+-activated nonselective current (INSCa), as well as a modified T-type Ca2+ current to enable larger Ca2+ influx to activate the nonselective current (ICaT), and a Na+/Ca2+ exchanger to balance the larger Ca2+ influx (INCX). The total ionic current is
| (10) |
The corresponding change in cytosolic [Ca2+]i is
| (11) |
The Low-Cl(NSCa) model variation generates depolarizations with a similar resting membrane potential, amplitude and frequency to the other model variations (Table 1). As with the Low-Cl(NaV) variation, the plateau phase is less pronounced than in the High-Cl models. The fast upstroke phase is also not captured well by the Low-Cl(NSCa) variation, and the slow wave duration at half-amplitude is 27–47% shorter than the High-Cl model durations (Fig. 5B; Table 1).
During Ano1 knockout simulations the remaining membrane potential oscillations are 1.5 mV in amplitude and occur 43% faster than the wild-type oscillations, corresponding to the change in frequency in the Ca2+ oscillations (Fig. 5, B and D; Table 1).
In summary, the amplitude and frequency of the wild-type depolarizations in the Low-Cl simulations are within the established range for murine small intestine slow waves, and Ano1 knockout simulations inhibit membrane depolarization. However, the ability of the models to reproduce the characteristic plateau phase of a slow wave is less clear. Both the Low-Cl(NaV) and Low- Cl(NSCa) models rapidly repolarize immediately after the peak because repolarizing currents are greater in magnitude than depolarizing currents at the peak potential, resulting in a shorter slow wave duration than the High-Cl model variations. The Low-Cl(NSCa) model also does not adequately reproduce the fast upstroke phase of a slow wave. This reflects the altered balance of inward and outward currents compared with the High-Cl models as the Ano1 current reverses at −50 mV.
ICC Model: Impact of Varying Ca2+ Currents
In addition to testing the effect of altering ECl, this study also tests whether a variety of different ion currents are plausible candidates for the plateau current that maintains the plateau phase of the slow wave. When varying the plateau current, the impact of altering the Ca2+ influx has a notable impact on the quantitative and qualitative characteristics of the simulated pacemaker activity in both wild-type and Ano1 knockout scenarios.
Three of the six model variations, High-Cl(NaV), High-Cl(NSV), and Low-Cl(NaV), have a relatively small voltage-dependent Ca2+ influx carried by the T-type Ca2+ channel. The Ca2+ oscillations produced by these variations all have similar amplitudes and frequencies. In the wild-type simulations, the magnitude of Ca2+ oscillations is smaller and the frequency is faster than in the Ano1 knockout simulations (Figs. 4, E and F, and 5C; Table 1).
The three other model variations, High-Cl(NSCa), High-Cl(CaV), and Low-Cl(NSCa), have a comparatively larger voltage-dependent Ca2+ influx carried by either a modified version of the T-type Ca2+ channel [High-Cl(NSCa) and Low-Cl(NSCa)] or a longer lasting Ca2+ current designated ICaV [High-Cl(CaV)]. In these variations, larger and slower Ca2+ oscillations are generated in the wild-type simulations than in the Ano1 knockout scenario; for example, the High-Cl(NSCa) wild-type Ca2+ oscillations peak at 1.9 μM compared with 0.53 μM in Ano1 knockout simulations. The exception is the High-Cl(CaV) model variation, which does not oscillate in the Ano1 knockout scenario (Figs. 4, G and H, and 5D; Table 1).
Furthermore, the wild-type Ca2+ oscillations produced by the three models with large Ca2+ influx are larger in amplitude and slower in frequency than those from the four smaller Ca2+ influx models. For example, in wild-type simulations with High-Cl(NSCa), [Ca2+]i peaks at 1.9 μM (Fig. 4G), whereas with High-Cl(NaV) and High-Cl(NSV) [Ca2+]i peaks at 0.6 μM (Fig. 4, E and F).
In the Low-Cl(NSCa) model variation, the Ca2+ oscillations in the wild-type simulations are similar in magnitude and frequency to those from the High-Cl(NSCa) variation, due to the similarities in the Ca2+-activated nonselective plateau current in these two models. Conversely, the Ca2+ oscillations in the Low-Cl(NSCa) Ano1 knockout simulations are smaller and faster than in any of the other model variations because of the additional Ca2+ extrusion mechanism, the plasma membrane NCX, included in this model (Fig. 5D).
The High-Cl(CaV) model variation has a significantly larger Ca2+ influx than the other variations, with wild-type [Ca2+]i peaking as high as 4.7 μM, compared with 1.9 μM in High-Cl(NSCa) or 0.6 μM in High-Cl(NaV) and High-Cl(NSV) (Fig. 4, E–H). As a result, the membrane potential and Ca2+ oscillations are significantly slower in the High-Cl(CaV) model variation, and in the Ano1 knockout simulation the lack of voltage-dependent Ca2+ entry results in complete loss of Ca2+ oscillations. Furthermore, while the resting membrane potential and amplitude of the depolarizations are within an appropriate range for slow waves recorded from ICC, the frequency and the morphology of the depolarizations are not. In particular, the characteristic plateau phase is not evident and instead a rapid repolarization follows immediately after the peak of the upstroke phase (Fig. 4, D and H; Table 1).
The main pattern that emerges from these results is that simulations with larger Ca2+ oscillations, corresponding to larger Ca2+ influx, tend to have slower frequencies; this holds true for both wild-type and Ano1 knockout simulations. Consequently, the model variations that have a larger voltage-dependent Ca2+ influx have more substantial changes in frequency in Ano1 knockout compared with wild-type simulations, associated with significant changes in the amplitude of Ca2+ oscillations in the absence of voltage-dependent Ca2+ influx (Figs. 4–5; Table 1).
DISCUSSION
To our knowledge, this article describes the first mathematical model of ICC to implement Ano1 as a pacemaker channel and to incorporate SOCE. We also present a novel mathematical model of the Ano1 Ca2+-activated Cl− channel based on electrophysiological measurements of Ano1 currents.
Ano1 Model
Multiple isoforms of Ano1 are produced by alternative splicing of four different exons, a, b, c, and d. The Ano1 model presented here is based on the properties of mouse Ano1(a,c) expressed in HEK 293 cells (70). However, the expression of alternative splice variants is known to alter the kinetics and Ca2+ sensitivity of the channel (47).
It is possible that the Ano1(a,c) variant used to develop the Ano1 model presented in this study is not the most prevalent splice variant in ICC. Verifying which Ano1 splice variants are commonly expressed in human and mouse ICC and characterizing the electrophysiological properties of these variants would allow more precise modeling of the role of Ano1 in ICC. Different Ano1 isoforms were shown to be expressed at different rates in human diabetic gastroparesis compared with nondiabetic controls, but there was also variable expression of Ano1 isoforms in the control subjects (43). The expression of human Ano1 variants is controlled by a recently identified promoter, which may impact on the properties of Ano1 currents (42), and different Ano1 variants can interact, further modifying their behavior (47). These factors may complicate attempts to determine which isoform or isoforms should be included in an ICC model.
ICC Model Development
One of the general limitations of modeling biophysical processes is that models can be sensitive to minor parameter changes, and care must be taken to ensure this does not inadvertently alter the model results. In the process of developing this ICC model it became apparent that the most important parameter was the Cl− reversal potential. Altering ECl has a significant impact on the ability of the model to generate slow waves in response to an initial depolarization by Ano1 channels. Furthermore, the channels responsible for maintaining depolarization during the plateau phase have not yet been identified. Consequently, instead of presenting a single model of ICC pacemaker activity, the dependence of the baseline model on ECl was explored in depth by developing six different model variations.
Voltage-gated Ca2+ influx is also shown to be a significant factor in the ability to generate slow waves. However, the qualitative results of the High-Cl model variations are relatively insensitive to model parameters other than ECl. As shown in Fig. 4, it is possible to simulate slow wave-like depolarizations when the plateau current is carried by a voltage-gated Na+ channel, a voltage-gated nonselective channel, or a Ca2+-activated nonselective channel. The exception is the High-Cl(CaV) model variation that includes a large voltage-gated Ca2+ current, which is unable to generate slow wave-like events because of the effect of the large Ca2+ influx on the intrinsic Ca2+ cycle.
Conversely, with the Low-Cl model variations the ability to reproduce slow wave-like events is highly dependent on the parameters used. Many of the parameter sets tested were unable to generate slow waves at all. However, those that were able to generate oscillatory depolarizations produced qualitatively and quantitatively similar results to those shown in Fig. 5, in which the plateau phase is not well reproduced.
Therefore, although a single pacemaker hypothesis underlies each of the model variations, this article does not present an exact replication of the pacemaker mechanism in ICC. Rather, we assess the viability of some of the components and processes that may contribute to ICC slow wave activity. We test the ability of four candidate ion channels to generate the plateau phase of the slow wave in response to an initial depolarization by Ano1 current and consider how ECl affects this mechanism.
Impact of Altering ECl
The High-Cl(NaV), High-Cl(NSV), and High-Cl(NSCa) model variations present mathematically plausible mechanisms for generating slow waves, thereby supporting the hypothesis that Ano1 acts as a pacemaker channel.
Conversely, the quantitative characteristics of the Low-Cl models are within the appropriate range for slow waves (Table 1) but the results do not qualitatively resemble ICC slow waves (Fig. 5, A and B). In particular, the prolonged plateau phase of slow waves is not adequately reproduced by the Low-Cl models, because the large outward current carried by Ano1 at the peak potential contributes to rapid repolarization.
The simulation results indicate that a typical slow wave morphology is more readily produced when ECl is near or above the peak slow wave potential, whereas the ability to generate slow waves is complicated by lowering ECl well below the peak potential. The short slow wave duration of the Low-Cl model variations restricts their use in other simulations, but the results can inform further experimental research.
Factors affecting Cl− equilibrium potential.
Previous estimates of the equilibrium or reversal potentials of Cl− currents in ICC varied widely, ranging from −10 (63) to −52 mV (48). Experimental (29) and computational (10) studies have suggested that Cl− channels contribute an inward current to maintain the plateau phase of the slow wave.
Subsequent measurements of [Cl−]i in ICC-MY from murine jejunum show that ECl is around −50 mV in situ or −41 mV in explant culture (76), suggesting that Cl− channels generate outward current during the plateau phase and could contribute to repolarization of the slow wave. However, our model results suggest that the reversal potential of Ano1 Cl− current is likely to be closer to the slow wave peak potential than to resting membrane potential.
It is possible that the [Cl−]i measured in situ does not accurately reflect the [Cl−]i seen by Ano1 channels during slow wave recordings. During microelectrode recordings, [Cl−]i may be raised by the high KCl concentration within the microelectrode tip. Glass microelectrodes are typically filled with an aqueous solution of 3 M KCl, and this highly concentrated filling solution causes a leak of K+ and Cl− ions into the impaled cell. The result is Cl− loading, in which significant changes in [Cl−]i and ECl can occur, thus altering the reversal potential of Cl− currents (28). For example, Cl− leak rates of 4.4 fmol/s and elevations in [Cl−]i up to 72 μM/min were observed in nonexcitable cells when using a 1 M KCl electrode filling solution (4). In a cell ∼1 pl in volume, the estimated volume of a murine ICC (10, 73), a leak rate on the order of 1 fmol/s will cause up to a 1 mM/s rise in [Cl−]i, which corresponds to a 4–8% increase per second in ICC-MY where [Cl−]i is reported to be 12.8 to 26.1 mM (76). Even accounting for mechanisms to balance [Cl−]i, such as diffusion out of the cell or the action of Cl− transporters, a 1 mM/s Cl− leak into the cell can have a dramatic effect on the reversal potential of Cl− currents.
An important implication of ECl being raised by a Cl− leak into the cell is that the slow wave morphology observed during microelectrode recordings may not accurately reflect the true morphology of slow waves in ICC. This could account for the difficulties we encountered in reproducing the typical slow wave morphology when ECl was set to −50 mV in our Low-Cl model variations. Physiological [Cl−]i can also be altered in whole cell patch-clamp recordings of slow waves in cultured and isolated ICC, due to dialysis of the intracellular solution with the pipette solution (34). Manipulation of [Cl−]i using whole cell patch clamp has been used in some studies to identify the Cl− selectivity of ion currents (75), but in other studies dialysis may alter the physiological [Cl−]i, making it difficult to determine the precise behavior of Cl− currents and slow waves in ICC.
An alternative explanation for a discrepancy between the [Cl−]i measured in situ (76) and the [Cl−]i that facilitates simulation of slow wave-like depolarizations in this study is that Ano1 channels are located within Cl− microdomains. Microdomains of Ca2+ are most common because of the highly buffered state of Ca2+ in the cytosol, but microdomains of other ions also occur, particularly close to ion transporters, such as Na+ microdomains observed near Na+/K+ ATPase and NCX (22). Cl− microdomains in ICC could form due to accumulation of Cl− by ion transport proteins in the cell membrane. ICC-MY are known to express several Cl− transporters, including a Na-K-Cl cotransporter (NKCC1) and three varieties of K-Cl cotransporters (9, 68). NKCC1 can maintain [Cl−]i above electrochemical equilibrium, and in murine small intestine ICC-MY this function is critical for the pacemaker mechanism (68).
Impact of Varying Ca2+ Currents
Other than ECl, the main determinant of the viability of the model variations presented in this study was the magnitude of Ca2+ influx associated with the plateau current.
The High-Cl(CaV) model variation, which includes a long-lasting voltage-activated Ca2+ current large enough to depolarize the cell above −20 mV, is not a valid model of slow wave activity. The large Ca2+ influx that accompanies depolarization alters the intrinsic Ca2+ cycle, resulting in low frequency spiking events instead of slow waves (Fig. 4D) and generating Ca2+ transients much larger than those observed in other cell types (54), but a smaller Ca2+ current would not cause sufficient depolarization for a slow wave. Thus Ca2+ currents are unlikely to contribute a major component of the plateau current.
However, it is plausible that a voltage-gated Ca2+ current is responsible for activating the plateau current, as in the High-Cl(NSCa) and Low-Cl(NSCa) model variations (Figs. 4C and 5B). The Ca2+ transients in these two model variations are somewhat larger than those observed in cardiac myocytes (54). If the plateau channel model was more sensitive to Ca2+, it could be activated by the smaller voltage-dependent Ca2+ influx used in the High-Cl(NaV) and High-Cl(NSV) model variations, but this would obviate the need for Ano1 to initiate slow waves. Alternatively, the Ca2+-activated nonselective channel could be colocalized with the T-type Ca2+ channel. This is consistent with previous pacemaker hypotheses in which the plateau phase occurs in response to voltage-dependent Ca2+ influx via T-type Ca2+ channels located in microdomains with IP3Rs and Ca2+-dependent cation channels (33, 52). Modeling microdomains containing T-type Ca2+ channels and the plateau channel were outside the scope of the present study.
Mathematically plausible models of pacemaker activity in which voltage-dependent Ca2+ influx does not play a crucial role are also presented in our study. In the High-Cl(NaV) model variation, the plateau current is a voltage-dependent Na+ current, and in the High-Cl(NSV) model variation, the plateau current is a voltage-dependent nonselective current (Fig. 4, A and B). T-type Ca2+ channels are present but are not essential for producing the plateau phase, or for the Ca2+ cycle, as evidenced by the continuation of Ca2+ oscillations in the Ano1 knockout simulations. Nevertheless, Ca2+ influx via SOC channels remains an intrinsic component of the pacemaker mechanism in these model variations.
Although T-type Ca2+ channels may not be crucial for generating slow waves in isolated ICC, voltage-dependent Ca2+ currents appear to play an important role in the propagation of slow waves through ICC networks (52). We intend to use this ICC model to simulate the behavior of ICC networks in future studies.
Effects of Ca2+ influx on Ano1 knockout simulations.
All the model variations except for High-Cl(CaV) demonstrate continuation of Ca2+ oscillations in the Ano1 knockout simulations, suggesting that Ca2+ oscillations occur independently of slow waves. These oscillations result from cyclical release and uptake of ER Ca2+ combined with SOCE. The frequency and magnitude of the Ca2+ oscillations in Ano1 knockout simulations also depend on the properties of the voltage-gated Ca2+ channel and the plasma membrane Ca2+ extrusion mechanism included in each model variation.
In the High-Cl(NaV), High-Cl(NSV), and Low- Cl(NaV) model variations, the amplitude of Ca2+ oscillations in the wild-type simulation is smaller than in the Ano1 knockout simulation (Figs. 4, E and F, and 5C). This result is unexpected, because the Ca2+ cycle in the wild-type simulations is augmented by a voltage-dependent Ca2+ influx that is inactive in the Ano1 knockout simulations. However, the increased amplitude of Ca2+ oscillations in the Ano1 knockout scenario is due to an increased driving force for SOCE at the more negative membrane potentials.
Conversely, in the High-Cl(NSCa) and Low-Cl(NSCa) model variations, the amplitude of Ca2+ oscillations in the wild-type simulations is much larger than in the Ano1 knockout simulations because of the larger voltage-dependent Ca2+ influx in the wild-type simulations (Figs. 4G and 5D). These model variations also demonstrate increased frequencies in Ano1 knockout simulations resulting from the decreased amplitude of Ca2+ oscillations, likely due to the greater capacity of the plasma membrane Ca2+ pumps (see Table A1 in the appendix).
The 43% increase in frequency in the Low-Cl(NSCa) Ano1 knockout simulations appears to contradict experimental evidence showing that Ca2+-dependent currents recorded from ICC under voltage clamp oscillate at similar frequencies to slow waves (61, 63). However, the impact of Ca2+ influx on the simulated Ca2+ transient depends on the Ca2+ model used. The Low-Cl(NSCa) model variation includes simple phenomenological models of two Ca2+ extrusion mechanisms: a high-affinity plasma membrane Ca2+ ATPase (PMCA) and a low-affinity Na+/Ca2+ exchanger (NCX) (37). Introducing a more complex model of an adaptive Ca2+ extrusion mechanism may enable the slow wave model to adjust to the changes in Ca2+ influx observed in the wild-type and Ano1 knockout simulations to maintain similar frequencies of Ca2+ oscillations.
Impact of Ano1 Knockout on Slow Waves
One of the key assumptions of the baseline model is that slow waves should be absent in an Ano1 knockout scenario. In recordings from Ano1 knockout mice the membrane potential of SMC is quiescent (23). However, to our knowledge, there have been no membrane potential recordings from ICC in Ano1 knockout mice, so we cannot be certain that the absence of slow waves in SMC reflects a complete loss of slow waves in ICC.
In the Ano1 knockout simulations presented here, slow wave activity is inhibited but membrane potential oscillations are not completely abolished, except in the High- Cl(CaV) model in which both membrane potential and Ca2+ oscillations ceased. The residual membrane potential oscillations in the Ano1 knockout scenarios are generated primarily by the cyclical activation and deactivation of the SOC current in response to changes in ER Ca2+ (Figs. 4 and 5). Therefore, our results predict that Ano1 knockout mice retain small Ca2+-driven depolarizations that are not transmitted to the SMC.
Leak currents are required to minimize the depolarizing effect of SOC current during Ano1 knockout simulations. The Na+ leak current may be carried by a Na+ leak channel (NALCN) recently identified in murine small intestine ICC (25). The K+ leak current is likely to be carried by KCNK3 (also called TASK-1), which encodes a background K+ channel that is abundantly expressed in ICC-MY (9).
Role of SOCE
Another of the key assumptions made in the model development is that slow waves are initiated when Ca2+ influx via SOC channels activates Ano1 channels. Store depletion and refill cycles in nonexcitable cells typically occur on slow time scales, on the order of tens of seconds, due to the time it takes for STIM1 to translocate to the plasma membrane (13), whereas pacemaker activity in mouse small intestine ICC can have a period <2 s (61). However, rapid SOCE has been observed in skeletal muscle cells, in which a splice variant of STIM1 proteins is permanently localized to the plasma membrane, allowing SOC channels to activate within milliseconds of depletion occurring (11, 13). Therefore, SOCE can function at the frequencies of Ca2+ oscillations observed in ICC.
The inhibitory effects of cyclopiazonic acid, thapsigargin, and SK&F96365 on ICC pacemaker activity suggest that SOCE plays a key role in ICC (36, 64). 2-APB, which has been routinely described as an IP3R inhibitor in the ICC field (38), is a more reliable inhibitor of SOCE than IP3Rs (5), lending further support to the hypothesis that SOC channels are important for initiating the pacemaker cycle. Similarly, inhibition of pacemaker activity by Ni2+ is commonly used to indicate a role for T-type Ca2+ channels in ICC (27, 29) but similar concentrations of Ni2+ also inhibit SOC channels (18). The application of Ni2+ or Ca2+-free external solution inhibited a Ca2+-activated Cl− current in ICC (75), indicating that Ca2+ influx, rather than Ca2+ release, is important for activating Ano1 in ICC. Therefore, it is likely that Ano1 channels in ICC are colocalized with SOC channels.
Nevertheless, it is plausible that the Ca2+ pathway for Ano1 activation in ICC may instead be IP3R channels in sections of ER proximal to the plasma membrane. The lack of slow waves in IP3R1 knockout mice (59) and inhibition of slow wave activity when inhibiting IP3 production with phospholipase C inhibitors (38, 40) show that IP3Rs are a crucial component of the pacemaker Ca2+ cycle in ICC. Modeling the activation of Ano1 by IP3Rs localized near the cell membrane could be implemented with the same method that was used to model localization of Ano1 to SOC channels in this study, with little impact on the rest of the model.
CONCLUSIONS
We have developed the first mathematical model of ICC that implements Ano1 as a pacemaker channel and incorporates SOCE. We present a series of model variations that enable us to draw several conclusions: Firstly, the models presented here support the theory that Ano1 can initiate slow waves in response to cyclical activation of SOC channels. The simulations reproduce the observation that blocking or knocking out Ano1 channels causes loss of slow wave activity. Secondly, ECl plays an important role in modulating the shape of the slow wave. If ECl is close to the potentials measured in ICC-MY (76), then Ano1 current may contribute to repolarizing the cell but the plateau phase is not well reproduced. Conversely, if ECl is at least as high as the slow wave peak, membrane potential oscillations that recreate experimentally recorded slow waves can be easily simulated. It is possible that ECl is artificially raised by the microelectrode recording techniques used to measure membrane potentials, such that recorded slow wave traces are different to those present in undisturbed ICC. Thirdly, voltage- or Ca2+-activated nonselective channels or Na+ channels are plausible candidates for generating the plateau current, but large or prolonged Ca2+ currents are unlikely to contribute a major component of the slow wave depolarization. Fourthly, membrane potential oscillations in ICC-MY from Ano1 knockout mice may not be completely abolished but are minimized by background currents. Further experiments are needed to confirm or refute these conclusions and to provide more evidence about the contributions of various ion channels to slow waves generated by pacemaker ICC in the gastrointestinal tract. In particular, it is important to confirm the report of [Cl−]i in ICC (76) and to search for any evidence that the reversal potential of Ano1 currents differs from the expected value for ECl.
GRANTS
R. Lees-Green was supported by a University of Auckland Doctoral Scholarship. This work was funded, in part, by grants from the Health Research Council of New Zealand and National Institute of Diabetes and Digestive and Kidney Diseases Grants DK-64775 and DK-57061.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: R.L.G., S.J.G., G.F., J.S., and L.K.C. conception and design of research; R.L.G. performed experiments; R.L.G. analyzed data; R.L.G., S.J.G., G.F., J.S., and L.K.C. interpreted results of experiments; R. L.G. prepared figures; R.L.G. drafted manuscript; R.L.G., S.J.G., G.F., J.S., and L.K.C. edited and revised manuscript; R.L.G., S.J.G., G.F., J.S., and L.K.C. approved final version of manuscript.
ACKNOWLEDGMENTS
We acknowledge the contributions from Andrew Pullan who passed away during the course of this research.
Appendix
The equations used in our model are detailed below. Parameter values common to all model variations are given in Table A1, while parameter values and gating variables that differ across the model variations are in Tables A2 and A3, respectively.
Table A1.
Parameter values common to all model variations
| Parameter | Value | Reference |
|---|---|---|
| Cell constants | ||
| Cm | 25 pF | 21, 27 |
| v | 1 × 10−12 l | 10 |
| vcyto | 0.7 × 10−12 l | 10 |
| ver | 0.1 × 10−12 l | 10 |
| F | 96 485 C/mol | |
| R | 8.314 J·mol−1·K−1 | |
| T | 310.0 K | |
| Plasma membrane current parameters | ||
| [Ca2+]o | 2 mM | 10, 16 |
| [Cl−]o | 166 mM | 76 |
| [K+]i | 140 mM | 67 |
| [K+]o | 5 mM | 67 |
| [Na+]i | 30 mM | 10 |
| [Na+]o | 140 mM | 10 |
| EK | −89.0 mV | C |
| ENa | 41.2 mV | C |
| ENS | 0 mV | 30, 49 |
| gSOC | 0.1 nS | |
| Cytosolic Ca2+ flux parameters | ||
| KSOC | 200 μM | 6, 57 |
| KPMCA | 0.1 μM | |
| bc | 0.01 | 14 |
| IP3R parameters | ||
| P | 0.5 μM | 65 |
| k1 | 4000 μM−1·s−1 | 65* |
| k2 | 2.0 μM−1·s−1 | 65* |
| k3 | 4000 μM−1·s−1 | 65* |
| k4 | 2.0 μM−1·s−1 | 65* |
| k5 | 200 μM−1·s−1 | 65* |
| k−1 | 520 s−1 | 65* |
| k−2 | 2.1 s−1 | 65* |
| k−3 | 3772 s−1 | 65* |
| k−4 | 0.29 s−1 | 65* |
| k−5 | 16.4 s−1 | 65* |
| kIPR | 7.0 s−1 | |
| Jleak | 0.01 s−1 | |
| SERCA pump parameters | ||
| Ve | 80 μM/s | |
| Ke | 0.1 μM | 65 |
| Ano1 model parameters | ||
| EC50(0mV) | 1.39 μM | 70 |
| kc | 0.012 48 mV−1 | 70 |
| Vh | −100 mV | |
| kv | 0.0156 mV−1 | 70 |
| Ano1-SOC localization parameters | ||
| Dc | 250 μm2/s | 55 |
| Dm | 75 μm2/s | 55 |
| Km | 1 μM | 55 |
| Bm | 50 μM | 55 |
| r | 0.05 μm | |
| vscale | 1015 μm3/l | C |
| nSOC | 50 | 16 |
C denotes that the parameter value was calculated using other parameters; SERCA is sarco-endoplasmic reticulum ATPase; SOC is store-operated Ca2+ channel; see text for other definitions. References are given where available; other parameter values were chosen to reproduce correct slow wave activity.
Inositol 1,4,5-trisphosphate receptor (IP3R) ki values are double the values in Ref. 65 to reproduce correct Ca2+ oscillation frequency.
Table A2.
Parameter values that differ across model variations
| Parameter | Value | Reference |
|---|---|---|
| Cl− parameters | ||
| [Cl−]i | ||
| H | 78 mM | C |
| L | 25.85 mM | 76 |
| ECl | ||
| H | −20.2 mV | C |
| L | −49.7 mV | C |
| Ion channel maximal conductances | ||
| gAno1 | ||
| H(NSV,NSCa) | 20 nS | |
| H(NaV,CaV), L(NaV) | 15 nS | |
| L(NSCa) | 10 nS | |
| gCaT | ||
| H(NaV,NSV,CaV), L(NaV) | 3 nS | 10 |
| H(NSCa), L(NSCa) | 4 nS | |
| gKb | ||
| H(NSV,NSCa,CaV) | 9 nS | |
| H(NaV), L(NaV,NSCa) | 5 nS | |
| gNab | ||
| H(NSV,NSCa,CaV) | 2 nS | |
| H(NaV), L(NaV,NSCa) | 1 nS | |
| gNaV | ||
| H(NaV) | 6 nS | |
| L(NaV) | 10 nS | |
| gNSV | ||
| H(NSV) | 30 nS | |
| gNSCa | ||
| H(NSCa), L(NSCa) | 30 nS | |
| gCaV | ||
| H(CaV) | 6.2 nS | |
| gKt | ||
| L(NaV) | 6 nS | |
| gKERG | ||
| L(NaV) | 3 nS | |
| Ca2+ pump maximal fluxes | ||
| VPMCA | ||
| H(NaV,NSV), L(NaV) | 50 μM/s | |
| H(NSCa) | 100 μM/s | |
| H(CaV) | 1500 μM/s | |
| L(NSCa) | 110 μM/s | |
| VNCX | ||
| L(NSCa) | 225 μM/s |
C denotes that the parameter value was calculated using other parameters; see text for other definitions. References are given where available; other parameter values were chosen to reproduce correct slow wave activity. Model variations in which each parameter value is used are denoted by H for High-Cl and L for Low-Cl.
Table A3.
Gating variable parameters
| Variable | Vh, mV | K, mV | a | τx, s | Reference |
|---|---|---|---|---|---|
| dCaT | |||||
| H(NaV,NSV,CaV), L(NaV) | −26 | −6 | 1 | 0.006 | 10 |
| H(NSCa) | −40 | −3 | 1 | 0.006 | |
| L(NSCa) | −45 | −3 | 1 | 0.003 | |
| fCaT | |||||
| H(NaV,NSV,CaV), L(NaV) | −66 | 6 | 1 | 0.04 | 10 |
| H(NSCa), L(NSCa) | −55 | 5 | 1 | 0.1 | |
| dNaV | |||||
| H(NaV) | −25 | −5.6 | 1 | Eq. 40 | 3* |
| L(NaV) | −39 | −5.6 | 1 | Eq. 46 | 3 |
| fNaV | |||||
| L(NaV) | −55 | −4.5 | 0.53 | 1.0 | |
| dNSV | |||||
| H(NSV) | −30 | −5 | 1 | 0.005 | |
| fNSV | |||||
| H(NSV) | −50 | 5 | 0.3 | 0.8 | |
| dCaV | |||||
| H(CaV) | −26 | −6 | 1 | 0.006 | 10 |
| dKt | |||||
| L(NaV) | −20 | −4.6 | 1.0 | 0.003 | |
| fKt | |||||
| L(NaV) | −45 | 4.4 | 1.0 | 0.045 | |
| dKERG | |||||
| L(NaV) | −35 | −7.1 | 1.0 | Eq. 49 | |
| fKERG | |||||
| L(NaV) | −42 | 4 | 1.0 | 0.003 |
Parameters for voltage-dependent gating variables for x∞ = a/[1 + e(Vm − Vh/k)] + (1 − a) and for τx, where x = dCaT, fCaT, dNaV, fNaV, dCaV, dNSV, fNSV, dKt, fKt, dKERG, or fKERG. Model variations in which each parameter value is used are denoted by H for High-Cl and L for Low-Cl. References are given where available; other parameter values were chosen to reproduce correct slow wave activity; see text for other definitions.
Vh modified from values in Ref. 3.
State Variables
Membrane potential.
| (12) |
where Iion for each model variation is defined in Eqs. 4–7, 9, and 10.
Ion channel gating variables.
| (13) |
for x = OAno1, dCaT, fCaT, dNaV, fNaV, dCaV, dNSV, fNSV, dKt, fKt, dKERG, or fKERG. Parameter values for x∞ and τx are listed in Table A3, except for OAno1∞ and τAno1 given in Eqs. 24 and 29, respectively, τdNaV given in Eqs. 40 and 46, and τdKERG given in Eq. 49.
Calcium concentration.
The change in [Ca2+]ER is given by:
| (14) |
The change in [Ca2+]i is given by:
| (15) |
as in Eq. 3, except in High-Cl(CaV) and Low-Cl(NSCa) where it is replaced by Eqs. 8 and 11, respectively.
IP3R inactivation.
The proportion of IP3R channels inactivated by Ca2+ (y), as a function of Cai and IP3 concentration (P), from Ref. 65:
| (16) |
| (17) |
| (18) |
where Ki = k−i/ki.
Calcium Flux
Ca2+ flux across the plasma membrane.
Plasma membrane Ca2+ ATPase:
| (19) |
Na+/Ca2+ exchanger, from Ref. 37:
| (20) |
Ca2+ flux across the ER membrane.
Total Ca2+ release from the ER, adapted from Ref. 65:
| (21) |
| (22) |
Ca2+ uptake into the ER, from Ref. 65:
| (23) |
Ano1 Model
Steady-state open probability of the Ano1 channel model, developed using data from Ref. 70:
| (24) |
| (25) |
Ca2+concentration near Ano1 channels as a function of Ca2+ flux through SOC channels from Ref. 55:
| (26) |
| (27) |
| (28) |
Time constant for the Ano1 channel model, developed using data from Ref. 70:
| (29) |
| (30) |
| (31) |
| (32) |
Ion Currents
Ion currents common to all models.
SOC channel:
| (33) |
| (34) |
Ano1 Ca2+-activated Cl− channel:
| (35) |
Na+ background current:
| (36) |
K+ background current:
| (37) |
T-type Ca2+ current:
| (38) |
Ion current specific to High-Cl(NaV).
Voltage-gated Na+ channel:
| (39) |
| (40) |
Ion currents specific to High-Cl(NSV).
Voltage-gated nonselective channel:
| (41) |
Ion currents specific to High-Cl(NSCa).
Ca2+-activated nonselective channel:
| (42) |
| (43) |
Ion current specific to High-Cl(CaV).
Voltage-gated Ca2+ channel:
| (44) |
Ion currents specific to Low-Cl(NaV).
Voltage-gated Na+ channel:
| (45) |
| (46) |
Transient K+ channel:
| (47) |
ERG-like K+ channel:
| (48) |
| (49) |
Ion currents specific to Low-Cl(NSCa).
Ca2+-activated nonselective channel:
| (50) |
| (51) |
Na+/Ca2+ exchanger, from Ref. 37:
| (52) |
Nernst equilibrium potential.
| (53) |
| (54) |
REFERENCES
- 1.Angermann JE, Forrest AS, Greenwood IA, Leblanc N. Activation of Ca2+-activated Cl- channels by store-operated Ca2+ entry in arterial smooth muscle cells does not require reverse-mode Na+/Ca2+ exchange. Can J Physiol Pharmacol 90: 903–921, 2012 [DOI] [PubMed] [Google Scholar]
- 2.Beyder A, Farrugia G. Targeting ion channels for the treatment of gastrointestinal motility disorders. Therap Adv Gastroenterol 5: 5–21, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Beyder A, Rae JL, Bernard CE, Strege PR, Sachs F, Farrugia G. Mechanosensitivity of Nav1.5 a voltage-sensitive sodium channel. J Physiol 588: 4969–4985, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blatt MR, Slayman CL. KCl leakage from microelectrodes and its impact on the membrane parameters of a nonexcitable cell. J Membr Biol 72: 223–234, 1983 [DOI] [PubMed] [Google Scholar]
- 5.Bootman MD, Collins TJ, Mackenzie L, Roderick HL, Berridge MJ, Peppiatt CM. 2- Aminoethoxydiphenyl borate (2-APB) is a reliable blocker of store-operated Ca2+ entry but an inconsistent inhibitor of InsP3-induced Ca2+ release. FASEB J 16: 1145–1150, 2002 [DOI] [PubMed] [Google Scholar]
- 6.Brandman O, Liou J, Park WS, Meyer T. STIM2 is a feedback regulator that stabilizes basal cytosolic and endoplasmic reticulum Ca2+ levels. Cell 131: 1327–1339, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Britton FC, Leblanc N, Kenyon JL. Calcium activated chloride channels. In: Physiology and Pathology of Chloride Transporters and Channels in the Nervous System, edited by Alvarez-Leefmans FJ, Delpire E. San Diego, CA: Academic, 2010, p. 233–256 [Google Scholar]
- 8.Caputo A, Caci E, Ferrera L, Pedemonte N, Barsanti C, Sondo E, Pfeffer U, Ravazzolo R, Zegarra-Moran O, Galietta LJV. TMEM16A, a membrane protein associated with calcium-dependent chloride channel activity. Science 322: 590–594, 2008 [DOI] [PubMed] [Google Scholar]
- 9.Chen H, Ördög T, Chen J, Young DL, Bardsley MR, Redelman D, Ward SM, Sanders KM. Differential gene expression in functional classes of interstitial cells of Cajal in murine small intestine. Physiol Genomics 31: 492–509, 2007 [DOI] [PubMed] [Google Scholar]
- 10.Corrias A, Buist ML. Quantitative cellular description of gastric slow wave activity. Am J Physiol Gastrointest Liver Physiol 294: G989–G995, 2008 [DOI] [PubMed] [Google Scholar]
- 11.Darbellay B, Arnaudeau S, Bader CR, Konig S, Bernheim L. STIM1L is a new actin-binding splice variant involved in fast repetitive Ca2+ release. J Cell Biol 194: 335–346, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.De Young GW, Keizer J. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc Natl Acad Sci USA 89: 9895–9899, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Edwards JN, Murphy RM, Cully TR, von Wegner F, Friedrich O, Launikonis BS. Ultrarapid activation and deactivation of store-operated Ca2+ entry in skeletal muscle. Cell Calcium 47: 458–467, 2010 [DOI] [PubMed] [Google Scholar]
- 14.Fall CP, Keizer JE. Mitochondrial modulation of intracellular Ca2+ signaling. J Theor Biol 210: 151–165, 2001 [DOI] [PubMed] [Google Scholar]
- 15.Farrugia G. Interstitial cells of Cajal in health and disease. Neurogastroenterol Motil 20, Suppl 1: 54–63, 2008 [DOI] [PubMed] [Google Scholar]
- 16.Faville RA, Pullan AJ, Sanders KM, Koh SD, Lloyd CM, Smith NP. Biophysically based mathematical modeling of interstitial cells of Cajal slow wave activity generated from a discrete unitary potential basis. Biophys J 96: 4834–4852, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Feske S, Gwack Y, Prakriya M, Srikanth S, Puppel SH, Tanasa B, Hogan PG, Lewis RS, Daly M, Rao A. A mutation in Orai1 causes immune deficiency by abrogating CRAC channel function. Nature 441: 179–185, 2006 [DOI] [PubMed] [Google Scholar]
- 18.Flemming R, Xu SZ, Beech DJ. Pharmacological profile of store-operated channels in cerebral arteriolar smooth muscle cells. Br J Pharmacol 139: 955–965, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gibbons SJ, Strege PR, Lei S, Roeder JL, Mazzone A, Ou Y, Rich A, Farrugia G. The alpha1H Ca2+ channel subunit is expressed in mouse jejunal interstitial cells of Cajal and myocytes. J Cell Mol Med 13: 4422–4431, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gomez-Pinilla PJ, Gibbons SJ, Bardsley MR, Lorincz A, Pozo MJ, Pasricha PJ, Van de Rijn M, West RB, Sarr MG, Kendrick ML, Cima RR, Dozois EJ, Larson DW, Ördög T, Farrugia G. Ano1 is a selective marker of interstitial cells of Cajal in the human and mouse gastrointestinal tract. Am J Physiol Gastrointest Liver Physiol 296: G1370–G1381, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goto K, Matsuoka S, Noma A. Two types of spontaneous depolarizations in the interstitial cells freshly prepared from the murine small intestine. J Physiol 559: 411–422, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hauck C, Frishman WH. Systemic hypertension: the roles of salt, vascular Na+/K+ ATPase and the endogenous glycosides, ouabain and marinobufagenin. Cardiol Rev 20: 130–138, 2012 [DOI] [PubMed] [Google Scholar]
- 23.Hwang SJ, Blair PJ, Britton FC, O'Driscoll KE, Hennig GW, Bayguinov YR, Rock JR, Harfe BD, Sanders KM, Ward SM. Expression of anoctamin 1/TMEM16A by interstitial cells of Cajal is fundamental for slow wave activity in gastrointestinal muscles. J Physiol 587: 4887–4904, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jin X, Shah S, Liu Y, Zhang H, Lees M, Fu Z, Lippiat JD, Beech DJ, Sivaprasadarao A, Baldwin SA, Zhang H, Gamper N. Activation of the Cl- channel ANO1 by localized calcium signals in nociceptive sensory neurons requires coupling with the IP3 receptor. Sci Signal 6: ra73, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim BJ, Chang IY, Choi S, Jun JY, Jeon JH, Xu WX, Kwon YK, Ren D, So I. Involvement of Na+-leak channel in substance P-induced depolarization of pacemaking activity in interstitial cells of Cajal. Cell Physiol Biochem 29: 501–510, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kim BJ, Lim HH, Yang DK, Jun JY, Chang IY, Park CS, So I, Stanfield PR, Kim KW. Melastatin-type transient receptor potential channel 7 is required for intestinal pacemaking activity. Gastroenterology 129: 1504–1517, 2005 [DOI] [PubMed] [Google Scholar]
- 27.Kim YC, Koh SD, Sanders KM. Voltage dependent inward currents of interstitial cells of Cajal from murine colon and small intestine. J Physiol 541: 797–810, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kirby MT, Hampson RE, Deadwyler SA. Cannabinoid receptor activation in CA1 pyramidal cells in adult rat hippocampus. Brain Res 863: 120–131, 2000 [DOI] [PubMed] [Google Scholar]
- 29.Kito Y, Suzuki H. Properties of pacemaker potentials recorded from myenteric interstitial cells of Cajal distributed in the mouse small intestine. J Physiol 553: 803–818, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Koh SD, Jun JY, Kim TW, Sanders KM. A Ca2+-inhibited nonselective cation conductance contributes to pacemaker currents in mouse interstitial cell of Cajal. J Physiol 540: 803–814, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kuruma A, Hartzell HC. Dynamics of calcium regulation of chloride currents in Xenopus oocytes. Am J Physiol Cell Physiol 276: C161–C175, 1999 [DOI] [PubMed] [Google Scholar]
- 32.Kuruma A, Hartzell HC. Bimodal control of a Ca2+-activated Cl channel by different Ca2+ signals. J Gen Physiol 115: 59–80, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lees-Green R, Du P, O'Grady G, Beyder A, Farrugia G, Pullan AJ. Biophysically based modeling of the interstitial cells of Cajal: current status and future perspectives. Front Comput Physiol Med 2: 29, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liem LK, Simard JM, Song Y, Tewari K. The patch clamp technique. Neurosurgery 36: 382–392, 1995 [DOI] [PubMed] [Google Scholar]
- 35.Liou J, Kim ML, Heo WD, Jones JT, Myers JW, Ferrell JE, Meyer T. STIM is a Ca2+ sensor essential for Ca2+-store-depletion-triggered Ca2+ influx. Curr Biol 15: 1235–1241, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu HN, Ohya S, Furuzono S, Wang J, Imaizumi Y, Nakayama S. Co-contribution of IP3R and Ca2+ influx pathways to pacemaker Ca2+ activity in stomach ICC. J Biol Rhythms 20: 15–26, 2005 [DOI] [PubMed] [Google Scholar]
- 37.Livshitz L, Acsai K, Antoons G, Sipido K, Rudy Y. Data-based theoretical identification of subcellular calcium compartments and estimation of calcium dynamics in cardiac myocytes. J Physiol 590: 4423–4446, 2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lowie BJ, Wang XY, White EJ, Huizinga JD. On the origin of rhythmic calcium transients in the ICC-MP of the mouse small intestine. Am J Physiol Gastrointest Liver Physiol 301: G835–G845, 2011 [DOI] [PubMed] [Google Scholar]
- 39.Luik RM, Wang B, Prakriya M, Wu MM, Lewis RS. Oligomerization of STIM1 couples ER calcium depletion to CRAC channel activation. Nature 454: 538–542, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Malysz J, Donnelly G, Huizinga JD. Regulation of slow wave frequency by IP3-sensitive calcium release in the murine small intestine. Am J Physiol Gastrointest Liver Physiol 280: G439–G448, 2001 [DOI] [PubMed] [Google Scholar]
- 41.Maruyama T, Kanaji T, Nakade S, Kanno T, Mikoshiba K. 2APB, 2-aminoethoxydiphenyl borate, a membrane-penetrable modulator of ins(1,4,5)P3-induced Ca2+ release. J Biochem 122: 498–505, 1997 [DOI] [PubMed] [Google Scholar]
- 42.Mazzone A, Bernard CE, Gibbons SJ, Fernandez-Zapico ME, Farrugia G. Identification and characterization of a human Ano1 gene promoter (Abstract). Gastroenterology 144: S-56, 2013 [Google Scholar]
- 43.Mazzone A, Bernard CE, Strege PR, Beyder A, Galietta LJV, Pasricha PJ, Rae JL, Parkman HP, Linden DR, Szurszewski JH, Ördög T, Gibbons SJ, Farrugia G. Altered expression of Ano1 variants in human diabetic gastroparesis. J Biol Chem 286: 13393–13403, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Means SA, Sneyd J. Spatio-temporal calcium dynamics in pacemaking units of the interstitial cells of Cajal. J Theor Biol 267: 137–152, 2010 [DOI] [PubMed] [Google Scholar]
- 45.Mignen O, Thompson JL, Shuttleworth TJ. Orai1 subunit stoichiometry of the mammalian CRAC channel pore. J Physiol 586: 419–425, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ng LC, McCormack MD, Airey JA, Singer CA, Keller PS, Shen XM, Hume JR. TRPC1 and STIM1 mediate capacitative Ca2+ entry in mouse pulmonary arterial smooth muscle cells. J Physiol 587: 2429–2442, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.O'Driscoll KE, Pipe RA, Britton FC. Increased complexity of Tmem16a/Anoctamin 1 transcript alternative splicing. BMC Mol Biol 12: 1–13, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Park SJ, Mckay CM, Zhu Y, Huizinga JD. Volume-activated chloride currents in interstitial cells of Cajal. Am J Physiol Gastrointest Liver Physiol 289: G791–G797, 2005 [DOI] [PubMed] [Google Scholar]
- 49.Parsons SP, Kunze WA, Huizinga JD. Maxichannels recorded in situ from ICC and pericytes associated with the mouse myenteric plexus. Am J Physiol Cell Physiol 302: C1055–C1069, 2012 [DOI] [PubMed] [Google Scholar]
- 50.Prakriya M, Lewis RS. Potentiation and inhibition of Ca2+ release-activated Ca2+ channels by 2-aminoethyldiphenyl borate (2-APB) occurs independently of IP3 receptors. J Physiol 536: 3–19, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rich A, Hanani M, Ermilov LG, Malysz J, Belzer V, Szurszewski JH, Farrugia G. Physiological study of interstitial cells of Cajal identified by vital staining. Neurogastroenterol Motil 14: 189–196, 2002 [DOI] [PubMed] [Google Scholar]
- 52.Sanders KM, Koh SD, Ward SM. Interstitial cells of Cajal as pacemakers in the gastrointestinal tract. Annu Rev Physiol 68: 307–443, 2006 [DOI] [PubMed] [Google Scholar]
- 53.Schroeder BC, Cheng T, Jan YN, Jan LY. Expression cloning of TMEM16A as a calcium activated chloride channel subunit. Cell 134: 1019–1029, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Shaw RM, Colecraft HM. L-type calcium channel targeting and local signalling in cardiac myocytes. Cardiovasc Res 98: 177–186, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Smith GD. Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys J 71: 3064–3072, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Smyth JT, Hwang SY, Tomita T, DeHaven WI, Mercer JC, Putney JW. Activation and regulation of store-operated calcium entry. J Cell Mol Med 14: 2337–2349, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Stathopulos PB, Zheng L, Li GY, Plevin MJ, Ikura M. Structural and mechanistic insights into STIM1-mediated initiation of store-operated calcium entry. Cell 135: 110–122, 2008 [DOI] [PubMed] [Google Scholar]
- 58.Stiber JA, Rosenberg PB. The role of store operated calcium influx in skeletal muscle signaling. Cell Calcium 49: 341–349, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Suzuki H, Takano H, Yamamoto Y, Komuro T, Saito M, Kato K, Mikoshiba K. Properties of gastric smooth muscles obtained from mice which lack inositol trisphosphate receptor. J Physiol 525: 105–111, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Takeda Y, Koh SD, Sanders KM, Ward SM. Differential expression of ionic conductances in interstitial cells of Cajal in the murine gastric antrum. J Physiol 586: 859–873, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Thomsen L, Robinson TL, Lee JC, Farraway LA, Hughes MJ, Andrews DW, Huizinga JD. Interstitial cells of Cajal generate a rhythmic pacemaker current. Nat Med 4: 848–851, 1998 [DOI] [PubMed] [Google Scholar]
- 62.Tian Y, Schreiber R, Kunzelmann K. Anoctamins are a family of Ca2+-activated Cl− channels. J Cell Sci 125: 4991–4998, 2012 [DOI] [PubMed] [Google Scholar]
- 63.Tokutomi N, Maeda H, Tokutomi Y, Sato D, Sugita M, Nishikawa S, Nakao J, Imamura T, Nishi K. Rhythmic Cl− current and physiological roles of the intestinal c-kit-positive cells. Pflügers Arch 431: 169–177, 1995 [DOI] [PubMed] [Google Scholar]
- 64.Torihashi S, Fujimoto T, Trost C, Nakayama S. Calcium oscillation linked to pacemaking of interstitial cells of Cajal: requirement of calcium influx and localization of TRP4 in caveolae. J Biol Chem 277: 19191–19197, 2002 [DOI] [PubMed] [Google Scholar]
- 65.Wang IY, Bai Y, Sanderson MJ, Sneyd J. A mathematical analysis of agonist- and KCl-induced Ca2+ oscillations in mouse airway smooth muscle cells. Biophys J 98: 1170–1181, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Ward SM, Ördög T, Koh SD, Abu Baker S, Jun JY, Amberg G, Monaghan K, Sanders KM. Pacemaking in interstitial cells of Cajal depends upon calcium handling by endoplasmic reticulum and mitochondria. J Physiol 525: 355–361, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.White EJ, Park SJ, Foster JA, Huizinga JD. Ether-a-go-go-related gene 3 is the main candidate for the E-4031-sensitive potassium current in the pacemaker interstitial cells of Cajal. Am J Physiol Gastrointest Liver Physiol 295: G691–G699, 2008 [DOI] [PubMed] [Google Scholar]
- 68.Wouters M, De Laet A, Donck LV, Delpire E, van Bogaert PP, Timmermans JP, de Kerchove d'Exaerde A, Smans K, Vanderwinden JM. Subtractive hybridization unravels a role for the ion cotransporter NKCC1 in the murine intestinal pacemaker. Am J Physiol Gastrointest Liver Physiol 290: G1219–G1227, 2006 [DOI] [PubMed] [Google Scholar]
- 69.Wright GWJ, Parsons SP, Huizinga JD. Ca2+ sensitivity of the maxi chloride channel in interstitial cells of Cajal. Neurogastroenterol Motil 24: e221–e234, 2012 [DOI] [PubMed] [Google Scholar]
- 70.Xiao Q, Yu K, Perez-Cornejo P, Cui Y, Arreola J, Hartzell HC. Voltage- and calcium-dependent gating of TMEM16A/Ano1 chloride channels are physically coupled by the first intracellular loop. Proc Natl Acad Sci USA 108: 8891–8896, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Xu SZ, Zeng F, Boulay G, Grimm C, Harteneck C, Beech DJ. Block of TRPC5 channels by 2-aminoethoxydiphenyl borate: a differential, extracellular and voltage-dependent effect. Br J Pharmacol 145: 405–414, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Yang YD, Cho H, Koo JY, Tak MH, Cho Y, Shim WS, Park SP, Lee J, Lee B, Kim BM, Raouf R, Shin YK, Oh U. TMEM16A confers receptor-activated calcium-dependent chloride conductance. Nature 455: 1210–1215, 2008 [DOI] [PubMed] [Google Scholar]
- 73.Youm JB, Kim N, Han J, Kim E, Joo H, Leem CH, Goto G, Noma A, Earm YE. A mathematical model of pacemaker activity recorded from mouse small intestine. Philos Trans A Math Phys Eng Sci 364: 1135–1154, 2006 [DOI] [PubMed] [Google Scholar]
- 74.Zhang SL, Yu Y, Roos J, Kozak JA, Deerinck TJ, Ellisman MH, Stauderman KA, Cahalan MD. STIM1 is a Ca2+ sensor that activates CRAC channels and migrates from the Ca2+ store to the plasma membrane. Nature 437: 902–905, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zhu MH, Kim TW, Ro S, Yan W, Ward SM, Koh SD, Sanders KM. A Ca2+-activated Cl- conductance in interstitial cells of Cajal linked to slow wave currents and pacemaker activity. J Physiol 587: 4905–4918, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Zhu Y, Parsons SP, Huizinga JD. Measurement of intracellular chloride ion concentration in ICC in situ and in explant culture. Neurogastroenterol Motil 22: 704–709, 2010. (Corrigendum. Neurogastroenterol Motil 22: 1042, 2010) [DOI] [PubMed] [Google Scholar]