AGG interruptions within the maternal FMR1 gene reduce the risk of offspring with fragile X syndrome

Abstract

Purpose

The ability to accurately predict the likelihood of expansion of the CGG repeats in the FMR1 gene to a full mutation is of critical importance for genetic counseling of women who are carriers of premutation alleles (55–200 CGG repeats) and who are weighing the risk of having a child with fragile X syndrome. The presence of AGG interruptions within the CGG repeat tract are thought to decrease the likelihood of expansion to a full mutation during transmission, thereby reducing risk, although their contribution has not been quantified.

Methods

We retrospectively analyzed 267 premutation alleles for number and position of AGG interruptions, length of pure CGG repeats, and CGG repeat lengths present in the offspring of the maternal transmissions. Additionally, we determined the haplotypes of four markers flanking the 5’ UTR locus in the premutation mothers.

Results

We found that the presence of AGG interruptions significantly increased genetic stability while specific haplotypes had a marginal association with transmission instability.

Conclusions

The presence of AGG interruptions reduced the risk of transmission of a full mutation for all maternal (premutation) repeat lengths below ~100 CGG repeats, with a differential risk (0 versus 2 AGG) exceeding 60% for alleles in the 70-to 80-CGG repeat range.

INTRODUCTION

The Fragile X Mental Retardation 1 (FMR1) gene encoding the FMR1 Protein (FMRP) is essential for normal brain development and synaptic plasticity.¹ The 5’ non-coding CGG-repeat tract, when expanded beyond the normal range (5–44 CGG repeats), leads to fragile X syndrome (FXS, OMIM 300624) and additional fragile X-associated disorders.^2,3 The American College of Medical Genetics guidelines classify expanded alleles as intermediate (45–54 CGG repeats), premutation (55–200 repeats), or full mutation (>200 repeats). Full mutation alleles are generally methylated within the promoter region; with consequent transcriptional silencing and absence of FMRP resulting in fragile X syndrome, the leading heritable form of intellectual disability and leading known single-gene form of autism.^4,5

A critical issue in genetic counseling is the accurate assessment of the likelihood that a female (premutation) carrier will have a child with a full mutation CGG repeat. Repeat-length instability during maternal transmission strongly favors size expansion of the CGG tract, with the probability of a full mutation allele in the offspring dependent upon the size of the maternal CGG repeat tract.^6–9 Although the basis for repeat instability is not known, it has been suggested that both cis and trans elements might play a role in trinucleotide repeat expansions. The role of trans factors in the instability of expanded alleles, which include many enzymes involved in DNA repair, has been suggested from studies in animal models.^10–12 Errors in base and nucleotide excision repair, that occur in response to oxidative damage, are two plausible mechanisms proposed in Huntington’s and FXS mouse models to explain increases in expansion of trinucleotide repeats when oxidative damage is induced.^13,14 In addition, cis elements, including AGG trinucleotides within the CGG repeat tract, which are typically separated by 9 to 11 CGG repeats and disrupting the otherwise pure CGG-repeat motif, appear to influence repeat instability during transmission.^15–17 Whereas normal alleles typically possess 2–3 AGG interruptions, premutation alleles generally possess 0–2 interruptions, with larger premutation alleles tending to have fewer AGG interruptions. The loss of AGG interruptions is therefore thought to increase the probability of transmission of a full mutation allele from a given repeat size of the maternal (premutation) allele.^15,18,19

To address the clinically important question of the influence of AGG repeats on premutation-to-full mutation transmission probability, we tested the hypothesis that the presence of AGG interruptions within a premutation FMR1 allele would lower the probability of conversion to full mutation during transmission, and with an effect size that would itself be a function of total repeat length.

We also determined haplotypes in 164 mothers using 4 markers flanking the CGG repeat tract (DXS548, FRAXAC1, ATL1 and IVS10+14), and evaluated in parallel the AGG profiles to determine whether differences in stability would be detected and to corroborate previous findings that haplotype profiles were related to the AGG interruption pattern.¹⁹

The study utilized DNA samples from 267 mothers harboring premutation alleles and their children, for whom total CGG repeat lengths were determined previously by both Southern Blot and PCR analysis. The total length of the CGG repeat tract, and the position of AGG interruptions, was determined using a newly available PCR based approach.^20,21 We evaluated the results of 373 transmission events, thereby defining for this cohort the association between AGG interruptions and total (and pure) CGG-repeat lengths, and the likelihood of a premutation-to-full mutation transmission.

We conclude that failure to account for AGG interruptions can result in profound errors in predicted risk for fragile X syndrome.

MATERIALS AND METHODS

Subjects

Individuals were recruited through the MIND Institute Clinic and provided informed consent under protocols approved by the UC Davis Institutional Review Board. Participants comprised mothers who were carriers with premutation FMR1 alleles, and whose children possessed expanded CGG-repeat alleles as determined previously by us using Southern Blot analysis and PCR amplification^20,22 The ages of the 234 mothers were known at the time of birth of each child. All females carrying a premutation allele were included in the study if they had at least one child with an expanded allele (>55 CGG repeats) regardless of the size of the CGG repeat.

Molecular Measures

DNA isolation, PCR, Southern Blot analysis, determination of location and number of AGG interruptions (Figure 1), by using both PCR and Eci I digestion (Supplementary Figure 1), and haplotypes genotyping were as previously described^{20,21,23–25} and detailed in Supplementary Appendices.

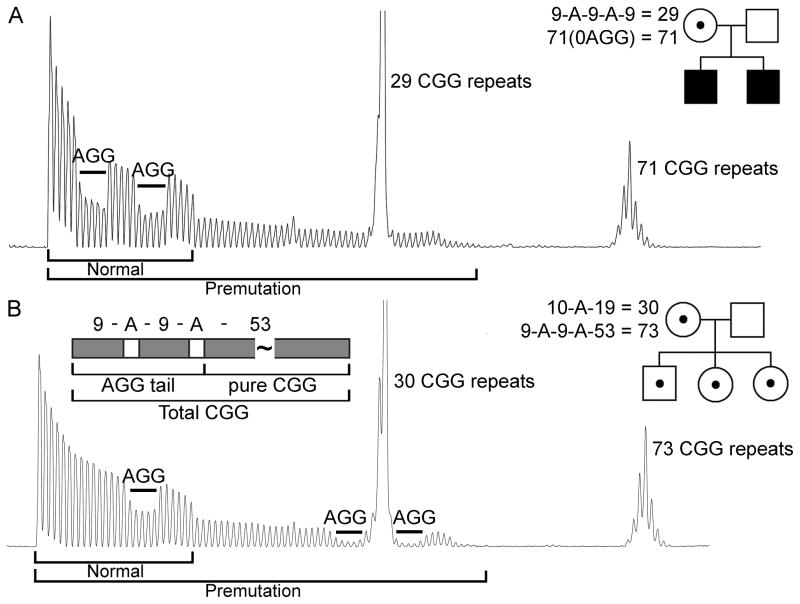
Figure 1.

Examples of electropherogram patterns of CGG-repeat-containing PCR products for two female premutation carriers, one with 2 AGG interruptions in the normal allele (29 CGG repeats) and no AGG in the premutation allele (71 CGG repeats) (A) and one with 1 AGG interruption in the normal (30 CGG repeats) and 2 AGG interruptions in the premutation allele (73 CGG repeats) (B). The corresponding pedigrees are provided for each subject, illustrating the effect of the presence of AGGs on transmission to a premutation (2 AGGs present in the maternal allele, 73 CGG) or to a full mutation (0 AGG present in the maternal allele, 71 CGG) offspring. In both females, the normal and the premutation allele lengths, shown as serial peaks, are illustrated at the bottom of each electrophoregram as a black line. Location and number of the AGG interruptions for each allele were determined as described in the Supplementary Appendix. A diagram showing the total CGG-repeat length (inclusive of AGGs), pure CGG-repeat length, and the AGG-containing CGG-repeat “tail” within an FMR1 premutation allele is also shown.

Statistical Methods

Logistic regression (using the number of full mutation and premutation children from each mother as a binomial outcome) was used to assess the relationship between transmission, maternal total CGG length (as a continuous variable), length of pure CGG stretch (as a continuous variable), number of AGG interruptions (as a categorical variable) and genotype and haplotype of flanking SNPs.

RESULTS

Data were collected on the total and pure CGG-repeat lengths (as defined in the Figure 1), the number and positions of AGG interruptions, and maternal age at the time of childbirth in 267 mothers with an FMR1 premutation allele. Additionally, identical data were obtained for a total of 373 children representing transmission events. A total of 296 transmission events resulted in expansion to full mutation alleles, and 77 resulted in premutation alleles. The current analysis counted only the CGG repeat tracts that were classified as expanded (premutation or full mutation) maternally-transmitted alleles; children who inherited the normal X chromosome from the mother were excluded from the analysis. For maternal premutation alleles, the mean total CGG length was 90.8 (range 55—175) and the mean pure CGG length was 84.9 (range 34—175). One hundred and fifty-five (58%) mothers had no AGG interruptions in the expanded premutation allele, 69 (26%) had 1 interruption, and 43 (16%) had 2 interruptions. Table 1 shows the resulting transmissions that occurred in each CGG size range (total and pure CGG length).

Table 1.

Transmission Results by Total (a) and Pure (b) CGG Length

Table 1a.
Maternal Total Length	No. Premutation	No. Full Mutation	% Full Mutationa	Total	No. 0 AGG	No. 1 AGG	No. 2 AGG
50–59	20	1	3%	21	10	2	9
60–69	25	1	3%	26	8	6	12
70–79	23	44	69%	67	39	24	4
80–89	7	78	93%	85	43	30	12
90–99	2	56	97%	58	22	22	14
100–109	0	54	100%	54	41	6	7
110–119	0	20	100%	20	15	2	3
120–129	0	30	100%	30	28	1	1
130–139	0	8	100%	8	8	0	0
140–149	0	1	100%	1	1	0	0

Table 1b.
Maternal Pure Stretch	No. Premutation	No. Full Mutation	% Full Mutationa	Total	No. 0 AGG	No. 1 AGG	No. 2 AGG
30–39	8	0	0%	8	0	0	8
40–49	15	0	0%	15	0	2	13
50–59	19	1	3%	20	10	6	4
60–69	21	23	49%	44	8	24	12
70–79	11	74	90%	85	39	32	14
80–89	3	67	95%	70	43	20	7
90–99	0	31	100%	31	22	6	3
100–109	0	44	100%	44	41	2	1
110–119	0	16	100%	16	15	1	0
120–129	0	28	100%	28	28	0	0

^a%Full mutation was calculated for each mother then averaged across mothers

Total CGG Length and Transmission Status

Modeling the probability of transmission as a function of total CGG length using logistic regression analysis, we found that the risk of premutation to premutation expansion and more so of premutation to full expansion increased significantly with total CGG length (P < 0.001). The estimated odds ratio for total CGG length, as a continuous variable from the logistic regression model, was 1.23 (95% CI: 1.17, 1.30). For this model, the risk of expansion to a full mutation increases most dramatically between 70 and 75 repeats, with a predicted probability of 0.34 (95% CI: 0.24, 0.46) at 70 repeats and 0.60 (95% CI: 0.50, 0.69) at 75 repeats, consistent with previous findings.⁸ Alleles with 90–99 CGG repeats expanded to a full mutation in 97% of cases, compared to estimates of 94%⁸ and 86.8%.⁷

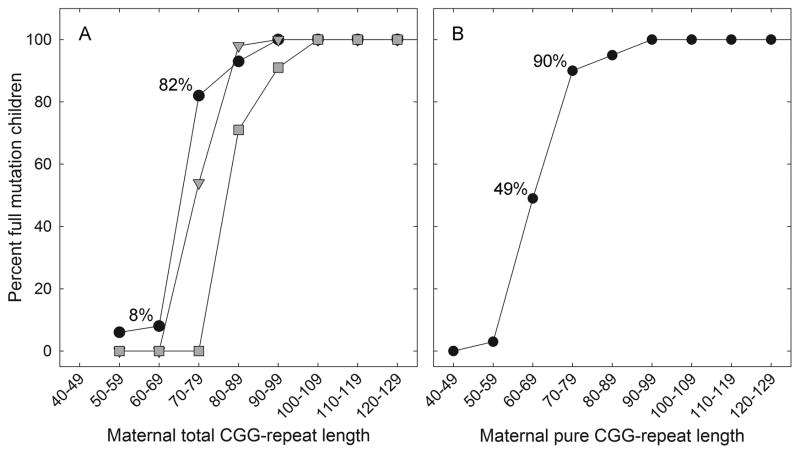
We also evaluated a logistic regression model with both total CGG length (as a continuous variable) and the number of AGG interruptions (as a categorical variable) as predictors of a full mutation expansion. As shown in Supplementary Table 1, the likelihood of transmission of a full mutation allele increased with increasing number of CGG repeats, and decreased with increasing number of AGG interruptions. Importantly, for a given total CGG repeat length, there was a substantial and statistically significant decrease in risk of a full mutation allele for maternal alleles with 2 interruptions relative to those with 0 interruptions (Figure 2A).

Figure 2.

Risk of expansion to a full mutation during maternal transmission. (A) Percent of alleles that expanded to a full mutation as a function of total CGG repeat length, for 0 (solid circle), 1 (gray triangles), or 2 (gray squares) AGG interruptions. (B) Percent full mutation expansions as a function of pure CGG repeat length within alleles that have either 0, 1, or 2 AGGs.

Pure CGG Repeat Length and Transmission Status

The observed results of transmission as a function of the pure CGG repeat lengths are shown in (Figure 2B). Modeling the probability of transmission as a function of pure CGG repeat length using logistic regression, the risk of expansion to a full mutation increased significantly with pure repeat length (P < 0.001), with an estimated odds ratio of 1.23 (95% CI: 1.17, 1.30) for pure CGG stretch (as a continuous variable). The risk of expansion to a full mutation increases most dramatically between 65 and 70 repeats, with a predicted probability of expansion to a full mutation of 0.48 (95% CI:0.37, 0.59) at 65 repeats and 0.72 (95% CI: 0.63, 0.79) at 70 repeats (Figure 2B).

The probability of transmission was also modeled (logistic regression) as a function of both tail length (sequence upstream of the most downstream AGG interruption; Figure 1) and pure CGG repeat length. The risk of transmission increased with increasing tail length (P = 0.005, odds ratio = 1.10; 95% CI: 1.03, 1.17) when adjusting for the length of the pure CGG repeat. The risk of transmission also increased with the length of the pure CGG repeat when adjusting for tail length (P < 0.001). An example of a different transmission outcome from two maternal premutation alleles of approximately the same number of CGG repeats but one with 0 and one with 2 AGG interruptions is illustrated in Figure 1.

Distributions of Long and Short Allele AGG Interspersion Patterns

Supplementary Table 2 shows the distributions of AGG interspersion patterns for 267 premutation and 264 normal alleles. McNemar’s test showed a significant difference in distribution of the most common interspersion patterns between normal and premutation alleles from the same mother (P < 0.001).

Flanking Markers as Predictor of Transmission Status

The probability of transmission was compared between long-allele genotypes of the flanking markers rs4949, rs25714, DXS548, and FRAXAC1 using logistic regression. The distribution of DXS548/FRAXAC1/rs4949/rs25714 haplotypes in the long and in the short alleles (express as percent) is shown in Supplementary Table 3 for the 164 premutation alleles and 157 normal alleles for which haplotypes could be resolved and data were available on all component genotypes. McNemar’s test showed a significant difference in haplotype distributions between normal and premutation alleles from the same mother (P < 0.001).

Although significant associations were observed between specific haplotypes and premutation or normal alleles (P < 0.001), supporting previous findings that haplotypes do correlate with risk of instability of the FMR1 CGG locus^26,27; we did not observe any significant association between the flanking markers and transmission to a full mutation. Supplementary Table 4 shows 4 haplotypes that were most frequent in the dataset, and the P-value resulting from using McNemar’s test to compare distribution of haplotypes between premutation and normal chromosomes, and P-values that resulted from logistic regression analysis that measured differences in risk of expansion to a full mutation during maternal transmission of a premutation allele by haplotype. Analysis of haplotype and risk of expansion in premutation alleles remains inconclusive as to whether there is an additional risk based on a cis-element, while we do not show significance, our data has large confidence intervals for the odd ratio, indicative of insufficient sample size.

The odds of transmission were lower for mothers with a FRAXAC1 allele length of 156, 158 (allele 2 and 1 respectively as in Macpherson et al., 1994)²⁷ or 160 bp than for mothers with a FRAXAC1 allele of 4 (152 bp), although this difference was not significant following adjustment for all pairwise comparisons (Tukey P = 0.091, odds ratio = 0.42, 95% CI = [0.19, 0.95]). No significant association was seen between the remaining flanking markers and transmission.

No difference in mean total CGG length (P = 0.584) or pure CGG repeat length (P = 0.917) was detected between SNP rs25714 genotypes by ANOVA modeling. Fisher's exact test did not show a significant association between rs25714 genotype and number of AGG interruptions (P = 0.431). Supplementary Table 5a shows the joint distribution of haplotype and AGG interspersion pattern for 164 premutation alleles. Chi-square testing (with P-values estimated through Monte Carlo simulation) was used to test for an association between haplotype and interspersion pattern for the table as a whole and for each cell. Premutation allele haplotype and interspersion pattern were significantly associated in general (P < 0.001); significantly more alleles than expected had the haplotype-interspersion pattern combinations X/7/3/A/C (P = 0.035 following Benjamini-Hochberg adjustment for multiple testing), 9-A-9-A-X/7/1/G/C (adjusted P = 0.021), and 9-A-9-A-X/2/1/G/C (adjusted P = 0.035). Supplementary Table 5b shows the joint distribution of haplotype and AGG interspersion pattern for 156 normal alleles. Chi-square testing (with P-values estimated through Monte Carlo simulation) was used to test for an association between haplotype and interspersion pattern for the table as a whole and for each cell. Normal allele haplotype and interspersion pattern were significantly associated in general (P < 0.001); significantly more alleles than expected had the haplotype-interspersion pattern combinations 9-A-9-A-X/7/4/G/T (adjusted P = 0.005), 10-A-9-A-X/7/3/A/C (adjusted P < 0.001), 13-A-X/7/3/G/C (adjusted P = 0.007), 9-A-9-A-X/7/3/G/C (adjusted P = 0.031), 9-A-12-A-X/6/4/G/C (adjusted P = 0.031), 9-AX/6/4/G/C (adjusted P = 0.004), and 10-A-X/6/3/A/C (adjusted P = 0.032). Significantly fewer alleles than expected had the haplotype-interspersion pattern combinations 9-A-9-A-X/7/3/A/C (adjusted P < 0.001) and 10-A-9-A-X/7/3/G/C (adjusted P = 0.005).

Maternal Age and Risk of Expansion to a Full Mutation

We assessed the contribution of maternal age to the risk of expansion to a full mutation using data from 234 mothers. Using a logistic regression model, maternal age was not statistically significant as a variable that contributed to risk of expansion to a full mutation when no other factors were considered (P-value = 0.500). Additionally, maternal age did not reach significance when considered with total CGG length (P-value = 0.091), total CGG length and number of AGG interruptions (P-value = 0.066), or pure CGG repeat length (P-value = 0.090), but did show marginal significance when tail length and pure CGG repeat length were used as variables of the logistic regression model (P-model = 0.040). When maternal age was added to logistic regression models that looked at other variables it did not change the conclusions regarding the other variables.

Selection of Best Model for Risk of Transmission Using the Akaike Information Criterion

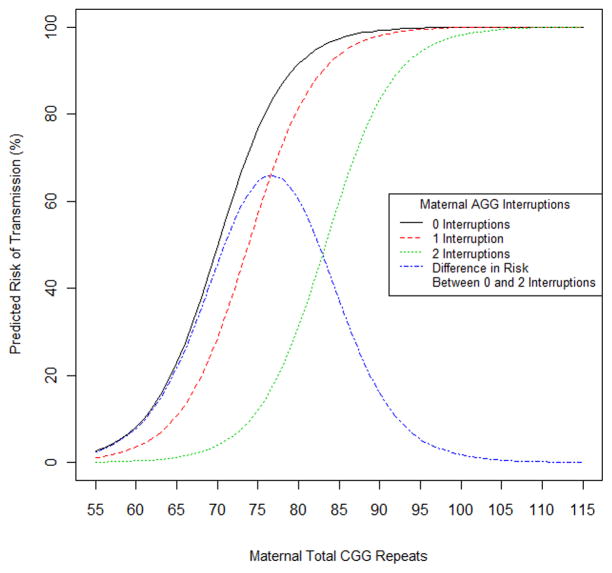
To determine which model best describes the risk of transmission in this dataset, we compared a number of models based on the Akaike Information Criterion (AIC).²⁸ The AIC provides a numerical measure of the goodness of fit of a model, while incorporating a penalty based on the number of covariates included in the model that gives preference to more parsimonious models. A model with a lower AIC is considered preferable to a model with a higher AIC. Models considered included any combination of the covariates, pure CGG repeat length, total CGG repeat length, tail length, and number of AGG interruptions (excluding models using both pure CGG and total repeat lengths due to the high correlation between these variables). While a number of the models considered had similar AIC values, the model including maternal total CGG repeat length and number of AGG interruptions had the lowest AIC (Supplementary Table 6). Based on this model, the predicted risk of transmission to a full mutation allele for a maternal allele where the CGG repeat number varies from 55–120; for 0, 1, and 2 AGG interruptions is shown in Table 2 and Supplementary Table 7 and depicted in Figure 3.

Table 2.

Predicted Risk of Transmission of Full Mutation Allele By Maternal Total CGG Repeat Length and Number of AGG Interruptions

	CGG Repeat Length	55a	60	65	70	75	80	85
Number of AGG interruptions	0	2.6% (0.7%, 9.5%)c	8.2% (2.9%, 21.1%)	22.9 (11.1%, 41.2%)	49.6% (32.9%, 66.3%)	76.5% (62.8%, 86.3%)	91.5% (83.5%, 95.9%)	97.3% (93.2%, 99%)
	1	1.1% (0.2%, 4.9%)	3.5% (1%, 11.4%)	10.7% (4.2%, 24.8%)	28.5% (15.2%, 46.9%)	56.9% (40.3%, 72.2%)	81.4% (68.8%, 89.7%)	93.6% (86.3%, 97.1%)
	2	0.1% (0%, 1%)	0.4% (0.1%, 2.5%)	1.2% (0.2%, 6%)	4% (1%, 14.3%)	12% (4%, 31%)	31.2% (13.9%, 56.1%)	60.1% (36.4%, 79.8%)
Differential riskb		2.5%	7.8%	21.7%	45.6%	63.5%	60.3%	37.2%
	CGG Repeat Length	90	95	100	105	110	115	120
Number of AGG interruptions	0	99.2% (97.2%, 99.8%)	99.7% (98.9%, 99.9%)	99.9% (99.5%, 100%)	100% (99.8%, 100%)	100% (99.9%, 100%)	100% (100%, 100%)	100% (100%, 100%)
	1	98% (94.4%, 99.3%)	99.4% (97.7%, 99.8%)	99.8% (99.1%, 100%)	99.9% (99.6%, 100%)	100% (99.8%, 100%)	100% (99.9%, 100%)	100% (100%, 100%)
	2	83.3% (64.7%, 93.1%)	94.3% (84.3%, 98.1%)	98.2% (93.6%, 99.5%)	99.5% (97.5%, 99.9%)	99.8% (99%, 100%)	100% (99.6%, 100%)	100% (99.8%, 100%)
Differential risk		15.9%	5.4%	1.7%	0.5%	0.2%	0%	0%

^aNumber designates the lower bound for the given bin (e.g., 55 = 55–59 CGG repeats)

^bDifference in risk of full mutation expansion (0 versus 2 CGG repeats), for a given total CGG repeat length.

^cNumbers in parenthesis denote the 95% confidence interval for the predicted risk

Figure 3.

Predicted risk of expansion during transmission by maternal total CGG repeat and AGG interruptions. Risk of expansion decreases when the number of AGG interruptions increases, for the same total CGG repeat length. The differential risk between one and two AGG interruptions is highest between 75 and 80 total CGG repeats.

DISCUSSION

AGG interruptions within the CGG-repeat element of the FMR1 gene are known to be associated with reduced propensity for repeat expansion to a full mutation during maternal transmission, although the molecular basis of the “AGG effect” is not known. Notwithstanding this lack of mechanistic understanding, it is imperative to quantify the influence of AGG interruptions on transmission instability to provide an accurate assessment of the risk of having a child with a full mutation FMR1 allele for mothers who are premutation carriers (~0.5 to 1% of all women). To this end, we characterized the CGG repeat locus in 267 carrier mothers of children with expanded (premutation or full mutation) CGG repeats, determining the total CGG repeat length (inclusive of AGGs), number and spacing of AGG interruptions, length of the longest run of pure CGG repeats, associated haplotypes; all as possible outcome predictors for transmission.

Consistent with previous studies,^7,8 the risk of a full mutation FMR1 allele in a child of a premutation carrier mother increased with increasing total repeat length, most dramatically for maternal FMR1 alleles with ~70 to 90 total repeats, or ~60–80 uninterrupted (pure) CGG repeats (Figure 2; Table 2). The most striking aspect of the AGG effect, and the most directly relevant to risk assessment, is the differential risk of expansion to a full mutation in a child for a given total repeat length in the mother, depending on the number of AGG interruptions. This difference in predicted risk is most pronounced for total repeat lengths in the range of 70 to 80 CGG repeats, where the difference in risk can exceed 60%. For example, at a total repeat length of 75, the predicted risk is 77% for alleles with no AGGs, but only 12% for alleles with 2 AGGs.

Among models that utilized combinations of total length, pure CGG repeat length, number of AGG interruptions, and CGG tail length; the risk of transmission was best described for the current dataset using a model that combined total CGG length and number of AGG interruptions using AIC.²⁸ Of course, the current optimization result could be biased by the relatively similar AGG patterns that were present in our dataset, since nearly all (98%) of the premutation alleles share four AGG patterns (Supplementary Table 2). Considering that tail length was shown to significantly associate with risk of expansion to a full mutation, it is possible that predictions made with additional data that incorporate less frequently occurring tail lengths of larger size, will better fit models that incorporate pure CGG repeat and/or tail length.

Previous studies have reported a higher risk of expansion to a full mutation between certain haplotypes, and showed separate lineages of mutations and founder effects to explain population specific prevalence of expanded alleles.^29,30 Although a difference in the distribution of haplotypes between the premutation and normal chromosomes was observed in this study, we were unable to detect any association between haplotypes and the outcome of maternal transmission, either before or after correcting for the length of the pure stretch. It is possible that the lack of association between the haplotypes and transmission outcome of premutation alleles could be due to an insufficient number of individuals relative to the number of unique haplotypes in the analysis.

In the current study, the location and number of AGG interruptions were determined in both the normal and the premutation alleles using a PCR assay that amplifies from the CGG repeat unit towards the 3’ of the FMR1 gene. This approach allows for AGG interruptions, which are physically near the 5’ end of the region, to be detected in reverse order on capillary electropherograms.^21,23 For longer, expanded alleles, AGG interruptions are detected later during electrophoresis than the AGG interruptions in normal range alleles. Therefore, it is very unlikely that an AGG interruption within the premutation allele is masked by the AGG interruption²³ on the normal allele (Figure 1).

The influence of AGG interruptions should be incorporated into the genetic counseling process as a modifier of risk for maternal transmission of the premutation to the full mutation, thus affording more accurate estimates of risk than were heretofore available. Both total CGG repeat and number/position of AGG interruptions can now be ordered in a clinical setting and be made available to the genetic counselor when counseling a patient regarding their risk of having a child with the full mutation. It is important to convey this more accurate risk information to families through the genetic counseling session(s), which will serve to further enhance their decision making process. To this end, we provide in Table 2 the predicted risk of expansion to a full mutation during maternal transmission, calculated by the total CGG length and number of AGG interruptions (see Supplementary Table 7). Clearly, these tables embody all of the limitations of cohort size and population bias at the level of AGG interspersion patterns; therefore, it is essential that additional studies be performed with larger cohorts and different populations to refine the models used to quantify the effects of both CGG repeat length and AGG interruptions on the risk of full mutation expansions during transmission. However, our findings have important clinical implications as they help to refine risk for carriers and improve genetic counseling. Indeed, understanding the molecular structure of the FMR1 gene related to the presence of AGG interruptions will provide substantially more accurate information that was not previously available for genetic counseling sessions; counselors will be able to provide information regarding the risk for maternal transmission of the premutation to the full mutation to at-risk families. In addition to having a major impact on our ability to predict the likelihood of CGG-repeat expansion from a premutation to a full mutation, the results of this study will have important implications for genetic counseling and interpretation of risk for carriers of intermediate “gray zone” and small premutation-range FMR1 alleles, for which instability is currently unknown. Alleles in this range (45–55 CGG repeats)³¹ are quite common in the general population;³² however their stability during mother-child transmission is unknown. Preliminary reports indicate that the presence of AGG interruptions predict instability of the CGG repeat, even in small FMR1 alleles³³, having a high impact in genetic counseling by risk assessment of smaller alleles. Finally, more studies are warranted in order to approach a unified model able to link and assess the contribution of both cis elements (AGG number and position, haplotypes, pure CGG tract) and trans factors (e.g., DNA repair proteins) governing repeat instability. This will have a great impact and implications for the mechanism(s) responsible of trinucleotide expansion, which lead to a number of human genetic disorders of a high burden to society.