Abstract
Transoral robotic surgery (TORS) offers a minimally invasive approach to resection of base of tongue tumors. However, precise localization of the surgical target and adjacent critical structures can be challenged by the highly deformed intraoperative setup. We propose a deformable registration method using intraoperative cone-beam CT (CBCT) to accurately align preoperative CT or MR images with the intraoperative scene. The registration method combines a Gaussian mixture (GM) model followed by a variation of the Demons algorithm. First, following segmentation of the volume of interest (i.e., volume of the tongue extending to the hyoid), a GM model is applied to surface point clouds for rigid initialization (GM rigid) followed by nonrigid deformation (GM nonrigid). Second, the registration is refined using the Demons algorithm applied to distance map transforms of the (GM-registered) preoperative image and intraoperative CBCT. Performance was evaluated in repeat cadaver studies (25 image pairs) in terms of target registration error (TRE), entropy correlation coefficient (ECC), and normalized pointwise mutual information (NPMI). Retraction of the tongue in the TORS operative setup induced gross deformation >30 mm. The mean TRE following the GM rigid, GM nonrigid, and Demons steps was 4.6, 2.1, and 1.7 mm, respectively. The respective ECC was 0.57, 0.70, and 0.73 and NPMI was 0.46, 0.57, and 0.60. Registration accuracy was best across the superior aspect of the tongue and in proximity to the hyoid (by virtue of GM registration of surface points on these structures). The Demons step refined registration primarily in deeper portions of the tongue further from the surface and hyoid bone. Since the method does not use image intensities directly, it is suitable to multi-modality registration of preoperative CT or MR with intraoperative CBCT. Extending the 3D image registration to the fusion of image and planning data in stereo-endoscopic video is anticipated to support safer, high-precision base of tongue robotic surgery.
Keywords: deformable image registration, Gaussian mixture model, Demons algorithm, cone-beam CT, image-guided surgery, transoral robotic surgery
1. INTRODUCTION
Head and neck carcinoma is the sixth most common cancer worldwide and afflicts approximately half a million people each year (Parkin et al., 2005). In the United States, the incidence of cancers involving the oral cavity and pharynx has increased for at least six consecutive years (2007–2012) as estimated by the American Cancer Society (Jemal et al., 2007, Jemal et al., 2008, Jemal et al., 2009, Jemal et al., 2010, Siegel et al., 2011, Siegel et al., 2012). In 2012, more than 40,000 individuals were diagnosed with oropharyngeal cancer, resulting in nearly 8000 deaths (Siegel et al., 2012). Traditional surgical approaches are invasive and involve high morbidity, including transcervical and transmandular approaches with need for tracheotomy and feeding tube placement. Radiation with or without chemotherapy offers an adjuvant or alternative treatment but may result in higher rates of gastrostomy tube dependence due to chronic mucosal injury and tissue fibrosis (Weinstein et al., 2010). Transoral robotic surgery (TORS) provides a minimally invasive approach to resection of oropharyngeal cancer with reduced morbidity, elimination of tracheostomy, decreased operative and hospitalization time, and improved postoperative function (swallowing) in comparison to open procedures (Van Abel and Moore, 2012), and reduced toxicity in comparison to chemo-radiotherapy (Weinstein et al., 2010). However, precise localization of the surgical target (tumor) and adjacent critical tissues (lingual nerves and arteries) can be challenging because these tumors tend to have significant submucosal extension that are hidden from direct visualization. Furthermore, preoperative CT and/or MR typically acquired in natural pose (neck in neutral position, mouth closed, and tongue in repose), to define and visualize such structures before surgery are of limited value for precise localization in the highly deformed intraoperative setup (neck flexed, mouth open, and tongue retracted). Acquisition of the preoperative images in an anatomical pose similar to the intraoperative setup would be impractical and painful (without anesthesia) due to instrumentation and retraction of the tongue. Intraoperative cone-beam computed tomography (CBCT) acquired with the patient in the operative setup could be used to account for such deformation.
Addition of a C-arm capable of high-quality intraoperative 3D imaging to an already crowded operating workspace is a challenge to collision-free setup. Integration of the robot and C-arm in a manner permitting simultaneous operation during the procedure is an area of ongoing research, offering the benefit of CBCT and fluoroscopy on demand during intervention. A simple, feasible clinical workflow for CBCT-guided TORS is illustrated in figure 1, bringing the C-arm and robot to the operating table at distinct points in the procedure. Specifically, following patient setup (but prior to docking the robot), C-arm CBCT is acquired as a basis for deformable registration of preoperative image and planning data to the deformed, intraoperative context. Then, the C-arm is removed from tableside, and the robot is docked and proceeds normally (but with the benefit of the CBCT image and deformably registered preoperative data for localization and guidance). Since the visibility of soft tissues can be fairly limited in CBCT due to noise and artifacts, direct localization of the target and critical tissues can be difficult. To overcome this challenge, the proposed registration method uses CBCT as the basis to transform preoperative images and planning data to the intraoperative scene, permitting visualization of such tissues in the (geometrically registered) preoperative images, in planning data registered and overlaid on CBCT, and/or by registration and fusion of planning data in stereo-endoscopic video.
Figure 1.
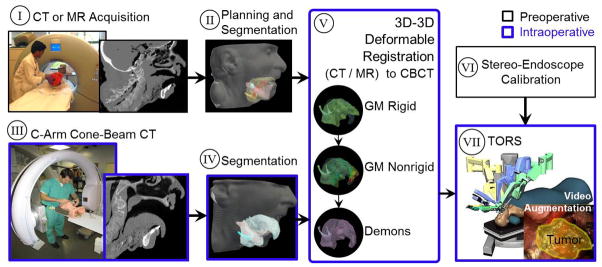
Potential clinical workflow for CBCT-guided TORS. Preoperative steps include (I) CT or MR imaging, (II) planning and segmentation, and (VI) endoscopic video calibration. Intraoperative steps include (III) patient setup and C-arm CBCT prior to docking the robot, (IV) segmentation, (V) deformable registration of preoperative images and intraoperative CBCT, and (VII) robot-assisted tumor resection with stereoscopic video visualization. Note the large deformation associated with the TORS operative setup, evident in images (I–II) and (III–IV). The proposed method for 3D deformable image registration (V) is detailed in this paper. Endoscopic video calibration (VI) and CBCT-to-robot registration (VII) are the subject of ongoing and future work (Liu et al., 2012).
Registration algorithms generally can be considered in two broad categories: feature-based and intensity-based approaches. Feature-based approaches employ points, curves, surfaces, and/or finite elements (Ong et al., 2010) in computing the deformation, rather than image intensities directly. They therefore tend to operate independently of the underlying imaging modality and can be robust against image artifacts; however, they can encounter difficulty in feature detection and correspondence. The iterative closest point method, for example, is a widely used, relatively fast point matching algorithm (Besl and McKay, 1992, Lange et al., 2003, Woo Hyun et al., 2010, Woo Hyun et al., 2012) but requires one-to-one correspondence between point features that can be difficult to achieve in real anatomy. Other studies (Tsin and Kanade, 2004, Jian and Vemuri, 2005, Wang et al., 2008, Wang et al., 2009, Chen et al., 2010, Tustison et al., 2011, Jian and Vemuri, 2011) have incorporated robust statistics and information-theoretic measures to account for such unknown correspondence, outliers, and noise in point set registration. Jian and Vemuri proposed a robust point set registration based on the statistically robust L2 measure of the Gaussian mixture (GM) representations of the point sets (Jian and Vemuri, 2005, Jian and Vemuri, 2011), allowing various transformation models (e.g., rigid, affine, thin-plate spline (TPS), Gaussian radial basis functions, and B-Spline) in a computationally efficient manner due to the closed-form solution of the L2 distance between two GMs.
Intensity-based approaches, on the other hand, maximize an image similarity metric and can apply to single-modality (e.g., CT-to-CT) or multi-modality (e.g., MR-to-CT) image registration. Implementations using statistical measures such as mutual information (MI) (Wells Iii et al., 1996, Mattes et al., 2003, Coselmon et al., 2004) and its normalized variants (Studholme et al., 1999, Rueckert et al., 1999, Rohlfing et al., 2003, Rohlfing et al., 2004) can be modality-independent (i.e., similarity assessed in terms of image statistics, rather than image intensity directly) but can be computationally expensive due to the estimation of image intensity distributions at every iteration during optimization. Algorithms based on sum of square differences (SSD) or absolute difference (AD) of intensity values, by comparison, are relatively fast and parallelizable but require images with consistent intensity values. To exploit the efficiency of SSD or AD type measures, input images can be encoded to a consistent intensity space in which voxel values describe some characteristic of the original images. The distance transformations (DT), for example, encode each voxel by the shortest distance to the surface of the structure of interest, providing shape information (e.g., boundary and medial line) that can be used as a basis for registration, especially for low-contrast images (e.g., subtle soft tissue variations in CT or CBCT). In (Cazoulat et al., 2011), the distance transform computed on segmented organs of interest in CT planning images for prostate radiotherapy were registered to daily CBCT using the Demons algorithm for surface matching between organ contours. Demons operating on distance map transforms can therefore offer a computationally fast algorithm applicable to images varying in image intensity (including CT, MR, and/or CBCT), provided a segmentation from which the distance transform can be computed. Demons is intrinsically fast (Sharp et al., 2007, Vercauteren et al., 2009, Nithiananthan et al., 2009, Nithiananthan et al., 2011) and analogous to minimization of SSD in an approximate gradient descent scheme (Pennec et al., 1999, Cachier et al., 1999). Variants of the Demons algorithm have been widely applied in image-guided interventions, including image-guided head-and-neck surgery (Nithiananthan et al., 2009, Nithiananthan et al., 2011, Nithiananthan et al., 2012), image-guided neurosurgery (Risholm et al., 2009, Risholm et al., 2010), head-and-neck radiotherapy (Hou et al., 2011), and prostate radiotherapy (He et al., 2005, Godley et al., 2009). Castadot et al. conducted a study comparing the accuracy of deformable registration methods, including Demons, free-form deformation, and level-set variants for head and neck adaptive radiotherapy (Castadot et al., 2008), showing Demons variants to perform well in terms of geometric volume overlap and image similarity.
To resolve the large deformation associated with the operative setup in transoral base of tongue surgery as opposed to patient positioning for pre-operative CT or MR imaging, we propose a deformable registration method that hybridizes a feature-based initialization (using GM models) followed by a Demons refinement (operating on distance transforms). The combined registration is intensity-invariant and thereby allows registration of preoperative CT and/or MR to intraoperative CBCT. Other aspects of the system, such as image quality and dose in C-arm CBCT (Daly et al., 2006, Fahrig et al., 2006, Bachar et al., 2007, Daly et al., 2011, Schafer et al., 2011, Schafer et al., 2012) and overlay of registered planning data in stereoscopic video (Liu et al., 2012), are the subject of other work. Section 2 details the registration method, and Sections 3 and 4 analyze the resulting registration performance in cadaver studies, with a detailed sensitivity analysis of algorithm parameters provided in the Appendix. Section 5 concludes with discussion of the advantages and limitations of the registration method and outlines future work required for clinical translation.
2. REGISTRATION METHODS
2.1 Overview of the Method
A deformable registration framework was implemented to solve the nonrigid transformation from the moving image (pre-operative CT or MR, denoted I0) to the fixed image (intraoperative CBCT, denoted I1). The framework comprises four main steps as shown in figure 2 and summarized as follows. First, the volume of interest (VOI) (i.e., tongue and hyoid bone) is segmented in both the moving image (I0) and the fixed image (I1). The resulting segmentation “masks” provide surface meshes from which point clouds are defined. Second, GM registration is used to compute a rigid initial alignment of point clouds (GM rigid), followed by a deformation (GM nonrigid) using a thin-plate spline. The use of continuous probability distributions to model the discrete point sets and minimization of L2 distance as a measure of distribution similarity makes the algorithm invariant to permutations of points within the set (Kondor and Jebara, 2003) and less sensitive to outliers, missing data, and unknown correspondences. Finally, a fast-symmetric-force variant of the Demons algorithm (Vercauteren et al., 2007) is applied to the DT images (Maurer et al., 2003) computed from the moving and fixed masks after GM registration. Because the Demons step operates on the DT images (and not directly on image intensities), the entire registration process is independent of image intensity and therefore allows registration of preoperative CT or MR to intraoperative CBCT. The proposed registration framework was implemented based on the Insight Segmentation and Registration Toolkit (ITK) (Ibanez et al., 2002, Ibanez et al., 2005) and open-source point set registration using GM (Jian and Vemuri, 2011). The four steps in the registration framework are detailed in the following sections, and notation of parameters pertinent to each step is summarized in table I.
Figure 2.
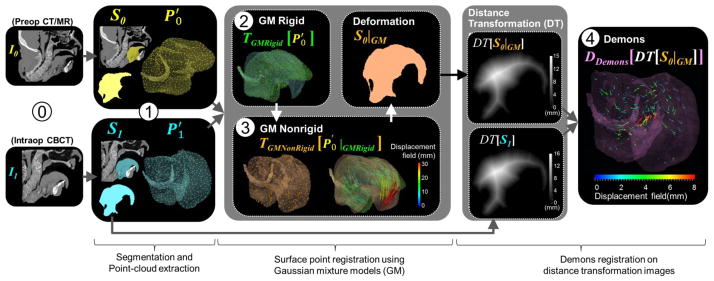
Deformable registration framework for CBCT-guided TORS. ⓪ Acquisition of preoperative image (I0) and intraoperative CBCT (I1). ➀ Segmentation of the VOI and extraction of surface point clouds. ➁ GM rigid and ➂ GM nonrigid registration. ➃ Refinement using the Demons algorithm applied to distance map transforms of the moving and fixed images.
2.2. Segmentation of Model Structures
The VOI is first segmented in both I0 and I1. Automatic segmentation can be challenging due to image artifacts and the low contrast of soft tissues in CT or CBCT, and simple region growing and active contour methods were found to result in erroneous segmentation boundaries. Advanced segmentation algorithms (Commowick et al., 2008, Qazi et al., 2011, Shyu et al., 2011, Zhou et al., 2011) are areas of ongoing research, and since the focus of initial work reported below was the registration process (not the segmentation process), we employed semi-automatic segmentation to identify the VOIs (denoted S0 and S1) by active contour region growing refined by manual contouring. Segmentation included the superior surface of the tongue (air-tissue boundary) and extended laterally within the bounds of the mandible (bone-tissue boundary) and inferiorly to the hyoid (more challenging soft tissue boundaries) using ITK-Snap (Yushkevich et al., 2006). A fill-holes operation was applied, followed by isosurface extraction based on Delaunay triangulation (Gelas et al., 2008b) to generate meshes of the VOI from S0 and S1. The meshes were downsampled using incremental edge-collapse decimation (Gelas et al., 2008a) for computational efficiency. Finally, the mesh vertices ( and ) were extracted as input to GM registration.
2.3. Gaussian Mixture Registration
2.3.1 Gaussian Mixture Models
The GM registration steps (i.e., GM rigid and nonrigid) started with “normalization” of the moving and fixed point sets ( and ) to provide initial alignment and scaling of each set such that each point can be treated approximately equally (Hartley, 1997, Tustison et al., 2011). To normalize , for example, each point was transformed to an object-centered coordinate system by subtracting the centroid location ( ), followed by isotropically scaling with (Kanatani, 2005, Tustison et al., 2011):
| (1) |
where represents a 3×n matrix of the moving points, is a 3×n matrix whose column vector elements are , and ||·||F denotes the Frobenius norm.
GM models are widely used to describe the underlying distribution of point sets (Wang et al., 2008, Myronenko and Song, 2010, Sandhu et al., 2010, Jian and Vemuri, 2011). A GM is defined as a linear combination of Gaussian densities:
| (2) |
where x is a position vector in R3, Θ = (w1, …, wn, μ1, …, μn, Σ1, … Σn) is a set of mixture parameters of the n Gaussian density components, wi is a weighting coefficient satisfying , and φi(x|μi, Σi) is a Gaussian component i:
| (3) |
where μi is a mean vector for component i, Σi is a 3×3 covariance matrix, and |·| denotes the determinant. We modeled each normalized point set using an overparameterized GM (Jian and Vemuri, 2011). The set of normalized moving points P0 = [x0,1, x0,2, … x0,n], for example, was modeled as a linear combination of n equally-weighted isotropic Gaussian densities:
| (4) |
where the 1/n term implies equal weighting, and φ0,i(x|x0,i, σ2I) denotes an isotropic Gaussian component i with a mean vector marking a point x0,i in P0 and a width of σ (units mm). The full covariance matrix (including off-diagonal elements) was not needed for the overparameterized mixture, since the combination of a large number of Gaussian components is sufficient to capture the underlying unknown distribution of P0. Similarly, the GM representation of P1 was the sum of n equally-weighted isotropic Gaussian densities with isotropic covariance σ2I.
A statistically robust L2 distance was used to measure dissimilarity between two mixtures, defined as (Williams and Maybeck, 2006, Jian and Vemuri, 2011, Scott, 2001):
| (5) |
where Θ0(T) is a set of mixture parameters of P0 after transformation T, and Θ1 is the set of mixture parameters for P1. The L2 distance cost function only involved terms coupling φ(x|Θ0(T)), since φ(x|Θ1) was fixed during optimization. The remaining integrals were further simplified using the Gaussian identity ∫ φ(x|μ0, Σ0) φ(x|μ1, Σ1) dx = φ(0|μ0 – μ1, Σ0 – Σ1) as in (Wand and Jones, 1995) to Gaussian kernels, which were evaluated in closed form (Jian and Vemuri, 2011).
2.3.2 GM Rigid
The registration process is initialized by rigid transformation computed in the GM rigid step. The rigid transformation (TR,t) describes the rotation (R) and translation (t) of P0 with respect to P1 and can be applied to a normalized moving point x0,i in P0 as:
| (6) |
TR,t was estimated by minimizing the L2 distance between the GM models of P0 and P1. Since the L2 norm of the moving mixture is invariant under rigid transformation (i.e., ∫ φ(x|Θ0(TR,t))2 dx = ∫ φ(x|Θ0)2 dx, the cost function only involved the inner product between the two mixtures:
| (7) |
where Θ0(TR,t) is a set of the GM parameters for the rigidly transformed mixture of P0, and Θ1 is the set of the GM parameters of the mixture of P1. Minimizing d in equation (7) maximizes the similarity between the two mixtures, since the integral represents the overlap of the two mixtures (Williams and Maybeck, 2006).
Minimizing the cost function was performed iteratively using the limited memory Broyden-Fletcher-Goldfarb-Shanno method with bounded constraints (L-BFGS-B) (Byrd et al., 1995, Zhu et al., 1997) in a hierarchical multiscale scheme to improve robustness against local minima. The nominal number of hierarchical levels was set to 3, and the number of iterations per level was [10, 20, 30]. The coarser levels involved a larger width of the distribution ( ), and the width at subsequent levels ( ,ℓ > 1) was reduced at each level. An increased number of iterations was used at the finer levels to better capture the underlying point sets, since execution time per iteration at each level was approximately equal - i.e., the execution time depended on the number of points (which was similar at every level), not on the width of the distribution. (See also the sensitivity analysis of such parameters in the Appendix.)
The final transformation (TGMRigid) is the concatenation of the inverse normalization of , the resulting rigid transformation (TR,t), and the normalization of :
| (8) |
where TGMRigid is a 3×4 affine transformation matrix, ω0 and ω1 are the scales of and , and are the centroids of and , R is the rotation matrix, and t is the translation vector of TR,t.
2.3.3 GM Nonrigid
Following the GM rigid step, deformation of the point sets was computed using the GM nonrigid registration (step ➂ in figure 2). The deformation defined a nonrigid mapping from the moving point set after GM rigid ( ) to the fixed point set ( ). Normalization of comprised a scale of ω1 (equal to the scale of ) and a centroid of . The final deformation was a concatenation of the normalization and TPS transformation estimated using GM models of the point sets after normalization (P0|GMRigid and P1). The TPS transformation was parameterized by affine components (A and t) and a warp component (WU) which can be applied to each point in P0|GMRigid as:
| (9) |
where x0,i|GMRigid is a point i in P0|GMRigid, A is a 3×3 affine coefficient matrix, t is a 3×1 translation vector, W is a 3×n warp coefficient matrix, and U(x0,i|GMRigid) = [U(x0,i|GMRigid, x0,k|GMRigid)] is a n×1 vector of TPS basis functions. The TPS basis function for 3D was defined as U(qi, qk) = −||qi – qk|| where qi and qk are points in R3 and ||·|| is the Euclidean distance (Jian and Vemuri, 2011).
The TPS was estimated with the regularization term involving bending energy proportional to WKWT(Bookstein, 1989, Belongie et al., 2002). The kernel K is the n×n matrix containing ki,j = U(x0,i|GMRigid, x0,j|GMRigid). The cost function was the combination of a distance measure and the bending energy represented by:
| (10) |
where Θ(TW,A,t) is the set of GM parameters of the warped mixture of P0|GMRigid, and Θ1 is the set of GM parameters of the mixture of P1.
The cost function was iteratively minimized using the limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method (Liu and Nocedal, 1989) in a hierarchical multiscale manner, with the number of levels fixed at three and the number of iterations per level fixed to [50, 150, 300]. In addition to adjusting the width of the Gaussian kernel ( ) in each step of the hierarchy, the strength of regularization was also adjusted at each level though variation of λGMNonRigid. The larger the value of λGMNonRigid, the smoother the resulting deformation (i.e., the more affine and less deformed).
The final deformation (TGMNonRigid) was the concatenation of the inverse normalization of , the resulting TPS transformation (TW,A,t), and the normalization of :
| (11) |
where is a point i in , ω1 and are the scale and centroid of , A and t are the affine components of TW,A,t, WUis the warp component of TW,A,t, TGMRigid is the GM rigid transformation as in equation (8), and is the centroid of . The resulting TGMNonRigid was used to interpolate a displacement for each voxel in the moving volume to a corresponding voxel in the fixed volume, with the GM nonrigid displacement field denoted DGMNonRigid.
2.4. Demons Registration
2.4.1 Distance Transformation
A DT of the segmented mask assigns each voxel a value given by the distance to the closest feature voxel (i.e., to voxels on the boundary of the mask). Although DT is fairly computationally expensive, we used the fast DT algorithm of Maurer et al. based on dimensionality reduction and partial Voronoi diagram construction (Maurer et al., 2003). DTs were computed for both the fixed mask (S1) and the moving mask after GM rigid and nonrigid registration (denoted simply as S0|GM). As a result, voxels in the deeper aspects of the tongue (away from the boundary) exhibit increasing DT values. Voxels at the boundary and external to the mask were assigned to zero. A histogram equalization transform (Nyul et al., 2000) was applied to the DT images prior to Demons registration to normalize voxel values (i.e., image intensity in the DT image).
2.4.2 Multi-resolution Demons Registration
Demons provides a non-parametric mapping of voxels from the moving image space to the fixed image space (Thirion, 1998) described as a displacement field DDemons containing a displacement vector for each voxel. Calculation of displacement vectors was based on an optical flow equation assuming small displacements and a similar intensity space between images (Thirion, 1998, Sharp et al., 2007). The Demons process alternates between iterative estimation of an update field and regularization using Gaussian filters to impose smoothness on deformation.
Variants of Demons have been proposed to increase the convergence rate (Vercauteren et al., 2007), reduce the dependence on image intensities (Guimond et al., 1999, Nithiananthan et al., 2011), improve the update field computation (He et al., 2005, Vercauteren et al., 2009), and incorporate a stopping criterion (Nithiananthan et al., 2009, Peroni et al., 2011). We used the symmetric force variant (i.e., an update field computed from the average gradient of the fixed image and the moving image) (Thirion, 1995, Vercauteren et al., 2007) and the hybrid regularization scheme (Cachier et al., 2003). Vercauteren et al. improved the convergence rate of the symmetric force variant by using the efficient second-order minimization — referred to as fast-symmetric force Demons (Vercauteren et al., 2007). An update displacement vector at a voxel x of an update field at the current iteration it is computed for the symmetric force variant as:
| (12) |
where is an update displacement vector at the voxel x at the iteration it, A is the fixed image (in this work, the DT image of the fixed mask, DT[S1]), B is the moving image (i.e., the DT image of the moving mask after GM registration, DT[S0|GM]), the term |B(it)(x) − A(0)(x)| estimates the image difference (including noise), and ∇⃗A(0)(x) and ∇⃗B(it)(x) are gradient images of A and B, respectively. The normalization K (Vercauteren et al., 2009, Cachier et al., 2003) is:
| (13) |
where the mean squared value of the voxel size of DT[S1] makes the force computation invariant to voxel scaling at each multi-resolution level (detailed below) (Nithiananthan et al., 2009), and MSL is the maximum update step length (Godley et al., 2009), which was bounded by (Cachier et al., 1999, Vercauteren et al., 2009).
Following estimation of the update field, a regularization is applied incorporating two deformation models - fluid and elastic models (Cachier et al., 2003) as follows:
| (14) |
where * denotes convolution, is the estimated displacement field at the current iteration it, is the update field at the current iteration, GσUpdateField is a Gaussian filter with a width of σUpdateField, and GσDisplacementField is a Gaussian filter with a width of σDisplacementField. The kernel GσUpdateField results in a fluid-like deformation model capable of resolving large deformations but usually does not preserve topology. The kernel GσDisplacementField, on the other hand, regularizes the displacement field and results in elastic-like deformation that preserves topology but may not resolve large deformations (Cachier et al., 2003). The original Demons (Thirion, 1998) could be considered as an elastic deformation model since only the displacement field was regularized.
A multiresolution pyramid was used to improve robustness and increase computational efficiency (Cachier et al., 1999, He et al., 2005, Nithiananthan et al., 2009). Both DT[S0|GM] and DT[S1] were repeatedly downsampled to coarser resolution by a factor of 2 (e.g., downsampling factors of 8, 4, 2, and 1). The convergence criterion was based on the percent change in mean square error (MSE) of voxel values between the current and previous five iterations (Peroni et al., 2011), specifically MSE less than a threshold of PT(1) = 0.01% for the coarsest level and PT(ℓ) = PT(ℓ−1) × 4 for the subsequent levels ℓ > 1.
3. EXPERIMENTAL METHODS
3.1. Cadaver Setup
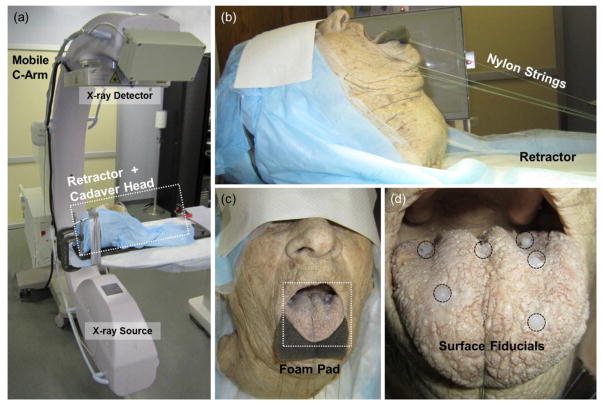
Registration accuracy and the sensitivity to various algorithm parameters were analyzed in cadaver studies. A cadaver head specimen of a male adult without teeth was lightly preserved using a phenol-glycerin solution to maintain flexibility of joints and soft tissues. Six 1.5 mm diameter Teflon spheres were glued to the surface of the tongue (figure 3), and eight 1.5 mm Teflon spheres were implanted within the tongue (figure 4). The Teflon spheres provide unambiguous fiducial markers for analysis of target registration error (TRE). The cadaver was mounted on a CT-compatible board incorporating nylon string to open the mouth and retract the tongue in a manner simulating the TORS setup as shown in figure 3. The setup placed the anatomy in a realistic intraoperative pose but did not include the mouth gag and tongue retractor typical of a clinical TORS procedure that would be expected to cause additional artifact in CBCT. Modifying such devices to a CT-compatible form (e.g., Al, Ti, or carbon fiber) and application of various artifact reduction techniques (under development) were not considered in the current experiments, since the focus was the registration process, assuming a CBCT image of quality sufficient for definition of the S1 mask.
Figure 3.
Cadaver setup emulating the intraoperative setup for CBCT-guided TORS. (a) Prototype mobile C-arm for intraoperative CBCT. (b) Cadaver mounted in a CT-compatible frame using nylon strings to retract the jaw and tongue. (c) A foam pad separated the tongue slightly from the lower lip to simplify segmentation. (d) Six Teflon spheres attached on the surface of the tongue. Eight additional spheres were implanted within the tongue (figure 4).
Figure 4.
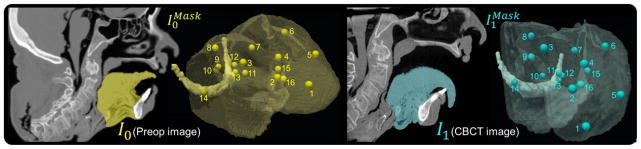
Images and segmentation of a cadaver specimen. (left) Preoperative CT (I0) and segmented subvolume ( ) showing 16 target points. (right) Corresponding CBCT (I1) in the intraoperative state (mouth open and tongue retracted) and subvolume ( ).
3.2. Image Acquisition
CT images (I0) of the cadaver in preoperative state (mouth closed and tongue in repose) were acquired (Philips Brilliance CT, Head Protocol, 120 kVp, 277 mAs) and reconstructed at (0.7×0.7×1.0) mm3 voxel size. An example sagittal slice of the preoperative CT is shown in figure 4. Subsequently, intraoperative CBCT images (I1) were acquired in intraoperative state (mouth open and tongue extended by nylon strings) using a mobile C-arm prototype (100 kVp, 230 mAs) and reconstructed at (0.6×0.6×0.6) mm3 voxel size. The mobile C-arm (figure 3(a)) incorporated a flat-panel detector, motorized rotation, geometric calibration, and 3D reconstruction software (Siewerdsen et al., 2005, Siewerdsen et al., 2007, Siewerdsen, 2011). A sagittal slice CBCT image with the head in the intraoperative pose is shown in figure 4.
3.3. Analysis of Registration Accuracy
3.3.1. Entropy Correlation Coefficient and Normalized Pointwise Mutual Information
Mutual information (MI) is a similarity metric common to multimodality image registration since it does not assume functional relations between intensity spaces. MI can be measured in terms of the Shannon entropies. The join entropy of the images A and B, for example, is represented by H(A, B) = − Σi p(i) log p(i) where p(i) is a joint probability density and i = [iA, iB] is a pair of intensities from two corresponding voxels in A and B. Since MI lacks a fixed upper bound and is sensitive to changes of the overlapping region between the two images (Maes et al., 1997, Studholme et al., 1999, Pluim et al., 2000, Pluim et al., 2001, Maes et al., 2003, Pluim et al., 2003), two normalized variants of MI have been introduced: i) normalized mutual information (Studholme et al., 1999); and ii) entropy correlation coefficient (ECC) as (Maes et al., 1997, Maes et al., 2003):
| (15) |
ECC ranges from 0 (independence) to 1 (dependence) with direct relation to NMI as ECC(A, B) = 2 − 2/NMI(A, B)(Pluim et al., 2003). In the results below, ECC was used as a global similarity metric due to its intuitive upper and lower bounds.
Local similarity can be evaluated using pointwise mutual information (PMI) to measure the B statistical dependence between a pair of intensities (i) from two corresponding voxels in A and B (Rogelj et al., 2003). PMI is represented as the ratio of the actual joint probability over the expected joint probability if the two intensities are independent:
| (16) |
The voxel intensities iA and iB are statistically independent if the joint probability density is the product of the marginal probability densities i.e., p(i) = p(iA) p(iB). PMI is sensitive to low-frequency intensities and lacks fixed bounds (Bouma, 2009, Jurić et al., 2012). Bouma therefore proposed normalized PMI (NPMI) as (Bouma, 2009):
| (17) |
where normalization by − log p(i) gives lower weight to low frequency intensity pairs. NPMI ranges from −1 (no co-occurrence), to 0 (independence), to 1(co-occurrence) (Fan et al., 2012). Since we measured the extent to which iA and iB specify each other (i.e., image similarity), we were interested in cases for which NPMI > 0. The NPMI was evaluated locally throughout the VOI.
3.3.2. Target Registration Error
The geometric accuracy of the registration framework was assessed in terms of TRE using the fourteen Teflon spheres mentioned above and two unambiguous anatomical features on the hyoid bone (left and right prominences) as shown in figure 4. TRE measures the distance between each corresponding target point defined in the fixed image and the moving image after registration:
| (18) |
where is a target point defined in the fixed image, and is the corresponding target point in the moving image after registration. Thus was used to measure TRE following GM rigid (➁ in figure 2), was used to measure TRE following GM nonrigid (➂), and was used to measured TRE following Demons (➃).
3.4. Registration Accuracy and Sensitivity to Algorithm Parameters
The sensitivity of the registration process to the individual parameters in table 1 was investigated in univariate analysis for a single image pair (preoperative CT and intraoperative CBCT), where each parameter was varied over a broad range holding all other parameters fixed. In each case, a reliable operating range and nominal value were identified by considering the effect on TRE and runtime.
Table 1.
Summary of notation and registration parameters.
| Step | Symbol | Definition | |
|---|---|---|---|
| Images | I0 | Moving image (e.g., preoperative CT or MR) | |
| I1 | Fixed image (intraoperative CBCT) | ||
| I|transformation | An image I after a given transformation (e.g., GM rigid, GM nonrigid, distance transformation, Demons) | ||
| ➀Pre-processing | Model structures | Sk | Segmentation of the volume of interest (VOI) i.e. tongue and hyoid bone in Ik |
|
|
VOI in Ik | ||
| Point cloud extraction |
|
A set of n surface points extracted from components in Sk (i.e., tongue and hyoid bone) | |
| Pk=[xk,1,xk,2,…,xk,3] | after normalization. | ||
|
|
Spatial location of a point in in R3 | ||
| xk | after normalization. | ||
| n | Number of points in Pk | ||
| Gaussian mixture registration | Gaussian Mixture (GM) | φ(x|Θk) | Gaussian mixture density of Pk with a set of mixture parameters Θk. |
| ➁ GM Rigid |
|
Width of the isotropic Gaussian components at each registration level ℓ. | |
| TGMRigid | GM rigid transformation | ||
| ➂ GM Nonrigid |
|
Width of the isotropic Gaussian components at each registration level ℓ. | |
|
|
Regularization parameter at each registration level ℓ. | ||
| TGMNonRigid | GM nonrigid transformation | ||
| DGMNonRigid | GM nonrigid displacement field | ||
| GM | Concatenation of GM rigid and GM nonrigid registrations (combined transform of steps ➁ and ➂) | ||
| ➃ Demons registration | Demons | DT | Distance transformation |
| σUpdateField | Width of the Gaussian filter to regularize the update field | ||
| σDisplacementField | Width of the Gaussian filter to regularize the displacement field | ||
| MSL | Maximum update step length | ||
| DDemons | Demons displacement field |
First, the sensitivity of the GM rigid step (➁ in figure 2) was analyzed as a function of the parameters n (number of surface points in the GM models) and σGMRigid (width of the isotropic Gaussian components). The first was varied over a range n = 200–3000, and the second was varied across the three levels of hierarchical pyramid (denoted [Level1, Level2, Level3]) from σGMRigid = [0.125, 0.075, 0.025] to [32.0, 19.2, 6.4] mm in steps of ×2 for each set. In addition, the sensitivity of the algorithm to at each level ℓ was investigated by varied in steps of ×2 over the range , and .
Second, the sensitivity of the GM nonrigid step (➂ in figure 2) was analyzed as a function of the parameters n, σGMNonRigid (width of the Gaussian kernels), and λGMNonRigid (regularization). As above, the number of points was varied from n = 200–3000, and σGMNonRigid was varied in the hierarchical pyramid over the range [0.0625, 0.0125, 0.00625] to [4, 0.8, 0.4] mm in steps of ×2. The width of the isotropic Gaussians at each level was investigated by varying in steps of ×2 over the ranges , and . Similarly, the regularization was varied across the three levels of the pyramid as λGMNonRigid = [0.175, 0, 0], [0.175, 0.175, 0.175], and [0.175, 0.175/2, 0.175/4], and varied at only level 1 over the range with no regularization at the other levels ( for ℓ >1).
Finally, the sensitivity of the Demons registration step (➃ in figure 2) was analyzed as a function of the parameters σUpdateField (width of the Gaussian filter for smoothing the update field), σDisplacementField (width of the Gaussian filter for smoothing the displacement field), and MSL. For fair comparison in analysis of σUpdateField and σDisplacementField, the number of iterations per pyramid level was fixed to [100, 50, 25] rather than using separate stopping criteria. The three-level hierarchical pyramid was constructed with downsampling factors of [4, 2, 1] voxels. The parameter ranges investigated were σDisplacementField = 0–5 voxels, σUpdateField = 0–5 voxels, and MSL = 0.5–8 voxels.
3.5. Overall Registration Performance
Five preoperative CT images and five intraoperative CBCT images acquired with complete readjustment of the cadaver head between each acquisition (i.e., relaxing and repositioning the head and retraction of the nylon string in figure 3) yielded 25 pairs of CT and CBCT images. Overall geometric accuracy of registration was measured in terms of TRE, and image similarity was measured in terms of NPMI (evaluated locally) and ECC (evaluated globally) using the nominal values of algorithm parameters suggested by the sensitivity analysis.
4. RESULTS
4.1. Registration Accuracy and Sensitivity to Algorithm Parameters
The Appendix details the analysis of the sensitivity of the registration process (e.g., TRE evaluated as a function of each parameter in table 1), and results are summarized in table 2. The table shows the operating range (i.e., the range of values for each parameter for which the registration was stable and provided registration accuracy within ~2 mm) as well as the nominal value (i.e., the value of each parameter giving acceptable registration accuracy (e.g., TRE ~2 mm) and consistent with other considerations of computational complexity and runtime) for each parameter.
Table 2.
Summary of sensitivity analysis. For each step in the registration process of table 1, a stable operating range and nominal value were determined as detailed in the Appendix.
| Step | Parameters | Operating Range | Nominal Values |
|---|---|---|---|
| ➁ GM Rigid | n | 800–2,000 | 800 |
|
| |||
| σGMRigid | [0.25, 0.15, 0.05] to [16.0, 9.6, 3.2] | [0.25, 0.15, 0.05] | |
|
| |||
| ➂ GM Nonrigid | n | 800–2,000 | 800 |
|
| |||
| σGMNonRigid | ℓ = 1: | [0.25, 0.05, 0.025] | |
| ℓ>1: | |||
| to | |||
|
| |||
| λGMNonRigid | ℓ = 1: | [0.16, 0,0] | |
| ℓ > 1: | |||
|
| |||
| ➃ Demons | σUpdateField | 3.5–4.5 | 4 |
|
| |||
| σDisplacementField | 0–2 | 0 | |
|
| |||
| MSL | 6–8 | 6 | |
For the GM rigid and nonrigid steps (➁–➂), an identical operating range and nominal value was identified for the number of points (specifically, range n = 800–2000 and nominal value n = 800) in order to directly connect the GM rigid and nonrigid steps without having to redefine the point sets. GM rigid exhibited better alignment of structures at the base of tongue for σGMRigid set to [0.25, 0.15, 0.05] mm in the three respective levels of the hierarchical pyramid, with a stable operating range of [0.25, 0.15, 0.05] to [16.0, 9.6, 3.2] mm. Similarly for GM nonrigid, was set to [0.25, 0.05, 0.025] mm with an operating range of (in the first level) followed by or in subsequent levels. To resolve large deformations, a fairly small degree of regularization (λGMNonRigid) was applied in the first level of GM nonrigid registration (range ~0.005–0.32), followed by no regularization, giving nominal regularization of λGMNonRigid = [0.16, 0, 0] in the three levels.
Finally, for the Demons step (➃), registration was most accurate given a fluid deformation model (i.e., smoothing the update field, σUpdateField) rather than an elastic model (i.e., smoothing only the displacement field, σDisplacementField). A stable operating range in σUpdateField was identified as 3.5–4.5 voxels, with a nominal value of 4 voxels. Meanwhile, σDisplacementField exhibited an operating range of 0–2 voxels, with a nominal value of 0 voxels. Demons was fairly insensitive to MSL in terms of TRE, with an operating range of 6–8 voxels and a nominal value of 6 voxels selected to speed convergence. The runtime of the Demons step was further reduced to ~2 minutes using a three-level hierarchical pyramid with downsampling factors of [8, 4, 2] voxels, since the fourth (full-resolution) level gave negligible improvement but carried the highest computational load.
Figures 5 and 6 and table 3 summarize the registration results associated with each step (➁ – ➃ in figure 2) evaluated from a single image pair (preoperative CT and intraoperative CBCT) at the nominal parameters shown in table 2. Note this single image pair was distinct from the 25 pairs evaluated in the next section. Figure 5 shows sagittal slices corresponding to steps ➀ – ➃. The moving image following GM rigid ( ) is overlaid in green, that following GM nonrigid ( ) is overlaid in orange, and that following Demons ( ) is overlaid in pink. Comparing each to the fixed CBCT image ( overlaid in cyan) shows the evolution of the registration at each step. At step ➁ we see gross rigid alignment of the center of mass. At step ➂, the GM nonrigid displacement field (DGMNonRigid) shows the transformation mapping the tongue onto the fixed CBCT image. Note the large (~30 mm) displacement at the tip, bringing into fairly close overall alignment with . The Demons displacement at step ➃ (motion vectors superimposed with magnitude scaled by a factor of 2 for easier visualization) is seen to refine the registration primarily in deeper portions of the base of tongue (i.e., at points far from the surface and hyoid points that drove the GM registration in steps ➁–➂).
Figure 5.
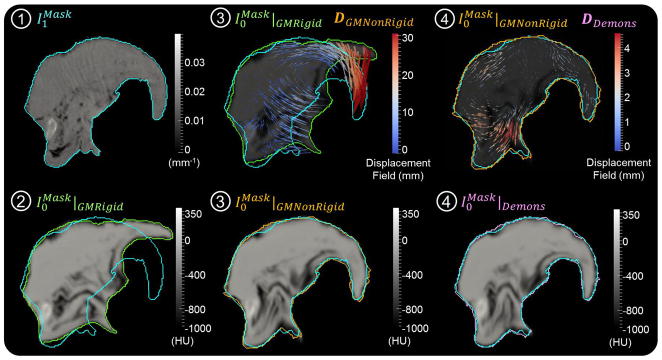
Sagittal slices illustrating the moving image at each step (➀ – ➃) of figure 2. Step ➀ shows the fixed CBCT image (contour overlay in cyan shown at each step). Step ➁ shows the GM rigid initialization (contour in green) along with the moving CT image. Step ➂ shows both the deformation field (DGMNonRigid) and the resulting image from the GM nonrigid step (contour overlay in orange). Step ➃ shows the deformation field (vector magnitudes scaled by a factor of 2 for purposes of visualization) and the final resulting image arising from the Demons step (contour overlay in pink).
Figure 6.
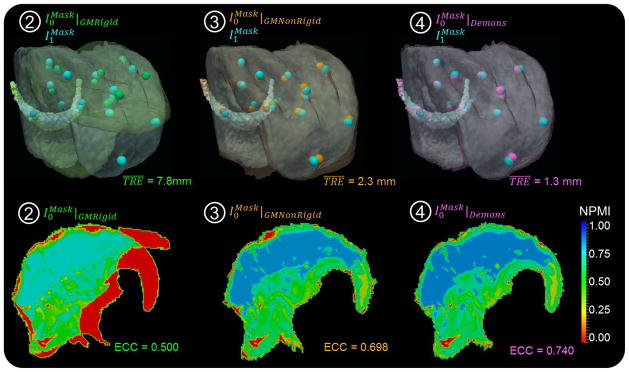
Registration accuracy. The TRE, global ECC, and local NPMI are shown following each step of the registration framework: ➁ GM rigid; ➂ GM nonrigid; and ➃ Demons. The first row shows semi-opaque overlays of the VOI in fixed and moving images, and the second row shows sagittal slices of NPMI maps.
Table 3.
Registration accuracy and runtime of the registration framework (total runtime of ~5 minutes).
| Metric | ➁ GM Rigid | ➂ GM Nonrigid | ➃ Demons |
|---|---|---|---|
| TRE | 7.8±7.3 mm (median 4.4 mm) | 2.3±1.1 mm (median 2.1 mm) | 1.3±0.7 mm (median 1.1 mm) |
| NPMI | 0.40±0.31 (median 0.46) | 0.58±0.27 (median 0.66) | 0.62±0.25 (median 0.67) |
| ECC | 0.500 | 0. 698 | 0.740 |
| Runtime | 1.3 seconds | 2.2 minutes | 2.6 minutes |
A difference in air infiltration in the cadaver tongue was clearly evident, with air expulsed from vessels and fissures upon retraction and reinfiltrating upon relaxation. The difference in air-tissue content is most evident along the inferior aspect of the tongue; however, because these features were not included in the point clouds for GM registration, and because the Demons registration operated on DT images, the discrepancy did not affect the registration process, and fairly good alignment was achieved. (The mismatch was evident in reduced values of NPMI and ECC, as noted below, but not in registration accuracy.) The CT and CBCT images overlaid as background context in each step of figure 5 also illustrate the differences in image quality in each modality (typically sharper and noisier for CBCT with a higher degree of shading artifacts, compared to smoother and more uniform for CT). Again, since the image intensities are not directly used in the registration (i.e., the framework is independent of the underlying intensity or modality), the registration process was robust against such differences in image intensity.
The registration accuracy and runtime associated with each registration step (➁–➃) are summarized in figure 6 and table 3. The TRE improved from 7.8±7.3 mm (median 4.4 mm) following GM rigid (step ➁) to 2.3±1.1 mm (median 2.1 mm) following GM nonrigid (step ➂), and 1.3±0.7 mm (median 1.1 mm) following Demons (step ➃). The semi-opaque overlays of volumes show that the Demons step not only refined the GM registration in deeper tissues (as evident in the Demons deformation field of figure 5) but also in surface matching. Similarity analyzed between the moving and fixed images showed corresponding improvement, with global ECC improving from 0.500 following GM rigid (➁) to 0.698 following GM nonrigid (➂) and 0.740 following Demons (➃). The sagittal slices of NPMI maps show similar improvement throughout the VOI, from 0.40±0.31 (median 0.46) following GM rigid (➁) to 0.58±0.27 (median 0.66) following GM nonrigid (➂) and 0.62±0.25 (median 0.67) following Demons (➃). Although the differences in air infiltration did not affect the registration accuracy, the expulsion of air from the tissue during tongue retraction was responsible for the relatively low value of image similarity (ECC and NPMI).
The total runtime of the initial implementation was measured on a desktop workstation (Dell Precision T7500, Intel Xeon E5405 2x Quad CPU at 2.00 GHz, 12-GB RAM at 800 MHz, Windows 7 64-bit). For images of size (512×512×168) and (300×320×230) voxels for I0 and I1, respectively, the nominal algorithm parameters of table 2, and with a hierarchical pyramid of size [8, 4, 2] in each step, the total runtime was ~5 minutes – including 12 s for point-cloud extraction, 1.3 s for the GM rigid step, 2.2 min for the GM nonrigid step, and 2.6 min for the Demons step. Although the runtime was relatively slow, and there is room for improvement in the implementation and parallelization of the algorithm, it is potentially within logistical requirements of the serial workflow depicted in figure 1.
4.2. Overall Registration Performance
Figures 7 and 8 summarize the overall registration performance evaluated using 25 image pairs (preoperative CT and intraoperative CBCT) and using the nominal values of registration parameters in table 2. Figure 7 illustrates the performance of each registration step (➁ – ➃) using box-and-whisker plots showing the median (red line), interquartile (box plot), and range (whiskers). Considering the first and third quartiles of the data (q1 and q3, respectively), outliers were defined outside the upper bound [q3 + 2(q3 − q1)] and marked as asterisks. The TRE evaluated from 16 target points (spheres and hyoid) in 25 image pairs improved from 4.6 ± 3.8 mm (median 3.3 mm) following the GM rigid step (➁) to 2.1 ± 1.1 mm (median 1.9 mm) following GM nonrigid (➂), and 1.7 ± 0.9 mm (median 1.5 mm) following Demons (➃). The interquartile range in TRE following Demons (➃) was 1.06 – 2.21 mm, and the range was 0.09 – 4.51 mm. The fairly broad range (and upper bound) in TRE was primarily due to target points at the tip of the tongue. Adjustment of registration parameters within the proposed operating range was possible to allow more deformation (e.g., increasing the number of points (n) in GM registration and/or reducing λGMNonRigid) and improve overall TRE, particularly at the tip of the tongue. For example, setting n = 900 and λGMNonRigid = [0.005,0,0] improved overall TRE from (2.3 ± 1.5) mm to (1.6 ± 0.8) mm at the cost of runtime (increasing from 4.9 min to 7.6 min).
Figure 7.
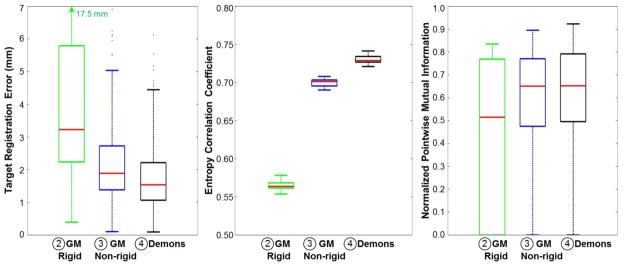
Overall registration performance as a function of registration step (➁, ➂, and ➃) evaluated from 25 pairs of CT and CBCT images. The TRE, global ECC, and local NPMI improved with each step, yielding mean geometric accuracy within ~2 mm.
Figure 8.
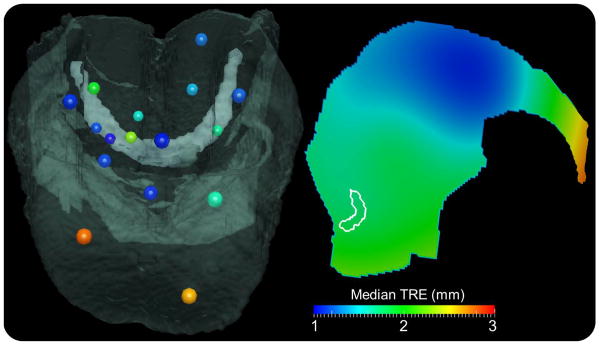
Median TRE at each of 16 target fiducials measured from 25 CT-CBCT image pairs for the complete registration process (➁–➃). (left) Target fiducials colored by magnitude of median TRE (colorbar), with a semi-opaque overlay of a CBCT volume and fiducial diameters scaled for depth perspective. (right) A sagittal slice of the 3D interpolated median TRE showing overall spatial dependence of registration accuracy.
Image similarity also improved globally at each step, with ECC increasing from 0.57 ± 0.01 (median 0.564) following GM rigid (➁) to 0.70 ± 0.01 (median 0.701) following GM nonrigid (➂), and finally 0.73 ± 0.01 (median 0.729) following Demons (➃). NPMI exhibited similar improvement throughout the VOI from (➁) 0.46 ± 0.31 (median 0.515) to (➂) 0.57 ± 0.24 (median 0.650) and finally (➃) 0.60 ± 0.23 (median 0.653) at the output of the full registration process. In each case, the fairly low absolute value in image similarity was due to mismatch in CT and CBCT image characteristics and – more importantly – the expulsion / re-infiltration of air from vessels and fissures in the tongue upon retraction / relaxation.
Figure 8 illustrates the spatial distribution of (median) TRE at each of the 16 target fiducials evaluated from 25 pairs of CT and CBCT images. On the left, a semi-opaque overlay of one of the CBCT volumes is shown with the 16 target points colored according to the magnitude of median TRE. On the right is a sagittal image representation of median TRE interpolated from the measured value at each target point over the VOI. A contour of the hyoid is shown in white for context. The 3D interpolation of the measured median TRE used multiquadric radial basis functions with a shape parameter selected using the method suggested by Foley (Foley, 1987, Rippa, 1999). The accuracy of registration is best (~1–2 mm) in the middle portion of the tongue and worst (~2.5–3.0 mm) at the tip of the tongue. Deep caudal aspects of the base of tongue exhibited median TRE ~2 mm, suggesting fairly good geometric accuracy in the main region of interest for TORS.
5. CONCLUSION AND DISCUSSION
A registration framework integrating two well-established methodologies — GM models and the Demons algorithm — was developed to resolve the large deformations associated with base of tongue surgery. The method forms an important component of a system under development for CBCT-guided TORS, where intraoperative CBCT provides a basis for deformably registering preoperative images and planning data into the highly deformed intraoperative context. The framework includes surface points to initialize the rigid and deformable registration of segmented subvolumes followed by a refinement based on the Demons algorithm applied to distance transformations (rather than image intensities directly). The method is therefore insensitive to image intensities and choice of imaging modality, allowing application to preoperative and/or intraoperative CT, CBCT, and/or MR.
The sensitivity analysis yielded nominal values of algorithm parameters and a knowledgeably selected operating range over which the algorithm behaved within desired levels of geometric accuracy, stability, and runtime. The analysis showed that the Demons algorithm applied to distance map transforms performed better for a fluid deformation model over an elastic deformation model due to the inherently small gradients in the distance map images and the fairly large displacements to be accommodated in the retracted tongue. A hierarchical pyramid with downsampling of [8, 4, 2] in combination with a simple stopping criterion improved the convergence rate and geometric accuracy by preventing excessive iterations, resulting in total runtime of ~5 min and TRE of ~2 mm in its initial implementation. The overall registration performance evaluated in cadaver studies demonstrated mean TRE of 1.7 mm, mean NPMI of 0.60, and mean ECC of 0.73 (the latter similarity metrics exhibiting fairly low values due to content mismatch (air expulsion) rather than geometric misalignment). Registration error was highest at the tip of the tongue; considering only the 8 targets in the base of tongue, the TRE was improved to 1.49 ± 0.69 mm. Recent studies in transoral surgery demonstrate improved surgical outcomes with increased local tumor control from surgical resection with adequate negative margins, and support that close margins (2 – 5 mm) may be equivalent to widely negative margin (> 5 mm) (Nason et al., 2009, Hinni et al., 2012, Hinni et al., 2013). The increased accuracy of this TORS system under development (allowing precision to < 2 mm) will likely improve the surgeon’s ability to achieve negative margins.
The complete registration process with nominal parameters in table 2 performed better than or similarly to alternative variations of the framework – for example: i.) a hybrid fluid-elastic Demons (σUpdateField = σDisplacementField = 2 voxels) applied to the entire CT and intraoperative CBCT image volumes directly (each scaled to Hounsfield units but without segmentation of the VOI, definition of point clouds, or any GM registration) and initialized with a basic MI-based rigid registration gave TRE of 59.3 ± 36.1 mm, showing the challenge associated with registering the entire bulk anatomy and the utility of working with a relevant subvolume; ii) GM rigid (➁) followed by Demons (➃) (and eliminating the GM nonrigid step (➂)) yielded TRE of 2.5 ± 2.1 mm; iii) GM rigid (➁) followed by Demons operating directly on the CT and CBCT image subvolumes (rather than on their distance map transforms) yielded TRE of 4.5 ± 3.9 mm; iv.) GM rigid (➁) and GM nonrigid (➂) followed by Demons operating directly on image subvolumes (rather than distance maps) yielded a TRE of 3.8 ± 2.8 mm; and v) similar to iv) using ➁ and ➂ but followed by elastic Demons (σDisplacementField = 4 voxels) operating directly on image subvolumes yielded TRE of 1.5 ± 0.8 mm. While the last case performed comparably to the nominal framework, the accuracy would be expected to degrade in the presence of artifacts (e.g., streaks from dental fillings), whereas Demons applied to a distance map transform would not. An alternative method in which the distance map transforms are recalculated during the iterative optimization process of the Demons algorithm was not investigated in the current work but could have a benefit (at the cost of increased computation time) in that the distance values in the DT images would not be affected by the tri-linear interpolation step. Since the DT images tend to lack fine-detailed features, error due to blur in the interpolation step was believed to be small. The overall finding regarding Demons operating on distance map transforms suggests a useful implementation in which the process is insensitive to image intensity differences and robust against artifacts and noise, provided a consistent segmentation of the VOI.
The registration framework involves a combination of methods reported by various investigators in previous work - in this case, model-based (GM) initialization (analogous to work by (Jian and Vemuri, 2011) and (Tustison et al., 2011)) followed by Demons refinement (analogous to (He et al., 2005),(Suh et al., 2011), and (Nithiananthan et al., 2012)). An analogous two-step strategy was shown previously to resolve large soft tissue deformations in CBCT images of the inflated and deflated lung in thoracic surgery - in that case employing a mesh evolution (rather than a GM model) for initialization and refined by an intensity-corrected Demons variant (Uneri et al., 2012, Uneri et al., 2013). Such combination of disparate approaches within an integrated framework could potentially apply to other soft-tissue contexts as well.
Various alternative methods have been proposed to transform multimodality images into a common intensity space and could be used in place of the distance map transformation employed in this work. Wachinger and Navab encoded the input images in terms of Shannon entropy images and Laplacian eigenmaps based on manifold learning to represent information content and image structure, respectively (Wachinger and Navab, 2012). Similarly, local phase can be used to represent structural information in input images while eliminating intensity dependence (Mellor and Brady, 2004, Mellor and Brady, 2005). Local frequency maps of images computed using Gabor filters and the Riesz transform were used in nonrigid registration based on a robust L2E estimator in (Liu et al., 2002) and (Jian et al., 2005), respectively. These structure-based encoding methods, however, are best suited to images that exhibit strong contrast differences in structures of interest (e.g, white and gray matter in MR, bone and soft tissue in CT, etc.) and can be of limited use with low-contrast images. Analogous to distance map transform, level set representation is computed from segmentation of a region of interest. It provides boundary information well suited for surface registration - for example, Suh and Wyatt’s level-set registration of colon boundaries defined in CT acquired in patient prone and supine positions, using the Demons algorithm to improve detection of polyps in CT colonography (Suh and Wyatt, 2006). Level-set representations combined with the Demons algorithm have also been used to study peripheral arterial disease in SPECT-CT of murine skeletal structures and body contours (Suh et al., 2011). However level-set representations provide relatively less shape information compared to distance transformations.
Although other registration methods were not explicitly compared in the current work, and a fair, quantitative comparison among registration schemes is beyond the current scope, there are numerous methods reported in the literature that may be applicable in whole or part to the tongue surgery context. For example, a coherent point drift (CPD) algorithm could be employed in the point set registration (Myronenko and Song, 2010). The algorithm solved the point matching by maximizing the likelihood between GM models of the transformed moving point set and fixed points in an expectation maximization framework. Since the maximum likelihood estimator can be sensitive to outliers, the algorithm included an additional Gaussian component to reduce outliers and improve robustness (Hu et al., 2010, Jian and Vemuri, 2011). Jian and Vemuri et al. demonstrated improved performance of their proposed method over the CPD algorithm (Jian and Vemuri, 2011). Tustison et al. proposed a labeled point-set registration algorithm to estimate B-Spline transformation by minimizing the Jensen-Havrda-Charvet-Tsallis divergence between the GM representations of the labeled point sets — i.e., each labeled point subset represented specific anatomy (Tustison et al., 2011). The algorithm included a parameter adjusting the degree of robustness against noise and outliers in the divergence measure. Large-scale soft-tissue deformation was addressed by Bondar et al., who developed a symmetric thin-plate spline robust point matching (S-TPS-RPM) algorithm for CT image registration in the context of cervical cancer (Bondar et al., 2010). The method estimated symmetric deformation by computing forward and backward transformations using unidirectional TPS-RPM (Vasquez Osorio et al., 2009) to ensure inverse consistency and demonstrated the ability to resolve large deformations with improved accuracy in comparison to TPS-RPM. This method presents a possible alternative to the nonrigid point set registration described above; however, the authors noted sensitivity of the method to noise, outliers, missing data, and difficulty with unknown correspondences, and Myronenko et al. demonstrated improved robustness for CPD in comparison to TPS-RPM (Myronenko and Song, 2010). Moreover, finite element methods have been employed to resolve large deformations in the liver (Brock et al., 2008a, Dumpuri et al., 2010), lungs (Zhang et al., 2004, Adil et al., 2011), prostate (Crouch et al., 2003, Chi et al., 2006, Brock et al., 2008b), and even in multi-organ systems (thorax and abdomen) (Brock et al., 2005) and could potentially yield accurate registration employing biomechanical modeling of the tongue (Buchaillard et al., 2007, Stavness et al., 2011). Hualiang et al. integrated a finite-element and Demons approach to resolve soft-tissue deformation in 4DCT of the lungs and CBCT of the prostate (Hualiang et al., 2012). The method used the Demons algorithm to compute displacements at boundary nodes defined in the high-contrast region, where Demons is likely to achieve accurate registration. This method could similarly apply to the tongue, invoking Demons for nodes defined at the air-tissue interface along the superior aspect of the tongue and at the tissue-bone interface about the hyoid and inner boundary of the mandible.
The runtime of the initial implementation was relatively slow (~5 min) but was potentially within logistical requirements of the workflow depicted in figure 1. A more integrated arrangement of a C-arm and robot (allowing CBCT and fluoroscopy on demand during the intervention) could similarly employ the registration framework described here to register preoperative images and planning data to the most up-to-date CBCT and would benefit from faster implementation of the algorithm. Improvements underway include a modified GM nonrigid step using compact-support radial basis functions (Yang et al., 2011), incorporation of a stopping criterion in the GM nonrigid step, and GPU implementation of the GM nonrigid and Demons calculations (Sharp et al., 2007, Xuejun et al., 2010). Alternative algorithms for nonrigid point set registration will also be investigated, such as the labeled point set registration using B-Spline transformation (Tustison et al., 2011). A variant in which the DT images are recalculated within the Demons optimization process is an area of possible future investigation. Routine application of the method in practice will require streamlined, semi-automatic segmentation of the tongue, without manual refinement of contouring as employed in this initial work. Future work could also include the addition of internal features to the segmentation point sets and distance maps — e.g., the lingual vessels — to provide increased internal constraint and potentially improve registration performance in deeper tissues.
Acknowledgments
This research was supported in part by the Thai Royal Government Scholarship, the Department of Computer Science (Johns Hopkins University), Siemens Healthcare, and NIH R01-CA-127444. The authors gratefully acknowledge Dr. Bing Jian (Google Inc.) and Dr. Jerry L. Prince (Johns Hopkins University) for valuable discussion regarding Gaussian mixture model registration. Dr. Rainer Graumann and Dr. Gerhard Kleinszig (Siemens XP) provided collaboration on development of the prototype mobile C-arm for CBCT. The authors extend their thanks to Mr. Ronn Wade (University of Maryland, State Anatomy Board) for assistance with the cadaver specimen.
Appendix: Sensitivity to Algorithm Parameters
The sensitivity of the registration process was evaluated in terms of TRE and runtime as a function of parameters intrinsic to the GM Rigid, GM Nonrigid, and Demons registration steps shown in figure 2. In each case, the TRE and runtime are reported at the output of a particular registration step (not necessarily the entire process), giving a basic univariate analysis in which each individual parameter was freely varied holding all others fixed to their nominal value. Results were analyzed from a single CT-CBCT image pair distinct from the 25 pairs forming the main body of results reported in Section 4.2. The same 16 target points as shown in figure 4 were used, except for the GM Rigid case, where distinct behavior was observed between the base and tip of the tongue, and the former was analyzed as the more pertinent region of interest. Runtime was measured for the workstation and volume sizes detailed in section 4.1. Nominal values and reasonable operating range in algorithm parameters are summarized in table 2.
A.1 Sensitivity Analysis: GM Rigid
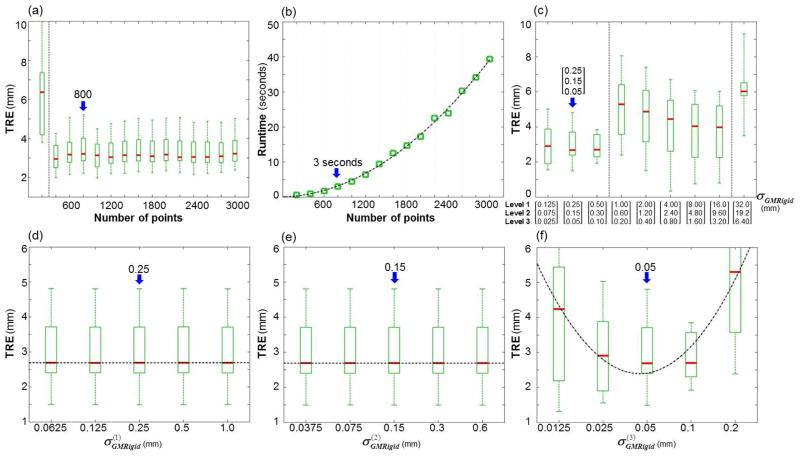
The sensitivity of the GM rigid step to its intrinsic parameters is summarized in figure A.1. As shown in figure A.1(a), GM rigid registration was insensitive to the number of points (minimal change in TRE) for n > 400 points. Since the GM rigid calculation was relatively fast (compared to the nonrigid steps) and did not depend strongly on n (i.e., runtime in seconds) as shown in figure A.1(b), in order to directly connect the GM rigid and nonrigid steps (without redefining points), the operating range and nominal value of n for the GM rigid step were taken as identical to those for GM nonrigid (n = 800–2000 and a nominal value of 800; see below). Figure A.1(c) shows that smaller values of σGMRigid (ranging [0.125, 0.075, 0.025] – [0.5, 0.3, 0.1] mm) allowed better modeling of motion at the base of the tongue, whereas larger values (ranging [1.0, 0.6, 0.2] – [16.0, 9.60, 3.20] mm) more easily aligned the tip of the tongue (and increased error at the base). Figure A.1(d,e) shows that GM rigid was insensitive to and in terms of TRE. However, as shown in figure A.1(f), the value of at the final level was more important — large enough to suppress mismatch features but small enough to capture the underlying points. Therefore, given a value of in level 1, the value in subsequent levels (ℓ > 1) was , where s was in the range 1.5 – 6. Taking smaller nominal values of σGMRigid = [0.25, 0.15, 0.05] mm better aligned structures at the base-of-tongue, while larger values up to σGMRigid = [16.0, 9.6, 3.2] mm increased accuracy at the tip of the tongue.
Figure A.1.
Sensitivity analysis and selection of registration parameters for GM rigid registration. The box-and-whisker plots show median TRE (red line), interquartile, and range. (a,b) TRE and runtime measured as a function of the number of points (n) in the GM models. (c–f) TRE measured versus the width (σGMRigid) of the isotropic Gaussian for various hierarchical pyramids. Blue arrows mark values selected as nominal.
A.2 Sensitivity Analysis: GM Nonrigid
Figure A.2 summarizes the sensitivity of the GM nonrigid step. As illustrated in figure A.2(a,b), the process demonstrated a slight improvement in TRE with higher values of n but a significant increase in runtime due to the thin-plate spline (Morse et al., 2005, Zagorchev and Goshtasby, 2006). To achieve TRE ~ 2 mm, the operating range was set to n = 800–2000 points, with the nominal value selected to be 800 points for runtime ~2 minutes. Figure A.2(c,d) demonstrates that small (but nonzero) regularization ( ) at the first level of the hierarchical pyramid provided reasonable affine constraint, and subsequent levels (ℓ > 1) benefited from a lack of regularization, allowing larger deformation and giving a nominal λGMNonRigid = [0.16, 0, 0]. As shown in figure A.2(e), σGMNonRigid in the range of [0.25, 0.05, 0.025] – [2.0, 0.4, 0.2] mm minimized TRE, implying σGMNonRigid smaller than this range could not suppress mismatch features and outliers, while larger σGMNonRigid could not capture the underlying points. Unlike GM rigid, the GM nonrigid step was sensitive to and but insensitive to , because the “action” was primarily in the first two levels: maximum deformation of 22.1 mm, 9.3 mm, and 1.6 mm after levels ℓ = 1, 2, and 3, respectively. Smoothness of the GM models was therefore important at the first two levels to allow such deformation. The resulting operating range was , followed by or in the subsequent level ℓ, with a nominal setting of [0.25, 0.05, 0.025] mm.
Figure A.2.
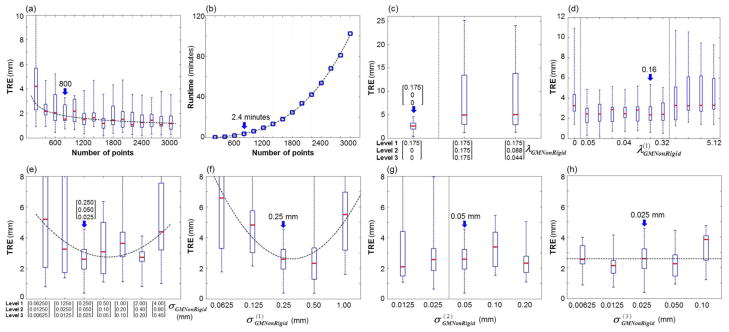
Sensitivity analysis and selection of registration parameters for GM nonrigid registration. The box-and-whisker plots show median TRE (red line), interquartile, and range. (a,b) TRE and runtime measured as a function of the number of points (n) in the GM models. (c,d) TRE measured versus regularization ( ) in the hierarchical levels ℓ = [1, 2, 3]. (e–h) TRE measured versus the width (σGMNonRigid) of the isotropic Gaussian for the three-level pyramids. Blue arrows mark values selected as nominal.
A.3 Sensitivity Analysis: Demons
The sensitivity of the Demons step to its intrinsic parameters is summarized in figure A.3. As shown in figure A.3(a,b), smoothing the update field using σUpdateField (i.e., a “fluid” deformation model) yielded improvement in TRE but increased runtime. An operating range of σUpdateField = 3.5–4.5 voxels was selected to minimize TRE, with a nominal value of 4 voxels. On the other hand, figure A.3(c,d) shows that smoothing the displacement field using σDisplacementField (i.e., an “elastic” deformation model) did not improve TRE (in fact, slightly degraded TRE) but increased runtime. Therefore, an operating range of σDisplacementField = 0–2 voxels was selected, with a nominal value of 0 voxels (i.e., no smoothing). The improved performance for a more fluid deformation model is believed to be due to the fairly small gradients of the DT images. Figure A.3(e,f) shows the algorithm to be fairly insensitive to changes in MSL in terms of TRE, but lower values of MSL increased runtime, requiring more iterations to converge and suggesting an operating range MSL = 6 – 8 voxels. The computation time was further reduced by using a three-level hierarchical pyramid with downsampling factors of [8, 4, 2] voxels instead of 4 levels [8, 4, 2, 1] or 3 levels [4, 2, 1], eliminating the full-resolution level without significant loss in TRE. For example, the [8, 4, 2, 1] and [8, 4, 2] pyramids achieved TRE of 1.27±0.64 mm and 1.31±0.67 mm, respectively, at runtimes of 11.9 and 2.6 minutes, respectively.
Figure A.3.
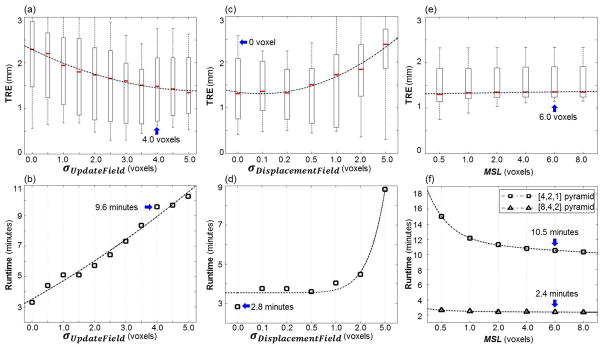
Sensitivity analysis and selection of registration parameters for Demons registration. The box-and-whisker plots show median TRE (red line), interquartile, and range. (a,b) TRE and runtime measured as a function of the Gaussian filter width (σUpdatetField) in smoothing the update field. (c,d) TRE and runtime measured as a function of the Gaussian filter width (σDisplacementField) in smoothing the displacement field. (e,f) TRE and runtime measured as a function of MSL. The runtime is shown in (f) for both [4,2,1] and [8,4,2] pyramids. Blue arrows mark values selected as nominal.
References
- Adil AM, Joanne M, Mike V, Kristy B. Toward efficient biomechanical-based deformable image registration of lungs for image-guided radiotherapy. Physics in Medicine and Biology. 2011;56:4701. doi: 10.1088/0031-9155/56/15/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bachar G, Siewerdsen JH, Daly MJ, Jaffray DA, Irish JC. Image quality and localization accuracy in C-arm tomosynthesis-guided head and neck surgery. Med Phys. 2007;34:4664–77. doi: 10.1118/1.2799492. [DOI] [PubMed] [Google Scholar]
- Belongie S, Malik J, Puzicha J. Shape matching and object recognition using shape contexts. IEEE Trans Pattern Anal Mach Intell. 2002;24:509–522. doi: 10.1109/TPAMI.2005.220. [DOI] [PubMed] [Google Scholar]
- Besl PJ, Mckay HD. A method for registration of 3-D shapes. IEEE Trans Pattern Anal Mach Intell. 1992;14:239–256. [Google Scholar]
- Bondar L, Hoogeman MS, Vasquez Osorio EM, Heijmen BJ. A symmetric nonrigid registration method to handle large organ deformations in cervical cancer patients. Med Phys. 2010;37:3760–72. doi: 10.1118/1.3443436. [DOI] [PubMed] [Google Scholar]
- Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Trans Pattern Anal Mach Intell. 1989;11:567–585. [Google Scholar]
- Bouma G. Normalized (pointwise) mutual information in collocation extraction. Proc of the Biennial GSCL Conference. 2009:31–40. [Google Scholar]
- Brock KK, Hawkins M, Eccles C, Moseley JL, Moseley DJ, Jaffray DA, Dawson LA. Improving image-guided target localization through deformable registration. Acta Oncologica. 2008a;47:1279–1285. doi: 10.1080/02841860802256491. [DOI] [PubMed] [Google Scholar]
- Brock KK, Nichol AM, Menard C, Moseley JL, Warde PR, Catton CN, Jaffray DA. Accuracy and sensitivity of finite element model-based deformable registration of the prostate. Med Phys. 2008b;35:4019–25. doi: 10.1118/1.2965263. [DOI] [PubMed] [Google Scholar]
- Brock KK, Sharpe MB, Dawson LA, Kim SM, Jaffray DA. Accuracy of finite element model-based multi-organ deformable image registration. Med Phys. 2005;32:1647–59. doi: 10.1118/1.1915012. [DOI] [PubMed] [Google Scholar]
- Buchaillard S, Brix M, Perrier P, Payan Y. Simulations of the consequences of tongue surgery on tongue mobility: implications for speech production in post-surgery conditions. The International Journal of Medical Robotics and Computer Assisted Surgery. 2007;3:252–261. doi: 10.1002/rcs.142. [DOI] [PubMed] [Google Scholar]
- Byrd RH, Lu P, Nocedal J, Zhu C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J Sci Comput. 1995;16:1190–1208. [Google Scholar]
- Cachier P, Bardinet E, Dormont D, Pennec X, Ayache N. Iconic feature based nonrigid registration: the PASHA algorithm. Computer Vision and Image Understanding. 2003;89:272–298. [Google Scholar]
- Cachier P, Pennec X, Ayache N. Technical Report RR-3706. INRIA; 1999. Fast non-rigid matching by gradient descent: study and improvements of the “Demons” algorithm. [Google Scholar]
- Castadot P, Lee JA, Parraga A, Geets X, Macq B, Gregoire V. Comparison of 12 deformable registration strategies in adaptive radiation therapy for the treatment of head and neck tumors. Radiother Oncol. 2008;89:1–12. doi: 10.1016/j.radonc.2008.04.010. [DOI] [PubMed] [Google Scholar]
- Cazoulat G, Simon A, Acosta O, Ospina J, Gnep K, Viard R, Crevoisier R, Haigron P. Prostate Cancer Imaging. Image Analysis and Image-Guided Interventions. Springer; Berlin Heidelberg: 2011. Dose Monitoring in Prostate Cancer Radiotherapy Using CBCT to CT Constrained Elastic Image Registration. [Google Scholar]
- Chen T, Vemuri B, Rangarajan A, Eisenschenk S. Group-Wise Point-Set Registration Using a Novel CDF-Based Havrda-Charvát Divergence. International Journal of Computer Vision. 2010;86:111–124. doi: 10.1007/s11263-009-0261-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chi Y, Liang J, Yan D. A material sensitivity study on the accuracy of deformable organ registration using linear biomechanical models. Med Phys. 2006;33:421–433. doi: 10.1118/1.2163838. [DOI] [PubMed] [Google Scholar]
- Commowick O, Gregoire V, Malandain G. Atlas-based delineation of lymph node levels in head and neck computed tomography images. Radiother Oncol. 2008;87:281–9. doi: 10.1016/j.radonc.2008.01.018. [DOI] [PubMed] [Google Scholar]
- Coselmon MM, Balter JM, Mcshan DL, Kessler ML. Mutual information based CT registration of the lung at exhale and inhale breathing states using thin-plate splines. Med Phys. 2004;31:2942–2948. doi: 10.1118/1.1803671. [DOI] [PubMed] [Google Scholar]
- Crouch J, Pizer S, Chaney E, Zaider M. Medical Image Computing and Computer-Assisted Intervention - MICCAI 2003. Springer; Berlin Heidelberg: 2003. Medially Based Meshing with Finite Element Analysis of Prostate Deformation. [Google Scholar]
- Daly MJ, Chan H, Nithiananthan S, Qiu J, Barker E, Bachar G, Dixon BJ, Irish JC, Siewerdsen JH. Clinical implementation of intraoperative cone-beam CT in head and neck surgery. 2011;7964:796426. [Google Scholar]
- Daly MJ, Siewerdsen JH, Moseley DJ, Jaffray DA, Irish JC. Intraoperative cone-beam CT for guidance of head and neck surgery: Assessment of dose and image quality using a C-arm prototype. Medical Physics. 2006;33:3767–3780. doi: 10.1118/1.2349687. [DOI] [PubMed] [Google Scholar]
- Dumpuri P, Clements LW, Dawant BM, Miga MI. Model-updated image-guided liver surgery: Preliminary results using surface characterization. Progress in Biophysics and Molecular Biology. 2010;103:197–207. doi: 10.1016/j.pbiomolbio.2010.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahrig R, Dixon R, Payne T, Morin RL, Ganguly A, Strobel N. Dose and image quality for a cone-beam C-arm CT system. Med Phys. 2006;33:4541–50. doi: 10.1118/1.2370508. [DOI] [PubMed] [Google Scholar]
- Fan J, Kalyanpur A, Gondek DC, Ferrucci DA. Automatic knowledge extraction from documents. IBM Journal of Research and Development. 2012;56(5):1–5. 10. [Google Scholar]
- Foley TA. Interpolation and approximation of 3-D and 4-D scattered data. Computers & Mathematics with Applications. 1987;13:711–740. [Google Scholar]
- Gelas A, Gouaillard A, Megason S. Surface Meshes Incremental Decimation Framework. Insight Journal. 2008a:1–8. [Google Scholar]
- Gelas A, Gouaillard A, Megason S. Triangular Meshes Delaunay Conforming Filter. Insight Journal. 2008b:1–4. [Google Scholar]
- Godley A, Ahunbay E, Peng C, Li XA. Automated registration of large deformations for adaptive radiation therapy of prostate cancer. Med Phys. 2009;36:1433–41. doi: 10.1118/1.3095777. [DOI] [PubMed] [Google Scholar]
- Guimond A, Roche A, Ayache N, Meunier J. Multimodal brain warping using the demons algorithm and adaptative intensity corrections. INRIA Research Report. 1999:3796. doi: 10.1109/42.906425. [DOI] [PubMed] [Google Scholar]
- Hartley RI. In defense of the eight-point algorithm. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1997;19:580–593. [Google Scholar]
- He W, et al. Validation of an accelerated ‘demons’ algorithm for deformable image registration in radiation therapy. Physics in Medicine and Biology. 2005;50:2887. doi: 10.1088/0031-9155/50/12/011. [DOI] [PubMed] [Google Scholar]
- Hinni ML, et al. Surgical margins in head and neck cancer: A contemporary review. Head & Neck. 2012:1–9. doi: 10.1002/hed.23110. [DOI] [PubMed] [Google Scholar]
- Hinni ML, Zarka MA, Hoxworth JM. Margin mapping in transoral surgery for head and neck cancer. Laryngoscope. 2013;123:1190–1198. doi: 10.1002/lary.23900. [DOI] [PubMed] [Google Scholar]
- Hou J, Guerrero M, Chen W, D’souza WD. Deformable planning CT to cone-beam CT image registration in head-and-neck cancer. Med Phys. 2011;38:2088–94. doi: 10.1118/1.3554647. [DOI] [PubMed] [Google Scholar]
- Hu Y, Rijkhorst E-J, Manber R, Hawkes D, Barratt D. Medical Imaging and Augmented Reality. Springer; Berlin Heidelberg: 2010. Deformable Vessel-Based Registration Using Landmark-Guided Coherent Point Drift. [Google Scholar]
- Hualiang Z, Jinkoo K, Haisen L, Teamour N, Benjamin M, Indrin JC. A finite element method to correct deformable image registration errors in low-contrast regions. Physics in Medicine and Biology. 2012;57:3499. doi: 10.1088/0031-9155/57/11/3499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibanez L, Ng L, Gee J, Aylward S. Registration patterns: the generic framework for image registration of the insight toolkit. Proceedings of IEEE International Symposium on Biomedical Imaging; 2002. pp. 345–348. [Google Scholar]
- Ibanez L, Schroeder W, Ng L, Cates J Consortium, T. I. S. The ITK Software Guide Second Edition Updated for ITK version 2.4. Published, Kitware Inc; 2005. Available from: http://www.itk.org/ [Google Scholar]
- Jemal A, Siegel R, Ward E, Hao Y, Xu J, Murray T, Thun MJ. Cancer statistics, 2008. CA Cancer J Clin. 2008;58:71–96. doi: 10.3322/CA.2007.0010. [DOI] [PubMed] [Google Scholar]
- Jemal A, Siegel R, Ward E, Hao Y, Xu J, Thun MJ. Cancer statistics, 2009. CA Cancer J Clin. 2009;59:225–49. doi: 10.3322/caac.20006. [DOI] [PubMed] [Google Scholar]
- Jemal A, Siegel R, Ward E, Murray T, Xu J, Thun MJ. Cancer statistics, 2007. CA Cancer J Clin. 2007;57:43–66. doi: 10.3322/canjclin.57.1.43. [DOI] [PubMed] [Google Scholar]
- Jemal A, Siegel R, Xu J, Ward E. Cancer statistics, 2010. CA Cancer J Clin. 2010;60:277–300. doi: 10.3322/caac.20073. [DOI] [PubMed] [Google Scholar]
- Jian B, Vemuri B, Marroquin J. Information Processing in Medical Imaging. Springer; Berlin Heidelberg: 2005. Robust Nonrigid Multimodal Image Registration Using Local Frequency Maps. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jian B, Vemuri BC. A robust algorithm for point set registration using mixture of Gaussians. IEEE International Conference on Computer Vision; 17–21 Oct. 2005; pp. 1246–1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jian B, Vemuri BC. Robust Point Set Registration Using Gaussian Mixture Models. IEEE Trans Pattern Anal Mach Intell. 2011;33:1633–1645. doi: 10.1109/TPAMI.2010.223. [DOI] [PubMed] [Google Scholar]
- Jurić D, Banek M, Dembitz Š. Agent and Multi-Agent Systems. Technologies and Applications. Springer; Berlin Heidelberg: 2012. Informativeness of Inflective Noun Bigrams in Croatian. [Google Scholar]
- Kanatani K. Handbook of Geometric Computing. Springer; Berlin Heidelberg: 2005. Uncertainty Modeling and Geometric Inference. [Google Scholar]
- Kondor R, Jebara T. A Kernel Between Sets of Vectors. Proceedings of the 20th International Conference Machine Learning; 2003. pp. 361–368. [Google Scholar]
- Lange T, Eulenstein S, Hunerbein M, Schlag PM. Vessel-based non-rigid registration of MR/CT and 3D ultrasound for navigation in liver surgery. Comput Aided Surg. 2003;8:228–40. doi: 10.3109/10929080309146058. [DOI] [PubMed] [Google Scholar]
- Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical Programming. 1989;45:503–528. [Google Scholar]
- Liu J, Vemuri BC, Marroquin JL. Local frequency representations for robust multimodal image registration. IEEE Trans Med Imaging. 2002;21:462–9. doi: 10.1109/TMI.2002.1009382. [DOI] [PubMed] [Google Scholar]
- Liu WP, Reaungamornrat S, Deguet A, Sorger JM, Siewerdsen JH, Richmon J, Taylor RH. Toward Intraoperative Image-Guided TransOral Robotic Surgery. Proc. of Hamlyn Med Robotics Symposium; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16:187–98. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- Maes F, Vandermeulen D, Suetens P. Medical image registration using mutual information. Proc of IEEE. 2003;91:1699–1722. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
- Mattes D, Haynor DR, Vesselle H, Lewellen TK, Eubank W. PET-CT image registration in the chest using free-form deformations. IEEE Trans Med Imag. 2003;22:120–128. doi: 10.1109/TMI.2003.809072. [DOI] [PubMed] [Google Scholar]
- Maurer CR, Jr, Rensheng Q, Raghavan V. A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans Pattern Anal Mach Intell. 2003;25:265–270. [Google Scholar]
- Mellor M, Brady M. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2004. Springer; Berlin Heidelberg: 2004. Non-rigid Multimodal Image Registration Using Local Phase. [Google Scholar]
- Mellor M, Brady M. Phase mutual information as a similarity measure for registration. Medical Image Analysis. 2005;9:330–343. doi: 10.1016/j.media.2005.01.002. [DOI] [PubMed] [Google Scholar]
- Morse BS, Yoo TS, Rheingans P, Chen DT, Subramanian KR. Interpolating implicit surfaces from scattered surface data using compactly supported radial basis functions. ACM SIGGRAPH courses. 2005:78–87. [Google Scholar]
- Myronenko A, Song X. Point set registration: coherent point drift. IEEE Trans Pattern Anal Mach Intell. 2010;32:2262–75. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- Nason RW, Binahmed A, Pathak KA, Abdoh AA, Sándor GKB. What is the adequate margin of surgical resection in oral cancer? Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, and Endodontology. 2009;107:625–629. doi: 10.1016/j.tripleo.2008.11.013. [DOI] [PubMed] [Google Scholar]
- Nithiananthan S, Brock KK, Daly MJ, Chan H, Irish JC, Siewerdsen JH. Demons deformable registration for CBCT-guided procedures in the head and neck: convergence and accuracy. Med Phys. 2009;36:4755–64. doi: 10.1118/1.3223631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nithiananthan S, Schafer S, Mirota DJ, Stayman JW, Zbijewski W, Reh DD, Gallia GL, Siewerdsen JH. Extra-dimensional Demons: a method for incorporating missing tissue in deformable image registration. Med Phys. 2012;39:5718–31. doi: 10.1118/1.4747270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nithiananthan S, et al. Demons deformable registration of CT and cone-beam CT using an iterative intensity matching approach. Med Phys. 2011;38:1785–98. doi: 10.1118/1.3555037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyul LG, Udupa JK, Zhang X. New variants of a method of MRI scale standardization. IEEE Trans Med Imaging. 2000;19:143–50. doi: 10.1109/42.836373. [DOI] [PubMed] [Google Scholar]
- Ong R, Ou J, Miga M. Non-rigid registration of breast surfaces using the laplace and diffusion equations. BioMedical Engineering OnLine. 2010;9:8. doi: 10.1186/1475-925X-9-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkin DM, Bray F, Ferlay J, Pisani P. Global cancer statistics, 2002. CA Cancer J Clin. 2005;55:74–108. doi: 10.3322/canjclin.55.2.74. [DOI] [PubMed] [Google Scholar]
- Pennec X, Cachier P, Ayache N. Medical Image Computing and Computer-Assisted Intervention –MICCAI’99. Springer; Berlin Heidelberg: 1999. Understanding the “Demon’s Algorithm”: 3D Non-rigid Registration by Gradient Descent. [Google Scholar]
- Peroni M, Golland P, Sharp GC, Baroni G. Ranking of stopping criteria for log domain diffeomorphic demons application in clinical radiation therapy. Conf Proc IEEE Eng Med Biol Soc. 2011:4884–7. doi: 10.1109/IEMBS.2011.6091210. [DOI] [PubMed] [Google Scholar]
- Pluim JP, Maintz JB, Viergever MA. Image registration by maximization of combined mutual information and gradient information. IEEE Trans Med Imaging. 2000;19:809–14. doi: 10.1109/42.876307. [DOI] [PubMed] [Google Scholar]
- Pluim JP, Maintz JB, Viergever MA. Mutual-information-based registration of medical images: a survey. IEEE Trans Med Imaging. 2003;22:986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- Pluim JPW, Maintz JBA, Viergever MA. Mutual information matching in multiresolution contexts. Image and Vision Computing. 2001;19:45–52. [Google Scholar]
- Qazi AA, Kim J, Jaffray DA, Pekar V. A feature-based approach for refinement of model-based segmentation of low contrast structures. Conf Proc IEEE Eng Med Biol Soc. 2011;2011:7977–80. doi: 10.1109/IEMBS.2011.6091967. [DOI] [PubMed] [Google Scholar]
- Rippa S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Advances in Computational Mathematics. 1999;11:193–210. [Google Scholar]
- Risholm P, Samset E, Talos I-F, Wells W. Information Processing in Medical Imaging. Springer; Berlin Heidelberg: 2009. A Non-rigid Registration Framework That Accommodates Resection and Retraction. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risholm P, Samset E, Wells Iii W. Validation of a nonrigid registration framework that accommodates tissue resection. 2010. p. 762319–762319. [Google Scholar]
- Rogelj P, Kovačič S, Gee JC. Point similarity measures for non-rigid registration of multi-modal data. Comput Vis Image Und. 2003;92:112–140. [Google Scholar]
- Rohlfing T, Maurer CR, Jr, Bluemke DA, Jacobs MA. Volume-preserving nonrigid registration of MR breast images using free-form deformation with an incompressibility constraint. IEEE Trans Med Imag. 2003;22:730–741. doi: 10.1109/TMI.2003.814791. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Maurer JCR, O’dell WG, Zhong J. Modeling liver motion and deformation during the respiratory cycle using intensity-based nonrigid registration of gated MR images. Med Phys. 2004;31:427–432. doi: 10.1118/1.1644513. [DOI] [PubMed] [Google Scholar]
- Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans Med Imag. 1999;18:712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- Sandhu R, Dambreville S, Tannenbaum A. Point set registration via particle filtering and stochastic dynamics. IEEE Trans Pattern Anal Mach Intell. 2010;32:1459–73. doi: 10.1109/TPAMI.2009.142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer S, et al. Mobile C-Arm Cone-Beam CT for Guidance of Spine Surgery: Image Quality, Radiation Dose, and Integration with Interventional Guidance. Medical Physics. 2011;38:4563–4575. doi: 10.1118/1.3597566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer S, Stayman JW, Zbijewski W, Schmidgunst C, Kleinszig G, Siewerdsen JH. Antiscatter grids in mobile C-arm cone-beam CT: effect on image quality and dose. Med Phys. 2012;39:153–9. doi: 10.1118/1.3666947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott DW. Parametric Statistical Modeling by Minimum Integrated Square Error. Technometrics. 2001;43:274–285. [Google Scholar]
- Sharp GC, Kandasamy N, Singh H, Folkert M. GPU-based streaming architectures for fast cone-beam CT image reconstruction and demons deformable registration. Physics in Medicine and Biology. 2007;52:5771. doi: 10.1088/0031-9155/52/19/003. [DOI] [PubMed] [Google Scholar]
- Shyu K, Pham V, Tran T, Lee P. Unsupervised active contours driven by density distance and local fitting energy with applications to medical image segmentation. Machine Vision and Applications. 2011:1–17. [Google Scholar]
- Siegel R, Naishadham D, Jemal A. Cancer statistics, 2012. CA Cancer J Clin. 2012;62:10–29. doi: 10.3322/caac.20138. [DOI] [PubMed] [Google Scholar]
- Siegel R, Ward E, Brawley O, Jemal A. Cancer statistics, 2011: the impact of eliminating socioeconomic and racial disparities on premature cancer deaths. CA Cancer J Clin. 2011;61:212–36. doi: 10.3322/caac.20121. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH. Cone-Beam CT with a Flat-Panel Detector: From Image Science to Image-Guided Surgery. Nucl Instrum Methods Phys Res A. 2011;648:S241–S250. doi: 10.1016/j.nima.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen JH, et al. Multimode C-arm fluoroscopy, tomosynthesis, and cone-beam CT for image-guided interventions: from proof of principle to patient protocols. Proc of SPIE Medical Imaging. 2007:65101A–65101A. [Google Scholar]
- Siewerdsen JH, Moseley DJ, Burch S, Bisland SK, Bogaards A, Wilson BC, Jaffray DA. Volume CT with a flat-panel detector on a mobile, isocentric C-arm: pre-clinical investigation in guidance of minimally invasive surgery. Med Phys. 2005;32:241–54. doi: 10.1118/1.1836331. [DOI] [PubMed] [Google Scholar]
- Stavness I, Lloyd JE, Payan Y, Fels S. Coupled hard–soft tissue simulation with contact and constraints applied to jaw–tongue–hyoid dynamics. International Journal for Numerical Methods in Biomedical Engineering. 2011;27:367–390. [Google Scholar]
- Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition. 1999;32:71–86. [Google Scholar]
- Suh JW, Scheinost D, Dione DP, Dobrucki LW, Sinusas AJ, Papademetris X. A non-rigid registration method for serial lower extremity hybrid SPECT/CT imaging. Med Image Anal. 2011;15:96–111. doi: 10.1016/j.media.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suh JW, Wyatt CL. Deformable Registration of Prone and Supine Colons for CT Colonography. 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; Aug. 30 –Sept. 3 2006; pp. 1997–2000. [DOI] [PubMed] [Google Scholar]
- Thirion JP. Fast non-rigid matching of 3D medical images. INRIA Technical Report. 1995;2547:1–37. [Google Scholar]
- Thirion JP. Image matching as a diffusion process: an analogy with Maxwell’s demons. Medical Image Analysis. 1998;2:243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- Tsin Y, Kanade T. Computer Vision -ECCV. Springer; Berlin Heidelberg: 2004. A Correlation-Based Approach to Robust Point Set Registration. [Google Scholar]
- Tustison NJ, Awate SP, Gang S, Cook TS, Gee JC. Point Set Registration Using Havrda-Charvat-Tsallis Entropy Measures. IEEE Trans Med Imag. 2011;30:451–460. doi: 10.1109/TMI.2010.2086065. [DOI] [PubMed] [Google Scholar]
- Uneri A, Nithiananthan S, Schafer S, Otake Y, Stayman JW, Kleinszig G, Sussman MS, Prince JL, Siewerdsen JH. Deformable registration of the inflated and deflated lung in cone-beam CT-guided thoracic surgery: Initial investigation of a combined model- and image-driven approach. Med Phys. 2013;40:017501–15. doi: 10.1118/1.4767757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uneri A, et al. Deformable registration of the inflated and deflated lung for cone-beam CT-guided thoracic surgery. Proc of SPIE Medical Imaging. 2012:831602–831602. doi: 10.1117/12.911440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Abel KM, Moore EJ. The rise of transoral robotic surgery in the head and neck: emerging applications. Expert Rev Anticancer Ther. 2012;12:373–80. doi: 10.1586/era.12.7. [DOI] [PubMed] [Google Scholar]
- Vasquez Osorio EM, Hoogeman MS, Bondar L, Levendag PC, Heijmen BJ. A novel flexible framework with automatic feature correspondence optimization for nonrigid registration in radiotherapy. Med Phys. 2009;36:2848–59. doi: 10.1118/1.3134242. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Malis E, Perchant A, Ayache N. Insight into Efficient Image Registration Techniques and the Demons Algorithm. Proc of Inf Process Med Imaging. 2007;4584:495–506. doi: 10.1007/978-3-540-73273-0_41. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: efficient non-parametric image registration. Neuroimage. 2009;45:S61–72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- Wachinger C, Navab N. Entropy and Laplacian images: structural representations for multi-modal registration. Med Image Anal. 2012;16:1–17. doi: 10.1016/j.media.2011.03.001. [DOI] [PubMed] [Google Scholar]
- Wand MP, Jones MC. Kernel Smoothing. London, UK: Chapman & Hall; 1995. [Google Scholar]
- Wang F, Syeda-Mahmood T, Vemuri BC, Beymer D, Rangarajan A. Closed-Form Jensen-Renyi Divergence for Mixture of Gaussians and Applications to Group-Wise Shape Registration. Proceedings of the 12th International Conference on Medical Image Computing and Computer-Assisted Intervention: Part I.; London, UK: Springer-Verlag; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Vemuri BC, Rangarajan A, Eisenschenk SJ. Simultaneous nonrigid registration of multiple point sets and atlas construction. IEEE Trans Pattern Anal Mach Intell. 2008;30:2011–22. doi: 10.1109/TPAMI.2007.70829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein GS, O’malley BW, Jr, Cohen MA, Quon H. Transoral robotic surgery for advanced oropharyngeal carcinoma. Arch Otolaryngol Head Neck Surg. 2010;136:1079–85. doi: 10.1001/archoto.2010.191. [DOI] [PubMed] [Google Scholar]
- Wells WM, III, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical Image Analysis. 1996;1:35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- Williams JL, Maybeck PS. Cost-function-based hypothesis control techniques for multiple hypothesis tracking. Mathematical and Computer Modelling. 2006;43:976–989. [Google Scholar]
- Woo Hyun N, Dong-Goo K, Duhgoon L, Jae Young L, Jong Beom R. Automatic registration between 3D intra-operative ultrasound and pre-operative CT images of the liver based on robust edge matching. Physics in Medicine and Biology. 2012;57:69. doi: 10.1088/0031-9155/57/1/69. [DOI] [PubMed] [Google Scholar]
- Woo Hyun N, Dong-Goo K, Duhgoon L, Jong Beom R. Robust registration of 3-D ultrasound and CT images of the liver for image-guided intervention. IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 14–17 April 2010; pp. 1201–1204. [Google Scholar]
- Xuejun G, et al. Implementation and evaluation of various demons deformable image registration algorithms on a GPU. Physics in Medicine and Biology. 2010;55:207–219. doi: 10.1088/0031-9155/55/1/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Xue Z, Liu X, Xiong D. Topology preservation evaluation of compact-support radial basis functions for image registration. Pattern Recognition Letters. 2011;32:1162–1177. [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. NeuroImage. 2006;31:1116–28. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Zagorchev L, Goshtasby A. A comparative study of transformation functions for nonrigid image registration. IEEE Trans Image Process. 2006;15:529–38. doi: 10.1109/tip.2005.863114. [DOI] [PubMed] [Google Scholar]
- Zhang T, Orton NP, Mackie TR, Paliwal BR. Technical note: A novel boundary condition using contact elements for finite element based deformable image registration. Med Phys. 2004;31:2412–2415. doi: 10.1118/1.1774131. [DOI] [PubMed] [Google Scholar]
- Zhou J, Tian Q, Chong V, Xiong W, Huang W, Wang Z. Segmentation of skull base tumors from MRI using a hybrid support vector machine-based method. Proceedings of the Second international conference on Machine learning in medical imaging.; Toronto, Canada: Springer-Verlag; 2011. [Google Scholar]
- Zhu C, Byrd RH, Lu P, Nocedal J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans Math Softw. 1997;23:550–560. [Google Scholar]