Abstract
Structural porosity is a decisive property for soil productivity and soil environmental functions. Hydraulic properties in the structural range vary over time in response to management and environmental influences. Although this is widely recognized, there are few field studies that determine dominant driving forces underlying hydraulic property dynamics. During a three year field experiment we measured temporal variability of soil hydraulic properties by tension infiltrometry. Soil properties were characterized by hydraulic conductivity, effective macroporosity and Kosugi's lognormal pore size distribution model. Management related influences comprised three soil cover treatment (mustard and rye vs. fallow) and an initial mechanical soil disturbance with a rotary harrow. Environmental driving forces were derived from meteorological and soil moisture data. Soil hydraulic parameters varied over time by around one order of magnitude. The coefficient of variation of soil hydraulic conductivity K(h) decreased from 69.5% at saturation to 42.1% in the more unsaturated range (− 10 cm pressure head). A slight increase in the Kosugi parameter showing pore heterogeneity was observed under the rye cover crop, reflecting an enhanced structural porosity. The other hydraulic parameters were not significantly influenced by the soil cover treatments. Seedbed preparation with a rotary harrow resulted in a fourfold increase in macroporosity and hydraulic conductivity next to saturation, and homogenized the pore radius distribution. Re-consolidation after mechanical loosening lasted over 18 months until the soil returned to its initial state. The post-tillage trend of soil settlement could be approximated by an exponential decay function. Among environmental factors, wetting-drying cycles were identified as dominant driving force explaining short term hydraulic property changes within the season (r2 = 0.43 to 0.59). Our results suggested that beside considering average management induced changes in soil properties (e.g. cover crop introduction), a dynamic approach to hydrological modeling is required to capture over-seasonal (tillage driven) and short term (environmental driven) variability in hydraulic parameters.
Abbreviations: K(h), hydraulic conductivity; ε, effective macroporosity; ϕ, total porosity; θs, water content at saturation; θr, residual water content; hm, median pressure head; rm, median pore radius; σ, standard deviation of pore size distribution
Keywords: Macroporosity, Temporal variability, Tension infiltrometer, Wetting–drying cycles, Cover cropping, Tillage
Highlights
-
•
Variability of hydraulic properties decreases from macropore to unsaturated range.
-
•
Management effects are over-seasonal, environmental effects within the season.
-
•
Mechanical disturbance has a higher impact compared to plant based measures.
-
•
Rye increases pore heterogeneity, tillage gives a temporarily higher median radius.
-
•
Wetting–drying intensity is a dominant driving force of hydraulic properties.
1. Introduction
Agricultural productivity and most environmental functions of the soil depend on an intact soil structure (Blum et al., 2006). Regarding soil hydraulics, soil structure controls the two fundamental relations for water flow in the saturated and near-saturated range, i.e. the retention and hydraulic conductivity functions (Cresswell et al., 1992).
Soil structural porosity is a highly dynamic property subject to numerous natural and human influences. Therefore knowledge of its spatial and temporal variability is fundamental to accurately describe soil processes like water infiltration and storage (van Es et al., 1999). Changes in soil structure occur on different time scales (Kay, 1990). Land use changes result in long-term adaptation of soil properties (e.g. Fuentes et al., 2004, Scheffler et al., 2011, Schwärzel et al., 2010). Tillage and crop rotation modify soil structure on an intermediate over-seasonal scale (e.g. Green et al., 2003, Moret and Arrúe, 2007, Roger-Estrade et al., 2000, Schwen et al., 2011, Snyder et al., 2000, Strudley et al., 2008). Within a cropping season soil structure responds to environmental conditions such as the amount and intensity of rainfall, wet–dry and freeze–thaw cycles, (e.g. Angulo-Jaramillo et al., 1997, Peng et al., 2007, Rousseva et al., 2002).
In agricultural soils, environmental and management related factors interact in driving temporal dynamics of structure related soil hydraulic properties (Mapa et al., 1986). Tillage operations and crop rotation are key management decisions that can improve or deteriorate soil structural porosity and water permeability (Munkholm et al., 2013). For example, no-tillage is considered particularly adapted to conserve soil structure (Bronick and Lal, 2005). The transition from regular soil loosening to no-tillage requires several years to achieve a stable, natural soil structure (Wright et al., 1999). Munkholm et al. (2003) demonstrated that soils under long term no-tillage with low “self-mulching potential” (low clay and organic matter content) can also tend to increased bulk density and reduced water permeability.
Crop rotation influences structural porosity via plant canopy and mulch coverage which protect aggregates at the soil surface against disruption by heavy rainfall (Blanco-Canqui et al., 2006). Also the different amount and quality of aboveground as well as root derived organic matter input and their microbiological decomposition are related to soil structure formation and stabilization (Angers and Caron, 1998, Feeney et al., 2004, Gregory, 2006). Particularly roots can modify pore properties in various ways, such as temporal pore clogging (Scanlan and Hinz, 2008), biopore formation upon decay (Rasse and Smucker, 1998), local compaction, enhanced wetting–drying (Whalley et al., 2004) and hydrophobicity of rooted pore walls (Czarnes et al., 2000).
The introduction of cover crops is a widely applied measure to improve soil quality and fertility within the crop rotation. Cover crops correspond to what Yunusa and Newton (2003) called primer-plants, i.e. plants without a direct economic benefit, but effective in conditioning the soil for cash crops and in conserving environmental resources. Folorunso et al. (1992) and Joyce et al. (2002) reported improved rainfall infiltration in cover-cropped plots compared to a fallow rotation. Carof et al. (2007) and Bodner et al. (2008) did not find a significantly higher hydraulic conductivity under cover crops, but showed a stabilization of near saturated hydraulic properties over time. Williams and Weil (2004) considered cover crops as an effective way to alleviate soil compaction due to root induced biopores being used by the following crop to penetrate the soil.
Horn and Smucker (2005) reviewed the role of various environmental driving forces for soil structure formation. Capillary forces enhance soil aggregation upon drying, while rewetting may increase structural instability (Lado et al., 2004, Leij et al., 2002, Peng et al., 2007). Rainfall intensity is an indicator for the disaggregating force of raindrop impact on surface aggregates (Singh et al., 2012). These dynamic environmental driving forces interact with stabilizing agents in a given soil such as organic matter (e.g. exudates) and ion composition (e.g. Ca++) as well as management (e.g. tillage, cover cropping).
The importance of temporal soil structure dynamics is widely recognized (e.g. Green et al., 2003, Stange and Horn, 2005) and there is substantial qualitative knowledge about structure forming factors. However, only few studies attempted to demonstrate the relation of structure dependent hydraulic properties and processes with their driving forces under field conditions. The present study analyses the temporal variability of field hydraulic properties in the near saturated range and aims to reveal major environmental and management induced driving forces. A main hypothesis of the study is that management factors modify soil structural porosity over a longer time scale, while within season variability can be explained by environmental driving forces. Our objective is to identify factors and time scales to be taken into consideration for a dynamic description of hydrological processes in an agricultural field, and to highlight the potential of agricultural management measures to influence soil hydraulic properties in the structural range.
2. Materials and methods
2.1. Experimental site
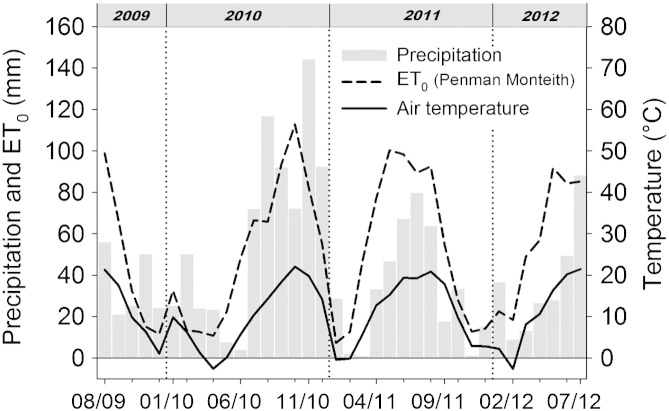
Field measurements were conducted on an arable field near Raasdorf, Lower Austria (48°14′N 16°35′E, 156 m asl) between 2009 and 2012. Climatically the site is characterized by sub-humid conditions (pannonic) with an average annual precipitation of 525 mm, a mean annual temperature of 9.8 °C, and a mean relative humidity of 75%. Weather data were recorded by an automated weather station (Adcon Telemetry GmbH, Austria) at the experimental site. Fig. 1 shows rainfall, temperature and reference evapotranspiration (ET0) for the three experimental years.
Fig. 1.
Precipitation, air temperature and reference evapotranspiration (ET0) at the experimental site.
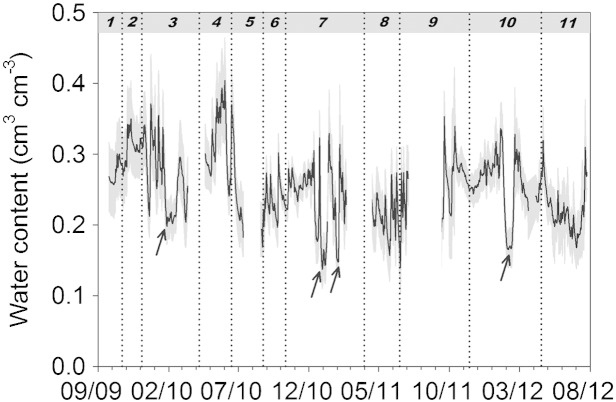
Capacitance sensors (CProbe, Adcon Telemetry GmbH, Austria) were installed in each experimental plot via access tubes for continuous soil water measurement. Fig. 2 shows the soil water dynamics in the upper soil layer during the experimental period.
Fig. 2.
Soil water content in the surface near soil layer. Gray area shows the standard deviation (n = 9), vertical dotted lines indicate measurement dates and numbers define periods between infiltration measurements. Arrows show periods of frozen soil. Gaps are due to sensor removal during harvest and seeding operations.
The soil at the site is classified as Chernosem in the WRB (IUSS, 2007). Basic soil properties are given in Table 1.
Table 1.
Soil properties of the experimental field.
| Horizon | Depth cm |
Sand kg kg− 1 |
Silt kg kg− 1 |
Clay kg kg− 1 |
Texture USDA |
Corg kg kg− 1 |
Field capacity cm3 cm− 3 |
Wilting point cm3 cm− 3 |
|---|---|---|---|---|---|---|---|---|
| A | 0–40 | 0.19 | 0.56 | 0.24 | SiL | 0.025 | 0.32 | 0.15 |
| AC | 40–55 | 0.23 | 0.54 | 0.23 | SiL | 0.015 | 0.27 | 0.10 |
| C | > 55 | 0.22 | 0.62 | 0.16 | SiL | 0.008 | 0.25 | 0.07 |
The field trial was established on a site under no tillage since 1996. Three different soil cover treatments were integrated during the fallow period between cash crops of a three year crop rotation. Cash crops were durum wheat (Triticum turgidum L. subsp. durum, 2010), field pea (Pisum sativum L., 2011) and durum wheat (2012). The soil cover treatments consisted of (i) bare soil without any plant cover between main crops, and two different cover crops, being (ii) mustard (Sinapis alba L.) and (iii) rye (Secale cereale L). The two cover crops differed in the duration of green canopy coverage and their root systems. Rye is a winter-hard cover crop while mustard is killed by frost during winter. Rye has a fibrous homorrhizal root system, while mustard is an allorhizal plant with a tap root (Kutschera et al., 2009). The soil in this crop rotation is left uncovered for around eight months (August to March) in case of not including a cover crop. The three soil cover treatments were arranged in a randomized complete block design (RCBD) with three replicates. Each plot had a length of 20 m and a width of 3 m.
Table 2 gives an overview of management measures and measurements during the study period. In spring 2010, before seeding of durum wheat into the cover crop residues, a shallow seed bed preparation of the top five centimeter soil was performed using a rotary harrow. In the subsequent years the soil again returned to no-tillage without any further mechanical soil disturbance.
Table 2.
Management measures and tension infiltrometer measurement dates.
| Experimental year | Date | Activity |
|---|---|---|
| 2009/10 | 20 August 2009 | Seeding of cover crops (mustard, rye) |
| 9 September 2009 | Tension infiltrometer measurement | |
| 21 October 2009 | Tension infiltrometer measurement | |
| 2 December 2009 | Tension infiltrometer measurement | |
| 13 December 2009 | Frost period killing mustard cover crop | |
| 10 March 2010 | Herbicide application to kill winter hard rye cover crop and weeds | |
| 8 April 2010 | Tension infiltrometer measurement | |
| 20 April 2010 | Seed bed preparation (rotary harrow) and seeding of durum wheat | |
| 15 June 2010 | Tension infiltrometer measurement | |
| 14 July 2010 | Harvest of durum wheat | |
| 2010/11 | 19 August 2010 | Seeding of cover crops (mustard, rye) |
| 26 August 2010 | Tension infiltrometer measurement | |
| 11 October 2010 | Tension infiltrometer measurement | |
| 5 December 2010 | Frost period killing mustard cover crop | |
| 22 March 2011 | Herbicide application to kill winter hard rye cover crop and weeds | |
| 31 March 2011 | Tension infiltrometer measurement | |
| 12 April 2011 | Direct seeding of field pea | |
| 16 June 2011 | Tension infiltrometer measurement | |
| 7 July 2011 | Harvest of field pea | |
| 2011/12 | 20 August 2011 | Seeding of cover crops (mustard, rye) |
| 29 November 2011 | Tension infiltrometer measurement | |
| 26 January 2012 | Frost period killing mustard cover crop | |
| 18 March 2012 | Herbicide application to kill winter hard rye cover crop and weeds | |
| 19 April 2012 | Tension infiltrometer measurement | |
| 21 April 2012 | Direct seeding of durum wheat | |
| 22 July 2012 | Tension infiltrometer measurement | |
| 25 July 2012 | Harvest of durum wheat |
2.2. Tension infiltrometer measurements
Infiltration experiments were conducted twelve times between September 2009 and July 2012 (cf. Fig. 2 and Table 2). The measurements were performed using a tension infiltrometer (Soil Measurement Systems Inc., Tucson, AZ). The infiltrometer disc had a diameter of 20 cm and was separate from the supply and tension control tubes. Measurements were taken at the soil surface where most structural dynamics were expected. The soil surface was prepared by carefully removing mulch and any above-ground plant material. A nylon mesh to avoid macropore clogging and a fine layer of quartz sand (diameter: 0.08–0.2 mm) to ensure good hydraulic contact were placed between the disc and the soil. The supply pressure heads were − 10, − 4, − 1, and 0 cm. The first two pressure heads were maintained for approximately 40–60 min, and the last two pressure heads were applied for about 10–20 min. Preliminary tests found these durations to be sufficient to achieve steady-state infiltration. The water level in the supply tube was observed visually in intervals of 15 s during the first 5 min after application of a supply pressure, and in increasing intervals of 2–10 min afterwards. All infiltration experiments were conducted in the non-trafficked interrow area of a plot. Before each infiltration measurement, soil samples were taken with steel cores (250 cm3) in the vicinity of the measurement location to obtain the initial water content, bulk density and total porosity. Immediately after each infiltration measurement, another core sample was collected directly below the infiltration disc to quantify the final water content.
2.3. Data analysis
All infiltration experiments were analyzed by the following procedures: In a first step, the near-saturated hydraulic conductivity vs. pressure head relationship K(h) was derived using the analytical approach of Wooding (1968). In a second step, effective macroporosity was calculated from K(h) following the procedure of Bodhinayake et al. (2004). Finally the cumulative infiltration data were used to inversely estimate the parameters of the Kosugi soil water retention model (Kosugi, 1996).
2.3.1. Near-saturated hydraulic conductivity
We followed the procedure described by Reynolds and Elrick (1991) and Ankeny et al. (1991) to determine the saturated and near-saturated hydraulic conductivity K(h). Infiltration from a circular source with a constant pressure head at the soil surface can be approximated analytically according to Wooding (1968) by
| (1) |
where q is the steady-state infiltration rate (cm3 s− 1), and rd is the radius of the disc (cm). The unsaturated hydraulic conductivity K(h) is described by the exponential model of Gardner (1958):
| (2) |
where h is the pressure head (cm), Ks is the saturated hydraulic conductivity (cm s− 1), and α is the sorptive number (cm− 1). Since the solution of Wooding has two unknown variables, K(h) and α, two steady-state fluxes at different tensions are required. Reynolds and Elrick (1991) among others derived the unsaturated hydraulic conductivity in the middle of an interval between two applied pressure heads hi and hi + 1, assuming α to be constant over this interval.
2.3.2. Effective macroporosity
The effective macroporosity of a soil can be estimated from the difference between the infiltration rates at two pressure heads (Bodhinayake et al., 2004, Buczko et al., 2006). We used the approach of Bodhinayake et al. (2004) where the water-conducting macroporosity ε(a,b) (cm3 cm− 3) is calculated from the hydraulic conductivity in the pressure head interval corresponding to the two pore radii a and b by
| (3) |
here, η is the dynamic viscosity of water (kg cm− 1 s− 1), σ is the surface tension of water (kg s− 2), ρ is the density of water (kg cm− 3), and g is the acceleration due to gravity (cm s− 2). Integration of Eq. (3) was done numerically using Matlab (Mathworks, USA). Effective macroporosity is given as the sum of pores ≥ 0.15 mm.
2.3.3. Inverse estimation of soil water retention parameters
The inverse analysis of tension infiltrometer data requires a numerical solution of the Richards' equation for radially symmetric Darcian flow. We followed the procedure presented by Šimůnek et al. (1998). Soil water retention was described by the model of Kosugi (1996) which is based on a lognormal pore-size distribution. We used the Kosugi model due to the physical interpretability of its parameters. Soil water retention Se(h) is given by
| (4) |
where Se (−) is the effective saturation corresponding to with θ (cm3 cm− 3) being the volumetric water content, θr (cm3 cm− 3) being the residual water content and θs (cm3 cm− 3) being the saturation water content. Erfc is the complementary error function, hm (cm) is the median pressure head and σ (−) is the standard deviation of the log-transformed pressure head. The median pore radius (rm) can be calculated from the median pressure head hm using the Young–Laplace equation.
Parameter estimation is done by minimizing the objective function as defined by Šimůnek and Van Genuchten (1996) using the program HYDRUS 2D/3D (Šimůnek et al., 2006) which applies a Levenberg–Marquardt nonlinear minimization algorithm. Initial parameter estimates were derived from the texture based pedotransfer function Rosetta (Schaap et al., 2001) (input parameters: soil texture and bulk density). To reduce the amount of unknown variables, θr was fixed to 0.067 cm3 cm− 3, as predicted by Rosetta, and Ks values were used from the Wooding analysis (Šimůnek et al, 1998). The remaining parameters θs, σ, and hm were then inversely estimated.
2.4. Driving force parameters
Different parameters may act as driving forces for the temporal variability of soil hydraulic properties. In our experiment management induced driving forces included three soil covers arranged as randomized plots on the field. Cover crop plants were characterized by their aboveground (soil cover, biomass) and root properties (root–shoot ratio, root length density). A further management impact on the entire experimental field was the mechanical soil disturbance at seedbed preparation in spring 2010.
Environmental driving forces included cumulative rainfall, rainfall intensity, cumulative reference evapotranspiration and three parameters reflecting soil wetting and drying (trend in soil moisture, intensity of wetting–drying, frequency of wetting–drying cycles). These parameters were calculated from meteorological data and surface near soil water content in the period between two consecutive infiltration measurements. The trend in soil moisture was obtained by linear regression of water content vs. time. Wetting–drying cycle intensity and cycle frequency were calculated by spectral analysis of the de-trended soil water content time series using the SAS (SAS Institute Inc., 2004) procedure PROC SPECTRA.
2.5. Statistical evaluation
Analysis of variance was performed using the MIXED procedure in SAS that computes Wald-type F-statistics using generalized least squares (GLSE) based on restricted maximum likelihood estimates of the variance components (Littell et al., 1998). Denominator degrees of freedom were approximated by the Kenward Roger method (Kenward and Roger, 1997). In case of significant differences in the Wald-F-statistic for p < 0.05, treatment means were compared using a two-sided t test. To account for the serial correlation of non-randomized repeated measures on the same experimental unit, i.e. pressure head sequence in the K(h) data and measurement date, an adequate correlation model must be fit to the data (Piepho et al., 2004). This was done within the procedure MIXED using the Akaike Information Criterion (AIC).
3. Results and discussion
3.1. Near saturated hydraulic conductivity
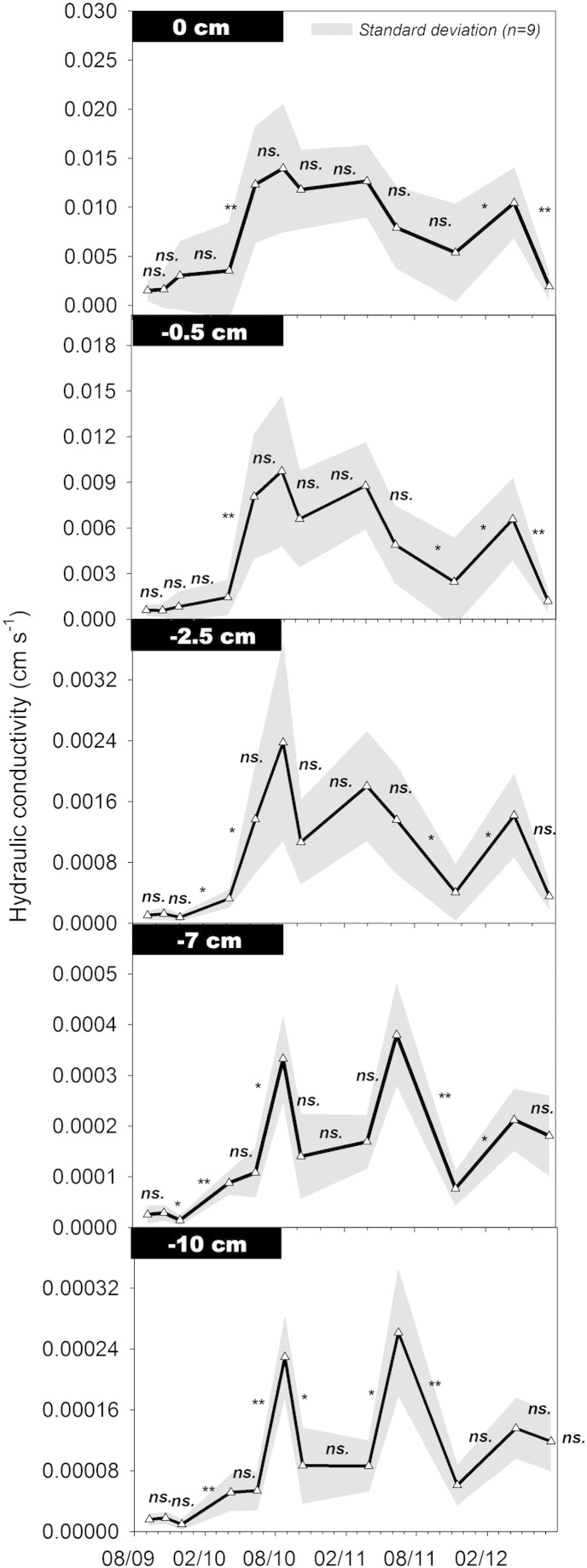
Near saturated hydraulic conductivity K(h) was calculated from infiltration measurements using Wooding's analytical solution at twelve measurement dates over the three year crop rotation (Fig. 3). All years included at least one measurement in the growing cover crop in autumn, one after winter before cash crop seeding and one in early summer before cash crop harvest.
Fig. 3.
Temporal variability of near saturated and saturated soil hydraulic conductivity at different pressure heads. Statistical comparison indicates if changes between two consecutive measurement dates are significant at p < 0.05 (ns. non-significant, * significant at p < 0.05, ** significant at p < 0.01).
Table 3 shows the results of the analysis of variance. The p-values reveal the dominant role of temporal variance on K(h) at all pressure heads. In average 62.5% of the total variance in K(h) was due to the temporal effect. This was substantially higher compared to spatial effects, which are indicated by replication and inter-plot (error) variance and explained 20.2% of the total variance. Also Messing and Jarvis (1993) found higher temporal than spatial variability in K(h) measured by tension infiltrometers.
Table 3.
Results of analysis of variance (p-values) for hydraulic conductivity K(h) and related pore parameters (ε effective macroporosity, ϕ total porosity, rm median pore radius, σ pore radius standard deviation).
| K(h) | ε | ϕ | rm | σ | |
|---|---|---|---|---|---|
| TREAT | 0.528ns | 0.928ns. | 0.305ns. | 0.449ns. | 0.030* |
| DATE | < 0.0001*** | < 0.0001*** | < 0.0001*** | < 0.0001*** | < 0.0001*** |
| TREAT ∗ DATE | 0.965ns | 0.633ns | 0.899ns | 0.525ns | 0.404ns |
| PRESS | < 0.0001*** | – | – | – | – |
| TREAT ∗ PRESS | 0.065ns | – | – | – | – |
| DATE ∗ PRESS | < 0.0001*** | – | – | – | – |
TREAT soil cover treatment, DATE measurement date, PRESS pressure head.
K(h) varied by around one order of magnitude between measurement dates. At saturation K(h) ranged from a minimum of 1.5e− 3 cm s− 1 (September 2009) to a maximum of 1.4e− 2 cm s− 1 (August 2010). At the lowest pressure head (− 10 cm), K(h) was between 9.4e− 6 cm s− 1 (December 2009) and 2.6e− 4 cm s− 1 (June 2011). The average coefficient of variation decreased from 69.5% at h = 0 cm to 42.1% at h = − 10 cm. Higher variability in hydraulic processes driven by larger pores has also been described by Schwen et al. (2011) and Castellini and Ventrella (2012).
Management effects reflected by the temporal dynamics of K(h) were mainly tillage, while soil cover treatment had neither a significant main nor interaction effect (cf. Table 3). At the higher pressure heads (0 cm to − 2.5 cm) K(h) significantly increased between April and June 2010, while this did not occur at lower pressure heads (− 7 cm and − 10 cm). After the infiltration measurement in April 2010, a shallow tillage operation for cash crop seedbed preparation was done. This mechanical soil disturbance resulted in a three to five fold increase in K(h) next to saturation. The post-tillage increase was followed by a decreasing trend which expressed the process of soil reconsolidation. This trend was strongest at saturation (r2 = 0.62, p = 0.019*) and decreased towards K(h) at − 2.5 cm (r2 = 0.36, p = 0.11ns). Until November 2011, K(h) between saturation and − 2.5 cm pressure head was significantly higher compared to the state before mechanical soil disturbance. Also Mapa et al. (1986) and Moret and Arrúe (2007) among others reported a temporary increase in hydraulic conductivity after tillage. The subsequent decreasing trend is influenced by environmental factors such as rainfall.
The tillage driven dynamics (loosening and reconsolidation) were not found for K(h) measured at − 7 cm and − 10 cm. At the lower pressure heads there were two marked peaks (26 August 2010, 16 June 2011) with K(h) values being above the average by half an order of magnitude. At both dates initial water contents recorded before infiltration measurements were at the lowest values during the entire experiment (0.22 cm3 cm− 3 and 0.16 cm3 cm− 3 respectively). This points to a dominant environmental influence in the more unsaturated range compared to management effects (cf. 3.4.2).
3.2. Effective macroporosity and total porosity
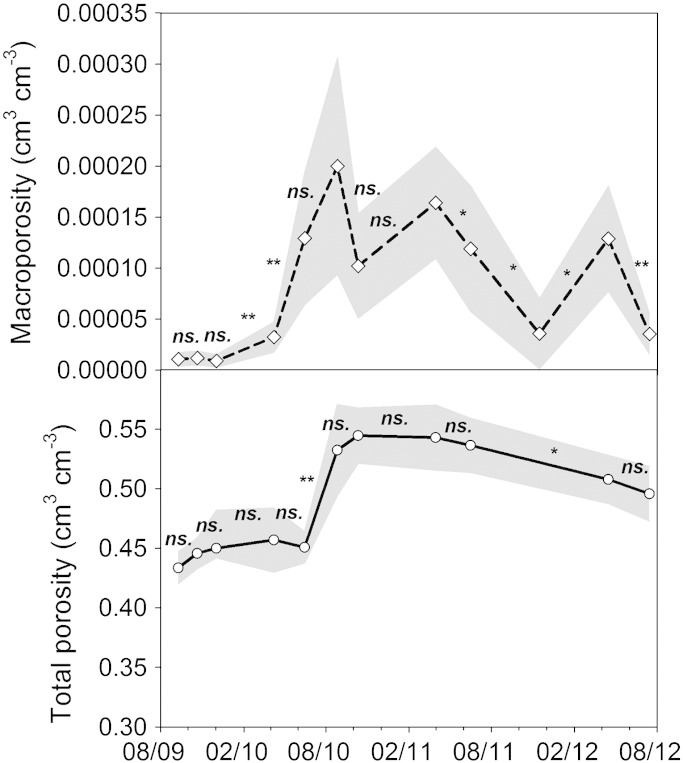
For a better understanding of pore properties underlying the flow process, we show effective macroporosity and total porosity. Macroporosity (ε) was calculated according to Bodhinayake et al. (2004) as the sum of pores ≥ 0.15 mm (equivalent to − 10 cm pressure head). Total porosity (ϕ) was measured with soil core samples (250 cm3) before infiltration measurements. Fig. 4 shows the temporal dynamics of ε and ϕ.
Fig. 4.
Temporal variability of effective macroporosity and total porosity. Statistical comparison indicates if changes between two consecutive measurement dates are significant at p < 0.05 (ns. non-significant, * significant at p < 0.05, ** significant at p < 0.01).
ε was in the range of values given in Bodhinayake et al. (2004) and Daraghmeh et al. (2008) and made up 0.02% of total porosity. We note that here ε represents an effective parameter, i.e. the water-conducting macropore fraction. Effective parameters obtained from field infiltration experiments are generally lower compared to those measured in the laboratory by e.g. desorption (Reynolds et al., 1995).
Statistical results for both parameters are given in Table 3. The different soil cover treatments did not have a significant influence, while both parameters showed a significant temporal variability. ε ranged from 9.0e− 6 cm3 cm− 3 (December 2009) to 2.0e− 4 cm3 cm− 3 (August 2010). ϕ varied between 0.43 cm3 cm− 3 (September 2009) and 0.54 cm3 cm− 3 (October 2010). The variability of ε was substantially higher compared to ϕ with coefficients of variation being 55.2% for ε and only 4.7% for ϕ.
ε showed a substantial increase between April and June 2010 and a decreasing tendency after a peak value in August 2010. The decreasing trend in ε (r2 = 0.39, p = 0.10ns.) was less apparent compared to K(h) at 0 cm and − 0.5 cm pressure head. It was interrupted by remarkable peaks, particularly between November 2011 and April 2012 which indicates important short term environmental influences.
ϕ increased significantly between June and August 2010. The increase in ϕ occurred during the same period as a peak in K(h) at lower pressure heads (cf. Fig. 3). The subsequent decreasing trend as well as short term variations were very low compared to macropore dynamics. Ciollaro and Lamaddalena (1998) also did not find a significant change in total porosity by tillage in a study on tillage induced changes of hydraulic properties. Similar to our findings, however, they reported a strong response of macropore dependent properties to mechanical soil disturbance.
Large macropores are characterized by high temporal variability (Jarvis, 2007); still they are only a small fraction of total porosity which is therefore more stable over time. The two parameters also suggested distinct driving forces for different pore classes. The effect of mechanical soil disturbance was apparent only in ε, while the increase in ϕ occurred in a period of intense soil drying, indicating a dominant influence of environmental factors.
3.3. Retention parameters
We calculated the parameters of the Kosugi water retention model from cumulative infiltration data by inverse simulation. The Kosugi model describes the pore size distribution by four parameters, i.e. saturation and residual water content (θs and θr), median pore radius (rm) and pore radius standard deviation (σ). An advantage of this model is the better physical interpretation of its parameters compared to curve fitting parameters in other retention functions (Kosugi et al., 2002). Here we report only rm and σ that essentially govern the shape of the pore size distribution. Hayashi et al. (2006) demonstrated that these parameters are proper indicators for structural porosity. A high rm for a given soil texture class reveals the importance of macroporosity as a product of biotic and abiotic structure forming processes. A narrow pore size distribution (low σ) with a high frequency of the dominant pore radius class is characteristic for structureless soils. The formation of a secondary, structure related, pore system increases the range of pore radii (high σ) and shows a more evenly distributed frequency of the single pore classes.
The significance of factors explaining the variance in Kosugi parameters is given in Table 3. Beside the temporal effect, which is highly significant for both parameters, σ is also significantly influenced by the soil cover treatments.
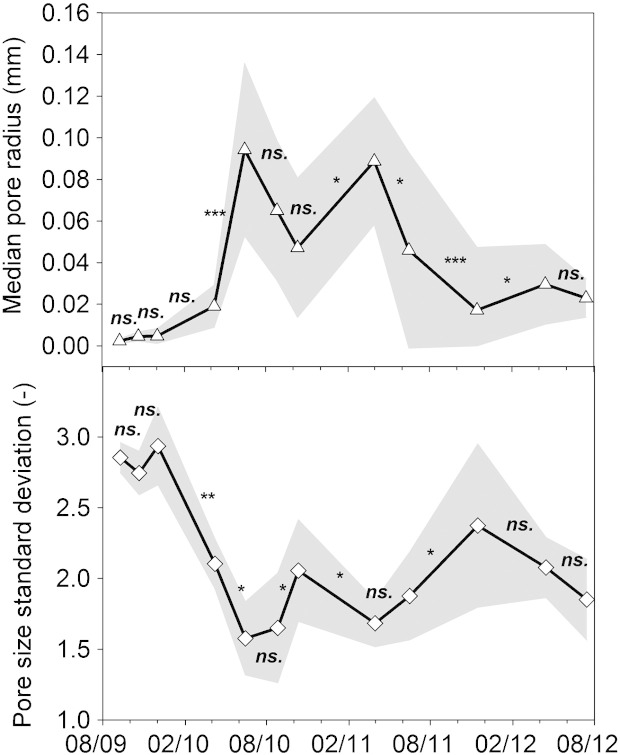
Fig. 5 shows the temporal dynamics of the Kosugi parameters. Rm was in the range of 0.002 mm to 0.09 mm, σ varied between 1.58 and 2.94. The coefficient of variation of rm was 67.1% and 13.4% for σ. Similar to ε and K(h) next to saturation, rm increased by half an order of magnitude between April and June 2010 in response to mechanical soil disturbance. The peak value of 0.09 mm in June 2010 was followed by a significant decreasing trend (r2 = 0.60, p = 0.023*) interrupted by a second peak in April 2011. In November 2011 rm had a value not significantly different from before mechanical disturbance.
Fig. 5.
Temporal variability of the parameters from Kosugi's water retention model. Statistical comparison indicates if changes between two consecutive measurement dates are significant at p < 0.05 (ns. non-significant, * significant at p < 0.05, ** significant at p < 0.01, *** significant at p < 0.001).
The range of pore radii, expressed by the Kosugi-parameter σ, was 2.84 at the beginning of the experiment and decreased significantly after December 2009 to reach its lowest value in June 2010. Thereafter it remained at a low value of 1.94 in average.
Kosugi parameters were inversely related to each other (Figure not shown, r2 = 0.73, p = 0.0004***). We suggest that this is an indication of both site characteristics and management. Soils with a strongly silt dominated texture, low in clay and intermediate organic matter tend to naturally consolidate under long term no-tillage due to reduced capacity of aggregation and structure stabilization (Grant and Blackmore, 1990, Munkholm et al., 2003). The significant decrease of rm short after the mechanical loosening showed this tendency as probably large inter-aggregate pores created by the tillage event were unstable. Horn et al. (1994) remarked that the formation of soil structural porosity is not only expressed by an enhanced macroporosity, but also a heterogenization of the pore system as a result of finer intra-aggregate pores. The larger range of pore radius classes (larger σ) in the undisturbed soil before harrowing in spring 2010 indicates the structure related secondary pore system at this site. The rotating tillage implement homogenized the soil and partially destroyed secondary aggregates and pore structures, which resulted in a decrease of σ. There was also a consistent reduction in σ over winter which is statistically significant in 2009/10 and 2010/11. During the comparatively mild winter 2011/12 the same tendency was visible, but not statistically significant. Over-winter freezing–thawing could have induced aggregate breakdown (Oztas and Fayetorbay, 2003) which would explain the structure homogenization expressed in the reduction of σ. Oztas and Fayetorbay (2003) showed that this effect is less pronounced with decreasing wetness. The dry autumn and winter seasons 2011/12 (cf. Fig. 1) thus could have reduced over winter structure degradation.
3.4. Driving forces of hydraulic property dynamics
Our measurements showed that field soil hydraulic parameters vary substantially over time. This points to the necessity of understanding the underlying driving forces. Although several authors discussed the qualitative role of biotic and abiotic structure forming agents on hydraulic processes (Angers and Caron, 1998, Bronick and Lal, 2005, Horn and Smucker, 2005, Oades, 1993), there are few field studies trying to demonstrate quantitatively the relation between hydraulic parameters with their driving forces in a natural field environment.
3.4.1. Management driving forces
Cover cropping is considered an effective agro-environmental measure to ameliorate soil physical properties (Dabney et al., 2001). The crop rotation (durum wheat–pea–durum wheat) in our experiment implied a long fallow period (8 month) to study the effect of the different soil cover treatments consisting of two cover crops (mustard, rye) compared to bare soil. The cover crops differed in the time of providing a green canopy cover (rye > mustard) and in their root properties (fibrous vs. taproot system).
Table 4 shows aboveground dry-matter, maximum soil coverage, root–shoot ratio and root length density of the two cover crop treatments. Mustard had a higher aboveground biomass compared to rye and achieved nearly complete soil coverage before winter while rye covered around 60% of the soil surface. Rye showed a higher translocation of biomass to the root system as indicated by the root–shoot ratio. Also root length density of the fibrous rye root system was higher compared to mustard.
Table 4.
Cover crop above ground and root system traits (Values in brackets give the inter-annual variation over the three experimental years).
| Above ground traits |
Root system traits |
|||
|---|---|---|---|---|
| Dry matter kg ha− 1 |
Soil coverage % |
Root–shoot ratio – |
Root length density cm3 cm− 3 |
|
| Mustard | 3715.5 (± 1298.8) | 97.2 (± 15.6) | 0.27 (± 0.09) | 3.7 (± 0.5) |
| Rye | 1401.4 (± 463.1) | 62.3 (± 12.3) | 0.44 (± 0.07) | 4.2 (± 0.8) |
In spite of the long period of bare soil in the fallow treatment, the different soil covers did not show a significant influence on most soil hydraulic properties (cf. Table 3). Yunusa and Newton (2003) compared annual and perennial herbaceous and woody species as primer plants to improve soil permeability. They concluded that annuals are not sufficiently effective in biopore formation to increase soil permeability. Also several studies on crop rotation and tillage effects on soil physical properties did not find a crop related influence, while mostly tillage had a dominant effect (e.g. Capowiez et al., 2009, Chang and Lindwall, 1992, Hammel, 1989). In our experiment the rotation had the same cash crops, while only soil cover treatments after cash crop harvest differed. Due to no-tillage management over most of the experimental duration, cash crop residues protected also the soil surface of fallow plots. These two reasons could have reduced the impact of the different soil cover treatments on most hydraulic parameters.
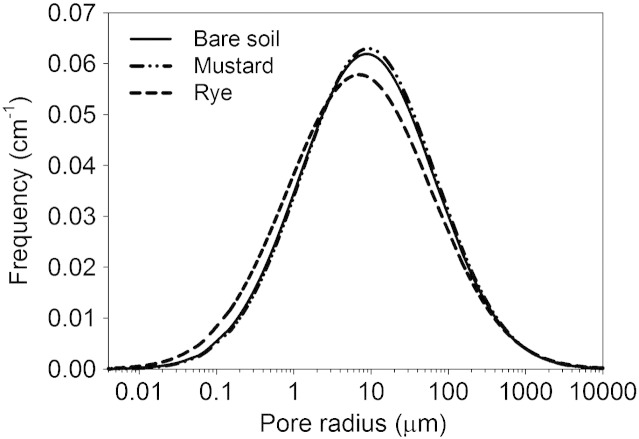
The only parameter significantly influenced by the soil cover treatments was the pore radius standard deviation σ of the Kosugi model. Rye had a significantly higher average σ-value (2.15) compared to the other treatments (fallow: 2.02, mustard: 2.03). The significant main effect without interaction with time indicated a general adaptation of the system properties to this management change. Fig. 6 shows the resulting mean soil pore size distribution under the three soil cover treatments.
Fig. 6.
Effect of different soil cover treatments on pore size distribution. Main difference according to statistical evaluation is due to pore radius standard deviation (Kosugi parameter σ).
We suggest that this slight differentiation in pore size distribution is caused by the root system of rye. Rooting intensity of the top soil is higher in rye compared to mustard and root growth also continues in early spring until herbicide application before cash crop seeding. Liu et al. (2005) demonstrated that exudates of grass cover crop roots improved soil aggregation. Liesch et al. (2011) found increased water permeability when integrating a rye cover crop into a maize production system and related this finding to the intense rye rooting. Scanlan (2009) suggested that an increased heterogeneity of the pore size distribution could result from roots growing inside preexisting pores in an intensely rooted soil. These findings support our interpretation that the increase in σ under rye was root induced.
Mechanical soil disturbance by a rotary harrow during seed bed preparation in April 2010 caused a strong increase for several hydraulic parameters followed by a decreasing trend. The process of loosening and subsequent reconsolidation was most pronounced for K(h) near saturation (h = 0 cm and − 0.5 cm; r2 = 0.62 and 0.57) and rm (r2 = 0.60). Also ε (r2 = 0.39) and K(h) at h = − 2.5 cm (r2 = 0.36) had the same tendency, but with a low coefficient of determination. Also Cameira et al. (2003) among others found that parameters with strong influence of large macropores are most responsive to tillage induced changes, while parameters influenced by smaller pore classes are less affected. Mechanical disturbance modified hydraulic parameters on an over-seasonal time scale. The original state before disturbance was achieved after approximately 18 months (November 2011). The decreasing trend could be described by a linear or, alternatively, an exponential decrease (figure not shown). The latter is probably more appropriate to capture the process of soil reconsolidation after mechanical disturbance. Moret and Arrúe (2007) considered post-tillage reconsolidation mainly a function of rainfall amount, while Mubarak et al. (2009) pointed to wet–dry cycles as dominant driving force.
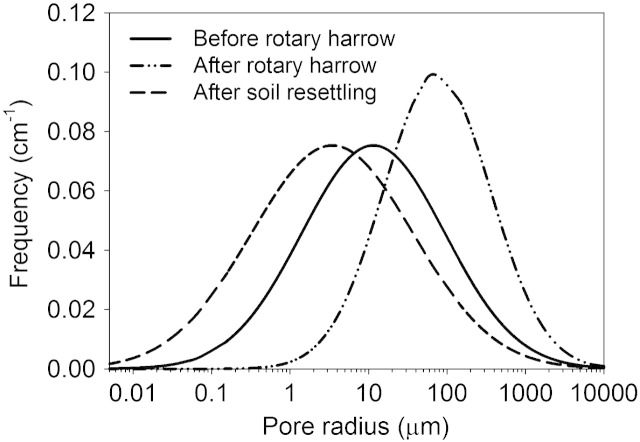
Fig. 7 resumes the overall effect of mechanical soil disturbance on the pore system. The undisturbed structure with a wide range of pore classes and a maximum in the smaller pore range (April 2010) shifted to a more homogeneous pore size distribution with a maximum at a higher radius after mechanical disturbance by a rotary harrow (June 2010). Thereafter the soil tended to return to its original state (November 2011). We notice that contrary to rm, which returned to its original state around 18 months after the temporary tillage induced increase, σ still had a significantly lower value at the end of the experiment. This shows that even a single tillage operation caused a sustainable alteration of soil structure.
Fig. 7.
Effect of mechanical soil disturbance by a rotary harrow on pore size distribution with state before disturbance, post-tillage shift and final state.
3.4.2. Environmental driving forces
Besides management influences, environmental factors may substantially modify soil structural properties (Horn and Smucker, 2005). We analyzed several environmental parameters for their role as driving forces of the temporal variability in soil hydraulic properties. These parameters were derived from meteorological and soil water measurements and are given in Table 5. Meteorological data were used to calculate cumulative rainfall and evapotranspiration between two consecutive infiltration measurements. Rainfall intensity was calculated as maximum 30 min rain amount (I30).
Table 5.
Quantification of environmental driving forces for temporal variability of soil hydraulic properties.
| Perioda | Driving forces |
|||||
|---|---|---|---|---|---|---|
| Σ Rainfall mm |
Maximum I30 mm h− 1 |
Σ ET mm |
Moisture trend cm3 cm− 3 d− 1 |
Cycle intensity – |
Cycle period d |
|
| 1 | 28.4 | 3.0 | 70.2 | 1.5E-03 | 0.9 | 27.0 |
| 2 | 60.0 | 2.0 | 23.7 | 6.9E-04 | 7.2 | 42.0 |
| 3 | 61.2 | 1.6 | 108.4 | − 8.5E-04 | 37.4 | 53.0 |
| 4 | 217.4 | 7.4 | 162.1 | 3.9E-04 | 51.0 | 55.0 |
| 5 | 253.4 | 17.0 | 232.9 | − 1.6E-03 | 5.3 | 28.0 |
| 6 | 110.8 | 3.2 | 75.4 | 2.4E-04 | 5.4 | 9.2 |
| 7 | 118.2 | 3.8 | 115.7 | − 3.5E-04 | 40.8 | 27.2 |
| 8 | 79.0 | 4.0 | 231.8 | − 2.2E-04 | 6.5 | 10.3 |
| 9 | 260.6 | 14.2 | 316.6 | 3.6E-04 | 20.1 | 21.0 |
| 10 | 80.4 | 1.8 | 129.7 | − 2.1E-04 | 55.2 | 42.3 |
| 11 | 133.8 | 9.8 | 260.7 | − 8.7E-04 | 8.8 | 46.0 |
Periods between two consecutive measurement dates (cf. Fig. 2).
The moisture trend was calculated as the slope of a linear regression through water content vs. time between two consecutive infiltration measurement dates. It indicates if the respective period was characterized by a general soil wetting or drying.
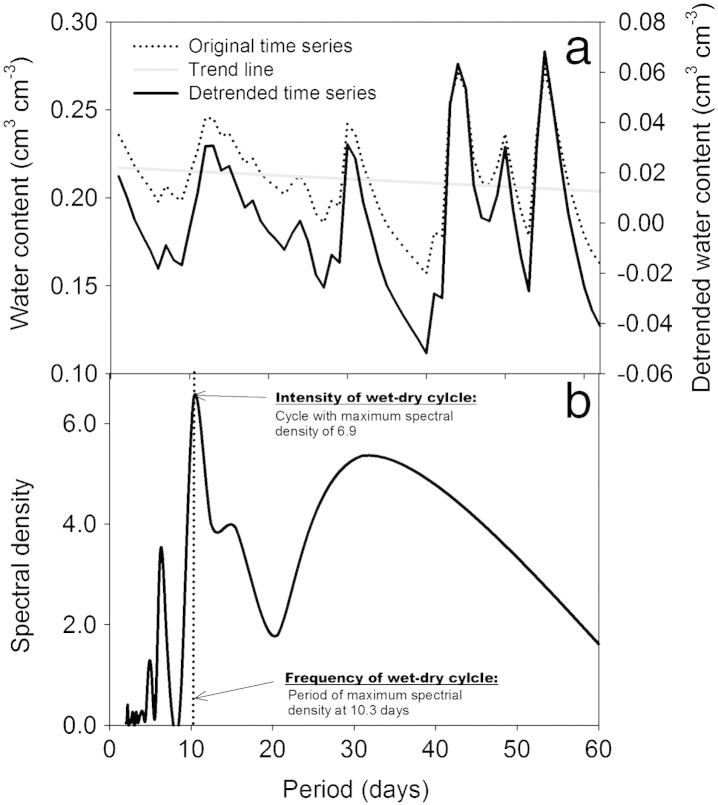
To quantify cyclic wetting–drying events, we used spectral analysis of the de-trended water content time series (Nielsen and Wendroth, 2003). Spectral analysis can reveal both, the intensity of a cyclic pattern and its frequency (period length). Fig. 8 exemplifies this approach to quantification of wetting–drying behavior from field water content data.
Fig. 8.
Quantification of wetting–drying for water content measurement. (a) De-trending of water content time series for spectral analysis, (b) periodogram showing maximum spectral density and the corresponding frequency.
The predictive power of environmental driving force parameters for fluctuations of the hydraulic parameters between consecutive measurements was analyzed by linear regression. Table 6 shows those environmental variables with highest predictive power for the respective soil property and whether the predictor is related positively or negatively to the dependent hydraulic variable.
Table 6.
Best predictor among environmental driving forces for the temporal change in soil hydraulic property parameters (r2 coefficient of determination, p significance of regression model, positive or negative sign in brackets indicates direction of influence).
| Δproperty | Best predictor (slope) | r2 | p |
|---|---|---|---|
| Δk(h) h = 0 cm | Wet–dry cycle intensity (+) | 0.43 | 0.03* |
| Δk(h) h = 0.5 cm | Wet–dry cycle intensity (+) | 0.54 | 0.01* |
| Δk(h) h = 2.5 cm | Wet–dry cycle intensity (+) | 0.37 | 0.05* |
| Δk(h) h = 7 cm | Moisture trend (−) | 0.21 | 0.15ns |
| Δk(h) h = 10 cm | Moisture trend (−) | 0.22 | 0.14ns |
| Δε | Wet–dry cycle intensity (+) | 0.44 | 0.03* |
| Δrm | Wet–dry cycle intensity (+) | 0.55 | < 0.01** |
| Δσ | Wet–dry cycle frequency (−) | 0.59 | 0.01** |
| Δϕ | Rainfall intensity (+) | 0.46 | 0.04* |
K(h) hydraulic conductivity, ε effective macroporostiy, rm median pore radius, σ pore radius standard deviation, ϕ total porosity.
For most parameters we could find a significant predictor, except for hydraulic conductivities in the more unsaturated range (h = − 7 cm and − 10 cm). Particularly the intensity of wetting drying explained a significant proportion of the temporal variance of several hydraulic property parameters. Several authors assumed wetting–drying to underlie temporal variability in their hydraulic properties measurements (e.g. Castellini and Ventrella, 2012, Mubarak et al., 2009, Murphy et al., 1993). Including a second variable in the regression model would have only slightly improved the coefficient of determination and in most cases did not significantly contribute to the explained variance. This indicates a dominant influence of the given variable among the tested environmental driving forces.
High intensity wetting–drying cycles resulted in an increase of those parameters related to soil's macroporosity (rm and ε) and macropore driven flow processes (K(h) at 0 cm and − 0.5 cm). This is in agreement with a laboratory study of Peng et al. (2007) who found a general increase in porosity (between 2.6 and 16.5% depending on clay content) with wetting–drying cycle intensity and highest changes in the macropore fraction. Mubarak et al. (2009) observed an increase in field hydraulic conductivity in a limited irrigation system as a result of more intense wetting–drying.
Soil parameters were more responsive to the intensity of wetting–drying compared to the frequency of cycles, which was also found by Peng et al. (2007). Only pore radius standard deviation was affected by cycle frequency. Here short period soil moisture fluctuations resulted in higher pore heterogeneity.
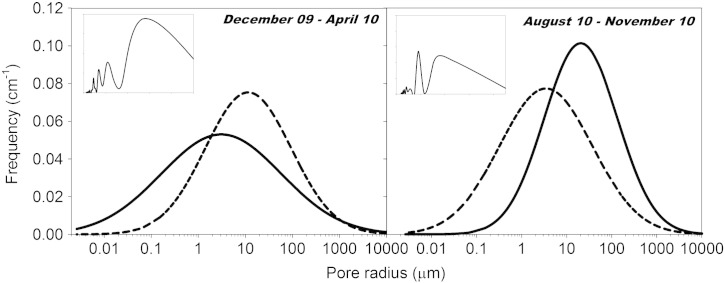
Fig. 9 gives an example of the shift in pore size distribution for two periods with different wetting–drying behavior. Over winter (December 2009 to April 2010), pore size distribution became narrower with an increase in median pore radius. This period was characterized by intense wetting–drying at low cycle frequency. The autumn period 2010 (August to November) on the contrary was characterized by more frequent, but low intensity cycles. The evolution of pore size distribution during this period showed an increase in pore heterogeneity with a shift towards a lower median radius.
Fig. 9.
Pore size evolution at two periods with different wetting–drying pattern. Periodogram with cyclic pattern in the respective period is shown in the left corner (high intensity and lower frequency cycles left; high frequency and lower intensity cycles right).
Total porosity was significantly influenced by rainfall intensity. However this relation has to be taken with care. There was only one substantial change in Φ (between June and August 2010), while variability was very low during the remaining time. Such a pattern may substantially bias a linear regression model.
In the more unsaturated range of K(h) we did not find significant relations to any of our predictor variables. Soil moisture trend had the highest r2 with K(h) at − 7 cm and − 10 cm. The enhanced unsaturated hydraulic conductivity upon prolonged soil drying might indicate an increase in intra-aggregate fissure (Smucker et al., 2007). The low r2 and lack of significance however point to an overall lower temporal variability in the more unsaturated range. The dynamic contribution of soil structure is quickly decreasing beyond the range of large macropores and the static effect of texture becomes dominant (Wagner et al., 2001).
4. Conclusions
In a three year field study we measured the temporal variability of soil hydraulic properties in the near saturated range and analyzed potential driving forces to explain the observed system dynamics. Temporal changes were most evident for those hydraulic parameters driven by macropores and decrease towards the more unsaturated range. The temporal variability in pore properties and flow processes was related to agricultural management measures as well as environmental factors. The distinct driving forces induced changes at different time scales. A change in crop rotation by integrating different soil cover treatments during the post-harvest fallow period led to an average system adaptation with different frequency distributions of pore radius classes. The winter hard, intensely rooted rye cover crop increased pore heterogeneity, indicating an enhanced soil structure formation. Still the overall impact of the plant based measure was substantially less compared to a mechanical soil disturbance. A single seedbed preparation with a rotary harrow significantly changed structural porosity on an over-seasonal time scale. Mechanical soil loosening increased macroporosity and hydraulic conductivity next to saturation, while it homogenized the pore radius frequency distribution. The effect of mechanical loosening lasted over 18 months until the soil returned to its original state in most hydraulic parameters.
Short term variability was found in all hydraulic properties and was more pronounced for parameters expressing macropore dynamics. The macropore range was mainly influenced by intense wetting–drying cycles. In the more unsaturated range periods of prolonged soil drying resulted in a temporal increase in hydraulic conductivity. Our field measurements confirmed the dominant role of wetting–drying intensity for soil pore evolution.
The study shows the necessity to consider time dependence in hydraulic functions when modeling water flow processes under field conditions. While post-tillage trends in hydraulic properties could be approximated by an exponential decay functions, spectral analysis allowed a quantification of field wetting–drying behavior to be used as predictor variable for describing short term fluctuations in hydraulic functions. A major challenge remains capturing the causal factors of a plant based management measure on soil structural porosity. Further research of root–soil interactions is required to advance our understanding in this field and define applicable management solutions.
Acknowledgment
The present study was funded by the Austrian Science Foundation (FWF) by grant number P 21836-B16. The authors are grateful for the financial support provided to their work.
Footnotes
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-No Derivative Works License, which permits non-commercial use, distribution, and reproduction in any medium, provided the original author and source are credited.
References
- Angers D.A., Caron J. Plant-induced changes in soil structure: processes and feedbacks. Biogeochemistry. 1998;42:55–72. [Google Scholar]
- Angulo-Jaramillo R., Moreno F., Clothier B.E., Thony J.L., Vachaud G., Fernandez-Boy E., Cayuela J.A. Seasonal variation of hydraulic properties of soils measured using a tension disk infiltrometer. Soil Science Society of America Journal. 1997;61:27–32. [Google Scholar]
- Ankeny M.D., Ahmed M., Kaspar T.C., Horton R. Simple field method for determining unsaturated hydraulic conductivity. Soil Science Society of America Journal. 1991;55:467–470. [Google Scholar]
- Blanco-Canqui H., Lal R., Post W.M., Izaurralde R.C., Owens L.B. Corn stover impacts on near-surface soil properties of no-till corn in Ohio. Soil Science Society of America Journal. 2006;70:266–278. [Google Scholar]
- Blum W.E.H., Warkentin B.P., Frossard E. Soil, human society and the environment. Geological Society, London, Special Publications. 2006;266:1–8. [Google Scholar]
- Bodhinayake W., Si B.C., Xiao C.J. New method for determining water-conducting macro- and mesoporosity from tension infiltrometer. Soil Science Society of America Journal. 2004;68:760–769. [Google Scholar]
- Bodner G., Loiskandl W., Buchan G., Kaul H.-P. Natural and management-induced dynamics of hydraulic conductivity along a cover-cropped field slope. Geoderma. 2008;146:317–325. [Google Scholar]
- Bronick C.J., Lal R. Soil structure and management: a review. Geoderma. 2005;124:3–22. [Google Scholar]
- Buczko U., Bens O., Huttl R.E. Tillage effects on hydraulic properties and macroporosity in silty and sandy soils. Soil Science Society of America Journal. 2006;70:1998–2007. [Google Scholar]
- Cameira M.R., Fernando R.M., Pereira L.S. Soil macropore dynamics affected by tillage and irrigation for a silty loam alluvial soil in southern Portugal. Soil and Tillage Research. 2003;70:131–140. [Google Scholar]
- Capowiez Y., Cadoux S., Bouchant P., Ruy S., Estrade J.R., Richard G., Boizard H. The effect of tillage type and cropping system on earthworm communities, macroporosity and water infiltration. Soil and Tillage Research. 2009;105:209–216. [Google Scholar]
- Carof M., De Tourdonnet S., Coquet Y., Hallaire V., Roger-Estrade J. Hydraulic conductivity and porosity under conventional and no-tillage and the effect of three species of cover crop in northern France. Soil Use and Management. 2007;23:230–237. [Google Scholar]
- Castellini M., Ventrella D. Impact of conventional and minimum tillage on soil hydraulic conductivity in typical cropping system in Southern Italy. Soil and Tillage Research. 2012;124:47–56. [Google Scholar]
- Chang C., Lindwall C.W. Effects of tillage and crop rotation on physical properties of a loam soil. Soil and Tillage Research. 1992;22:383–389. [Google Scholar]
- Ciollaro G., Lamaddalena N. Effect of tillage on the hydraulic properties of a vertic soil. Journal of Agricultural Engineering Research. 1998;71:147–155. [Google Scholar]
- Cresswell H.P., Smiles D.E., Williams J. Soil structure, soil hydraulic properties and the soil water balance. Australian Journal of Soil Research. 1992;30:265–283. [Google Scholar]
- Czarnes S., Hallett P.D., Bengough A.G., Young I.M. Root- and microbial-derived mucilages affect soil structure and water transport. European Journal of Soil Science. 2000;51:435–443. [Google Scholar]
- Dabney S.M., Delgado J.A., Reeves D.W. Using winter cover crops to improve soil and water quality. Communications in Soil Science and Plant. 2001;32:1221–1250. [Google Scholar]
- Daraghmeh O.A., Jensen J.R., Petersen C.T. Near-saturated hydraulic properties in the surface layer of a sandy loam soil under conventional and reduced tillage. Soil Science Society of America Journal. 2008;72:1728–1737. [Google Scholar]
- Feeney D., Daniell T.J., Hallett P.D., Ritz K., Young I.M. Eurosoil 2004. Proceedings, Freiburg. 2004. Fungi and root induced meso- and microscale soil structural changes. (2004) [Google Scholar]
- Folorunso O.A., Rolston D.E., Prichard T., Loui D.T. Soil surface strength and infiltration as affected by winter cover crops. Soil Technology. 1992;5:189–197. [Google Scholar]
- Fuentes J.P., Flury M., Bezdicek D.F. Hydraulic properties in a silt loam soil under natural prairie, conventional till, and no-till. Soil Science Society of America Journal. 2004;68:1679–1688. [Google Scholar]
- Gardner W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Science. 1958;85:228–231. [Google Scholar]
- Grant C.D., Blackmore A.V. Self mulching behavior in clay soils—its definition and measurement. Australian Journal of Soil Research. 1990;29:155–173. [Google Scholar]
- Green T.R., Ahuja L.R., Benjamin J.G. Advances and challenges in predicting agricultural management effects on soil hydraulic properties. Geoderma. 2003;116:3–27. [Google Scholar]
- Gregory P.J. Roots, rhizosphere and soil: the route to a better understanding of soil science? European Journal of Soil Science. 2006;57:2–12. [Google Scholar]
- Hammel J.E. Long-term tillage and crop rotation effects on bulk density and soil impedance in Northern Idaho. Soil Science Society of America Journal. 1989;53:1515–1519. [Google Scholar]
- Hayashi Y., Kosugi K., Mizuyama T. Changes in pore size distribution and hydraulic properties of forest soil resulting from structural development. Journal of Hydrology. 2006;331:85–102. [Google Scholar]
- Horn R., Smucker A. Structure formation and its consequences for gas and water transport in unsaturated arable and forest soils. Soil and Tillage Research. 2005;82:5–14. [Google Scholar]
- Horn R., Taubner H., Wuttke M., Baumgartl T. Soil physical properties related to soil structure. Soil and Tillage Research. 1994;30:187–216. [Google Scholar]
- IUSS . FAO; Rome: 2007. World Reference Base for Soil Resources. [Google Scholar]
- Jarvis N.J. A review of non-equilibrium water flow and solute transport in soil macropores: principles, controlling factors and consequences for water quality. European Journal of Soil Science. 2007;58:523–546. [Google Scholar]
- Joyce B.A., Wallender W.W., Mitchell J.P., Huyck L.M., Temple S.R., Brostrom P.N., Hsiao T.C. Infiltration and soil water storage under winter cover cropping in California's Sacramento Valley. Transactions of ASAE. 2002;45:315–326. [Google Scholar]
- Kay B.D. Rates of change of soil structure under different cropping systems. Advances in Soil Science. 1990;12:1–52. [Google Scholar]
- Kenward M.G., Roger J.H. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics. 1997;53:983–997. [PubMed] [Google Scholar]
- Kosugi K. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resources Research. 1996;32:2697. [Google Scholar]
- Kosugi K., Hopmans J.W., Dane J.H. Parameteric models. In: Dane J.H., Topp G.C., editors. Methods of Soil Analysis. Part 4. Physical Methods. Inc., Madison; Wisconsin, USA: 2002. pp. 739–757. (Soil Science Society of America). [Google Scholar]
- Kutschera L., Lichtenegger E., Sobotik M. DLG-Verlag; Frankfurt Main: 2009. Wurzelatlas der Kulturpflanzen gemäßigter Gebiete mit Arten des Feldgemüsebaues. [Google Scholar]
- Lado M., Paz A., Ben-Hur M. Organic matter and aggregate-size interactions in saturated hydraulic conductivity. Soil Science Society of America Journal. 2004;68:234–242. [Google Scholar]
- Leij F.J., Ghezzehei T.A., Or D. Modelling the dynamics of the soil pore-size distribution. Soil and Tillage Research. 2002;64:61–78. [Google Scholar]
- Liesch A.M., Krueger E.S., Ochsner T.E. Soil structure and physical properties under rye–corn silage double-cropping systems. Soil Science Society of America Journal. 2011;75:1307–1314. [Google Scholar]
- Littell R.C., Henry P.R., Ammerman C.B. Statistical analysis of repeated measures data using SAS procedures. Journal of Animal Science. 1998;76:1216–1231. doi: 10.2527/1998.7641216x. [DOI] [PubMed] [Google Scholar]
- Liu A., Ma B.L., Bomke A.A. Effects of cover crops on soil aggregate stability, total organic carbon, and polysaccharides. Soil Science Society of America Journal. 2005;69:2041–2048. [Google Scholar]
- Mapa R.B., Green R.E., Santo L. Temporal variability of soil hydraulic properties with wetting and drying subsequent to tillage. Soil Science Society of America Journal. 1986;50:1133–1138. [Google Scholar]
- Messing I., Jarvis N.J. Temporal variation in the hydraulic conductivity of a tilled clay soil as measured by tension infiltrometers. Journal of Soil Science. 1993;44:11–24. [Google Scholar]
- Moret D., Arrúe J.L. Dynamics of soil hydraulic properties during fallow as affected by tillage. Soil and Tillage Research. 2007;96:103–113. [Google Scholar]
- Mubarak I., Mailhol J.C., Angulo-Jaramillo R., Ruelle P., Boivin P., Khaledian M. Temporal variability in soil hydraulic properties under drip irrigation. Geoderma. 2009;150:158–165. [Google Scholar]
- Munkholm L.J., Schjønning P., Rasmussen K.J., Tanderup K. Spatial and temporal effects of direct drilling on soil structure in the seedling environment. Soil and Tillage Research. 2003;71:163–173. [Google Scholar]
- Munkholm L.J., Heck R.J., Deen B. Long-term rotation and tillage effects on soil structure and crop yield. Soil and Tillage Research. 2013;127:85–91. [Google Scholar]
- Murphy B.W., Koen T.B., Jones B.A., Huxedurp L.M. Temporal variation of hydraulic properties for some soils with fragile structure. Australian Journal of Soil Research. 1993;31:179–197. [Google Scholar]
- Nielsen D.R., Wendroth O. Catena publisher; Reiskirchen, Germany: 2003. Spatial and Temporal Statistics. Sampling Field Soils and Their Vegetation. [Google Scholar]
- Oades J.M. The role of biology in the formation, stabilization and degradation of soil structure. Geoderma. 1993;56:377–400. [Google Scholar]
- Oztas T., Fayetorbay F. Effect of freezing and thawing processes on soil aggregate stability. Catena. 2003;52:1–8. [Google Scholar]
- Peng X., Horn R., Smucker A. Pore shrinkage dependency of inorganic and organic soils on wetting and drying cycles. Soil Science Society of America Journal. 2007;71:1095–1103. [Google Scholar]
- Piepho H.P., Büchse A., Richter C. A mixed modelling approach for randomized experiments with repeated measures. Journal of Agronomy and Crop Science. 2004;190:230–247. [Google Scholar]
- Rasse D.P., Smucker A.J.M. Root colonization of previous root channels in corn and alfalfa rotations. Plant and Soil. 1998;204:203–212. [Google Scholar]
- Reynolds W.D., Elrick D.E. Determination of hydraulic conductivity using a tension infiltrometer. Soil Science Society of America Journal. 1991;55:633–639. [Google Scholar]
- Reynolds W.D., Gregorich E.G., Curnoe W.E. Characterization of water transmission properties in tilled and untilled soil using tension infiltrometers. Soil and Tillage Research. 1995;33:117–131. [Google Scholar]
- Roger-Estrade J., Richard G., Boizard H., Boiffin J., Caneill J., Manichon H. Modelling structural changes in tilled topsoil over time as a function of cropping systems. European Journal of Soil Science. 2000;2000:455–474. [Google Scholar]
- Rousseva S., Torri D., Pagliai M. Effect of rain on the macroporosity at the soil surface. European Journal of Soil Science. 2002;53:83–94. [Google Scholar]
- Scanlan C.A. School of Earth and Environment; 2009. Processes and Effects of Root-Induced Changes to Soil Hydraulic Properties. PhD Thesis at the University of Western Australia. [Google Scholar]
- Scanlan C.A., Hinz C. vol. 10. 2008. A conceptual model to quantify plant root induced changes in soil hydraulic conductivity and water retention; pp. EGU2008–A-05854. (Geophysical Research Abstracts). (EGU General Assembly 2008) [Google Scholar]
- Schaap M.G., Leij F.J., van Genuchten M.T. ROSETTA: a computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. Journal of Hydrology. 2001;251:163–176. [Google Scholar]
- Scheffler R., Neill Ch., Krusche A.V., Elsenbeer H. Soil hydraulic response to land-use change associated with the recent soybean expansion at the Amazon agricultural frontier. Agriculture, Ecosystems & Environment. 2011;144:281–289. [Google Scholar]
- Schwärzel K., Carrick S., Wahren A., Feger K.-H., Bodner G., Buchan G.D. Soil hydraulic properties of recently tilled soil under cropping rotation compared with 2-years-pasture: measurement and modelling the soil structure dynamics. Vadose Zone Journal. 2010;10:354–366. [Google Scholar]
- Schwen A., Bodner G., Scholl P., Buchan G.D., Loiskandl W. Temporal dynamics of soil hydraulic properties and the water-conducting porosity under different tillage. Soil and Tillage Research. 2011;113:89–98. [Google Scholar]
- Šimůnek J., van Genuchten M.T. Estimating unsaturated soil hydraulic properties from tension disc infiltrometer data by numerical inversion. Water Resources Research. 1996;32:2683–2696. [Google Scholar]
- Šimůnek J., Angulo-Jaramillo R., Schaap M.G., Vandervaere J.P., van Genuchten M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension-disc infiltrometer data. Geoderma. 1998;86:61–81. [Google Scholar]
- Šimůnek J., van Genuchten M.T., Sejna M. Prague, Czech Republic; Technical Manual PC Progress: 2006. The HYDRUS Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. [Google Scholar]
- Singh M.J., Khera K.L., Santra P. Selection of soil physical quality indicators in relation to soil erodibility. Archives of Agronomy and Soil Science. 2012;58:657–672. [Google Scholar]
- Smucker A.J.M., Park E.-L., Dorner J., Horn R. Soil micropore development and contributions to soluble carbon transport within macroaggregates. Vadose Zone Journal. 2007;6:282–290. [Google Scholar]
- Snyder V.A., Rivadeneira J., Lugo H.M. Temporal changes in soil structure and hydraulic properties in the plow layer of an oxisol following tillage. Advances in Geoecology. 2000;32:314–324. [Google Scholar]
- Stange F.C., Horn R. Modeling the soil water retention curve for conditions of variable porosity. Vadose Zone Journal. 2005;4:602–613. [Google Scholar]
- Strudley M.W., Green T.R., Ascough J.C. Tillage effects on soil hydraulic properties in space and time: state of the science. Soil and Tillage Research. 2008;99:4–48. [Google Scholar]
- Van Es H.M., Ogden C.B., Hill R.L., Schindelbeck R.R., Tsegaye T. Integrated assessment of space, time, and management-related variability of soil hydraulic properties. Soil Science Society of America Journal. 1999;63:1599–1608. [Google Scholar]
- Wagner B., Tarnawski V.R., Hennings V., Müller U., Wessolek G., Plagge R. Evaluation of pedo-transfer functions for unsaturated soil hydraulic conductivity using an independent data set. Geoderma. 2001;102:275–297. [Google Scholar]
- Whalley W.R., Leeds-Harrison P.B., Leech P.K., Riseley B., Bird N.R.A. The hydraulic properties of soil at root-soil interface. Soil Science. 2004;169:90–99. [Google Scholar]
- Williams S.M., Weil R.R. Crop cover roots may alleviate of soil compaction effects on soybean crop. Soil Science Society of America Journal. 2004;68:1403–1409. [Google Scholar]
- Wooding R.A. Steady infiltration from a shallow circular pond. Water Resources Research. 1968;4:1259–1273. [Google Scholar]
- Wright S.F., Starr J.L., Paltineanu I.C. Changes in aggregate stability and concentration of glomalin during tillage management transition. Soil Science Society of America Journal. 1999;63:1825–1829. [Google Scholar]
- Yunusa I.A.M., Newton P.J. Plants for amelioration of subsoil constraints and hydrological control: the primer-plant concept. Plant and Soil. 2003;257:261–281. [Google Scholar]