Bayesian Sensitivity Analysis of Statistical Models with Missing Data

Abstract

Methods for handling missing data depend strongly on the mechanism that generated the missing values, such as missing completely at random (MCAR) or missing at random (MAR), as well as other distributional and modeling assumptions at various stages. It is well known that the resulting estimates and tests may be sensitive to these assumptions as well as to outlying observations. In this paper, we introduce various perturbations to modeling assumptions and individual observations, and then develop a formal sensitivity analysis to assess these perturbations in the Bayesian analysis of statistical models with missing data. We develop a geometric framework, called the Bayesian perturbation manifold, to characterize the intrinsic structure of these perturbations. We propose several intrinsic influence measures to perform sensitivity analysis and quantify the effect of various perturbations to statistical models. We use the proposed sensitivity analysis procedure to systematically investigate the tenability of the non-ignorable missing at random (NMAR) assumption. Simulation studies are conducted to evaluate our methods, and a dataset is analyzed to illustrate the use of our diagnostic measures.

1. Introduction

It is common to have missing data in surveys, clinical trials, and longitudinal studies. Various statistical methods have been developed to handle missing data. These methods depend on the missing data mechanism that generates the missing values and other modeling assumptions at various stages, and the resulting estimates and tests can be sensitive to these assumptions. Sensitivity analyses are commonly performed to perturb the model assumptions and/or individual observations to check the sensitivity of a specific influence measure (e.g., a parameter of interest). There is an extensive literature on sensitivity analysis for missing data problems in frequentist analysis (Copas and Eguchi (2005), Little and Rubin (2002), Zhu and Lee (2001), Copas and Li (1997), van Steen et al. (2001), Troxel (1998), Jansen et al. (2006), Jansen et al. (2003), Verbeke et al. (2001), Troxel et al. (2004), Shi, Zhu and Ibrahim (2009), Hens et al. (2006), Daniels and Hogan (2008)).

The literature on influence measures include Copas and Eguchi (2005), Zhu and Lee (2001), Troxel et al. (2004), Copas and Li (1997), van Steen et al. (2001), Troxel (1998), Jansen et al. (2006), Jansen et al. (2003), Hens et al. (2006), Verbeke et al. (2001), Shi, Zhu and Ibrahim (2009), and Daniels and Hogan (2008). For instance, in frequentist analysis, Copas and Eguchi (2005) developed a general formulation for assessing the bias of maximum likelihood estimates in the presence of small model perturbations for missing data problems. The local influence method in Cook (1986) was successfully applied to carry out sensitivity analyses for various statistical models with missing data (van Steen et al. (2001), Troxel (1998), Jansen et al. (2006), Hens et al. (2006), Jansen et al. (2003), Verbeke et al. (2001)). Shi, Zhu and Ibrahim (2009) further systematically investigated the local influence methods proposed in Zhu et al. (2007) for GLMs with missing at random (MAR) covariates as well as not missing at random (NMAR) covariates, often referred to as nonignorable missing covariates.

In contrast, in the Bayesian literature, several analogues of Cook (1986) were developed to carry out model assessment by using either the curvature of some influence measures (Millar and Stewart (2007), Linde (2007), Lavine (1991)) or the Fréchet derivative of the posterior with respect to the prior (Dey, Ghosh and Lou (1996), Gustafson (1996a), Gustafson (1996b), Berger (1994)). Daniels and Hogan (2008) examined several global and local sensitivity methods in the Bayesian analysis of pattern mixture models (Little (1994), Andridge and Little (2011)). Recently, Zhu, Ibrahim and Tang (2011) developed a general framework of Bayesian influence analysis for assessing various perturbation schemes to the data, the prior and the sampling distribution for a class of statistical models without missing data.

The aim of this paper is to develop a formal Bayesian sensitivity analysis in statistical models with missing data. We introduce various perturbations to the modeling of the missing data mechanism, individual observations, and the prior. We develop a geometric framework, called the Bayesian perturbation manifold, to characterize the intrinsic structure of these perturbations. We examine several influence measures for sensitivity analysis and for quantifying the effect of various perturbations to statistical models with missing data.

In the paper, we develop a Bayesian perturbation manifold for a large class of statistical models with missing data; examine three Bayesian influence measures including the ϕ-divergence, the posterior mean distance, and the Bayes factor; focus on assessing missing data mechanism, while simultaneously perturbing other distributional assumptions, the prior, and individual observations.

To motivate our methodology, we consider data on 1116 female sex workers in Philippine cities from a study of the relationship between Acquired Immune Deficiency Syndrome (AIDS) and the use of condoms (Morisky et al. (1998)), which is discussed in more detail in Section 3. The data contains items about knowledge of AIDS, attitude toward AIDS, belief, and self efficiency of condom use. Nine variables in the original data set (items 33, 32, 31, 43, 72, 74, 27h, 27e, and 27i in the questionnaire) were taken as responses. The primary interest here was to find how the threat of AIDS is associated with aggressiveness of the sex worker and the fear of contracting AIDS. The responses and covariates are missing at least once for 361 workers (32.35%). In Section 3, we carry out a Bayesian analysis of a structural equations model with both missing covariates and responses to analyze this data set, and present a formal Bayesian sensitivity analysis.

The rest of this paper is organized as follows. In Section 2, we construct a Bayesian perturbation manifold to characterize various perturbations to statistical models with missing data and derive its associated geometric quantities. We propose global and local influence measures to quantify the effects of perturbing missing data mechanism, while simultaneously perturbing the data, the prior, and other model assumptions on the posterior quantities. In Section 3, we present simulation studies and a data analysis to illustrate the importance of the proposed method in assessing the missing data mechanism and other potential misspecifications.

2. Bayesian sensitivity analysis

2.1. Statistical models with missing data

Let z_obs = (z_1,o, . . . , z_n,o) and z_mis = (z_1,m, . . . , z_n,m) be the observed and missing data, respectively, and z_com = (z_1,c, . . . , z_n,c) = (z_mis, z_obs) be the complete data, where z_i,c = (z_i,o, z_i,m) for i = 1, . . . , n. In applications, the dimensions of z_i,c, z_i,o and z_i,m may be different across i. For instance, the number of observations may vary across clusters for clustered data.

For missing data problems, we consider a statistical model p(z_com | θ) for the complete data such that p(z_com | θ) is the product of a model for the observed data p(z_obs | θ) and a model for the missing data given the observed data p(z_mis | z_obs, θ). This class of statistical models for missing data includes generalized linear models with missing covariates and/or responses, generalized linear mixed models, nonlinear models, parametric survival models, and many others. To carry out Bayesian inference, we usually use Markov chain Monte Carlo (MCMC) methods to simulate samples from the posterior distribution of the observed data

$$p(\theta \mid {\mathbf{z}}_{obs})\propto p({\mathbf{z}}_{obs}\mid \theta )p\left(\theta \right)\propto \int p({\mathbf{z}}_{com}\mid \theta )p\left(\theta \right)d{\mathbf{z}}_{mis}.$$ (2.1)

Example 1 (Missing Covariates Data). Consider n independent observations z_com = {z_i,c = (x_i, c_i, r_i, y_i), i = 1, . . . , n}, where y_i is the response variable, x_i is a p₁ × 1 vector of completely observed covariates, and c_i = (c_i,m, c_i,o) is a p₂ × 1 vector of partially observed covariates, where c_i,m and c_i,o denote the missing and observed components of c_i, respectively. Let r_i be a p₂ × 1 vector whose j^th component, r_ij, equals 1 if the j^th component of c_i, denoted by c_ij, is observed, and 0 if c_ij is missing. We assume that p(x_i, c_i, r_i, y_i|θ) = p(y_i|x_i, c_i, θ)p(x_i, c_i|θ) p(r_i|y_i, x_i, c_i, θ), where θ denotes the vector of unknown parameters. In this case, z_i,m = c_i,m and z_i,o = (x_i, c_i,o, r_i, y_i) for all i.

We assume the generalized linear model (GLM)

$$p(y_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i,\beta ,\tau )=\text{exp}[a_i^{-1}\left(\tau \right)\{y_i{\eta }_i\left(\beta \right)-b_1\left({\eta }_i\left(\beta \right)\right)\}+b_2(y_i,\tau )]$$ (2.2)

for i = 1, . . . , n, where a_i(·), b₁(·), and b₂(·,·) are known functions, η_i = η(μ_i) and ${\mu }_i=g\left(({\mathbf{x}}_i^{\prime },{\mathbf{c}}_i^{\prime })\beta \right)$, in which g(·) is a known link function, β = (β₁, . . . , β_p)′ and p = p₁ + p₂. We assume that

$$p({\mathbf{x}}_i,{\mathbf{c}}_i\mid \alpha )=p(c_{i{p}_2}\mid c_{i,p_2-1},\cdots ,c_{i1},{\mathbf{x}}_i,{\alpha }_{2p_2})\times \cdots \times p(c_{i1}\mid {\mathbf{x}}_i,{\alpha }_{21})p({\mathbf{x}}_i\mid {\alpha }_1).$$ (2.3)

Similarly, we model the missing-data mechanism as

$$p({\mathbf{r}}_i\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,\xi )=p(r_{i{p}_2}\mid r_{i,p_2-1},\cdots ,r_{i1},y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_{p_2})\times \cdots \times p(r_{i1}\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_1).$$ (2.4)

To carry out a full Bayesian analysis, we need to specify a prior for θ. We can take an independent prior for θ such that p(θ) = p(τ)p(β)p(ξ)p(α). For τ and β, we can take τ ~ gamma(α₀/2, λ₀/2) and β ~ N(μ₀, Σ₀), where α₀, λ₀, μ₀(p×1), and Σ₀(p × p positive definite matrix) are pre-specified hyperparameters. If λ_min(Σ₀) converges to ∞, then N(μ₀, Σ₀) tends to an improper prior. In contrast, if λ_max(Σ₀) is very small, then N(μ₀, Σ₀) tends to a strongly informative prior. For α, we can take an independent prior p(α) = p(α₁)p(α₂₁) · · · p(α_2p2). To make valid Bayesian inferences about β, requires an appropriate prior p(θ) and the correct specification of the sampling distributions (2.2)-(2.4), so it is crucial to assess the robustness of both the prior and the sampling distribution with respect to posterior estimate of β. Particularly, there is a growing awareness of the need for a formal method for investigating the sensitivity of inference to the missing-data mechanism (Copas and Eguchi (2005), Little and Rubin (2002), Zhu and Lee (2001), Troxel et al. (2004), Copas and Li (1997), van Steen et al. (2001), Troxel (1998), Jansen et al. (2006), Jansen et al. (2003), Verbeke et al. (2001), Shi, Zhu and Ibrahim (2009), Daniels and Hogan (2008), Ibrahim, Chen and Lipsitz (2005)).

Example 2 (Missing Response Data). We consider n independent observations z_com = {z_i,c = (x_i, r_i, y_i), i = 1, . . . , n}, where y_i = (y_i,m, y_i,o) is a p_y × 1 response vector, in which y_i,m and y_i,o denote the missing and observed components of y_i, respectively, and x_i is a p_x × 1 vector of completely observed covariates. Moreover, r_i is a p_y × 1 vector, whose j^th component, r_ij, equals 1 if the j^th component of y_i, denoted by y_ij, is observed, and 0 if y_ij is missing. It is common to model the joint distribution of (y_i, r_i) given x_i such that

$$p({\mathbf{y}}_i,{\mathbf{r}}_i\mid {\mathbf{x}}_i,\theta )=p({\mathbf{y}}_{i,m},{\mathbf{y}}_{i,o}\mid {\mathbf{x}}_i,{\theta }_I)p({\mathbf{r}}_i\mid {\mathbf{y}}_{i,m},{\mathbf{y}}_{i,o},{\mathbf{x}}_i,{\theta }_N),$$ (2.5)

where θ_I is the vector of parameters of interest and θ_N includes all parameters in the missing data mechanism p(r_i|y_i,m, y_i,o, x_i, θ_N). In this case, z_i,m = y_i,m and z_i,o = (x_i, y_i,o, r_i) for all i.

To carry out a full Bayesian analysis, we need to specify a prior for θ and the missing data mechanism. For instance, a well-known ignorability condition (Rubin, 1976) is commonly used to carry out posterior inference on θ_I without specifying the missing data mechanism. Specifically, a missing data mechanism is said to be ignorable if it is MAR, (2.5) is true and p(θ) = p(θ_I)p(θ_N). Although it is computationally easier to assume the ignorability condition, most missing data mechanisms are nonignorable (Daniels and Hogan (2008)). An alternative method for nonignorable missing data is to use the extrapolation factorization

$$p({\mathbf{y}}_i,{\mathbf{r}}_i\mid {\mathbf{x}}_i,\theta )=p({\mathbf{y}}_{i,m}\mid {\mathbf{y}}_{i,o},{\mathbf{r}}_i,{\mathbf{x}}_i,{\theta }_N)p({\mathbf{y}}_{i,o},{\mathbf{r}}_i\mid {\mathbf{x}}_i,{\theta }_I).$$ (2.6)

In this case, p(y_i,m|y_i,o, r_i, x_i, θ_N) is an extrapolation model and cannot be identifiable by the observed data, while p(y_i,o, r_i|x_i, θ_I) is an observed data model. Here, the components in θ_N are called sensitivity parameters (Daniels and Hogan (2008)).

2.2. Bayesian Perturbation Manifold

We introduce a perturbation vector ω = ω(z_com, θ) in a set Ω to perturb the complete-data model p(z_com, θ) = p(θ)p(z_com | θ). To ensure that the perturbation ω is meaningful and sensible, we require the following. (1) p(z_com, θ | ω) is the probability density of (z_com, θ) for the perturbed model as ω varies in a set Ω; (2) There is an ω⁰ ∈ Ω such that p(z_com, θ | ω⁰) = p(z_com, θ) and p(z_obs, θ | ω⁰) = ∫ p(z_com, θ | ω⁰)dz_mis = p(z_obs, θ) for all (z, θ). The ω⁰ can be regarded as the ‘central point’ of Ω representing no perturbation. See Gustafson (2006) and Daniels and Hogan (2008) for general discussions of model expansion from a Bayesian viewpoint.

Example 1 (Continued) We are interested in perturbing the missing-data mechanism p(r_i|y_i, x_i, c_i, ξ) in (2.4). For instance, when (2.4) is assumed to be MAR, we can consider a general perturbation scheme

$$p({\mathbf{r}}_i\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,\xi ,\omega )=p(r_{i{p}_2}\mid r_{i,p_2-1},\cdots ,r_{i1},y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_{p_2},\omega )\cdots p(r_{i1}\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_1,\omega ),$$ (2.7)

where ω = (ω₁, . . . , ω_m)^T is an m×1 vector. The perturbation (2.7) is commonly used to perturb the given GLM with MAR covariates in the direction of NMAR (Shi, Zhu and Ibrahim (2009), Verbeke et al. (2001)). We can also consider the individual-specific infinitesimal perturbation (Verbeke et al. (2001), Hens et al. (2006), Jansen et al. (2006), Jansen et al. (2003))

$$p({\mathbf{r}}_i\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,\xi ,{\omega }_i)=p(r_{i{p}_2}\mid r_{i,p_2-1},\cdots ,r_{i1},y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_{p_2},{\omega }_i)\cdots p(r_{i1}\mid y_i,{\mathbf{x}}_i,{\mathbf{c}}_i,{\xi }_1,{\omega }_i).$$ (2.8)

Large effect of ω_i in (2.8) can provide insight into which cases have large influence. Influence measures developed for the perturbation (2.8) are closely related to Bayesian case influence measures, such as the conditional predictive ordinate (Geisser (1993), Gelfand et al. (1992)).

We develop a geometric framework, called a Bayesian perturbation manifold, to delineate the effect of introducing each perturbation ω in Ω. Under some conditions, $\mathcal{M}=\{p({\mathbf{z}}_{com},\theta \mid \omega ):\omega \in \Omega \}$ is a Riemannian Hilbert manifold (Lang (1995)). On $\mathcal{M}$, we consider a smooth curve C(t) given by

$$C\left(t\right)=\{p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right)):[-∊,∊]\to \mathcal{M},C\left(0\right)=p({\mathbf{z}}_{com},\theta \mid \omega ),\text{and}\int \stackrel{.}{\ell }{({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))}^{2}p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))d{\mathbf{z}}_{com}d\theta <\infty \},$$ (2.9)

in which $\stackrel{.}{\ell }({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))=d\log p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))∕dt$ is called the tangent (or derivative) vector. The tangent vectors for all possible curves of the form C(t) form the tangent space of $\mathcal{M}$ at ω, denoted by $T_{\omega }\mathcal{M}$. The inner product of any two tangent vectors v₁(ω) and v₂(ω) in $T_{\omega }\mathcal{M}$ is given by

$$<{\mathit{v}}_1,{\mathit{v}}_2>\left(\omega \right)=\int \left\{{\mathit{v}}_1\left(\omega \right){\mathit{v}}_2\left(\omega \right)\right\}p({\mathbf{z}}_{com},\theta \mid \omega )d{\mathbf{z}}_{com}d\theta .$$ (2.10)

It can be shown that the length of the curve C(t) from t₁ to t₂ is

$$S_C(\omega \left(t_1\right),\omega \left(t_2\right))={\int }_{t_1}^{t_2}\sqrt{<\stackrel{.}{\ell }({\mathbf{z}}_{com},\theta \mid \omega \left(t\right)),\stackrel{.}{\ell }({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))>}dt.$$ (2.11)

We consider the concept of a geodesic as a direct extension of the straight line in Euclidean space on $\mathcal{M}$. For a real function f(ω) defined on $\mathcal{M}$, we take df[v](ω) = lim_t→0t^–1(f[p(z_com, θ | ω(t))] – f[p(z_com, θ | ω(0))]) as the directional derivative of f at the perturbation distribution p(z_com, θ | ω) in the direction of $\mathit{v}\left(\omega \right)\in T_{\omega }\mathcal{M}$. For any two smooth vector fields u(ω) and v(ω) in $T_{\omega }\mathcal{M}$, we define the directional derivative du[v](ω) = lim_t→0t^–1{u(ω(t)) – u(ω(0))} of a vector field u(ω), called the connection, at the perturbation distribution in the direction of v(ω). The popular Levi-Civita connection, denoted by ∇_vu(ω), is

$$d\mathit{u}\left[\mathit{v}\right]\left(\omega \right)-0.5\{\mathit{u}\left(\omega \right)\mathit{v}\left(\omega \right)p({\mathbf{z}}_{com},\theta \mid \omega )-\int \mathit{u}\left(\omega \right)\mathit{v}\left(\omega \right)p({\mathbf{z}}_{com},\theta \mid \omega )d{\mathbf{z}}_{com}d\theta \}.$$ (2.12)

A geodesic on the manifold $\mathcal{M}$ is a smooth curve τ(t) = p(z_com, θ | ω(t)) on $\mathcal{M}$ with $\stackrel{.}{\ell }({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))=\mathit{v}\left(\omega \left(t\right)\right)$ such that ∇_vv(ω(t)) = 0. The geodesic is (locally) the shortest path between points on $\mathcal{M}$. Finally, based on these geometric quantities of $\mathcal{M}$, we define $(\mathcal{M},\langle \mathit{u},\mathit{v}\rangle ,{\nabla }_{\mathit{v}}\mathit{u})$ as the Bayesian perturbation manifold (BPM) with an inner product < u, v > and the Levi-Civita connection ∇_vu.

Compared to the existing sensitivity analysis methods, a key advantage of using the BPM is that it provides a framework for quantifying simultaneous perturbations to the prior, the missing data mechanism and other distributional assumptions, and individual observations. Such simultaneous perturbations can be important, since it can allow one to disentangle the uncertainty about unverifiable missing data mechanism assumptions from the misspecification of the prior and other distributional assumptions, as well as the presence of outliers. According to the best of our knowledge, no methods currently exist for handling the simultaneous perturbations.

Example 1 (Continued) Consider the simultaneous perturbation model

$$p(\theta \mid {\omega }_{\theta })\prod _{i=1}^n\left\{p(y_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i,\beta ,\tau ,{\omega }_{iy})p({\mathbf{x}}_i,{\mathbf{c}}_i\mid \alpha ,{\omega }_{ic})p({\mathbf{r}}_i\mid {\mathbf{x}}_i,{\mathbf{c}}_i,y_i,\xi ,{\omega }_{ir})\right\},$$ (2.13)

where ω includes ω_θ and ${\omega }_i=({\omega }_{iy}^T,{\omega }_{ic}^T,{\omega }_{ir}^T)$ for all i and all components of ω are assumed to be independent of z_com and θ. The three terms on the right hand side of (2.13) are assumed to be probability densities and ω_θ, ω_iy, ω_ic, and ω_ir for all i have no components in common. In this case, the BPM is given by

$$\mathcal{M}=\{p(\theta \mid {\omega }_{\theta })\prod _{i=1}^{n}p({\mathbf{x}}_i,{\mathbf{c}}_i,{\mathbf{r}}_i,y_i\mid \theta ,{\omega }_i):({\omega }_{\theta },{\omega }_1,\cdots ,{\omega }_n)\in \Omega \},$$ (2.14)

where p(x_i, c_i, r_i, y_i|θ, ω_i) denotes the product of the three terms on the right hand side of (2.13). Consider ω(t) as a vector of smooth functions of t and v_h = dω(0)/dt. It follows from the arguments in Zhu, Ibrahim and Tang (2011) that $T_{\omega }\mathcal{M}$ is spanned by the functions ∂_ωθ logp(θ| ω_θ), ∂_ωiy logp(y_i|x_i, c_i, β, τ, ω_iy), ∂_ωic logp(x_i, c_i|α, ω_ic), and ∂_ωir logp(r_i|x_i, c_i, y_i, ξ, ω_ir), where ∂_ω = ∂/∂_ω. By using the chain rule, we have

$$\mathit{v}\left(\omega \left(0\right)\right)={\mathbf{v}}_h{\partial }_{\omega }\ell ({\mathbf{z}}_{com},\theta \mid \omega \left(0\right))\text{and}<\mathit{v},\mathit{v}>\left(\omega \left(0\right)\right)={\mathit{v}}_h^{T}G\left(\omega \left(0\right)\right){\mathit{v}}_h,$$ (2.15)

where

$$G\left(\omega \left(0\right)\right)=\int {\left[{\partial }_{\omega }\ell ({\mathbf{z}}_{com},\theta \mid \omega \left(0\right))\right]}^{\otimes 2}p({\mathit{z}}_{com},\theta \mid \omega )d{\mathit{z}}_{com}d\theta$$ (2.16)

is the Bayesian Fisher information matrix with respect to ω (Daniels and Hogan (2008)). Geometrically, ω_θ, ω_iy, ω_ic, and ω_ir are orthogonal to each other with respect to the inner product defined in (2.10) (Cox and Reid (1987)). Similar to Zhu et al. (2007), one can easily separate out the influence of the missing data mechanism from that of the data, the prior, and other distributional assumptions. Example 2 (Continued). The sensitivity parameters in (2.6) can be either fixed at a range of values, or assigned an appropriate distribution (Daniels and Hogan (2008)). Here we take the first approach and treat θ_N or its parametrization as a perturbation vector. Generally, we consider a simultaneous perturbation model

$$p(\theta \mid {\omega }_{\theta })\prod _{i=1}^n\left\{p({\mathbf{y}}_{i,m}\mid {\mathbf{y}}_{i,o},{\mathbf{r}}_i,{\mathbf{x}}_i,{\omega }_N)p({\mathbf{y}}_{i,o},{\mathbf{r}}_i\mid {\mathbf{x}}_i,{\theta }_I,{\omega }_I)\right\},$$ (2.17)

where ω includes ω_θ, ω_N, and ω_I, which represent the perturbation vectors to the prior, the extrapolation model, and the observed data model, respectively. For simplicity, we assume that ω_θ, ω_N, and ω_I do not share any common components and are independent of z_com and finite dimensional parameters. Moreover, it is assumed that p(θ|ω_θ), p(y_i,m|y_i,o, r_i, x_i, ω_N), and p(y_i,o, r_i|x_i, θ_I, ω_I) for all i are probability densities. Generally, it is possible that ω_N and ω_I may depend on z_com and vary across i.

Consider ω(t) as a vector of smooth functions of t and v_h = dω(0)/dt. In this case, $T_{\omega }\mathcal{M}$ is spanned by ∂_ωθ logp(θ |ω), ${\sum }_{i=1}^n{\partial }_{{\omega }_N}\log p({\mathbf{y}}_{i,m}\mid {\mathbf{y}}_{i,o},{\mathbf{r}}_i,{\mathbf{x}}_i,{\omega }_N)$, and ${\sum }_{i=1}^n{\partial }_{{\omega }_I}\log p({\mathbf{y}}_{i,o},{\mathbf{r}}_i\mid {\mathbf{x}}_i,{\theta }_I,{\omega }_I)$. Subsequently, we can calculate the Bayesian Fisher information matrix G(ω(0)) according to (2.16). Geometrically, ω_θ, ω_N, and ω_I are also orthogonal to each other with respect to the inner product defined in (2.10) (Cox and Reid (1987)).

2.3 Intrinsic influence measures

As the purpose of a sensitivity analysis is to assess the uncertainty of the parameter of interest as ω varies in Ω given the data at hand, we take an IFM to be a functional of p(θ|z_obs, ω) as ω varies in Ω, where p(θ | z_obs, ω) is the perturbed posterior distribution of θ given z_obs and ω. Generally, let IF(ω) = IF(p(θ | z_obs, ω)) be the intrinsic influence measure. Three common intrinsic influence measures are the ϕ-divergence function, the posterior mean, and the Bayes factor (Kass et al (1989), Kass and Raftery (1995)).

For the missing data mechanism, one can fix an ω₀ ∈ Ω corresponding to MAR and then develop a relative intrinsic influence measure (RIFM) as a functional of p(θ | z_obs, ω) and p(θ | z_obs, ω₀),

$$\mathrm{RI}(\omega ,{\omega }_0)=\mathrm{RI}(p(\theta \mid {\mathit{z}}_{obs},\omega ),p(\theta \mid {\mathit{z}}_{obs},{\omega }_0)).$$ (2.18)

For instance, RI(ω, ω⁰) can be the total variation distance of p(θ | z_obs, ω⁰) and p(θ | z_obs, ω) (Dey, Ghosh and Lou (1996)). One can take RI(ω, ω₀) = IF(ω) – IF(ω₀) as the difference between IFMs at ω and ω₀. See more examples in Section 2.4.

We also suggest rescaling RI(ω, ω₀) by using the minimal geodesic distance between p(z_com, θ | ω) and p(z_com, θ | ω₀), g(ω, ω₀), on the BPM $\mathcal{M}$. Thus, we define the intrinsic influence measure for comparing p(θ | z_obs, ω) to p(θ | z_obs, ω₀) as

$${\mathrm{IGI}}_{RI}(\omega ,{\omega }_0)=\frac{\mathrm{RI}{(\omega ,{\omega }_0)}^2}{g{(\omega ,{\omega }_0)}^2}.$$ (2.19)

The proposed IGI_RI(ω, ω₀) can be interpreted as the ratio of the change of the objective function relative to the minimal distance p(z_com, θ | ω) and p(z_com, θ | ω₀) on $\mathcal{M}$. In practice, one can identify the most influential ω in Ω, denoted by ${\widehat{\omega }}_I$, which maximizes IGI_RI(ω, ω₀) for all ω ∈ Ω.

We consider the local behavior of RI(ω(t), ω₀) as t approaches zero along all possible smooth curves p(z_com, θ | ω(t)} passing through ω(0) = ω₀. Since RI(ω(t), ω₀) is a function from R to R, it follows from a Taylor's series expansion that

$$\mathrm{RI}(\omega \left(t\right),{\omega }_0)=\mathrm{RI}(\omega \left(0\right),{\omega }_0)+\partial \mathrm{RI}\left(\omega \left(0\right)\right)t+0.5{\partial }^2\mathrm{RI}\left(\omega \left(0\right)\right)t^2+o\left(t^2\right),$$

where ∂RI(ω(0)) and ∂²RI(ω(0)) denote the first- and second order derivatives of RI(ω(t), ω⁰) with respect to t evaluated at t = 0. We need to distinguish ∂RI(ω(0)) ≠ 0 for some smooth curves ω(t) and ∂RI(ω(0)) = 0 for all smooth curves ω(t). For the case ∂RI(ω(0)) ≠ 0, ∂RI(ω(0)) = d(RI)[v](ω(0)) is the directional derivative of RI in the direction of $\mathbf{v}\in T_{\omega \left(0\right)}\mathcal{M}$ (Lang (1995)). The first-order local influence measure is defined as

$${\mathrm{FI}}_{RI}\left[\mathbf{v}\right]\left(\omega \left(0\right)\right)=\underset{t\to 0}{\text{lim}}{\mathrm{IGI}}_{RI}(\omega \left(0\right),\omega \left(t\right))=\frac{{\left\{d\left(\mathrm{RI}\right)\left[\mathbf{v}\right]\left(\omega \left(0\right)\right)\right\}}^2}{<\mathbf{v},\mathbf{v}>\left(\omega \left(0\right)\right)}.$$ (2.20)

We use the tangent vector v_FImax in $T_{\omega \left(0\right)}\mathcal{M}$ that maximizes FI_RI[v](ω(0)), to carry out a sensitivity analysis.

For the case ∂RI(ω(0)) = 0, we use ∂²RI(ω(0)) to assess the second-order local influence of ω to a statistical model (Zhu et al. (2007)). The second-order influence measure in the direction $\mathbf{v}\in T_{\omega \left(0\right)}\mathcal{M}$ is defined as

$${\mathrm{SI}}_{RI}\left[\mathbf{v}\right]\left(\omega \left(0\right)\right)=\frac{{\partial }^2\mathrm{RI}\left(\omega \left(0\right)\right)}{<\mathbf{v},\mathbf{v}>\left(\omega \left(0\right)\right)}.$$ (2.21)

Geometrically, SI_RI[v](ω(0)) is invariant to scalar transformations and smooth transformations. To carry out a sensitivity analysis, we use the tangent vector v_S,max in $T_{\omega \left(0\right)}\mathcal{M}$ that maximizes SI_RI[v](ω(0)) for all $\mathbf{v}\in T_{\omega \left(0\right)}\mathcal{M}$.

2.4. Bayesian Sensitivity Analysis

Our sensitivity analysis consists of four steps.

1. Introduce a Bayesian perturbation manifold based on p(z_com, θ | ω).

2. Calculate the geometric metric < v, v > (ω₀) of the perturbation manifold.

3. Choose an intrinsic influence measure IF(ω). If ∂RI(ω(0)) ≠ 0, then we calculate v_FI,max to assess local influence of minor perturbations to the model. If ∂RI(ω(0)) = 0, then we compute v_S,max. We inspect v_FI,max (or v_S,max) in order to detect the most influential components of ω.

4. For the most influential subcomponents of ω, we calculate IGI_RI(ω, ω₀) and ${\widehat{\omega }}_I={\mathrm{argmax}}_{\omega \in \Omega }{\mathrm{IGI}}_{RI}(\omega ,{\omega }_0)$.

In practice, we iteratively perform the four-step influence analysis as described above. We start with a simultaneous perturbation to z_com, p(θ) and p(z_com|θ). We decide a set of parametric perturbation characterized by a finite dimensional ω such that the perturbed model is large enough to cover a large class of candidate models for the data set. With parametric perturbations, it is computationally simple to carry out the Bayesian sensitivity analysis, and a perturbation model with a large number of perturbations can approximate most interesting perturbation models. we start with a local influence analysis to examine the sensitivity of all components and then focus on a few influential components using an intrinsic influence analysis. For instance, if a few influential hyper-parameters to the prior are identified, one further perturbs their associated prior distribution using the additive ε-contamination class and then carries out intrinsic influence analysis. After combining the information learned from our influence analysis, we might choose a new sampling distribution and/or a new prior. This procedure can be run iteratively until a certain satisfaction is reached.

2.5. Examples of Bayesian influence measures

We focus on assessing the influence of a perturbation scheme ω to the posterior distribution based on ϕ–divergence, the posterior mean distance, and the Bayes factor. The Bayes factor, the ϕ-diverfence, and the posterior mean quantify the effects of introducing ω on the overall assumed model, on the overall posterior distribution, and on the posterior mean of θ, respectively. Since the Bayes factor measures the overall difference between p(z_obs|ω) and p(z_obs|ω₀), it can be more sensitive to some discrepancies between the assumed model and the observed data. As the ϕ-diverfence measures the overall difference between p(z_mis, θ|z_obs, ω) and p(z_mis, θ|z_obs, ω₀), and such a difference may include mean, median, etc., it can be more sensitive to some changes of the posterior distributions, but the posterior mean distance is more sensitive to a subtle change in the posterior mean.

Example 3 (Bayes factor). The logarithm of the Bayes factor for comparing ω with ω₀ is

$$\begin{array}{cc}\hfill \mathrm{BF}(\omega ,{\omega }_0)& =\text{log}\left(p({\mathbf{z}}_{obs}\mid \omega )\right)-\text{log}\left(p({\mathbf{z}}_{obs}\mid {\omega }_0)\right)\hfill \\ \hfill & =\text{log}(\int p({\mathbf{z}}_{com}\mid \theta ,\omega )p(\theta \mid \omega )d{\mathbf{z}}_{mis}d\theta )-\text{log}(\int p({\mathbf{z}}_{com}\mid \theta )p\left(\theta \right)d{\mathbf{z}}_{mis}d\theta ).\hfill \end{array}$$

The value of BF(ω, ω₀) can be regarded as a statistic for testing hypotheses of ω against ω₀ (Kass and Raftery (1995)). Under some smoothness conditions, BF(ω, ω₀) is a continuous map from $\mathcal{M}$ to R.

We set RI(ω, ω₀) = BF(ω, ω₀), where ω(t) is a smooth curve on $\mathcal{M}$ with ω(0) = ω₀ and $d_t\log p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right)){\mid }_{t=0}=\mathbf{v}\left({\omega }_0\right)\in T_{\omega \left(0\right)}\mathcal{M}$, where d_t = d/dt. It can be shown that

$$\partial \mathrm{RI}\left(\omega \left(0\right)\right)=E\{d_t\text{log}p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))\mid {\mathbf{z}}_{obs},\omega \left(t\right)\}{\mid }_{t=0},$$

where the conditional expectation is taken with respect to p(z_mis, θ | z_obs, ω(t)). We can use MCMC methods to draw samples $\{({\theta }^{\left(s\right)},{\mathbf{z}}_{mis}^{\left(s\right)}):s=1,\dots ,S_0\}$ from p(z_mis, θ | z_obs) and then approximate ∂RI(ω(0)) by using $S_0^{-1}{\sum }_{s=1}^{S_0}{d}_t\log p({\mathbf{z}}_{obs},{\mathbf{z}}_{mis}^{\left(s\right)},{\theta }^{\left(s\right)}\mid {\omega }_0)$.

We consider a simultaneous perturbation to both the prior and the sampling distribution. We have

$${\mathrm{FI}}_{BF}\left[\mathbf{v}\right]\left(\omega \left(0\right)\right)=\frac{E{\{d_t\text{log}p({\mathbf{z}}_{com},\theta \mid \omega \left(0\right))\mid {\mathbf{z}}_{obs},{\omega }_0\}}^2}{<v,v>\left({\omega }_0\right)}.$$

For instance, for the perturbation to the prior given by p(θ; t) = p(θ) + t{g(θ) – p(θ)}, it can be shown that

$${\mathrm{FI}}_{BF}\left[\mathbf{v}\right]\left(\omega \left(0\right)\right)=\frac{\mathrm{E}{\{g\left(\theta \right)∕p\left(\theta \right)\mid {\mathbf{z}}_{obs}\}}^2}{{\text{var}}_P\{g\left(\theta \right)∕p\left(\theta \right)\}}=\frac{{\{p_g\left({\mathbf{z}}_{obs}\right)∕p\left({\mathbf{z}}_{obs}\right)\}}^2}{{\text{var}}_P\{g\left(\theta \right)∕p\left(\theta \right)\}},$$

where p(z_obs) = ∫ p(z_com; θ)p(θ)dz_misdθ and p_g(z_obs) = ∫ p(z_com; θ)g(θ)dz_misdθ. Since the ratio of p_g(z_obs) to p(z_obs) is the Bayes factor in favor of g(θ) against p(θ), the first-order local influence measure is the square of the normalized Bayes factor of g(θ) against p(θ).

Example 4 (ϕ–divergence). The ϕ–divergence between two posterior distributions for ω₀ and ω is

$${\Phi }_{RI}(\omega ,{\omega }_0)=\int \varphi \left(R({\mathbf{z}}_{mis},\theta \mid \omega ,{\omega }_0)\right)p({\mathbf{z}}_{mis},\theta \mid {\mathbf{z}}_{obs},{\omega }_0)d{\mathbf{z}}_{mis}d\theta ,$$

where R(z_mis,θ | ω, ω₀) = p(z_mis, θ | z_obs, ω)/p(z_mis, θ | z_obs, ω₀) and ϕ(·) is a convex function with ϕ(1) = 0, such as the Kullback-Leibler divergence or the χ²-divergence (Kass et al. (1989)).

We set RI(ω, ω₀) = Φ_RI(ω, ω₀), where ω(t) is a smooth curve on $\mathcal{M}$ with ω(0) = ω₀ and $d_t\log p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right)){\mid }_{t=0}=\mathbf{v}\left({\omega }_0\right)\in T_{\omega \left(0\right)}\mathcal{M}$. It can be shown that ∂RI(ω(0)) = 0 and

$${\partial }^2\mathrm{RI}\left(\omega \left(0\right)\right)=\ddot{\varphi }\left(1\right)\int {\left[d_t\text{log}p({\mathbf{z}}_{mis},\theta \mid {\mathbf{z}}_{obs},\omega \left(t\right))\right]}^{2}p({\mathbf{z}}_{mis},\theta \mid {\mathbf{z}}_{obs},{\omega }_0)d{\mathbf{z}}_{mis}d\theta {\mid }_{t=0},$$

where $\ddot{\varphi }\left(t\right)=d^2\varphi \left(t\right)∕d{t}^2$. We need a computational formula. Note that

$$d_t\text{log}p({\mathbf{z}}_{com},\theta \mid \omega \left(0\right))-\int \left[d_t\text{log}p({\mathbf{z}}_{com},\theta \mid \omega \left(0\right))\right]p({\mathbf{z}}_{mis},\theta \mid {\mathbf{z}}_{obs},{\omega }_0)d{\mathbf{z}}_{mis}d\theta .$$

In practice, we use MCMC methods to draw samples $\{({\theta }^{\left(s\right)},{\mathbf{z}}_{mis}^{\left(s\right)}):s=1,\dots ,S_0\}$ from p(θ, z_mis | z_obs, ω₀) and then approximate ∂²RI(ω(0)) using

$$\ddot{\varphi }\left(1\right)S_0^{-1}\sum _{s=1}^{S_0}{[d_t\text{log}p({\mathbf{z}}_{mis}^{\left(s\right)},{\mathbf{z}}_{obs},{\theta }^{\left(s\right)}\mid \omega \left(0\right))-S_0^{-1}\sum _{s^{\prime }=1}^{S_0}{d}_t\text{log}p({\mathbf{z}}_{mis}^{\left(s^{\prime }\right)},{\mathbf{z}}_{obs},{\theta }^{\left(s^{\prime }\right)}\mid \omega \left(0\right))]}^2.$$

For perturbation schemes to the prior distribution, it can be shown that

$$<\mathbf{v},\mathbf{v}>\left(\omega \left(0\right)\right)=\int {\left[d_t\text{log}p(\theta \mid \omega \left(0\right))\right]}^{2}p(\theta \mid \omega \left(0\right))d\theta$$

and ${\partial }^2\mathrm{RI}\left(\omega \left(0\right)\right)=\ddot{\varphi }\left(t\right)\mathrm{var}[d_t\log p(\theta \mid \omega \left(0\right))\mid {\mathbf{z}}_{obs},{\omega }_0]$, which are, respectively, the Fisher information matrices of ω(t) based on the prior and posterior distributions, where var(· | z_obs, ω₀) denotes the posterior variance. For instance, for p(θ | ω(θ)) = p(θ) + t{g(θ) – p(θ)}, we can show that

$${\mathrm{SI}}_{{\Phi }_{RI}}\left[v\right]\left\{\omega \left(0\right)\right\}=\frac{\ddot{\varphi }\left(1\right)\text{var}\{g\left(\theta \right)∕p\left(\theta \right)\mid {\mathbf{z}}_{obs}\}}{{\text{var}}_P\{g\left(\theta \right)∕p\left(\theta \right)\}},$$

where var_P(·) denotes the prior variance.

Example 5 (Posterior mean distance). We measure the distance between the posterior means of h(θ) for ω₀ and ω (Kass et al. (1989), Gustafson (1996b)). The posterior mean of h(θ) after introducing ω is

$$M_h\left(\omega \right)=\int h\left(\theta \right)p({\mathbf{z}}_{mis},\theta \mid {\mathbf{z}}_{obs},\omega )d{\mathbf{z}}_{mis}d\theta .$$

Cook's posterior mean distance for characterizing the influence of ω is then

$${\mathrm{CM}}_h(\omega ,{\omega }_0)={\{M_h\left(\omega \right)-M_h\left({\omega }_0\right)\}}^T{G}_h\{M_h\left(\omega \right)-M_h\left({\omega }_0\right)\},$$ (2.22)

where G_h is a positive definite matrix. Henceforth, G_h is the inverse of the posterior covariance matrix of h(θ) for p(θ | z_obs, ω₀).

We set RI(ω, ω₀) = CM_h(ω, ω₀), where ω(t) is a smooth curve on $\mathcal{M}$ with ω(0) = ω₀ and $d_t\log p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right)){\mid }_{t=0}=\mathbf{v}\left({\omega }_0\right)\in T_{\omega \left(0\right)}\mathcal{M}$. It can be shown that ∂RI(ω(0)) = 0 and ∂²RI(ω(0)) = M̧_h(v)^TG_hM̧_h(v), where

$${\stackrel{.}{M}}_h\left(\mathbf{v}\right)=d_t{M}_h\left(\omega \left(0\right)\right)=\text{Cov}\{h\left(\theta \right),d_t\text{log}p({\mathbf{z}}_{com},\theta \mid \omega \left(t\right))\mid {\mathbf{z}}_{obs},{\omega }^0\}{\mid }_{t=0}.$$

We can use MCMC methods to approximate M̧_h(v) and G_h.

2.6. A Simple Theoretical Example

We consider a simple example involving missing responses (Daniels and Hogan (2008)). Consider a data set z_com = ((y₁, r₁), · · · , (y_n, r_n))^T, where r_i = 1 if y_i is observed and 0 if y_i is missing. We focus on perturbing missing-data mechanism.

First, we fit a pattern mixture model for (y_i, r_i) such that

$$y_i\mid r_i=1\sim N({\mu }_1,{\sigma }^2),y_i\mid r_i=0\sim N({\mu }_0,{\sigma }^2),r_i\sim Ber\left(\varphi \right).$$ (2.23)

Model (2.23) assumes that the observed and missing responses differ in their mean but share the same variance. Since the observed data do not contain any information on μ₀, we assume μ₀ = μ₁ + ω_μ.

Here ω_μ can be regarded as a perturbation and θ = (μ₁, σ², ϕ). The complete-data likelihood function is

$$p({\mathbf{z}}_{com},\theta \mid {\omega }_{\mu })={\varphi }^{\sum _i{r}_i}{(1-\varphi )}^{n-\sum _i{r}_i}\left\{\prod _{i,r_i=0}p(y_i;{\mu }_1+{\omega }_{\mu },{\sigma }^2)\right\}\left\{\prod _{i,r_i=1}p(y_i;{\mu }_1,{\sigma }^2)\right\},$$

where p(y|μ, σ²) denotes the normal density function. Regardless of the prior for θ, it can be shown that $G\left({\omega }_{\mu }\right)={\sum }_{i=1}^n(1-r_i)∕{\sigma }^2$, which is independent of ω_μ, and thus $\mathcal{M}$ is flat and g(ω_μ,1, ω_μ,2) = c|ω_μ,1 – ω_μ,2|, where c is a scalar (Zhu et al. (2007)). Moreover, since the observed-data likelihood function ∫ p(z_com, θ|ω_μ)dz_mis does not depend on ω_μ, all IFs and IFMs based on p(θ|z_obs, ω_μ) are zero. This indicates that varying ω_μ does not influence the posterior inferences on θ given z_obs. Instead, if we consider the posterior mean μ₁ + (1 – ϕ)ω_μ, the mean of y_i, as the influence measure, then we have

$$\begin{array}{cc}\hfill & \mathrm{IF}\left({\omega }_{\mu }\right)=E[{\mu }_1+(1-\varphi ){\omega }_{\mu }\mid {\mathbf{z}}_{obs}]=E[{\mu }_1\mid {\mathbf{z}}_{obs}]+\{1-E[\varphi \mid {\mathbf{z}}_{obs}]\}{\omega }_{\mu },\hfill \\ \hfill & {\mathrm{IGI}}_{RI}({\omega }_{\mu ,1},{\omega }_{\mu ,2})=\frac{{[\mathrm{IF}\left({\omega }_{\mu ,1}\right)-\mathrm{IF}\left({\omega }_{\mu ,2}\right)]}^2}{g{({\omega }_{\mu ,1},{\omega }_{\mu ,2})}^2}=\frac{{\{1-E[\varphi \mid {\mathbf{z}}_{obs}]\}}^2{\sigma }^2}{\sum _{i=1}^n(1-r_i)},\hfill \end{array}$$

where E[·|z_obs] denote the expectations taken with respect to p(θ|z_obs). In this case, IF(ω_μ) does not belong to any of the three Bayesian influence measures considered in Section 2.4, but our invariant influence measure is applicable. Moreover, the constant IGI_RI(ω_μ,1, ω_μ,2) indicates that any inferences about the measure of y_i is completely driven by the assumptions regarding the size of ω_μ.

Second, we fit a selection model for (y_i, r_i) such that

$$y_i\sim N({\mu }_1,{\sigma }^2),r_i\sim Ber\left({\varphi }_i\right)\text{with logit}\left({\varphi }_i\right)={\xi }_1+{\omega }_{\xi }{y}_i,$$ (2.24)

where logit(·) denotes the logit function. In (2.24), ω_ξ = 0 corresponds to MAR, whereas ω_ξ ≠ 0 corresponds to NMAR. In this case, ω_ξ can be regarded as a perturbation and θ = (μ₁, σ², ξ₁). The complete-data likelihood function is

$$p({\mathbf{z}}_{com},\theta \mid {\omega }_{\xi })={\varphi }_i^{\sum _i{r}_i}{(1-{\varphi }_i)}^{n-\sum _i{r}_i}\prod _{i=1}^{n}p(y_i;{\mu }_1,{\sigma }^2).$$

If p(θ) is the prior for θ, it can be shown that

$$G\left({\omega }_{\xi }\right)=n\int y^2\frac{\text{exp}({\xi }_1+{\omega }_{\xi }y)}{{[1+\text{exp}({\xi }_1+{\omega }_{\xi }y)]}^2}p(y;{\mu }_1,{\sigma }^2)p\left(\theta \right)dyd\theta ,$$

which does not have a simple form. Moreover, since the observed-data likelihood function ∫ p(z_com, θ|ω_ξ)dz_mis does depend on ω_ξ, all IFs and IFMs based on p(θ|z_obs, ω_ξ) can be numerically calculated according to the formula given in Sections 2.3-2.4. Generally, in the selection model, varying ω_ξ does not influence the posterior inferences about θ given z_obs.

3. Simulation Study

We consider a two-level model. We assume that data are obtained from N individuals nested within J groups, with group j containing n_j individuals, where $N={\sum }_{j=1}^J{n}_j$. The level-1 units are the individuals and the level-2 units are the groups. At level-1, for each group j (j = 1, . . . , J), the within-group model is given by

$$y_{ij}={\mathbf{x}}_{ij}^T{\beta }_j+{\epsilon }_{ij},i=1,\dots ,n_j,$$ (3.1)

where y_ij is the outcome variable, x_ij is a q-vector with explanatory variables (including a constant), β_j is a q-vector of regression coefficients, and ε_ij is the residual. At level-2, we further assume β_j to be a vector of random regression coefficients,

$${\beta }_j=Z_j\gamma +{\mathbf{u}}_j,$$ (3.2)

where Z_j is a q × r matrix with explanatory variables (including a constant) obtained at the group level, γ is a r-vector containing fixed coefficients, and u_j is a q-vector of residuals. Assume that u_j is independent of ε_ij, u_j ~ N_q(0, Σ), and ${\epsilon }_{ij}\sim N(0,{\sigma }_{\epsilon }^2)$. We assume that the covariates x_ij and Z_j are completely observed for i = 1, . . . , n_j and j = 1, . . . , J, but the responses y_ij may be missing.

We simulated a data set according to (3.1)-(3.2). We set J = 100, q = 2, and r = 3, and then we chose varying values of n_j in order to create a scenario with different cluster sizes. Specifically, we set n₁ = . . . = n₁₀ = 3, n₉₁ = . . . = n₁₀₀ = 20, and n_i ∈ {5, 7, 8, 10, 12, 13, 15, 17} for i = 11, . . . , 90. We independently generated all components (except the intercept) of x_ij and Z_j as U(0, 1). We assumed that the y_ij's were missing at random (MAR) with missing data mechanism

$$\mathrm{Pr}(r_{ij}=1\mid {\mathbf{x}}_{ij},\phi )=\frac{\text{exp}({\phi }_0+{\phi }_x^T{\mathbf{x}}_{ij})}{1+\text{exp}({\phi }_0+{\phi }_x^T{\mathbf{x}}_{ij})},$$ (3.3)

where φ = (φ₀, φ_x), r_ij = 1 if y_ij is missing and r_ij = 0 if y_ij is observed. We set φ₀ = –2.0, φ_x = (0.5, 0.5)^T , γ = (0.8, 0.8, 0.8)^T , $\Sigma ={0.51}_2{1}_2^T+0.5I_2$, and ${\sigma }_{\epsilon }^2=1.0$. The missing fraction of the responses is about 18.4%. To add some outliers, we modified the simulated data set by generating new {y_ij : j = 1, 99, 100; i = 1, . . . , n_j} from a $N({\mathbf{x}}_{ij}^T{Z}_j\gamma +{\mathbf{x}}_{ij}^T{\mathbf{u}}_j,{\sigma }_{\epsilon }^2)$ distribution with u_j ~ N(5.61₂, 1.96I₂ + 0.3Σ) (j = 1, 99, 100).

We fit (3.1)-(3.3) to the simulated data set and used MCMC sampling to carry out the Bayesian influence analysis (Chen, Shao and Ibrahim (2000)). We took

$$p\left(\gamma \right)\stackrel{D}{=}N({\gamma }^0,H_{0\epsilon }),p\left({\sigma }_{\epsilon }^{-2}\right)\stackrel{D}{=}\Gamma ({\alpha }_{0\epsilon },{\beta }_{0\epsilon }),p\left(\Sigma \right)\stackrel{D}{=}I{W}_q({\rho }_0,R^0),$$

where γ⁰, H_0ε, α_0ε, β_0ε, R⁰, and ρ₀ are hyperparameters whose values are prespecified. We assumed that $p\left(\phi \right)\stackrel{D}{=}N({\phi }^0,H_{0\phi })$, where φ⁰ and H_0φ are the given hyperparameters. Furthermore, we set γ⁰ = (0.8, 0.8, 0.8)^T, $R^0=2I_2+{21}_2{1}_2^T$, φ⁰ = (–2.0, 0.5, 0.5)^T, H_0φ = I₃, α_ε0 = 10.0, β_ε0 = 8.0, ρ₀ = 10, and H_0ε = diag(0.2, 0.2, 0.2).

We simultaneously perturbed the distributions of u_j and the prior distributions of γ, Σ, and ${\sigma }_{\epsilon }^2$, whose perturbed complete-data joint (unnormalized) log-posterior density is given by

$$\ell ({\mathbf{z}}_{com},\theta \mid \omega )=\sum _{j=1}^J\{-q\text{log}(2\pi ∕{\omega }_j)-\text{log}\mid \Sigma \mid -{\omega }_j{\mathbf{u}}_j^T{\Sigma }^{-1}{\mathbf{u}}_j\}∕2+\{-r\text{log}(2\pi ∕\omega \gamma )-\text{log}\mid H_{0\epsilon }\mid -\omega \gamma {(\gamma -{\gamma }^0)}^T{H}_{0\epsilon }^{-1}(\gamma -{\gamma }^0)\}∕2-({\rho }_0-q-1)\text{log}\mid \Sigma \mid ∕2-{\omega }_{\Sigma }\mathrm{tr}\left(R^0{\Sigma }^{-1}\right)∕2-q{\rho }_0\text{log}\left(2\right)∕2+{\rho }_0\text{log}\mid {\omega }_{\Sigma }{R}_0\mid ∕2-\text{log}{\Gamma }_q({\rho }_0∕2)+\text{log}[p\left({\sigma }_{\epsilon }^{-2}\right)+{\omega }_{\sigma }\{g\left({\sigma }_{\epsilon }^{-2}\right)-p\left({\sigma }_{\epsilon }^{-2}\right)\}],$$

where $g\left({\sigma }_{\epsilon }^{-2}\right)$ is the density of a Gamma (α_0ε + 3, β_0ε + 1) distribution and ω = (ω₁, . . . , ω_J, ω_γ, ω_Σ, ω_σ )^T. In this case, ω⁰ = (1, 1, . . . , 1, 0)′ represents no perturbation. By differentiating $\ell ({\mathbf{z}}_{com},\theta \mid \omega )$ with respect to ω, after some calculations, we have

$$G\left({\omega }^0\right)=\text{diag}[q{I}_J∕2,r∕2,{\text{var}}_{\Sigma }\left\{\mathrm{tr}\left(R^0{\Sigma }^{-1}\right)\right\}∕4,{\text{var}}_{{\sigma }_{\epsilon }^2}\{g\left({\sigma }_{\epsilon }^{-2}\right)∕p\left({\sigma }_{\epsilon }^{-2}\right)\}],$$

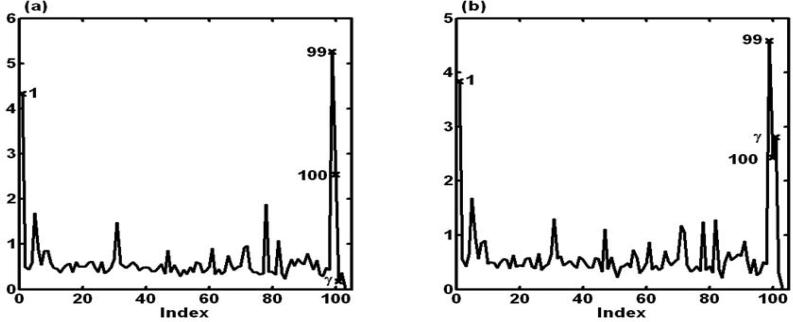
where var_Σ and ${\mathrm{var}}_{{\sigma }_{\epsilon }^2}$ denote the variance with respect to the priors of Σ and ${\sigma }_{\epsilon }^2$, respectively. Then, we chose a new perturbation scheme $\tilde{\omega }={\omega }^0+G{\left({\omega }^0\right)}^{1∕2}(\omega -{\omega }^0)$ and calculated the associated local influence measures ${\mathbf{v}}_{F,\max }=\mathrm{argmax}{\mathrm{FI}}_{BF}\left[\mathbf{v}\right]\left\{\tilde{\omega }\left(0\right)\right\}$, SI_ΦIR[e_j], and SI_CMh[e_j], in which ϕ(·) was chosen to be the Kullback-Leibler divergence divergence and h(θ) = θ. Note that the numbers of observations in groups 1, 99, and 100 were, respectively, 3, 20, and 20. Groups 1, 99 and 100 were detected to be influential by all our local influence measures. Selected results for SI_ΦIR[e_j] are presented in Fig. 1(a).

Figure 1.

Simulation Study: group index plots of local influence measures for simultaneous perturbation: (a) SI_ΦIR[e_j] can detect the three influential groups (1, 99, and 100); (b) SI_ΦIR[e_j] can simultaneously detect the three influential groups (1, 99, and 100) and the perturbed prior distribution p(γ).

We used the same setup, except that we employed a perturbed prior distribution for $\gamma :p\left(\gamma \right)\stackrel{D}{=}N(4{\gamma }^0,H_{0\epsilon })$, and then applied the same MCMC method, perturbation scheme, and local influence measures. Groups 1, 99, and 100 and the perturbed prior distribution of γ were identified to be influential by all our local influence measures. Selected results for SI_ΦD[e_j] are presented in Fig. 1 (b).

Next, we explored the potential deviations of the MAR mechanism in the direction of NMAR. We simulated a data set using the same setup except that the missing data mechanism for y_ij was

$$\mathrm{Pr}(r_{ij}=1\mid {\mathbf{x}}_{ij},y_{ij},\phi ,{\phi }_y)=\frac{\text{exp}({\phi }_0+{\phi }_x^T{\mathbf{x}}_{ij}+{\phi }_y{y}_{ij})}{1+\text{exp}({\phi }_0+{\phi }_x^{T}s{\mathbf{x}}_{ij}+{\phi }_y{y}_{ij})},$$ (3.4)

with φ_y = 0.5 to make the missing data fraction approximately equal to 25%.

Similar to sensitivity analysis methods in missing data problems (Molenberghs and Kenward (2007), Little and Rubin (2002)), we fit model (3.1)-(3.2) and (3.4), with φ_y fixed at a value ω_y, to the simulated data set. When ω_y = 0, the missing data is MAR and hence the missing data mechanism in (3.4) is ignorable. Thus, by varying ω_y in an interval Ω₁, we can treat ω_y as a perturbation scheme to the sampling distribution and then calculate the associated local influence measures. Specifically, we chose ω = (ω_y) and obtained a curve C(t) on $\mathcal{M}$ at t = ω.

We used the same prior distributions for γ, φ, ${\sigma }_{\epsilon }^2$, and Σ as before and used MCMC sampling to carry out the Bayesian influence analysis. We calculated the intrinsic influence measures IGI_f(ω⁰, Ω₁) for Φ_D(ω) and M_h(θ), in which we chose ϕ(·) as the Kullback-Leibler divergence divergence, set h(θ) = γ and treated ω⁰ = 0 as no perturbation. We set Ω₁ = [–2.0, 2.0] and approximated Ω₁ via K₀ = 41 grid points ω_g,(k) = –2.0 + 0.1k for k = 0, . . . , 40. For a given ω ∈ Ω₁, d(ω⁰, ω) was calculated via a composite trapezoidal rule.

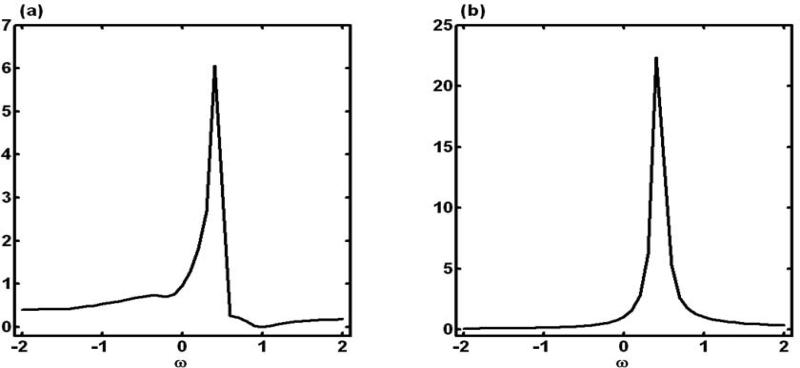
Figures 2 (a) and 2 (b) present plots of IGI_IR(ω⁰, ω) against ω ∈ Ω₁ for Φ_IR(ω) and M_h(ω), respectively. The intrinsic influence measures reach maxima near the true value of φ_y = 0.5. This indicates that the nonignorable missing data mechanism is tenable for the simulated data. We also followed a standard sensitivity analysis to compute the posterior means and standard deviations of γ for different φ_y in Table 1. Although we observed that the posterior distribution of γ varies with φ_y, it is hard to tell why φ_y = 0.5 is more meaningful. We also carried out a local influence analysis under this NMAR setting (not presented here) and observed that the proposed local influence method can pick up anomalous features of the data that are not necessarily associated with the missing data mechanism (Jansen et al. (2006)).

Figure 2.

Simulation Study: plots of IGI_IR(ω⁰, ω) against ω ∈ Ω₁ for (a) Φ_IR(ω) and (b) M_h(ω), in which h(θ) = γ.

Table 1.

Posterior means (PMs) and standard errors (SDs) of γ at different values of φ_y

	True γ0 = (0.8, 0.8, 0.8)T
	γ 1		γ 2		γ 3
	PM	SD	PM	SD	PM	SD
φy = 0.5	0.831	0.174	0.721	0.251	0.809	0.255
φy = 0.3	0.777	0.170	0.697	0.249	0.786	0.247
φy = 0.15	0.738	0.167	0.661	0.243	0.776	0.249
φy = 0.0	0.697	0.177	0.622	0.247	0.749	0.250

4. Real data example

We consider a small portion of a data set from a study of the relationship between acquired immune deficiency syndrome (AIDS) and the use of condoms (Morisky et al. (1998)). This subset contains 11 items on such topics as knowledge about AIDS and beliefs, behaviours and attitudes towards condoms use collected from 1116 female sex workers. Nine items, denoted by y = (y₁, . . . , y₉)^T, were taken as responses. Items (y₁, y₂, y₃) are related to a latent variable, η, which can be roughly interpreted as threat of AIDS, while items (y₄, y₅, y₆) and (y₇, y₈, y₉) are, respectively, related to latent variables ξ₁ and ξ₂, that can be interpreted as aggressiveness of the sex worker and worry of contracting AIDS (Lee and Tang (2006)). All response variables were treated as continuous. A continuous item x₁ on the duration as a sex worker and an ordered categorical item x₂ on the knowledge about AIDS were taken as covariates. The response variables and covariates are missing at least once for 361 of them (32.35%) (see Table 4 of Lee and Tang (2006)). The covariate x₂ is completely observed.

Let y_i = (y_i1, . . . , y_i9)^T and ${\varpi }_i={({\eta }_i,{\xi }_{i1},{\xi }_{i2})}^T$. We considered the measurement and structural equations given as

$$\begin{array}{cc}\hfill {\mathbf{y}}_i& =\mu +\Lambda {\varpi }_i+{\epsilon }_i,\hfill \\ \hfill {\eta }_i& =b_1{x}_{i1}+b_2{x}_{i2}+{\gamma }_1{\xi }_{i1}+{\gamma }_2{\xi }_{i2}+{\delta }_i,\text{for}i=1,\dots ,1116,\hfill \end{array}$$

where μ = (μ₁, . . . , μ₉)^T and

$${\Lambda }^T=\left(\begin{array}{ccccccccc}\hfill {1.0}^{\ast }\hfill & \hfill {\lambda }_{21}\hfill & \hfill {\lambda }_{31}\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill \\ \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {1.0}^{\ast }\hfill & \hfill {\lambda }_{52}\hfill & \hfill {\lambda }_{62}\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill \\ \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {0.0}^{\ast }\hfill & \hfill {1.0}^{\ast }\hfill & \hfill {\lambda }_{83}\hfill & \hfill {\lambda }_{93}\hfill \end{array}\right),$$

in which 0.0* and 1.0* are regarded as fixed values to identify the scale of the latent factor. We took ε_i distributed as N(0, Ψ), where Ψ = diag(ψ₁, . . . , ψ₉), and ${\varpi }_i$ and ε_i are independent. In the structural equation, Γ = (b₁, b₂, γ₁, γ₂) is a vector of unknown parameters, ξ_i = (ξ_i1, ξ_i2)^T is distributed as N(0, Φ), δ_i is distributed as N(0, ψ_δ), and ξ_i and δ_i are independent.

We took the missing data as NMAR, and hence the missingness mechanism of the response variables is non-ignorable (Ibrahim and Molenberghs (2009)). Let r_yij = 1 if y_ij is missing and r_yij = 0 if y_ij is observed. For the missing data mechanism of the response variables, we took logit{pr(r_yij = 1 | y_i)} = φ₀ + φ₁y_i1 + . . . + φ₉y_i9, where φ = (φ₀, φ₁, . . . , φ₉)^T. We also assumed that the covariate x_i1 is NMAR. Let r_xi1 = 1 if x_i1 is missing and r_xi1 = 0 if x_i1 is observed. It was assumed that x_i1 was $N(0,{\tau }_x^2)$ distribution and logit{pr(r_xi1 = 1 | φ_x)} = φ_x0 + ωx_i1. When ω = 0, the missingness mechanism reduces to MAR.

We fitted the proposed structural equation models to the AIDS data set and used MCMC sampling to carry out the Bayesian influence analysis. We specified the prior distributions for μ, Λ, Ψ, Γ, ω, Φ, ψ_δ, φ, φ_x0, and τ_x as those in Lee and Tang (2006). A total of 40, 000 MCMC samples was used to compute the intrinsic and local influence measures.

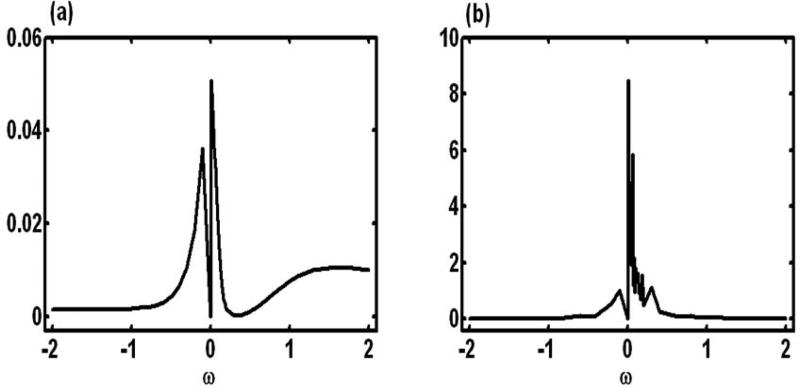
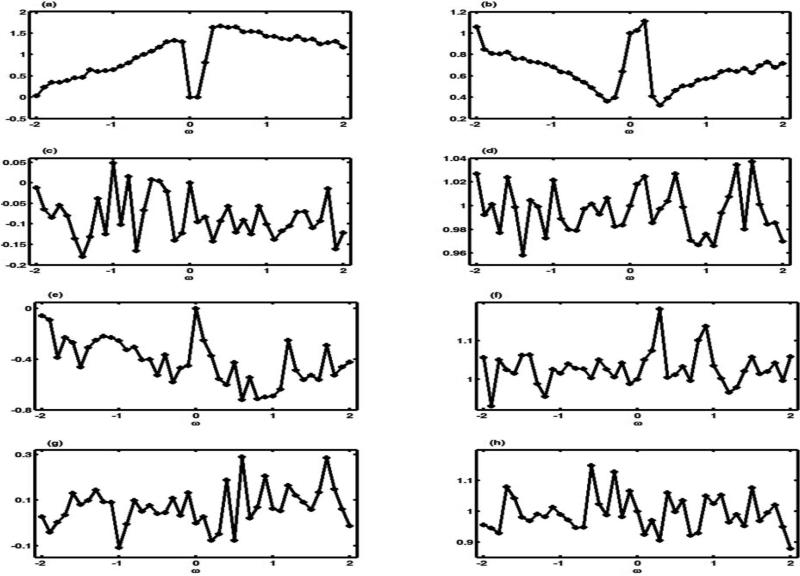
By varying ω in an interval [–2, 2], we can treat ω as a perturbation parameter to the sampling distribution. In this case, ω⁰ = 0 represents no perturbation. We calculated two intrinsic influence measures for the Kullback-Leibler divergence and the posterior mean distance, denoted by CM_h(ω). Specifically, CM_h(ω, ω⁰) = {M_h(ω) – M_h(ω⁰)}^T C_h{M_h(ω) – M_h(ω⁰)}, where M_h(ω) = ∫ h(θ)p(θ | z, ω)dθ, in which h(θ) = Γ, and C_h is the posterior covariance matrix of Γ based on p(Γ |z, ω⁰). We calculated IGI_RI(ω⁰, ω) at 41 evenly spaced grid points in [–2, 2] (Fig. 3). An inspection of Figure 3 shows that the largest IGI_RI(ω⁰, ω) values are close to 0.1 for both the Kullback-Leibler divergence and M_h(ω). This indicates that the nonignorable missing data mechanism may be tenable for the AIDS data. We also carried out a standard sensitivity analysis and computed posterior means and standard deviations of at different values of ω, as shown in Figure 4. Although we observe that the posterior means and standard deviations of Γ vary with ω, it is difficult to make any meaningful inference here.

Figure 3.

AIDS data analysis results: plots of IGI_RI(ω⁰, ω) against ω ∈[–2, 2] for (a) Φ_RI(ω) and (b) M_h(ω), in which h(θ) = Γ.

Figure 4.

AIDS data analysis results: plots of (posterior means-posterior mean at ω = 0)/(posterior standard deviation at ω = 0) ((a),(c),(e),(g)) and the ratio of posterior standard deviations over posterior standard deviation at ω = 0 ((b),(d),(f),(h)) of b₁, b₂, γ₁, γ₂ as a function of ω ∈ [–2, 2].

We also calculated the local influence measures of the Kullback-Leibler divergence under a simultaneous perturbation scheme. The simultaneous perturbation scheme ω includes variance perturbations ω_c for individual observations, perturbations ω_s to coefficients in the structural equations model, perturbations ω_ξ to the sampling distribution of ξ_i, perturbations ω_μ to the prior distribution of μ, perturbations ω_Γ to the prior distribution of Γ, perturbations ω_φ to the prior distribution of φ, and perturbations ω_x to the missing data mechanism. The corresponding kernel of the joint log-posterior density of (z, θ) based on the complete data is given by

$$\text{log}p(z,\theta \mid \omega )\equiv \ell (z,\theta \mid \omega )=l_c\left({\omega }_c\right)+l_s\left({\omega }_s\right)+l_{\xi }\left({\omega }_{\xi }\right)+l_{\mu }\left({\omega }_{\mu }\right)+l_{\Gamma }\left({\omega }_{\Gamma }\right)+l_{\phi }\left({\omega }_{\phi }\right)+l_x\left({\omega }_x\right),$$ (4.1)

where

$$\begin{array}{cc}\hfill l_c\left({\omega }_c\right)& =\{-p\sum _{i=1}^n\text{log}(2\pi ∕{\omega }_i)-\sum _{i=1}^n{\omega }_i{(y_i-\mu -\Lambda {\varpi }_i)}^T{\Psi }^{-1}(y_i-\mu -\Lambda {\varpi }_i)\}∕2,\hfill \\ \hfill l_s\left({\omega }_s\right)& =\{-\sum _{i=1}^n{({\eta }_i-b_1{x}_{i1}-b_2{x}_{i2}-{\gamma }_1{\xi }_{i1}-{\gamma }_2{\xi }_{i2}-{\omega }_{\gamma 1}{\xi }_{i1}^2-{\omega }_{\gamma 2}{\xi }_{i2}^2-{\omega }_{\gamma 3}{\xi }_{i1}{\xi }_{i2})}^2∕{\psi }_{\delta }\}∕2,\hfill \\ \hfill l_{\xi }\left({\omega }_{\xi }\right)& =\{-n{q}_2\text{log}(2\pi ∕{\omega }_{\xi })-n\text{log}\mid \Phi \mid -{\omega }_{\xi }\sum _{i=1}^n{\xi }_i^T{\Phi }^{-1}{\xi }_i\}∕2,\hfill \\ \hfill l_{\mu }\left({\omega }_{\mu }\right)& =\{-p\text{log}(2\pi ∕{\omega }_{\mu })-\text{log}\mid {\Sigma }_0\mid -{\omega }_{\mu }{(\mu -{\mu }_0)}^T{\Sigma }_0^{-1}(\mu -{\mu }_0)\}∕2,\hfill \\ \hfill l_{\Gamma }\left({\omega }_{\Gamma }\right)& =\{-(s+t)\text{log}(2\pi ∕{\omega }_{\Gamma })-\text{log}\mid H_{\Gamma }\mid -{\omega }_{\Gamma }{(\Gamma -{\Gamma }^0)}^T{H}_{\Gamma }^{-1}(\Gamma -{\Gamma }^0)\}∕2,\hfill \\ \hfill l_{\phi }\left({\omega }_{\phi }\right)& =\{-(p+1)\text{log}(2\pi ∕{\omega }_{\phi })-\text{log}\mid H_{\phi }\mid -{\omega }_{\phi }{(\phi -{\phi }^0)}^T{H}_{\phi }^{-1}(\phi -{\phi }^0)\}∕2,\hfill \\ \hfill l_x\left({\omega }_x\right)& =\sum _{i=1}^n[r_{xi1}({\phi }_{x0}+{\omega }_x{x}_{i1})-\text{log}\{1.0+\text{exp}({\phi }_{x0}+{\omega }_x{x}_{i1})\}].\hfill \end{array}$$

In this case, ${\omega }^0={({\omega }_c^{0T},{\omega }_s^{0T},{\omega }_{\xi }^0,{\omega }_{\mu }^0,{\omega }_{\Gamma }^0,{\omega }_{\phi }^0,{\omega }_x^0)}^T$ represents no perturbation, in which ${\omega }_c^0={(1,\dots ,1)}^T$, ${\omega }_s^0={(0,0,0)}^T$, ${\omega }_{\xi }^0={\omega }_{\mu }^0={\omega }_{\Gamma }^0={\omega }_{\phi }^0=1$ and ${\omega }_x^0=0.1$.

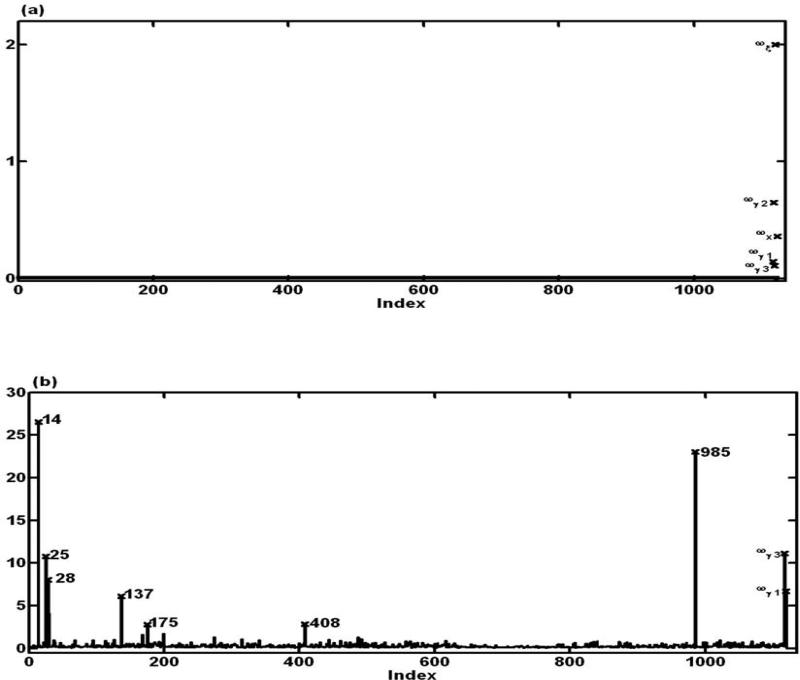
We calculated ${\partial }_{\omega }\ell (z,\theta \mid \omega )$ and then obtained its metric tensor as

$$G\left({\omega }^0\right)=\text{diag}\{G_c\left({\omega }_c^0\right),G_s\left({\omega }_s^0\right),G_{\xi }\left({\omega }_{\xi }^0\right),G_{\mu }\left({\omega }_{\mu }^0\right),G_{\Gamma }\left({\omega }_{\Gamma }^0\right),G_{\phi }\left({\omega }_{\phi }^0\right),G_x\left({\omega }_x^0\right)\},$$

where $G_c\left({\omega }_c^0\right)=\mathrm{diag}(p∕2,\dots ,p∕2)$, $G_{\xi }\left({\omega }_{\xi }^0\right)=n{q}_2∕2$, $G_{\mu }\left({\omega }_{\mu }^0\right)=p∕2$, $G_{\Gamma }\left({\omega }_{\Gamma }^0\right)=(s+t)∕2$, $G_{\phi }\left({\omega }_{\phi }^0\right)=(p+1)∕2$, $G_s\left({\omega }_s^0\right)=\mathrm{diag}[3n{E}_{\varphi ,{\psi }_{\delta }}({\varphi }_{11}^2∕{\psi }_{\delta }),3n{E}_{\varphi ,{\psi }_{\delta }}({\varphi }_{22}^2∕{\psi }_{\delta }),n{E}_{\varphi ,{\psi }_{\delta }}\{({\varphi }_{11}{\varphi }_{22}+2{\varphi }_{12}^2)∕{\psi }_{\delta }\}]$, and $G_x\left({\omega }_x^0\right)=E_{{\phi }_{x0},r_x,x_1}{\left[{\sum }_{i=1}^n\{r_{xi1}-\exp ({\phi }_{x0}+{\omega }_x^0{x}_{i1})∕(1.0+\exp ({\phi }_{x0}+{\omega }_x^0{x}_{i1}))\}\right]}^2$. The diagonal elements of the metric tensor G(ω⁰) reveal that ω_γ1, ω_γ2, ω_γ3, ω_ξ, and ω_x have larger effects compared to other perturbations (see Fig. 5(a)). Then, we chose a new perturbation scheme $\tilde{\omega }={\omega }^0+G{\left({\omega }^0\right)}^{1∕2}(\omega -{\omega }^0)$ and calculated the associated local influence measures SI_ΦIR[e_j] for the Kullback-Leibler divergence divergence. The local influence measures based on the ϕ-divergence are able to detect cases {14, 25, 28, 137, 175, 408, 985} as influential observations (see Fig. 5(b)), while ω_γ1 and ω_γ3 indicate that it may be important to include ${\xi }_{i1}^2$ and ξ_i1ξ_i2 in the structural model (see Fig. 5(b)).

Figure 5.

AIDS data analysis results: index plots of (a) metric tensor g_jj(ω⁰) and (b) local influence measures SI_ΦIR[e_j] for simultaneous perturbation.

5. Discussion

We have developed a Bayesian sensitivity analysis methods for assessing various perturbations to statistical methods with missing data. We have developed a Bayesian perturbation manifold to characterize the intrinsic structure of the perturbation model and quantifying the degree of each perturbation in the perturbation model. We have developed global and local influence measures for selecting the most influential perturbation based on various objective functions and their statistical properties. Finally, we have also examined a number of examples to highlight the broad spectrum of applications of this method for Bayesian influence analysis in missing data problems.

Many issues merit further research. Our Bayesian sensitivity analysis method can be extended to more complex data structures (e.g., survival data) and other parametric and semiparametric models with nonparametric priors. In further research, we will generalize our methodology to the setting of estimating equations and empirical likelihood of generalized estimating equations for missing data problems. We will develop Bayesian sensitivity analysis methods to deal with the well-known masking and swamping effects in the diagnostic literature.