Abstract
Purpose
To improve myocardial and blood T1 measurements with a multi-variable T1 fitting model specifically modified for a segmented multi-shot FLASH sequence.
Methods
The proposed method was first evaluated in a series of phantoms simulating realistic tissues, and then in healthy rats (n = 8) and rats with acute myocardial infarction (MI) induced by coronary artery ligation (n = 8).
Results
By accounting for the saturation effect caused by sampling α-train pulses, and the longitudinal magnetization recovery between readouts, our model provided more accurate T1 estimate than the conventional three-parameter fit in phantoms under realistic gating procedures (error of −0.42 ± 1.73% vs. −3.40 ± 1.46%, respectively, when using the measured inversion efficiency, β). The baseline myocardial T1 values in healthy rats was 1636.3 ± 23.4 ms at 7 T. One day post ligation, the T1 values in the remote and proximal myocardial areas were 1637.5 ± 62.6 ms and 1740.3 ± 70.5 ms, respectively. In rats with acute MI, regional differences in myocardial T1 values were observed both before and after the administration of gadolinium.
Conclusion
The proposed method has improved T1 estimate in phantoms and could advance applications utilizing quantitative myocardial T1 mapping in rodents.
Keywords: myocardial and blood T1, segmented multi-shot gradient echo, T1 regression model, acute myocardial infarction, rats
INTRODUCTION
There are many applications that can benefit from accurate measurements of the myocardial and blood T1 values. For example, the detection (1,2) and distinction between acute and chronic myocardial infarction (MI) by tissue characterization of edema (3) or fibrosis (4,5), and the measurement of myocardial blood flow (6–9) with arterial spin labeling (ASL), all require quantitative and accurate T1 values of the myocardium and blood.
Late gadolinium enhancement (LGE) imaging is commonly used to detect MI, based on the T1 contrast between the necrosis and normal remote myocardial tissue. To properly identify the size of the infarction, one needs to determine the null time of healthy myocardium which is controlled by both the intrinsic tissue T1 and the gadolinium concentration varying along the washing-out following contrast injection (1,2). The null image of healthy myocardium is usually decided by repeating an inversion-prepared imaging with different inversion delays (TI). This is very time-consuming and inefficient. If a myocardial T1 map is available for assessment, the demanding imaging time and errors in deciding the null image could be alleviated (10). Nevertheless, LGE cannot differentiate acute MI from chronic one, and this information is critical for patient risk assessment and treatment decision. T2-weighted images, in combination with LGE, can distinguish edema-filled acute MI from fibrosis-rich chronic MI (11–13). The long TE, T2-weighted cardiac edema images, however, often suffer from motion artifacts, poor signal-to-noise ratio, and low image contrast between the myocardium and blood pool. These problems can impose a particular challenge for small animal imaging at high field. T1-weighted images or T1 maps, on the other hand, can be used as an alternative to characterize edema in acute MI without the need of contrast agent (3), and also fibrosis in chronic MI or other cardiac disease with the administration of contrast agent (4,5,14).
The ASL technique, which uses magnetically-labeled water as an endogenous contrast, is a useful method to quantify myocardial blood flow (MBF). The quality of MBF determined by this means, though, is highly dependent on the accuracy of T1 (15). For instance, a 2.5% error in myocardial T1 can result in a 134% error in MBF calculated by ASL when MBF = 1 ml/min/g; although this MBF error gradually reduced with an increasing MBF (an error of 36% when MBF = 4 ml/min/g). Because of the technical challenges of acquiring a high-resolution, gadolinium-enhanced first-pass perfusion imaging in small animals, researchers are still keen to improve current ASL techniques in order to gain accurate T1 and thus MBF measurements (9,16–19). In addition, other emerging applications, such as, measuring the myocardial extracellular volume fraction to detect diffuse fibrosis not revealed by LGE, also requires accurate and high-resolution myocardial and blood T1 maps (5,20–22).
There have been continuous efforts to quantify the myocardial and blood T1 values in patients and animals using a Look-Locker based, multiple-point sampling of the T1 recovery curve, with either a single-shot FLASH (23–26), multi-shot FLASH (9,10,16,17,19,26–28), steady-state free precession (SSFP) (29–32), or EPI-based readout (33). A FLASH-based readout is preferred for cardiac applications in small animals because it is less susceptible to artifact caused by cardiac and respiratory motions or field inhomogeneity at high field (23,34). Additionally, small animals have rapid heart rate, and a very short data acquisition window during each heartbeat. Therefore, a gated, segmented multi-shot FLASH readout appears to be mandatory for a high-resolution myocardial T1 measurement, although low-resolution single-shot FLASH has also been used in early studies (6–8). In these studies employing a multi-shot FLASH readout (9,10,16,17,26–28), a conventional three-parameter fit model originally developed for a single-shot FLASH (24) has often been used to fit the T1. This model generally causes an underestimation of the T1 because the assumption of steady-state magnetization resulted from the long α-train in a single-shot FLASH is no longer satisfied. Plus, the recovery of the longitudinal magnetization during the time period between consecutive Look-Locker image readouts also needs to be considered, especially when dual cardiac/respiratory gating is used. In the study of Vandsburger et al. (19), a modified T1 regression model was used to adapt the varying TR between α-trains caused by the dual cardio-respiratory gating with a correction factor based on the previous work of Gunther et al. (35). However, they didn’t elaborate their T1 regression model, and it’s not clear if the magnetization relaxation between consecutive Look-Locker images (on the scale of hundreds of ms for cardio-respiratory gated acquisition) was accounted for. Also, they didn’t validate their results with an independent gold standard method, like IR-SE, to provide an absolute accuracy of the T1 in phantoms.
Possible underestimation of the T1 values could lead to errors in the subsequent calculations of MBF, infarction size or extracellular volume fraction when absolute values are needed. Therefore, it is still necessary to improve the accuracy of myocardial and blood T1 values and thus the reliability of following measurements of perfusion or infarction size, etc. The overall goal of this study is to improve the myocardial and blood T1 measurements with a new T1 regression fit model adapted for a dual respiratory/ECG gated, segmented multi-shot FLASH-based Look-Locker acquisition. The effectiveness of the proposed method was first examined in a series of phantoms and then in a rat model with acute MI.
METHODS
Pulse Sequence
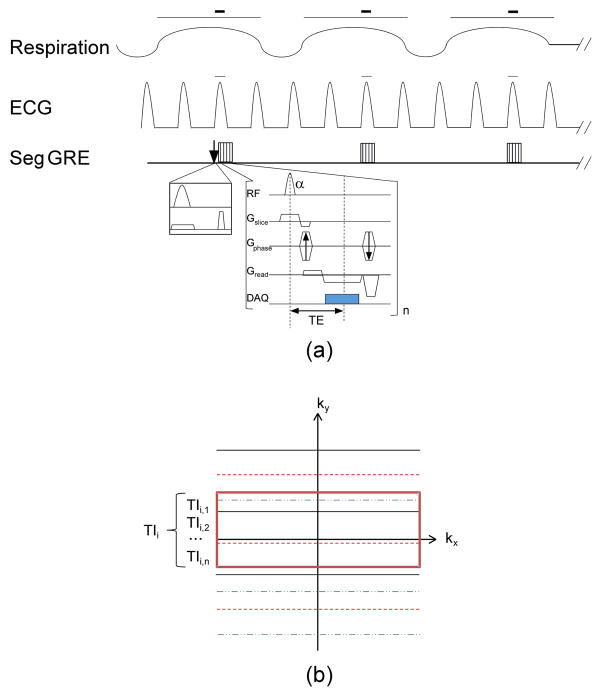
Because of the short data acquisition window for cardiac imaging in rodents, a segmented FLASH sequence was employed to sample the T1 recovery curve after a non-slice selective, inversion-recovery (IR) preparation pulse in the Look-Locker scheme and multiple shots. A schematic diagram of the sequence was shown in Fig. 1a. After an initial TI (TI1) of 10 ms, a segment of phase-encoding lines in each Look-Locker image was acquired with a small α-train during the longitudinal magnetization recovery. The k-space lines in each segment were acquired in an interleaved fashion. The inversion pulse and data acquisition for each Look-Locker image were gated by the dual respiratory and ECG signals from the rat.
Fig. 1.
A schematic diagram of the proposed T1 sequence gated by both respiration and ECG signal. (a) After a slice-selective or non-selective IR pulse at the start of R-wave in the first respiration cycle, data acquisition of a segment of k-space lines for the first Look-Locker image occurred after a short TI1 (10 ms); after the first R-wave was detected in the second respiration cycle, a segment of k-space lines for the second Look-Locker image was acquired approximately at TI1 + respiration interval; and so on to the desired number of Look-Locker images. Then, a new inversion pulse was applied and the above procedure was repeated for another segment until the entire k-space was filled. The red bars indicate the dual respiratory/cardiac gating where the inversion pulse and/or data acquisition occurred. (b) For each segment of k-space lines of an image, the data were acquired in an interleaved version (each line style represents the k-space lines belonging to one segment). Times at which the central k-space line of each segment was acquired (denoted by those within the central red rectangle) were averaged by the total number of shots n and then represented the final TIi of that reconstructed ith Look-Locker image.
T1 Regression Model
Derived from the Bloch Equations (36), the longitudinal magnetization Mz at any time t can be written as
| [1] |
where M0 is the equilibrium magnetization, Mz (t0) is the initial magnetization at time t0.
Based on Eq. [1], in a multi-shot, segmented FLASH sequence, Mz right before the central k-space line (kth step) in the Nth Look-Locker image is
| [2] |
where α is the flip angle of the RF pulse, TR is the repetition time between two α pulses, and Mz(N,1)− is the longitudinal magnetization before the 1st RF pulse of the Nth image.
Likewise, in each segment N, the transient Mz right before the last (nth) RF pulse can be expressed by the initial magnetization before the 1st RF pulse of that segment, Mz(N,1)−, as
| [3] |
or equally, by the magnetization before the central k-space line k in the same segment, Mz(N,k)−, as
| [4] |
Also, based on Eq. [1], Mz right before the 1st RF pulse of the segment in the Nth image, Mz(N,1)−, can be expressed as
| [5] |
where Mz(N-1,n)− is the transient longitudinal magnetization before the last (nth) RF pulse of the segment in the (N-1)th Look-Locker image, n is the total number of phase encoding lines in each segment, and TN is the recovery time between the segments of the (N – 1)th and Nth images and is expressed as
| [6] |
| [7] |
where TIN and TIN-1 (N ≠ 1) are the recovery times between the IR pulse and Nth or (N –1)th image, respectively.
Since Mz(N,k)− at the central k-space mainly determines the image signal intensity SN, as Mz(N,k)− sinα, Eq. [4] can be rewritten as
| [8] |
Similarly, we get
| [9] |
Substitute Eq. [9] into Eqs. [5] and [2], we obtain
| [10] |
where Ak-1 is defined as and B is equal to cos αe−TR/T1.
With β as the actual efficiency of the inversion pulse, from Eq. [10] and known imaging parameters of α, k, n, N and TR, T1 and M0 can be estimated through a multivariable non-linear regression model:
| [11] |
where YN is SN/sinα; X1 = 1 (N = 1) or 0 (N ≠ 1); and X2 = TN, X3 = SN-1/sina (N ≠ 1) or 0 (N = 1). In Eq. [11], SN, X1, X2, and X3 are used as the free parameters to predict T1 and M0.
With this model, the recovery of Mz during the time intervals between consecutive readout segments of the Look-Locker images (on the scale of hundreds of ms for gated acquisition) has been accounted for during the T1 calculation. That is, instead of assuming a steady state of Mz as in the three-parameter fit originated from a single-shot FLASH (24), we have calculated the actual saturation effect caused by the sampling α-train pulses, considered the recovery of Mz during readout intervals, and used the magnetization at the center k-space line which primarily determines the signal intensity of the images in the T1 regression fittings with TIs. The regression analysis of T1 and M0 was performed with non-linear least squares algorithm of the Levenberg-Marquardt method using MATLAB R2009a (MathWorks, Natick, MA), with an initial estimate of T1 = 200 ms and M0 = 50.
Phantom Study
All the phantom and in vivo experiments were performed on a 7 T/21 cm Bruker Biospec, Avance III scanner (Bruker Biospin, Billerica, MA), with a 12-cm, BGA-12S gradient set and a 72-mm birdcage transceiver. The sequence and T1 regression model described were first evaluated in phantoms doped with different concentrations of copper sulfate and agarose, simulating the realistic T1 and T2 values of physiological tissues. Specifically, four phantoms simulated the T1 and T2 values of the myocardium and blood before and after the Gadolinium injection. Another six phantoms had a T1 of approximately 1.2 s, while T2 around 40, 60 and 180 ms; and a T1 close to 1.9 s, while T2 approximated 40, 60 and 180 ms at 7 T.
To simplify the imaging procedures, the single-slice, multi-shot FLASH based T1 measurements were first pseudo-triggered by inserting a 400 ms fixed delay between each Look-Locker image segment to study the four phantoms simulating the myocardium and blood before and after contrast administration. The number of Look-Locker images was 12 for short T1 values (the last TI approximated 1.4 s), and 24 for long T1 values (the last TI approximated 10 s), to provide sufficient time for a nearly full recovery of the inverted magnetization.
The single-slice, multi-shot FLASH based T1 measurement was then gated by the actual respiratory and ECG signal from a rat sitting outside the scanner to study the six phantoms with varying T2 and T1 values. The rat was ventilated and anesthetized with 2% isoflurane in 2:1 O2: N2O gas mixture at a stroke volume of 1.0 ml/100 g body weight, and a rate of approximately 61 bpm. Three ECG leads were attached to the rat chest for ECG gating; and the rat temperature was maintained at 36.8°C through a rectal thermometer. ECG, respiration and rectal temperature were monitored throughout the study using a MR-compatible small animal system (SA Instruments, Stony Brook, NY). The RR intervals of the ECG varied from 130 – 220 ms in individual rats. The inversion pulse and data acquisition were both ECG and respiration gated during the T1 curve sampling. The initial TI (TI1) was 10 ms and was within the same gating window of the inversion pulse. The following data acquisition occurred right after the first R-wave of the cardiac cycle and was located within the next 480 ms gating window of the expiration phase in the respiratory cycle. The dual gating of respiration and ECG resulted in a delay of approximately 1 s between the Look-Locker images. During the imaging, the actual time stamps between the inversion pulse and central k-space line of each segment in the Look-Locker image series were recorded with the BioBench software and a Labview ACQ board (National Instruments, Austin, TX). The final TI of the Look-Locker image i was calculated as the average of the TIs (TIi,j) of the central k-space line in all segments (Fig. 1 b) to adjust the variations of delays because of the inharmonic frequencies of ECG and respiration. The total number of Look-Locker images = 8, resulting in a sampling time of approximately 7 s for the T1 recovery curve. Another 3 s delay was also inserted after the segment of the last Look-locker image to allow for full recovery of the Mz prior to next inversion. The total data acquisition time was approximately 5.3 min for a single slice T1 measurement when the number of k-space lines per segment = 4.
The inversion pulse was a non-slice selective, adiabatic hyperbolic secant pulse with a duration of 5 ms and bandwidth of 3520 Hz. The excitation pulse for the segmented FLASH was a sinc pulse with a duration of 0.6 ms and bandwidth of 10350 Hz. To optimize the imaging parameters for measuring the myocardial and blood T1, we first varied the flip angle (α) of the excitation as 4°, 8°, 10°, 12°, and the number k-space lines per segment as 1, 2, 3, and 4. Then, based on these results, major imaging parameters were applied as follows: α = 10°, TR = 4.7 ms, TE =1.7 ms, FOV = 40×40 mm, matrix size = 128×128, in-plane resolution of 312×312 μm, slice thickness = 1.5 mm, acquisition bandwidth= 50 kHz, and the number of k-space lines per segment = 4.
An IR-SE measurement with the same non-slice selective, adiabatic hyperbolic secant inversion pulse was performed as the gold standard for the T1 measurement, using the following parameters: TR = 11 s, TE =6.9 ms, FOV = 40×40 mm, matrix size = 128×128, slice thickness = 1.5 mm, acquisition bandwidth= 50 kHz, number of k-space lines per segment = 1, a hermite shaped excitation pulse with a duration of 1 ms and bandwidth of 5400 Hz, a hermite shaped refocusing pulse with a duration of 0.633ms and bandwidth of 5400 Hz, and TIs = 15, 200, 500, 700, 900, 1000, 1200, 1400, 1600, 5000, and 8000 ms. Depending on the TI values, the total scan time for an IR-SE sequence ranged from 24 min to 41 min. To investigate the actual inversion efficiency of the adiabatic pulse for different T1 and T2 values, the SE pulse was applied with and without the inversion pulse. The inversion factor, β, was then calculated as the signal intensity with the inversion pulse divided by that without the inversion pulse. T2 values of the phantoms were also roughly estimated using a similar SE sequence of multiple TEs (SE-MTE) with the following parameters: TR=11 s, number k-space lines per segment = 1, 18 echoes with an echo spacing = 9 ms, and the same resolution as the in the T1 measurement.
Animal Study
Animal preparation
The Brown Norway rats (Harlan Laboratories Inc., Indianapolis, IN) used in this study were 2–3 months old, and weighed 230–320 g. Animal protocols were approved by the Institutional Animal Care and Use Committee of Carnegie Mellon University. All animals received humane care in accordance with the guidelines and regulations of the Care and Use of Laboratory Animals, published by the NIH.
Before MRI, a femoral vein catheter was placed in the rat for contrast agent administration. Four healthy rats (weight 296 ± 28 g) were used as controls for assessing baseline myocardial and blood T1 values, and each was measured twice on different days. In another eight rats (244 ± 9 g), MI was induced by a permanent ligation of the left anterior descending (LAD) coronary artery at the edge of left atrium (37). Then, in vivo MRI was performed for these rats one day later. After the MRI, the heart was perfused with saline and then with 2% (w%) triphenyltetrazolium chloride (TTC) for approximately 5 min until the normal myocardium turned brick-red in color, whereas the infarcted regions were still in pale white or light pink. The heart was then excised and sliced at the corresponding MRI imaging position for photograph.
In vivo MRI
All imaging was performed on the same 7 T scanner depicted above. Rats were anesthetized as described in the phantom and were imaged in the prone position. An IntraGate FLASH sequence was used to localize the heart in the short-axis view with the following parameters: TR = 27 ms, TE = 2.1 ms, number of repetition = 20, FOV = 60×60 mm, slice thickness = 1.5 mm, and number of slices = 3.
The multi-shot FLASH based T1 measurements were performed in a single-slice, short-axis plane near the mid-ventricular level in healthy rats, and distal to the ligated LAD coronary artery in rats with MI, as identified by abnormal wall motion observed in myocardial tagging images in the long-axis view. The inversion pulse and data acquisition were ECG and respiration gated during the T1 imaging. Plus, the ratio (R) of the slice thickness between the inversion pulse and imaging pulse has shown substantial impact on the accuracy of in vivo T1 measurements. In addition to a non-selective, adiabatic hyperbolic secant inversion pulse, a selective inversion pulse with R = 3 was also applied as a reference. Other major imaging parameters were the same as the phantom study: α = 10°, TR = 4.7 ms, TE =1.7 ms, FOV = 40×40 mm, matrix size = 128 × 128, in-plane resolution of 312 μm, slice thickness = 1.5 mm, acquisition bandwidth = 50 kHz, number of k-space lines per segment = 4, and number of Look-Locker images = 8.
For LGE imaging, a bolus intravenous injection of 0.2 mM/kg body weight of OmniScan (GE Healthcare Inc., Princeton, NJ) was given through the femoral vein. T1 measurements and LGE images were performed again between 10–20 min after the injection, and repeated until 50–60 min when the myocardial T1 returned to the pre-contrast level.
Data Analysis
For the phantom studies, the average signal intensity (S) within a circular region of interest (ROI) of each tube was obtained for T1 analysis for both the IR-prepared multi-shot FLASH and IR-SE experiments. For the IR-SE, T1 was determined by a non-linear regression fit of S=a*(1−(1+b)*exp(−TI/T1)), where a was a scaling factor and b denoted the efficiency of the inversion pulse. To demonstrate the accuracy of our T1 regression fitting for the gated multi-shot FLASH based T1 sampling experiment, S and T1 were analyzed via two fit models: (i) our proposed T1 fitting in Eq. [11], first with an assumed perfect inversion factor β = 1 and then with the actual β measured from IR-SE signal intensities; and (ii) the conventional three-parameter fit with a correction factor as shown below (24,38), also with an assumed β = 1 and then with the actual β measured from IR-SE:
| [12] |
| [13] |
where A and B were constants, and estimated in the regression analysis along with T1*. For the simplified phantom experiment gated with a fixed delay, the S was only fitted with the proposed T1 fit Eq. [11] and three-parameter fit Eq. [12–13] with an assumed β = 1. The T1 values obtained from the multi-shot FLASH acquisition and with both fitting methods under two different β values were then compared with those measured with IR-SE, and the errors of T1 values (%) were calculated. A Bland-Altman plot of the T1 values obtained from a fixed gating delay and analyzed using these two fitting models only with β = 1 was performed separately in comparison with those obtained from IR-SE to assess the agreement between these methods. A range of agreement was defined as mean bias ± 1.96 SD.
For the rat studies, pixel-wise T1 maps were generated by the proposed nonlinear fitting of S and TI using Eq. [11] before and after gadolinium administration. Then, ROIs were selected on the T1 maps. An ROI was drawn in the LV cavity to obtain the blood T1 value. The selection of a myocardial ROI followed the following rules: in rats with acute MI, one regional ROI was drawn in remote myocardium area supplied by normal left circumflex artery (LCx); and another ROI was drawn in an area proximal to the ligated lower LAD artery and was referred to by the hyperintensity in LGE images. In healthy rats, three regional ROIs were drawn in the LAD, LCx, and septal (SEP) myocardial regions, and an average T1 in these three regions was obtained to represent a global T1 value. All ROIs were drawn carefully in the central myocardium (50%) to avoid artifact present at the edges.
All the T1 values reported in the animal study were acquired using a non-slice selective inversion pulse to achieve better inversion profile and to prevent the perfusion effect of spins. A Paired t-test was performed for the T1 values in the remote and proximal myocardial areas in rats with acute MI. An un-paired t-test was also performed for the myocardial T1 values between the healthy rats and remote myocardium, and between healthy and proximal myocardium in rats with acute MI. A p-value < 0.05 was defined as statistically significant.
RESULTS
Phantom Study
Table 1 shows the actual inversion efficiency β with regard to different T1 and T2 values studied. For the adiabatic pulse we used, β was approximately 0.98 with T2 close to 180 ms; and decreased to 0.95 when T2 approximated 40 ms. β might be dependent on T1 as well (38). However, this was not obvious for the limited number of T1 values we studied.
TABLE 1.
The inversion efficiency, β, of the adiabatic hyperbolic secant pulse used with respect to different T1 and T2 values under our experimental settings. The duration of the inversion pulse = 5 ms, and its bandwidth = 3520 Hz.
| Relaxation time (ms) | T1 ≈ 1200 | T1 ≈ 1900 | ||||
|---|---|---|---|---|---|---|
| T2 = 45 | T2 = 60 | T2 = 181 | T2 = 43 | T2 = 56 | T2 = 178 | |
| Inversion Efficiency β | 0.95 | 0.97 | 0.98 | 0.95 | 0.96 | 0.98 |
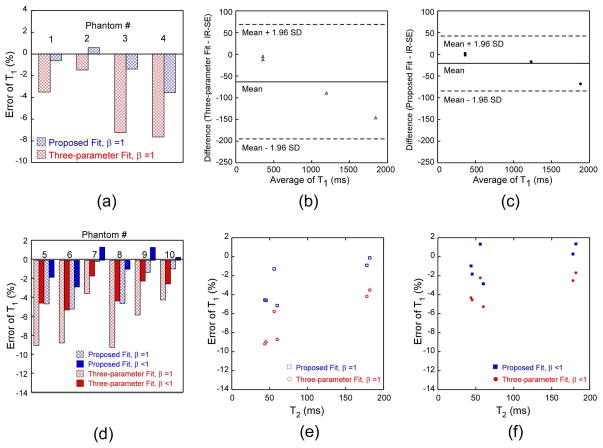
Tables 2a and 2b present the errors of T1 obtained with different imaging parameters and fitting procedures. These results illustrate that, whether the phantom experiment was gated with a simplified fix delay or the actual respiratory and ECG signals from a rat, when α was 8° or 10°, the most accurate T1 values were obtained with our proposed T1 fit model, which was further improved by considering the actual inversion efficiency β. Since α = 10° gave a relatively higher signal-to-noise ratio than α = 8°, we chose α = 10° for the reminder of the experiments in this study. When we varied the number of k-space lines per segment from 1 to 4, for both the fixed and realistic gating procedures, the accuracy of T1 did not change extensively for our proposed T1 fit model using the actual inversion factor β. Consequently, we selected 4 k-space lines per segment to reduce the scan time to approximately 5 min. More importantly, it should be noted from Table 2b that under both the assumed β =1 and actual β < 1 conditions, our proposed T1 fit model has corrected the underestimation of T1 values commonly seen in the widely used three-parameter fit and outperformed it in T1 accuracy.
TABLE 2.
The effect of excitation flip angle α and the number of k-space lines per segment (Seg) on the accuracy of T1 measurements with a segmented multi-shot FLASH sequence when using the proposed T1 regression fit and the three-parameter fit. (a) For the simplified phantom experiments simulating the myocardium and blood, images were gated with a fixed delay, and the signal intensities of the T1 sampling curve were fitted with an assumed β value of 1. (b) For the six phantoms with a similar T1 but varied T2 values, the data acquisition were gated with the actual respiratory and ECG signals of a rat, and images were analyzed by these two fitting procedures twice: first with an assumed perfect inversion of β=1 and then with the actual β measured from IR-SE. The T1 errors shown in the table were the average error for the series of phantoms studied in each group, in comparison with the T1 values obtained from IR-SE.
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| T1 Error (%) | Flip Angle α (Seg = 4) | Segmentation Number (α = 10°) | ||||||
| 4° | 8° | 10° | 12° | 1 | 2 | 3 | 4 | |
| Three-Parameter Fit with β =1 | −1.04 | −4.61 | −5.29 | −7.73 | −3.01 | −4.46 | −6.32 | −5.29 |
| Proposed T1 Fit with β =1 | 2.22 | 0.20 | 0.50 | −1.30 | 0.15 | −1.11 | 0.56 | 0.50 |
| (b) | ||||||||
|---|---|---|---|---|---|---|---|---|
| T1 Error (%) | Flip Angle α (Seg = 4) | Number of Seg (α = 10°) | ||||||
| 4° | 8° | 10° | 12° | 1 | 2 | 3 | 4 | |
| Three-Parameter Fit with β =1 | −4.83 | −5.41 | −6.72 | −8.76 | −2.82 | −6.95 | −6.86 | −6.72 |
| Three-Parameter Fit with β <1 | −1.45 | −2.05 | −3.40 | −5.52 | −0.65 | −3.65 | −3.54 | −3.40 |
| Proposed T1 Fit with β =1 | −3.13 | −1.51 | −2.77 | −3.77 | −0.80 | −3.21 | −3.10 | −2.77 |
| Proposed T1 Fit with β <1 | −1.04 | 0.75 | −0.42 | −1.32 | 0.39 | −0.97 | −0.82 | −0.42 |
Tables 3a and 3b summarize the T1 error in the phantoms measured with the IR prepared multi-shot FLASH, in comparison with those obtained from IR-SE (gold standard). We have found that whether the signal intensities from the FLASH-based T1 sampling curve were analyzed with an assumed β =1 or an actual value of β < 1, the proposed T1 fit always provided more accurate T1 estimate than the conventional three-parameter fit for the range of the T1 and T2 values studied (Table 3a and Fig. 2a), and this was still valid even when the data acquisitions were gated by the actual respiratory and ECG signals from a rat (Table 3b and Fig. 2d). Specifically for phantoms gated by this realistic procedure, when we assumed a perfect inversion of β = 1, the three-parameter fit significantly underestimated the T1 values (error of −6.72 ± 2.56%) in comparison with the gold standard, whereas our proposed regression fit relatively improved the T1 estimate (error of -2.77 ± 2.23%, Fig. 2d). When we used the actual inversion efficiency β in the T1 fittings, both the proposed fit and the three-parameter fit yielded better T1 estimates (Table 3b and Fig. 2d). However, our proposed T1 fit model still outperformed the three-parameter fit with an average error of −0.42 ± 1.73% vs. −3.40 ± 1.46%, respectively.
TABLE 3.
Summary of the T1 errors in phantoms that measured from the multi-shot segmented FLASH and analyzed with the proposed T1 regression fit and the three-parameter fit, in comparison with the T1 values obtained from IR-SE. For the segmented FLASH sequence, the flip angle α= 10° and the number of k-space lines per segment = 4. (a) For the simplified phantom experiments gated with a fixed delay, the signal intensities of the T1 sampling curve were fitted only with an assumed β=1. (b) For the data acquisition gated with the actual respiratory and ECG signals from a rat, the signal intensities were fitted twice, each first with an assumed perfect inversion of β=1 and then with the measured actual β value.
| (a) | ||||
|---|---|---|---|---|
| Phantom No. | 1 | 2 | 3 | 4 |
| Relaxation Time (ms) | T1= 1238 | T1= 361 | T1= 1914 | T1= 358 |
| T2 = 54 | T2 = 52 | T2 = 162 | T2 = 163 | |
| Three-Parameter Fit with β =1 | −7.25 | −3.52 | −7.67 | −1.49 |
| Proposed T1 Fit with β =1 | −1.40 | −0.63 | −3.58 | 0.58 |
| (b) | ||||||
|---|---|---|---|---|---|---|
| Phantom No. | 5 | 6 | 7 | 8 | 9 | 10 |
| Relaxation Time (ms) | T1 ≈ 1200 | T1 ≈ 1900 | ||||
| T2 = 45 | T2 = 60 | T2 = 181 | T2 = 43 | T2 = 56 | T2 = 178 | |
| Three-Parameter Fit with β =1 | −8.96 | −8.72 | −3.50 | −9.17 | −5.77 | −4.18 |
| Three-Parameter Fit with β <1 | −4.52 | −5.24 | −1.66 | −4.28 | −2.20 | −2.48 |
| Proposed T1 Fit with β =1 | −4.60 | −5.14 | −0.12 | −4.55 | −1.29 | −0.91 |
| Proposed T1 Fit with β <1 | −1.80 | −2.82 | 1.38 | −0.95 | 1.36 | 0.32 |
Fig. 2.
T1 error in the phantoms obtained with our proposed T1 regression model and the three-parameter fit when compared to the actual T1 values obtained from IR-SE. (a) T1 error for the four phantoms simulating the myocardium and blood before and after gadolinium administration when the T1 measurement was gated with a fixed delay, and the signal intensities of the T1 sampling curve were fitted with only an assumed β=1. The Bland-Altman analysis of these T1 values calculated from (b) the conventional three-parameter fit and (c) the proposed T1 fit with β=1 when compared to the T1 values obtained from IR-SE. (d) T1 error for the other six phantoms when the data acquisition was gated with the actual respiratory and ECG signals of a rat, and the signal intensities were fitted with the two models twice, first with an assumed perfect inversion of β=1 and then with the measured actual β value. The dependence of this T1 error on T2 values for the two fitting models when (e) β = 1 and (f) β < 1.
The Bland-Altman analysis of the T1 values obtained under the simplified conditions (gated with a fixed delay and an assumed β =1 ) has found that the three-parameter fit produced a mean bias of -63.6 ms in comparison with IR-SE; and the 95% limits of agreement were between −195.5 and 68.2 ms (Fig. 2b). Whereas, the Bland-Altman analysis of the T1 values achieved under the same situations but analyzed by the proposed T1 fit with β =1 had a mean bias of −21.5 ms compared to IR-SE; and the 95% limits of agreement were between −84.9 and 42.0 ms (Fig. 2c). We have also investigated the effect of T2 on the inversion efficiency and thus the T1 errors obtained with the proposed T1 fit and the three-parameter fit when β = 1 (Fig. 2e) and β < 1 (Fig. 2f) during the fittings, respectively. We can see that when a perfect inversion was assumed (β = 1), the T1 error was larger for lower T2 values and was decreasing with an increased T2, especially for the three-parameter fit model (Fig. 2e). This was possibly caused by the poor inversion efficiency for low T2 values. After using the measured actual β value in the fittings, however, the dependence of the T1 errors on T2 became insensitive, particularly for our proposed T1 fit model (Fig. 2f).
Animal Study
Representative slice-selective IR prepared multi-shot FLASH images of a rat heart at different TIs acquired one day post LAD ligation are illustrated in Fig. 3.
Fig. 3.
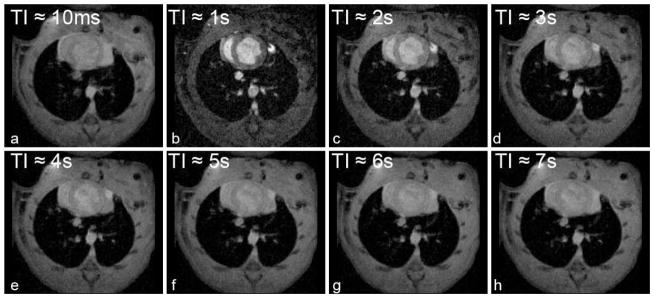
Representative images acquired with a slice-selective IR-prepared, segmented multi-shot FLASH at different recovery time points (TIs) in a rat with acute MI.
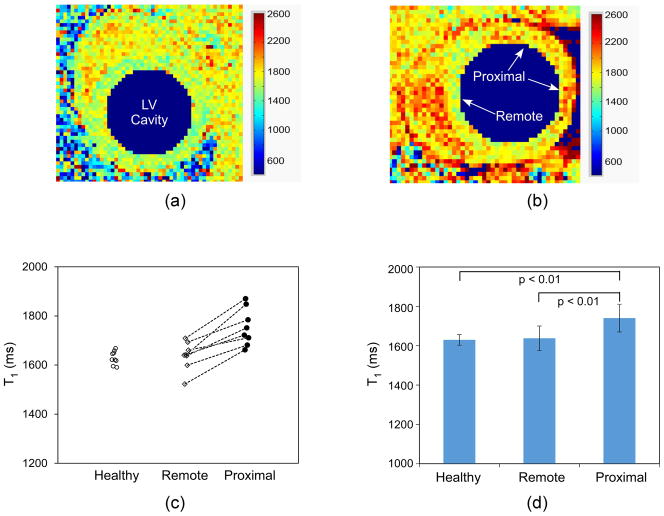
Fig. 4a shows a representative baseline myocardial T1 map in a healthy rat; while Fig. 4b shows the myocardial T1 map obtained in a rat one day post LAD ligation. For healthy hearts, the T1 value was uniform throughout the left ventricle myocardium (Fig. 4a); whereas, in hearts with LAD ligation, higher T1 values were observed in lateral and anterior-lateral areas proximal to the LAD ligation than those in septal and septal-inferior areas which were remote to the ligation (Fig. 4b). Myocardial T1 values from the healthy rats, and from areas remote and proximal to the LAD ligation in the eight rats with acute MI were plotted in Fig. 4c. The increased T1 values observed proximal to the LAD ligation were likely due to edema following ligation. The larger standard deviation of T1 values found in rats with acute MI may result from the extent and regional differences in edema distributions. The average myocardial T1 value in healthy rats was 1636.3 ± 23.4 ms; and the average blood T1 from the LV cavity was 1810.6 ± 53.0 ms. In rats with acute MI, the average myocardial T1 values in the remote and proximal area of the ligation were 1637.5 ± 62.6 ms and 1740.3 ± 70.5 ms, respectively (Fig. 4d). The blood T1 value in these rats with ligation was 1854.7 ± 87.1 ms. Statistical analysis showed that myocardial T1 in the proximal area was significantly different from that in the remote area of the same rat, and was also significantly different from that in healthy rats (all p-values < 0.05).
Fig. 4.
Representative baseline myocardial T1 before contrast agent injection. Myocardial T1 map of (a) a healthy rat showed uniform T1 value throughout the left ventricle (LV) myocardium; (b) whereas, myocardial T1 map of a rat with acute MI revealed regional higher T1 in the proximal area of ligation (anterior-lateral and lateral myocardium), probably because of edema occurred right after the ligation; The blood T1 in the LV cavity was deliberately suppressed to better demonstrate the LV myocardium contour. (c) Plot of each individual baseline myocardial T1 values of the eight measurements in healthy rats, and in the remote and proximal regions towards LAD ligation in the eight rats with acute MI; (d) The mean baseline myocardial T1 values and their SD in the healthy rats, and in the remote and proximal regions of the rats with ligation. T1 in the proximal regions supplied by the ligated arteries was significantly different from that in the remote area of the same rat, and from the one in healthy rat.
Fig. 5a displays a representative LGE image of an infarcted rat heart at approximately 14 min following the administration of gadolinium one day post LAD ligation. The infarction was observed as a region of signal hyperintensity; however, the boundary between the infarction and normal myocardium was not clear. Fig. 5b shows a corresponding computer-aided, color-coded display of the infarction zone from Fig. 5a. The pink color indicates the infarction zone, defined as pixels having a signal intensity ≥ 5 times standard deviation above the average signal found in the remote myocardium (39). In the corresponding myocardial T1 map calculated from the same scan, pixels in the infarction zone were characterized by dramatically lower T1 (Fig. 5c). One could clearly identify the edge between the infarcted and normal myocardium with the disparity of their T1 values, and this region agreed well with the color-coded infarction display (Fig. 5b). At this early time point following MI, we speculate that no diffuse fibrosis has formed yet, and therefore no short T1 values were observed beyond the infarction zone (40). The infarction zone indicated in the LGE images (Fig. 5b) and by the regional low values of T1 (Fig. 5c) matched well with that revealed by the TTC staining (Fig. 5d). Within 10–20 min after the administration of contrast agent, the average blood and myocardial T1 values in healthy rats were 556.7 ± 68.5 ms and 968.7 ± 56.5 ms, respectively. In rats with acute MI, the average blood T1 was 616.8 ± 139.6 ms; while the average myocardial T1 values remote to the ligation and in the infarction zone were 969.3 ± 136.7 ms and 488.8 ± 92.7 ms, respectively.
Fig. 5.

(a) LGE image of a rat heart with MI; (b) Computer-aided, color-coded display of the infarction zone from the LGE image of Fig. 5a. The pink color indicated pixels with signal intensity ≥ 5 times standard deviation above the average pixel intensity in the remote area of the LAD ligation. (c) Corresponding myocardial T1 map (in the unit of ms) of the same heart at the same time point post Gd injection as in (a) showed dramatically lower T1 values in the infarction zone defined by Fig. 5b, displaying clear edge with the normal remote myocardium; No low T1 was found beyond the specified infarction zone, implicating no fibrosis was formed at this time point after ligation. (d) TTC staining of the same rat demonstrated that the infarction zone (in white or light pink color) was in the anterior-lateral and lateral myocardium, in good agreement with the LGE and T1 results.
DISCUSSION
In this study, we have introduced a multi-variable T1 regression fit model modified for a dual respiration/ECG gated, segmented multi-shot FLASH-based Look-Locker sequence in rats. By taking account the actual saturation effect induced by the short α-train pulses and the recovery of Mz during intervals between consecutive Look-Locker image readouts, we have amended the T1 underestimation commonly seen in the three-parameter fit and improved the accuracy of T1 estimate as shown in our phantom studies (Table 2, Table 3 and Fig. 2). We used the actual Mz at the center k-space line, and simply averaging TI values in all segments of the same Look-Locker image for the T1 relaxation curve fitting. In a similar dual respiration/ECG gated data acquisition with spiral k-space trajectory, a strategy to further sort the acquired k-space data of the segmented FLASH with corresponding TI values was reported (19). They corrected the inconsistent TIs resulted from dual respiratory and ECG gating in mice with a fuzzy C-means algorithm and assigned it to each Look-Locker image retrospectively. This has improved the T1 estimate in comparison with a prospective TI assignment, and agreed with that obtained with a fixed and constant sampling interval.
In contrast, most other myocardial T1 studies in rodents employed only ECG gating for a fast data acquisition and T1 curve sampling by restricting the respiratory motion with a mechanical ventilator (7,8,17,41), applying a pseudo dual respiratory/ECG gating for the inversion pulse only and then retrospectively removing or replacing the echoes corrupted by respiratory motion (9,16,28), or even without respiration suppression (10,26,27). All of these procedures could result in significant image motion artifact and thus possible erroneous T1 values. Among those publications using segmented multi-shot FLASH data acquisition in rodents, either for assessing myocardial perfusion (9,16,17,19,28), infarction size (10,26), or simply measuring baseline T1 values (27), the reported myocardial T1 values were inconsistent from study to study, after considering the fact that tissue T1 values are generally increasing with an increased field strength. For example, Schneider et al. (10), Bohl et al. (26), and Li et al. (27) all reported myocardial T1 values of approximately 1.0–1.2 s in mice at 9.4 T; whereas Kober et al. (9) reported a myocardial T1 of 1.3 s in rats at 4.7 T, and both Streif et al. (17) and Vandsburger et al. (19) reported T1 values of approximately 1.6 s in mice at 7 T. Our measurements at 7 T were close with the T1 values reported by Vandsburger et al and Streif et al. The discrepancies of T1 values in these studies could be attributed to different strategies of image gating. When only a cardiac gating was used for data acquisition, image artifact caused by the un-restricted respiratory motion could be problematic for T1 fitting (10,26,27). There were also studies in which the dual respiratory/cardiac gating was applied only for the inversion pulse; the following readout was still ECG-triggered, and those echoes contaminated by respiratory motion were then removed (9,16) or replaced (28) retrospectively before the T1 fitting. By this means, one can reduce the effect of respiration motion, which, on the other hand, might require longer measurement time to collect sufficient repeated echoes and more imaging postprocessing work.
A direct way to minimize the respiratory motion artifact is to use a dual respiratory/ECG gating, as shown in this study and the study of Vandsburger et al. (19). A limitation of the dual gating was the relatively few data points available for T1 fitting because the sampling intervals were determined by the respiration (i.e. ventilation) rate regardless of the varied heart rate of 270–460 bpm among individual rats studied. In this study, we only had eight data points for the T1 curve fitting, obtained in approximately 7 s following the inversion pulse. To better sample the T1 recovery curve, especially including a data set close to the null point of the T1 will improve the accuracy of T1 estimate. Images near the null point, however, could be more susceptible to the background noise and induce ambiguities of the polarity of the magnitude images during the fitting and bias the resulted T1. Including more data points on both sides of the null point would help the fitting if condition allowed. Also, techniques that utilized the phase-sensitive reconstruction and preserved the image polarity would improve the quality of the T1 estimate (42). For a multi-shot FLASH readout, the total data acquisition time (about 5.3 min in this study), however, was mainly limited by the time required for Mz to return to equilibrium before applying a new inversion pulse for the next round of segments of readout. In this study, we intentionally added an additional 3 s delay after each series of Look-Locker image readout segments, making the total inversion delay of approximately 10 s and slightly longer than five times of the longest T1 value measured. It would be better to have additional readout segments during each gated expiration window (approximate 480 ms) in order to take advantage of the long Mz recovery time and increase the number of data points available for T1 fitting. Instead, we deliberately skipped the second ECG window because sometimes it was located outside the expiration window for a cardiac cycle of approximately 130–220 ms in rats as a consequence of the inharmonic frequencies of respiration and ECG. With this strategy, we could avoid missed readout in the gating window and further inconsistency of the TIs among different segments of the same image. Using a slightly different initial TI (TI1) to acquire additional datasets as the MOLLI method (29) could also increase the T1 sampling efficiency and estimate accuracy, although this would put the first Look-Locker image in a slightly different cardiac phase and could induce mis-registration between images.
Another limitation of the study was that we have only validated the improvement in T1 estimate with the proposed fit model indirectly in static phantoms because of the lack of gold standard for in vivo T1 quantification. Using the actual respiratory and ECG signals from a rat to gate the phantom data acquisition of the T1 sampling images with a multi-shot FLASH based Look-Locker sequence as did in our study has reproduced the duration and variation of the TIs between readouts actually occurred in animal studies under the dual respiration/ECG gating schemes and made our phantom results more realistic. Although the phantom results elaborated the effectiveness of our model, it did not reveal the respiratory and cardiac motion of the heart and the perfusion effect of moving spins happening under physiological situations. The third limitation of this study was that the effect of T2 and T1 on the inversion efficiencies of different types of adiabatic pulses, and thus the T1 measurements (38,43) only came to our attention after we submitted our manuscript for peer review. Throughout our study, we have used a hyperbolic secant pulse for inversion. With an independent measurement of the inversion efficiency β and including it in the proposed T1 fitting model has greatly improved the accuracy of myocardial T1 measurement than with just an assumed perfect inversion (error of −0.42 ± 1.73% vs. −2.77 ± 2.23% for our phantom data) and reduced its dependence on T2 values (Fig. 2f). Similarly, using a pixel-wised β for in vivo studies could also improve the accuracy of myocardial T1 mapping. Alternatively, choosing an inversion pulse that is relatively independent on T2 and T1 values, such as a tangent/hyperbolic tangent pulse (38), could facilitate the myocardial T1 measurement and achieve similar T1 accuracy by avoiding additional measurement of the inversion efficiency.
For in vivo rodent studies, the myocardial T1 map provides an easy way to visualize the area containing edema or infarction, and could provide further quantitative information of MBF, MI percentage or extracellular volume fraction etc. However, as noted in Fig. 4c, the variations of the presence, extent or regional distributions of edema in the myocardium after coronary artery ligation could lead to variations of the baseline T1 in each pixel and in both the proximal and remote ROIs selected, especially from individual to individual. This could impose a potential difficulty to specify a single threshold value of T1 in distinguishing normal tissue from edema. Still, baseline myocardial T1 measurement could provide complementary information for LGE images to indicate the presence of reversible injury. The quantitative analyses of infarction percentage, identifying reversible injury from infarction, or the compositions of edema and fibrosis in MI and their longitudinal changes along ventricular remodeling, however, are beyond the scope of this study.
In conclusion, using a new T1 regression fit model that takes into account the saturation effect of the short sampling α-train and the Mz recovery during a gated, segmented multi-shot FLASH acquisition, we have improved the accuracy of T1 measurement in phantoms and outperformed the three-parameter fit. With this improvement, we can clearly distinguish the regional difference of T1 values in the remote and proximal areas in rats with MI. Therefore, the developed T1 techniques may serve as a promising tool to advance related applications utilizing quantitative T1 values.
Acknowledgments
We are indebted to Li Liu for preparing the phantoms for our experiments. We also thank Brent Barbe and Lisa McGaw for their technical assistance in animal experiments and animal care. Our research is supported by research grants from the National Institutes of Health (R01HL-081349 and P41EB-001977 for C Ho).
APPENDIX
Derived from the Bloch Equations (36), the longitudinal magnetization Mz at any time t can be written as
| [1] |
where M0 is the equilibrium magnetization, Mz (t0) is the initial magnetization at time t0.
Meanwhile, the longitudinal magnetization after the ith RF pulse (ith k-space step) in the Nth Look-Locker image, Mz(N,i)+, can be expressed with the longitudinal magnetization before this RF pulse, Mz(N,i)−, as
| [App.1] |
and α is the flip angle of the RF pulse.
According to Eq. [1] and Eq. [App.1], in a multi-shot, segmented FLASH sequence, the longitudinal magnetization after the application of the 1st RF and a waiting time of TR, but right before we apply the 2nd RF, Mz(N,2)−, in the segment of the Nth Look-Locker image is
| [App.2] |
where TR is the repetition time between two α pulses, Mz(N,1)− is the longitudinal magnetization right before the 1st RF pulse in the segment of the Nth image.
And right after the application of the 2nd RF pulse, the longitudinal magnetization Mz(N,2)+ is
| [App.3] |
Similarly, the longitudinal magnetization right before we apply the 3rd RF, Mz(N,3)−, in the segment of the Nth Look-Locker image is
| [App.4] |
If we repeat this procedure, and with the mathematic equation of
| [App.5] |
we can get the longitudinal magnetization right before the central k-space line (kth step) in the segment of the Nth Look-Locker image, Mz(N,k)−, as
| [2] |
Likewise, in each segment N, the transient Mz right before the last (nth step) RF pulse can be expressed by Mz(N,1)− as
| [3] |
or equally by the magnetization before the central k-space line k in the same segment, Mz(N,k)−, as
| [4] |
References
- 1.Simonetti OP, Kim RJ, Fieno DS, Hillenbrand HB, Wu E, Bundy JM, Finn JP, Judd RM. An improved MR imaging technique for the visualization of myocardial infarction. Radiology. 2001;218(1):215–223. doi: 10.1148/radiology.218.1.r01ja50215. [DOI] [PubMed] [Google Scholar]
- 2.Judd RM, Kim RJ. Imaging time after Gd-DTPA injection is critical in using delayed enhancement to determine infarct size accurately with magnetic resonance imaging. Circulation. 2002;106(2):E6–E6. doi: 10.1161/01.cir.0000019903.37922.9c. [DOI] [PubMed] [Google Scholar]
- 3.Goldfarb JW, Arnold S, Han J. Recent myocardial infarction: assessment with unenhanced T1-weighted MR imaging. Radiology. 2007;245(1):245–250. doi: 10.1148/radiol.2451061590. [DOI] [PubMed] [Google Scholar]
- 4.Sparrow P, Messroghli DR, Reid S, Ridgway JP, Bainbridge G, Sivananthan MU. Myocardial T1 mapping for detection of left ventricular myocardial fibrosis in chronic aortic regurgitation: pilot study. AJR Am J Roentgenol. 2006;187(6):W630–635. doi: 10.2214/AJR.05.1264. [DOI] [PubMed] [Google Scholar]
- 5.Amano Y, Takayama M, Kumita S. Contrast-enhanced myocardial T1-weighted scout (Look-Locker) imaging for the detection of myocardial damages in hypertrophic cardiomyopathy. J Magn Reson Imaging. 2009;30(4):778–784. doi: 10.1002/jmri.21921. [DOI] [PubMed] [Google Scholar]
- 6.Belle V, Kahler E, Waller C, Rommel E, Voll S, Hiller KH, Bauer WR, Haase A. In vivo quantitative mapping of cardiac perfusion in rats using a noninvasive MR spin-labeling method. J Magn Reson Imaging. 1998;8(6):1240–1245. doi: 10.1002/jmri.1880080610. [DOI] [PubMed] [Google Scholar]
- 7.Waller C, Kahler E, Hiller KH, Hu K, Nahrendorf M, Voll S, Haase A, Ertl G, Bauer WR. Myocardial perfusion and intracapillary blood volume in rats at rest and with coronary dilatation: MR imaging in vivo with use of a spin-labeling technique. Radiology. 2000;215(1):189–197. doi: 10.1148/radiology.215.1.r00ap07189. [DOI] [PubMed] [Google Scholar]
- 8.Waller C, Hiller KH, Kahler E, Hu K, Nahrendorf M, Voll S, Haase A, Ertl G, Bauer WR. Serial magnetic resonance imaging of microvascular remodeling in the infarcted rat heart. Circulation. 2001;103(11):1564–1569. doi: 10.1161/01.cir.103.11.1564. [DOI] [PubMed] [Google Scholar]
- 9.Kober F, Iltis I, Izquierdo M, Desrois M, Ibarrola D, Cozzone PJ, Bernard M. High-resolution myocardial perfusion mapping in small animals in vivo by spin-labeling gradient-echo imaging. Magn Reson Med. 2004;51(1):62–67. doi: 10.1002/mrm.10676. [DOI] [PubMed] [Google Scholar]
- 10.Schneider JE, Lanz T, Barnes H, Stork LA, Bohl S, Lygate CA, Ordidge RJ, Neubauer S. Accelerated Cardiac Magnetic Resonance Imaging in the Mouse Using an Eight-Channel Array at 9. 4 Tesla. Magn Reson Med. 2011;65(1):60–70. doi: 10.1002/mrm.22605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abdel-Aty H, Zagrosek A, Schulz-Menger J, Taylor AJ, Messroghli D, Kumar A, Gross M, Dietz R, Friedrich MG. Delayed enhancement and T2-weighted cardiovascular magnetic resonance imaging differentiate acute from chronic myocardial infarction. Circulation. 2004;109(20):2411–2416. doi: 10.1161/01.CIR.0000127428.10985.C6. [DOI] [PubMed] [Google Scholar]
- 12.Simonetti OP, Finn JP, White RD, Laub G, Henry DA. “Black blood” T2-weighted inversion-recovery MR imaging of the heart. Radiology. 1996;199(1):49–57. doi: 10.1148/radiology.199.1.8633172. [DOI] [PubMed] [Google Scholar]
- 13.Miller S, Helber U, Brechtel K, Nagele T, Hahn U, Kramer U, Hoffmeister HM, Claussen CD. MR imaging at rest early after myocardial infarction: detection of preserved function in regions with evidence for ischemic injury and non-transmural myocardial infarction. Eur Radiol. 2003;13(3):498–506. doi: 10.1007/s00330-002-1544-6. [DOI] [PubMed] [Google Scholar]
- 14.Goldfarb JW, Arnold S, Roth M. Gadolinium pharmacokinetics of chronic myocardial infarcts: Implications for late gadolinium-enhanced infarct imaging. J Magn Reson Imaging. 2009;30(4):763–770. doi: 10.1002/jmri.21901. [DOI] [PubMed] [Google Scholar]
- 15.Zhang H, Shea SM, Park V, Li D, Woodard PK, Gropler RJ, Zheng J. Accurate myocardial T1 measurements: toward quantification of myocardial blood flow with arterial spin labeling. Magnet Reson Med. 2005;53(5):1135–1142. doi: 10.1002/mrm.20461. [DOI] [PubMed] [Google Scholar]
- 16.Kober F, Iltis I, Cozzone PJ, Bernard M. Myocardial blood flow mapping in mice using high-resolution spin labeling magnetic resonance imaging: influence of ketamine/xylazine and isoflurane anesthesia. Magn Reson Med. 2005;53(3):601–606. doi: 10.1002/mrm.20373. [DOI] [PubMed] [Google Scholar]
- 17.Streif JU, Nahrendorf M, Hiller KH, Waller C, Wiesmann F, Rommel E, Haase A, Bauer WR. In vivo assessment of absolute perfusion and intracapillary blood volume in the murine myocardium by spin labeling magnetic resonance imaging. Magn Reson Med. 2005;53(3):584–592. doi: 10.1002/mrm.20327. [DOI] [PubMed] [Google Scholar]
- 18.Iltis I, Kober F, Dalmasso C, Lan C, Cozzone PJ, Bernard M. In vivo assessment of myocardial blood flow in rat heart using magnetic resonance imaging: effect of anesthesia. J Magn Reson Imaging. 2005;22(2):242–247. doi: 10.1002/jmri.20352. [DOI] [PubMed] [Google Scholar]
- 19.Vandsburger MH, Janiczek RL, Xu Y, French BA, Meyer CH, Kramer CM, Epstein FH. Improved arterial spin labeling after myocardial infarction in mice using cardiac and respiratory gated look-locker imaging with fuzzy C-means clustering. Magn Reson Med. 2010;63(3):648–657. doi: 10.1002/mrm.22280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jerosch-Herold M, Sheridan DC, Kushner JD, Nauman D, Burgess D, Dutton D, Alharethi R, Li D, Hershberger RE. Cardiac magnetic resonance imaging of myocardial contrast uptake and blood flow in patients affected with idiopathic or familial dilated cardiomyopathy. Am J Physiol Heart Circ Physiol. 2008;295(3):H1234–H1242. doi: 10.1152/ajpheart.00429.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Flett AS, Hayward MP, Ashworth MT, Hansen MS, Taylor AM, Elliott PM, McGregor C, Moon JC. Equilibrium contrast cardiovascular magnetic resonance for the measurement of diffuse myocardial fibrosis: preliminary validation in humans. Circulation. 2010;122(2):138–144. doi: 10.1161/CIRCULATIONAHA.109.930636. [DOI] [PubMed] [Google Scholar]
- 22.Schelbert EB, Testa SM, Meier CG, Ceyrolles WJ, Levenson JE, Blair AJ, Kellman P, Jones BL, Ludwig DR, Schwartzman D, Shroff SG, Wong TC. Myocardial extravascular extracellular volume fraction measurement by gadolinium cardiovascular magnetic resonance in humans: slow infusion versus bolus. J Cardiovasc Magn Reson. 2011;13:16. doi: 10.1186/1532-429X-13-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Haase A. Snapshot Flash Mri - Applications to T1, T2, and Chemical-Shift Imaging. Magnet Reson Med. 1990;13(1):77–89. doi: 10.1002/mrm.1910130109. [DOI] [PubMed] [Google Scholar]
- 24.Deichmann R, Haase A. Quantification of T1 Values by Snapshot-Flash Nmr Imaging. J Magn Reson. 1992;96(3):608–612. [Google Scholar]
- 25.Steinhoff S, Zaitsev M, Zilles K, Shah NJ. Fast T(1) mapping with volume coverage. Magnet Reson Med. 2001;46(1):131–140. doi: 10.1002/mrm.1168. [DOI] [PubMed] [Google Scholar]
- 26.Bohl S, Lygate CA, Barnes H, Medway D, Stork LA, Schulz-Menger J, Neubauer S, Schneider JE. Advanced methods for quantification of infarct size in mice using three-dimensional high-field late gadolinium enhancement MRI. Am J Physiol Heart Circ Physiol. 2009;296(4):H1200–1208. doi: 10.1152/ajpheart.01294.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li W, Griswold M, Yu X. Rapid T1 mapping of mouse myocardium with saturation recovery Look-Locker method. Magn Reson Med. 2010;64(5):1296–1303. doi: 10.1002/mrm.22544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Campbell-Washburn AE, Price AN, Wells JA, Thomas DL, Ordidge RJ, Lythgoe MF. Cardiac arterial spin labeling using segmented ECG-gated Look-Locker FAIR: variability and repeatability in preclinical studies. Magn Reson Med. 2013;69(1):238–247. doi: 10.1002/mrm.24243. [DOI] [PubMed] [Google Scholar]
- 29.Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified Look-Locker inversion recovery (MOLLI) for high-resolution T-1 mapping of the heart. Magnet Reson Med. 2004;52(1):141–146. doi: 10.1002/mrm.20110. [DOI] [PubMed] [Google Scholar]
- 30.Messroghli DR, Greiser A, Frohlich M. Optimization and validation of a fully-integrated pulse sequence for modified look-locker inversion-recovery (MOLLI) T1 mapping of the heart. J Magn Reson Imaging. 2007;26(4):1081–1086. doi: 10.1002/jmri.21119. [DOI] [PubMed] [Google Scholar]
- 31.Messroghli DR, Walters K, Plein S, Sparrow P, Friedrich MG, Ridgway JP, Sivananthan MU. Myocardial T1 mapping: application to patients with acute and chronic myocardial infarction. Magn Reson Med. 2007;58(1):34–40. doi: 10.1002/mrm.21272. [DOI] [PubMed] [Google Scholar]
- 32.Zun Z, Wong EC, Nayak KS. Assessment of myocardial blood flow (MBF) in humans using arterial spin labeling (ASL): feasibility and noise analysis. Magn Reson Med. 2009;62(4):975–983. doi: 10.1002/mrm.22088. [DOI] [PubMed] [Google Scholar]
- 33.Poncelet BP, Koelling TM, Schmidt CJ, Kwong KK, Reese TG, Ledden P, Kantor HL, Brady TJ, Weisskoff RM. Measurement of human myocardial perfusion by double-gated flow alternating inversion recovery EPI. Magnet Reson Med. 1999;41(3):510–519. doi: 10.1002/(sici)1522-2594(199903)41:3<510::aid-mrm13>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 34.Zaitsev M, Steinhoff S, Shah NJ. Error reduction and parameter optimization of the TAPIR method for fast T(1) mapping. Magnet Reson Med. 2003;49(6):1121–1132. doi: 10.1002/mrm.10478. [DOI] [PubMed] [Google Scholar]
- 35.Gunther M, Bock M, Schad LR. Arterial spin labeling in combination with a look-locker sampling strategy: inflow turbo-sampling EPI-FAIR (ITS-FAIR) Magn Reson Med. 2001;46(5):974–984. doi: 10.1002/mrm.1284. [DOI] [PubMed] [Google Scholar]
- 36.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Physical Principles and Sequence Design. Wiley-Liss; 1999. Magnetic Resonance Imaging; p. 58. [Google Scholar]
- 37.Lutgens E, Daemen MJAP, de Muinck ED, Debets J, Leenders P, Smits JFM. Chronic myocardial infarction in the mouse: cardiac structural and functional changes. Cardiovasc Res. 1999;41(3):586–593. doi: 10.1016/s0008-6363(98)00216-8. [DOI] [PubMed] [Google Scholar]
- 38.Kellman P, Herzka DA, Hansen MS. Adiabatic inversion pulses for myocardial T1 mapping. Magn Reson Med. 2013 doi: 10.1002/mrm.24793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schulz-Menger J, Bluemke DA, Bremerich J, Flamm SD, Fogel MA, Friedrich MG, Kim RJ, von Knobelsdorff-Brenkenhoff F, Kramer CM, Pennell DJ, Plein S, Nagel E. Standardized image interpretation and post processing in cardiovascular magnetic resonance: Society for Cardiovascular Magnetic Resonance (SCMR) Board of Trustees Task Force on Standardized Post Processing. J Cardiovasc Magn Reson. 2013;15:35. doi: 10.1186/1532-429X-15-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Iles L, Pfluger H, Phrommintikul A, Cherayath J, Aksit P, Gupta SN, Kaye DM, Taylor AJ. Evaluation of diffuse myocardial fibrosis in heart failure with cardiac magnetic resonance contrast-enhanced T1 mapping. J Am Coll Cardiol. 2008;52(19):1574–1580. doi: 10.1016/j.jacc.2008.06.049. [DOI] [PubMed] [Google Scholar]
- 41.Waller C, Engelhorn T, Hiller KH, Heusch G, Ertl G, Bauer WR, Schulz R. Impaired resting perfusion in viable myocardium distal to chronic coronary stenosis in rats. Am J Physiol Heart Circ Physiol. 2005;288(6):H2588–2593. doi: 10.1152/ajpheart.01060.2004. [DOI] [PubMed] [Google Scholar]
- 42.Xue H, Shah S, Greiser A, Guetter C, Littmann A, Jolly MP, Arai AE, Zuehlsdorff S, Guehring J, Kellman P. Motion correction for myocardial T1 mapping using image registration with synthetic image estimation. Magn Reson Med. 2012;67(6):1644–1655. doi: 10.1002/mrm.23153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rodgers CT, Piechnik SK, Delabarre LJ, Van de Moortele PF, Snyder CJ, Neubauer S, Robson MD, Vaughan JT. Inversion recovery at 7 T in the human myocardium: Measurement of T(1), inversion efficiency and B(1) (+) Magn Reson Med. 2012 doi: 10.1002/mrm.24548. [DOI] [PMC free article] [PubMed] [Google Scholar]