Single-shot characterization of enzymatic reaction constants K_m and k_cat by an acoustic-driven, bubble-based fast micromixer

Abstract

In this work we present an acoustofluidic approach for rapid, single-shot characterization of enzymatic reaction constants K_m and k_cat. The acoustofluidic design involves a bubble anchored in a horseshoe structure which can be stimulated by a piezoelectric transducer to generate vortices in the fluid. The enzyme and substrate can thus be mixed rapidly, within 100 ms, by the vortices to yield the product. Enzymatic reaction constants K_m and k_cat can then be obtained from the reaction rate curves for different concentrations of substrate while holding the enzyme concentration constant. We studied the enzymatic reaction for β-galactosidase and its substrate (resorufin β-D-galactopyranoside) and found K_m and k_cat to be 333±130 =M and 64±8 s⁻¹ respectively, which are in agreement with published data. Our approach is valuable for studying the kinetics of high-speed enzymatic reactions and other chemical reactions.

Introduction

Enzymes have played an important role in many disciplines such as biochemistry,^1,2 medicine,^3,4 food science,^5,6 and biochemical engineering.^7,8 One key issue in enzyme-based assays and studies is the accurate characterization of the enzymatic reaction constants.^9–11 The Michaelis-Menten (M-M) kinetics is one of the most used models to describe the bulk reactions of enzymes,^12,13 and the M-M constant (K_m) and turnover number (k_cat) are two of the most important constants in enzymatic reactions. K_m quantifies the affinity between enzyme and substrate; k_cat quantifies the turnover rate of the reaction. A typical strategy used to calculate K_m and k_cat is the Lineweaver-Burk plot (L-B plot).¹⁴ This method uses a linear regression of the reciprocal of both the initial reaction rate (v₀) and the substrate concentration (C₀) from the M-M kinetics equation to calculate the enzymatic reaction constants.

Microfluidics¹⁵ has emerged as a powerful platform for chemical,^16–18 biological,^19–22 and physical^23–27 processes due to its simple fabrication, ultra-low sample consumption, and ease of use. Using a microfluidic device to measure the enzymatic reaction constants requires two key factors: first, several parallel experiments must be conducted with different substrate concentrations but a constant enzyme concentration; second, enzyme and substrate must be mixed as quickly as possible to quantify the initial reaction and minimize the time that substrate or enzyme is inhomogeneous due to partial mixing. Following these two requirements, several microfluidic-based approaches have been developed to measure enzymatic reaction constants.^28–42 These approaches can potentially examine many enzymatic reactions in parallel while consuming smaller amounts of samples and reagents than conventional methods. In these approaches, however, the kinetics of high-speed enzymatic reactions is often difficult to characterize because the mixing is slow. The mixing time is on the order of ten seconds if the mixing is driven by diffusion.^30,31,35,37 The mixing time is about 1 s when convection, such as Dean flow, is introduced.^29,38 The relatively long mixing time makes these approaches only applicable to enzymatic reactions with long reaction times—in these reactions the reaction time has to be significantly longer than the mixing time. Thus, there is a strong need for developing rapid microfluidic mixers for accurate on-chip characterization of high-speed enzymatic reactions. In this regard, the Ismagilov group and other researchers have successfully measured the enzymatic reaction constants using multiphase flow with induced vortex mixing within a droplet to rapidly mix the enzyme and substrate.^{33,34,39–42} This approach successfully improved mixing efficiency in droplets, however, it introduced an organic solvent that may increase the complexity of experiments and/or change the properties of the reaction kinetics due to the interfacial effects. It would be advantageous to have a system that induces fast mixing without the use of organic solvents.

Acoustofluidic micromixers can effectively enhance mixing efficiency without the use of organic solvents. In our previous work, an acoustic-driven bubble leads to ultrafast mixing in a microfluidic channel.^43,44 When a bubble is introduced in the microfluidic channel and driven by acoustic waves, the oscillating gas-liquid interface will cause vortices in the channel to achieve millisecond level mixing. This method is well suited for use in measuring enzymatic reaction constants.

In this article, we report an on-chip, single-shot characterization system that uses an acoustic bubble-based microfluidic mixer to measure the enzymatic reaction constants. “Single-shot” means the concentration of enzyme and substrate are adjusted by altering the flow rates of the pumps during a single experiment. Our “single-shot” method allows streamlining of the experiments to save time in parallel experiments and ensures that all experimental parameters are consistent. The enzyme and substrate were fully mixed in just a few milliseconds by the oscillating bubble. The fast enzymatic reaction between β-D-galactopyranoside (β-Gal) and its substrate, resorufin β-D-galactopyranoside, was tested using this system. This reaction led to a fluorescent product to facilitate the detection. The intensity of the fluorescent signals indicated the concentration of product generated from the reaction. The reaction time was calculated based on the flow rates and the geometry of the channel. Our bubble-based, high-speed mixer reduced the mixing time into the milliseconds range, significantly increasing the versatility in characterizing enzymatic reaction constants without the use of organic solvents or measures to affect the reaction. In addition, our continuous flow design can record all the information in the initial phase of the enzymatic reaction with high resolution, which has advantages over conventional methods that can only record separated data points.

Experiments

Device fabrication

The polydimethylsiloxane (PDMS) based microfluidic channel was fabricated using the standard soft lithography and mold replica technique.⁴⁵ The channel design is shown in Fig. 1. The channel width, depth, and length are 570 μm, 65 μm, and 1.5 cm, respectively. A horseshoe structure is positioned at the center of the channel to trap a bubble inside (insert in Fig. 1). The width, depth, and length for the horseshoe structure are 60 μm, 65 μm, and 90 μm, respectively. The PDMS channel was treated with oxygen plasma and bonded to a glass slide. The bubble was trapped inside the horseshoe structure by injecting reaction buffer from the outlet of the channel. A piezoelectric transducer (Model No. 273-073, RadioShack Corp.) was bonded adjacent to the PDMS microfluidic device on the same glass substrate using epoxy. The piezoelectric transducer was driven by a function generator (Hewlett Packard 8116A) using a square wave with a frequency equal to the natural resonance frequency (31 kHz) of the trapped bubble.

Figure 1.

Schematic of the experimental setup. The inset shows the horseshoe structure with a bubble trapped inside.

On-chip enzymatic reaction

In our experiments, the enzyme characterized was β-galactosidase (from E. Coli). The reaction buffer contains 100 mM Tris, 2.0 mM KCl, 0.1 mM MgCl₂, 0.1% BSA (w/w), and 0.05% Tween 20 (w/w) at pH 7.8. The enzyme was dissolved in reaction buffer to form the enzyme solution. The substrate, resorufin-β-D-galactopyranoside, was stored in dimethyl sulfoxide at –20°C. The chemicals above were purchased from Sigma-Aldrich. Immediately before use, the thawed stock solution was diluted with the reaction buffer to form substrate solution. The enzyme solution, reaction buffer, and substrate solution were injected into the reaction channel with syringe pumps (KD Scientific Corp.). The reaction buffer was injected in the middle inlet to separate the enzyme and substrate and to prevent reaction before mixing (Fig. 1). The standard material of reaction product, sodium resorufin, was used to correlate the fluorescent intensity with the concentration of the product. All experiments were carried out at room temperature.

Optical detection setup

While the enzyme and substrate do not emit fluorescence, the enzymatic reaction is a fluorescence-generating reaction. The reaction product, resorufin, has a maximum emitting fluorescent intensity at 585 nm, while the maximum exciting wavelength is 570 nm. A fluorescent intensity detection system was constructed to monitor the change in product concentration. A transmission microscope (Elipse Ti, Nikon Corp.), combined with two bandpass filters (530–570 nm and 580–650 nm, respectively) and one dichroic mirror (transmission above 575 nm), was used to observe the fluorescent light. A CCD camera (CoolSNAP HQ2, Photometrics) was connected to the microscope for capturing images. The parameters used in the optical setup were held fixed over all the experiments.

Results and Discussion

Fast mixing

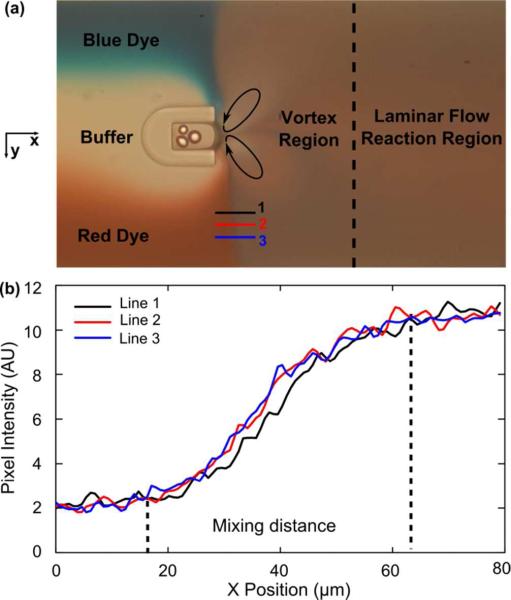
The gas-liquid interface oscillates when the bubble is stimulated by the acoustic waves from the piezoelectric transducer. This oscillation has a maximum amplitude at the fundamental resonance frequency of the bubble, which depends on the size of the bubble and the properties of the liquid. For a water-based reaction environment, a bubble, with dimensions of 60 μm (width) × 90 μm (length) × 65 μm (height), has a resonance frequency at ~31 kHz. Under these conditions, the bubble will get stable oscillation and can maintain its shape for more than 10 min. The bubble's oscillatory frequency was the same as that of the stimulating signal, and its oscillation amplitude was approximately 5 μm. The oscillating bubble changed the flow field near its surface and caused fast mixing in the fluid. To visualize and characterize the rapid mixing in our bubble-based mixer, blue, clear, and red fluids are shown to represent the substrate, buffer, and enzyme respectively we used in the experiment (Fig. 2a). The flow rates of the three fluids were set as 0.4, 0.3, 0.4 μl/min, which were the same as in our enzymatic reaction experiments. When the piezoelectric transducer activates, three distinct regions of streamlines exist in the channel by using fluorescent polystyrene particles with a diameter of 1 μm (Fig. S1, Supporting Information). The first region, in which the streamlines are parallel indicating laminar flow, occurs before the fluid reaches the bubble. The second region is the vortex region in which rapid mixing takes place. The vortex flow pattern is similar to the streaming pattern near a bubble, driven by bulk acoustic waves.^46–48 Significantly downstream of the bubble exists the third region where the effect of the bubble oscillation is negligible and the streamlines are again parallel. All concentration measurements were made in the third region.

Figure 2.

(a) Mixing caused by an oscillating bubble surface. Water and dyes were used to demonstrate mixing effect of enzyme and substrate. (b) line analysis to calculate mixing time.

In order for the substrate and enzyme to be fully mixed before significant amount of product is generated, the mixing time must be significantly shorter than the reaction time. The average mixing time (t_avg) could be estimated by:

$$t_{avg}=\frac{d_{mix}}{v_{avg}},$$ (1)

where d_mix was the average mixing distance and v_avg was the average velocity of flow in the channel. The average mixing distance d_mix was characterized using a grey value plot (Fig. 2a lines 1-3) in the region from unmixed to mixed. The distance in the x direction of the sloped part of the grey value curve (Fig. 2b) was the mixing distance. Data from three separate locations (lines 1–3) were plotted to get the average mixing distance (around 45 μm). The average velocity of flow in the channel (v_avg) could be calculated by flow rate and channel dimension. Under the experimental conditions (total flow rate: 1.1 μl/min), t_avg was about 89 ms. Such a mixing time is significantly shorter than the enzymatic reaction time (several seconds). Therefore, we could assume that the reagents were fully mixed before the reaction started. Moreover, our acoustic bubble based mixer could still achieve excellent mixing when the total flow rate increased—at a flow rate of 10 μl/min, the mixing time was even shorter (~10 ms).

Calibration curve

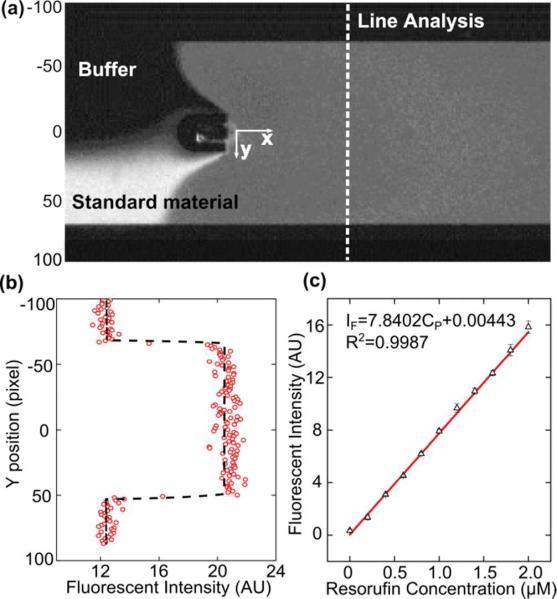
A standard curve of product samples with different concentrations was generated to obtain the relationship between the concentration and fluorescent intensity of product. Standard product material with a concentration of 2 μM was mixed with buffer in different ratios to form a series of concentrations. After mixing by the oscillating bubble, the concentrations were 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, and 2.0 μM. After mixing, the fluorescent intensity was detected by a CCD camera. All experimental conditions for fluorescence detection were the same as in our enzymatic reaction experiments. Figure 3a shows a single image recorded during the calibration experiment. In this picture, the flow rate ratio between standard material and buffer was 1:1. The fluorescent intensity along the channel-width direction (y direction) is plotted in Fig. 3b. The difference between the fluorescence of the liquid and the dark background was used as effective fluorescent intensity. The entire calibration experiment was repeated three times to produce the calibration curve shown in Fig. 3c. The points represent the mean for each test and the error bar represents the standard deviation. A least squares fit of the data was performed to generate the relation equation:

$$I_F=7.8402C_p+0.00443.$$ (2)

Here, I_F is fluorescent intensity (arbitrary unit) and C_P is the concentration of product (μM). This equation was used to correlate product concentration with fluorescent intensity in the following sections.

Figure 3.

(a) Optical image recorded during the calibration experiment. (b) Fluorescent intensity at the detection line. The difference between liquid in the channel and background was used as effective fluorescent intensity. (c) The standard curve of product fluorescent intensity.

Enzymatic reaction rate

In our device, fast mixing allows us to measure v₀ in a short time (sub-second range). For this enzymatic reaction, the enzyme concentration was 5 mg/l, which is sufficient to cause a detectable fluorescent change in the 1-second range. Accordingly, we chose a substrate concentration series ranging from 91 to 545 μM with an interval of 91 μM. The concentration series was generated by using different flow rate ratios between substrate stock solution (1 mM) and reaction buffer (Fig. S7, Supporting Information).

Total flow rate is an important factor, which decides the reaction time in the channel. When the flow rate is larger, the residence time is shorter, which means that the enzyme has a shorter time to generate product. As a result, the product concentration is smaller. Based on the preliminary research, the total flow rate was always held at 1.1 μl/min (enzyme: 0.5 μl/min; substrate: 0.6–0.0 μl/min; buffer: 0.0–0.6 μl/min). The average residence time in the channel was about 4 s, which is long enough to produce an obvious change in fluorescent intensity along the length of the channel. The velocity profile in the channel was another key factor. Because the channel width (570 μm) was much larger than the channel depth (65 μm), the velocity across the width of channel was almost uniform except at the edges, and the velocity across the depth of channel was parabolic causing concentration changes near the edges.^49,50 As a simplification, we neglected the parabolic velocity profile in the depth direction and used the average velocity to calculate the reaction time. We established a mathematic model (details in the Supporting Information) to theoretically predict the difference in the product generated between plug flow and laminar flow to be less than 5%. The Peclet number is still much larger than one at the flow rates we used, so the axial dispersion effect can also be safely neglected.

The images taken by the CCD camera were imported to a Matlab program for data analysis. Figure 4a shows a single experimental image demonstrating how the fluorescent intensity was analyzed in the experiment. Analysis of the grey scale value across the channel width was used to detect fluorescent intensity. The grey scale plots of two representative results at different X positions (blue and red line in Fig. 4a) are shown in Fig. 4b. These plots are the average values over 10 pixels in the X-direction. It can be seen that the upstream data (blue circles) have less fluorescence when compared to the downstream data (red squares). As the reagents move down the channel more product is generated. At the edge of the channel the velocity is lower because of the laminar flow profile in the channel, so the intensity, and likewise concentration of product, increases more rapidly. Therefore, we only used the data at the center of the channel (between Y= –200 and 200 μm) to calculate the fluorescence value at each X position. The mean and standard deviation of this fluorescent intensity in Fig. 4b were correlated to product concentration by the calibration curve (Fig. 3c) and displayed as one data point in Fig. 4c. Also the X distance was correlated with reaction time by channel dimension and flow rate. The reaction time was calculated by dividing the X distance by plug flow velocity (496 μm/s). The fluorescence at each X position starting at the surface of the bubble (x=0 μm, t=0 s) to the very end of the straight channel (x=1784 μm, t=3.6 s) was analyzed with a resolution of 1 pixel (Vx = 4.96 μm; Δt = 0.01 s) and plotted as a function of product concentration versus reaction time in Fig. 4c. This was repeated for each substrate concentration (C₀) between 91 and 545 μM (Fig S4, Supporting Information). At the beginning of each set of data the trend was flat because the reaction had yet to start. The baseline fluorescence is not exactly the same for each initial concentration because the substrate sample contains some fluorescent product due to degradation.

Figure 4.

(a) Enzymatic reaction carried out in the channel. The fluorescent intensity was detected in the channel with equal distance intervals. (b) The fluorescent intensity at the starting point of reaction (circle) and the point after a certain reaction time (square). The fluorescent intensity at the middle of the curves was used as effective fluorescent intensity in Fig. 4c. (c) Initial reaction rate (v₀) curve with substrate concentration ranging from 91 μM to 545 μM. The concentration of enzyme was set as 5 mg/l.

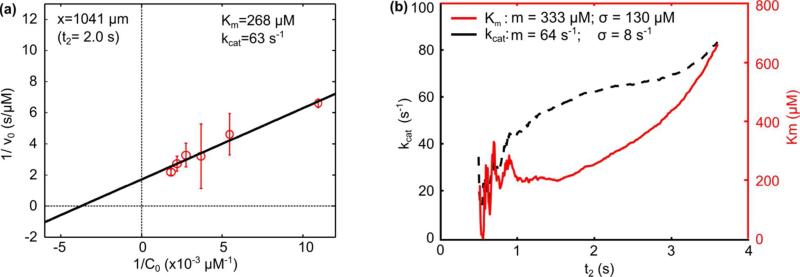
Once the reaction starts, the fluorescence increases linearly in accordance with M-M kinetics. The linear increase part began at point x=198 μm (t=0.4 s), and this point was shown in Fig. 4a by the blue line. From this point, a least squares, linear fit can be used to find the reaction rate (v₀) because this initial part of enzyme reaction has a linear trend and the slope of the linear fit is v₀. Using the calculated value of v₀, the reaction constants K_m and k_cat can be calculated via the L-B plot analysis described in the next section. Since our system records information during the initial reaction at high resolution, we could conveniently choose different initial reaction times to analyze. The reaction time is defined from the start of the linear region (t = 0.4 s, blue line in Fig. 4a) to some later time, which we denote as t₂. As an example, we analyze the system using t₂ = 2.0 s (red line in Fig. 4a). This is the value of t₂ used to generate the linear fits shown in Fig. 4c. The calculated v₀ values are plotted in Fig. 5a and used to determine K_m and k_cat as described in the next section. This process is repeated for values of t₂ from 0.5 s to 3.6 s with a resolution of 0.01 s.

Figure 5.

(a) Lineweaver–Burk plot to characterize K_m and k_cat on single initial reaction time. (b) K_m and k_cat analysis under different reaction time.

Lineweaver-Burk plot

The L-B plot derived from the M-M mechanism is described by:⁷

$$\frac{1}{v_0}=\frac{K_m}{V_{\max }}\frac{1}{C_0}+\frac{1}{V_{\max }},$$ (3)

where 1/v₀ has a linear relationship with 1/C₀, the slope is K_m/V_max, the y-intercept is 1/V_max (where V_max is the maximum reaction rate), and the x-intercept is –1/K_m. From the relationship in Eqn. 3, K_m and k_cat can be calculated. Continuing the example where t₂ = 2 s (between blue and red line in Fig. 4a), Fig. 5a was generated from the values of v₀ determined from the linear fits shown in Fig. 4c. The enzymatic reaction was repeated three times and the mean and standard deviation of v₀ were calculated. The reciprocal of v₀ was plotted against the reciprocal of C₀ in Fig. 5a where the points represent the mean and the error bars represent the standard deviation of v₀. A least squares linear fit of the mean values was calculated and the slope of the fitting line was K_m/V_max, and the y-intercept was 1/ V_max. K_m for this example at t₂ = 2 s was 268 μM and the value of k_cat can be calculated by¹³

$$V_{\max }=k_{cat}\left[E\right],$$ (4)

where [E] is the concentration of the enzyme. Thus for t₂ = 2 s, the value of k_cat was 63 s⁻¹.

To fully characterize the reaction constants for different initial reaction times, we repeated this entire analysis process for different values of t₂ between 0.5 and 3.6 s with a resolution of 0.01 s. The results were shown in Fig. 5b. Theoretically, K_m and k_cat should keep constant. However, due to the slight decrease in v₀ as t₂ increases and the amplified error due to the two reciprocals in the linear regression (Fig. 5a), K_m and k_cat are not constant with respect to t₂. To produce an average K_m and k_cat to compare with other published data, we calculated the mean and standard deviation of K_m and k_cat over a range of t₂. We ignored the data over the range t₂ = 0.5–1 s, because in this period the number of data points was low, causing erratic linear fits to produce v₀, thus K_m and k_cat fluctuate during this period. From t₂=1 s to 3.6 s, K_m had a mean of 333 μM and a standard deviation of 130 μM, and k_cat had a mean of 64 s⁻¹ and a standard deviation of 8 s⁻¹. This data should be an accurate, comprehensive description of our device because it considers the error from both parallel experiments (as represented by error bars in Fig. 5a) and different reaction times (as represented by the presented standard deviations of K_m and k_cat).

We listed our results and the data from previously reported work in Table 1. To compare the difference between our results and published data, a two-tailed t-test was conducted. We assumed the null hypothesis that there was no significant difference between these three independent studies. When it was unknown, the number of tests performed was assumed to be three for the t-test. The P-values calculated for each comparison are given in Table 2. Using a significance level of 0.1, the t-test indicates that we cannot reject the null hypothesis in comparing K_m between group 1 and 3, 2 and 3, and k_cat between group 2 and 3, which states that these results have no significant difference. On the other hand, there is difference between group 2 and 3 in comparing k_cat.

Table 1.

Comparing results of K_m and k_cat.

No.	Km (μM)	kcat (/s)	Author
1	550±200	70±30	Hadd35
2	335±65	39±5	Jambovane51
3	333.4±129.7	63.74±7.915	This work

Table 2.

P-value from t-test for K_m and k_cat.

Compare Group No.	P for Km	P for kcat
1 and 3	0.214	0.792
2 and 3	0.930	0.058

Overall, our results compared reasonably well with the reported data from Hadd³⁵et al. and Jambovane⁵¹et al. There are several reasons for the discrepancies between our results and published data. First, although the enzyme and substrate were the same in each work, the enzyme activity might vary in different batches and the properties of reaction buffer might not be consistent. The enzyme activity is dependent on its environment and these small differences could change enzyme activity. Second, the flow model we used was an ideal plug flow, meaning each portion of the fluid has the same residence time; however, the flow condition in the experiments was more complicated, including a parabolic velocity profile and slight flow instabilities from the syringe pumps and channel inlets. Third, the lack of fast mixing in the previous works affected the final results. Fourth, factors in the data analysis method and sample processing such as line analysis interval affect the results. In our case, the values of K_m and k_cat were dependent on the reaction time. We have shown this trend in Fig. 5b. Jambovane also mentioned that using alternate methods for data analysis could cause variation of as much as 13% for K_m and 24% for k_cat.⁵¹

Conclusions

In summary, we performed a single-shot enzymatic reaction using a bubble-based micromixer. This device could simply and quickly characterize enzymatic reaction constants. Each data set was collected in 1 s. Fast mixing of enzyme and substrate in under 100 ms was achieved by an acoustically driven bubble anchored in a horseshoe structure. Our design overcame the low mixing speed and efficiency of earlier microfluidic designs. The “single-shot” detection system does not require preparation of additional samples for each parallel experiment, as adjusting flow rates conveniently alters the concentration ratio. The continuous flow reaction allowed all product concentration information in initial enzymatic reaction to be recorded with high resolution. The β-galactosidase-catalyzed hydrolysis of resorufin β-D-galactopyranoside was tested as a model system and K_m and k_cat in this reaction were measured to be 333 μM, with a standard deviation of 130 μM, and 64 s⁻¹ with a standard deviation of 8 s⁻¹, respectively. These values are in fair agreement with published results. Our approach reduced mixing time into the milliseconds range, significantly increasing the efficiency in characterizing enzymatic reaction constants. It represents the ability to study kinetics of high-speed enzymatic reactions with small amounts of enzymes, substrates, or inhibitors.