Abstract
We present a new MRI-based attenuation correction (AC) approach for integrated PET/MRI systems that combines both segmentation- and atlas-based methods by incorporating dual-echo ultra-short echo-time (DUTE) and T1-weighted (T1w) MRI data and a probabilistic atlas. Segmented atlases were constructed from CT training data using a leave-one-out framework and combined with T1w, DUTE, and CT data to train a classifier that computes the probability of air/soft tissue/bone at each voxel. This classifier was applied to segment the MRI of the subject of interest and attenuation maps (μ-maps) were generated by assigning specific linear attenuation coefficients (LACs) to each tissue class. The μ-maps generated with this “Atlas-T1w-DUTE” approach were compared to those obtained from DUTE data using a previously proposed method. For validation of the segmentation results, segmented CT μ-maps were considered to the “silver standard”; the segmentation accuracy was assessed qualitatively and quantitatively through calculation of the Dice similarity coefficient (DSC). Relative change (RC) maps between the CT and MRI-based attenuation corrected PET volumes were also calculated for a global voxel-wise assessment of the reconstruction results. The μ-maps obtained using the Atlas-T1w-DUTE classifier agreed well with those derived from CT; the mean DSCs for the Atlas-T1w-DUTE-based μ-maps across all subjects were higher than those for DUTE-based μ-maps; the atlas-based μ-maps also showed a lower percentage of misclassified voxels across all subjects. RC maps from the atlas-based technique also demonstrated improvement in the PET data compared to the DUTE method, both globally as well as regionally.
Keywords: PET, MRI, attenuation correction, segmentation, atlas
Introduction
Integrated PET/MR is an area of rapidly growing interest in the medical imaging community. Combined systems capable of simultaneous data acquisition, in particular, offer a number of advantages over imaging subjects on separate scanners: quantitative PET data and high resolution structural and functional MRI are automatically co-registered, PET data can be motion corrected using spatial information derived from MR [1], and temporal correlation between the MR and PET signals may provide greater insight into biological function in health and disease [2,3]. Several simultaneous PET/MR systems have been developed and tested for human imaging [4,5]. These scanners, however, lack an integrated transmission source or CT system due to spatial constraints, and therefore a critical challenge in employing them for quantitative PET imaging is developing an accurate attenuation correction (AC) method that relies solely on the MR data.
MR-based AC is challenging because unlIke the Hounsfield Units (HU) of CT data, the intensity values of MRI are a function of proton density and tissue relaxation times, which are not directly related to the linear attenuation coefficients (LACs) that characterize 511 keV photon attenuation in PET. Voxel-wise maps of LACs (μ-maps), however, have been obtained by assigning the appropriate LAC to each tissue class (air, soft tissue, or bone) segmented from MRI data. MRI segmentation is an advanced field, but nearly all algorithms are designed to segment structures or tissue types within the brain (i.e. white matter, gray matter, etc.) [6-8]. Segmentation of MRI into air, soft tissue, and bone is difficult since there is aLmost no signal from bone or from air when using conventional MR sequences and they both appear dark on the MR images. Distinguishing the two is crucial, however, since they have the largest difference in LACs. Furthermore, the state-of-the-art integrated MR-PET systems have long axial fields of view (e.g. 19.25 and 25.8 cm in the case of the Siemens BrainPET prototype and Biograph mMR scanners, respectively), acquire emission data in 3D mode which means that numerous lines of response (LORs) pass through internal air spaces such as the frontal, nasal, maxillary and mastoid sinuses [9].
Earlier AC methods did not attempt to segment the internal air cavities [10-12]. Instead, they manually fitted an ellipse to the head, estimated the contour of the head or generated a rough approximation of the skull through filtered back-projection of the reciprocal sinogram. Zaidi et al. [13] proposed a method to obtain μ-maps from MRI by segmenting the skull and nasal air spaces using a fuzzy clustering technique. This method, however, required manual intervention for accurate delineation of the skull and resulted in statistically significant overestimation of regional cerebral glucose metabolism in multiple regions of interest (ROIs). Atlas-based methods for AC have also been investigated, but current techniques rely heavily [14] or entirely [15] on local anatomical information represented by the atlas and therefore may not generalize well to all subjects, especially patients who have undergone neurosurgical procedures or have substantial pathology. These techniques are also highly sensitive to registration errors between the atlas and the subject of interest.
Methods for obtaining MR-based μ-maps exclusively from DUTE sequences have previously been proposed [9,16]. In those approaches, optimal MR acquisition parameters and algebraic combination of the DUTE volumes obtained at the two echo times allowed air and bone voxels to be readily distinguished. Subsequently, a Dixon sequence was proposed in addition to the DUTE data to also allow the segmentation of fat tissue [17]. While these techniques produced good overall agreement with segmented CT data, there were still misclassified voxels in some regions of the brain (e.g. ventricles), the skull thickness was underestimated and substantial errors still remained in the sinus region, which may bias PET results in adjacent structures. In Poynton et al. [18] an atlas-based approach for bone segmentation of T1-weighted (T1w) structural MPRAGE MRI was presented, which showed promising agreement with CT, but did not apply the method to PET AC and used a two class, binomial model for constructing the atlas.
To address the limitations of the segmentation-based approaches, a method to derive substitute CTs from the MR data acquired using two DUTE sequences with different flip angles and a T2-weighted SPACE sequence was suggested [19]. Using a Gaussian mixture regression model, the intensities in the MR images were linked to the HUs in the corresponding CT images on a voxel-by-voxel basis. In particular, this method relies on similar image values of head and brain tissues for different subjects in both CT and MRI. While CT quantification is very accurate and reproducible due to the nature of the Hounsfield units’ definition and the full calibration of the CT scanners, accurate and reproducible image quantification remains still one of the main challenges in MRI. While promising results have been reported using this method [20], further validation is still required.
In this work, a novel combination of segmentation and atlas-based classifier is derived to compute MR-based μ-maps. A probabilistic air/soft tissue/bone atlas is constructed from CT training data and the corresponding DUTE and MPRAGE are used to train a classifier that calculates the probability of each class at each voxel in the subject of interest. This approach incorporates local anatomical information through the atlas prior and the lkelihood model captures global, joint MR intensity properties of each class from corresponding T1w MPRAGE and DUTE MRI. Results from the classifier show local and global improvement over using only DUTE for segmentation. The quantitative analysis of the PET data attenuation corrected using the different methods suggests the Atlas-T1w-DUTE approach could provide results that are comparable to those obtained with the segmented CT approach, which was previously proposed as the “silver standard” for segmentation-based AC methods, producing results that are within 5% of those obtained using the scaled CT method.
Methods
Data acquisition
MR and CT data from 13 glioblastoma patients were used in this work. The study was approved by the local Institutional Review Board. The PET data were acquired on a prototype MR-compatible brain PET scanner (“BrainPET”) designed to fit inside the MAGNETOM Trio, a total-imaging-matrix (TIM) 3T human MRI scanner (Siemens Healthcare Inc.). BrainPET uses magnetic field-insensitive avalanche photodiodes as scintillation photon detectors. The inner and outer physical diameters of the gantry are 35 cm and 60 cm, respectively. The PET data processing and image reconstruction workflow were previously described [9]. Briefly, the emission data were acquired in list-mode format, sorted in the line-of-response (LOR) space, and compressed axially in the sinogram space for fast reconstruction [21]. This axial compression (span=9, maximum ring difference=67) generated 1,399 sinograms, each consisting of 256 radial elements and 192 angular projections. The images were reconstructed with the ordinary Poisson ordered-subsets expectation maximization algorithm from prompts, variance-reduced random coincidences [23], detector sensitivity (obtained from a plane source), scatter [22], and attenuation, the latter two accounting for the head and radiofrequency coil. The reconstructed volume consisted of 153 slices with 256×256 pixels (1.25×1.25×1.25 mm3).
A PET-compatible circularly polarized transmit combined with an 8-channel receive radiofrequency coil specifically designed for this scanner was used to acquire the MR data. MPRAGE and DUTE data were obtained during the PET data acquisition. The 3D multi echo MPRAGE data were acquired after administration of MR contrast agent (Magnevist) with the following parameters TE=1.64 ms, TR=1200 ms, matrix =256×256, pixel size=1×1 mm2, 256 slices, thickness=1 mm. The DUTE sequence used in this study had the following parameters: TE1/TE2=0.07/2.46 ms; TR=200 ms; flip angle=10°; radial projections=32,000; bandwidth=1,532 Hz/pixel; FOV=320 mm; base resolution=192; and acquisition time=3:20 min:sec.
CT data for each patient were obtained according to the clinical protocol: 140 kVp, 150 mAs, 512×512 in-plane voxels, with voxel sizes ranging from 0.492×0.492 mm2 to 0.668×0.668 mm2; the CT spanned 87 to 104 slices, each 2.5 mm thick. The CT and MR-PET studies were performed less than one month apart, and no surgical procedures that would alter the morphology of the skull or brain were performed between the scans. This is important since voxels must belong to the same tissue class (air, soft tissue, or bone) in the CT and MR data of each subject to ensure accurate training of the classifiers. Surgical intervention after the CT and before the MR, for example, could result in voxels showing intact skull in the CT, but fluid in the MR.
Probabilistic atlas construction
Probabilistic atlases were computed from the CT data for use in the Atlas-T1w-DUTE-based segmentation technique described later in this article. First, the structural MRI was intensity normalized using FreeSurfer [23], and the normalized data were used for all subsequent registration and analysis. The CT volume was co-registered to the corresponding structural MRI volume for each subject, using 6 degrees of freedom (DOF) and mutual information as the cost function. The structural data were then registered to a standard space using the MNI152T1 atlas as the reference [24], 12 DOF and normalized correlation ratio as the cost function. Although non-linear registration techniques often provide better results for inter-subject registration, they can introduce substantial mis-registration in subjects with pathology (i.e. brain tumors). To reduce this risk, 12 DOF affine registration was used for this step. The resulting transformations were applied to the corresponding CT. All registrations in this step were performed using FLIRT, which is part of FSL [25,26]. The transformed CT datasets were then segmented into bone (300-2,000 HUs [27], softtissue (-500 to 300 HUs), and air cavities (<-500 HUs) to produce three binary label maps for each subject.
Probabilistic atlases are often constructed by counting the number of occurrences of each tissue class at each voxel and normalizing the result to obtain a probability distribution. In the three-class situation, this corresponds to maximum lIkelihood (ML) estimation of the parameters of a multinomial distribution, i.e., if k~Multinomial (n, p), then, the ML estimate of p given observed k is ˆp=k/n. Here, n is the number of trials (i.e. the number of CT observations at a given voxel), k is the number of occurrences of each tissue label (soft tissue, air, or bone) at the given voxel, and p is the probability of each tissue class that needs to be estimated from the observed data. The ML estimates were obtained from the binary label maps to produce an atlas containing the probability of air, soft tissue, and bone at each voxel. Thirteen separate atlases were constructed using a leave-one-out framework in which one subject is withheld as the “test” subject and a corresponding atlas is constructed from the remaining twelve “training” data sets. A fourteenth atlas was also constructed from all thirteen data sets to be used for generating the μ-maps for future subjects.
Attenuation map generation
For each subject, the DUTE volumes (i.e. the two volumes acquired at each echo time) were first divided by the corresponding smoothed volumes obtained after applying a 3D Gaussian low pass filter with a 20 mm radius kernel. This removed image inhomogeneities due to nonuniform coil sensitivity [9]. The intensity-normalized DUTE volumes were registered using SPM8 to the MPRAGE volumes using 12 DOF [28] and normalized mutual information as the cost function, to account for any motion between the structural and DUTE acquisitions. Rather than use simply the smoothed DUTE volume from the first echo (DUTE1) and the second echo (DUTE2), we applied two additional transformations to improve contrast between the three tissue classes (air, soft tissue, and bone) as described previously [9]. The first transformed DUTE image, DUTEtr1, was computed according to (DUTE1-DUTE2)/DUTE2 2 to enhance signal from bone voxels. The numerator allows identification of voxels with a large signal change (i.e. bone), while the denominator identifies voxels with the lowest signal in the DUTE2 data (i.e. bone and air). Similarly, the second transformed DUTE image, DUTEtr2, was computed to enhance identification of air voxels according to (DUTE1+DUTE2)/DUTE1 2. Furthermore, a mask of the head including voxels from all classes was obtained by applying a morphologic closing operation to the MPRAGE data. This step was required for excluding the voxels outside the subject’s head. The transformed DUTE images were then normalized to the maximum value within the subject’s head and thresholded with empirical values of 0.02 and 0.5 respectively for 3D intensity histogram construction addressed in the following paragraph. Each atlas was then registered to the corresponding subject by inverting the previously calculated transformations between subject space and standard space.
For each subject and each tissue class (air, soft tissue, and bone), all voxels belonging to that tissue class are identified in the corresponding CT training data and a 3D intensity histogram is constructed from the corresponding structural MRI, DUTEtr1, and DUTEtr2 training data. Each location, (Ii, Ij, Ik), in the histogram denotes the number of voxels in the class of interest (identified from CT training data) with the set of bin labels {Ii, Ij, Ik}, where Ii is the ith intensity bin in the structural MRI, Ij is the jth intensity bin in DUTEtr1, and Ik is the kth intensity bin in DUTEtr2. Normalizing each 3D intensity histogram by the total number of voxels in the histogram gives the lIkelihood terms for each tissue class, P(Ii, Ij, Ik|Lm), where Lm is the tissue class label obtained from the CT training data with m ∈ {air, soft tissue, bone}.
Thus, the lIkelihood provides the probability of observing a voxel with a set of MR intensities that fall within bins Ii, Ij, and Ik given it belongs to a certain tissue class (e.g. bone).
The prior probabilities of each tissue class, P(Lm|Xn), were obtained from the co-registered atlas, where Xn, denotes the voxel location. The posterior probability of each class at each voxel was computed according to (Equation 1):
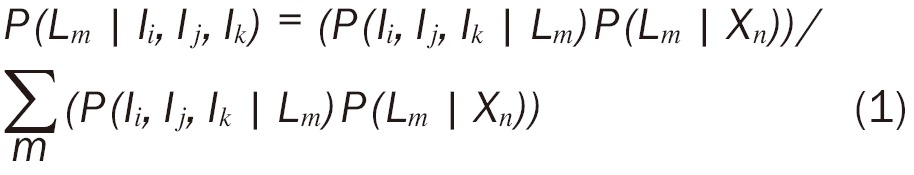 |
The trained classifier was then applied to segment the MRI of the subject of interest, providing a posterior probability of each tissue class at each voxel.
Thresholding was performed on the posterior probability maps to limit the effects where air or bone probabilities would dominate over soft tissue; first, voxels were assigned as bone where the bone posterior probabilities were greater than the other two classes; subsequently an empirical threshold of 0.8 was applied as a lower bound for assignment of air. The final subject-specific μ-map was generated from the assigned labels by assigning LACs of 0, 0.096 and 0.151 cm-1 to air, soft tissue, and bone, respectively. Voxels outside the head mask were assigned LACs of 0.
Additionally, DUTE-based μ-maps were computed for comparison to the proposed method. Similar to [9], bone LAC (0.151 cm-1) was assigned to all voxels in DUTEtr1 volume above an empirically determined threshold (0.012) and the LAC for air (0 cm-1) was assigned to all voxels in DUTEtr2 above a second empirically determined threshold (0.14).
For comparison, segmented CT-based μ-maps were obtained from each subject’s CT data by assigning the appropriate LACs to each voxel using the binary label maps computed above.
Quantitative evaluation of the Atlas-T1w-DUTE method
Segmentation accuracy
The accuracy of each MR-based segmentation approach (Atlas-T1w-DUTE and DUTE) was evaluated by both visual comparison to the segmented CT μ-map and calculation of the Dice Similarity Coefficient (DSC) [29] for each tissue class (air, soft tissue, and bone). The DSC is defined as the number of intersecting voxels divided by the average number of all considered voxels, and provides a quantitative measure of the agreement between two volume sets. A DSC of 1 indicates that the two volumes are exactly the same, while a DSC of 0 indicates that the volumes have no overlapping voxels. The head mask previously computed from each subject’s MPRAGE data was selected to provide a common region of comparison for the segmentation results. This mask was then applied to binary segmentations of each tissue class that were obtained from each μ-map by thresholding. The DSC was computed from the masked volumes to quantify agreement between the estimated and segmented CT μ-maps.
Effect on PET data quantification
PET images reconstructed using the MR-based AC methods were compared to those obtained using the segmented CT-based method. In each case, the complete μ-map was obtained by adding the μ-map of the head to that of the radiofrequency coil. The complete μ-maps were first smoothed using a 4 mm FWHM Gaussian filter and then forward projected and exponentiated to generate the AC factors (ACFs). The PET data were reconstructed as described above using the ACFs obtained from these μ-maps and the results were assessed qualitatively and quantitatively. The relative changes (RC) were computed according to: RC=100×(CMR-Csegmented_CT)/Csegmented_CT, where Csegmented_CT are the values from the PET reconstruction using segmented CT for AC and CMR are the values from the PET images obtained using the Atlas-T1w-DUTE or DUTE methods. The overall accuracy of the PET images was quantified by calculation and analysis of absolute RC values of all brain voxels for each patient; the mean and standard deviation for each subject were computed.
The gaps between the PET modules in the transaxial and axial directions in the case of the BrainPET scanner, make it more susceptible to data inconsistencies that can lead to artifacts and mask or amplify the bias introduced by inaccurate AC. To demonstrate that the measured changes are indeed related to differences in the μ-maps, simulations were also carried out assuming a gapless scanner with the same geometry as the BrainPET and ignoring other factors such as detector normalization, scatter correction, etc., as previously described [9]. Briefly, “true” emission sinograms were obtained by forward projecting volumes in which uniform activity is assigned to each subject’s brain. Sinograms derived from the segmented CT μ-maps were used to attenuate the “true” emission sinograms, and then images were reconstructed using the ACF obtained from the Atlas-T1w-DUTE- and DUTE μ-maps. The RC values were calculated in a similar fashion to those derived from the measured PET data.
The local performance of the MR-based AC methods was also examined. 12 brain regions of interest were defined using an automated anatomical labeling (AAL)-based atlas [30] and warped using DARTEL in SPM8 to each individual patient.
Results
Probabilistic atlas construction
Results of the atlas construction for a representative subject are shown in Figure 1. Axial and sagittal views of the probability maps of soft tissue and bone after co-registration of the atlas to subject space are shown in Figure 1A and 1B, respectively. The probabilistic atlas successfully describes anatomical variability among subjects in the training data set. Large variability (low probabilities) can be seen in the sinuses and other internal air spaces.
Figure 1.
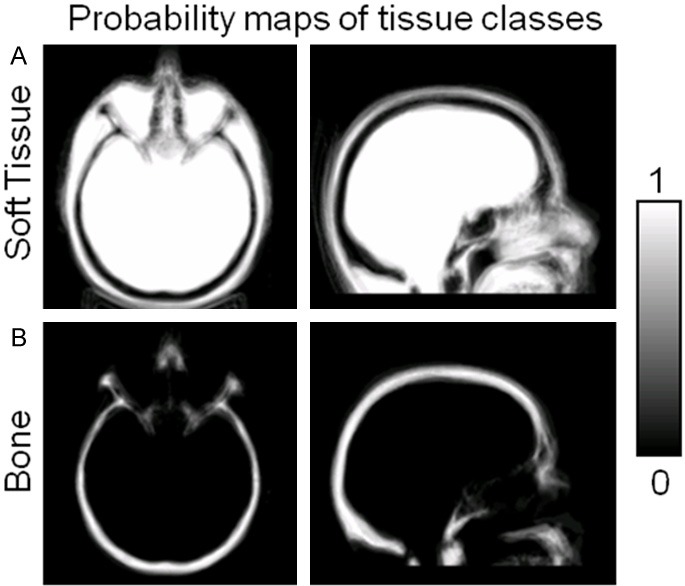
Representative atlas constructed from CT training data. The atlas provides probability maps of soft tissue (A), bone (B), and air (not shown), with each voxel taking continuous values between 0 and 1.
Segmentation accuracy
The segmentation results for each method were evaluated qualitatively by comparing μ-maps from the MR-based methods to those obtained from segmented CT images. μ-maps for a representative subject are shown in Figure 2 in the transverse and sagittal orientations. The DUTE method (Figure 2B) shows overall agreement with segmented CT (Figure 2A), especially in the more superior slices, but substantial errors in the sinus region and more inferior regions of the skull can be seen. The DUTE method fails to fully segment the internal air cavities, overestimating bone and soft tissue, while underestimating air (Figure 2B, bottom row). The Atlas-T1w-DUTE method (Figure 2C) shows good overall agreement with segmented CT and an improvement over the DUTE method, especially in the sinus region; internal air spaces are now clearly visible, giving better overall agreement with the μ-map from segmented CT.
Figure 2.
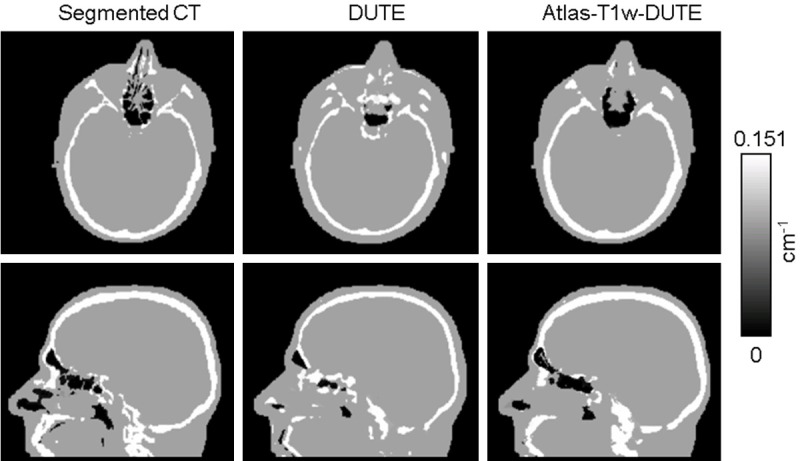
Representative μ-maps computed with each method for an axial and a sagittal slice. The DUTE method (B) shows overall agreement with the segmented CT (A), but substantial errors are still present. The Atlas-T1w-DUTE method (C) shows the best overall agreement with the CT-based μ-map and internal air spaces are now clearly visible.
DSC values quantifying agreement between the Atlas-T1w-DUTE result and CT-based μ-map in Figure 2 were 0.85, 0.97, and 0.72, for bone, soft tissue, and air, respectively. For all subjects, the Atlas-T1w-DUTE method shows improvement over DUTE for each tissue class. The mean DSCs for DUTE across all subjects were 0.58, 0.92, and 0.55 for bone, soft tissue and air, respectively, while the corresponding DSCs for Atlas-T1w-DUTE were 0.81, 0.96, and 0.69. DSC results for all subjects are shown in Figure 3. The box plots show the first, second and third quartiles and the minimum and maximum DSC values across all patients for each segmentation method and each tissue class (air, soft tissue, bone). The atlas-based method shows improvement over DUTE for each tissue class. The median (second quartile) DSCs for DUTE across all subjects were 0.58, 0.92, and 0.55 for bone, soft tissue and air, respectively, while the corresponding DSCs for Atlas-T1w-DUTE were 0.82, 0.96, and 0.72.
Figure 3.
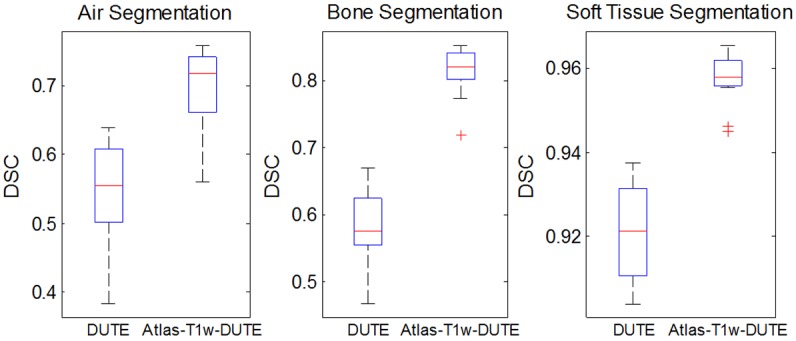
Dice similarity coefficients (DSC) for all subjects, tissue classes and methods. The atlas-based method shows improvement in DSC values for all tissue classes: bone, soft tissue, and air. Median DSC values for Atlas-T1w-DUTE show substantial improvement over DUTE.
The segmentation results were further evaluated by computing the percentage of misclassified voxels as shown in Figure 4, where “water” refers to soft tissue. This plot shows that the Atlas-T1w-DUTE method resulted in the lowest total percentage of misclassified voxels in all subjects, which agrees with our previous qualitative assessment of the segmentation results. Misclassification of bone as air and air as bone have the greatest impact on the accuracy of subsequent PET reconstructions since the difference between the LACs of these two tissue classes is the largest (LACbone-LACair=0.151 cm-1). The sum of these two errors is reduced in the Atlas-T1w-DUTE method relative to the DUTE method in all subjects.
Figure 4.
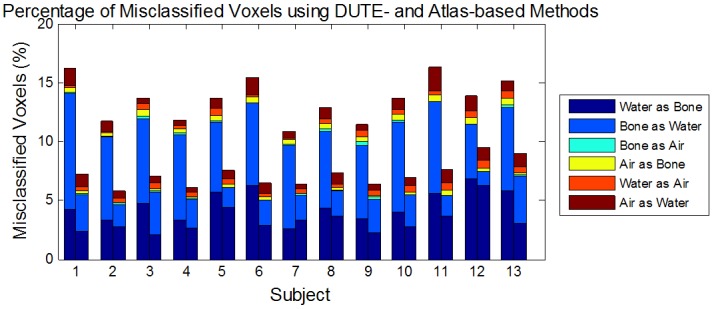
Voxel classification errors for each patient and segmentation method. The percentage of misclassified voxels in the estimated DUTE (left bar) and Atlas-T1w-DUTE (right bar) μ-maps are shown for each patient and each type of error: Water as Bone, Bone as Water, Bone as Air, Air as Bone, Water as Air, and Air as Water (here “Water” refers to “soft tissue”). The Atlas-T1w-DUTE method shows the lowest total percentage of misclassified voxels in all subjects. In addition, the Atlas-T1w-DUTE method shows reduction in bone/air and air/bone errors in all subjects relative to the DUTE results. This is particularly important given the large difference in LAC values between these classes.
Effects on PET data quantification
PET images were reconstructed as described above using μ-maps computed with the MR- and segmented CT-based AC methods. PET images for a representative subject are shown in the top row of Figure 5. The Atlas-T1w-DUTE-based (Figure 5C) and DUTE-based corrected images (Figure 5B) show strong qualitative agreement with those based on the segmented CT (Figure 5A).
Figure 5.
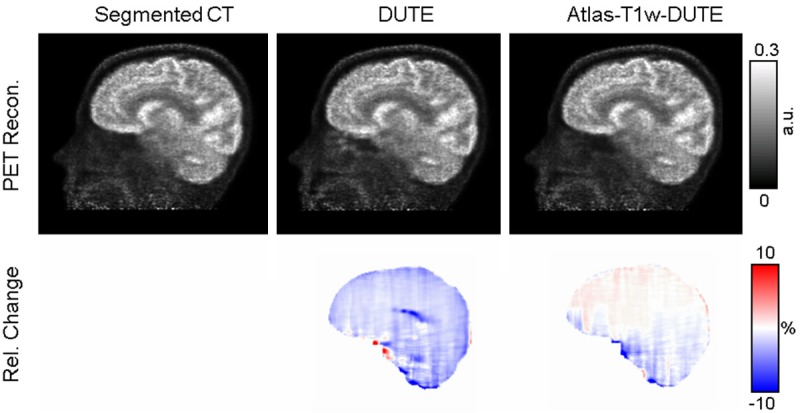
Representative PET images from the data reconstructed using the segmented CT (A), DUTE (B), and Atlas-T1w-DUTE (C) μ-maps from a representative subject are shown in row 1. The corresponding Relative Change maps computed using each estimated reconstruction and the CT-based reconstruction (as the “silver standard”) are shown in row 2.
The RC maps for the same subject are shown in the bottom row of Figure 5. The Atlas-T1w-DUTE method shows smaller RC in many brain regions relative to the DUTE RC map, which shows regions with RC values near ± 20%. For this subject, an average of 2.02% and 0.94% was observed for absolute RC values using the DUTE and AtlasT1-DUTE methods, respectively. The standard deviation was 2.30% and 1.24% for the DUTE and Atlas-T1w-DUTE methods, respectively. This suggests a global improvement in RC values for the Atlas-T1w-DUTE method in this subject. Across all subjects, the mean of the absolute RC values was 3.24% for the DUTE method, versus 1.75% for Atlas-T1w-DUTE. The standard deviation of the absolute RC values across all subjects was 5.37% and 2.64% for the DUTE and Atlas-T1w-DUTE methods, respectively.
Comparable results were obtained from the simulated data. Across all subjects, the mean of the absolute RC values was 2.84% for the DUTE method, versus 1.82% for Atlas-T1w-DUTE. The standard deviation of the absolute RC values across all subjects was 4.83% and 2.45% for the DUTE and Atlas-T1w-DUTE methods, respectively.
For the ROI-based analysis, in all 12 regions the mean of the absolute RC values also consistently showed an improvement for the atlas-based method compared to the DUTE-based method (Figure 6). Qualitatively, the larger regions had smaller RC values while small structures in the limbic system and the cerebellum showed slightly higher RC values and greater variability. In addition, gray matter regions close to the skull also had higher RC values.
Figure 6.
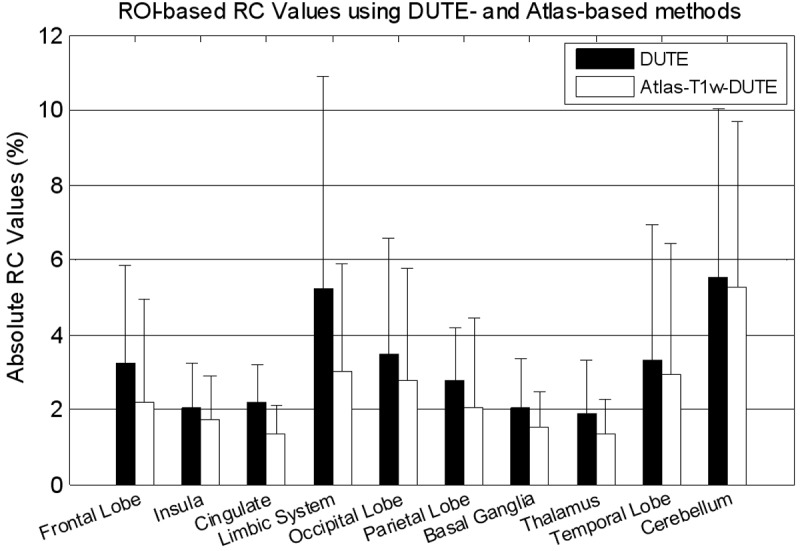
Mean absolute RC values for PET activity, reconstructed with different μ-map generation methods, in different regions of the brain.
Discussion
Obtaining accurate air/bone segmentations from MR data is critical for accurate AC and quantitative imaging on integrated PET/MR scanners. In this work, we proposed an approach combining both segmentation and atlas-based techniques in order to improve the performance compared to standard segmentation methods in terms of global and local PET data quantification accuracy.
Our goal with the first implementation of the DUTE-based AC method [9] was to demonstrate that acceptable μ-maps could be obtained from DUTE data. Indeed, very accurate segmented μ-maps could probably be obtained using only the data acquired with an ideal DUTE sequence (i.e. high spatial resolution, high SNR at the short echo time, no spatial distortion between the volumes obtained at the two echoes, etc.). However, the existing DUTE sequence is less than ideal and additional information about the subject’s anatomy (i.e. from additional sequences or anatomical priors) is necessary to facilitate the segmentation task. Furthermore, local misclassifications due to this method, such as erroneous bone or air assignments in the brain, can lead to large relative errors in the PET images. Although several MR sequences that provide various types of contrast could be used for this purpose, in this work, we proposed to use a MPRAGE sequence and probabilistic atlas to obtain these data. This MPRAGE sequence (or a very similar implementation) is used for obtaining high spatial resolution morphological data in virtually all the brain studies performed at our center. Furthermore, we have recently proposed a method for performing MR motion correction for this sequence (currently available as a work-in-progress package on the Siemens scanners). In combination with the MR-assisted PET motion correction implemented for the BrainPET [29], this would eliminate the mis-registration between the attenuation map and the emission data, which typically occurs due to subject motion and produces artifacts in the reconstructed images.
Results of the Atlas-T1w-DUTE classifier showed improvement over the DUTE method: qualitative comparison to segmented CT μ-maps showed excellent agreement, DSC values were substantially higher in all tissue classes, and the percentage of misclassified voxels due to air/bone misclassification errors was also reduced in all subjects. The Atlas-T1w-DUTE classifier also showed improvement over DUTE in terms of PET quantification: the PET images demonstrated better agreement to those corrected using the ACFs derived from segmented CT μ-maps, mean bias and variability in absolute RC values were substantially reduced. More importantly, the local errors in the μ-maps generated from the DUTE method were also eliminated and this is the main advantage of the proposed method.
The mean variability reflects how robust the segmentation method is across datasets with varying anatomical and image intensity properties in contrast to the variability in RC values for a single subject, which provides a global measure of the segmentation accuracy across the netire volume of interest (i.e. the head). The higher variability observed when using the DUTE method is lIkely due to greater variance in DUTE intensities across separate acquisitions relative to the MPRAGE, which tends to be more consistent across sessions. In the atlas-based methods, the mean variability also reflects how well the trained classifier generalizes to new “test subjects”. Anatomical differences between the subject and atlas may account for some of the variability in the atlas-based results, although mean variability is still reduced in the Atlas-T1w-DUTE relative to the DUTE approach. The generalization of the atlas-based classifier could be further improved by acquiring larger training data sets, normalizing DUTE intensities, scaling the “test” data to minimize the Kullback-Leibler (KL) divergence between the test and training data as described in [18], or applying other information theory techniques.
While the results of the Atlas-T1w-DUTE method are encouraging, several factors may reduce the accuracy of this approach, and thus merit further discussion. While not an issue for the data analyzed in this study, distortions in the MRI data due to gradient non-linearities or signal loss due to dental implants may affect the accuracy of registration between the distorted region(s) and non-distorted data (i.e. MNI atlas). However, these errors could be mitigated by giving more weight in the registration procedure to those regions that have higher SNR (in the case of signal drop out). The MPRAGE data in this study were acquired after administration of MR contrast agent. Although this changes the contrast in some brain regions, it does not affect the bone/air segmentation. Accurate image coregistration is important for alignment of MR and CT data, coregistration of DUTE and MPRAGE volumes (to correct for distortions that may arise in the two UTE images) and of the atlases to each individual subject. Because the coregistration accuracy in this study was visually assessed, errors could still be present and affect the final PET data quantification. To minimize such errors, we used high-resolution CT scans, confirmed that no surgical procedures were carried out between the CT and MR-PET scans of each patient, and used a 12-DOF affine transformation for image registration. The μ-maps derived from the segmented CT data were used as the “silver standard” for evaluating the proposed MR-based AC methods. Although we have previously shown that compared to the AC method that uses scaled CT data this introduces minimal errors in the final reconstructed PET images [9], we are currently investigating methods for generating continuous-valued μ-maps from the MR data.
One common limitation of atlas-based approaches is that the modified anatomy in certain patient populations could introduce bias. This is less of an issue for our method compared to pure atlas-based methods because it does not rely exclusively on the atlas information. Instead, we use a probabilistic approach that allows global intensity properties of DUTEtr1, DUTEtr2 and MPRAGE data for each tissue class to be modeled, reducing the strong reliance on local information found in previous atlas-based techniques. As a proof, μ-maps for newly diagnosed glioblastoma patients post-surgical intervention were successfully generated in this work.
Although the Atlas-T1w-DUTE method was developed and tested using data acquired on the BrainPET prototype, it is relatively straightforward to implement on other integrated PET/MR scanners (e.g. the whole-body Biograph mMR from Siemens Healthcare, Inc. or the Ingenuity TF PET/MR from Philips Healthcare). In this case, a new training data set will lIkely be required to account for software (e.g. MR sequence and acquisition parameters) and hardware (e.g. RF coil sensitivity, longer axial field of view) differences between the two scanners.
Conclusion
AC is critical for accurate quantification of radiotracer concentration and clinical assessment of PET images. The recent development of integrated PET/MR systems that lack a transmission system or integrated CT has greatly increased the need for an MR-based AC technique. In this work, such an approach for deriving segmented μ-maps from DUTE and MPRAGE data by combining segmentation and atlas-based techniques was presented. The qualitative and quantitative analysis of the μ-maps and the corresponding PET images attenuation corrected based on these μ-maps demonstrated the Atlas-T1w-DUTE is substantially superior to the previously implemented DUTE-based approach, both in terms of global and local accuracy. In sum, these experiments suggest that the Atlas-T1w-DUTE method could be a viable option for AC in integrated PET/MR scanners, its performance being comparable to the segmented CT-based approach. Implementation of an accurate MR-based AC technique is essential for the widespread adoption of integrated PET/MR scanners, which have the potential to substantially advance our understanding of neurological diseases by simultaneously leveraging the technological strengths of both modalities.
Acknowledgements
Funding for this work was provided by NIH grants: R01CA137254-03, 5R01AT005280-03, 1P01AT006663-01, 5T32GM008313, 5T90DA022759-05, and T32EB001680 2013 NDSEG-AFOSR fellowship.
Disclosure of conflict of interest
None.
References
- 1.Catana C, Benner T, van der Kouwe A, Byars L, Hamm M, Chonde DB, Michel CJ, El Fakhri G, Schmand M, Sorensen AG. MRI-assisted PET motion correction for neurologic studies in an integrated MR-PET scanner. J Nucl Med. 2011;52:154–161. doi: 10.2967/jnumed.110.079343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Catana C, Drzezga A, Heiss WD, Rosen BR. PET/MRI for Neurologic Applications. J Nucl Med. 2012;53:1916–1925. doi: 10.2967/jnumed.112.105346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Catana C, Guimaraes AR, Rosen BR. PET and MR Imaging: The Odd Couple or a Match Made in Heaven? J Nucl Med. 2013;54:815–824. doi: 10.2967/jnumed.112.112771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schlemmer HPW, Pichler BJ, Schmand M, Burbar Z, Michel C, Ladebeck R, Jattke K, Townsend D, Nahmias C, Jacob PK, Heiss WD, Claussen CD. Simultaneous MR/PET imaging of the human brain: feasibility study. Radiology. 2008;248:1028–1035. doi: 10.1148/radiol.2483071927. [DOI] [PubMed] [Google Scholar]
- 5.Drzezga A, Souvatzoglou M, Eiber M, Beer AJ, Furst S, Martinez-Moller A, Nekolla SG, Ziegler S, Ganter C, Rummeny EJ, Schwaiger M. First clinical experience with integrated whole-body PET/MR: comparison to PET/CT in patients with oncologic diagnoses. J Nucl Med. 2012;53:845–55. doi: 10.2967/jnumed.111.098608. [DOI] [PubMed] [Google Scholar]
- 6.Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 7.Fischl B, Salat DH, van der Kouwe AJW, Makris N, Segonne F, Quinn BT, Dale AM. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004;23:S69–S84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 8.Zaidi H, Ruest T, Schoenahl F, Montandon ML. Comparative assessment of statistical brain MR image segmentation algorithms and their impact on partial volume correction in PET. Neuroimage. 2006;32:1591–1607. doi: 10.1016/j.neuroimage.2006.05.031. [DOI] [PubMed] [Google Scholar]
- 9.Catana C, van der Kouwe A, Benner T, Michel CJ, Hamm M, Fenchel M, Fischl B, Rosen B, Schmand M, Sorensen AG. Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. J Nucl Med. 2010;51:1431–1438. doi: 10.2967/jnumed.109.069112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bergstrom M, Litton J, Eriksson L, Bohm C, Blomqvist G. Determination of object contour from projections for attenuation correction in cranial positron emission tomography. J Comput Assist Tomogr. 1982;6:365–372. doi: 10.1097/00004728-198204000-00022. [DOI] [PubMed] [Google Scholar]
- 11.Siegel S, Dahlbom M. Implementation and evaluation of a calculated attenuation correction for PET. IEEE Transactions on Nuclear Science. 1992;39:1117–1121. [Google Scholar]
- 12.Weinzapfel BT, Hutchins GD. Automated PET attenuation correction model for functional brain imaging. J Nucl Med. 2001;42:483–491. [PubMed] [Google Scholar]
- 13.Zaidi H, Montandon ML, Slosman DO. Magnetic resonance imaging-guided attenuation and scatter corrections in three-dimensional brain positron emission tomography. Med Phys. 2003;30:937–948. doi: 10.1118/1.1569270. [DOI] [PubMed] [Google Scholar]
- 14.Hofmann M, Steinke F, Scheel V, Charpiat G, Farquhar J, Aschoff P, Brady M, Scholkopf B, Pichler BJ. MRI-based attenuation correction for PET/MRI: a novel approach combining pattern recognition and atlas registration. J Nucl Med. 2008;49:1875–1883. doi: 10.2967/jnumed.107.049353. [DOI] [PubMed] [Google Scholar]
- 15.Montandon ML, Zaidi H. Atlas-guided non-uniform attenuation correction in cerebral 3D PET imaging. Neuroimage. 2005;25:278–286. doi: 10.1016/j.neuroimage.2004.11.021. [DOI] [PubMed] [Google Scholar]
- 16.Keereman V, Fierens Y, Broux T, De Deene Y, Lonneux M, Vandenberghe S. MRI-Based Attenuation Correction for PET/MRI Using Ultrashort Echo Time Sequences. J Nucl Med. 2010;51:812–818. doi: 10.2967/jnumed.109.065425. [DOI] [PubMed] [Google Scholar]
- 17.Berker Y, Franke J, Salomon A, Palmowski M, Donker HCW, Temur Y, Mottaghy FM, Kuhl C, Izquierdo-Garcia D, Fayad ZA, Kiessling F, Schulz V. MRI-based attenuation correction for hybrid PET/MRI systems: a 4-class tissue segmentation technique using a combined ultrashort-echo-time/Dixon MRI sequence. J Nucl Med. 2012;53:796–804. doi: 10.2967/jnumed.111.092577. [DOI] [PubMed] [Google Scholar]
- 18.Poynton C, Jenkinson M, Wells W. Atlas-based Improved Prediction of Magnetic Field Inhomogeneity for Distortion Correction of EPI data. Med Image Comput Comput Assist Interv. 2009;12:951–959. doi: 10.1007/978-3-642-04271-3_115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johansson A, Karlsson M, Nyholm T. CT substitute derived from MRI sequences with ultrashort echo time. Med Phys. 2011;38:2708–2714. doi: 10.1118/1.3578928. [DOI] [PubMed] [Google Scholar]
- 20.Larsson A, Johansson A, Axelsson J, Nyholm T, Asklund T, Riklund K, Karlsson M. Evaluation of an attenuation correction method for PET/MR imaging of the head based on substitute CT images. MAGMA. 2013;26:127–136. doi: 10.1007/s10334-012-0339-2. [DOI] [PubMed] [Google Scholar]
- 21.Hong IK, Chung ST, Kim HK, Kim YB, Son YD, Cho ZH. Ultra fast symmetry and SIMD-based projection-backprojection (SSP) algorithm for 3-D PET image reconstruction. IEEE Trans Med Imaging. 2007;26:789–803. doi: 10.1109/tmi.2007.892644. [DOI] [PubMed] [Google Scholar]
- 22.Watson CC. New, faster, image-based scatter correction for 3D PET. IEEE Transactions on Nuclear Science. 2000;47:1587–1594. [Google Scholar]
- 23.Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis - I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 24.Fonov V, Evans AC, Botteron K, Almli CR, McKinstry RC, Collins DL. Unbiased average age-appropriate atlases for pediatric studies. Neuroimage. 2011;54:313–327. doi: 10.1016/j.neuroimage.2010.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- 26.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang YY, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 27.Kinahan PE, Hasegawa BH, Beyer T. X-ray-based attenuation correction for positron emission tomography/computed tomography scanners. Semin Nucl Med. 2003;33:166–179. doi: 10.1053/snuc.2003.127307. [DOI] [PubMed] [Google Scholar]
- 28.Ashburner J, Friston KJ. Spatial transformation of images. In: Frackowiak RSJ, Friston KJ, Frith CD, Dolan RJ, Mazziotta JC, editors. Human Brain Function. Academic Press USA; 1997. pp. 43–58. [Google Scholar]
- 29.Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- 30.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated Anatomical Labeling of Activations in SPM Using a Macroscopic Anatomical Parcellation of the MNI MRI Single-Subject Brain. Neuroimage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]


