The Role of Molecular Dipole Orientation in Single-Molecule Fluorescence Microscopy and Implications for Super-Resolution Imaging

Abstract

Numerous methods for determining the orientation of single-molecule transition dipole moments from microscopic images of the molecular fluorescence have been developed in recent years. At the same time, techniques that rely on nanometer-level accuracy in the determination of molecular position, such as single-molecule super-resolution imaging, have proven immensely successful in their ability to access unprecedented levels of detail and resolution previously hidden by the optical diffraction limit. However, the level of accuracy in the determination of position is threatened by insufficient treatment of molecular orientation. Here we review a number of methods for measuring molecular orientation using fluorescence microscopy, focusing on approaches that are most compatible with position estimation and single-molecule super-resolution imaging. We highlight recent methods based on quadrated pupil imaging and on double-helix point spread function microscopy and apply them to the study of fluorophore mobility on immunolabeled microtubules.

1. Introduction

Over the past several decades, single-molecule detection techniques have proven to be an invaluable tool set for probing the heterogeneity of both biological and abiological systems.^[1–4] Measuring single-molecular parameters such as position, fluorescence lifetime, and emission spectrum reveals a wealth of information otherwise unseen by traditional ensemble-averaged methods. Another important parameter that has been probed over the years in both near- and far-field imaging is molecular orientation.^{[5, 6]} Today, single-molecule orientation tracking microscopy is a field in its own right, which has, for example, enabled the elucidation of the rotational dynamics of small molecules^[7] and has shed light on the stepping motions of biological molecular motors.^[8,9]

A molecule’s three-dimensional (3D) orientation intimately affects the way in which it interacts with the surrounding electromagnetic field. In particular, most molecules (e.g. fluorescent dyes) interact with the field primarily through their electric transition dipole moment. This fact has important and useful implications for the determination of single-molecule orientation in fluorescence microscopy, which is the subject of this review. We begin with a more general description of single-molecule orientation itself and shift toward a discussion of its relationship to the burgeoning field of single-molecule-based super-resolution imaging.

To aid our discussion we refer to the coordinate system depicted in Figure 1A in which the z axis corresponds to the optical axis of a microscope, θ is the polar angle of the dipole relative to the z axis, and ϕ is the dipole’s azimuthal angle about this axis. A fluorophore’s response to an incident electromagnetic wave will depend upon the polarization of the field. Considering only electric dipole transitions (an excellent approximation for most fluorescent molecules), the probability of absorption is proportional to |μ⃑_abs • E⃑|², where μ⃑_abs is the molecule’s absorption dipole moment and E⃑ is the (local) illuminating electric field. Thus, a molecule will be pumped more efficiently with a laser beam that is polarized parallel to its absorption dipole than with one polarized otherwise. Similarly, an excited molecule can couple to the vacuum modes of the electromagnetic field and emit through its emission dipole moment, resulting in a probability of emitting a photon of a given polarization proportional to |μ⃑_em • e⃑|², where μ⃑_em is the emission dipole moment and e⃑ is a unit vector in the direction of the electric field at a particular point in space. Taken together, these attributes imply that much orientational information can be gleaned by using combinations of polarizing elements in both/either the illumination and/or detection paths of a fluorescence microscope. Such methods are widely used, especially in the study of rotations of biological motor proteins^[8] or polymer chain orientations,^[10] and have been reviewed extensively elsewhere. Here, we discuss these methods briefly and then choose to elaborate on other classes of orientation measurements.

Figure 1.

Coordinate definitions and dipole emission distribution. A) A molecular dipole is represented by a double-barbed orange arrow. θ is the polar angle made with the optical (z) axis. ϕ is the azimuthal angle about the z axis. B) Contours of constant fluorescence intensity emitted by a dipole, as projected in two dimensions. The emitted intensity in a given direction is proportional to sin²β, where β is the angle between the transition dipole moment μ⃑ and the Poynting vector S⃑ of the emitted wave at a particular point in space. The pattern is rotationally symmetric about the dipole, forming a toroidal shape in three dimensions.

Most simply, one can achieve some level of orientational sensitivity by alternating the polarization of the pumping light in a standard wide-field illumination configuration,^{[9, 11]} as illustrated in Figure 2A. Alternatively or additionally, one can split the collected fluorescence into orthogonal polarization channels and then, for example, monitor the evolution of linear dichroism (LD), as defined in Equation (1):

$$\text{LD}=\frac{N_{\mathrm{T}}-N_{\mathrm{R}}}{N_{\mathrm{T}}+N_{\mathrm{R}}}$$ (1)

where N_T and N_R are the numbers of photons collected in the transmitted and reflected detection arms, respectively, as defined relative to a polarizing beam splitter. Such an implementation offers simplicity but has two major limitations in that 1) there exist degeneracies in the functional dependence of the collected intensity on ϕ, and 2) the ratio of N_T and N_R will depend upon the molecule’s inclination θ, but there is not enough information to directly determine this parameter.

Figure 2.

Three categories of methods for determining molecular orientation with far-field fluorescence microscopy. A) Polarized illumination and/or detection. The illustration depicts an example setup similar to those in refs. [9, 11] based on modulation of the illumination polarization using an electro-optic modulator (EOM). The basic epi-fluorescence setup consists of a Köhler lens (K. L.) which focuses the polarized illumination light onto the back aperture of the objective (Obj.) to produce a wide-field spot in the sample. Fluorescence is collected back through the objective and focused by a tube lens (T. L.) onto a charge-coupled device (CCD) camera. The dashed box before the T. L. represents where a polarizer might be placed if polarized detection were implemented. B) Methods which make use of the distinct spatial patterns of the polarized fields at the focus of the illumination light. The illustration depicts an example based on ref. [17]. X-polarized illumination light traverses an opaque annular mask which removes the low-angle rays before being focused to a diffraction-limited confocal spot by the objective. The resulting intensity patterns corresponding to the squares of each of the polarized incident fields are shown in the inset. Each of the three boxes in the inset is a square of length 1 μm. The number in the lower right of each box indicates the factor by which the intensity is scaled relative to that in the left box. Without the modulated illumination this number would be much larger for the middle and right boxes. The confocal spot is raster scanned over the sample and the collected fluorescence is focused through a confocal pinhole onto a point detector such as an avalanche photodiode (APD). C) Methods which rely on the spatial variation of emitted fluorescence. The illustration depicts an example similar to that in ref. [47] based on defocused imaging. The epi-illumination (or TIRF) configuration is again employed with a slight defocusing of the optics which causes the images of molecules to depend highly on orientation. Simulated images of six example molecules at various orientations are shown in the inset (scale bar: 1 μm). Related methods make use of the information available at the back focal plane (BFP) of the microscope, which is marked with a dashed line.

To overcome these limitations, a number of modifications can be made to the system. Fourkas has shown that by detecting emission through four channels polarized at 0°, 45°, 90°, and 135° one can break these degeneracies and determine θ given a sufficient number of photons detected^[12]. Goldman and co-workers have employed a more sophisticated polarization-alternating total-internal reflection (TIRF) illumination scheme in order to effectively overcome these limitations.^[13] In TIRF illumination, the evanescent field produced at the water-glass slide interface of the sample contains an enhanced z-polarized component, which increases the probability of pumping molecules with smaller θ values and thus strengthens sensitivity in the determination of θ. Polarization control/analysis-based orientation methods can achieve excellent temporal resolution in macromolecular tracking, down to the sub-millisecond regime if sufficient detected photons are available.^[14] A recent theoretical study by Foreman and Török explored the fundamental limits of polarization-based methods.^[15]

Another category of orientation techniques relies on the spatial variation of polarization of the illuminating light (Figure 2B). When an x-polarized beam is focused through a high-numerical aperture (NA) objective, a significant amount of polarization mixing is introduced such that non-negligible y- and z-polarized components are manifested in the focal plane.^[16] The amount and direction of polarization mixing incurred by each ray entering the back focal plane of the objective is highly dependent on the angular and radial coordinates of the ray relative to the aperture. This results in spatial non-uniformity of the intensity patterns of each polarization component in the focal plane. Each of these non-uniform intensity patterns is mutually distinct among the three polarization components, discernible by the number and placement of their intensity nodes (Figure 2B inset). Thus, by implementing confocal scanning one will detect a single fluorophore with an intensity pattern that directly indicates its orientation: an x-oriented molecule will show up with the shape of the squared x-polarized field. The analogous statements are true for y- and z-oriented molecules, and molecules with arbitrary orientations will be displayed with patterns that are some linear combinations of the patterns of the basis orientations. Practically, one must spatially modulate the amplitude and/or the phase of the light incident on the back aperture of the objective in order to introduce sufficient relative amounts of mixed polarization to achieve sensitivity to y- and z-oriented molecules. Sick and coworkers have done so by introducing an annular aperture into the illumination optics.^[17] The patterns depicted in the inset of Figure 2B were obtained by calculating the focused electric field under annular illumination according to the equations given by Gu.^[18]

Similarly, Débarre and co-workers used a bone-shaped amplitude/phase mask to achieve a comparable result.^[19] A further twist on such approaches can be realized by exciting the molecule with azimuthally or radially polarized doughnut modes.^[20] Due to the scanning nature of all these techniques they are not well suited for detecting many molecules in parallel, which makes them non-ideal for incorporation into single-molecule super-resolution imaging (see Section 2).

A third major category of orientation techniques exploits the spatial distribution of the light emitted by a fluorescent molecule (Figure 2C). The previous discussion on the probability of emitting a photon of a certain polarization implies that the distribution of the light emitted by a molecule is not spherically symmetric. In particular, the molecule emits no light in the direction parallel to its dipole moment, as any transversely polarized electromagnetic wave traveling in this direction would have a dot product with the dipole moment that evaluates to zero. More generally, in the far-field, a molecule emitting through its emission dipole moment resembles a classical oscillating dipole. In terms of the angle-dependent probability of detecting photons, its radiation pattern is proportional to sin²β, where β is the angle between the Poynting vector of the emitted light and the dipole moment (Figure 1B). A microscope objective lens collects a subset of these unevenly emitted rays, which ultimately results in an image of finite extent that exhibits corresponding variations in the intensity profile. Moreover, as the subset of rays that are collected by the objective is dependent on the orientation of the molecule relative to the optics, the molecule’s image pattern is highly dependent on its orientation. Inversely, one can determine the 3D molecular orientation from the unique patterns displayed in the images of the single molecules. Sepiol et al. first demonstrated this for terrylene molecules in a polymer matrix at low temperatures.^[21] Soon after, Dickson and co-workers reported the first room-temperature observations of this phenomenon (using TIR excitation to enhance z-polarized pumping components).^[22] Since then, many methods for determining molecular orientation that rely on measuring the spatial distribution of single-molecule fluorescence have been developed. In Sections 3 and 4 we focus our attention on the mechanics of these methods. Such techniques provide especially attractive candidates for the incorporation into single-molecule-based super-resolution microscopy experiments as they are compatible with epi-fluorescence illumination and detection and do not require alternating illumination polarizations. Furthermore, the spatial anisotropy of a single-molecule fluorescence image has important implications for these super-resolution methods, and only recently has the super-resolution community started to address them. The role of molecular orientation in super-resolution microscopy is the subject of Section 2.

2. Implications of Molecular Orientation for Super-Resolution Microscopy

The advent of super-resolution fluorescence microscopy has made imaging with resolution beyond the diffraction limit fairly common in recent years.^{[23, 24]} Targeted super-resolution techniques such as stimulated emission depletion^[25] and ground-state depletion microscopies^[26] are largely robust to orientation effects as they do not rely on single-molecule detection and the position of the source of fluorescence necessarily coincides with the position of the laser beams, which is known a priori. Still, a previous theoretical study has shown that molecular orientation can, in fact, more subtly affect resolution in these methods, depending in part on the polarization of the lasers.^[27] Another major subset of super-resolution techniques does make use of single-molecule detection, and these methods are the primary focus here. This category includes fluorescence-photoactivated localization microscopy,^{[28, 29]} stochastic optical reconstruction microscopy,^[30] and point accumulation for imaging in nanoscale topography.^[31] We hereafter refer to these techniques by the collective term single-molecule active control microscopy (SMACM). SMACM relies on two major principles: 1) the photophysics or photochemistry of the fluorophores labeling a structure of interest must be actively controlled by the experimenter (e.g. by photoactivation, chemical additives, light intensity, etc.) such that in any image frame only a sparse subset of labels are fluorescing and thus their diffraction-limited images are well-separated in space; 2) each isolated diffraction-limited molecular image is fit with a model function of choice in order to estimate the position of each molecule with precision well below the diffraction limit (typically tens of nanometers). The most common fitting strategy is to approximate the molecular point spread function (PSF) as a two-dimensional (2D) Gaussian function and to find the center of the Gaussian through least squares (LS) fitting or maximum likelihood estimation (MLE). With the collection of molecular positions thus available, the underlying structure is reconstructed in a pointillist fashion.

An apparent logical inconsistency arises. If the center of the fitted symmetric Gaussian shape reflects the true position of the molecule, then there is an underlying assumption that the image of a single molecule is symmetric and Gaussian-like. However, Section 1 described the anisotropic emission patterns that give rise to potentially asymmetric, non-Gaussian single-molecule images. Enderlein and co-workers addressed this issue in the context of the SMACM precursor through fluorescence imaging with one nanometer accuracy (FIONA).^[32] Their theoretical work revealed that fitting molecular emission patterns with 2D Gaussians can result in mislocalizations of molecules that are located in the focal plane by tens of nanometers when molecular orientation is fixed on the time scale of the measurement. Stallinga and Rieger corroborated this conclusion with their own theoretical study, in which they also noted that this mislocalization generally worsens with increased levels of defocus.^[33] Both studies found that the problem is essentially removed for molecules within the focal plane when an objective of NA less than about 1.20–1.25 is used and when imaging molecules near a water-glass interface. However, it is common for SMACM experiments to make use of higher-NA oil immersion objectives in order to maximize fluorescence collection, in which case the error persists for in-focus molecules. In a typical epi-illumination (non-TIRF) wide-field (i.e. without a confocal pinhole) SMACM experiment, molecules located far from the focal plane are excited and allowed to fluoresce. The finite extent of an objective’s depth-of-field means that molecules located hundreds of nanometers from the focal plane can be detected and fit. The localization error persists for these molecules regardless of the NA of the objective. Engelhardt and co-workers demonstrated experimentally that the localization bias incurred (using the also-common centroid calculation rather than Gaussian fitting for finding molecular positions) for out-of-focus molecules located within the microscope’s depth-of-field can, in fact, exceed 100 nm.^[34] The worsening of dipole-induced localization error with defocus is even more troubling in the context of 3D SMACM methods,^[35–38] which inherently rely on the detection of molecules located far from the focal plane. Localization biases, that is, systematic errors, of tens or >100 nanometers threaten to overwhelm the typically-obtained statistical localization precisions of a few tens of nanometers in the SMACM experiments. It is thus necessary that the SMACM community addresses molecular orientation in a meaningful way.

Until now we only described molecules that are fixed in their orientation during the course of an image acquisition. At the other extreme, an organic dye or fluorescent protein that is completely unrestricted in its rotational motion (but tethered such that it does not translate) will explore all of the orientation space during the course of a single image acquisition, and thus acts as an isotropic emitter. Hence a rotationally unconstrained fluorophore will not suffer from dipole-induced localization bias. Recently, Vaughan and co-workers took care to ensure their antibody-conjugated Cy3B labels exhibited sufficient rotational mobility so as not to corrupt their high-resolution images of in vitro polymerized microtubules.^[39] However, other previous workers have shown that it is not always sound to assume total rotational mobility in typical SMACM experiments. Gould and co-workers measured molecular anisotropies in their F-PALM study of Dendra2-labeled actin expressed in fixed mouse fibroblasts by splitting emission into two orthogonal polarization channels.^[40] Anisotropy is defined in Equation (2):

$$\frac{I_{\Vert }-I_{\perp }}{I_{\Vert }+2I_{\perp }}$$ (2)

where I_|| and I_⊥ refer to the intensities of the detected fluorescence polarized parallel and perpendicular to the linearly polarized illumination laser, respectively. They found regions of significant anisotropy (|r | >0.5), whereas a sample containing totally rotationally mobile labels would have an anisotropy of zero for every molecule. In a similar study Testa and co-workers found a significant population of anisotropically emitting tdEosFP labeling β-actin in living PtK2 cells.^[41] These studies, combined with the apparent utility and the ubiquity of fluorescent protein fusions as labels, indicate that there indeed are conditions in which SMACM can be expected to suffer from dipole-induced localization bias in both living and fixed cells. Despite these examples it is still uncommon to characterize rotational mobility of labels when presenting SMACM data.

In reality it is unlikely that SMACM labels are either completely rotationally mobile or immobile. Instead, fluorophore labels are likely to exhibit some intermediate rotational mobility. The question then becomes: “how much rotational mobility is needed to bound the localization error within a certain range?” This regime is the subject of a recent theoretical study by Lew and Backlund et al.^[42] Single fluorophores were modeled as emitting dipoles free to rotate within an angular range bounded by a cone. By tuning the half-angle α of the cone, rotational mobility was varied among the totally immobile (α= 0°), totally mobile (α=90°), and a number of intermediate cases. In doing so, the functional dependence of the dipole-induced localization error on orientational mobility was determined. It was found that in order to bound the localization bias below 10 nm for typical imaging conditions it is necessary to ensure that α>60°. Based on this number, a normalized steady-state bulk anisotropy value less than 0.14 would be sufficient to achieve this level of accuracy (on average).^[43]

In the same study the authors also detailed the effects of partial rotational mobility on example SMACM image reconstructions. Depending on the underlying distribution of the average molecular orientations, insufficient rotational mobility can either cause degraded resolution or distortions in the resulting reconstruction. Figure 3A shows the former case, wherein two crossing microtubules were simulated for which the center axes are offset in z by 200 nm. Mean molecular orientations were drawn uniformly from a sphere such that there was no correlation between position and orientation, and the simulated labels were allowed to wobble in a cone of a prescribed α. The depicted less rotationally mobile case (α=15°) appears dimmer than the more mobile case (α=60°), which is due to the freezing of molecules at orientations exhibiting lower absorption probability and fluorescence collection efficiency. The histograms in Figure 3B show that this effect is significant enough to hinder the ability to resolve the outer edges of one microtubule or to resolve the two microtubules from one another.

Figure 3.

Effects of rotational mobility on simulated SMACM reconstructions. A) Simulated super-resolution reconstructions of two crossing dual-antibody-labeled microtubules modeled as hollow cylinders of diameter 40 nm whose center axes are separated in z by 200 nm. The top panel shows results for a wobble cone angle of α=15° while the bottom shows the α=60° case. Color-scale units are SM localizations per 0.5 nm². B) Histograms of the binned localizations within the boxes shown in (A). The top two panels are these distributions in the white and yellow boxes of the α=15° case, along with the fit to the sum of two Gaussians (cyan). The bottom two panels show the corresponding histograms for the α=60° case, along with the fit (magenta). C) Simulated super-resolution reconstructions of a section of a cell membrane modeled as a hemispherical cap of radius 1.5 μm for the α=15° and α=60° cases. Color-scale units are SM localizations per 0.5 nm². D) Diagram showing an xz slice of the simulated membrane in (C). Because the dipoles (orange) are embedded with orientation orthogonal to the membrane they experience apparent lateral shifts (purple) in the direction of the cell edge with magnitude proportional to distance from the focal plane. Scale bars: 200 nm. Reprinted from ref. [42] with permission from the American Chemical Society.

If instead the underlying distribution of mean orientations is correlated with the position, then insufficient rotational mobility can cause systematic distortions in the reconstruction. This effect is demonstrated in Figure 3C. Here a cell membrane is modeled as a hemispherical cap of radius 1.5 μm, and only molecules within 260 nm of the focal plane (located at mid-plane of the hemisphere) contributed to the final reconstruction. Mean orientations were assigned such that each molecule was orthogonal to the cell surface^[44] and the molecules were again allowed to wobble within a cone of prescribed width. Now in the more constrained case the edge of the cell becomes brighter and sharper than in the less constrained case. In the more constrained case the molecules are frozen near orientations that cause a localization bias toward the edge of the cell, resulting in the observed concerted effect (Figure 3D).

This study shows that molecular orientation is a parameter that must be addressed in SMACM experiments unless a significant degree of rotational mobility can be guaranteed. If such mobility is not evident then care must be taken to either ignore localizations that can be classified as spurious or to correct the mislocalizations directly. Mislocalization correction may require direct measurement of molecular orientation in parallel with position estimation. In Sections 3 and 4 we present a detailed account of several major orientation determination methods which rely on the spatial patterns of molecular emission. As mentioned in Section 1, these methods provide potential candidates for incorporation into SMACM imaging. We organize the discussion into techniques that rely solely on the intensity distribution measured in the image plane (Section 3) and techniques that derive useful information from the modulation of light in the back focal plane of the microscope (Section 4). Section 4 highlights two recently developed methods from the Moerner lab based on quadrated pupil imaging^[45] and the double-helix point spread function (DH-PSF).^[46]

3. Orientation Determination through Image Plane Spatial Distributions

3.1. Defocused Orientation Imaging

One commonly used orientation imaging modality is based on defocusing of the optics (i.e. displacement of the molecule away from the focal plane). This idea is inspired by the early observation that controlled introduction of aberrations can enhance the spatial variation in single-molecule dipole images, providing for more accurate orientation discrimination.^[22] Böhmer and Enderlein showed that the easily applied defocus aberration provides such an ability.^[47] This powerful method typically works by moving the microscope objective ~1 μm towards the sample and collecting a relatively long camera exposure of ~1–20 s. The obtained image (e.g. Figure 2C inset) is then compared to a library of simulated images based on full vectorial diffraction calculations and the orientation with the best match is assigned.^[48] The need to simulate a full range of orientations makes the method somewhat computationally involved, and better resolution in angle determination inherently requires simulating image templates on increasingly finer orientation grids. Furthermore, the act of defocusing increases the spatial extent of each molecular image, which spreads the budgeted photons across more pixels. Long exposures are thus necessary to overcome the photon dilution, which in turn may make defocused imaging non-ideal for SMACM where exposures below 100 ms are often desired.

The unique diffraction patterns observed in defocused imaging are highly sensitive to the z position of the molecule, and, in particular, its position relative to the index of refraction discontinuities in the surrounding media, which produce additional aberrations. In particular, defocused imaging is most often used with the molecules positioned at an air–glass interface or embedded in a polymer very near the air–polymer interface. This fact makes defocused imaging useful for studying the rotations of molecules embedded in polymers^{[49, 50]} and even for determining the thickness of a thin polymer layer.^[48] In the wide-field imaging of 3D biological objects by contrast, molecular labels will appear at varied distances from the interfaces of the imaging media. As the z position of these labels is not known a priori and because the exact thicknesses and refractive indices of the components of the media are often difficult to measure precisely, defocused imaging is less suitable for such 3D objects.

Toprak and co-workers applied defocused orientation imaging to the study of myosin V stepping near a glass-water interface.^[51] In this experiment they combined orientation determination with position estimation by two methods. For some data they estimated both sets of parameters from the same images. Because of the aforementioned spread of photons, a degradation of precision in position estimation relative to focused imaging can occur. To overcome this, they alternately recorded in- and out-of-focus images and interleaved their estimations of position and orientation. While it may not be impossible to incorporate such a treatment into a general SMACM experiment, one would need each localized molecule to be actively emitting for at least two sequential image frames.

3.2. Fitting of the Full Dipole PSF

Mortensen and co-workers recently demonstrated the ability to simultaneously fit molecular position and orientation from focused images of immobile single molecules.^[52] They did so by using the full theoretical PSF (based on vectorial diffraction theory as was the case in Section 3.1), which depends parametrically on orientation, and fitting using MLE. They applied this MLE with the theoretical PSF (MLEwT) to the imaging of isolated, in-focus rhodamine molecules near the cover slip and achieved the Cramer–Rao lower bound (CRLB) in precision for both position and orientation estimation. The low computational speed (0.4 molecules s⁻¹) is a major drawback of MLEwT and may prevent its incorporation into SMACM imaging.^[53] Further, this method is sensitive to aberrations for the same reasons as simple defocused imaging is. Among such aberration considerations is the fact that MLEwT as presented only applies to in-focus molecules, which is not optimal for the imaging of biological structures that are extended in z.

Very recently Zhang and co-workers presented an alternative method that shares the ability to simultaneously discern orientation and position for both in- and out-of-focus molecules without manipulation of the standard optics.^[53] However, instead of employing MLE they make use of artificial neural networks (ANNs) that require training with simulated dipole images. They reported orientation and position precisions equivalent to those obtained with MLEwT with greatly reduced computational time (~10⁵ times faster). They also directly demonstrated modest reduction of dipole-induced localization bias from ~50 to ~20 nm for quantum rods at a defocus of z = 300 nm. Most interestingly, they applied their ANN method to real SMACM data obtained in both 2D and 3D (by incorporating biplane imaging,^[36] thus demonstrating that implementation of the method does not require a priori knowledge of the focal position). The ANN-based method may thus be an attractive option for future SMACM imaging with orientation determination.

3.3. Other Parametric Fitting Methods

Aguet and co-workers recast the dipole image formulation in terms of a weighted sum of six basis templates (per defocus level).^[54] The weighting coefficients are trigonometric functions of orientation angles that can be inverted to give orientation. Casting the problem into this form allows one to formulate the estimation of orientation and position as the optimization of a 3D steerable filter. They applied their method to the high-SNR imaging of defocused Cy5 molecules at an air-glass interface under TIRF illumination and achieved good localization precisions (ones to tens of nm) and orientation estimation precisions (~1–5°). While they directly addressed the modest localization bias of 5–20 nm that occurs for in-focus dipoles when fit with a Gaussian estimator, larger mislocalizations for out-of-focus molecules were not treated. The model allows for estimation of z, but it is only demonstrated over the small z range applicable to TIRF microscopy. A highly valuable result of their work is that for a given defocus, one must only calculate six images rather than a full sampling of orientation space. Burghardt has since presented a similar method.^[55]

Some of these methods based on precise fitting of the non-symmetric emission shapes of in-focus molecules have only been demonstrated for relatively high signal levels of ~3000–30 000 photons per frame,^{[52, 54]} despite the fact that typical SMACM experiments record signal photon rates on the order of 1000 photons per frame or lower. In their advocation of an alternative method, Stallinga and Rieger sought to address both this fact and the removal of large localization biases at moderate defocus levels.^[56] In this theoretical study they described a fitting technique which combines polarized detection and simplified PSF modeling. The use of an Azzam polarimeter splits collected fluorescence into four channels polarized at 0, 45, 90, and 135°. The four images are then projected onto different quadrants of an EMCCD camera. To fit each image they developed a modification of the traditional 2D Gaussian method allowing for the donut shape of vertically oriented dipole images and the asymmetry of intermediately oriented dipole images. They did so by multiplying the Gaussian by a weighted combination of the first few Hermite polynomials. The set of images was then fit to the model using MLE. Their simulations demonstrated the success of their method with only 500 total signal photons (i.e. the sum of photons in all four channels) on a background of 25 photons per pixel. They obtained localization precisions below 5 nm and orientation precisions below 5°. They also directly demonstrated the reduction of localization bias to within 5 nm for the otherwise severe case of θ=45° at the edge of the depth-of-field. Furthermore, the model does not require a priori knowledge of the molecule’s z position, which suggests utility in imaging biological objects which extend beyond the TIRF region. While these claims are impressive, to our knowledge this method has yet to be applied to experimentally obtained images.

4. Orientation Determination through Back Focal Plane Manipulation

While Section 3 dealt with accessing molecular orientation by measuring the intensity distributions in the image plane, we now turn to methods which capitalize on the characteristic distribution of light emitted by a single dipole as seen in the back focal plane (BFP) of the microscope. To easily access the BFP in a commercial fluorescence microscope (dashed line in Figure 2C), one typically adds a 4f optical processing system after the intermediate image plane (i.e. the conventional camera position) of the microscope (Figure 4A). A first lens is placed one focal length from this intermediate image plane. The plane that is one focal length behind this lens is conjugate to the BFP of the microscope and allows one to easily add optical components without taking apart the microscope. We use “BFP” interchangeably to mean this conjugate plane. Some representative plots of the BFP intensity patterns due to single molecules are shown in Figure 4B for various orientations. Note the bright ring of intensity at the outer edge of the patterns that results from the collection of high-angle rays by a high-NA objective. This ring is intensified by the collection of supercritical light in the presence of a discontinuity in the index of refraction in the sample (e.g. an air–glass interface). By comparing the outer rings of the BFP patterns of various orientations it becomes evident that this region contains a great deal of orientational information. To complete the 4f optical processing system, a second lens placed one focal length behind this conjugate plane then focuses the light onto the camera placed at the final image plane.

Figure 4.

Illustration of the back focal plane. A) Schematic showing the 4f optical system which is added to a standard microscope in order to facilitate access to the BFP. The intermediate image plane is where the camera would normally be placed in a standard microscope configuration. Methods which utilize Fourier plane processing place an SLM or a phase/amplitude mask at the position of the plane conjugate to the BFP. B) Examples of BFP intensity patterns for molecules at various θ.

Lieb and co-workers first showed that by instead placing a camera directly at the BFP one could measure these intensity patterns and determine molecular orientation by comparing to simulations.^[57] However, this method is not suited for high-resolution imaging, because detecting the intensity in the BFP destroys the position information in image space. Further, in wide-field imaging, the BFP contains overlapping information for all molecules in the field-of-view. A number of methods have since been developed which seek to transmit the orientational information encoded in the BFP into the image plane in order to preserve compatibility with imaging.

4.1. Point Scanning BFP Methods

Several methods have been proposed which incorporate BFP manipulation with confocal microscopy. While these methods are not ideal for SMACM integration due to their serial nature, we include them here for the sake of completeness. Hohlbein and Hübner presented a theoretical description of such a method in which an annular mirror separated the light from the outer ring of the BFP and projected this directly on a point detector.^[58] The lower spatial frequency content is allowed to pass through the annulus to be split by a polarizing beam splitter and subsequently focused onto two more point detectors. Börner and co-workers recently applied this method experimentally.^[59] Foreman and co-workers proposed a similarly-spirited method in which a non-polarizing beam splitter placed after the objective first splits the fluorescence into two parts.^[60] One part is split further by a polarizing beam splitter and focused onto two point detectors. The other portion split by the first beam splitter passes through a phase mask placed in the BFP. The mask imparts a π-phase delay on the left half of the BFP and leaves the right half unmodulated. This portion is then focused onto a third point detector. Sikorski and Davis proposed another method based on spatially varying modulation of light in the BFP.^[61] Through the use of two spatial light modulators (SLMs) they suggest rotating the polarization of portions of the BFP such that one can optimally detect molecules of a prescribed but arbitrary ϕ.

4.2. Quadrated Pupil Imaging

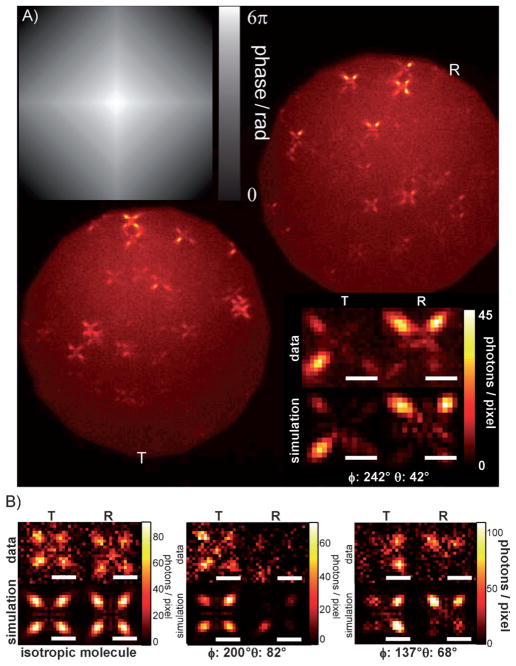
Backer et al. recently demonstrated a method for determining molecular orientation that relies on phase modulation of light in the BFP in the context of wide-field imaging.^[45] In this method, called quadrated pupil imaging, the collected emission is first split into orthogonally polarized R and T channels [as defined in Eq. (1)] with a polarizing beam splitter. A single SLM is placed at the shared BFP of each channel, and the phase mask in Figure 5A is encoded onto the SLM. This square pyramidal mask serves to shunt light toward the diagonals of each quadrant of the pupil. In the final image this manifests as a four-pointed star in both channels for each single emitter (Figure 5A, upper right and lower left). Because the different channels and quadrants are illuminated uniquely for each molecular orientation, the integrated intensity around each of the eight lobes in the image is a signature of the underlying orientation. In the published study, these eight observations were fit by MLE to determine molecular orientation for several single DCDHF-N-6 molecules^[62] spun in a thin layer of poly methyl methacrylate (PMMA). The lower right inset in Figure 5A shows the measured and matched simulated images of one example molecule. For this particular molecule the orientation was determined to be (θ_quadrated = 42.2°±1.8°, ϕ_quadrated = 242.2°±1.7°), within reasonable agreement of the orientation as determined by defocused imaging for the same molecule, (θ_defocus = 36°±3.9°, ϕ_defocus = 260.7°±3.2°). Here the precisions for the quadrated imaging estimates surpassed those of defocused imaging and approached the CRLB. It is important to note that the residual discrepancy between the angles estimated by quadrated and defocused imaging does not necessarily indicate a shortcoming of the quadrated method since the values obtained from defocused (and somewhat aberrated) imaging do not necessarily reflect the ground truth.

Figure 5.

Quadrated pupil imaging. A) Phase mask implemented for quadrated pupil imaging (top left). Image of a field of DCDHF-N-6 molecules embedded in PMMA as seen in both the R (top right) and T (bottom left) polarization channels. Molecular orientations are fixed in this sample, causing molecules to appear as a pair of four-pointed stars with lobes of unequal intensity. Experimental images of an example molecule and the images of the corresponding best-fit orientation are shown (bottom right). The best-fit orientation is printed at the bottom of this panel. B) Images of three example Alexa 647 molecules from the immunolabeled microtubule sample. The sample contains both freely rotating dipoles as indicated by lobes of equal intensity (left) and molecules with more constrained orientation as indicated by lobes of unequal intensity (middle and right). All scale bars: 1 μm. A portion of this Figure is reprinted from ref. [45] with permission from the Optical Society of America.

Because the quadrated pupil method does not require precise fitting of fine features in the image, it is quite robust to minor aberrations not captured by ideal simulations. In particular, its SM images are mostly invariant over a z range of ±150 nm and thus, it performs relatively uniformly over this range. Though the four-pointed images do not lend themselves to high-precision localization estimates, one can conceivably implement a scheme analogous to the alternating defocused and focused imaging described in Section 3.1 by toggling on and off the SLM power. In contrast to physically moving an objective in and out of focus, toggling an SLM can be done at very high rates with no sample perturbation.

In addition, the quadrated pupil is a useful diagnostic tool for determining if a fluorophore is rotationally mobile, and hence whether or not it may be considered an isotropic emitter. Unlike bulk anisotropy techniques that recover average parameters describing the amount of rotational mobility present in a sample overall, quadrated pupil imaging enables one to observe the orientational behavior of individual molecules, and consequently identify subpopulations of molecules in a heterogeneous sample. To illustrate this point, microtubules immunolabeled with Alexa Fluor 647 were imaged using our quadrated pupil technique, under conditions typical of super-resolution imaging. In cultured BSC-1 cells, the primary rabbit antibody stained alpha tubulin (abcam ab18251), while the secondary goat anti-rabbit antibody (Invitrogen A21244) was labeled with Alexa Fluor 647. The sample was imaged in a buffer containing β-mercaptoethylamine thiol and the glucose, glucose oxidase, and catalase oxygen-scavenging system to produce blinking as described in other SMACM experiments.^{[63, 64]} For this sample, we found that the majority of molecules detected exhibited fluorescence images consistent with those of isotropic emitters. The left panel of Figure 5B shows a representative image of such a single molecule, as well as simulated images of an isotropic point-source modulated by the quadrated pupil. However, a small portion of the single-molecule images exhibited highly asymmetric features, indicating that the rotational motion of these molecules had been restricted. The middle and right panels of Figure 5B show examples of orientationally constrained molecules, as well as simulated images corresponding to the most likely dipole orientation of these emitters. The presence of such stably oriented molecules in the microtubule sample confirms that one must at least consider the effects of orientation when imaging this common SMACM structure. Whether it is significantly beneficial to remove or correct localizations arising from molecular orientation effects depends on the proportion of these immobile labels relative to the total population of fluorophores. We explore this point more quantitatively in Section 4.3.

4.3. Double-Helix Point Spread Function Microscopy

Another newly validated method from the Moerner group is based on DH-PSF (double-helix point spread function) imaging.^[46] The DH-PSF was originally applied to microscopy in order to provide a means for precise 3D position estimation in SMACM and single-particle tracking.^{[38, 64–66]} Briefly, the DH-PSF is an engineered PSF which is convolved with the standard PSF such that a single emitter is recorded as two closely-spaced lobes of light that revolve around one another as a function of axial position (Figure 6A). The precise position of the emitter can be determined by (for instance) fitting the image to the sum of two Gaussians. The midpoint between the Gaussians gives the lateral position, while the angle made by the line connecting the two Gaussians relative to the horizontal gives the axial position. To create the DH-PSF a special phase mask (Figure 6B), which can be encoded on an SLM, is placed at the BFP of the microscope. Thus, the uneven illumination of the phase mask in the BFP due to molecular orientation creates additional complexity in the DH-PSF image which can be exploited to infer (θ, ϕ).

Figure 6.

Determination of molecular orientation and position with the DH-PSF. A) Path of the DH-PSF lobes as a function of z carves out the shape of a double helix. The center pale blue plane marks xy image when the molecule is in focus and the lobes are horizontal. Planes are spaced apart by 1 μm axially. B) DH-PSF phase mask. C) Histograms of estimations of molecular orientation of one example molecule as measured at many z positions. A Gaussian fit is overlaid in magenta and the purple arrows mark the independently estimated orientation from defocused imaging. D) Four images of the same example molecule at a single z position. The four images were obtained in the transmitted channel with the mask rotated 90° (red), the transmitted channel with the mask upright (gold), the reflected channel with the mask rotated (green), and the reflected channel with the mask upright (blue). Scale bar: 1 μm. E) 2D histograms of lateral localizations of same example molecule as measured at many z positions. The top panel shows the uncorrected case and the bottom panel shows the corrected case (using the average estimated orientation). Bin size: 15 nm; displayed axes length: 100 nm. Reprinted from ref. [46] with permission from the U.S. National Academy of Sciences.

In particular, it was found that molecular orientation is reflected in the asymmetry of the amplitudes of the two lobes, which can be captured by defining the parameter lobe asymmetry (LA) given by Equation (3):

$$\text{LA}=\frac{A_1-A_2}{A_1+A_2}$$ (3)

where A₁ and A₂ are the amplitudes of the Gaussian fits. Simulations showed that in general the LA is larger in magnitude for molecules that exhibit large localization biases, suggesting the use of LA as a proxy for localization error (vide infra). Furthermore, as the use of a liquid-crystal SLM usually requires first polarizing the emission anyway, the LD [Eq. (1)] was also utilized to aid orientation estimations. To demonstrate the method the authors imaged single DCDHF-N-6 molecules spun in PMMA and measured 3D position, LA, and LD many times for each single molecule over a ~1 μm axial range. The measured z, LA, and LD values were then compared to simulations in order to assign (θ, ϕ) at each z position. The results of this orientation estimation for an example molecule are shown in Figure 6C. Throughout this section we present results for the same single molecule; results for other examples can be found in ref. [46] and its accompanying supporting information. To validate this novel method, estimates of orientation obtained from defocused imaging were also produced for the same molecules. For the molecule in Figure 6C–E the results gave (θ_DH-PSF = 61°±2°, ϕ_DH-PSF = 141°±4°) and (θ_defocus = 63°±3°, ϕ_defocus = 143°±5°). Good agreement with the established method was thus obtained, as well as similar angular precisions. In contrast to defocused imaging, however, the DH-PSF method works well over a large z range and allows for simultaneous high-precision determination of (x,y,z). Also interestingly, the authors found the need to compensate for spherical, astigmatic, and comatic aberrations in defocused imaging. These corrections were not required for DH-PSF imaging, presumably because the DH-PSF mask imparts a large enough wave-front distortion that renders distortions due to minor aberrations insignificant.

Due to the unique pyramidal mirror microscope geometry employed (as described in detail in ref. [46]), it proved useful to record two sequential acquisitions (resulting in four total images due to the use of two polarization channels) for each estimation of orientation: one with the phase mask oriented upright on the SLM and the other with the mask rotated by 90°. For the same example molecule, these four (falsely colored) images are shown for a single z position in Figure 6D. While the use of four images rather than two certainly aided accuracy by removing degeneracies, it may be possible to obtain similar results by using a modified microscope geometry. Thus, even though the need to toggle the phase mask enforces a similar constraint on imaging efficiency as in the position determination discussion in Section 4.2 or the alternating defocus/in-focus modality described in Section 3.1, the use of separate SLMs for each polarization channel, for instance, would allow for accurate orientation determination from a single acquisition.

In this study the authors directly addressed large localization biases and the consequential apparent lateral shifts of molecules as a function of z. The 2D localization histograms shown in Figure 6E demonstrate the accurate modeling and correction of these shifts for the same example molecule. These histograms represent density maps of binned xy-localizations of the same single molecule measured many times over the full z range (here only shown for the “green” channel). The top panel of Figure 6E shows an elongated, irregular shape with transverse length ~100 nm due to the z-dependent dipole-induced mislocalization. By correcting the position estimates with the DH-PSF analysis the more concentrated and symmetric distribution of lateral localizations shown in the bottom panel is obtained. The residual spread in the corrected values approaches the bound set by photon and camera noise.

A study by Agrawal and co-workers compares the theoretical limits of position and orientation estimation of the polarization-sensitive DH-PSF method to other methods by calculating the CRLBs.^[67] They found that the polarization-sensitive DH-PSF and a polarization-sensitive bifocal plane imaging scheme provide for high, relatively z-invariant accuracy and precision in both 3D position and orientation estimation when compared to a simple defocused imaging or polarization-sensitive defocused imaging configuration. Hence the polarization-sensitive DH-PSF method is an excellent candidate to simultaneously measure orientations and correct mislocalizations in 3D SMACM, especially if it can be demonstrated with the use of a single camera acquisition. More immediately, however, since the observed LA correlates with localization bias, we propose the use of LA as a diagnostic for the prominence of this bias.

To quantify this bias prominence in a real 3D SMACM image, we again imaged microtubules immunolabeled with Alexa 647 as described in Section 4.2. The DH-PSF microscope enabled the 3D super-resolved reconstruction shown in Figure 7A, in which z position is color-coded. Each molecular fit has an associated LA and LD which we compiled in the histograms shown in Figure 7B. A population of labels which all exhibit full rotational mobility would produce δ-function distributions centered at LA =0 and LD =0 (in the absence of noise). The finite widths (σ_LA,R = 0.11, σ_LA,T = 0.11, σ_LD = 0.12) of these distributions coupled with qualitative inspection of a subset of molecular images strongly suggest the presence of some biased localizations. However, these distribution widths are much smaller than one would expect if each label were completely immobile. We also examined the spatial distribution of LA and LD, as shown for a typical subregion in Figure 7C. These sub-images do not exhibit a strong spatial dependence of these parameters. Removing fits with |LA | >0.2 in either channel (21 % of all fits) did not result in a noticeable improvement in image quality, indicating that for this particular sample the proportion of biased molecules is sufficiently low and spatially disperse to justify ignoring molecular orientation effects.

Figure 7.

Position and orientation-dependent parameters of Alexa Fluor 647-immunolabeled microtubules in a BSC-1 cell measured with the DH microscope. A) Two-dimensional histogram of the median z position of Alexa 647 localizations recorded within each pixel. These localizations span a depth range of ~1.3 μm. Comparison to a diffraction-limited 2D image taken at low pumping intensity (upper-right) shows the inherent 3D resolution improvement achievable with the DH microscope. Bin size =30 nm, scale bar =5 μm. B) Distributions of lobe asymmetry (LA) measured over all molecules detected in the reflected channel (left) and transmitted channel (middle), as well as the distribution of linear dichroism (LD, right), over the entire region plotted in (A). C) Spatial dependence of LA for molecules detected in the reflected channel (left) and transmitted channel (middle), as well as the spatial dependence of LD (right), plotted over the sub-region outlined by the white rectangle in (A). Bin size =30 nm, scale bar =1 μm.

5. Conclusion and Outlook

Over the years, a number of methods have been developed which allow for the determination of single-molecule orientation from fluorescence images. These techniques can be broadly grouped into those that rely solely on the modulation of the absorption/emission polarization(s), those that rely on the spatial dependence of absorption, and those that take advantage of the spatial distributions of emitted fluorescence. The third category includes methods that do not employ manipulation of the emission at the BFP (e.g. defocused imaging and template matching, fitting of the full dipolar PSF) and those that do (e.g. quadrated pupil imaging, DH-PSF microscopy). The methods of this third category are most compatible with SMACM because of 1) the potential to measure orientation from a single camera snapshot for each molecule, 2) the use of simple widefield epi-fluorescence pumping and collection, and 3) the ability to detect many molecules in parallel. Recent studies have shown that molecular orientation plays an important role in SMACM since these single-molecule super-resolution imaging modalities depend explicitly on the accurate localization of individual emitters, which is hindered by the inherently anisotropic emission patterns of single-molecule dipoles. This becomes especially important when fluorescent labels are not sufficiently rotationally mobile. Despite this fact, only a handful of published SMACM studies carefully characterize the rotational mobility/prominence of localization bias in the imaged samples.

Motivated by this fact, we here characterized the mobility and localization bias prominence in a sample of microtubules labeled with Alexa 647 using both quadrated pupil and DH-PSF imaging. The quadrated pupil images showed specific examples of fluorophores that were nearly completely rotationally immobile, for which localization bias would be significant. Using the DH-PSF, however, we characterized the full population of labels and concluded that further correction is unnecessary for this particular sample, because these immobile molecules represent a sufficiently small and randomly dispersed sub-population. Nevertheless, this example should not be misinterpreted to dismiss the role of localization bias in all SMACM samples. It is only meant to be an objective study of one commonly used test sample, imaged by immunofluorescence where the labels are mostly sufficiently floppy. The prominence of the bias will vary from sample to sample and ideally should be characterized in a similar manner in conjunction with any SMACM measurement. Candidate samples for revealing more prominent sub-populations of biased localizations are the actin-based samples of refs. [40, 41], which exhibited significant anisotropies. More generally, the distributions of orientational mobility of single fluorescent protein fusions must be measured in future work.

While the characterization of orientation/mobility distribution for the sake of localization bias will become increasingly important as the resolution attainable in SMACM approaches the molecular scale, parallel estimation of orientation along with (3D) position in SMACM will also provide an interesting new way to probe details of local environments at very high resolution. As described in Section 1, the simultaneous estimation of position and orientation in single-biomotor tracking permitted by polarization techniques has provided invaluable information on the stepping motions of these important enzymes. At the same time, bulk anisotropy measurements are often used to quantify the ensemble orientational behavior of important biological molecules embedded in extended structures.^{[44, 68–70]} The combination of SMACM and orientation imaging methods would allow for the detailed characterization of the types of extended structures previously studied in bulk at the subdiffraction, single-molecule level.

Biographies

Mikael P. Backlund is currently a Ph.D. candidate in physical chemistry and a Robert and Marvel Kirby Stanford Graduate Fellow at Stanford University. He graduated with Highest Honors from the University of California, Berkeley in 2010, where he received his B.Sc. in chemistry with a minor in mathematics. His research interests include single-molecule microscopy, optical imaging, molecular biophysics, and single-particle tracking.

Matthew D. Lew is a Ph.D. candidate in electrical engineering, a 3Com Corporation Stanford Graduate Fellow, and a National Science Foundation Graduate Research Fellow at Stanford University. He received the B.Sc. degree with Honor in electrical engineering from the California Institute of Technology in 2008 and the M.Sc. degree in electrical engineering from Stanford University in 2010. His work in the Moerner Lab has involved the design and application of novel optical elements to more efficiently encode 3D position and molecular orientation in far-field fluorescence images. His research interests include single-molecule fluorescence, optical imaging systems, and point spread function engineering.

Adam S. Backer received his B.Sc. degree in engineering and physics from Brown University in 2008 and an M. Phil. in engineering from Cambridge University as a recipient of the Charles Craig Studentship in 2009. In 2010 he received a National Defense Science and Engineering Graduate Fellowship, and in 2011 he joined the Moerner lab to pursue his interest in single-molecule superresolution microscopy. His research focuses on using wavefront engineering to enhance 3D superresolution imaging modalities, and single-molecule orientation measurements. He is currently a Ph.D. candidate at the Institute for Computational and Mathematical Engineering at Stanford University.

Steffen J. Sahl is presently a postdoctoral fellow at Stanford University, USA, having earned his doctorate in physics (Heidelberg University, Germany) for thesis work at the Max Planck Institute for Biophysical Chemistry, Göttingen, Germany, in 2010. Steffen also holds degrees in physics from Cambridge University, England. His research interests are in single-molecule optical analysis and imaging, in particular the further development of three-dimensional super-resolution fluorescence microscopies, and applying these methods to better understand the aggregation behavior of amyloid proteins in neurodegenerative disease.

W. E. (William Esco) Moerner, the Harry S. Mosher Professor of Chemistry and Professor, by courtesy, of Applied Physics, at Stanford University, has conducted research in the areas of physical chemistry and biophysics of single molecules, development of 2D and 3D super-resolution imaging for cell biology, nanophotonics, photorefractive polymers, and trapping of single biomolecules in solution.