Abstract
Iterative image reconstruction with sparsity-exploiting methods, such as total variation (TV) minimization, investigated in compressive sensing claim potentially large reductions in sampling requirements. Quantifying this claim for computed tomography (CT) is nontrivial, because both full sampling in the discrete-to-discrete imaging model and the reduction in sampling admitted by sparsity-exploiting methods are ill-defined. The present article proposes definitions of full sampling by introducing four sufficient-sampling conditions (SSCs). The SSCs are based on the condition number of the system matrix of a linear imaging model and address invertibility and stability. In the example application of breast CT, the SSCs are used as reference points of full sampling for quantifying the undersampling admitted by reconstruction through TV-minimization. In numerical simulations, factors affecting admissible undersampling are studied. Differences between few-view and few-detector bin reconstruction as well as a relation between object sparsity and admitted undersampling are quantified.
Index Terms: Compressed sensing (CS), computed tomography (CT), data models, image sampling, iterative methods
I. Introduction
Recently, iterative image reconstruction (IIR) algorithms have been developed for X-ray tomography [1]–[10] based on the ideas discussed in the field of compressive sensing (CS) [11]–[14]. These algorithms promise accurate reconstruction from less data than is required by standard image reconstruction methods. This is made possible by exploiting sparsity, i.e., few nonzeroes in the image or of some transform applied to the image. One can argue about whether these algorithms are truly novel or not: edge-preserving regularization and reconstruction based on the total variation (TV) semi-norm [15]–[18] have a clear link to sparsity in the object gradient and have been considered before the advent of CS, and algorithms specifically for object sparsity have been developed for blood vessel imaging with contrast agents [19]. Nevertheless, the interest in CS has broadened the perspective on applying optimization-based methods for IIR algorithm development for computed tomography (CT), and it has motivated development of efficient algorithms involving variants of the ℓ1-norm [10], [20]–[25].
What is seldom discussed, however, is that the theoretical results from CS do not extend to the CT setting. CS only provides theoretical guarantees of accurate undersampled recovery for certain classes of random measurement matrices [13], not deterministic matrices such as CT system matrices. While the mentioned references demonstrate empirically that CS-inspired methods do indeed allow for undersampled CT reconstruction, there is a fundamental lack of understanding of why, and the conditions under which, this is the case. One problem in uncritically applying sparsity-exploiting methods to CT is that there is no quantitative notion of full sampling.
Most IIR, including sparsity-exploiting, methods employ a discrete-to-discrete (DD) imaging model1 which requires that the object function be represented by a finite-sized expansion set and sampling specified over a finite set of transmission rays. This contrasts with most analysis of CT sampling, which is performed on a continuous-to-discrete (CD) model. For analyzing analytic algorithms such as filtered back-projection (FBP), a continuous-to-continuous (CC) model such as the X-ray or Radon transform is chosen, and discretization of the data space is considered, yielding results for the corresponding CD model. Analysis of the CD model is performed independent of object expansion. If the expansion set for the DD model is chosen to be point-like, e.g., pixels/voxels, there may be similarity between CD and DD models justifying some crossover of intuition on sampling, but in general sufficient-sampling conditions can be different for the two models. That a more fine-grained notion of sufficient sampling is needed for the DD model can be seen by considering the representation of the object function on a 128 × 128 versus a 1024 × 1024 pixel array. Clearly, the latter case requires more samples than the former, but sampling conditions derived from the CD model cannot make this distinction. Sufficient sampling for the DD model becomes even less intuitive for nonpoint-like expansion sets such as natural pixels, wavelets, or harmonic expansions. Yet, to quantify the level of undersampling admitted by a sparsity-exploiting IIR method, full sampling needs to be defined for the corresponding DD model, and to that end we introduce several sufficient-sampling conditions (SSCs).
Specifically, in the present article, SSCs for the DD model are derived from the condition number of the corresponding system matrix. Multiple SSCs are defined to characterize both invertibility and stability of the system matrix. To perform the analysis, a class of system matrices is defined so that the system matrix depends on few parameters. The class is chosen so that it has wide enough applicability to cover thoroughly a configuration/expansion combination of interest, but not so wide as to make the analysis impractical. For the present study, we select a system matrix class for a 2-D circular fan-beam geometry using a square-pixel array. The SSCs are chosen so that they provide a useful characterization of any system matrix class, but the particular values associated with the SSCs in this work apply only to the narrow system matrix class defined. While the article presents a strategy for defining full sampling, the analysis must be redone with any alteration to the system matrix class.
After deriving the SSCs for the particular circular fan-beam CT system matrix class, we apply sparsity-exploiting IIR in the form of constrained TV-minimization. We consider the specific application of CT to breast imaging and use a realistic and challenging discrete phantom. We use the SSCs as reference points of full sampling for quantifying the undersampling admitted by each of the conducted reconstructions. Specifically, we demonstrate significant differences in undersampling admitted for reconstruction from few views compared to few bins. We study how variations to the reconstruction optimization problem, to the image quality metric, to the discretization method for the system matrix, and to the sparsity of the phantom image affect the results.
In Section II we describe the CT imaging model and present the particular system matrix class we employ for circular fan-beam CT reconstruction. In Section III we give a background on sparsity-exploiting methods. In Section IV the SSCs are presented and their application is illustrated for the 2-D circular fan-beam case. Finally, Section V illustrates an example study on quantifying admissible undersampling by constrained TV-minimization employing the discussed SSCs.
II. Class of System Matrices for the Discrete-to-Discrete Imaging Model
A. The X-Ray Transform
Explicit image reconstruction algorithms such as FBP are based on inversion formulas for the CC cone-beam or X-ray transform model
| (1) |
where g, the line integral over the object function f from source location s⃗ in the direction θ⃗, is considered data. Fan-beam FBP, for example, inverts this model for the case where the source location s⃗ varies continuously on a circular trajectory surrounding the subject, and at each s⃗ the ray-direction θ⃗ is varied continuously through the object in the plane of the source trajectory.
B. The Discrete-to-Discrete Model
For most IIR algorithms, the CC imaging model is discretized by expanding the object function in a finite expansion set, for example, in pixels/voxels. Furthermore, the discrete digital sampling of the CT device is accounted for by directly using the sampled data without interpolation. The effect of both of these steps is to convert the imaging model to a discrete-to-discrete (DD) formulation
| (2) |
where g⃗ represents a finite set of ray-integration samples, f⃗ are coefficients of the object expansion, and X is the system matrix modeling ray integration. This DD imaging model is almost always solved implicitly, because the matrix X, even though sparse, is beyond large for CT applications: X is in the domain of a giga-matrix for 2-D imaging and a tera-matrix for 3-D imaging.
A central point motivating the strategy of the present work is that the DD imaging model has a more focused scope than the CD model, because the former can often be derived from the CD model by expanding the continuous image domain with a finite set of functions. How the discretization of the CD model is done for CT to achieve the DD imaging model is not standardized. Many expansion elements have been used in CT studies; in addition to pixels, for example blobs [27], wavelets [28], [29], and natural pixels [30], [31]. Also, the matrix elements using only the pixel expansion set can be calculated in different ways that all tend toward the CC model in the limit of shrinking pixel size and detector bin size. Different modeling choices will necessarily alter X. This tremendous variation in X means that it is important to fully specify X for each study, and it is important to recharacterize X for any change in the model. For example, changing pixel size can have large impact on the null space of the system matrix in the DD model.
In order to describe precisely and provide a delimitation of the system matrices considered in the present work, we introduce the notion of a system matrix class. Any given system matrix depends on numerous model parameters determining the scanning geometry, sampling and discrete expansion set. A system matrix class consists of the system matrices arising from fixing a number of these parameters and leaving a subset of the parameters free. The system matrix class can then be studied by varying these free parameters.
C. The System Matrix Class Used in the Present Study
In CT, projections are acquired from multiple source locations which lie on a curve trajectory and the source location s⃗(λ) is specified by the scalar parameter λ. The circular trajectory is the most common, and is what we use here
where R0 is the distance from the center-of-rotation to the X-ray source, and set to R0 = 40 cm in the present work. The detector bin locations are given by
where D is the source-to-detector-center distance (D = 80 cm in the present work), and u specifies a position on the detector. The ray direction for the detector-geometry independent data function is
The 2π arc is divided into Nviews equally spaced angular intervals, so that the source parameters follow:
| (3) |
where
| (4) |
The detector is subdivided into Nbins
| (5) |
where DL is the detector length (DL = 41.3 cm), umin = −DL/2, Δu = DL/Nbins, and j ∈ [0, Nbins − 1]. The detector length is determined by requiring it to detect all rays passing through the largest circle inscribed within the square N × N image array for which we use the side length 20 cm. We restrict the unknown pixel values to lie within this circular field-of-view (FOV), and the number of unknown pixel values Npix is
| (6) |
where the actual value, which has to be an integer, is given with each simulation below.
Effectively, the dimensions of the projector X are M = Nviews × Nbins rows (number of ray integrations) and Npix columns (number of variable pixels). To obtain the individual matrix elements, the line-intersection method is employed, where Xm,n is the intersection length of the mth ray with the nth pixel. This description completely specifies the system matrix class for the present circular fan-beam CT study, and the free parameters of this class are N, Nviews, and Nbins.
III. CT Image Reconstruction by Exploiting Gradient-Magnitude Sparsity
Reconstruction of objects from undersampled data within the DD imaging model corresponds to a measurement matrix X with fewer rows than columns. The infinitely many solutions are narrowed down by selecting the sparsest one, i.e., the one that has the fewest number of nonzeroes, either in the image itself or after some transform has been applied to it. Mathematically, the reconstruction can be written as the solution of the constrained optimization problem
| (7) |
Here, Ψ is a sparsifying transform, for instance a discrete wavelet transform, and ||·||0 is the ℓ0-“norm” (although it is in fact not a norm), which computes its argument vector’s sparsity, that is, counts the number of nonzeroes. The equality constraint restricts image candidates to those agreeing exactly with the data.
Central results in CS derive conditions on X drawn from certain random system matrix classes such that f⃗* is exactly equal to the underlying unknown image that gave rise to the data g⃗. Two key elements are sparsity of Ψ(f⃗) and incoherence of X: exact recovery depends on the size of g⃗ being larger than some small factor of ||Ψ(f⃗)||0 [13], and the concept of incoherence is needed to ensure that the few measurements g⃗ available give meaningful information about the nonzero elements of Ψ(f⃗). Other important results in CS involve the relaxation of the non-convex ℓ0-“norm” to the convex ℓ1-norm
| (8) |
In contrast to (7), this convex problem is amenable to solution by a variety of practical algorithms, although the large scale of CT matrices still presents a challenge for algorithm development. Another important contribution from CS is the derivation of conditions under which the solution to (8) is identical to the solution to (7), so that the sparsest solution can be found by solving (8).
For application to medical imaging, it was suggested in [12] that a potentially useful Ψ would be to have Ψ compute the discrete gradient magnitude of f⃗, i.e., for the jth pixel
| (9) |
where Dj computes a finite-difference approximation of the gradient at each pixel j, and the two-norm also acts pixel-wise on the differences. In CT, for example, the typical image consists of regions having an approximately constant gray-level value separated by sharp boundaries between various tissue types. The magnitude of the spatial gradient of such images is zero within constant regions and nonzero along edges, so the gradient magnitude image can be sparse. The ℓ1-norm applied to the gradient magnitude image is known as the total variation (TV) semi-norm
| (10) |
and the optimization problem of interest becomes
| (11) |
However, the theoretical results from CS do not extend to the CT setting. Three properties that separate CT matrices from typical CS matrices are that CT matrices:
are structured and do not belong to random matrix classes for which CS results are proved [13];
can have rank smaller than the number of rows, which means that there exist vectors g⃗ in the data space that are inconsistent with X, and accordingly the linear imaging model (2) has no solution;
may be numerically ill-conditioned in case of having more rows than columns (data set size is greater than the image representation).
Nevertheless, it has been demonstrated empirically in extensive numerical studies with computer phantoms under ideal data conditions as well as with actual scanner data that highly accurate reconstructed images for “undersampled” projection data can be obtained from (8) and variants thereof.
It is precisely this last phrase which is of interest in the present paper: what exactly does it mean to have “undersampled” data for CT? Undersampled data implicitly relies on a certain level of sampling being sufficient—but no such precise concept exists for CT using the DD imaging model, to the best of our knowledge. Without a reference point for having sufficient sampling it is difficult to quantify admissible levels of undersampling. In the present paper, we aim to provide this reference point. Specifically in Section IV, we propose sufficient-sampling conditions (SSCs) to be computed for specific system matrix classes, and which serve as a reference for quantifying the admissible undersampling for sparsity-exploiting reconstruction. Application of the SSCs is demonstrated with numerical simulations of breast CT.
IV. Sufficient-Sampling Conditions
In considering sufficient sampling for circular fan-beam CT, the CC model is recast as a CD model by introducing a discrete sampling operator, usually taken to be evenly distributed delta functions, on the CT sinogram space. Making the assumption that the underlying sinogram function is band-limited, many useful and widely applicable results have been obtained, see for example Sec. 3.3 of [32] and [33]–[35]. Furthermore, for more advanced scanning geometries and sampling patterns there are available tools for analysis such as singular value decomposition (SVD), direct analysis of multi-dimensional aliasing, and the evaluation of the Fourier crosstalk matrix [36]–[38]. These important results, however, do not apply directly to IIR, since for the DD model we need to take into account the finite image expansion set.
We consider an empirical approach for characterizing sufficient sampling within a class of system matrices. The idea is to fix the image representation, which for the circular fan-beam system matrix class is the parameter Npix, and then vary the sampling parameters Nviews and Nbins to ensure accurate determination of the pixel values. This is done by establishing sufficient-sampling conditions (SSCs) based on matrix properties in the considered system matrix class. If the system matrix class is altered, the SSC-analysis must be redone.
A. SSC Definitions
The SSCs, we propose, characterize invertibility and ill-conditioning of the system matrix class. In considering the DD imaging model (2), the data g⃗ are restricted to the range of X. This separates out the issue of model inconsistency which does not have direct bearing on sampling conditions.
We define SSC1 to be sampling such that X has at least as many rows as columns. If there are fewer rows than columns, X necessarily has a nontrivial null space, and solutions of (2) will not be unique. Even if the number of rows is equal to or larger than the number of columns, there may still be a nontrivial null space, because the rows can be linearly dependent. In addition to SSC1, we define SSC2 to mean that X has a null space consisting only of the zero image, or equivalently, that the smallest singular value σmin of X is nonzero. Existence of a unique solution to (2) is ensured by SSC2. Both SSC1 and SSC2 can be evaluated for any system matrix class.
Neither of SSC1 and SSC2 address numerical instability and to address that, we employ the condition number of X, the ratio of the largest and smallest singular values
| (12) |
The condition number κ can be as small as 1 and the larger κ becomes, the more numerically unstable is solution of X f⃗ = g⃗. How to use κ to define a SSC requires some discussion.
Whereas sensing matrix classes studied in CS typically are well-conditioned—for instance the square discrete Fourier transform (DFT) matrix is orthogonal, thus having a condition number of 1—the system matrices encountered in X-ray CT can have a relatively large condition number [32], [39], which leads to numerical instability and thus large sensitivity to noisy measurements. Even if SSC2 holds, the condition number κ is finite but may still be large, potentially allowing other images than the desired solution to be numerically close to satisfying X f⃗ = g⃗. If we fix the image representation, which for the present 2-D circular fan-beam setup amounts to fixing Npix, and increase the sampling, allowing Nviews and Nbins to increase toward ∞, the condition number will decrease toward a limiting condition number
| (13) |
where the DC subscript refers to the fact that X is limiting to a discrete-to-continuous (DC) system matrix2. The limiting condition number κDC is the best-case κ for a fixed image representation, but κDC may still be larger than 1.
For actual CT scanners, it is not practical to allow Nviews and Nbins to increase without bound, and empirical experience shows diminishing improvements in doing this. To balance the impracticality of going to continuous sampling on the one hand against the need to optimize numerical stability on the other, we introduce SSC3 to mean that the condition number of X satisfies
| (14) |
where rsamp is a finite ratio parameter greater than 1. The smaller the choice of rsamp, the closer X is to the DC limit. This SSC can also be generally applied to other system matrix classes, but the appropriate parameter setting of rsamp will be specific to a particular class.
Finally, we introduce SSC4 specifically for the present 2-D circular fan-beam system matrix class. This SSC is taken to mean 2N samples in both the view and bin directions, i.e., Nviews = Nbins = 2N. This SSC is simple to evaluate, and we will demonstrate empirically that it is a useful condition, which acts as a good approximation for attaining SSC3 with rsamp = 1.5. This SSC is specific to the system matrix class investigated here. Even slightly different system matrix classes might not allow for the same SSC4 definition.
Our strategy is similar to analysis presented in early works on CT, such as in [39], but the point here is not novelty of the analysis; rather we need to establish a reference point by which to evaluate the sampling reduction admitted by sparsity-exploiting methods.
In what follows, the proposed SSCs are examined for the 2-D circular fan-beam system matrix class. First, small systems are considered, where X can be explicitly computed and analyzed so that the full set of singular values of X is attainable. Second, we argue that our conclusions generalize to larger, more realistic systems, where X is impractical to store in computer memory and it is only feasible to compute the smallest and largest singular values.
B. SSCs for Small Systems
We consider a small N = 32 image array with Npix = 812, and generate system matrices X for different numbers of views, Nviews ∈ [8, 128], and detector bins, Nbins ∈ [8, 128]. The condition number κ(X) is computed through direct SVD of X for all values of Nviews and Nbins within the specified parameter ranges, and κ(X) as a function of Nviews (for fixed Nbins = 64) and Nbins (for fixed Nviews = 64) is shown in Fig. 1. The plots show three phases: the left-most part, where the condition number is infinite; the middle, where the condition number becomes finite and decays slowly; and the right-most part, where it remains relatively stable. The positions of the different SSCs are shown at the top and bottom, and they serve as transition points between the three phases.
Fig. 1.
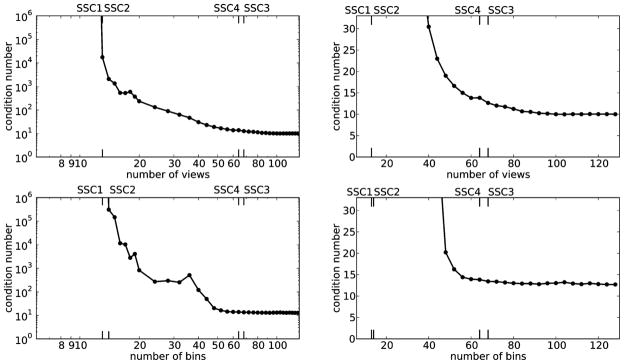
Condition numbers for system matrices (line-intersection) modeling circular fan-beam projection data from the 812-pixel circular FOV contained within a 32 × 32 pixel square. Top: number of bins is fixed at 64. Bottom: the number of views is fixed at 64. Left: Double-logarithmic plot for overview. Right: Linear plot of details. The abbreviations SSC1, SSC2, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A.
For varying the number of views, SSC1 occurs at Nviews = 13, where X is of size 832×812. In fact, also SSC2 occurs here, since κ has become finite. For varying the number of bins, SSC1 occurs at the same place, but SSC2 needs 14 bins. In general, we have no way to determine whether SSC1 and SSC2 occur in the same position for the whole system matrix class, which makes SSC1 less reliable as a general reference of full sampling. On the other hand, SSC2 is a reliable reference point for full sampling, however, SSC2 requires more work to determine, because its location can change with a change of system matrix class.
After passing SSC2, the condition number κ decreases. For larger Nviews and Nbins, the decay becomes slower, and we pick rsamp = 1.5 as a trade-off between a sufficiently small condition number and a finite number of views. As an approximation of κDC we take the value of κ at Nviews = Nbins = 4N = 128, yielding κDC = 9.17. Then SSC3 occurs at Nviews = 68 and at Nbins = 68, which suggests a symmetry in Nviews and Nbins. On the other hand, the decrease in κ during the middle part is not symmetric in the parameters Nviews and Nbins; the decrease in κ with Nviews is gradual while that of Nbins is step-like at Nbins = 48. Nevertheless, at the position of SSC3, there is only small further reductions in κ to be gained by going to larger Nviews and Nbins. The simpler condition SSC4 occurs at Nviews = 64 and Nbins = 64, and it approximates SSC3 with rsamp = 1.5 closely.
C. Altering the System Matrix Class
Altering the system matrix class will in general alter the SSCs. To demonstrate this effect, we replace the line-intersection based system matrix class by ray-tracing, using nearest-neighbor interpolation at the mid-line of each pixel row. The experiment is repeated and the obtained condition numbers are shown in Fig. 2, along with the ones based on line-intersection, for comparison. The shown SSCs are for ray-tracing. While the same overall trends are seen, there are some significant differences. First, for fixed Nviews = 64 we need Nbins = 16 to obtain SSC2, compared to 14 for line-intersection. This firmly establishes that SSC1 does not imply SSC2, and that the precise position of SSC2 cannot be inferred from knowing SSC2 of a similar system matrix. Second, the ray-tracing condition numbers are smaller than the same for line-intersection, for instance, kDC = 7.23 is 20% lower relative to the line-intersection version of X. That the ray-tracing condition numbers are lower does not necessarily mean that this method is “better” than the line-intersection method for real-world applications, because the other side of the story is model error, which is not considered here. Finally, the positions of SSC3 are different, for fixed Nbins = 64 coinciding with SSC4, while for fixed Nviews = 64 occurring at Nbins = 56. Still, for larger Nviews and Nbins there are only small further reductions in κ to be gained, and SSC4, at rsamp = 1.45, approximates SSC3 closely.
Fig. 2.
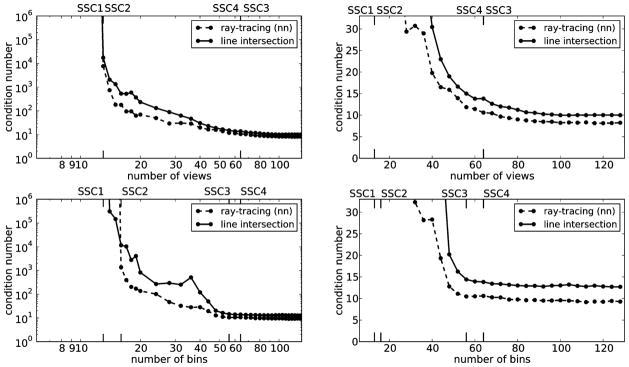
Condition numbers for system matrices (ray-tracing with nearest neighbor interpolation, and line-intersection for comparison) modeling circular fan-beam projection data from the 812 pixels circular FOV contained within a 32 × 32 pixel square. Top: number of bins is fixed at 64. Bottom: the number of views is fixed at 64. Left: double-logarithmic plot for overview. Right: linear plot of details. The labels SSC1, SSC2, SSC3, and SSC4 are the sufficient-sampling conditions, discussed in Section IV-A, for the ray-tracing system matrix.
One could imagine that other system matrix classes such as employing area-weighted integration instead of the linear integration or different basis functions could alter the condition numbers of X even more substantially. We do not include results for more system matrix classes, as our goal here is not to provide a comprehensive comparison between all conceivable classes, but merely to stress that different classes can have different SSCs, and to propose carrying out the same study for gaining insight in the particular system matrix class at hand.
D. SSCs for Larger Systems
The results shown in Figs. 1 and 2 give a sense about various sampling combinations, but the system size is unrealistically small. In this section we aim to extend the results to larger systems. For large X, it is not practical to compute the direct SVD for evaluating κ. Instead, we seek only to obtain σmin and σmax, which can be accomplished through the power and inverse power methods [40].
For characterizing the present circular, fan-beam system matrix class, κ(X) is computed for larger image arrays with sizes N = 32, 64, 128, 256. We focus on sampling conditions where Nbins = 2N and report the data sampling in views, Nviews, as multiples of N, ranging from 1.0 to 4.0. The left plot in Fig. 3 shows the condition number as a function of N for each sampling size on a double logarithmic scale. A clear linear trend is seen in all cases and the best linear fits and their slopes are also shown, in all cases very close to 0.50, and we conclude that κ scales with . For increasing Nviews, the condition numbers tend towards the bottom line, note in particular that not much difference is seen between Nviews = 3N and Nviews = 4N indicating that the limiting κ is approached. We conclude that κDC also scales with . As a result, it can expected that at SSC4, i.e., Nviews = Nbins = 2N, κ(X)/κDC ≈ 1.5, which was the case at N = 32. Hence, SSC4 will continue to approximate SSC3 closely, when the image size is increased. To further support this conclusion we show in the right plot of Fig. 3 the ratio rsamp = κ(X)/κDC as function of the number of views (normalized by N) for each N. The rsamp values are almost identical for all N and intersect the line rsamp = 1.5 very close to Nviews = 2N, which is precisely SSC4.
Fig. 3.
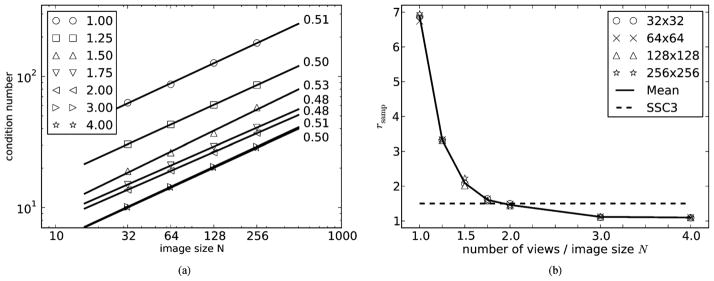
Left: condition numbers as function of image size. Each symbol represents different number of views ranging from N to 4N. Circular image arrays are used with sizes given by N = 32, 64, 128, 256. The number of bins is fixed at 2N. With each number of views is also shown the best linear fit and its slope is given. In all cases the condition number scales with . Right: same condition numbers normalized by the respective κDC at each N and plotted as function of view number normalized by image size N. The full line is the point-wise mean and the dashed line is the position of SSC3 with rsamp = 1.5. Independently of N, SSC3 with rsamp = 1.5 occurs very close to Nviews = 2N.
E. Summary of SSCs
The conditions SSC1 and SSC2 are useful reference points for invertibility of X and can be computed for any system matrix class. The size of the gap between SSC1, X being square, and SSC2, X having an empty null space, is governed by inherent linear dependence of the rows of the system matrix. Because the results show little difference between SSC1 and SSC2 for the present system matrix class and SSC1 is easier to compute, we use only SSC1 in the simulation studies in Section V.
For system matrix classes representing CT imaging, stability of the system matrix plays an important role, and accordingly we have introduced SSC3 which also can be computed for any system matrix class. For the present, circular fan-beam system matrix class, SSC3 at rsamp = 1.5 is a useful operating point, and this level of sampling is well approximated by the simple rule, SSC4, where Nviews = Nbins = 2N. We point out that for other system matrix classes, even those representing circular fan-beam CT, other operating points for SSC3 may be more appropriate and empirical studies must be performed to see if a simple condition, such as SSC4, can approximate accurately SSC3.
In the remaining part of the paper we demonstrate how we can use the SSCs as a reference for stating admissible undersampling factors in sparsity-exploiting reconstruction.
V. Numerical Experiments With SSCs and Sparsity-Exploiting Undersampled Reconstruction
In this section we investigate sparsity-exploiting IIR in numerical simulation studies. Our goal is to numerically demonstrate and quantify the undersampling admitted by sparsity-exploiting IIR, i.e., at which an accurate reconstruction is obtained. We use numerical simulation, because we are unaware of any theoretical results establishing undersampling guarantees for the present system matrix class. We focus here on exploiting gradient-magnitude sparsity by use of constrained TV-minimization.
Three important factors differentiate the present studies from previous simulation work with constrained TV-minimization:
use of phantoms with realistic complexity;
numerically accurate solution to the constrained TV-minimization problem;
quantitative references for full sampling—the central topic of the paper.
For each factor, we briefly discuss the significance.
Much simulation work on constrained TV-minimization has used regular, piece-wise constant phantoms, such as the Shepp–Logan phantom, to demonstrate the promise of the technique. For that purpose, such unrealistically simple phantoms were fine, and simulations were generally followed up by demonstration with actual CT projection data. For the present purpose of quantifying admissible undersampling, we need phantoms with similar complexity as would be encountered in CT applications, and as an example we focus on breast CT. The standard measure of complexity employed in CS is the image sparsity, i.e., the number of nonzeroes in the image, or in the case of TV-minimization the number of nonzeroes in the gradient-magnitude image. Accordingly, we choose a digital phantom with realistic gradient-magnitude sparsity modeling breast anatomic structure [41].
The accuracy requirement on the solver of constrained TV-minimization for the present study is extremely high. The optimization problems in Section V-B, below, are solved to high accuracy, which has been made possible only recently for large-scale CT problems involving the TV-semi-norm through development of advanced first-order methods [21], [22], [25]. This level of accuracy is necessary, because empirical image error results obtained by sweeping parameters of the system matrix class will be used for determining whether a numerically computed solution is close to the original. High-accuracy solutions remove any doubt about whether the resulting images, and the corresponding quantitative measures, depend on the algorithm used to solve constrained TV-minimization.
The SSCs defined above provide reference points useful for interpreting the empirical results of this section and help to quantify undersampling admitted by constrained TV-minimization.
A. Breast CT Background
Breast CT [42], [43] is being considered as a possible screening or diagnostic tool for breast cancer. The system requirements are challenging from an engineering standpoint, because this type of CT must operate with a total exposure similar to two full-field digital mammograms (FFDM). FFDMs for a screening exam entail two X-ray projections, while breast CT acquires on the order of 500 X-ray projections. The exposure previously used for only two views is now divided up among 250 times more projections. Accordingly, sparsity-exploiting IIR algorithms for CT may have an impact on the breast CT application. The potential to reconstruct volumes from fewer views than a typical CT scan might allow an increased exposure per view.
For the present study, we employ the breast phantom originally described in [41] and displayed in Fig. 4. It consists of Npix = 51 468 pixels within the circular image region, contained in a 256 × 256 array. The breast phantom has a small region of interest (ROI) containing five tiny ellipses which model microcalcifications. The gray values range from 1.0 to 2.3, normalized to the background fat tissue, hence unit-less. The modeled tissues and corresponding gray values are fat at 1.0, fibroglandular tissue at 1.10, skin at 1.15, and microcalcifications ranging from 1.9 to 2.3. The sparsity in the gradient magnitude image is 10019, or roughly one fifth of Npix. Because we are investigating the utility of gradient-magnitude sparsity-exploiting algorithms, it is important that the test phantom have a realistic sparsity level relative to the actual application.
Fig. 4.

Left: 256 × 256 pixelized breast CT phantom used in the present study. Middle: same with ROI around microcalcifications shown magnified as inset. Right: the gradient magnitude image, which has a sparsity of 10019 nonzero pixel values.
B. Simulation Optimization Problems and Algorithms
Our goal is to evaluate quantitatively what level of undersampling reconstruction through (11) allows. Similar to the analysis of the linear imaging model (2), only data g⃗ in the range of X is considered. Although not a realistic assumption for actual CT data, this “inverse crime” scenario [44] is appropriate for obtaining a reference of the underlying admissible undersampling. For the numerical studies, we solve a relaxed form of (11), where the data equality constraint is replaced by an inequality allowing for a small deviation ε from data as measured by the distance D between the data g⃗ and the projection X f⃗ of some image f⃗
| (15) |
where
Scaling the data error D with Nviews and Nbins is done to enable comparison across images reconstructed from different view and detector bin numbers. The constrained TV-minimization problem is
| (16) |
Accurate solution of (16) is nontrivial; although the objective is convex, it is not quadratic. The algorithm employed here solves its Lagrangian using an accelerated first-order method, using only the objective and its gradient, and is explained in detail in [21]. An important technical detail for this algorithm is that it requires that the image TV-term be differentiable. For the algorithm implementation we use a smoothed TV-term, , with a small smoothing parameter, η = 10−10. One convergence check on the algorithm is performed by evaluating
| (17) |
where R(f⃗) denotes a generic regularization term, and for constrained TV-minimization R(f⃗) = ||f⃗||TV. The conditions for convergence, derived in [4], are that the gradients of the data-error and regularization terms are back-to-back, cos α = −1, and D(X f⃗, g⃗) = ε. The latter condition assumes that the data-error constraint is active, which is the case for all the simulations performed here. For the present results, iteration is terminated when both
| (18) |
are satisfied.
C. Admitted Undersampling by ℓ2-TV
We are interested in two separate notions of accurate reconstruction: exact reconstruction and stable reconstruction. By the former, we mean that the reconstructed image is identical to the original. Exact reconstruction is only possible when ε = 0, because the regularizing effect of a nonzero ε introduces a bias relative to the original image. Having ε = 0 is only relevant for noise-free data, which means that stability is not an issue. Since SSC2 ensures a unique solution to (2), it can be used as a full sampling reference point for exact reconstruction. In practice, for the considered system matrix class, we found little difference in locations of SSC1 and SSC2, and we will therefore use SSC1 as a surrogate for SSC2.
Stable reconstruction is the corresponding concept for fixed, nonzero ε, where we cannot hope for exact reconstruction. Instead, we are interested in the degree of sampling at which further increase in sampling leads to no further improvement in the reconstruction. This point of stable reconstruction can be compared to SSC3, since that is the point where no further improvement of the system matrix condition number occurs. Since SSC4 was seen to approximate SSC3 for the present system matrix class and is simple to determine, it could also be considered to use SSC4 instead for the reference point.
In the simulations, we take the image array to be the same as that of the breast phantom N = 256. The parameters of the circular, fan-beam system matrix class are varied in a fashion parallel to the condition number plots of Fig. 1: first, Nbins is fixed at 2N and Nviews is varied in the range [32, 512]; and second, Nviews is fixed at 2N and Nbins is varied in the range [32, 512].
Computing SSC1 and SSC4 is straightforward and they occur at Nviews = 101 and Nviews = 512, respectively. Computation of SSC3 was performed using the procedure outlined in Section IV-D. For the fixed-bin case, SSC3 occurs at Nviews = 492, with rsamp = 1.51 and for the fixed-view case at Nbins = 456.
In order to assess the undersampling with respect to exact reconstruction admitted by exploiting image gradient-magnitude sparsity, we need access to the solution of ℓ2-TV for a data-equality constraint, ε = 0. We are unaware of efficient algorithms that make ℓ2-TV with ε = 0 feasible to solve in acceptable time for systems of realistic size. With the algorithm described in Section V-B, we can obtain an approximation by solving ℓ2-TV with ε = 10−3, 10−4, and 10−5 and thus study the reconstruction error as ε approaches zero. As an error measure, we use the root-mean-square-error (RMSE)
| (19) |
where f⃗* is the solution to ℓ2-TV and f⃗0 is the original phantom.
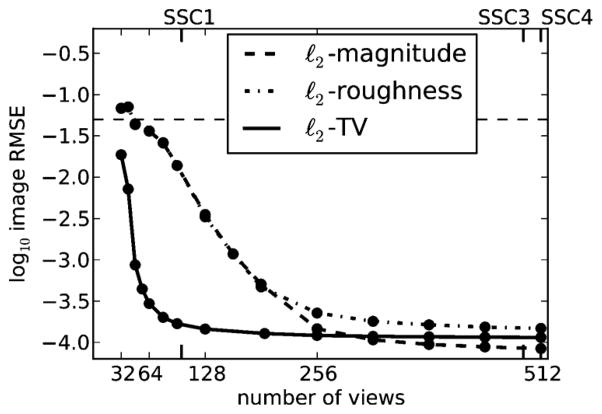
The computed RMSEs for the results from ℓ2-TV are displayed in Fig. 5. As in Section IV we show SSC-locations at the top and bottom. The horizontal line shows the minimum gray level contrast, 0.05, in the test phantom and provides a reference for the RMSE. An image RMSE much less than the minimum gray-level contrast is an indicator that the reconstructed image is visually close to the original phantom (barring pathological distributions of the image error).
Fig. 5.
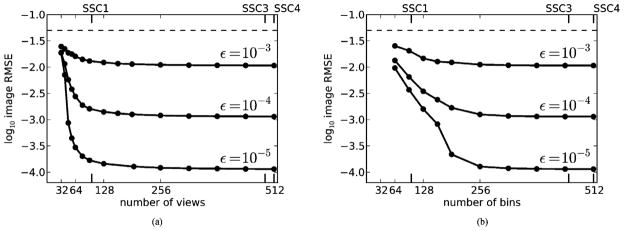
Image RMSE, δ, for the data distance D(X f⃗, g⃗) constrained by ε = 10−3, 10−4, and 10−5. The image size is 256 × 256. Left: fixed Nbins = 2N = 512, as function of Nviews. Right: fixed Nviews = 2N = 512, as function of Nbins. The labels SSC1, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A.
For the plots of δ versus Nviews, we note a steep drop in δ as Nviews increases past 40 views and the drop is increasingly rapid as ε decreases. Based on these curves we extrapolate that exact reconstruction would be attained for Nviews ≈ 50 at ε = 0. Because SSC1 occurs at Nviews = 101, we note an admitted undersampling with respect to exact reconstruction of a factor of 2 for the present simulation. Note that use of SSC1 leads to a conservative estimate, because SSC2 can only be larger than SSC1.
For the plots of δ versus Nbins, the image RMSE curves drop much more gradually at each of the ε’s investigated. Based on these curves it is only clear that δ is tending to zero at Nbins = 190 as function of ε. Comparing to SSC1 at Nbins = 101, we do not observe any level of admitted undersampling in the bin-direction with respect to exact reconstruction. Extending the range of ε to smaller values may yield a different conclusion.
This difference reflects an asymmetry in sampling of the two parameters of X. We note that the asymmetry was also observed in the condition number dependence on Nviews and Nbins for the N = 32 simulations in Section IV-B. For the present N = 256 simulations, a relatively large κ(X) = 3.2 · 104 is seen for Nbins = 128 and Nviews = 512, compared to κ(X) = 1.5 · 103 for Nbins = 512 and Nviews =128. The results demonstrate a larger potential for successful TV-based reconstruction from few views compared to using few bins.
Regarding stable reconstruction, we note that the curves in Fig. 5 all exhibit a plateau, where δ levels off with increasing Nviews or Nbins, meaning that no gain in image RMSE is achieved by increasing sampling. Thus, the left-most point of these plateaus is the point of stable reconstruction. For the plot varying Nviews, we see that stable reconstruction begins at Nviews ≈ 80, which is a factor of 6 fewer than SSC3. For the plot varying Nbins, the stable reconstruction begins at Nbins ≈ 200, a factor of approximately 2 fewer than SSC3.
These results show quantitatively that significant undersampling in Nviews, particularly with respect to stable reconstruction, is admitted for ℓ2-TV. This conclusion is achieved with a phantom modeling a realistic level of gradient-magnitude sparsity. We do point out, however, that these empirical results only apply to the presented simulation. To support the present conclusion for admitted undersampling, we vary in Section VI different aspects of the ℓ2-TV study.
D. Altering the Optimization Problem
To support the use of the gradient-magnitude sparsity exploiting ℓ2-TV for admitting undersampling, we compare results with two other optimization problems
| (20) |
and
| (21) |
where ∇ represents a numerical gradient operation and is computed by forward finite-differencing. The Lagrangian form of these optimizations are two forms of Tikhonov regularization commonly used for IIR.
The solutions to ℓ2-magnitude and ℓ2-roughness are obtained with linear conjugate gradients (CG) applied to the Lagrangians of these problems with the multiplier being adjusted until the data-error constraint holds with equality. The convergence criteria are the same as what is specified in (18) except that for ℓ2-magnitude and for ℓ2-roughness.
We focus on the ε = 10−5 case and plot image RMSEs for ℓ2-magnitude, ℓ2-roughness and ℓ2-TV as function of Nviews for fixed Nbins = 512 in Fig. 6. We note little difference between results from ℓ2-magnitude and ℓ2-roughness but a large gap between these results and those of ℓ2-TV. The optimization problems ℓ2-TV and ℓ2-roughness differ only on the norm of the image-gradient in the regularization term, while ℓ2-roughness and ℓ2-magnitude differ by the presence of the gradient. It is clear from Fig. 6 that for this simulation, the ℓ1-norm has the greater impact.
Fig. 6.
Image RMSE, δ, for ℓ2-magnitude, ℓ2-roughness, and ℓ2-TV reconstructions as a function of the number of views for the number of bins fixed at 512, and the data distance D(X f⃗, g⃗) constrained by ε = 10−5. The horizontal dashed line shows the level of the minimum gray-level contrast in the breast phantom. The labels SSC1, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A.
For large Nviews, the ℓ2-TV RMSE is actually slightly larger than that of ℓ2-magnitude. The reason is the regularizing effect of having a nonzero ε, which causes a small bias of the solutions compared to the original image. The relative size of the biases are not known in advance. We conclude that the ℓ2-TV solution is not to prefer over the ℓ2-magnitude and ℓ2-roughness solutions when Nviews approaches the SSC3 (rsamp = 1.5). Nevertheless, there is a certain “sampling window,” for the present phantom, approximately for Nviews ∈ [50, 256], where the TV-solution is superior to Tikhonov regularization in terms of RMSE.
In Fig. 7, we overlay the results of ℓ2-magnitude onto the results of ℓ2-TV from Fig. 5 in order to investigate possible un-dersampling admitted by ℓ2-magnitude. The results of ℓ2-roughness are not shown because they are similar to those of ℓ2-magnitude and to prevent clutter in the figure. Going from left to right, both plots show a gradual decrease of δ for ℓ2-magnitude as Nviews and Nbins increase with δ leveling off at Nviews ≈ 300 and Nbins ≈ 400. For the investigated range of ε, ℓ2-magnitude does not admit any undersampling with respect to exact reconstruction, but does show a marginal undersampling with respect to stable reconstruction as the corresponding δ-curves reach the plateau before SSC3 and SSC4. In summary, the un-dersampling admitted by ℓ2-magnitude is substantially less that that admitted by ℓ2-TV for this simulation; particularly in considering view number undersampling with respect to stability.
Fig. 7.
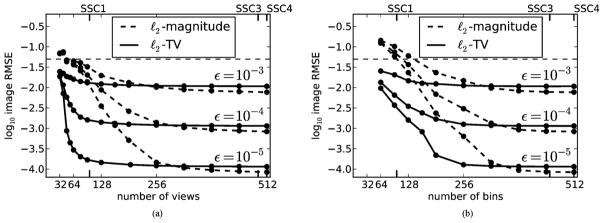
Image RMSE, δ, for ℓ2-magnitude and ℓ2-TV reconstructions and ε = 10−3, 10−4, and 10−5. Left: fixed Nbins = 2N = 512, as function of Nviews. Right: fixed Nviews = 2N = 512, as function of Nbins. The horizontal dashed line shows the level of the minimum gray-level contrast in the breast phantom. The labels SSC1, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A.
E. Altering the Image Evaluation Metric
Conclusions based on evaluating reconstructed images with a single summarizing metric, such as the RMSE, can be misleading. While our aim is not a fully realistic image evaluation, we want to show how the results can potentially change with a change of metric. For example, with the task of microcalcification detection in mind, one might consider the RMSE of only the ROI of the microcalcifications displayed in Fig. 4. This RMSE is denoted δROI. Fig. 8 shows the corresponding plot for δROI. While there are numerical differences between the δ and δROI plots, the trends are similar, giving us further confidence that the RMSE of the entire image, δ, can be used for investigating admitted undersampling.
Fig. 8.

Image RMSE as in Fig. 6 but for δROI, i.e., the RMSE restricted to the ROI around the microcalcifications.
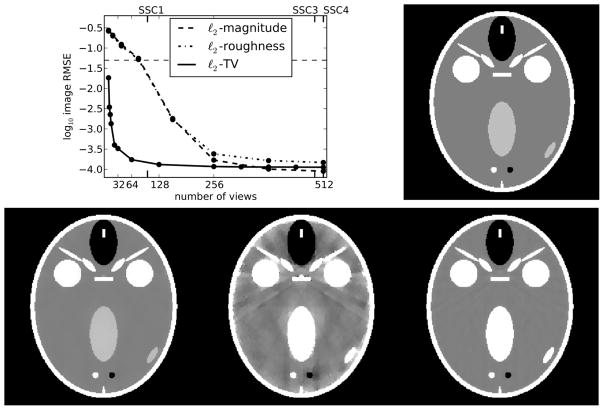
Another way to evaluate images is by visual comparison. The reconstructed images in Fig. 9 are shown for a range in Nviews showing the transition to accurate image reconstruction by ℓ2-TV. That the ℓ2-magnitude and ℓ2-roughness show strong artifacts for this range is expected as their corresponding image RMSEs are at the level of the minimum phantom contrast level. Interestingly, the microcalcifications can be identified and well-characterized in all reconstructions, although more clearly with more views. It may be argued that, from a utility point of view, that 32 views would suffice if we are solely interested in the microcalcifications and disregard the prominent artifacts of the background image. The ROI of the ℓ2-TV reconstructed images are shown with a narrow gray scale window in the bottom row to reveal the high level of accuracy at Nviews = 50. We emphasize that our goal is not a discussion about different artifacts but simply support our conclusions on undersampling from Section V-C by illustrating the behavior in the transition region around Nviews = 50.
Fig. 9.

First, second, third, and fourth columns show reconstructions from 32, 40, 48, 64 view data. The first, second, and third rows show ℓ2-magnitude, ℓ2-roughness, and ℓ2-TV images with ε = 10−5. The gray scale window is [0.95, 1.20] for the complete image, and [0.9, 1.8] for the ROI blow-ups. The fourth row shows the ℓ2-TV ROIs enlarged in an extremely narrow gray scale, [1.09, 1.11], in order to scrutinize the transition to sufficient sampling based on the object sparsity. These images show that 50 views is sufficient for this system and object.
F. Altering the System Matrix Class
To illustrate the change in results due to change in the system matrix class, the RMSE, δ, is again computed as function of Nviews for Nbins = 2N = 512 and for ε = 10−3, 10−4, and 10−5 but using a system matrix set up through ray-tracing with nearest-neighbor interpolation at the mid-line of each pixel row, as in Section IV-C. Results are plotted in Fig. 10. The overall trends are similar to those for line-intersection, however SSC3 occurs already at Nviews = 408, with rsamp =1.49. By closer comparison with the line-intersection results, it is seen that the nearest-neighbor RMSEs are smaller than the line-intersection RMSE at the same Nviews. This example serves to illustrate that the SSCs will change when the system matrix class is altered.
Fig. 10.
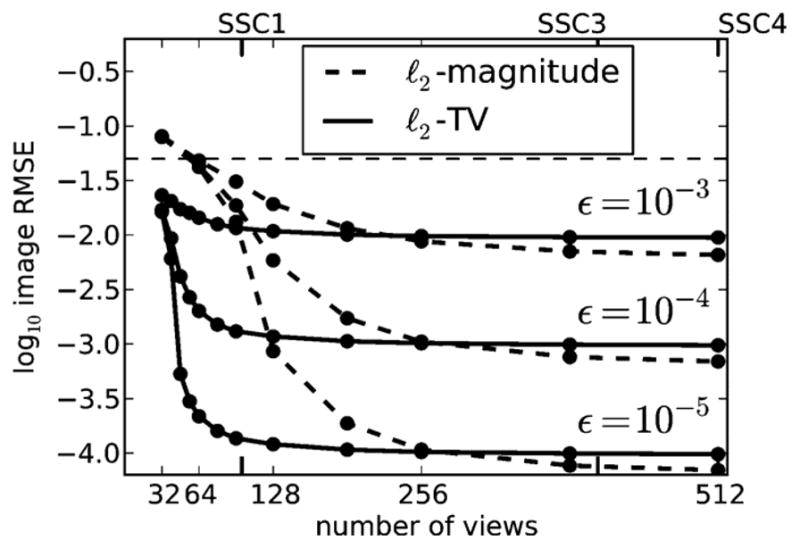
Image RMSE, δ, for ℓ2-magnitude and ℓ2-TV reconstructions, as in Fig. 6 for varying ε, computing X with ray-tracing and nearest-neighbor interpolation. Nbins is fixed at 512. The labels SSC1, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A.
While the present alteration is relatively minor, it is enough that the approximation SSC4 of to SSC3 is worse, and larger differences can be expected with more radical changes such as the use of nonpoint-like image expansion functions.
In terms of admissible undersampling for ℓ2-TV with the altered system matrix class, we see very similar undersampling factors for both exact and stable reconstruction as for the line-intersection class.
G. Altering the Phantom Sparsity
The breast phantom study is repeated employing a variation of the FORBILD head phantom [45] which is highly sparse in the gradient-magnitude image. The present version of the phantom, which is seen in Fig. 11, does not have the ear objects of the original phantom, and the contrast levels have been increased so that the minimum gray-level contrast is the same as for the breast phantom. The gradient magnitude sparsity is 2492, or approximately a quarter of the breast phantom. In Fig. 11, the obtained δ for ℓ2-magnitude, ℓ2-roughness and ℓ2-TV are shown as function of Nviews with Nbins = 2N = 512 and ε = 10−5.
Fig. 11.
Top: Image RMSE, δ, for ℓ2-magnitude, ℓ2-roughness, and ℓ2-TV reconstructions, as in Fig. 6, except that the data are generated from the head phantom shown on the right. The labels SSC1, SSC3, and SSC4 are the sufficient-sampling conditions discussed in Section IV-A. Bottom: images reconstructed for Nviews = 12 shown in a gray scale window of [0.9, 1.1] on the left and a narrow gray scale window of [0.99, 1.01] in the middle. On the right is the reconstructed image for Nviews = 32 in the narrow gray scale window [0.99, 1.01]. At Nviews = 12 the RMSE is 0.005 resulting in visible artifacts for the image shown in the 1% gray scale window, while the RMSE is a factor of 10 less for Nviews = 32.
The ℓ2-magnitude and ℓ2-roughness curves are almost identical to those of the breast phantom. The SSCs are unchanged, because the same system matrix class is used. That two so different looking phantoms show such similar δ-behavior suggests that the reconstruction quality of ℓ2-magnitude and ℓ2-roughness depend only weakly on the particular phantom.
For ℓ2-TV, on the other hand, the step-like transition occurs already at Nviews = 12, for which the reconstruction is shown in Fig. 11. We expect that this phantom would be recovered exactly at Nviews = 12 in the limit ε → 0, leading to an admitted undersampling with respect to exact reconstruction of a factor of approximately 8. Stable reconstruction occurs at Nviews ≈ 64, i.e., an undersampling also of a factor 8 with respect to stability.
Interestingly, the exact reconstruction result hints at the existence of a simple relation between sparsity and admitted undersampling. Compared to the breast phantom, there is a gain in undersampling by 8/2 = 4. In comparison, we note that the change in gradient magnitude sparsity relative to the breast phantom is 10019/2492 ≈ 4. That is, reducing the sparsity by a certain factor leads to an improvement in the admitted undersampling by the same factor. This result, if shown to hold, could be important for practical application of CS-inspired sparsity-exploiting methods, since it provides quantitative insight into how many views would suffice for reconstructing images of given sparsity. Another conclusion that can be drawn is that simulations with images of too low sparsity compared to a realistic level in the imaging scenario of interest are bound to yield overoptimistic promises of undersampling potential. This could have been anticipated but the result establishes this expectation quantitatively.
We caution, however, that the result is based on only two phantoms and further study is required. For more robust conclusions, the present studies need to be performed on ensembles of phantoms in order to verify that admitted undersampling for constrained TV-minimization depends primarily on the gradient-magnitude image sparsity.
We also note that while we may have exact reconstruction of the head phantom at Nviews = 12 and the reconstructed image at ε = 10−5 appears very accurate in the [0.9, 1.1] gray scale window, it is in fact not an exact reconstruction. By narrowing the gray scale to [0.99, 1.01], also shown in Fig. 11, prominent artifacts become visible. This underlines that exact reconstruction is not the relevant notion for a fixed, nonzero ε. Instead, stable reconstruction, at Nviews = 64, yields an accurate reconstruction, and for the present case already at Nviews = 32 (also shown in Fig. 11) the artifacts are reduced to a negligible level in the [0.99, 1.01] gray scale window.
VI. Summary
We argue that a quantitative notion of a sufficient-sampling condition (SSC) for X-ray CT using the DD imaging model is necessary in order to provide a reference for evaluating the undersampling potential of sparsity-exploiting methods. We propose and apply four different SSCs to a class of system matrices describing circular, fan-beam CT with a pixel expansion. While SSC1 and SSC2 characterize invertibility of the system matrix, SSC3 characterizes numerical stability for inversion of the system matrix. A simple-to-compute SSC4 is seen to approximate SSC3 closely for the circular, fan-beam full angular range CT geometry.
We employ the SSCs as reference points of full sampling to quantify undersampling admitted by reconstruction through TV-minimization on a breast CT simulation. Relative to SSC1, we observe some undersampling potential of TV-minimization for exact reconstruction and large undersampling relative to SSC3 and SSC4 for stable reconstruction. We find few-view reconstruction to admit larger undersampling than few-detector bin reconstruction, and we show evidence of a simple quantitative relation between image sparsity and the admitted undersampling.
More generally, the proposed SSCs can help to engineer and understand other sparsity-exploiting IIR algorithms by providing full sampling reference points for quantification of admissible undersampling in other imaging applications of interest. This analysis can guide decisions on alternative optimization problems, object representations, sampling configurations, and integration models.
Acknowledgments
This work was supported in part by the project CSI: Computational Science in Imaging under Grant 274-07-0065 from the Danish Research Council for Technology and Production Sciences, and in part by the National Institutes of Health (NIH) R01 under Grant CA158446, Grant CA120540, and Grant EB000225.
The authors are very grateful to the referees for providing valuable feedback that significantly improved the quality of the paper.
Footnotes
See [26, Ch. 15] for an overview of different imaging models.
We conjecture that the limiting condition number is finite and well-defined based on empirically observing convergence to a constant with increasing Nviews and Nbins for the considered system matrix class.
The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of the National Institutes of Health.
Contributor Information
Jakob S. Jørgensen, Email: jakj@imm.dtu.dk, Department of Applied Mathematics and Computer Science, Technical University of Denmark, 2800 Lyngby, Denmark
Emil Y. Sidky, Email: sidky@uchicago.edu, Department of Radiology, University of Chicago, Chicago, IL 60637 USA
Xiaochuan Pan, Email: xpan@uchicago.edu, Department of Radiology, University of Chicago, Chicago, IL 60637 USA.
References
- 1.Sidky EY, Kao CM, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J X-ray Sci Technol. 2006;14:119–139. [Google Scholar]
- 2.Song J, Liu QH, Johnson GA, Badea CT. Sparseness prior based iterative image reconstruction for retrospectively gated cardiac micro-CT. Med Phys. 2007;34:4476–4483. doi: 10.1118/1.2795830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35:660–663. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol. 2008;53:4777–4807. doi: 10.1088/0031-9155/53/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sidky EY, Pan X, Reiser IS, Nishikawa RM, Moore RH, Kopans DB. Enhanced imaging of microcalcifications in digital breast tomosynthesis through improved image-reconstruction algorithms. Med Phys. 2009;36:4920–4932. doi: 10.1118/1.3232211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pan X, Sidky EY, Vannier M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction? Inverse Prob. 2009;25:123009–123009. doi: 10.1088/0266-5611/25/12/123009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bian J, Siewerdsen JH, Han X, Sidky EY, Prince JL, Pelizzari CA, Pan X. Evaluation of sparse-view reconstruction from flat-panel-detector cone-beam CT. Phys Med Biol. 2010;55:6575–6599. doi: 10.1088/0031-9155/55/22/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ritschl L, Bergner F, Fleischmann C, Kachelrieß M. Improved total variation-based CT image reconstruction applied to clinical data. Phys Med Biol. 2011;56:1545–1561. doi: 10.1088/0031-9155/56/6/003. [DOI] [PubMed] [Google Scholar]
- 9.Han X, Bian J, Eaker DR, Kline TL, Sidky EY, Ritman EL, Pan X. Algorithm-enabled low-dose micro-CT imaging. IEEE Trans Med Imag. 2011 Mar;30(3):606–620. doi: 10.1109/TMI.2010.2089695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Defrise M, Vanhove C, Liu X. An algorithm for total variation regularization in high-dimensional linear problems. Inverse Prob. 2011;27:065002. [Google Scholar]
- 11.Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52:1289–1306. [Google Scholar]
- 12.Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory. 2006 Feb;52(2):489–509. [Google Scholar]
- 13.Candès EJ, Wakin MB. An introduction to compressive sampling. IEEE Signal Process Mag. 2008 Mar;21(2):21–30. [Google Scholar]
- 14.Candès EJ, Romberg JK, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Comm Pure Appl Math. 2006;59:1207–1223. [Google Scholar]
- 15.Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Phys D. 1992;60:259–268. [Google Scholar]
- 16.Delaney AH, Bresler Y. Globally convergent edge-preserving regularized reconstruction: An application to limited-angle tomography. IEEE Trans Image Process. 1998 Feb;7(2):204–221. doi: 10.1109/83.660997. [DOI] [PubMed] [Google Scholar]
- 17.Persson M, Bone D, Elmqvist H. Total variation norm for three-dimensional iterative reconstruction in limited view angle tomography. Phys Med Biol. 2001;46:853–866. doi: 10.1088/0031-9155/46/3/318. [DOI] [PubMed] [Google Scholar]
- 18.Elbakri IA, Fessler JA. Statistical image reconstruction for polyenergetic X-ray computed tomography. IEEE Trans Med Imag. 2002 Feb;21(2):89–99. doi: 10.1109/42.993128. [DOI] [PubMed] [Google Scholar]
- 19.Li M, Yang H, Kudo H. An accurate iterative reconstruction algorithm for sparse objects: Application to 3-D blood vessel reconstruction from a limited number of projections. Phys Med Biol. 2002;47:2599–2609. doi: 10.1088/0031-9155/47/15/303. [DOI] [PubMed] [Google Scholar]
- 20.Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans Image Process. 2009 Nov;18(11):2419–2434. doi: 10.1109/TIP.2009.2028250. [DOI] [PubMed] [Google Scholar]
- 21.Jensen TL, Jørgensen JH, Hansen PC, Jensen SH. Implementation of an optimal first-order method for strongly convex total variation regularization. BIT. 2012;52:329–356. [Google Scholar]
- 22.Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imag Vis. 2011;40:120–145. [Google Scholar]
- 23.Ramani S, Fessler JA. A splitting-based iterative algorithm for accelerated statistical X-ray CT reconstruction. IEEE Trans Med Imag. 2012 Mar;31(3):677–688. doi: 10.1109/TMI.2011.2175233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rashed EA, Kudo H. Statistical image reconstruction from limited projection data with intensity priors. Phys Med Biol. 2012;57:2039–2061. doi: 10.1088/0031-9155/57/7/2039. [DOI] [PubMed] [Google Scholar]
- 25.Sidky E, Jørgensen JH, Pan X. Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle-Pock algorithm. Phys Med Biol. 2012;57:3065–3091. doi: 10.1088/0031-9155/57/10/3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Barrett HH, Myers KJ. Foundations of Image Science. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- 27.Matej S, Lewitt RM. Practical considerations for 3-D image reconstruction using spherically symmetric volume elements. IEEE Trans Med Imag. 1996 Feb;15(1):68–78. doi: 10.1109/42.481442. [DOI] [PubMed] [Google Scholar]
- 28.Delaney AH, Bresler Y. Multiresolution tomographic reconstruction using wavelets. IEEE Trans Image Process. 1995 Jun;4(6):799–813. doi: 10.1109/83.388081. [DOI] [PubMed] [Google Scholar]
- 29.Unser M, Aldroubi A. A review of wavelets in biomedical applications. Proc IEEE. 1996;84:626–638. [Google Scholar]
- 30.Buonocore MH, Brody WR, Macovski A. A natural pixel decomposition for two-dimensional image reconstruction. IEEE Trans Biomed Eng. 1981 Feb;28(2):69–78. doi: 10.1109/TBME.1981.324781. [DOI] [PubMed] [Google Scholar]
- 31.Gullberg GT, Zeng GL. A reconstruction algorithm using singular value decomposition of a discrete representation of the exponential Radon transform using natural pixels. IEEE Trans Nucl Sci. 1994 Dec;41(6):2812–2819. [Google Scholar]
- 32.Natterer F. The Mathematics of Computerized Tomography. New York, NY: Wiley; 1986. [Google Scholar]
- 33.Natterer F. Sampling in fan beam tomography. SIAM J Appl Math. 1993;53:358–380. [Google Scholar]
- 34.Izen SH, Rohler DP, Sastry KLA. Exploiting symmetry in fan beam CT: Overcoming third generation undersampling. SIAM J Appl Math. 2005;65:1027–1052. [Google Scholar]
- 35.Faridani A. Proc Symp Appl Math. Atlanta, GA: Amer. Mathematical Soc; 2006. Fan-beam tomography and sampling theory; pp. 43–66. [Google Scholar]
- 36.Barrett HH, Gifford H. Cone-beam tomography with discrete data sets. Phys Med Biol. 1994;39:451–476. doi: 10.1088/0031-9155/39/3/012. [DOI] [PubMed] [Google Scholar]
- 37.Barrett HH, Denny JL, Wagner RF, Myers KJ. Objective assessment of image quality. II. Fisher information, Fourier crosstalk, and figures of merit for task performance. J Opt Soc Amer A. 1995;12:834–852. doi: 10.1364/josaa.12.000834. [DOI] [PubMed] [Google Scholar]
- 38.Rivière PJL, Pan X. Sampling and aliasing consequences of quarter-detector offset use in helical CT. IEEE Trans Med Imag. 2004 Jun;23(6):738–749. doi: 10.1109/tmi.2004.826950. [DOI] [PubMed] [Google Scholar]
- 39.Huesman RH. The effects of a finite number of projection angles and finite lateral sampling of projections on the propagation of statistical errors in transverse section reconstruction. Phys Med Biol. 1977;22:511–521. doi: 10.1088/0031-9155/22/3/012. [DOI] [PubMed] [Google Scholar]
- 40.Saad Y. Numerical Methods for Large Eigenvalue Problems. Manchester, U.K: Manchester Univ. Press; 1992. [Google Scholar]
- 41.Reiser I, Nishikawa RM. Task-based assessment of breast tomosynthesis: Effect of acquisition parameters and quantum noise. Med Phys. 2010;37:1591–1600. doi: 10.1118/1.3357288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Boone JM, Nelson TR, Lindfors KK, Seibert JA. Dedicated breast CT: Radiation dose and image quality evaluation. Radiology. 2001;221:657–667. doi: 10.1148/radiol.2213010334. [DOI] [PubMed] [Google Scholar]
- 43.Glick SJ. Breast CT. Annu Rev Biomed Eng. 2007;9:501–526. doi: 10.1146/annurev.bioeng.9.060906.151924. [DOI] [PubMed] [Google Scholar]
- 44.Kaipio J, Somersalo E. Statistical and Computational Inverse Problems. New York: Springer; 2005. [Google Scholar]
- 45.Lauritsch G, Bruder H. Forbild head phantom [Online] Available: http://www.imp.uni-erlangen.de/phantoms/head/head.html.