Abstract
Personalized tumor growth model is valuable in tumor staging and therapy planning. In this paper, we present a patient specific tumor growth model based on longitudinal multimodal imaging data including dual-phase CT and FDG-PET. The proposed Reaction-Advection-Diffusion model is capable of integrating cancerous cell proliferation, infiltration, metabolic rate and extracellular matrix biomechanical response. To bridge the model with multimodal imaging data, we introduce intracellular volume fraction (ICVF) measured from dual-phase CT and Standardized Uptake Value (SUV) measured from FDG-PET into the model. The patient specific model parameters are estimated by fitting the model to the observation, which leads to an inverse problem formalized as a coupled Partial Differential Equations (PDE)-constrained optimization problem. The optimality system is derived and solved by the Finite Difference Method. The model was evaluated by comparing the predicted tumors with the observed tumors in terms of average surface distance (ASD), root mean square difference (RMSD) of the ICVF map, average ICVF difference (AICVFD) of tumor surface and tumor relative volume difference (RVD) on six patients with pathologically confirmed pancreatic neuroendocrine tumors. The ASD between the predicted tumor and the reference tumor was 2.4±0.5 mm, the RMSD was 4.3±0.4%, the AICVFD was 2.6±0.6%, and the RVD was 7.7±1.3%.
Keywords: Tumor growth modeling, Multimodal images, Intracellular Volume Fraction, Metabolic rate
1. Introduction
Quantitatively characterizing the tumor spatial-temporal progression is valuable in staging tumor and designing optimal treatment strategies. In clinical practice, due to the lack of the characterization of the spatially heterogeneous pattern of the cancer progression, a conservative therapy is usually adopted by treating a margin of normal-appearing tissue surrounding the tumor as part of the tumor. This conservative approach necessities a better understanding of the spatial-temporal progression of the tumor.
Tumor growth not only relies on the properties of cancer cells, but also depends on dynamic interactions among cancer cells, and between cells and their constantly changing microenvironment. The complexity of the cancer system motivates the study of the tumor growth using mathematical models (Swanson et al., 2000; Clatz et al., 2005; Hogea et al., 2008).
Cancer modeling can be classified into four scales: atomic, molecular, microscopic, and macroscopic (Deisboeck et al., 2011). Atomic scale modeling studies the structure and dynamic properties of proteins, peptides, and lipids, as well as their dependency on the features of the environment using molecular dynamics. Molecular scale modeling studies average properties of a population of proteins, peptides, and lipids. Microscopic scale, i.e. tissue or multicell, studies cell-cell and cell-microenvironment interactions. Macroscopic scale studies dynamics of the gross tumor behavior including morphology, shape, extent of vascularization, and invasion, which are observable by clinical imaging data. Tumor modeling requires the knowledge of the underlying tumor physiological parameters. Clinical imaging data offers the benefit of non-invasive, in-vivo and timely measurement of these parameters. In this paper, we focus on the image-driven tumor modeling on the macroscopic scale.
In the image-driven tumor modeling field, Swanson et al. (2000) assumed an infiltrative growth of the tumor cells, while considering differences in cell diffusion in white and gray matter. Clatz et al. (2005) modeled locally anisotropic migration patterns by integrating information from diffusion tensor images (DTI). Hogea et al. (2008) included the mechanical properties of the lesion on surrounding structures to model mass effect.
In this paper, we not only consider mass effect, but also the cell metabolic rate. To incorporate cell metabolism into the tumor growth modeling, we combine the energy conservation law presented in (West et al., 2001) with cell proliferation law (Swanson et al., 2000). As pointed by West et al. (2001), ontogenetic development is fuelled by metabolism and occurs primarily by cell division. The incoming metabolic energy is allocated to two parts: one part for the maintenance of the existing cells and the other part for the creation of new cells. This work was further extended by Herman et al. to study the relationship between tumor vascularization and growth (Herman et al., 2011). FDG-PET (2-[18F] Fluoro-2-deoxyglucose positron emission tomography) is widely used in oncology to find regions in the body which are more active and need more energy, which motivates us to use FDG-PET to measure metabolic rate and incorporate it into the tumor growth modeling. Tracer kinetic modeling is a formal way to calculate glucose metabolic rate (Huang et al., 1980); however, this modeling approach usually requires taking series of blood samples from the studied subject to give the time course of the tracer delivery and requires measuring the dynamics of the radiolabel in local tissues. Standardized Uptake Value (SUV) is a semi-quantitative measurement of the metabolic rate and does not need dynamic blood sampling and PET scanning, therefore is suitable for routine clinical use. In this paper, we present the quantitative relation between both glucose metabolic rate and SUV, and the proliferation rate of the model. Anatomical modality imaging data such as CT and MRI can be used to monitor the progress of the tumor boundary, which motivates the studies (Swanson et al., 2000; Clatz et al., 2005; Hogea et al., 2008) on using tumor boundary as the biomarker to estimate model parameters by comparing the predicted tumor boundary with the measured boundary. However, tumor boundary only provides quite limited tumor physiological information and in some cases cannot really reflect the growth of the tumor. For instance, the cancerous cell proliferation might not be reflected in the tumor boundary progression, which motivates us to find a way to extract the underlying physiological parameter related to the cell number. In this paper, we introduce Intracellular Volume Fraction (ICVF) into tumor growth modeling and present the principle and method to estimate ICVF using dual-phase CT.
In this paper, we focus on integrating FDG-PET and CT into tumor modeling. Our work is based on the extension of a Reaction-Diffusion model (Swanson et al., 2000). The Reaction-Diffusion model plays a fundamental role in modeling spatial-temporal dynamics in system biology. The Reaction-Diffusion model describes the change of the cell density or population. However, 1) the Reaction-Diffusion model does not incorporate cell metabolic rate and 2) due to the difficulty to calculate the cell number, the pre-diction of the Reaction-Diffusion model, i.e., the cell number has to be converted to the front progression in order to connect the model with the clinical observation (tumor boundary). In this paper, we 1) develop a Reaction-Diffusion model enabling the incorporation of the cell metabolic rate and 2) present a method to calculate ICVF using dualphase CT. As a result, the model prediction can be directly related to clinical imaging data.
The proposed model is formalized as a coupled PDE system (forward problem). The patient specific parameters (control variables) are estimated by fitting the model prediction to the observed tumor leading to a coupled PDE-constrained optimization problem (an inverse problem). To obtain realistic solution, Tikhonov regularization was introduced to regularize the solution. The optimality system was derived and solved by the Finite Difference Method (FDM).
The proposed model was evaluated on pancreatic neuroendocrine tumors. A dedicated protocol was developed to accumulate longitudinal CT and FDG-PET of untreated pancreatic tumors. The only work on the pancreatic tumor modeling that we are aware of is (Haeno et al., 2012), in which the authors used a compartment model to divide the cell population into three subpopulations: primary tumor cells, metastasis-enabled cells and metastasized cells. The migration rate between subpopulations and the growth rate and death rate within each subpopulation were estimated based on autopsy data. In this paper, we focus on the way to combine routine clinical multimodal images to study the growth of the primary solid tumor.
2. Material and methods
In this section, we first present the whole framework of the modeling and evaluation; second, derive a Reaction-Advection-Diffusion model incorporated with cell metabolic rate and mass effect; third, describe how to adapt the model to associate it with routine dual- phase CT and FDG-PET; finally, describe the process for parameter estimation using longitudinal imaging data.
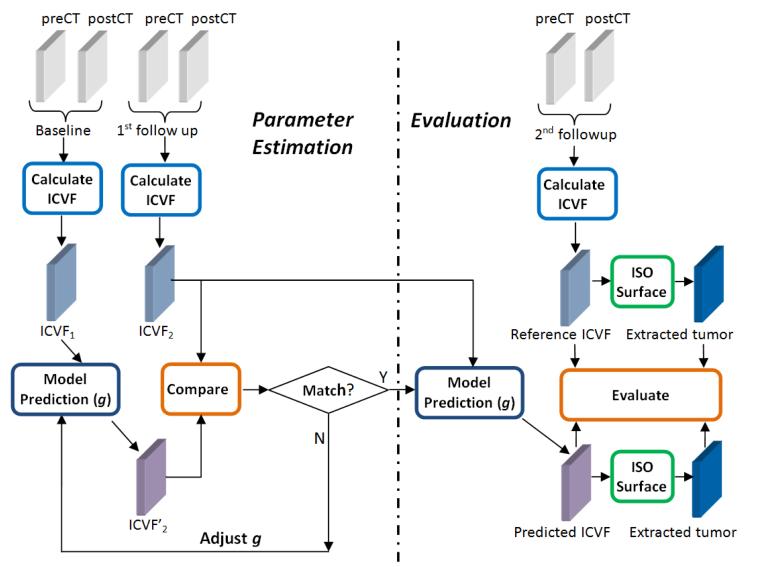
The flow chart of the proposed method is illustrated in Fig. 1. The flow chart includes two parts: parameter estimation and evaluation. We introduce ICVF as the biomarker for both model parameter estimation and evaluation. In the parameter estimation part, ICVF calculation takes longitudinal dual-phase CT images as inputs. At each time point, ICVF is measured based on pre- and post-contrast CT images (see Section 2.2 for details). The measured ICVF at the 1st follow-up is compared with the predicted ICVF growing from the base line to find the optimal parameters g by minimizing the deviation between the two ICVF maps. Once the model parameter g is estimated, the tumor grows from the 1st follow-up with estimated model parameter. The predicted ICVF and the extracted tumor surface are compared with the measured ICVF and tumor surface at the 2nd follow-up for evaluation.
Figure 1.
Flow chart of the method. The left side is parameter estimation and the right side is model evaluation. ICVF rather than tumor boundary is used as the biomarker for both parameter estimation and evaluation. In the parameter estimation part, the baseline and the 1st follow-up are involved, in which each time point includes dual-phase CT scans: pre-contrast CT (preCT) and post-contrast CT (postCT). In the evaluation part, the 2nd follow-up is used to compare with the model prediction. g is a vector of the unknown model parameters.
To use dual-phase CT to calculate ICVF, the non-rigid registration for the imaging data at one time point, i.e., between pre- and post-contrast CT, needs to be performed. To incorporate PET into the model, we also need to non-rigidly align the post-contrast CT and PETCT, and then apply the transform to the PET. The non-rigid registration method we used was the Free-Form Deformation (FFD) (Lee et al., 2002) based method. To align the longitudinal data, we performed the rigid registration between longitudinal postcontrast CT using an ITK implementation of an affine transform-based registration (Yoo et al., 2002). For the tumor segmentation, we used a Level Set segmentation implemented in ITK-SNAP (Yushkevich et al., 2006).
2.1 Derive the tumor growth model
According to the tumor logistical growth model presented in (Swanson et al., 2000), the number of the newly created cells within unit time can be described by,
| (1) |
where N is the number of cells, a function of time t. ρ is spatial-temporal invariant proliferation rate. This model describes that the tumor grows exponentially at the beginning and then gradually slows down as approaching the carrying capacity K.
As a tumor progresses, the parts with sufficient nutrients and oxygen grow faster, and those suffering vascular inefficiencies will develop into necrosis, suggesting a heterogeneous or spatial-temporal varying proliferation function ρ(x, t). The metabolic energy conservation law presented by West et al. (2001) quantitatively describes the relationship between the metabolic energy and the ontogenetic growth, providing the theoretical foundation to explore the heterogeneity of the proliferation rate. The energy conservation law states that the incoming energy required for tumor growth is allocated to two parts,
| (2) |
where the first term represents the energy to maintain the existing cells and the second term represents the energy to create new cells. Bc is the metabolic rate of a single cell, and Ec is the energy required to create a cell. Both Bc and Ec are assumed constant during tumor growth. We replace in equation (2) with ,
| (3) |
The proliferation rate ρ in equation (3) is a function of time t. However, in clinical practice, ρ is only available at specific time points when B and N are measurable. Thus, we approximate ρ at time t between 0 and T through a linear interpolation,
| (4) |
where B0, BT, N0 and NT are the measured metabolic rate and cell number at time 0 and T, respectively. Apply model (1) to each voxel (millions of cells within 1mmm3) at position x, and add a diffusion term as that in the Reaction-Diffusion model (Swanson et al., 2000) to account for cancerous cell infiltration into surrounding tissues, leading to a new Reaction-Diffusion model enabling the incorporation of the cell metabolism,
| (5) |
where the first term is the diffusion term, and the second term is the reaction (proliferation) term. is the diffusivity or infiltration rate. Equation (5) describes that the rate of cell number change equals the sum of the net dispersal of cancerous cells and the net proliferation of cancerous cells. The cell number at position x is not only affected by the proliferation and diffusion (Brownian movement) but also affected by the underlying mechanical deformation (so-called mass effect), which is caused by the growing cells impacting on the extracellular matrix. Tumor cells live in an extracellular matrix (ECM) (Suresh, 2007), which clusters and binds the cells together to form tissues. Integrins are cell surface receptors which create clusters known as focal adhesions to bind the cell surface and the ECM, which provides the biological interpretation on why the cells can move with the ECM. As the tumor grows, the pressure produced by the gradient of local cell density will drive the ECM to deform, which in turn drifts cells. Viewing cells as the source of the body force and the ECM as the studied material, we can use established theories in continuum mechanics to study the kinematics and the mechanical behavior of the ECM. To account for mass-effect, we model the ECM as a material of linear instantaneous elasticity. An advection term is added into model (5) as that in (Hogea et al., 2008) to account for the tumor cells being displaced as a consequence of the underlying mechanical deformation,
| (6) |
where the tumor cell drift velocity depends on the displacement vector u induced by the balance between the Cauchy stress tensor ρ and the body force b. λ and are μ unknown Lame’s coefficients in linear elasticity. The body force originated from the growing cells is proportional to the local gradient of the tumor cell density,
| (7) |
where p is an unknown positive constant.
Model (6) allows the incorporation of cell metabolic rate and accounts for cell proliferation, infiltration, metabolism and mass effect, but not directly connected to clinical imaging data. We will adapt the model in the following two subsections in order to associate the model parameters with measurements from CT and FDG-PET. The proposed model accounts for the cell metabolic rate and directly connects to routine CT and FDG-PET, which makes our model fundamentally different from the model in (Hogea et al., 2008).
2.2 Associate the model with dual-phase CT
The Reaction-Diffusion model predicts the tumor cell number. To measure this physiological parameter, we introduce dual-phase CT into the modeling. In this section, we describe the principle on how to use dual-phase CT to measure Intracellular Volume Fraction and present the image processing pipeline to measure ICVF.
2.2.1 Principle of ICVF calculation using dual-phase CT images
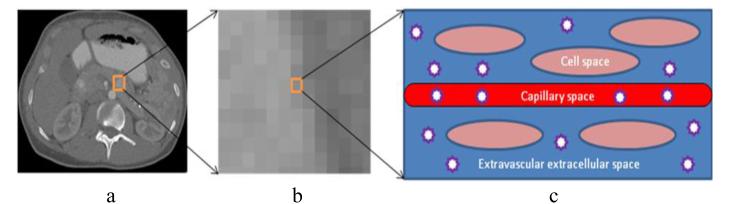
A tissue is considered to be made of three well-defined regions (see Fig. 2): (1) a vascular space through which the blood flows; (2) an extravascular extracellular space (EES) which provides the support structure of the tissue; and (3) the cellular space.
Figure 2.
Iodinated contrast medium distribution in a three-compartment physiology model. Left: a typical CT image with a tumor ROI denoted by an orange box. Middle: one voxel within the ROI. Left: three-compartment physiology model of the voxel: cell space, capillary space, and extravascular extracellular space (EES). The stars represent the iodinated contrast molecules constrained within the capillary space and the EES.
Iodine contrast agent in a target organ or blood plasma causes greater absorption and scattering of x-ray radiation, which results in an increase in CT attenuation and contrast medium enhancement in the CT image. For a given voltage, the proportionality of contrast enhancement to iodine concentration is near constant (Bae, 2010). Iodinated contrast media consist of relatively small molecules (molecular weight, 800-1,600) that are highly diffusible. Intravascular contrast media are distributed rapidly and extensively outside the blood vessels in volumes approaching that of the extracellular space (ECV), i.e., extravascular extracellular space plus capillary space, after injection (Kormano and Dean, 1976). Before the derivation of the ICVF calculation equation, we define the following parameters,
vp: volume of the vascular space,
vc: volume of the cellular space,
vEES: volume of the EES,
vECV: volume of the vascular space plus EES, i.e., vp + vEES,
vtissue: volume of the tissue space, i.e., vECV + vc,
vECV: contrast media concentration within extracellular space,
vtissue: contrast media concentration within the tissue.
Because the Hounsfield Unit (HU) enhancement of CT is proportional to the concentration of the tissue within one voxel (Bae, 2010) (not the concentration of ECV), for one voxel within the tumor, we have,
| (8) |
where HUpost_tumor and HUpre_tumor are the HU of the voxel of the tumor in the post-contrast and pre-contrast CT, respectively. k is a constant. According to mass conservation,
| (9) |
where ECVF is the ratio of the volume of extracellular space and the volume of the tissue space. Replace Cpost_tumor in equation (8) with (9),
| (10) |
Directly using equation (10) to calculate ECVF of the tumor encounters the trouble that both k and CECV are unknown. We take the voxel of the blood pool as the reference since we know the ECVF of the blood pool is 1.0 − Hctblood, where the hematocrit Hctblood is the volume percentage (%) of red blood cells in blood, which varies from patient to patient, but can be measured by the blood sample (Purves et al., 2004). Apply equation (10) on the voxel of the blood pool with the assumption that iodine contrast agent reaches dynamic equilibrium between the tumor and blood pool,
| (11) |
| (12) |
To alleviate the influence of the noise, we use the average HU enhancement of the blood pool. ECVF’s complement ICVF can be calculated as,
| (13) |
2.2.2 ICVF calculation framework
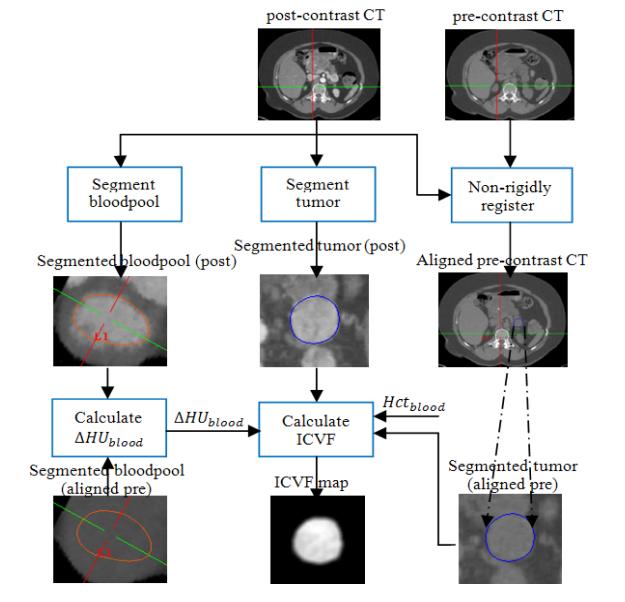
Fig. 3 illustrates the image processing pipeline to calculate ICVF from the pre- and post-contrast CT images. The procedures were performed on the baseline and all followups. Firstly, pre-contrast CT was non-rigidly registered with post-contrast CT. Then, the tumor and blood pool were segmented on post-contrast CT.
Figure 3.
Image processing pipeline of ICVF calculation.
ΔHUblood = HUpost_bloodpool − HUpre_bloodpool was calculated based on the segmented blood pools on the aligned pre-contrast CT and post-contrast CT. Hctblood was obtained by the blood sample. When ΔHUblood,Hctblood, the segmented tumors on both aligned pre-contrast CT and post-contrast CT were available, the ICVF map within the tumor were calculated using equation (13).
The measured ICVF maps are compared with the predicted ICVF maps to estimate tumor growth parameters.
In equation (6), the cell number N is difficult to be directly measured by CT image. We adapt the Reaction-Advection-Diffusion equation by replacing N(x, t) with Kθ(x, t) based on the assumption that all cells have similar volumes,
| (14) |
where (replace N0 and NT in (4) with Kθ0 and KθT, respectively)
| (15) |
where a = KBc and b = KEc. Both parameters a and b> have specific biological meanings, representing the energy to maintain K cells and create K cells, respectively. Similarly, replacing N in (7) with Kθ leads to .
2.3 Associate the model with FDG-PET
The formal way to calculate glucose metabolic rate, an approximation of metabolic rate B, was originally presented in (Huang et al., 1980), in which the glucose metabolic rate MRglc can be calculated by,
| (16) |
where LC is a lumped constant that accounts for the transport and phosphorylation difference between FDG and glucose, and is the glucose concentration in arterial plasma. [K1K3/(K2 + K3)] (commonly called the uptake constant) can be estimated given dynamic FDG-PET scans and blood samples, usually not available in routine clinical practice.
The energy for organism growth is supplied by different metabolic pathways. The metabolic energy of the tumor can be approximated by that supplied by glycolytic pathway due to the established model of the Warburg effect (Warburg, 1956): cancer cells use glycolysis for energy production regardless of the availability of oxygen because glycolysis produces energy much faster than oxidative phosphorylation despite the loss in efficiency.
Normally, when the scanning time is longer than 45 min post-injection, the uptake constant can be approximated by (Huang et al., 1980),
| (17) |
where PET(t) denotes the radioactive tracer FDG concentration in the tissue at time t that is measurable with PET. k is a constant that is not dependent on the particular subject being studied. Replace the uptake constant in (16) with (17),
| (18) |
where , a lumped unknown parameter. The numerator in (18) is widely used as Standardized Uptake Value, which is proportional to MRglc since both k and LC are constants.
Replace B0 and BT in equation (15) with, c × SUV0 and c × SUVT respectively,
| (19) |
where α = c/b, β = a/b.
Equation (6) with its Reaction-Advection-Diffusion equation replaced with equation (14) constitutes our proposed model (or state equations from an optimal control standpoint (Gunzburger, 2003)). This model connects to dual-phase CT via ICVF and static FDG-PET via SUV using equation (19) or connects to ICVF and dynamic FDG-PET using equation (15). Using dynamic FDG-PET with the model needs an additional tracer kinetic model involved to estimate metabolic rate , but has the benefit that two biologically meaningful parameters a and b can be estimated.
ρ (x, t) is the generalization of the spatial-temporal invariant ρ in (Swanson et al., 2000; Clatz et al., 2005; Hogea et al., 2008), leading to a heterogeneous growth model.
In equation (19), when = constant for all position x and a = β, ρ(x, t) is reduced to (equivalent to a constant ρ), leading to a homogeneous model. Heuristically, a higher FDG-PET value denotes a more aggressive growth. But, this aggressiveness can be caused by more less-aggressive cells or less more-aggressive cells. Thus, simply weighting the proliferation rate with the PET value cannot truly reflect the aggressiveness of the growth. The benefit using energy conservation law (2) to explore the heterogeneity of the proliferation rate described as equation (15) and (19) lies in the removal of the influence of the cell number/fraction.
The proposed model constitutes the forward problem with unknown control parameter and state variable g = (α, β, D, λ, μ, q) and state variable ϕ = (ρ, u, v), which will be solved in the following section using the optimal control theory.
2.4 Model parameter estimation
Problem definition: Given measured SUV: SUV0, SUVT, and measured ICVF: ρ0, ρT at time 0 and T in the spatial domain Ω, estimate model parameter: g = (α, β, D, λ, μ, q).
To estimate the parameters, the predicted tumor ICVF map is compared to the measured ICVF map to find the parameters leading to the best fit for the functional,
| (20) |
where the first term measures the degree of similarity, and the second term is Tikhonov regularization term to recover a locally unique solution close to a reference solution gr = (αr, βr, Dr, λr, μr, qr). S is a scaling matrix to scale model parameters into the same order of magnitude. The diagonal entries of S are Sα, Sβ, SD, Sλ, Sμ, Sq, and the nondiagnoal entries are zero. γ controls the balance of these two terms, which is obtained by a trial-and-error strategy. Functional (20) along with model (state) equations constitutes a coupled PDE-constrained optimization problem. The Lagrange multiplier or adjoint variable is introduced to change (20) to an un-constrained Lagrangian functional,
| (21) |
Apply the first order necessary KKT (Karush-Kuhn-Tucker) conditions to (21), yielding an optimality system: state equations, i.e., the model equation, adjoint equations (22), optimality conditions (23).
| (22) |
| (23) |
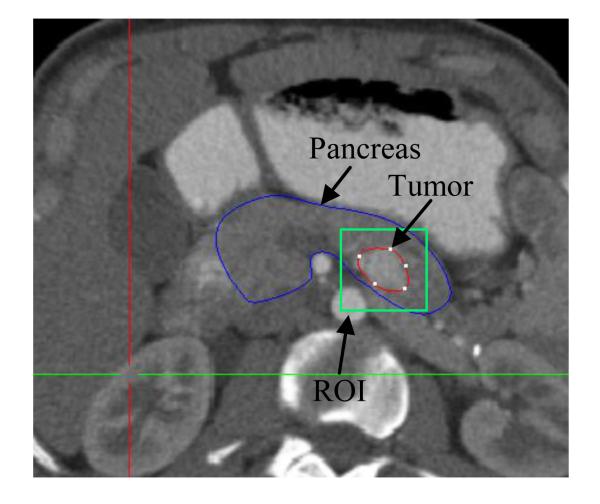
We specify a ROI (spatial domain Ω as shown in Fig. 4) centered at the geometrical center of the tumor with size 50 × 50 × 50mm3 for registration and FDM. The rigid registration between the post-contrast CT at time 0 and T is performed within the ROI rather than the whole image to avoid the influence of the intensity variation in the non-ROI region. The optimality system is resolved by the FDM within the ROI. Very few pancreatic tumors can have a size larger than 30 × 30 × 30mm3. We add 10 mm margin and assume there are no cells progressed to the boundary (ρ = 0) and no mass effect occurring on the boundary (u = 0), yielding the following boundary and initial conditions,
| (24) |
Figure 4.
ROI for the parameter estimation. The blue contour is the pancreas, and the green box is the ROI. The size of the ROI is predefined as 50 × 50 × 50mm3, and the center of the ROI is the geometrical center of the segmented tumor (red contour).
Boundary and initial conditions (24) complete the optimality system. Note that the adjoint reverses the propagation of information leading to the initial condition of the adjoint equations backward in time with a terminal condition at t = T.
Model parameters in g, reflecting different properties of tumor growth, are different in the order of magnitude. To obtain a realistic solution, we force the potential solution to be close to a reference solution gr, which is estimated as follows,
■ , where Ec = 2.1 × 10−5J, the energy to create one cell (West et al., 2001), K=106, 6.2 × 10−5 g· J− is the mass of glucose to produce 1 Joule energy.
■ , where Bc is the scaled metabolic rate of an average cell in an intact mammal (West et al., 2002).
■ Dr = 0.13mm2/day is according to the suggested average diffusion by Fisher in (Swanson et al., 2000).
■ where Young’s modulus E = 3000Pa and Poisson’s ratio come from brain biomechanics (Wittek et al., 2007).
■ qr = 200Pa is based on the one dimensional mass effect simulation in (Hogea et al., 2008).
■ The diagonal entries of the scaling matrix S are: sα = 103, sβ = 102, sD = 10, sλ = 10−3, sμ = 10−3, sq = 10−2, which scale the reference model parameters to the range [1, 10].
The reference solution is derived from literature and is just a rough estimation of the real solution. It is not necessary to be accurate since it is only used to define a region in which the real solution is located.
3. Results
To study tumor growth, we have developed a dedicated protocol spanning for several years to collect patients with pancreatic tumors. The desirable longitudinal data needs to satisfy the requirements: 1) the tumor should be big enough (volume > 20mm3) to allow us to ignore the error induced by segmentation and registration, 2) at least three time points and each time point includes both dual-phase CT and FDG-PET, and 3) without any treatments. Usually, a tumor will be surgically removed when it becomes sufficiently big. The contradictive requirements 1) and 3) lead to the difficulty to obtain desirable data.
In this work, we selected 6 patients with pathologically confirmed pancreatic neuroendocrine tumors from over 100 patients for the model evaluation. The scanning interval is about one year for each patient. We are still collecting data and will incorporate them in the modeling in the future. The patient information is listed in Table 1.
Table 1.
Patient information. All patients have pancreatic neuroendocrine tumors.
| Gender | Age | Location | Grade | #Tumor | |
|---|---|---|---|---|---|
| Patient 1 | male | 57 | head | 3 | 1 |
| Patient 2 | female | 48 | tail | 1 | 1 |
| Patient 3 | male | 51 | tail | 2 | 1 |
| Patient 4 | male | 62 | head | 1 | 1 |
| Patient 5 | female | 37 | head | 3 | 1 |
| Patient 6 | male | 58 | body | 1 | 1 |
Pancreatic protocol CT scan was performed by using GE LightSpeed Ultra. The patients were placed supine on the table, head first, centered at the sternal notch. A bolus of 115ml (adult with body weight ≤ 82kg) or 130ml (adult with body weight > 82kg) of iodinated contrast (Isovue 300; Bracco Diagnostics, Inc, Princeton, NJ) was given intravenously. The rate of automated intravenous injection of contrast was 2ml/second. The images were obtained 50 minutes after the contrast injection with image dimension 512 × 512 × 247 and voxel size 0.7 × 0.7 × 1.89 mm.
Data overview
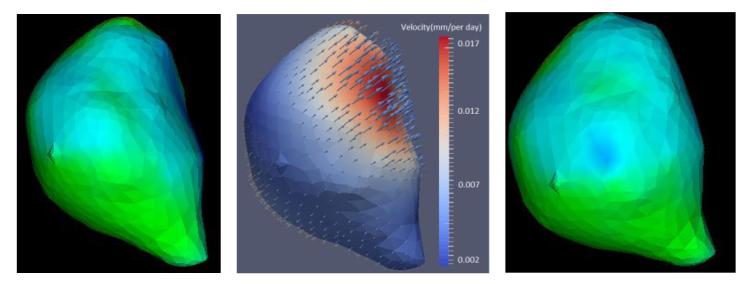
Table 2 lists all data used for model parameter estimation and the estimated parameters. Carefully examining Table 2, we found that a general pattern of the ICVF is that it increases slowly as the ICVF increases, which might be caused by less room for cell growth when ICVF is larger. For instance, for patient 2, it only increases one percent from 86% to 87% for one year period even the energy uptake is very large (over 10.0). This slow increasing behavior agrees well with the logistical growth model (Eq. 1), which has been incorporated into our proposed model. Another interesting observation is that if the energy uptake is high (larger than 10), the ICVF usually can reach a value close to 80% (patients 1, 2, 4 and 5), which might disclose that if the energy uptake is high, tumor cells can grow fast. For the velocity term, we observe that the cell moves outwards, as shown in Fig. 6. We speculate that the underlying reason lies in the pressure induced by the internal high cell density, which drives the cell to move towards surrounding regions with low cell density.
Table 2.
Measured ICVF, SUV and estimated parameters of two patients. Hct blood comes from blood samples, ΔHU is the average enhancement of the voxels located in the blood pool. Unit: ICVF (%), Dose (MBq), Weight (Kg), SUV (g/ml), D (mm2/day), α (g −1 · ml · day−1), β (day −1), λ (Pa), μ (Pa), q (Pa), Glc (mg/dl). γ = 0.6. The scanning interval is about one year. In the parameter column, there are two groups of estimated parameters. One group of parameters is estimated by considering cell metabolic rate and the other group not (in the parenthesis). The p-values for the statistical comparison for all parameters are listed at the bottom row of the table.
| ICVF | SUV | Parameter g | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Id | base | 1st | 2nd | base | 1st | 2nd | ||||
| 1 | Hctblood | 0.43 | 0.43 | 0.44 | Dose | 345.23 | 350.42 | 361.44 | α(10−3) | 4.5(4.8) |
| β(10−2) | 9.8(9.5) | |||||||||
| ΔHU | 256 | 222 | 245 | Weight | 78.7 | 77.8 | 75.4 | D | 0.02(0.02) | |
| Glc | 82 | 84 | 84 | λ | 4532.6(4289.6) | |||||
| ICVF | [0,68] | [0,73] | [0,77] | SUV | [0,12.4] | [0,13.5] | [0,14.9] | μ | 498.8(488.3) | |
| q | 81.7(83.5) | |||||||||
| 2 | Hctblood | 0.42 | 0.41 | 0.42 | Dose | 397.38 | 397.38 | 397.38 | α(10−3) | 2.3(2.5) |
| β(10−2) | 7.2(7.4) | |||||||||
| ΔHU | 279 | 230 | 252 | Weight | 73.0 | 72.0 | 72.0 | D | 0.02(0.02) | |
| Glc | 102 | 98 | 98 | λ | 5223.1(5206.2) | |||||
| ICVF | [0,81] | [0,86] | [0,87] | SUV | [0,14.5] | [0,18.4] | [0,18.4] | μ | 657.3(650.5) | |
| q | 125.8(122.2) | |||||||||
| 3 | Hctblood | 0.42 | 0.42 | 0.42 | Dose | 397.38 | 397.38 | 397.38 | α(10−3) | 4.7(4.1) |
| β(10−2) | 7.7(7.3) | |||||||||
| ΔHU | 254 | 240 | 242 | Weight | 82.6 | 83.5 | 83.2 | D | 0.02(0.01) | |
| Glc | 96 | 98 | 98 | λ | 3345.8(3462.1) | |||||
| ICVF | [0,41] | [0,62] | [0,69] | SUV | [0,8.2] | [0,7.4] | [0,8.9] | μ | 395.6(405.2) | |
| q | 105.2(89.4) | |||||||||
| 4 | Hctblood | 0.42 | 0.43 | 0.3 | Dose | 356.31 | 360.38 | 360.38 | α(10−3) | 3.1(2.8) |
| β(10−2) | 3.3(2.7) | |||||||||
| ΔHU | 305 | 289 | 310 | Weight | 85.1 | 86.8 | 84.7 | D | 0.01(0.01) | |
| Glc | 88 | 82 | 80 | λ | 2109.4(2245.6) | |||||
| ICVF | [0,55] | [0,68] | [0,75] | SUV | [0,13.2] | [0,15.8] | [0,15.6] | μ | 309.4(300.5) | |
| q | 71.4(73.2) | |||||||||
| 5 | Hctblood | 0.41 | 0.42 | 0.42 | Dose | 397.38 | 397.38 | 397.38 | α(10−3) | 4.1(4.4) |
| β(10−2) | 5.7(5.1) | |||||||||
| ΔHU | 270 | 245 | 251 | Weight | 68.2 | 68.0 | 70.0 | D | 0.03(0.03) | |
| Glc | 101 | 96 | 98 | λ | 3489.2(3511.2) | |||||
| ICVF | [0,67] | [0,76] | [0,79] | SUV | [0,15.3] | [0,15.5] | [0,15.9] | μ | 489.2(455.1) | |
| q | 113.2(127.5) | |||||||||
| 6 | Hctblood | 0.43 | 0.42 | 0.44 | Dose | 356.31 | 360.38 | 360.38 | α(10−3) | 4.2(3.8) |
| β(10−2) | 3.2(3.2) | |||||||||
| ΔHU | 266 | 278 | 291 | Weight | 77.0 | 76.8 | 76.5 | D | 0.02(0.02) | |
| Glc | 81 | 79 | 83 | λ | 2268.9(2288.3) | |||||
| ICVF | [0,47] | [0,60] | [0,66] | SUV | [0,6.4] | [0,7.2] | [0,7.7] | μ | 342.6(335.0) | |
| q | 89.0(85.6) | |||||||||
P-value (paired t-test, significant level: 0.05): D(0.36), α(0.63), β(0.09), λ(0.92) μ(0.15),q(0.85)
Figure 6.
Velocity visualization. The left and right figures are the tumors of two adjacent follow-ups. The color denotes the ICVF distribution. The middle figure is the estimated velocity. The color denotes the magnitude of the velocity and the arrow points to the direction of the velocity.
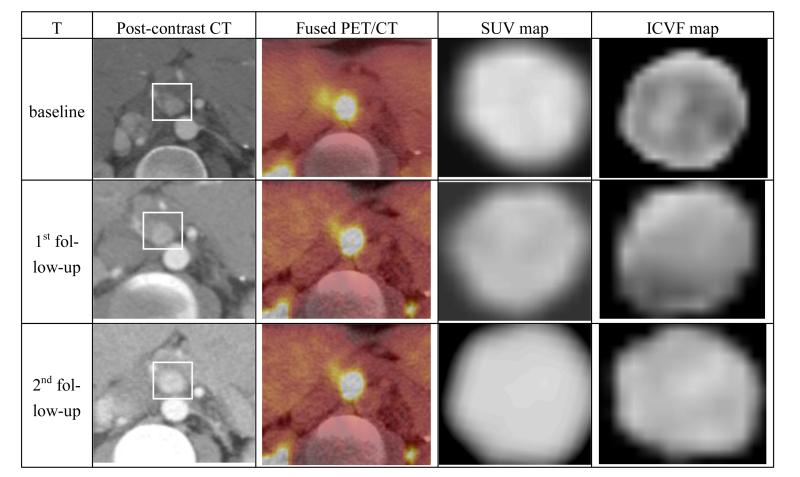
We evaluated the proposed model by comparing the predicted ICVF map and tumor with the measured ICVF map and tumor at the 2nd follow-up. The predicted ICVF map was produced by growing the ICVF (using the model equation) from the 1st follow-up for the period between the 1st and 2nd follow-up with the parameters estimated from the longitudinal data at the baseline and the 1st follow-up. The predicted tumor is an isosurface extracted from the predicted ICVF map based on a threshold. Fig.5 shows the longitudinal post-contrast CT, fused PET/CT, estimated SUV map (with decay correction) and the ICVF maps.
Figure 5.
Longitudinal original and intermediate results. The rows correspond with the baseline, the 1st follow-up, and the 2nd follow-up and the columns correspond with post-contrast CT, fused PET/CT, estimated SUV and ICVF maps. The white bounding box highlights the tumor.
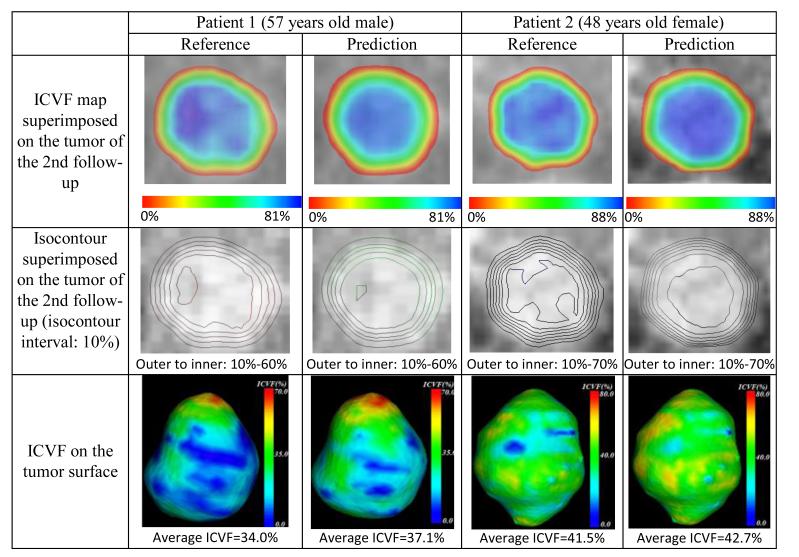
Fig.7 shows the comparison between the reference results of the 2nd follow-up and the prediction results of two patients. The corresponding ICVF range, SUV range and parameters of the two patients are listed in Table 2. The first row of Fig. 6 demonstrates a similar distribution of the ICVF map between the reference and the prediction results for both patients: the cell number decreases from the center to the rim of the tumor. The predicted center region (blue) is more homogeneous than the reference part, which might be caused by the exclusion of the complex heterogeneous tumor microenvironment from our model.
Figure 7.
Comparison between the reference (the 2nd follow-up) and the prediction of two patients regarding ICVF map, isocontour and ICVF on the tumor surface.
The comparison of the isocontours of the ICVF map is shown in the second row. The inner most contour shows larger discrepancy, but the outer contours agree well with each other, suggesting a more heterogeneous cell distribution in the center region of the reference tumor, which also can be observed in the gray scale ICVF (the last column of Fig.5). In the third row, we compare the ICVF on the surface of the segmented tumor. We focus on this surface because it is the one that can be identified in the image data with our naked eyes.
Both patients show similar ICVF distribution, and the second patient demonstrates a more homogeneous ICVF distribution than the first patient. We assume the average ICVF on the tumor surface to be the threshold that defines the detectable tumor boundary, which makes sense since ICVF is a main factor affecting HU of CT. We use this threshold to extract the isosurface (predicted tumor) from the predicted ICVF map to compare with the segmented tumor in terms of average surface distance and relative volume difference.
The quantitative evaluation regarding the root mean square difference (RMSD) of the ICVF map, the average ICVF difference (AICVFD) on tumor surface, the average surface distance (ASD) between the predicted tumor surface and the segmented tumor surface, and the tumor relative volume difference (RVD, the ratio of the volume difference and the volume of the segmented tumor) are listed in Table 3, in which the RMSD is 4.3±0.4%, the AICVFD is 2.6±0.6%, the ASD is 2.4±0.5 mm, and the RVD is 7.7±1.3%. The ICVF value is slightly large, but the boundary prediction (clinically relevant) is very promising (around 2.4mm). Actually, there is no work to compare with our work regarding ICVF because we are the first one introducing ICVF into the tumor growth modeling.
Table 3.
Quantitative evaluation. ICVF ([min%, max%]), RMSD (%), AICVFD (%), ASD (mm), RVD (%).The value out of the angular bracket was obtained using the proposed model, and the value in the angular bracket was obtained without considering the metabolic rate. The value in the parenthesis of the ASD is the threshold to extract the predicted tumor from the predicted ICVF map.
| Id | ICVF | Predicted ICVF | RMSD | AICVFD | ASD | RVD |
|---|---|---|---|---|---|---|
| 1 | [0,77] | [0,81]<0,83> | 4.2<5.1> | 3.1<3.7> | 2.0<2.4>(34.0) | 8.l<9.2> |
| 2 | [0,87] | [0,88]<0,88> | 5.1<5.2> | 1.2<1.4> | 2.2<2.3>(41.5) | 7.6<7.4> |
| 3 | [0,69] | [0,65]<0,64> | 4.6<5.2> | 3.1<3.8> | 3.3<3.9>(36.0) | 10.4<11.0> |
| 4 | [0,75] | [0,79]<0,80> | 3.7<3.5> | 2.7<2.8> | 3.1<3.2>(31.6) | 8.2<8.2> |
| 5 | [0,79] | [0,77]<0,77> | 3.8<4.4> | 3.5<4.7> | 1.5<2.1>(39.2) | 4.5<5.3> |
| 6 | [0,66] | [0,78]<0,81> | 4.1<4.6> | 2.2<2.7> | 2.4<2.8>(32.2) | 7.1<7.3> |
| mean ± std | [0,75±6] | [0,78±5]<0,79±6> | 4.3±0.4<4.7±0.5> | 2.6±0.6<3.2±0.9> | 2.4±0.5<2.8±0.5> | 7.7±1.3 < 8.1±1.4 > |
To infer the sensitivity of the model output to the adjusted parameters, we conducted global nonlinear non-monotonic sensitivity analysis as shown in Table 4. The global analysis was performed by an extended Fourier Amplitude Sensitivity Test (eFAST) (Marino et al., 2008), an extension of FAST (Collins et al., 1994). eFAST is a variance decomposition method to measure the sensitivity of the output to the input. As input parameters vary, the output of the model varies accordingly. The variation of the output is quantified by the variance of sampling data with size N. To determine the fraction of the variation caused by each parameter, eFAST first partitions the variance by varying different parameters at different frequencies, and then uses Fourier analysis to measure the strength of each parameter’s frequency in the model output, which serves as a measure of the model’s sensitivity to the input parameter.
Table 4.
eFAST global sensitivity analysis. Sample sizes 65 (resampling size 3). Si: the first order sensitivity index denoting the fraction of model output variance explained by the input variation of a given parameter i. STi:the total order sensitivity index denoting the remaining variance after the contribution of the complementary set is removed. Output(g) = ∫Ω (θ (x) – θT(x))2 dx
| eFAST | ||
|---|---|---|
| Si (first order) | STi (total order) | |
| Parameters | Output(g) | Output(g) |
| α | 0.2210 | 0.4776 |
| β | 0.2533 | 0.4451 |
| D | 0.4328 | 0.7403 |
| λ | 0.0369 | 0.1226 |
| μ | 0.0524 | 0.1709 |
| q | 0.0091 | 0.0083 |
In our eFAST analysis, the output was defined as the sum of square difference between the model prediction and the reference ICVF. The parameter space is assumed to follow a uniform distribution. We ran the eFAST analysis with sample size 65 (resampling size 3).
Both the first order and total order sensitivity indexes show the biological parameters: D, α and β are consistently higher than the three biomechanical parameters: μ, λ and q, which suggests the biological parameters affect the ICVF more than the biomechanical parameters. In the biological parameters, the diffusion D is highest (Si=0.43, STi=0.74), probably disclosing the aggressive infiltration of the pancreatic tumor. In the biome-chanical parameters, μ and λ dominate the explanation of the variation, which makes sense since these two parameters control the stiffness and incompressibility of the tissue.
Robustness
To evaluate the robustness of the parameter estimation, we also estimated the parameters using the first and second follow-ups. The parameters values are listed in the parenthesis of Table 2. We found that the estimated values are very close to the values estimated using the baseline and the first follow-up. Paired t-test shows there is no significant difference between these two group values: D(0.36), α(0.63), β(0.09), λ(0.92) μ(0.85). In our study, P-value equal or less than 0.05 is considered as significant difference.
Comparison
To evaluate the impact of metabolic rate on the tumor growth modeling, we compared the proposed model incorporated with metabolic rate with the model without metabolic rate. In another word, compare the model with proliferation rate as a function of cell creation and maintenance energy with a model using a constant proliferation rate. Table 3 shows the comparison regarding ICVF, RMSD, AICVFD, ASD and RVD. Patients 1, 3, 5 and 6 show obvious improvement when considering cell metabolic rate, but patients 2 and 4 not. Examining ICVF distribution, as shown in Fig. 8, we found patient 2 and 4 have homogeneous ICVF distribution. As a result, the metabolic rate might not be very helpful in exploring the heterogeneity. Therefore, there is no big difference between using and not using the metabolic rate for these two cases.
Figure 8.
Homogeneous ICVF distribution for two patients. The ICVF is encoded into the color. Both patient show homogeneous ICVF distribution.
Clinical significance
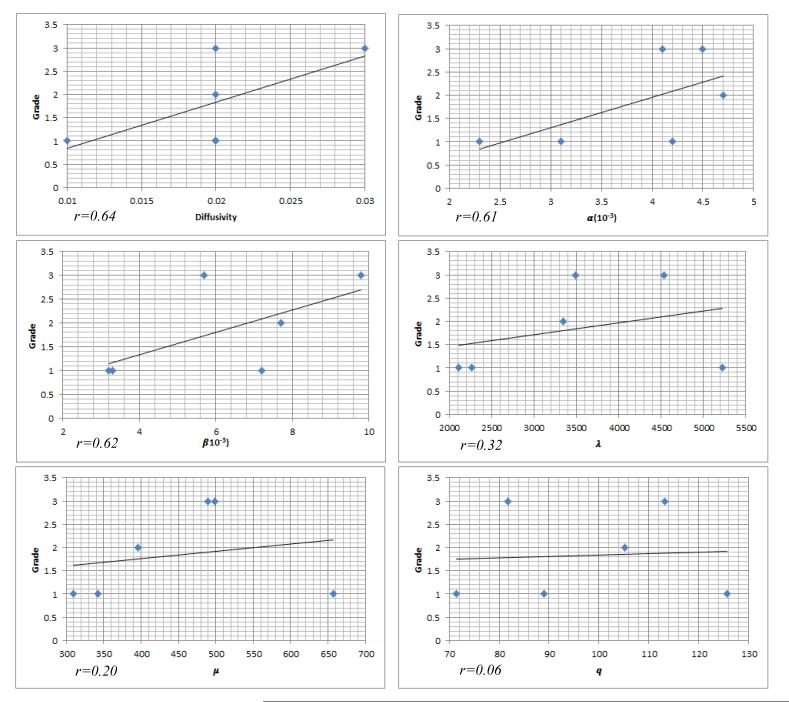
The estimated parameters might be used as a biomarker for diagnosis. To evaluate this, we performed simple linear regression and correlation analysis for each parameter. The results are shown in Fig. 9. The tumor grade is the response and the model parameter is the predictor. Fig. 9 shows the three biological parameters have higher correlation (greater than 0.6) with the tumor grade than the three biomechanical parameters (less than 0.35). The diffusion has highest correlation, which is consistent with our sensitivity analysis, in which the diffusion explains most tumor growth. The reason should be this parameter directly reflects the aggressiveness of the cancerous cell infiltrating into surrounding tissues.
Figure 9.
Relation between the model parameters and the tumor grade.
4. Discussion
In this paper, we focus on the growth modeling of the primary solid tumor. We consider multiple cancerous cell characteristics. Cancerous cells are characterized by uncontrolled growth, so the proliferation rate is widely in tumor growth modeling (Swanson et al., 2000; Clatz et al., 2005; Hogea et al., 2008). However, a simple constant proliferation might not completely capture the cell growth behavior. We explore cell proliferation heterogeneity by combing the metabolic energy conservation law and logistical growth law and derive the relation between the proliferation rate and cell creation and maintenance energy. Focusing on a position x, the cell number is changed not only due to the proliferation, but also the motion of the cells. In our tumor growth modeling, we consider two cell motions: diffusion and advection. Tumor cells are driven by cell densi- ty gradient and move from a high density region to a low density region. Diffusivity is a parameter needed to be estimated. Diffusion is a random Brownian motion, which has no relation with the advection. The advection term is used to incorporate mass effect. Tumor cells live in the ECM, which can bring the cell to move together. As tumor grows, the mass gradient will drive the moving of the ECM, which in turns causes the moving of the cell, i.e. mass effect. We model the ECM as a linear instantaneous elasticity material characterized by Lame’s coefficients. The driving force caused by the mass gradient is parameterized on an unknown constant q. Because there is a higher cell density in central region than in peripherals, the mass effect causes the ECM moving towards surrounding regions, leading to the cell moving outwards as shown in Fig. 6.
There are two kinds of parameters in our modeling: biological parameters and biomechanical parameters: μ, λ and q. To the best of our knowledge, there is no report about the pancreatic tumor biophysics modeling. The only work about pancreatic cancer modeling is (Haeno et al., 2012), in which authors focused on the tumor cell metastasis modeling rather than the biophysics modeling. To gain some experience of these parameters, we borrowed some values from Glioma of brain. These values do not need to be accurate, just for the purpose of regularization. Our robustness experiment demonstrates the effectiveness of the parameter estimation method.
5. Conclusions and Future Work
In this paper, we presented a tumor growth model, which is characterized by incorporating cell metabolic rate into the Reaction-Advection-Diffusion model and being driven by routine clinical imaging data based on ICVF and SUV. The ICVF is able to reflect current tumor cell invasion, but not the future progression. To predict tumor progression, tumor’s inherent biological and biomechanical parameters need to be estimated. In this paper, we developed a tumor growth model and used clinical imaging data to estimate model parameters. The experiment on pancreatic neuroendocrine tumors demonstrated the promise of the proposed model. Other than the characteristics of tumor itself such as the aggressiveness measured by the metabolic rate, tumor microenvironment is also essential for the study of tumor growth. In the future, besides dual-phase CT and FDG-PET, we will introduce DCE-MRI to measure vasculature/perfusion regions and FMISO-PET to measure hypoxia regions in order to model tumor microenvironment.
Highlights.
We present a macroscopic scale tumor growth model integrating cancerous cell proliferation, infiltration, metabolic rate and extracellular matrix biomechanical response
We present a tumor growth model directly associated with clinical CT and FDG-PET
We introduce Intracellular Volume Fraction (ICVF) into tumor modeling
We present the principle to calculate ICVF using dual-phase CT
Acknowledgments
Funding Sources
Funded by the National Institutes of Health (NIH) Intramural program.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Potential Conflict of Interest
The authors declare that they have no competing interests.
References
- Bae KT. Intravenous Contrast Medium Administration and Scan Timing at CT: Considerations and Approaches. Radiology. 2010;256:32–61. doi: 10.1148/radiol.10090908. [DOI] [PubMed] [Google Scholar]
- Clatz O, Sermesant M, Bondiau PY, Delingette H, Warfield SK, Malandain G, Ayache N. Realistic simulation of the 3-D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Transactions on Medical Imaging. 2005;24:1334–1346. doi: 10.1109/TMI.2005.857217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins DC, Avissar R. An evaluation with the Fourier amplitude sensitivity test (FAST) of which land-surface parameters are of greatest importance in atmospheric modeling. J. Climate. 1994;7(5):681–703. [Google Scholar]
- Deisboeck TS, Wang Z, Macklin P, Cristini V. Multiscale Cancer Modeling. Annu. Rev. Biomed. Eng. 2011;13:127–55. doi: 10.1146/annurev-bioeng-071910-124729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunzburger MD. Advances in Design and Control. SIAM: 2003. Perspectives in Flow Control and Optimization; pp. 14–21. [Google Scholar]
- Haeno H, Gonen M, Davis MB, Herman JM, Lacobuzio-Donahue CA, Michor F. Computational modeling of Pancreatic cancer reveals kinetics of metastasis suggesting optimum treatment strategies. Cell. 2012;148:362–375. doi: 10.1016/j.cell.2011.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herman AB, Savage VM, West GB. A Quantitative Theory of Solid Tumor Growth. Metabolic Rate and Vascularization, PLoS ONE. 2011;6(9):1–9. doi: 10.1371/journal.pone.0022973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogea C, Davatzikos C, Biros G. An image-driven parameter estimation problem for a reaction-diffusion glioma growth model with mass effects. J Math Biol. 2008;56:793–825. doi: 10.1007/s00285-007-0139-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang SC, Phelps ME, Hoffman EJ, Sideris K, Selin CJ, Kuhl DE. Noninvasive determination of local cerebral metabolic rate of glucose in man. Am J Physiol Endocrinol Metab. 1980;238:E69–E82. doi: 10.1152/ajpendo.1980.238.1.E69. [DOI] [PubMed] [Google Scholar]
- Kormano M, Dean PB. Extravascular contrast material: the major component of contrast enhancement. Radiology. 1976;121:379–382. doi: 10.1148/121.2.379. [DOI] [PubMed] [Google Scholar]
- Lee S, Wolberg G, Shin SY. Scattered data interpolation with multilevel B-splines. IEEE Transactions on Visualization and Computer Graphics. 2002;3(3):228–244. [Google Scholar]
- Marino M, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–96. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purves WK, Sadava D, Orians GH, Heller HC. Life: The Science of Biology. 7th Sinauer Associates; Sunderland, Mass: 2004. [Google Scholar]
- Suresh S. Biomechanics and biophysics of cancer cells. Acta Materialia. 2007;55:3989–4014. doi: 10.1016/j.actbio.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson KR, Alvord EC, Murray JD. A quantitative model for differential motility of gliomas in grey and white matter. Cell Prolif. 2000;33:317–329. doi: 10.1046/j.1365-2184.2000.00177.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warburg O. On the origin of cancer cells. Science. 1956;123(3191):309–314. doi: 10.1126/science.123.3191.309. [DOI] [PubMed] [Google Scholar]
- West GB, Brown JH, Enquist BJ. A general model for ontogenetic growth. Nature. 2001;413:628–631. doi: 10.1038/35098076. [DOI] [PubMed] [Google Scholar]
- West GB, Woodruff WH, Brown JH. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. PNAS Suppl. 2002;19(99):2473–8. doi: 10.1073/pnas.012579799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittek A, Miller K, Kikinis R, Warfield SK. Patient-specific model of brain deformation: Application to medical image registration. Journal of biomechanics. 2007;40(4):919–929. doi: 10.1016/j.jbiomech.2006.02.021. [DOI] [PubMed] [Google Scholar]
- Yoo TS, Ackerman MJ, Lorensen WE, Schroeder W, Chalana V, Aylward S, Metaxas D, Whitaker R. Engineering and Algorithm Design for an Image Processing API: A Technical Report on ITK - The Insight Toolkit. In: Westwood J, editor. Proc. of Medicine Meets Virtual Reality; IOS Press Amsterdam; 2002. pp. 586–592. [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–28. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]