3D Model of Frequency Representation in the Cochlear Nucleus of the CBA/J Mouse

Abstract

The relationship between structure and function is an invaluable context with which to explore biological mechanisms of normal and dysfunctional hearing. The systematic and topographic representation of frequency originates at the cochlea, and is retained throughout much of the central auditory system. The cochlear nucleus (CN), which initiates all ascending auditory pathways, represents an essential link for understanding frequency organization. A model of the CN that maps frequency representation in 3D would facilitate investigations of possible frequency specializations and pathologic changes that disturb frequency organization. Toward this goal, we reconstructed in 3D the trajectories of labeled auditory nerve (AN) fibers following multiunit recordings and dye injections in the anteroventral CN of the CBA/J mouse. We observed that each injection produced a continuous sheet of labeled AN fibers. Individual cases were normalized to a template using 3D alignment procedures that revealed a systematic and tonotopic arrangement of AN fibers in each subdivision with a clear indication of isofrequency laminae. The combined dataset was used to mathematically derive a 3D quantitative map of frequency organization throughout the entire volume of the CN. This model, available online (http://3D.ryugolab.com/), can serve as a tool for quantitatively testing hypotheses concerning frequency and location in the CN.

Hearing begins in the cochlea, where sounds of different frequencies stimulate hair cell receptors at different positions along the basilar membrane. This mapping is approximately exponential with distance, with a low-to-high frequency gradient established from the apex to the base, respectively (von Békéesy, 1960; Liberman, 1982). Stimulated hair cells, in turn, activate auditory nerve (AN) fibers with which they are connected, relaying information from the periphery to the central nervous system (reviewed by Nayagam et al., 2011). Because the activity of AN fibers reflects their cochlear point of origin, there is a place-frequency map in the cochlea (Liberman, 1982).

Early anatomists recognized that the AN projects into the cochlear nucleus (CN) following a stereotyped plan (Ramón y Cajal, 1909; Lorente de Nó, 1933). Fibers tuned to low best frequencies (BFs) are distributed at more ventral locations throughout the CN, and fibers with progressively higher BFs are distributed progressively dorsally (Fekete et al., 1984; Ryugo and May, 1993). This arrangement corroborates physiological observations of frequency tuning (Rose et al., 1959; Bourk et al., 1981; Spirou et al., 1993), suggesting that tonotopy in the CN is due to the spatial pattern of synaptic connections made by auditory nerve fibers on CN neurons (Ramón y Cajal, 1909; Lorente de Nó, 1933; Fekete et al., 1984; Ryugo and May, 1993).

Studies of tonotopy in the CN have largely been reduced to 1- or 2D, with few studies providing quantitative results in 3D space (Bourk et al., 1981; Müller, 1990; Luo et al., 2009). A complete model of frequency representation in the CN would be beneficial for evaluating possible frequency specializations in the animal or pathologic changes in tuning. Among the scant data currently available, there also exists no straightforward method for experimenters to freely view and interpret spatial data. Atlases of auditory structures have typically consisted of sets of standardized serial sections to which experimental sections must be matched for interpretation (e.g., Kiang et al., 1975; Willard and Ryugo, 1983; Franklin and Paxinos, 1997; Trettel and Morest, 2001; Cant and Benson, 2005). Such methods are approximate and highly subjective, requiring the experimenter to make assumptions about the angle at which their tissue was sectioned and relative similarity of an experimental section to a given atlas section.

The mouse has emerged as a model for mammalian auditory research (Willott, 1983, 2001; Steel and Kros, 2001; Liu, 2006). A number of studies have characterized aspects of frequency representation within the mouse cochlea (Ehret, 1975; Ou et al., 2000; Müller et al., 2005) or CN (Ryugo et al., 1981; Ehret and Fischer, 1991; Berglund and Brown, 1994; Luo et al., 2009), but none have provided the kind of detail that would enable a complete quantitative and comparative assessment of frequency representation in 3D. To this end, we adapted techniques used in insect neuroanatomy (Rein et al., 2002; Jenett et al., 2006) to construct a 3D template of the CBA/J mouse CN. Next we analyzed the trajectory of physiologically characterized labeled auditory nerve fibers resulting from injections in the CN and mapped each case to our 3D template using automated alignment algorithms. Finally, we used this composite dataset to develop a quantitative map of tonotopy in the CN of this mouse strain. This type of organization has been explored in other species (Feng and Vater, 1985; Müller, 1990), but we have expanded on past methods to allow us to generalize our findings across a number of experimental cases and to create an interactive model. This model can serve as a tool for visualizing CN tonotopy (e.g., virtual arbitrary slices) and a quantitative reference upon which hypotheses concerning frequency and location in the CN can be tested.

MATERIALS AND METHODS

Animals

Twenty-four adult CBA/J mice (2 male, 22 female; Jackson Laboratories, Bar Harbor, ME) were used in this study (Table 1). Mice ranged in age from 2.5–4 months (mean: 12.3 ± 1.7 weeks) and weighed between 17–30 g (mean: 23.9 ± 3.8 g). All procedures were in accordance with National Institutes of Health (NIH) guidelines and approved by the Animal Care and Use Committee of the Johns Hopkins University School of Medicine. All data are reported as mean ± standard deviation (SD).

TABLE 1.

Age/Weight, Cochlear Nucleus Volume, and Template Fitting for All Cases

Mouse statistics				CN statistics		Case used as candidate template				Case fit to final template RMS error (µm)
ID	Sex	Age (weeks)	Weight (g)	# Sections	Volume (mm3)	Mean ± SD RMS error (µm)			Core-to-seam (c2s) ratio
22	F	12	22	35	0.648	28.7	±	3.2	2.39	21.8
23	M	12	29	38	0.627	27.3	±	4.0	2.47	19.8
25	M	13	28	34	0.566	28.6	±	2.0	2.53	21.8
27	F	10	22	37	0.645	26.6	±	3.2	2.52	19.0
30	F	11	24	40	0.648	27.2	±	2.7	2.47	21.9
31	F	11	24.5	331	0.5751	34.5	±	3.2	2.31	24.1
32	F	11	24.6	41	0.603	30.0	±	3.3	2.45	28.0
33	F	12	24	38	0.594	31.7	±	2.6	2.31	28.8
35	F	11	18	37	0.561	29.1	±	4.1	2.48	18.9
36	F	12	19	41	0.664	26.1	±	3.0	2.54	20.6
37	F	12	20	36	0.552	32.2	±	3.5	2.48	23.7
38	F	12	17	39	0.608	26.5	±	3.0	2.54	20.1
39	F	12	24	40	0.675	27.4	±	4.1	2.41	21.7
40	F	14	30	41	0.687	23.9	±	2.8	2.56	13.8
42	F	10	20.5	34	0.673	26.1	±	3.1	2.50	16.1
44	F	12	24	36	0.621	26.8	±	3.2	2.45	17.2
45	F	12	22	37	0.555	26.4	±	3.4	2.50	18.5
49	F	14	29	40	0.650	29.3	±	3.5	2.27	23.3
51	F	14	24	321	0.6561	33.8	±	3.1	2.47	22.6
52	F	15	26	39	0.594	30.1	±	2.4	2.42	27.3
53	F	16	29	301	0.5211	39.1	±	4.3	2.22	26.7
55	F	11	21	37	0.583	29.3	±	3.6	2.42	21.6
56	F	11	22	261	0.5451	37.1	±	3.6	2.16	21.6
60L	F	16	30	652	0.563	26.3	±	3.3	2.50	23.6
60R	“	“	“	682	0.523	25.9	±	2.8	2.45	22.0
Mean		12.3	23.9	37.9	0.611					21.8
SD		1.7	3.8	2.3	0.047					3.6

¹Some sections missing and not included in section or volume means.

²Sectioned at 30 µm instead of 50 µm and not included in section mean.

Surgery

Mice were prepared for recordings using aseptic surgical techniques. Anesthesia was induced via an intraperitoneal (IP) injection containing a mixture of ketamine (100 mg/kg), xylazine (10 mg/kg), and 14.25% ethanol. Atropine (0.1–0.2 mg/kg, intramuscular [IM]) was administered to decrease oral secretions that interfered with respiration and dexamethasone (0.6 mg/kg, IM) was given to reduce brain swelling. When the animal exhibited no corneal reflex it was secured in a stereotaxic frame (Stoelting, Wood Dale, IL). Body temperature was maintained at 37°C with a temperature feedback-controlled heating pad. Through a midline incision a craniotomy overlying the inferior colliculus was made 2 mm lateral and 2 mm caudal to Lambda, after which the dura was opened. Upon conclusion of the experiment, gel foam was placed over the skull opening and the soft tissue pulled back up and sutured in place. The wound was irrigated with a topical antibiotic and closed with nylon sutures. Postsurgical treatment included the administration of lactated Ringer’s (~0.25 ml, IP), doxapram (10 mg/kg, IM) to stimulate respiration, and butorphanol (5 mg/kg, subcutaneous) for postsurgical analgesia.

Electrophysiology

Electrophysiological recordings were collected from mice in a heated, double-walled, sound-attenuated chamber (IAC, Bronx, NY). Stimulus delivery and neural recordings were controlled via custom routines in MatLab (MathWorks, Natick, MA). Acoustic stimuli were generated either by manually adjusting an analog test oscillator during search (4200B; Krohn-Hite, Brockton, MA) or via computer-controlled hardware (RP2, SM5; Tucker-Davis Technologies [TDT], Alachua, FL). Signals were attenuated (PA5; TDT), amplified (D-75A; Crown, Elkhart, IN), and delivered by a calibrated free-field speaker (40-5036 or Super Tweeter; Radio Shack, Fort Worth, TX) placed directly in front of the animal.

Single- and multiunit recordings were performed in the CN using glass micropipettes (1.2 mm outer diameter) containing fluorescein dextran-amine (MW10,000; D-1820; Molecular Probes/Invitrogen, Carlsbad, CA) or tetramethylrhodamine dextran-amine (MW 10,000; D-1817; Molecular Probes), each diluted to 10% w/v in a solution of 0.5M Tris buffer, pH 7.6, and 3M NaCl. Tip diameter was 10 µm (inner diameter) with 2–4 MΩ impedances. Signals were amplified (1800; A-M Systems, Carlsborg, WA), filtered (3202; Krohn-Hite), and digitized for analysis (PCI-6602; National Instruments, Austin, TX).

Search stimuli in the form of broadband noise or sinusoidal tone bursts (200 msec duration, 5 msec rise/fall) were delivered as the recording electrode was advanced into the brain using a motorized hydraulic micromanipulator (650; Kopf Instruments, Tujunga, CA). Entry was guided by atlas coordinates (Franklin and Paxinos, 1997), approaching the nucleus at a 16° posterior angle. Arrival into the CN was heralded by the presence of sound-evoked spike discharges. BF and threshold of a recording site were determined audiovisually while manually adjusting the tone burst frequency and attenuation. BF was then confirmed with an automated tuning curve protocol that measured responses to a 4-octave (oct.) sweep centered on the test frequency at 20 dB above threshold, sampling every 1/25-oct. At selected frequency locations fluorescent dextran-amine tracer was injected iontophoretically using a high-voltage, constant current source (CS 3; Midgard/Stoelting) set at 5 µA of positive current (50% duty cycle) for 6–10 minutes. After a rest period of 5 minutes the pipette was withdrawn. An injection at a second frequency region in the CN using a complementary fluorescent tracer was attempted in most animals.

Preparation of tissue for microscopy

Two weeks following dye injection, animals were deeply anesthetized with a lethal dose of sodium pentobarbital (100 mg/kg, IP) and perfused transcardially with 3% paraformaldehyde in 0.1M phosphate buffer (PB), pH 7.3. The ipsilateral cochlea was immediately perfused through the oval and round windows. Both the cochlea and brainstem were dissected from the skull and post-fixed overnight in the 3% paraformaldehyde solution. The brainstem was embedded in gelatin-albumin, cut in the transverse plane using a vibratome (Vibratome, Bannockburn, IL) at 50 µm thickness, mounted, and coverslipped in Krystalon (Harleco, Philadelphia, PA).

Each cochlea ipsilateral to the injection site was dissected in 0.1M PB using fine picks and forceps under a dissection microscope. After chipping away the otic capsule, the stria vascularis was removed and the osseous spiral lamina fractured centrally at the modiolus. Rosenthal’s canal, the osseous spiral lamina, and basilar membrane were removed together as apical, middle, and basal segments, and coverslipped using Vectashield (Vector Laboratories, Burlingame, CA) in separate slide wells. Histologic slides were kept refrigerated in the dark to preserve fluorescence.

One additional mouse that did not receive a dye injection was used to construct 3D surfaces of CN subdivisions using similar procedures as above with the following modifications: the perfusion solution contained 2%/2% paraformaldehyde/glutaraldehyde in 0.1M PB, pH 7.3 and the brainstem was sectioned at 30 µm thickness using an Integraslice vibrating microtome (Campden Instruments, Lafayette, IN). After unstained sections were photographed (see below), every third section was mounted, Nissl-stained, and coverslipped in Permount. The cochleae from this mouse were not preserved.

Cochlear nucleus reconstruction

Serial-section digital light micrographs at 25× and 100× (total magnification) were collected in the coronal plane from all brains with injection labeling. All images for a single case were collected as layers within a single document in Photoshop (Adobe Systems, San Jose, CA). The 100× images were restricted to the CN and registered to their 25× counterparts, which captured the entire brainstem. Low magnification images were then registered with one another using blood vessels and other anatomical landmarks to reestablish continuity along the anterior–posterior axis. Only rotational and translational manipulations were applied. Nondestructive level adjustments were applied uniformly across all sections to enhance the visualization of regions of interest. Once aligned, the 100× image stack was exported to a 3D software package, Amira (Visage Imaging, San Diego, CA), where the CN was outlined in each section using a graphics tablet (Cintiq 12WX/21UX; Wacom, Vancouver, WA).

Sections from the nonexperimental brain were collected at 100× through the entire CN of each hemisphere using unstained, free-floating sections placed on slides immediately prior to photographing. Later, every third section was mounted, stained with cresyl violet, cover-slipped, and rephotographed. Images from each hemisphere were aligned independently as above. The CN was outlined using a graphics tablet and the three primary subdivisions (dorsal; DCN, ventral; VCN, granule/small cell domain; GCD) were delimited following standard criteria (Mugnaini et al., 1980; Willard and Ryugo, 1983; Trettel and Morest, 2001). Outlines were exported as an image-stack for use in Amira. The left hemisphere from this case was digitally mirrored to match the orientation of all other cases.

Outlined image-stacks were used to reconstruct 3D surfaces of each CN. Each case was resampled in Amira and converted into a label-field that was used to generate a triangular surface using an unconstrained smoothing algorithm. A remeshing algorithm in Amira was applied to reduce the total number of vertices while preserving overall shape and to improve triangle quality, thereby reducing the computational burden.

Cochlear nucleus template search and normalization

We adapted techniques developed for insect neuroanatomy (Rein et al., 2002; Jenett et al., 2006) to conduct a bias-free search of a CN template using our dataset in two steps. First, every case was independently assessed as a candidate CN template by fixing its position and aligning all other noncandidate cases to it. 3D alignments were performed in Amira by iteratively computing a non-rigid/affine transformation matrix (12 degrees of freedom: three axes of rotation, three axes of translation, anisotropic scaling along each axis, and 3D skew) that minimized the root mean square (RMS) distance between points on the candidate and noncandidate surfaces (Procrustes method). Two metrics were used to evaluate overall fit quality: average RMS distance error, and the core-to-seam ratio (Jenett, 2006). Once all noncandidate surfaces were aligned to a given candidate, a 3D probability map was computed that detailed the percentage overlap of all CN surfaces in the dataset. From this probability map the core-to-seam ratio:

$$c2s=\frac{V_{\mathit{\text{core}}}}{V_{\mathit{\text{seam}}}},$$

was calculated for each candidate CN, where V_core is the volume of the region with a high probability (P ≥ 80%) of surface overlap and V_seam is the volume of the region with a low probability (20% < P < 80%) of surface overlap. A high core-to-seam (c2s) value indicates the candidate is a better choice for the template surface.

After an initial CN template was chosen from our dataset, a set of average CN surfaces was extracted from its probability map. Each surface corresponded to a discrete value (X%) in the range of overlap probabilities and was equivalent to the volume bounded by P ≥ X%. Every average CN surface was evaluated as a candidate by fixing its position and aligning all original CN surfaces to it as above. The surface with the highest c2s value was used as the final CN template surface. Normalization of our dataset was thus achieved by utilizing the alignment transformations to this final template. Transformation matrices were stored and used for all subsequent analyses of spatial data from a particular case. All imported image data from a single animal were confined to the same bounding box so that the transformation matrix was consistent across that case.

A separate iterative procedure was used to generate smooth CN subdivision surfaces from the left- (L-) and right- (R-) hemispheres of the nonexperimental mouse. At each step, the R-CN was fixed and the L-CN was aligned to it using rigid transformations (rotation and translation only). Once aligned, a vector field was computed for each surface that described the shortest path between each point on the test surface to its counterpart. The vertices of each surface were then adjusted by adding 50% of the value of its respective vector field, producing surfaces that were morphs of the parent surfaces. This procedure was repeated to minimize the RMS vector field magnitudes until the two surfaces were virtually indistinguishable from one another. The smoothed result was then aligned to the final CN template (but did not contribute to its creation). The same strategy was applied to DCN and VCN surfaces using whole-CN transformation matrices.

Cochlear labeling identification and reconstruction

Light and fluorescent micrographs of cochlear segments were taken at 25× and 100× (total magnification) and aligned in Photoshop using similar procedures as above. Rhodamine- and fluorescein-sensitive images were collected using appropriate filter sets and stored in the red and green channels of an RGB document, even if only one injection was made. This facilitated the extraction of labeled features from endogenous background signals that appeared in both channels. Slides were also flipped upside-down and rephotographed to capture any detail that may have been occluded by the osseous spiral lamina. Due to the thickness of the tissue, images were taken at multiple focal planes. When necessary, higher magnification micrographs were also taken to resolve ambiguities in fluorescent labeling. Images were examined in Photoshop for labeled radial fibers, which appeared as thin processes that extended outwards towards the inner hair cells (IHCs), and were only found in a single color channel. By cycling through multiple focus planes and between light and fluorescent micrographs, labeled fibers that terminated on IHCs were documented. The most apical and basal locations of positive labeling were marked and stored with the light micrographs. The position that fell midway between the borders of label was assigned the innervation site.

Light micrographs of cochlear segments were imported into Neurolucida (MicroBrightField, Williston, VT) for further analysis. The length of each segment was measured by tracing along the row of IHCs. These values were summed to produce total cochlea length. The position of each innervation site was determined by measuring and summing all segment lengths that were apical to it. Innervation site lengths were normalized to total cochlea length and stored as percent distance from apex (Viberg and Canlon, 2004).

Auditory nerve reconstruction

Fluorescent micrographs of the CN were taken at 100× at the same time as brightfield micrographs and subjected to identical alignment and export manipulations in Photoshop as described above. Images were analyzed to identify the location and trajectory of labeled AN fibers as they coursed through the CN. In some cases, levels were independently adjusted in each color channel to bring out weak signals and to balance the overall amount of background signal across channels. Additionally, color saturation could be enhanced, which tended to make independent red and green signals stand out from the background. Because our analysis focused on the location of labeled pixels, but not pixel luminance, these manipulations did not alter our findings.

Enhanced image stacks were imported into Neurolucida for tracing. Contours were drawn around the perimeter of labeled ANs in each section using a graphics tablet. The AN root (ANR) branch was identified by locating the contour series that moved ventrally and outwards toward the periphery. The location at which one contour diverged into two contours represented the AN bifurcation (Fekete et al., 1984). Continuing anteriorly from the bifurcation, one series of contours moved dorsally through the anteroventral CN (AVCN), corresponding to the ascending branch of the AN. The other contour progressed caudally through the posteroventral CN (PVCN) and into the DCN, describing the descending branch of the AN.

DCN and VCN contours were imported into MatLab for analysis as sets of x-, y-, and z-coordinates corresponding to contour vertices. Each contour was then resampled in order to create an evenly spaced set of vertices along the perimeter without changing the contour shape. Contour sets were then collapsed to line sets by computing the medial axis of each contour. The medial axis is the set of all points inside a contour having more than one closest point on the contour boundary. This transformation will typically produce a topological skeleton with multiple branch points. As such, we simplified the result by selecting the longest path that traversed the skeleton.

Model generation

Radial basis functions (RBFs) are an excellent method for modeling irregular, nonuniformly sampled data (Buhmann, 2003) and were used to derive 3D models of frequency representation throughout the entire volumes of the DCN and VCN. Briefly, RBFs are artificial neural networks containing a weighted sum of translations of a radially symmetric basic function augmented by a polynomial term, and take the form:

$$s(\mathbf{x})=p(\mathbf{x})+{\sum }_{i=1}^N{\lambda }_i\times \mathrm{\varphi }(\Vert \mathbf{x}-{\mathbf{x}}_i\Vert ),$$

where p(x) is a polynomial, λ_i is a real-valued weight, ϕ is a basic function, and ‖x − x_i‖ is the Euclidian distance of x from x_i. For our situation, the basic function consisted of a simple biharmonic (ϕ(r) = r) spline + linear polynomial. The weights, λ_i, were estimated based on the location and cochleotopic/frequency values of labeled AN fibers. To filter out inherent noise in the dataset, a smoothing operation was applied implicitly by replacing the basic function during evaluation with a new function, Ψ, where:

$$\mathrm{\Psi }(\mathbf{x})=\sqrt{{\Vert \mathbf{x}\Vert }^2+c^2},$$

with 100 µm chosen as a value for c, which is half the lowest spatial sampling frequency of our dataset (Carr et al., 2003).

RESULTS

Electrophysiology

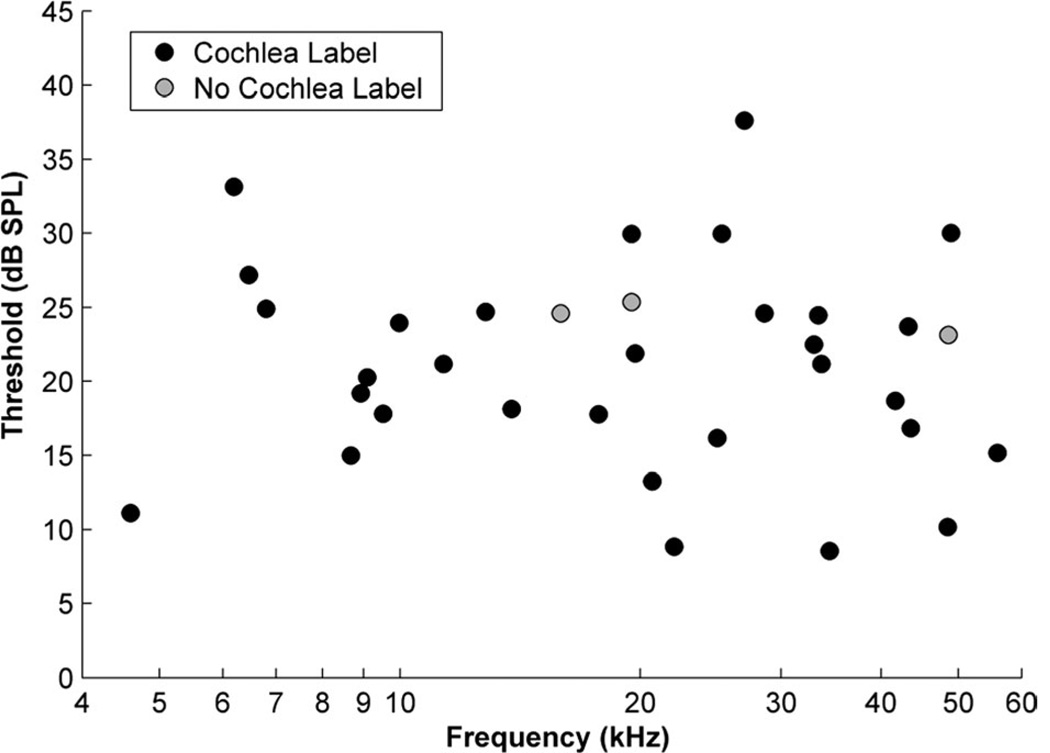
A total of 34 recording sites are reported from 23 mice. BFs ranged from 4.6–56 kHz with thresholds ranging from 8.6–34.6 dB SPL (Fig. 1; Table 2). Iontophoretic injections were made at each recording site.

Figure 1.

Plot of thresholds and best frequencies of multiunit auditory responses in the cochlear nucleus of CBA/J mice. Two groups of unit clusters are shown: those for which an injection was made and successfully traced to the cochlea (black circles) and those for which an injection was made but no label was found in the cochlea (gray circles).

TABLE 2.

Frequency Tuning, Cochlear Analysis, and Auditory Nerve Labeling for All Injections

Mouse ID/ injection	Recording		Cochlea labeling					Auditory nerve labeling
	Frequency (kHz)	Threshold (dB SPL)	Cochlea length (mm)	Midpoint (%)	Apical limit (%)	Basal limit (%)	Spread (%)	Injection location	Mean height of AN label (µm)
22-Fluo	22.1	8.8	5.42	60.3%	56.5%	64.1%	7.6%	VCN	—
23-Fluo	8.7	15.0	5.20	23.1%	11.0%	35.2%	24.2%	VCN	40.4
25-Fluo	9.5	17.8	5.68	20.9%	19.3%	22.5%	3.1%	VCN	39.8
27-Fluo	56.0	15.1	5.50	81.3%	74.8%	87.9%	13.1%	VCN	40.0
27-Rhod*	8.9	19.2	“	4.1%	0.9%	7.2%	6.3%	VCN	—
30-Fluo	9.1	20.3	5.38	23.8%	13.5%	34.1%	20.6%	VCN	33.9
30-Rhod	11.3	21.2	“	35.6%	29.9%	41.3%	11.4%	VCN	37.3
31-Fluo*	19.7	21.9	5.55	63.6%	61.7%	65.4%	3.8%	VCN	—
31-Rhod	33.7	21.2	“	62.2%	50.1%	74.3%	24.2%	VCN	50.2
32-Fluo	41.7	18.7	5.47	71.7%	65.8%	77.5%	11.7%	VCN	—
33-Rhod	25.0	16.2	5.45	53.0%	45.4%	60.6%	15.1%	VCN	41.6
35-Fluo	33.0	22.5	5.01	64.9%	52.9%	76.9%	24.0%	VCN	37.5
35-Rhod	48.6	23.1	“	—	—	—	—	VCN	48.0
36-Fluo	34.5	8.6	5.14	72.2%	68.5%	75.9%	7.4%	VCN	—
36-Rhod	20.7	13.2	“	51.8%	45.0%	58.5%	13.5%	VCN	44.0
37-Fluo	6.5	27.2	5.28	16.9%	4.9%	28.9%	24.0%	DCN	27.0
37-Rhod	49.0	30.0	“	87.0%	81.0%	92.9%	11.9%	VCN	41.5
38-Rhod	10.0	23.9	5.15	27.9%	17.7%	38.1%	20.4%	VCN	41.0
38-Fluo	17.7	17.8	“	35.9%	22.8%	48.9%	26.1%	VCN	—
39-Rhod	13.8	18.1	5.11	39.9%	27.1%	52.7%	25.6%	VCN	32.2
40-Rhod	6.8	24.9	5.36	8.8%	7.3%	10.2%	3.0%	VCN	39.1
40-Fluo	15.9	24.6	“	—	—	—	—	VCN	—
42-Fluo	6.2	33.1	5.23	13.5%	3.7%	23.2%	19.5%	VCN	37.0
44-Rhod	4.6	11.1	5.11	7.5%	1.6%	13.4%	11.8%	DCN	34.2
45-Rhod	27.0	37.6	5.18	64.8%	53.6%	75.9%	22.3%	VCN	45.3
45-Fluo	48.5	10.2	“	83.2%	78.2%	88.2%	10.0%	VCN	40.0
49-Fluo	28.6	24.6	5.27	71.8%	67.9%	75.7%	7.7%	VCN	41.8
51-Rhod	43.3	23.7	5.35	78.9%	76.6%	81.2%	4.6%	VCN	38.3
52-Rhod	33.4	24.5	4.79	80.9%	70.7%	91.0%	20.3%	VCN	35.5
53-Rhod	43.6	16.8	4.69	82.9%	79.7%	86.1%	6.4%	VCN	38.9
55-Rhod	12.8	24.7	4.91	41.1%	34.2%	48.0%	13.8%	VCN	32.1
55-Fluo	19.5	29.9	“	51.6%	46.7%	56.6%	9.9%	VCN	—
56-Rhod	19.5	25.4	5.01	—	—	—	—	VCN	—
56-Fluo	25.3	29.9	“	62.6%	57.0%	68.2%	11.2%	VCN	—
Mean			5.23				14.6%		39.0
SD			0.24				7.3%		5.1

^*Injection not isolated to CN and not included in means.

Cochlea place-frequency map

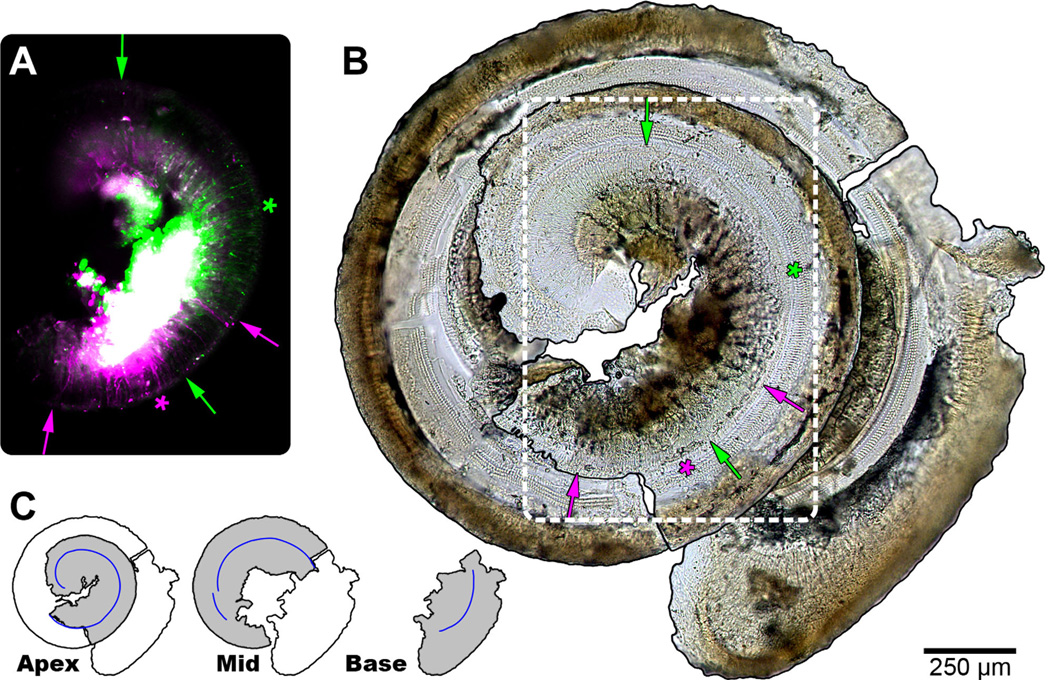
Cochleae were recovered in three or four segments containing Rosenthal’s canal, osseous spiral lamina, and basilar membrane. Reconstruction of the cochlear whole mounts required alignment of the pieces by attending to segment orientation, curvature, and edge shape. An example of a fully reconstructed cochlea from three segments is shown in Figure 2. Mean length of the organ of Corti, as measured along the row of IHCs, was 5.23 ± 0.24 mm (n = 23; Table 2).

Figure 2.

Summary of cochlear analysis. A: Composite fluorescent micrograph of the apical turn of a cochlea (#30; Table 1), corresponding to white dashed outline in B. Auditory nerve fibers labeled with either rhodamine (magenta) or fluorescein (green) are present. The large white region corresponds to the intense and unfocused signal from SGCs overlapping in both channels. Labeled radial fiber processes that reach to the IHCs were analyzed. The apical and basal extent of labeling of each tracer is indicated using arrows of matching color. The calculated midpoint of labeling is shown with asterisks. B: Photomontage of the osseous spiral lamina and basilar membrane of the dissected cochlea. A single row of IHCs and three rows of outer hair cells are evident. Arrows and asterisks as in A. C: Schematic representation of the separate apical, middle, and basal segments recovered from a cochlea and reconstructed in B. The pieces were arranged to resemble the spiral of the intact cochlea. The total measured extent of the row of IHCs is shown by the blue line segments. Scale bar = 250 µm in A–B.

Twelve mice received a single injection and 11 mice received two injections, giving 34 in total (Table 2). Retrograde fluorescent labeling was located in the cochlea as a result of tracer deposits in the CN for all but 3 of the 34 injections. Two of the remaining 31 injections were excluded from further analysis, as their injections were medial and invaded the vestibular nerve root, resulting in extensive labeling of auditory efferents in the cochlea (Brown et al., 1988). Successful labeling was indicated by a circumscribed volume of dye in the CN matching the stereotaxic coordinates of the electrode tip and confirmed by the presence of labeled radial fibers extending to IHCs (Fig. 2A). The location of innervation was defined by taking the midpoint between the apical and basal extremes of labeled radial fibers. Labeled fibers appear as thin threads that terminate on IHCs near the locus of labeled spiral ganglion cells (SGCs; Fig. 2A,B, arrows). The spread of labeling, reported as a percentage of total cochlea length, was variable (mean: 14.6% ± 7.3%, n = 29) and had no obvious relationship to cochlear position (R = −0.22, P = 0.25) or injection BF (R = −0.24, P = 0.21; Fig. 3). A summary of recordings and characteristic place in the cochlea is given in Table 2.

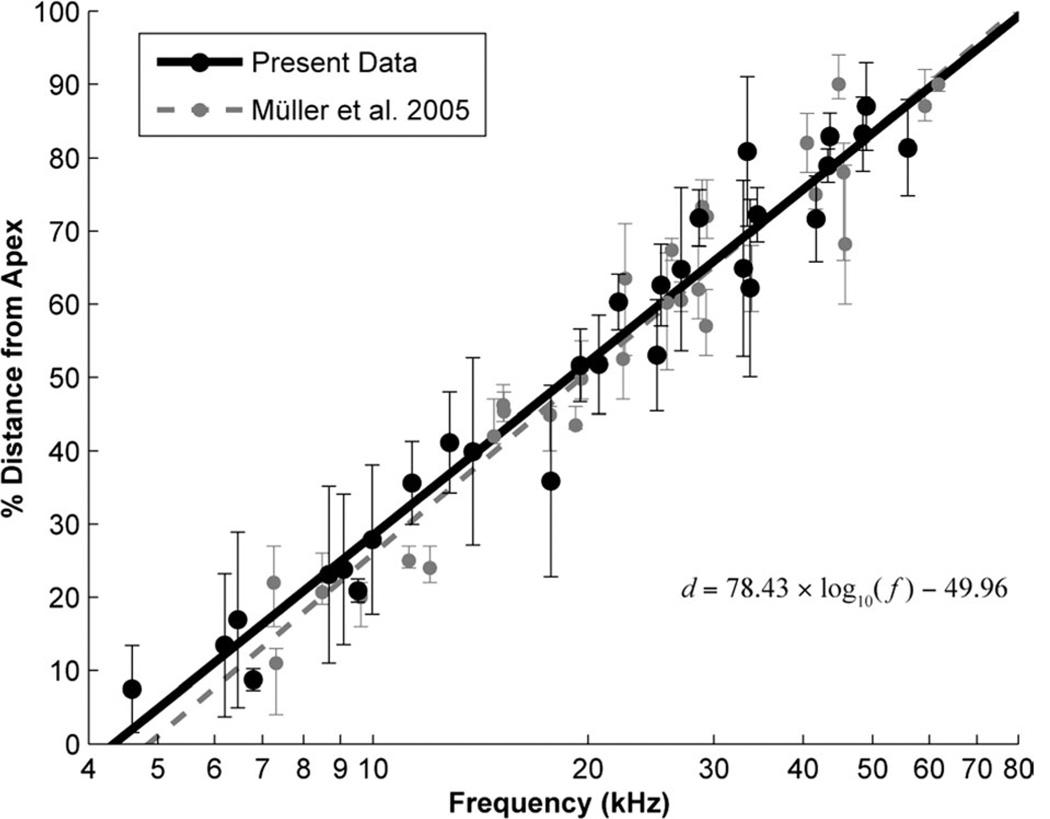
Figure 3.

Plot of cochlear place-frequency map for the CBA/J mouse. The place-frequency map was constructed by comparing the locations of labeled fibers in the cochlea (Fig. 2) to the best frequency of the injection site (Fig. 1). The midpoint of label (black circles) and the spread of labeling along the cochlea (vertical bars) are shown. A log-linear line of best fit was calculated (black solid line) and takes the form d = 78.43 × log₁₀ (f) − 49.96 (R² = 0.96), where f is the frequency in kHz and d is the normalized percent distance from the apex in the cochlea. For comparison, the individual measurements (gray circles/bars) and log-linear fit (gray dashed line) from Müller et al. (2005) are also shown. The equation for the Müller fit is d = 82.5 × log₁₀ (f) − 56.5. The correspondence of the plots is striking considering the different methods utilized.

A monotonic relationship is clearly demonstrated between BF at the injection site and innervation locus in the cochlea (Fig. 3). Linear regression of the midpoint of cochlear labeling against frequency on a logarithmic scale gives the function:

$$d=78.43\times {\text{log}}_{10}(f)-49.96,$$

where f is the frequency in kHz and d is the normalized percent distance from the apex of the cochlea (R² = 0.96). A general form of the mammalian cochlear frequency map has been devised by Greenwood (1961, 1990, 1996). This map takes the form of the equation:

$$f=A\times ({10}^{\mathrm{\alpha }d}-k),$$

where f is the frequency in Hz, d is the normalized distance from the apex of the cochlea, and A, α, and k are coefficients. α describes the gradient at the high-frequency end of the map, A shifts the entire curve along the log-frequency axis, and k induces curvature or warp to fit low-frequency data that are not well described by a single log-linear equation.

Our experiments produced primary data relating to both frequency (f) based on electrophysiology and position (d) based on cochlear labeling; thus, it was possible to apply Greenwood’s equation with respect to either parameter, allowing all coefficients to vary. Solving for frequency (Liberman, 1982; Müller, 1991; Müller et al., 1993) produced coefficient values of A = 8345, α = 0.95, and k = 0.58 (R² = 0.93) from our measurements. Solving for distance (Müller and Smolders, 2005; Müller et al., 2010) yields coefficient values of A = 5404, α = 1.16, and k = 0.27 (R² = 0.96). The decision to fit to one parameter versus the other can be influenced by differences in the variance of fitting errors. With our data, solving for distance produced a marginally better Greenwood fit.

Cochlear nucleus reconstruction

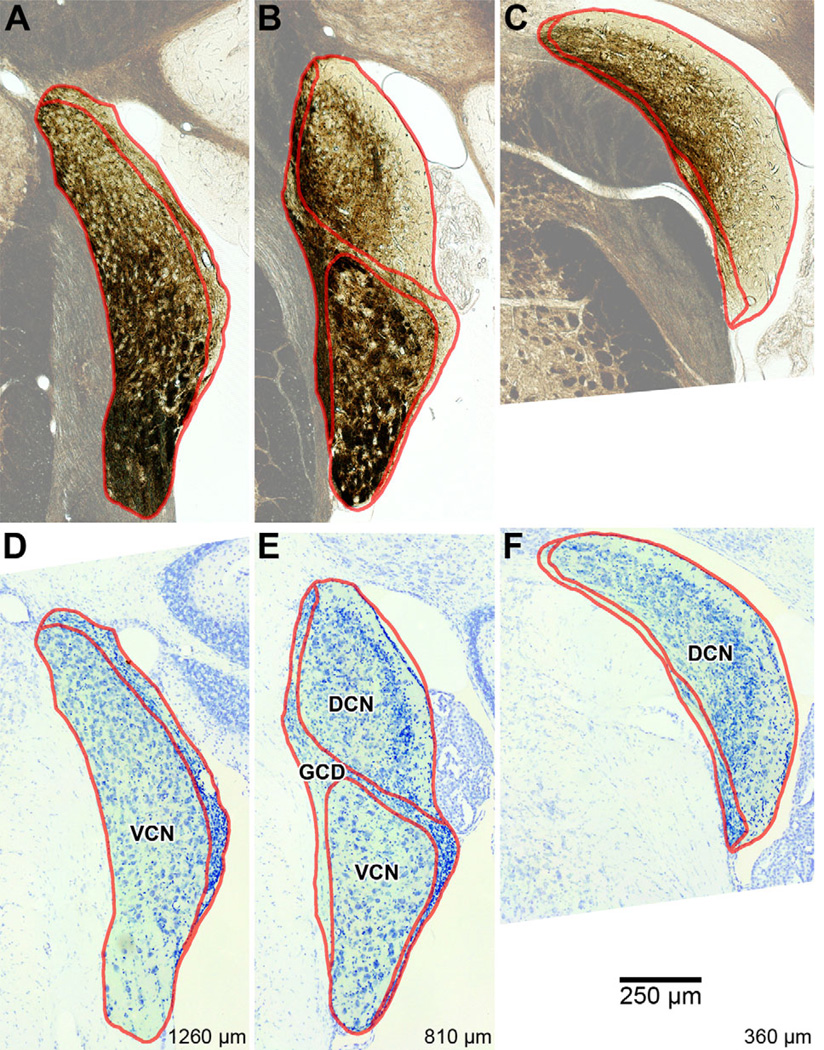
Serial sections were collected in the coronal plane through each CN. Cases that had received injections (n = 23) were cut at 50 µm, with the CN spanning between 34 and 41 sections (mean: 37.9 ± 2.3, n = 19; Table 1). This variability can be attributed to individual differences in the size of the nucleus, nonuniform reactions to histological processing, and/or changes in the cutting angle during sectioning. In four animals we were not able to recover all sections and thus they were not included in the mean. In order to preserve fluorescence (see below), sections were mounted, dehydrated, and cover-slipped prior to examination. The nonexperimental brain was sectioned at 30 µm, with L- and R-CNs spanning 65 and 68 sections, respectively (#60; Table 1). Deliberate misalignment of the brightfield condenser maximized light diffraction through the tissue and enhanced image contrast (Richter and Warner, 1974). This method of photographing tissue facilitated outlining the CN and its subdivisions (Fig. 4). Fiber tracts appear dark brown due to the scattering of focused light by myelin sheaths, with tracts that run orthogonal to the section plane appearing darker than those running in parallel. Empty pockets in the dense neuropil hint at the locations of some larger cell bodies, and match up with stained nuclei when the same sections are Nissl-stained.

Figure 4.

Photomicrographs of three evenly spaced coronal sections through the right cochlear nucleus of a CBA/J mouse (#60R; Table 2). Borders delineating the major subdivisions of DCN, VCN, and GCD are shown in red. Regions outside the CN were rendered semiopaque for emphasis. A–C: Photomicrographs of unstained sections. Areas rich in myelin appear dark brown. Values at bottom-right designate relative distance from the posterior edge of the CN. D–F: Photomicrographs of the same sections after staining with cresyl violet, showing cytoarchitecture.

The medial border of the CN was easily demarcated, as it shares an edge with the inferior cerebellar peduncle, trapezoid body, trigeminal nerve, vestibular branch of the eighth nerve, and middle cerebellar peduncle, each of which is dense in myelin and appears dark and/or texturally distinct from the CN (Fig. 4, upper). Outlining the major subdivisions (DCN, VCN, and GCD) was helped by the use of Nissl-stained sections (Fig. 4, lower). For our purposes, we grouped all miscellaneous subdivisions (small cell cap, acoustic stria, etc.) under the GCD heading, as we were chiefly concerned with the dorsal and ventral subdivisions. The GCD was identified in each section as a region of pale coloring (unstained) and/or containing many small cells (Nissl), and was considered to completely separate the ventral and dorsal divisions (Mugnaini et al., 1980). Published criteria (Willard and Ryugo, 1983; Trettel and Morest, 2001) were applied to this process. The DCN and VCN were thus defined as the remaining space in the CN after labeling the GCD.

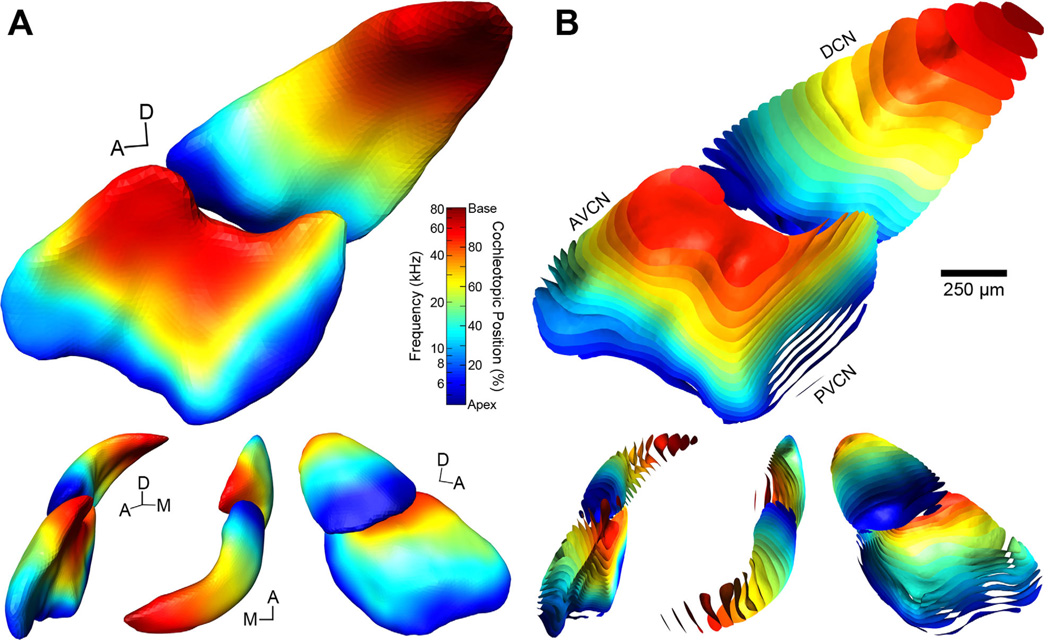
3D surfaces of each CN were generated from their stacked outlines. Volumes of complete cases ranged from 0.523–0.687 mm³ (mean: 0.611 ± 0.047 mm³; Table 1). Although age and weight were highly correlated (R = 0.66, P < 0.001, n = 24), neither factor bore a significant relation to CN volume (age: R = −0.34, P = 0.13; weight: R = −0.05, P = 0.61; n = 21). Each CN was qualitatively similar in shape (Fig. 5A), displaying a shallow concave surface along the interior aspect of the DCN, which curves over the trunk of the inferior cerebellar peduncle. At the medioposterior pole of the DCN, there are differences in the extent of this protrusion because the separation between DCN proper and the dorsal acoustic stria can be ambiguous. Anterior to the DCN a prominent ridge runs along the medial edge of the nucleus, giving rise to the subpeduncular corner (Fig. 5A, dorsal view). The ventral surface of the nucleus between AVCN and PVCN also varied slightly, owing to the occlusion of the CN by the incoming AN. Subdivision volumes were 0.187 and 0.170 mm³ for the L- and R-DCNs, respectively, and 0.273 and 0.261 mm³ for the L- and R-VCNs. Subtracting subdivision volumes from the CN volume yields estimated GCD volumes of 0.104 and 0.093 mm³ for the L- and R-sides.

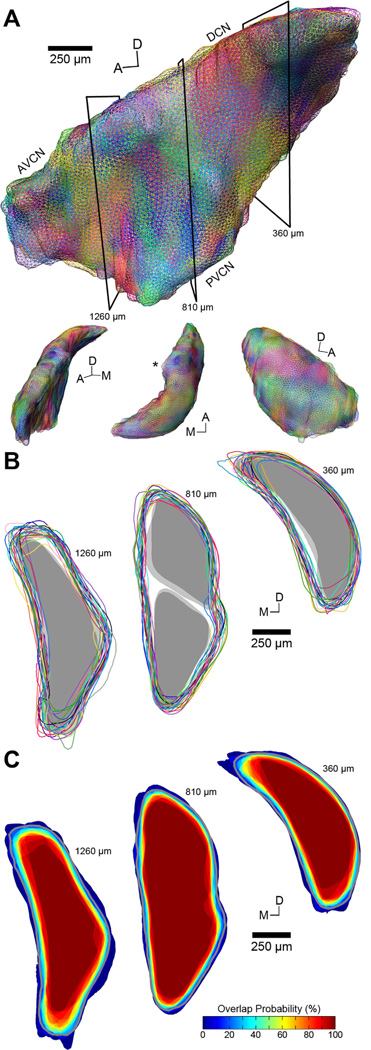
Figure 5.

Normalization of all cochlear nucleus surfaces to a template. A: Compilation of reconstructed 3D CN surfaces for all 25 cases (Table 2) rendered as wireframes. Surfaces are shown in top figure from a medial perspective. Each surface is randomly assigned a different color. In this example, one case (#40) has been selected as the template and all other cases are aligned to it using nonrigid transformations. The heterogeneity of colors visible on the surface emphasizes the similarity of CN shapes when registered to a template; no single case dominates. Black boxes indicate the orientation of cross-sections shown in B,C. Lower figures are from alternate viewing angles; L-R: anterior, dorsal, and lateral. Asterisk in dorsal perspective indicates the subpeduncular corner. Scale bar applies to large figure only. B: Coronal cross-sections through the AVCN (left), DCN and PVCN (middle), and DCN (right) show the boundaries of each CN after registration to the template. Each outline is paired to its corresponding surface in A. While there is some structural variability among the cases, the predominantly overlapping boundaries indicate that each CN is well matched to the template and thus to one another. Gray regions show the fit of the boundaries of DCN and VCN to the model. C: Probability maps of the sections shown in B indicate the amount of overlap between CNs after alignment to the template. The dark red core region of each section corresponds to a probability of 100% and is therefore contained within all 25 nuclei. More peripheral locations show decreasing degrees of surface overlap. The gray outline in each section indicates the border of the final template used for registration (see Results).

Cochlear nucleus normalization

Due to the nature of brain sectioning, it is unlikely that any two brains will be cut along the exact same plane relative to gross anatomy. Consequently, 3D reconstructions of individual CNs must be normalized to a “standard reference” template in order for meaningful comparisons to be made across subjects. Because the quality of any normalization will depend critically on the selection of a template surface to which all cases are aligned, we conducted a bias-free two-stage search for an average template that best represented the CN.

Each of the 25 CN surfaces in our dataset was individually evaluated as a candidate template. In each instance, the other 24 surfaces were aligned to the candidate using nonrigid transformations (Fig. 5A). Visually, surfaces were quite similar to one another, with the most variation apparent at the dorsomedial and anterior poles of the CN. The nonrigid transformation algorithm takes the entire surface geometry into account so that we did not need to approximate a whole CN for cases with missing sections. Coronal sections showing surface outlines are shown to demonstrate how closely the surfaces overlapped (Fig. 5B). Relative spatial relationships between surface boundaries following a nonrigid transformation are not affected by the absolute size of the reference surface. Consequently, each candidate surface was uniformly scaled to the average CN volume of the dataset (0.611 mm³) prior to alignment. This scaling allowed us to make more meaningful comparisons of average RMS distance error measurements between candidates. Average RMS errors ranged from 23.9–39.1 µm (Table 1). The four cases with partial CN surfaces predictably produced the highest errors, as they were poor representations of a typical CN surface. 3D probability maps were also computed for each candidate (Fig. 5C). From each map the c2s ratio was obtained. This statistic is invariant to changes in absolute scale, making it an excellent criterion for selecting a template. c2s ratios for the 25 surfaces ranged from 2.16–2.56 (Table 1). The surface with the highest c2s ratio (#40) also produced the lowest RMS error and was chosen as the initial template from which average CN surfaces were extracted.

Average CN surfaces were computed by taking the region bounded by P ≥ X% for each discrete value, X, in the 3D probability map, ranging from the extreme outer contour of 4% (1 out of 25 surfaces overlapping) to 100% probability of overlap (Fig. 5C). The shapes of average CN surfaces were strikingly similar at each value up through 84%; the remaining values produced truncated surfaces due to the four cases that were missing sections. Confirming this observation, the mean c2s ratio was 2.58 ± 0.01 for the first 21 average surfaces (4%–84%), dropping to 2.49 ± 0.05 for the remaining four cases. Correspondingly, the mean RMS error was 21.7 ± 0.6 µm for the first 21 average surfaces, climbing to 27.9 ± 1.4 µm for the last four cases. Although most surfaces were similarly suitable as templates, the average CN surface corresponding to 16% probability of overlap produced the highest overall c2s ratio and was thus chosen as the final template for the normalization of our dataset (Fig. 5C; gray lines). The mean RMS error after normalizing all 25 CN surfaces to the final template was 21.8 ± 3.6 µm (Table 1). It should be emphasized that each case, and all data related to it, was independently normalized to the final template and had no bearing on the placement of data arising from other cases.

Surfaces of the DCN and VCN were required for purposes of illustrating the frequency model developed below. Smooth surfaces were generated by iteratively morphing each hemisphere of a single animal (#60L/R) until they became virtually indistinguishable from one another. The morphing process produced a smoother surface than either of the original surfaces, but still retained significant characteristics of each subdivision. Prior to morphing, DCN and VCN surfaces were separated by RMS distances of 24.8 µm and 24.4 µm, respectively. Modified c2s ratios (volume of overlap vs. nonoverlap) were 3.10 for DCN and 4.15 for VCN. Following eight morph iterations, RMS distances dropped to 0.52 µm for DCN and 0.61 µm for VCN, and modified c2s ratios rocketed to 457.93 and 427.82, indicating near complete congruence.

Auditory nerve reconstruction

All tracer deposits in the CN were made on the right side; two injections were localized to the DCN and 30 were distributed throughout the AVCN. Two other injections were not confined to the CN and were therefore excluded from analyses. A typical result following dual injections shows that the approximate location of a particular injection site can be easily determined upon visual inspection (Fig. 6). In this example, both injections are clearly confined to the AVCN.

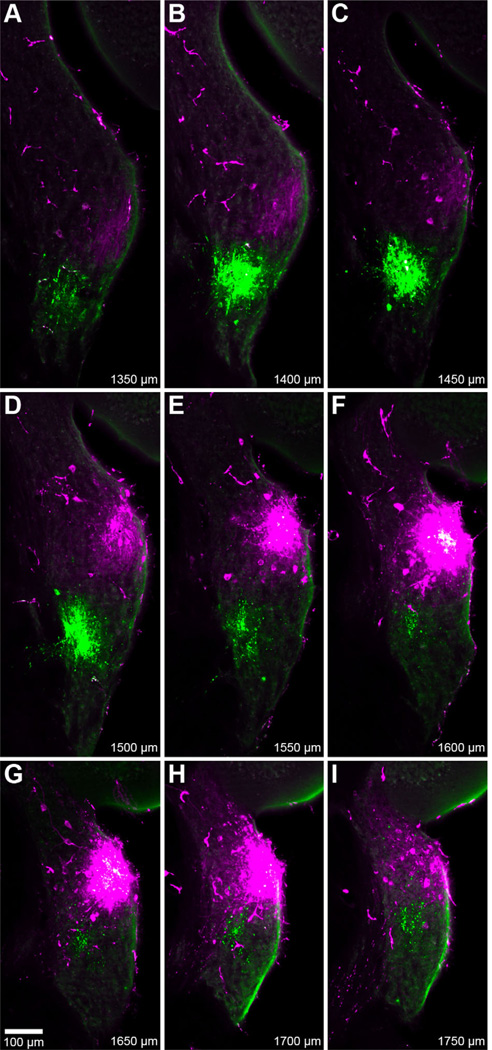
Figure 6.

Fluorescent photomicrographs of serial coronal sections, 50-µm thick, spanning a pair of cochlear nucleus injection sites (#30; Table 1). Both rhodamine (magenta, 11.3 kHz BF) and fluorescein (green, 9.1 kHz BF) injections were located in the AVCN. The most intense central region of rhodamine labeling was also detected with fluorescein filters, resulting in white pixels (e.g., panel F). Values at bottom-right designate relative distance from the posterior pole of the CN. The location of the rhodamine injection is both more dorsal and anterior to that of the fluorescein injection. Faint strands of labeled AN fibers can be found posteroventral to each injection.

CN injections result in labeling of AN fibers in the CN and cochlea in 24 of the 31 injections (Table 2; Fig. 7A–C). Fibers could be relatively faint when compared to the injection site but were nevertheless still distinguishable from the background signal. Comparing images from alternate color channels enabled us to distinguish labeled fibers throughout the CN with confidence. Rhodamine tended to produce a more robust signal than fluorescein. On the basis of fiber caliber, we propose that only the axons of type I SGCs are in our analysis.

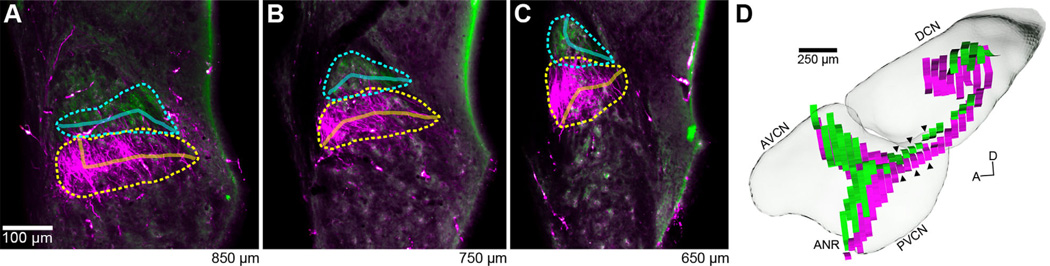
Figure 7.

Reconstructed auditory nerve fibers. A–C: Fluorescent photomicrographs show three coronal sections through the PVCN (#45; Table 1). AN fibers labeled with rhodamine (magenta; 27.0 kHz injection) or fluorescein (green; 48.5 kHz injection) can be seen passing through the dorsal region of the PVCN in each section. The location of fibers in each section was approximated by outlining the extent of visible label (rhodamine: dashed-yellow; fluorescein: dashed-cyan). Solid lines show the computed medial axes, which bisect each outline and are used to represent the location of labeled AN fibers. Values at bottom right designate relative distance from the posterior edge of the CN. D: 3D reconstruction of AN fibers from all sections, aligned and positioned within the template CN. Each “ribbon” corresponds to the medial axis computed from a single section. Ribbons for both rhodamine (magenta; 27.0 kHz) and fluorescein (green; 48.5 kHz) are shown. Black arrowheads indicate the positions of the three sections shown in A–C; leftmost arrowheads correspond to panel A. The fibers follow a stereotyped trajectory, entering as part of the auditory nerve root from the ventral surface and traversing dorsally before bifurcating, giving rise to the ascending and descending branches of the AN. There is a systematic relationship between AN position and frequency, with fibers tuned to higher frequencies (in this case, green), having a more dorsomedial position compared to those fibers tuned to lower frequencies. The CN is presented from a medial viewpoint.

Each set of labeled fibers followed a stereotypical pattern as it coursed through CN sections. Fibers progress ventrally through the ANR and towards the cochlea, and dorsally into the CN where they then bifurcate, sending an ascending branch through the AVCN, and a descending branch through the PVCN before terminating in the DCN. Short collateral branches are given off along the trajectories of the ascending and descending branches (for review, see Nayagam et al., 2011). The bifurcation point is identifiable when following the label through consecutive sections. The ascending branch progresses toward the anterior pole of the CN, often encountering the injection site (as most injections were in the AVCN). The exact trajectory of the ascending branch typically varied with respect to the BF of the injection site. The lowest BFs resulted in label that closely followed the ventrolateral edge of the AVCN, and higher BFs produced label that had a more dorsal and medial distribution. In the PVCN, the descending branch of labeled AN fibers tended to fill out in a horizontal band. The lowest BFs were tucked into the ventral edge of the PVCN with higher BFs occupying progressively more dorsal regions in a coronal slice. The descending fibers crossed through the GCD lamina and extended dorsolaterally into the DCN. Lower BFs made this transition at more anterior positions, with the highest BFs not entering the DCN until the most dorsoposterior aspect of the PVCN was reached.

After outlining the extent of label for each color channel, the resulting polygons were approximated as lines by computing the medial axis of each outline (Fig. 7A–C). We estimated the orthogonal spread (approximately perpendicular to the medial axis) of AN labeling in each case by calculating the mean height (range: 27.0–50.2 µm; mean: 39.0 ± 5.1 µm; n = 24; Table 2). There was no apparent relationship between the mean height of AN fiber labeling and the spread of labeling in the cochlea (R = −0.13, P = 0.61).

The trajectory of labeled AN fibers in a given case can best be appreciated when collectively viewing all the lines together in 3D within the CN (Fig. 7D). The separate branches of the AN (ANR, ascending, descending) are each readily identified, as is the transition from PVCN to DCN. A tonotopic relationship between pairs of labeled fiber bundles is maintained for all individual cases, with higher BF fibers consistently located in a more dorsal and/or medial position compared to fibers with lower BFs.

This relationship also holds when all AN lines are shown together, each designated in space by using the transformation matrices calculated during normalization (Fig. 8A). Individual lines are colorized based on the corresponding midpoint position of labeling in the cochlea, revealing a conspicuous but not unexpected display of frequency organization. Fibers originating from the most apical regions of the cochlea bifurcate and course anteriorly and posteriorly along the ventral floor of the VCN. As the fibers proceed towards the DCN, they turn laterally to pass through the GCD and occupy the ventral floor of the DCN. Fibers originating from more basal regions of the cochlea advance higher into the ANR region before bifurcating and dispersing while maintaining their relative spatial position within the nucleus. The descending branch passes through the GCD lamina and proceeds posteriorly to its terminal field in the DCN. Viewed from the medial axis, fibers intermingle in the ANR region. Ascending fibers progress all the way to the anterodorsal border of the AVCN, but descending fibers do not extend fully to the dorsal surface of the DCN.

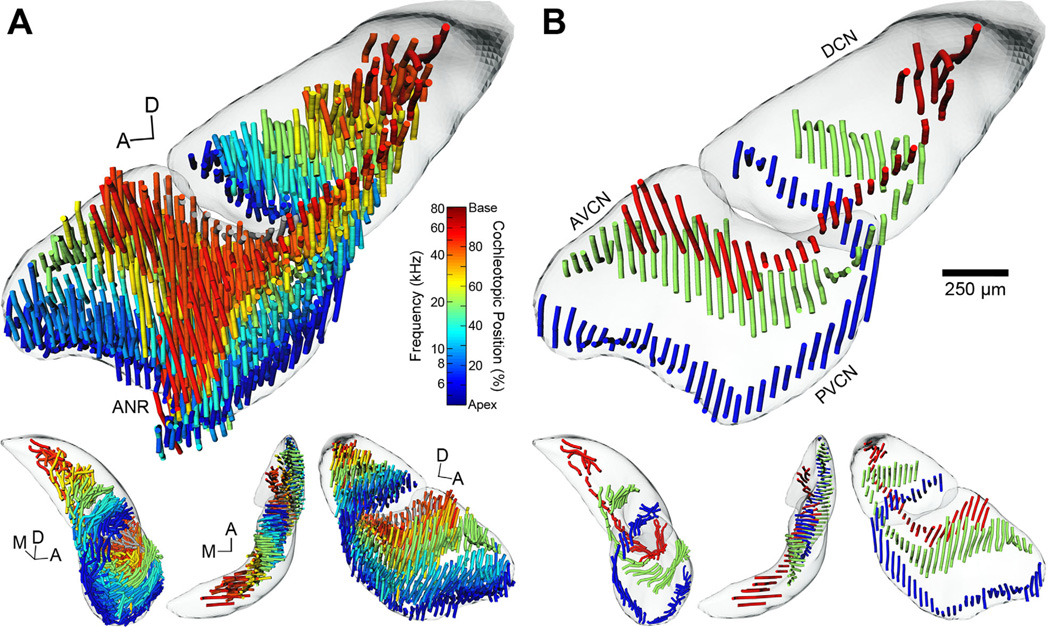
Figure 8.

3D tonotopic arrangement of auditory nerve fibers in the cochlear nucleus of the CBA/J mouse. A: The complete set of reconstructed AN fiber tracts from all experimental cases is shown after normalization to the template CN. Each tract is represented as a set of “noodles” and shaded according to its position of cochlear origin. Equivalent frequency/position values are provided (vertical color map) based on our place-frequency map of the cochlea (Fig. 3). A clear tonotopic trend is evident in all three major subdivisions. DCN and VCN surfaces are also shown and rendered semiopaque. The top figure is from a medial viewpoint. Lower figures are from alternate viewing angles; L-R: posterior, dorsal, and lateral. In the lower figures, the reconstructed ANR fibers have been removed (see text). B: Three cases from A are chosen to illustrate the trajectory of low-, middle-, and high-frequency AN fiber tracts more clearly. Examples shown correspond to values of 13.5%/6.4 kHz, 53.0%/20.5 kHz, and 87.0%/55.8 kHz. The reconstructed ANR fibers have been removed. Scale bar = 250 µm for large figures only.

There is a 3D organizational plan of primary inputs into the CN. AN fibers from progressively higher frequency locations describe parallel “U”-shaped laminae that stack upon one another in ascending order from apical to basal cochlear origin. This arrangement is made more apparent by only showing a single case each from a low-, middle-, and high-BF injection (Fig. 8B). Each AN/frequency-module is positioned slightly more dorsal and medial to the previous one such that a cochleotopic map is established throughout the volume of the CN.

3D model of frequency representation in the cochlear nucleus

We used RBFs, a type of artificial neural network, to generate quantitative maps that approximate frequency representation with respect to 3D position in the DCN and VCN. By creating such maps, we avoided having to reduce the dimensionality of our dataset. The weighting coefficients of the RBFs were estimated based on the location and values of the representational lines of labeled AN fibers (Fig. 8A), as these were well distributed throughout the volume of the CN. We disregarded the ANR branch because individual AN fibers may produce none or only a few collaterals restricted to the ANR region prior to bifurcation (Fekete et al., 1984). While these collaterals can complicate fine-scale frequency organization in the ANR region of the VCN (Bourk et al., 1981), they did not contribute to the dominant projection patterns of the ascending and descending branches.

As RBFs require discrete points for operation, we first resampled the AN lines as a set of points spaced at 50-µm intervals along the path of each line. This interval was equivalent to our section thickness, which in turn had determined the separation of individual lines in each case along the z-axis. The result was a uniform distribution of point sets in 3D that were segregated into two groups, corresponding to AN lines located in the VCN or DCN. The separation was done in order to avoid undesired interactions between the low frequency ventral edge of the DCN and the adjacent high frequency dorsal edge of the VCN (Fig. 8). Cochleotopic values associated with each point set were used for coefficient estimation rather than injection BFs, as these values were linear with respect to distance along the sensory epithelium. The final RBFs take as input a coordinate within a subdivision and return an expected cochleotopic position that approximates the cochlear origin of AN fibers innervating that location. Outputs were then converted to frequency values by using the cochlear place-frequency map (Fig. 3). Evaluating the RBFs over arbitrary point grids, with grid spacing setting the resolution of the map, can create visual 3D maps of frequency representation.

The coordinates of DCN and VCN surfaces were fed into the RBFs in order to visualize our model (Fig. 9A). Each vertex was shaded according to the output of the interpolant. It should be emphasized that the DCN and VCN surfaces did not contribute to the creation of the frequency model, and were only used as “canvases” upon which the model was illustrated.¹ The result is predictably similar to the distribution of AN labeling (Fig. 8). There is a regular progression of frequency representation in the AVCN, PVCN, and DCN, whose orientation advances along an anteroventral–posterodorsal axis. There is also a slight lateral–medial axis of change. The distribution of frequency in the PVCN runs approximately orthogonal to that of the AVCN, with the shift in direction occurring immediately posterior to the ANR region. This relationship is made clearer by visualizing the model as a set of isosurfaces bound to the exterior edge of each subdivision, with surfaces rendered at 5% intervals—equivalent to 0.21-oct. steps (Fig. 3)—along the cochleotopic axis (Fig. 9B). To highlight the internal structure of the model, a series of “virtual” slices in coronal, parasagittal, and horizontal planes are shown (Fig. 10).

Figure 9.

3D models of frequency representation in the cochlear nucleus of the CBA/J mouse. A: Volumetric DCN and VCN models constitute the predicted values of frequency representation at any coordinate. The exterior nodes of the DCN and VCN surfaces were shaded according to their predicted values. Frequency and cochleotopic values are interchangeable based on our place-frequency map of the cochlea (Fig. 3). Within the bounds of each subdivision, the model captures the trends found with respect to the tonotopic organization of auditory nerve fibers (Fig. 8). B: Isosurfaces constrained to subdivision boundaries are rendered for cochleotopic values at 5% intervals, corresponding to 0.21-oct. steps, and shaded accordingly. Viewed in this manner, we are able to observe the undulations of isofrequency laminae within the interior of the CN. The top figures are from medial viewpoints. Lower figures are from alternate viewing angles; L-R: anterior, dorsal, and lateral. Scale bar = 250 µm for large figures only.

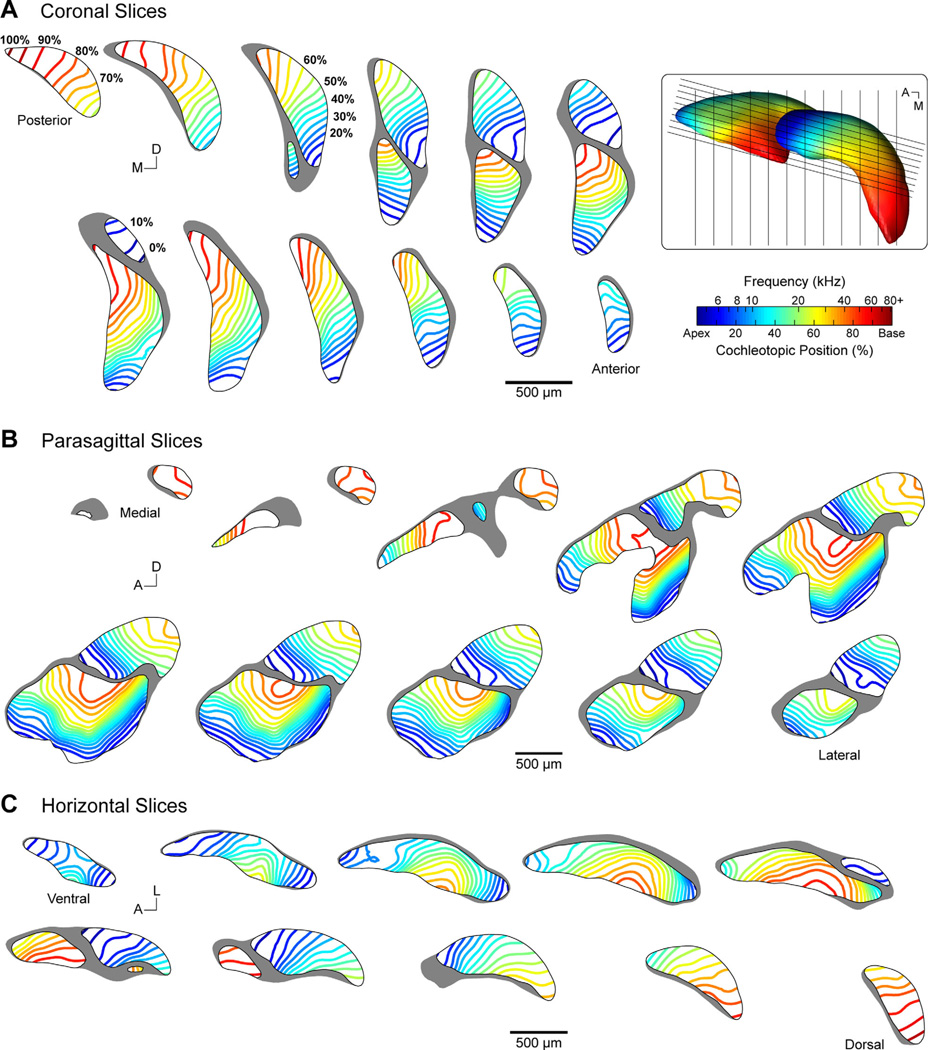
Figure 10.

Collection of virtual slices demonstrating tonotopy in the cochlear nucleus of the CBA/J mouse. Evenly spaced parallel slices are presented in coronal (A), parasagittal (B), and horizontal (C) planes. Isofrequency lines are rendered within each slice at 5% cochleotopic intervals, equivalent to 0.21-oct. steps, and correspond to the isosurfaces presented in B. Frequency and cochleotopic values are interchangeable based on our place-frequency map of the cochlea (Fig. 3). Slices in each row or column are aligned with one another along the orthogonal axis. Coronal and horizontal slices are spaced at 150 µm. Parasagittal slices are spaced at 50 µm and oriented 15° off the sagittal plane. Inset: Dorsal view of the 3D model. Black lines indicate the location of sectioning planes used for virtual slicing of coronal and parasagittal sections. Horizontal sections are taken along the plane of the image.

The subdivision surfaces allowed for the estimation of the amount of neural volume dedicated to equal partitions of cochlear representation. Each surface was segmented into blocks of 5% representation—equivalent to 0.21-oct.—and the volume of each block was computed. Blocks were equivalent to the space between adjacent isosurfaces in Figure 9B. Between cochleotopic values of 10%–85% there was a roughly equal amount of VCN volume dedicated to each block (mean: 0.0180 ± 0.0014 mm³ per block; Table 3). Beyond this range, however, there was a steep drop-off in per-block volume. This was undoubtedly due to the limits of our dataset when constructing the models. We did not detect a trend in VCN block volume with respect to frequency (R = −0.09, P = 0.72). In the DCN, between cochleotopic values of 10%–85%, there was slightly more variation in volume (mean: 0.0106 ± 0.0018 mm³ per block; Table 3). As in the VCN, volumes decreased at higher frequency ranges, but at lower ranges the percent volume per block actually increased before dropping below 0.0032 mm³ for the lowest frequency block. There was a modest, although not significant, decrease in DCN block volume with respect to frequency across the whole cochleotopic range (R = −0.37, P = 0.10). This effect likely reflects the tapering of the shape of the DCN along the ventrolateral to dorsomedial axis, which mirrors the general trend of the tonotopic gradient. Overall, we were unable to detect any obvious frequency overrepresentation within either subdivision of the CN.

TABLE 3.

Percent CN Volume Per Equal Partitions of Cochlear Representation

Cochleotopic range (%)	VCN	DCN
0–5	0.00%	1.69%
5–10	1.51%	7.21%
10–15	5.77%	8.14%
15–20	5.39%	5.15%
20–25	6.16%	4.62%
25–30	6.95%	4.75%
30–35	6.36%	5.41%
35–40	6.79%	5.67%
40–45	6.07%	5.65%
45–50	6.23%	5.75%
50–55	6.85%	5.98%
55–60	6.35%	5.70%
60–65	6.50%	5.63%
65–70	6.98%	6.63%
70–75	5.85%	5.20%
75–80	5.80%	4.09%
80–85	6.89%	5.69%
85–90	3.46%	4.21%
90–95	0.12%	1.92%
95–100	0.00%	0.91%

Use of the frequency model for analysis

The frequency model of the CN comprises two sets of RBFs, one set relating frequency organization in the DCN, and the other describing the VCN. With the model, making a prediction about frequency representation at a particular location is simply a matter of plugging a 3D coordinate into either function. To make this model accessible to researchers, we have created a web-based interface for online evaluation of these functions (http://3D.ryugolab.com/). In its initial implementation, one simply enters a set of formatted 3D coordinates into a text-field and decides which subdivision function to evaluate these coordinates in. Model predictions for each entry will be returned in frequency and/or cochleotopic units.²

DISCUSSION

In this study we used electrophysiological recording techniques, dye injections, light microscopic analyses, and computer graphics to describe the tonotopic organization of the mouse CN, and to develop a quantitative 3D model that encompasses frequency and anatomical position. The model applied a predictive artificial neural network to the projection pattern of physiologically characterized AN fibers that had been traced back to their cochlear origins. We observed AN fibers to be highly organized in the CN, and they exhibited a 3D modular stacking pattern throughout CN subdivisions with respect to frequency. By visualizing the model, we also note that the directionality of tonotopic gradients is variable; the precise orientation of isofrequency laminae is dependent on position, and cannot be well approximated by a single axis in each subdivision. We found an approximately equal amount of CN volume dedicated to equal segments of the sensory epithelium, demonstrating the absence of frequency specialization for this species. To make the model accessible, we have created an online interface (http://3D.ryugolab.com/) to permit researchers to make a straightforward comparison of other datasets against predicted frequency representation in the CN. We plan to integrate our model with preexisting atlases, so we will also make the relevant transformations (e.g., conversion to the stereotaxic coordinates of Franklin and Paxinos, 1997) available on the model website. Key concepts of our 3D analysis are presented in a summary video (Supporting Fig. 1).

Place-frequency maps of the cochlea

Our method of identifying the relative location of retrogradely labeled AN fibers in the organ of Corti has been used to calculate place-frequency maps in a number of species with great success (Liberman, 1982; Vater et al., 1985; Müller, 1991, 1996; Müller et al., 1991, 1992, 1993, 2005, 2010). Our cochlear map for the mouse is in close agreement with a recent retrograde study (Müller et al., 2005). The range of paired electrophysiological measurements of BF and sound-level threshold in this study were well matched to previous reports in CBA/J (Müller et al., 2005), CBA/CaJ (Taberner and Liberman, 2005), and NMRI (Ehret and Moffat, 1984) mouse strains, supporting the view that our map was obtained from healthy mice in a normal physiological state. That the map is well described by a log-linear fit suggests that the mouse is an auditory generalist, and lacks an acoustic fovea (Bruns and Schmieszek, 1980; Kossl and Vater, 1985; Vater et al., 1985; Müller et al., 1992).

The similarity between our place-frequency map and that of Müller et al. (2005) merits further discussion, considering that different methods of cochlear analysis were used (reconstructed sections vs. surface preparation). We observed a larger spread in our cochlear labeling, which may be attributed to tracer sensitivity, injection size, and/or analysis criteria. Our dataset contained four injections with BFs lower than Müller et al.’s lowest BF, causing our map to include an additional 0.16-oct. of lower frequencies. The use of surface preparations to analyze cochlear labeling meant we ran the risk of failing to recover the hook-region of the cochlea—a challenge for every dissection (Viberg and Canlon, 2004). Had we consistently underestimated the length of each cochlea prior to normalization, the effect would be to decrease the slope of the place-frequency map—increasing the upper limit of frequency representation—while leaving the low-frequency limit unchanged. Because our result is extremely similar to that of Müller et al. (2005), whose sectioning method inherently preserved the hook-region, we conclude that our measurements of cochlear length are reliable. It should be noted also that the maps based on recording, labeling, and direct mapping differ from those inferred from noise trauma (Ou et al., 2000) and behavioral measures (Ehret, 1975).

Auditory nerve reconstruction

AN fibers have been labeled via Golgi impregnation (Ramón y Cajal, 1909; Lorente de Nó, 1933; Ryugo and Fekete, 1982), single-fiber fills (Fekete et al., 1984; Ryugo and May, 1993; Tsuji and Liberman, 1997), extracellular tracer deposits in the cochlea (Leake and Snyder, 1989; Collinge and Schweitzer, 1991; Berglund and Brown, 1994), and extracellular tracer deposits in the AVCN (Feng and Vater, 1985; Müller, 1990; present study). Analyzed in coronal sections, labeled bundles of AN fibers appear as isofrequency “slabs” (Feng and Vater, 1985; Müller, 1990; Collinge and Schweitzer, 1991). It is impossible to reconstruct these fibers with the same fidelity as intracellular fills (e.g., Fekete et al., 1984), necessitating our use of approximation by outlining the “slabs” in each section. While discarding information about the area of labeling, the medial axis lines provided a reasonable estimate of the long-axis of labeling within a section. Even so, the medial axis computation was found to be quite sensitive to small imperfections in polygon shape. For example, in Figure 7A a slight bump on the dorsomedial corner of the rhodamine polygon caused the medial axis to make an abrupt dorsal turn rather than proceeding medially. These irregularities were the exception, however, and when present were confined to the ends of a given line. Another source of ambiguity was encountered when labeled AN fibers approached the injection site. The spread of label would obscure colocalized AN fibers, requiring us to approximate their location by outlining the injection site instead. Despite these limitations, our approximations appear to accurately represent the general projection plan of AN fibers throughout the CN.

When viewed from the medial axis, each 3D reconstruction closely resembled prior descriptions obtained from parasagittal sections with respect to both branch trajectories and BF-dependent bifurcation (e.g., Ramón y Cajal, 1909; Lorente de Nó, 1933; Sando, 1965; Osen, 1969; Fekete et al., 1984; Ryugo and May, 1993; Berglund and Brown, 1994). Affirming earlier descriptions (Sando, 1965; Osen, 1969), we observed that fibers exiting the PVCN twist laterally and dorsally at an approximately 90° angle to innervate the DCN, with fibers with low BFs coursing under fibers with higher BFs. We also noted a counterclockwise helical twist of the AN root as it exits the ventral surface of the CN, as described previously (Sando, 1965; Arnesen and Osen, 1978).

By combining anatomical data from multiple animals, we assume a common organization among individuals such that, following normalization, the same regions of the CN would represent the same frequencies in each animal (e.g., Bourk et al., 1981; Spirou et al., 1993). The presence of tonotopy when visualizing the composite dataset supports this idea. Further evidence comes when we consider just the three cases with BFs between 6–7 kHz. Each case was a different size, yet after normalization AN lines were essentially overlapping one another throughout all subdivisions of the CN. We cannot rule out the possibility that small variations may exist in AN organization of individual animals, but these results suggest that any such variance will be minor.

Quantitative maps of response properties

Studies of brain maps often use reductive techniques to facilitate analysis, but in doing so must make assumptions about organization. The mammalian cochlea exhibits a spiraling 3D structure but, due to the linear arrangement of IHCs, it can be abstracted as a 1D line for purposes of mapping frequency tuning (e.g., Liberman, 1982; Müller et al., 2005; present study). Studies of physiological properties in neocortex, taking advantage of its columnar arrangement (Mountcastle, 1997), are often reduced to 2D maps (Van Essen and Maunsell, 1980). Other structures, however, exhibit complicated organization in 3D that cannot easily be reduced for analysis (e.g., Malmierca et al., 1998; Nayagam et al., 2006). Given modern computing power, and the absence of evidence favoring reduction, we utilized 3D techniques to create a quantitative map of frequency tuning in the CN.

Maps of frequency organization have been created for various central auditory structures (Clopton et al., 1974; Rubel and Parks, 1975; Bourk et al., 1981; Sanes et al., 1989; Spirou et al., 1993; Luo et al., 2009; Tabor et al., 2012), and these reports form the conceptual groundwork for the present results. In most studies, linear regression was used to quantify a tonotopic gradient, thereby describing frequency tuning as a function of distance along a single noncardinal axis. This axis might be arbitrarily chosen or computed from 3D data points (Tabor et al., 2012), but ultimately assumes that the tonotopic gradient progresses in a single direction. It must be acknowledged that such reductions were generally made due to technical constraints on analytical methods available at the time of study. While sufficient for describing some structures, these assumptions may fail to capture all the details of others. The idea that frequency representation may be organized in concert with the laminar structure of nuclei to form isofrequency sheets or slabs (Rockel and Jones, 1973) has been demonstrated in the CN (e.g., Ryugo et al., 1981; Feng and Vater, 1985; Ryan et al., 1988; Müller, 1990; Ehret and Fischer, 1991). Our 3D reconstructions of AN fibers show that isofrequency sheets undulate throughout the CN, and that the direction of the tonotopic gradient is highly dependent on where one chooses to measure it. This observation motivated our use of RBFs, which can capture both global and local features of a gradient. The obvious drawback to this analytical approach is that tonotopy cannot be related by a simple one-line equation, but is instead governed by a large set of functions derived from our dataset. To address this accessibility challenge, we created the model website (http://3D.ryugolab.com/), allowing other research groups to evaluate our functions.

Frequency organization in the CN

Structure–function relationships are invaluable themes with which to investigate biological substrates of normal and abnormal hearing. Fundamental to this task is the idea of topographic maps (Fritsch and Hitzig, 1870; Leyton and Sherrington, 1917; Marshall et al., 1937; reviewed by Kaas, 1997). These maps are defined by orderly representations of sensory and motor systems within the brain. In this regard, the systematic and topographic representation of frequency is retained as a primary organizing principle throughout much of the central auditory system (reviewed by Clopton et al., 1974; Kandler et al., 2009). Physiologically characterized and labeled AN fibers in the cat (Fekete et al., 1984; Ryugo and May, 1993) have been mapped to the same locations in the AVCN and DCN as physiologically characterized single units (Bourk et al., 1981; Spirou et al., 1993), supporting this idea. Our model is consistent with the principal that frequency organization in the CN is determined by the pattern of AN innervation because labeled AN fibers were traced to their frequency-mapped source (cochlea) and their frequency-determined point of termination (CN). The foundation is solid due to its basis on 20 independently aligned cases, three containing two sets of labeled fibers.

3D frequency organization has recently been described in the C57Bl/6J mouse (Luo et al., 2009). The map is based on pooled physiological recordings from multiple electrode penetrations in multiple mice, and suggests a fairly stable intersubject map. Because we only obtained up to two BFs per animal, we were unable to investigate potential intersubject variations in frequency mapping. A much narrower frequency range was reported in each subdivision compared to our model, perhaps owing to the use of the C57 strain (Mikaelian, 1979), but a similar tonotopic trend was observed.

When computing our model, we intentionally removed labeled ANR fibers. The result of this omission is the impression of continuous isofrequency sheets coursing through the AVCN and PVCN. Electrophysiological evidence concludes that frequency representation in the ANR region has a different organization (Bourk et al., 1981), owing to the intermingling of root, ascending, and descending branches and their collaterals in this region (Fekete et al., 1984). As such, frequency predictions in this zone should be regarded with caution.

There exists a slight difference between the termination field of labeled AN fibers in the DCN and our final model. The AN terminates only in the deep layers of the DCN, yet we had allowed our model to extend all the way through the molecular layer. Systematic recordings in the cat DCN (Spirou et al., 1993) have shown that isofrequency contours extend through all layers of the DCN, suggesting that various cell types in the DCN (Young and Oertel, 2003) could be collected together as processing modules or slabs corresponding to lamina. Extrapolating our model through these additional layers allows us to account for this property.

In our model, it appears that roughly equal volumes of tissue in each subdivision are dedicated to representations of equal portions of the cochlea. This calculation is in line with findings in the gerbil (Müller, 1990), although findings in the cat DCN suggest that more space may be dedicated to high-frequency representations (Spirou et al., 1993). This interpretation, however, is based on linear distance rather than volume of the DCN (which is not uniform over its length) and could also be skewed due to curvature of the nucleus. In our model, isofrequency contours in the DCN appear to become more separated with increasing frequency—similar to observations in the cat (Spirou et al., 1993)—which might compensate for thinning of the nucleus to attain equal apportioning of tissue volume. In the bat, there is an expanded tissue representation of the echolocating frequency range in the CN (Feng and Vater, 1985), reflecting the specialization in its cochlea (Vater et al., 1985). The presence (or absence) of an acoustic “fovea” in the cochlea in a particular species could indicate that frequency tuning may be equivalently represented throughout its auditory pathways.

Atlases of the cochlear nucleus

A “block model” of the cat CN was created on the basis of cytoarchitectonic features so that electrophysiological data, such as unit type (Pfeiffer, 1966), or other anatomical details, such as cell type (Brawer et al., 1974) or amino acid histochemistry (Godfrey and Matschinsky, 1976), could be mapped onto a standardized atlas (Kiang et al., 1975). The limitation of this block model, however, was the use of a single cat that apparently had irregularities in its CN and difficulties in sharing the model across laboratories. The spirit and intent of the model are still valid and more recent advances in technology make the aim feasible.

Our atlas combined anatomical data obtained from multiple subjects, each with different CN volumes and minor variations in shape. By adapting normalization techniques developed for insects (Rein et al., 2002; Jenett et al., 2006) we sought to create an average CN template to which experimental cases were then aligned using nonrigid transformations. Alterative normalization strategies include uniformly scaling 2D sections to a standardized atlas (e.g., Cant and Benson, 2008), or scaling 3D reconstructions along each principal axis (e.g., Tabor et al., 2012). We could not adopt these approaches because 1) there are no mouse atlases of sufficient resolution for matching our sections; 2) we could not guarantee that sections were always oriented on the same plane; and 3) some of our 3D reconstructions were missing coronal sections, which would affect normalization along the anterior–posterior axis. An advantage of our method is that no assumptions were made about the ideal shape, orientation, or completeness of CN reconstructions; the creation of, and normalization to, the template was entirely automated and objective.

One prior study has estimated CN volumes in the CBA/J mouse (Webster and Trune, 1982). On average, CN values were approximately twice as great in our subjects (neither study accounted for shrinkage caused by histological processing). We note, however, that for the two cases in which we computed subdivision volumes, the ratio between DCN and VCN volumes agreed with their data. Absolute differences between measurements may be due to subject age, histological procedures, and/or method of analysis.

Subjective errors may still be introduced at the outset of our analysis during the stages of segmentation and serial-section reconstruction. Segmentation of CN borders was particularly difficult in fluorescent sections, where differences in texture were the primary way to distinguish between nuclei and fiber tracts. This circumstance could have presented variability in medial and ventral borders. It is also possible to introduce a minor but systematic skew when reconstructing sections, which may only be apparent when contrasting cases. Atlases based on high-resolution magnetic resonance imaging (MRI; e.g., Benveniste et al., 2000) avoid this issue, although manual intervention with segmentation is still required for some areas, and labeled elements are not, as of yet, resolvable. We used nonrigid, rather than uniform, surface transformations to help account for some of these potential reconstructive errors.

A number of anatomical mouse brain atlases have been created based on serial-section reconstructions (Franklin and Paxinos, 1997; Williams, 2000; Lein et al., 2007) and high-resolution MRI (Benveniste et al., 2000; MacKenzie-Graham et al., 2004; Kovacevic et al., 2005; Ma et al., 2005; Badea et al., 2007; Dorr et al., 2008; Johnson et al., 2010). Planar atlases specific to the mouse CN have also been developed that highlight cytoarchitectonic details (Martin, 1981; Webster and Trune, 1982; Willard and Ryugo, 1983; Trettel and Morest, 2001). Our model joins this tradition by providing high-resolution mapping of frequency tuning throughout the mouse CN. It is envisaged that, following guidelines under development by the Digital Atlasing Project (Hawrylycz et al., 2011), our data could be standardized and integrated into a canonical mouse atlas to enhance information sharing and comparisons across modalities. While many whole-brain atlases are currently based on the C57Bl/6J mouse—a strain noted for age-related high-frequency hearing loss (Mikaelian, 1979)—the strategies for incorporating anatomically linked data remain valid and could additionally facilitate comparisons between mouse strains with different hearing pathologies. We can now use this model to compare frequency representation in mice having various degrees of hearing loss in order to evaluate the nature of compensatory plasticity and frequency reorganization.

Abbreviations

A

Anterior

AN

Auditory nerve

ANR

Auditory nerve root

AVCN

Anteroventral cochlear nucleus

BF

Best frequency

CN

Cochlear nucleus

D

Dorsal

DCN

Dorsal cochlear nucleus

GCD

Granule/small cell domain

IHC

Inner hair cell

M

Medial

PVCN

Posteroventral cochlear nucleus

RBF

Radial basis function

RMS

Root mean square

SGC

Spiral ganglion cell

VCN

Ventral cochlear nucleus