Abstract
Background:
The Biomarker Strategy Design has been proposed for trials assessing the value of a biomarker in guiding treatment in oncology. In such trials, patients are randomised to either receive the standard chemotherapy treatment or a biomarker-directed treatment arm, in which biomarker status is used to guide treatment.
Methods:
Motivated by a current trial, we consider an adaptive design in which two biomarkers are assessed. The trial is conducted in two stages. In the first stage, patients in the biomarker-guided arm are assessed using a standard and an alternative cheaper biomarker, with the standard biomarker guiding treatment. An analysis comparing biomarker results is then used to choose the biomarker to use for the remainder of the trial. The new biomarker is used if the results for the two biomarkers are sufficiently similar.
Results:
We show that in practical situations the first-stage results can be used to adapt the trial without type I error rate inflation. We also show that there can be considerable cost gains with only a small loss in power in the case where the alternative biomarker is highly concordant with the standard one.
Conclusions:
Adaptive designs have an important role in reducing the cost and increasing the clinical utility of trials evaluating biomarker-guided treatment strategies.
Keywords: adaptive design, biomarker strategy design, concordance, personalised medicine, two-stage design
The existence of heterogeneity of the patient population in their response to anti-cancer therapies has long been appreciated and is a major feature of clinical research in this area. Chemotherapy treatment is highly effective in some cases, but is unpleasant for all and can lead to life-threatening treatment-induced toxicity and long-term health problems. There is therefore considerable interest in the development of methods for more accurately identifying those patients most likely to respond to treatment and selecting or targeting treatment accordingly. The aim is to avoid giving potentially harmful therapies to patients for whom benefit from the therapy is considered unlikely. Treatment decisions are often made through the division of patients into subgroups using biomarkers based on gene expression assays or immunohistochemical assays. Assays to guide the use of targeted therapy such as oestrogen receptor status in breast cancer (Early Breast Cancer Trialists' Collaborative Group (EBCTCG), 2005) and EGFR or K-Ras mutation status in non-small-cell lung cancer (Zhou et al, 2008) generally have high specificity. Multi-parameter assays to predict responsiveness to cytotoxic chemotherapy have also been developed. Examples include the classification of breast cancers into intrinsic subgroups (Perou et al, 2000; Sorlie et al, 2001), which display differential sensitivity to chemotherapy (Parker et al, 2009), and the Oncotype DX test (Paik et al, 2006), which is widely used to guide adjuvant chemotherapy decisions in early breast cancer. Other tests that could potentially be used to predict chemotherapy benefit in early breast cancer include MammaPrint (Van De Vijver et al, 2002; Drukker et al, 2013), Mammostrat (Ring et al, 2006; Bartlett et al, 2010), EndoPredict (Filipits et al, 2011), IHC4 and fluorescence IHC4 (Cuzick et al, 2011) and PAM50 (Parker et al, 2009; Dowsett et al, 2013) assays.
The assessment of effectiveness and cost-effectiveness of anti-cancer therapies is based on a phase III randomised controlled trial (RCT). Conventional RCTs with no biomarker evaluation aim only to estimate the treatment effect in the overall study population and do not enable evaluation of biomarker-guided therapy. For this latter purpose, specific alternative trial designs are required (Freidlin et al, 2010). One commonly used RCT design is the Biomarker-Strategy Design (Sargent et al, 2005). In such trials, patients are randomised to a control arm, in which case they receive the standard treatment irrespective of biomarker status, or a biomarker-directed treatment arm, in which case the biomarker status is used to guide treatment, usually between the standard treatment and some alternative. The primary comparison is then between the two randomised groups. The biomarker-strategy design has been shown to be less efficient than a marker-by-treatment interaction design for evaluating whether there is a difference in effectiveness (Mandrekar and Sargent, 2009; Simon, 2010). Nevertheless, the design remains popular with clinicians, and provides a way to test the clinical utility of a validated biomarker, including cost-effectiveness. In the case when there is high-quality historical data, then a more efficient alternative to the biomarker strategy design would be an enriched trial that only recruits patients with the biomarker status that is to be randomised between treatments. However, in the case that the historical data may not be high quality or representative of the population being investigated, the most robust evidence on the effect of the biomarker-guided therapy in the entire population would come from a trial that continues to recruit all patients.
Most RCT designs assessing biomarker-guided treatment focus on a single biomarker chosen before the start of the trial. In practice, a number of potential assays for patient selection may exist so that the choice of a single biomarker may itself present a challenge. In this setting, it may be desirable to conduct an RCT to both compare different potential biomarkers and to assess the effectiveness of biomarker-guided therapy. The aim of such a RCT is to both identify the best of a set of possible biomarkers and to assess the effectiveness of using this biomarker relative to the approach in which all patients receive standard therapy. If assays vary considerably in price, the cost-effectiveness of the use of different biomarkers might also need to be considered. We propose an adaptive design in which both assessment of the concordance between biomarkers and the comparison between the strategy and control arms can be done in one trial. Compared with first conducting a trial assessing the concordance and then a RCT, this saves time and allows first-stage patients to be included in the final analysis (at least when the original biomarker is used, as discussed later).
Our work is motivated by the OPTIMA (Optimal Personalised Treatment of early Breast Cancer using Multi-Parameter Analysis) trial of biomarker-guided adjuvant chemotherapy for oestrogen receptor-positive, HER2-negative breast cancer patients who would be given adjuvant chemotherapy as standard (Bartlett et al, 2012). In this trial, patients are randomised to be either in the control arm or in the test-guided arm. All patients in the control arm receive chemotherapy and endocrine therapy as is standard in this population. Patients in the test-guided arm all receive endocrine therapy, but receive chemotherapy in addition only if the test indicates that they are high risk. The trial will be conducted in two stages. In the first stage (the preliminary study), 150 patients will be randomised to each arm. All patients will have Oncotype DX testing (Paik et al, 2004) but only those patients in the test-guided arm will be allocated to treatment on the basis of the result of the Oncotype DX test. In addition to this test, a number of other assays will also be performed on all patients. The results from an analysis comparing the different tests within the preliminary study will determine which one (or possibly more) test(s) will be chosen to guide treatment for the test-guided therapy arm in the main trial, where a total of 1860 randomised patients are to be recruited to each arm. The value of the Oncotype DX test has been demonstrated in retrospective phase III trials in some populations (Gianni et al, 2005; Paik et al, 2006; Mina et al, 2007; Chang et al, 2008; Albain et al, 2010; Dowsett et al, 2010), but there is a need for further research to assess its true clinical value and cost-effectiveness given the current cost of £2580 (around $4000) per assay. There is considerable overlap between the methods and markers included in this test and the other tests considered, so that an alternative test might be used to guide treatment in the main trial if the preliminary results indicated that it corresponded closely to Oncotype DX and was simpler or more cost effective.
Materials and methods
Trial design
Considering a slightly simplified version of the approach used for the OPTIMA trial, we assume that there are two biomarker-based tests, which are available for guiding treatment. Biomarker 1 is considered to be a gold standard that has previously been validated as a predictive biomarker (i.e., the treatment effect of the treatment being investigated depends on the biomarker value) with biomarker 2 a cheaper potential alternative. The trial is split into two stages. In the first stage, a total of 2n1 patients are recruited to the trial, equally allocated between the biomarker-directed arm and the control arm. All patients are assessed using both biomarkers. In the biomarker-directed arm, patients who are positive on biomarker 1 are allocated to chemotherapy, and patients who are negative on biomarker 1 are allocated to an alternative treatment. On the control arm, all patients are allocated to chemotherapy.
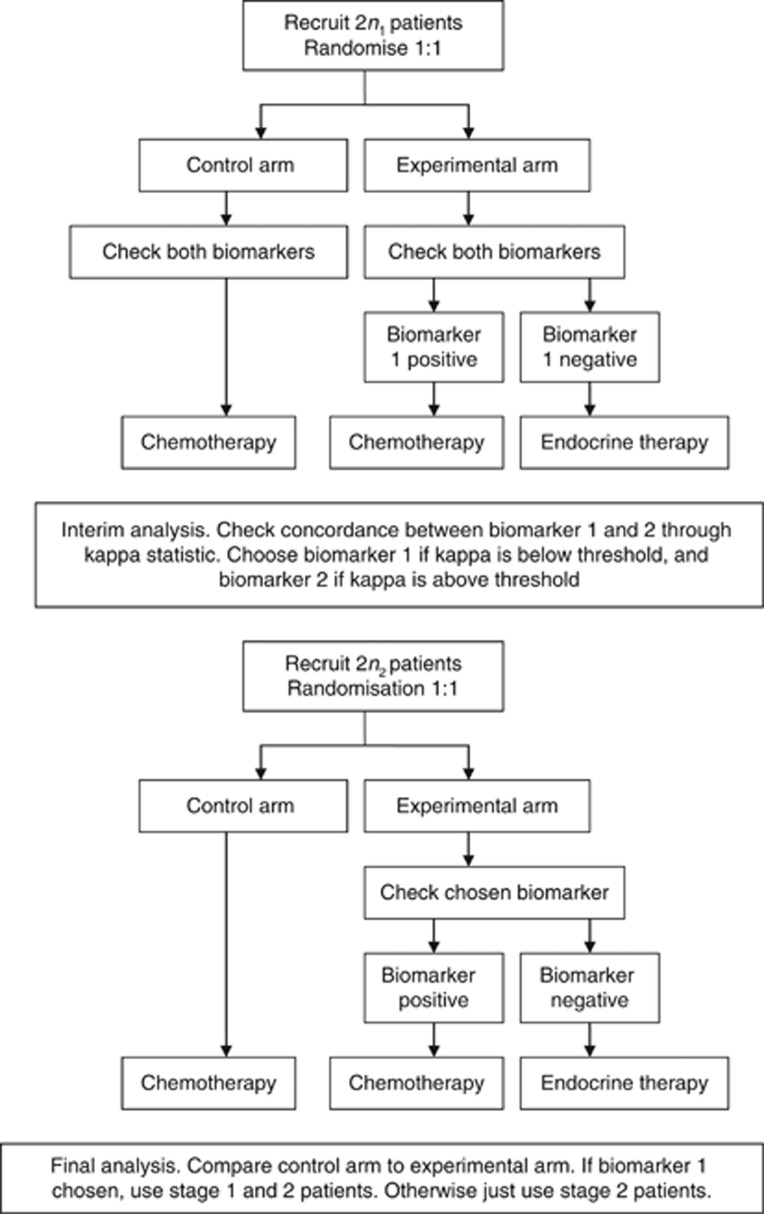
An interim analysis occurs after all stage 1 patients have been assessed on both biomarkers. At this analysis, the concordance between the two biomarkers, as assessed by Cohen's kappa statistic, is measured. If this concordance is sufficiently high, biomarker 2 is used in stage 2 of the trial, otherwise biomarker 1 is used. In the second stage of the trial, 2n2 patients are recruited, and equally allocated to the biomarker-directed arm and control arm. In the biomarker-directed arm, the chosen biomarker is used to guide which therapy patients receive, similar to stage 1. In the control arm, all patients receive chemotherapy (and so no patients are tested using the chosen biomarker). At the end of the trial, it is of interest to compare the relative difference in outcome between the control arm and the intervention arm. Figure 1 illustrates the trial design.
Figure 1.
Schema of adaptive design with selection between a gold standard (biomarker 1) and cheaper alternative (biomarker 2).
We assume that the primary treatment outcome is observed with significant delay, or is time to some event during long-term follow-up and that there is no intermediate informative outcome available. For example in OPTIMA, the outcome is invasive disease-free survival during a 5-year follow-up period. Consequently, at the interim analysis, very few patients are expected to have primary outcome data. We first consider the case in which the primary outcome is binary, and that the log odds ratio is used to summarise the difference in effect between the control and intervention arms. In this case, we can derive analytic expressions to enable us to study the properties of the design. Similar analytic formulae can be derived in the case of a normally distributed outcome. We do not consider normally distributed outcomes in this paper as they are rare in oncology trials. For time-to-event outcomes, the analytic method is less feasible, so instead we use simulation to assess designs.
Notation
The formula for Cohen's kappa statistic, calculated at the end of the first stage, is:
 |
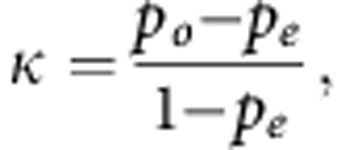where po is the observed probability of agreement between the biomarkers, and pe is the expected agreement between the biomarkers by chance, that is, if the assignments of the two biomarkers were independent.
We assume that the log odds ratio between the control and biomarker-directed arm is used to assess the biomarker-guided strategy at the end of the second stage. If biomarker 1 is selected at the interim analysis, both stage 1 and stage 2 patients are included in the final analysis; on the other hand, if biomarker 2 is selected, only stage 2 patients are included for both arms. This is because biomarker 1 is used to guide treatment in the first stage and it would bias the final analysis to include only the first-stage biomarker-directed arm patients on whom the two biomarkers agreed. The issue of including stage 1 patients in the latter case will be considered in the discussion.
The log odds ratio if biomarker 1 is selected is:
 |
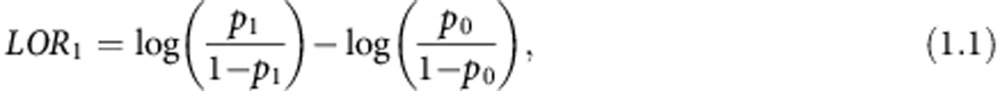where p1 is the probability of an event (invasive disease recurrence or death) in the biomarker-directed arm patients and p0 is the probability of an event in the control arm patients. In this case, both p1 and p0 are estimated from stage 1 and stage 2 patients. The log odds ratio if biomarker 2 is selected is:
 |
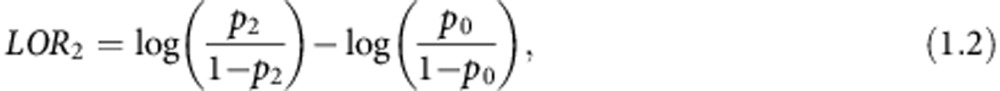where p2 is the probability of an event in the biomarker-directed arm patients from stage 2. In this case, both p2 and p0 are estimated from just stage 2 patients.
We assume, as in the OPTIMA trial, that the trial aims to show non-inferiority of the biomarker-guided arm. This requires specification of a non-inferiority margin. Non-inferiority is declared if the upper 95% confidence interval (CI) limit for the odds ratio is below the non-inferiority margin; that is, if the 95% CI is entirely below the non-inferiority margin. Different margins can be used; we assume one of 1.3 (0.262 on the log odds-ratio scale), which is a fairly stringent level to use (Rousson and Seifert, 2008).
The probability of invasive disease recurrence or death will depend on the true biomarker status of the patient and whether they were treated with chemotherapy or not. Thus there are, in principle, four types of patients: (1) those who are biomarker positive and treated with chemotherapy; (2) those who are biomarker positive and not treated with chemotherapy; (3) those who are biomarker negative and treated with chemotherapy; and (4) those who are biomarker negative and not treated with chemotherapy.
Hypotheses
The null hypothesis tested at the end of the trial will depend on the biomarker chosen at the interim analysis. If the gold-standard biomarker is selected, then the null hypothesis will be:
 |
Similarly, if the second biomarker is selected, the null hypothesis is:
 |
The power of the trial to declare non-inferiority will be the probability of the upper 95% CI of the respective log odds ratio to be below log(1.3). The distribution of the estimated upper 95% CI of LOR1 is asymptotically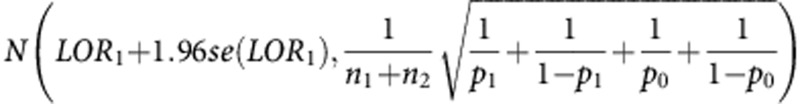 
, where se(LOR1) is the standard error of the estimated log odds ratio. The distribution of the estimated upper 95% CI of LOR2 is asymptotically 
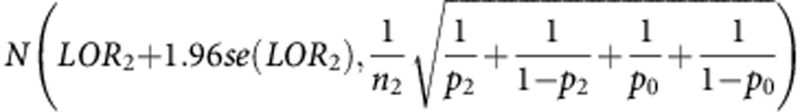. These formulae allow calculation of the power of the trial.
Joint distribution of Cohen's kappa and the log odds ratio
The observed values of κ, LOR1 and LOR2 are all functions of the same random variables, described further in the Supplementary Material. Thus, a technique called the delta method (see, e.g., Agresti (2002)) can be used to approximate the joint distribution of the three statistics. The joint distribution can be used to find the power (i.e., the probability of declaring non-inferiority) of the two-stage procedure when different interim selection rules are used. The process of finding the analytical joint distribution using the delta method is described in detail in the Supplementary Material.
Specifically of interest is the level of correlation between the estimated kappa statistic after the first stage and the log odds ratio after the second stage. This is because a non-zero correlation will mean that the distribution of the final test statistic is dependent on the selection rule used in the interim analysis after the first stage. This may cause operating characteristics of the main trial, such as the type I error rate, to deviate from the planned values. Using the delta method, we can obtain the correlation analytically (described further in the Supplementary Material). If the second biomarker is chosen at the interim analysis, the first-stage data are not used in the final analysis so that there is no correlation between the two stages. Thus, the correlation between kappa and the log odds ratio only needs to be considered in the case that the first biomarker is used in the second stage.
Time to event outcome simulation
Up to this point, we have restricted our attention to a binary end point. However, time-to-event outcomes such as overall survival or invasive disease-free-survival are more commonly used in large trials such as OPTIMA. The final analysis of OPTIMA will analyse invasive disease-free survival as a time-to-event outcome. Compared with the binary case, deriving the analytic joint distribution of Cohen's kappa statistic and a suitable time-to-event test statistic is less feasible. Therefore, we use simulations to evaluate the power of the adaptive trial design. Full details of the methods used for simulating data are described in the Supplementary Material.
Results
Correlation between kappa and the log odds ratio
The extent of the correlation depends on the sample sizes considered at the two stages (i.e., n1 and n2), the probabilities of an event for each of the four types of patients (biomarker positive and treated with chemotherapy; positive and untreated; negative and treated; negative and not treated), the proportion of patients who are positive for biomarker 1, and the sensitivity and specificity of biomarker 2. Generally, for realistic values, the correlation is very near to zero. For example, if 150 patients per arm are recruited in the first stage and 1500 per arm in the second stage, the probabilities of an event are 0.3, 0.5, 0.25 and 0.2 for positive/treated, positive/untreated, negative/treated and negative/untreated patients, respectively, the proportion of biomarker 1 positives is 0.2, and both sensitivity and specificity are set to 0.95, the correlation is 0.002. The correlation ranges between −0.015 and 0.015 for a broad range of realistic scenarios (Supplementary Table 1). Thus, basing the selection of a biomarker on the Cohen's kappa statistic will not typically affect the operating characteristics of the trial design. The correlation appears to increase (in absolute terms) as the proportion of biomarker 1 positives increases. Interestingly, it increases as the sensitivity and specificity increases up to a peak and then decreases again. The maximum correlation found, for 150 and 1500 patients per arm in the first and second stage, respectively, was 0.08. However, the correlation is only this high when the probabilities of an event takes extremely implausible values (i.e., that all patients who were negative for biomarker 1 but treated with chemotherapy would recur, whereas patients who were negative and not treated would never recur).
Impact of kappa threshold on power and cost of trial
The main potential benefit of selecting between two biomarkers is to allow a cheaper biomarker test to be used if it performs well. However, this would be undesirable if the selection rule allows low-quality biomarkers to be selected, and thus causes the power of the trial to be too low. It is also undesirable if the potential cost saving is low. Thus, assessing the selection rule with respect to the power of the trial and the reduction in cost is of great importance.
It is possible to use the analytic formulae derived in the Supplementary Material to get the power of the two-stage procedure. We investigated the power of the procedure and the expected cost of testing individuals. We varied the quality of biomarker 2, considering: an excellent quality biomarker 2 with sensitivity and specificity of 0.99; a good quality biomarker 2, with sensitivity and specificity of 0.95; and a poor quality biomarker 2, with sensitivity and specificity of 0.8. We consider a total of eight scenarios, where the probability of a patient being positive for biomarker 1 and the probabilities of an event for the four types of patient (positive/treated, positive/untreated, negative/treated, and negative/untreated) were varied. Scenario 1 assumes that biomarker-positive patients have a large reduction in probability of recurrence when treated, whereas biomarker-negative patients have no reduction. Scenarios 2 and 3 vary this relative benefit. Scenario 4 is the same as scenario 1 except that biomarker-negative patients receive a small benefit when treated. Scenario 5 assumes that biomarker-negative patients receive a small benefit when not treated. In scenario 6, biomarker 1 is purely prognostic, and biomarker-positive and -negative patients receive the same relative benefit from treatment; the probabilities of recurrence are chosen so that the odds ratio when biomarker 1 is chosen is equal to the inferiority margin. Scenarios 7 and 8 are the same as scenario 1 except the probability of a patient being positive for biomarker 1 is varied. Table 1 shows the eight scenarios and the resulting log odds ratio that would result from selecting biomarkers 1 and 2.
Table 1. Summary of simulation scenarios.
| |
|
|
|
LOR2
biomarker 2 quality |
||
|---|---|---|---|---|---|---|
| Scenario | p | ptp | LOR1 | Excellent | Good | Poor |
| 1 |
(0.2, 0.5, 0.2, 0.2) |
0.2 |
0.000 |
0.004 |
0.019 |
0.073 |
| 2 |
(0.2, 0.8, 0.2, 0.2) |
0.2 |
0.000 |
0.007 |
0.037 |
0.144 |
| 3 |
(0.2, 0.3, 0.2, 0.2) |
0.2 |
0.000 |
0.001 |
0.006 |
0.025 |
| 4 |
(0.2, 0.5, 0.2, 0.21) |
0.2 |
0.049 |
0.052 |
0.065 |
0.111 |
| 5 |
(0.2, 0.5, 0.2, 0.19) |
0.2 |
−0.051 |
−0.046 |
−0.029 |
0.035 |
| 6 |
(0.2, 0.5, 0.02, 0.04) |
0.2 |
0.268 |
0.275 |
0.301 |
0.393 |
| 7 |
(0.2, 0.5, 0.2, 0.2) |
0.1 |
0.000 |
0.008 |
0.009 |
0.037 |
| 8 | (0.2, 0.5, 0.2, 0.2) | 0.5 | 0.000 | 0.009 | 0.046 | 0.178 |
Abbreviation: LOR1=log odds ratio.
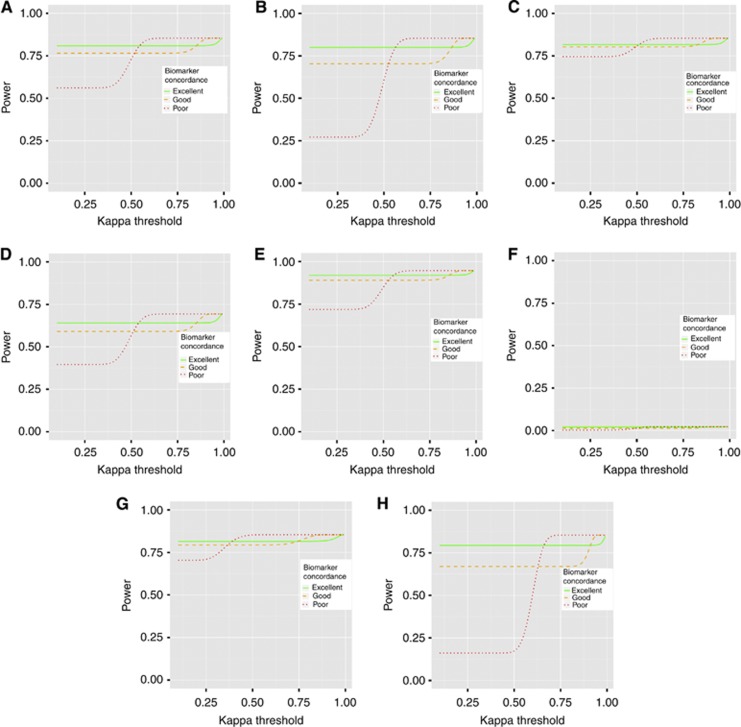
Figure 2 shows the power of the two-stage procedure for different interim decision rules. It becomes more likely that biomarker 1 will be used in the second stage as the kappa threshold increases. With 300 patients recruited in the first stage, the estimate of kappa has high precision, and therefore there is only a narrow window of the kappa threshold, which results in non-negligible uncertainty over which biomarker will be used in the second stage. In all cases, using biomarker 1 results in a higher power. This is for two reasons: (1) using biomarker 1 means that the first-stage patients are included in the final analysis; (2) the sensitivity and specificity of biomarker 2 are lower, implying that some patients are treated suboptimally. Generally, the drop in power is small for the excellent quality biomarker 2, medium for good quality biomarker 2, but unacceptably high for poor quality biomarker 2. The relative loss in power depends on the scenario, with an increased probability of patients being positive for biomarker 1 resulting in a higher drop in power. These results show that it is important to select a kappa threshold such that poor quality biomarker 2 has a negligible chance of being selected in the interim analysis. A kappa value of 0.8 appears suitable from the figures.
Figure 2.
Plots showing the power of the two-stage procedure to declare non-inferiority as the kappa threshold, at which biomarker 2 is selected, changes. (A–H) Scenarios 1–8 in Table 1. The eight scenarios use different probabilities of an event for the four patient groups (i.e., positive/treated, positive/untreated, negative/treated, negative/untreated). These are listed in Table 1. In scenario 6, the null hypotheses are true, so the lines give the type I error rate. Curves are shown for three possible performance characteristics of biomarker.
To quantify the loss of power because of decreased sample size when biomarker 2 is selected, the power of scenario 1, when biomarker 1 is selected but only second-stage data are used, is around 82%. This implies that for scenario 1 most of the power loss when an excellent biomarker 2 is selected was due to the lower sample size, and only a small amount due to the imperfect concordance. For a good biomarker 2, slightly more than half of the power loss is due to the imperfect concordance.
It should be noted that in some cases, using biomarker 2 will result in higher power, for example, if untreated positive patients have a lower chance of an event than treated patients, but these situations are unlikely if biomarker 1 is a validated predictive biomarker.
In Supplementary Figure 1, we show the power of the two-stage procedure under the same scenarios but for n1=50 and n2=1650 (i.e., the overall sample size remains the same but the interim analysis takes place earlier). There is more uncertainty in the estimate of kappa, but the power loss is also smaller in each scenario. Thus, it may be beneficial to reduce the number of patients used in the first stage.
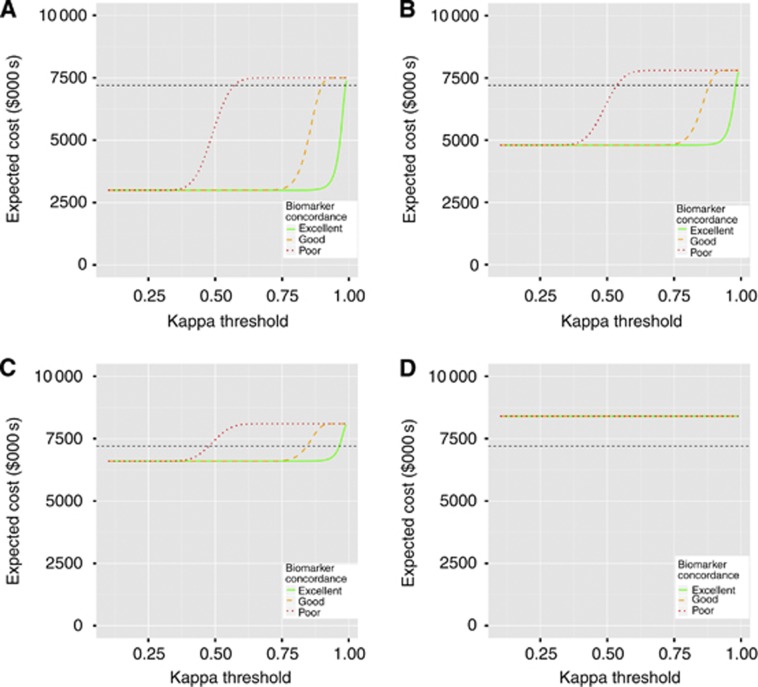
The expected cost of testing patients in the trial does not depend on the probabilities of an event, only on the quality of biomarker 2, and hence on how likely this biomarker is to be used in stage 2, and the ratio of the cost of each biomarker. Figure 3 shows the expected cost of testing patients if the gold standard biomarker costs $4000 per patient, approximately the current cost of Oncotype DX, and the cheaper biomarker varies in cost, with $1000, $2000, $3000 and $4000 per patient considered. The results show that if biomarker 2 is inexpensive, including it adds little to the maximum cost of the trial, but could result in a large reduction in cost. For example, if the cheaper biomarker is $2000, including it increases the maximum cost of testing individuals by 8% compared with testing everyone with the gold-standard but reduces the cost by around 35% (from $7 200 000 to $4 800 000) if the cheaper one is chosen. This potential saving depends on the ratio of the cost of the two biomarkers; if both tests cost the same, the two-stage procedure will always be more expensive.
Figure 3.
Plots showing the expected cost of the two-stage procedure as the kappa threshold, at which biomarker 2 is selected, changes for 150 patients per arm in the first stage. The four panels assume different costs of the cheaper biomarker: (A) $1000; (B) $2000; (C) $3000; (D) $4000. The gold-standard biomarker is assumed to cost $4000. The black dashed line in the figures shows the cost of a trial that only used biomarker 1 and did not have an interim analysis.
Supplementary Figure 2 shows the same plots when n1=50 and n2=1650. In this case, the potential savings from using the two-stage procedure are higher. If the cheaper biomarker is $2000, then choosing biomarker 2 at the interim analysis reduces the cost of testing by 44% (from $7 200 000 to $3 900 000).
Time-to-event end points
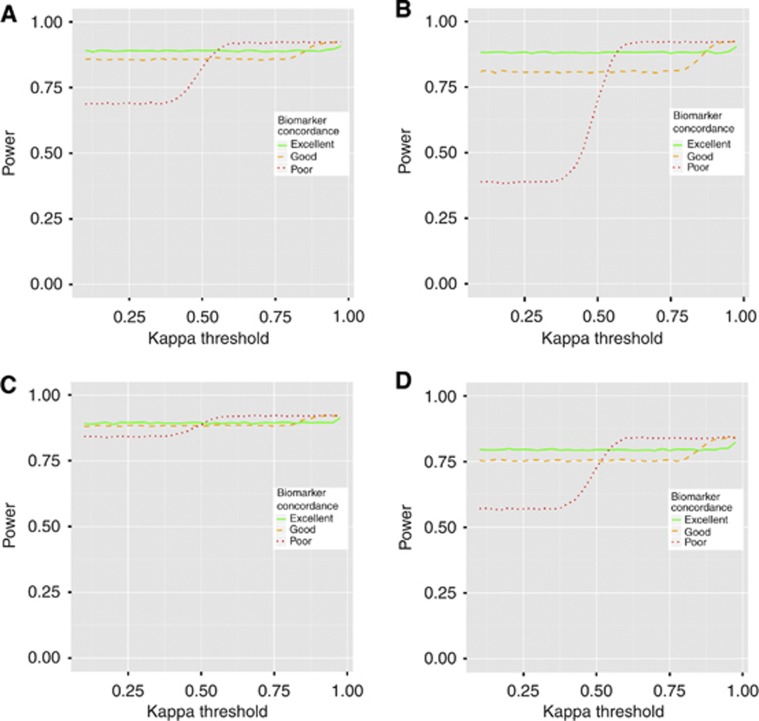
Scenarios that were analogous to the first four scenarios of Table 1 were used, except the hazard parameters in each of the four patient groups varied. The hazard rates are chosen so that, assuming the time-to-event is distributed as an exponential random variable, the probability of invasive disease before 5 years is equal to the probabilities in the scenarios used in the previous section. The follow-up time is assumed to be the time required for half of patients to have events. The remaining patients are right censored. The quality of biomarker 2 is varied in the same way as in the previous section.
Figure 4 shows results similar to Figure 2, except that the power is generally higher. The lines are also less smooth as they are based on a limited number of simulation replicates (25 000). The higher power is to be expected as a time-to-event analysis is typically more powerful than a binary analysis. We do not show plots of the expected cost of the trial, because this depends only on concordance between biomarkers, which is assumed to the same here as it was in the previous section. Thus, the potential cost savings will be the same as in the binary case.
Figure 4.
Plots showing the power of the two-stage procedure to declare non-inferiority for a time-to-event end point as the kappa threshold, at which biomarker 2 is selected, changes. The four scenarios use different hazard rates for the four patient groups (i.e., positive/treated, positive/untreated, negative/treated, negative/untreated). These are: (A) (0.045, 0.139, 0.045, 0.045), (B) (0.045, 0.322, 0.045, 0.045), (C) (0.045, 0.072, 0.045, 0.045), (D) (0.045, 0.139, 0.045, 0.047). Power at each value of the kappa threshold is estimated from 25 000 simulated replicates.
Discussion
In this paper, we have examined the potential advantages and disadvantages of including an interim analysis to select between a gold-standard and cheaper biomarker. The biomarkers are used to decide whether patients should get a treatment that can greatly benefit a small subgroup of patients, but has undesirable side effects. This is based on the OPTIMA trial in which a relatively small first stage is used to select between several biomarkers; the chosen biomarker is then used to guide treatment in a larger second stage. Although OPTIMA is the motivating trial, we have explored a wider range of scenarios so that the work is informative for other trials also. Although we have focused on biomarker-strategy designs, the general concept of allowing for a change in biomarker could be used in other biomarker designs also, such as enrichment trials and marker-by-treatment interaction designs.
Generally, if a considerably cheaper biomarker is available that may be as good as the gold standard, there is considerable benefit to including an interim analysis without many disadvantages. In the case where the cheaper biomarker is highly concordant with the gold standard, the expected cost of testing patients reduces considerably with only a small loss in power. The advantage of the adaptive design over a initial study assessing concordance and a subsequent study assessing difference in treatment effect is that the first-stage patients can be included when the original biomarker is used, providing a higher power. One scenario in which the adaptive design is likely to be inferior is when there is a high-quality retrospective data set available, in which biomarker status is available for patients who also have long-term follow-up data. In this case, a separate retrospective first stage to decide on the suitable biomarker would likely be more efficient, unless it is thought the effect of treatment has changed since the patients were observed.
In the case that the alternative biomarker is almost the same price, or is unlikely to have high concordance with the gold-standard biomarker, then there is less advantage to including an interim analysis. In this paper, only the costs of the trial itself were considered. There are other, longer term, advantages and disadvantages of selecting a cheaper biomarker. On the plus side, it will reduce the future cost of biomarker-guided treatment in the clinic. However, if the sensitivity or specificity of the chosen biomarker is truly less than the gold-standard biomarker, it may mean that future patients experience worse outcomes. This is another reason to ensure that the alternative biomarker is only chosen if it is highly concordant.
One of the reasons for the loss in power when the cheaper biomarker is used is that the first-stage patients are not included in the final analysis. It would be possible to include control patients, as their treatment does not depend on which biomarker is chosen. This would go some way to reducing the loss in power. However, it is not straightforward to include the first-stage biomarker-directed arm patients, unless the two biomarkers agreed perfectly. If there are patients on whom the biomarkers disagreed, then one would need to know whether those patients would have recurred if treatment was assigned using biomarker 2. If only patients for whom the two biomarkers agreed were included, then this would ignore two subgroups of patients, which may bias the final results. More sophisticated statistical methods that would allow inclusion of the first-stage patients would be a useful area for future research. In practice, if the concordance between biomarkers is extremely high (>0.95), then including the first-stage patients should not cause many problems. Alternatively, the sample size of the second stage could be increased when the second biomarker is chosen. This would reduce the potential benefit in terms of cost, but would mean the power loss was mitigated.
A complication that has been ignored in this paper is that biomarker 1 itself may not perfectly discriminate between patients who would benefit from treatment. In this case, it is possible that biomarker 2 is actually a higher quality biomarker than biomarker 1, but is not selected because the two have low concordance. In the scenario, we have considered, there is little that can be done to address this point. However, if there was final outcome information at the interim analysis, or a correlated intermediate outcome was available, then this, rather than the concordance of the biomarkers, could be used to pick the higher quality biomarker. The advantage of just considering concordance is that this is measured immediately, so there is no delay between recruiting and assessing patients. Delay can affect the efficiency of an adaptive design considerably – there may be less to gain from using an adaptive design if outcome information was used to assess which biomarker should be used. The case of selecting a biomarker when partial or complete outcome data are available is a problem that deserves attention.
There are several other complexities that we did not consider in this work. For example, missing data are a common problem in real trials. In the case of a biomarker-strategy design, if biomarker data are missing for a patient in the experimental arm, then they cannot be assigned to treatment. Missing biomarker data in a control arm patient are less problematic but may reduce the efficiency of the final analysis. If a first-stage patient has missing biomarker data, they will not contribute information to the concordance assessment at the interim analysis, so the estimate of kappa will be less precise – the first-stage sample size should be increased if missing biomarker data are common. As we are considering non-inferiority trials (although the methodology is equally applicable to superiority trials), there are issues over whether patients receive the assigned treatment and whether a per-protocol analysis is preferable to an intention-to-treat analysis – however, the adaptive design does not exacerbate any of these issues.
We have considered an adaptive design that chooses between two biomarkers, but it may be of interest to check many alternative biomarkers. Assuming that the selected biomarker is based on the kappa statistic, we have shown that this will not cause problems with the final analysis, no matter how many are checked. In addition, other metrics that measure concordance could be used other than the kappa statistic. As alternative metrics are generally highly correlated with kappa, we consider it unlikely that basing selection on any measure of concordance will lead to type I error inflation. In practice, we would recommend several factors are used to decide which biomarker should be chosen.
The work presented here shows that adaptive designs, such as the one used in OPTIMA, have an important part to play in reducing the cost and increasing the clinical utility of trials evaluating biomarker-guided treatment strategies.
Acknowledgments
JW is funded by the Medical Research Council (grant number U.1052.00.014). The OPTIMA trial is funded by the National Institute for Health Research Health Technology Assessment (NIHR HTA) Programme (project number 10/34/01). RCS is additionally supported by the National Institute for Health Research University College London Hospitals Biomedical Research Centre. The views and opinions expressed therein are those of the authors and do not necessarily reflect those of the HTA programme, NIHR, NHS or the Department of Health.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies this paper on British Journal of Cancer website (http://www.nature.com/bjc)
This work is published under the standard license to publish agreement. After 12 months the work will become freely available and the license terms will switch to a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License.
Supplementary Material
References
- Agresti A. Categorical Data Analysis. John Wiley & Sons; 2002. [Google Scholar]
- Albain KS, Barlow WE, Shak S, Hortobagyi GN, Livingston RB, Yeh I, Ravdin P, Bugarini R, Baehner FL, Davidson NE. Prognostic and predictive value of the 21-gene recurrence score assay in postmenopausal women with node-positive, oestrogen-receptor-positive breast cancer on chemotherapy: a retrospective analysis of a randomised trial. Lancet Oncol. 2010;11:55–65. doi: 10.1016/S1470-2045(09)70314-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartlett J, Canney P, Campbell A, Cameron D, Donovan J, Dunn J, Earl H, Francis A, Hall P, Harmer V. Selecting breast cancer patients for chemotherapy: the opening of the UK OPTIMA trial. Clin Oncol. 2012;25 (2:109–116. doi: 10.1016/j.clon.2012.10.005. [DOI] [PubMed] [Google Scholar]
- Bartlett JM, Thomas J, Ross DT, Seitz RS, Ring BZ, Beck RA, Pedersen HC, Munro A, Kunkler IH, Campbell FM. Mammostrat® as a tool to stratify breast cancer patients at risk of recurrence during endocrine therapy. Breast Cancer Res. 2010;12:R47. doi: 10.1186/bcr2604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang JC, Makris A, Gutierrez MC, Hilsenbeck SG, Hackett JR, Jeong J, Liu ML, Baker J, Clark-Langone K, Baehner FL. Gene expression patterns in formalin-fixed, paraffin-embedded core biopsies predict docetaxel chemosensitivity in breast cancer patients. Breast Cancer Res Treat. 2008;108:233–240. doi: 10.1007/s10549-007-9590-z. [DOI] [PubMed] [Google Scholar]
- Cuzick J, Dowsett M, Pineda S, Wale C, Salter J, Quinn E, Zabaglo L, Mallon E, Green AR, Ellis IO. Prognostic value of a combined estrogen receptor, progesterone receptor, Ki-67, and human epidermal growth factor receptor 2 immunohistochemical score and comparison with the Genomic Health recurrence score in early breast cancer. J Clin Oncol. 2011;29:4273–4278. doi: 10.1200/JCO.2010.31.2835. [DOI] [PubMed] [Google Scholar]
- Dowsett M, Cuzick J, Wale C, Forbes J, Mallon EA, Salter J, Quinn E, Dunbier A, Baum M, Buzdar A. Prediction of risk of distant recurrence using the 21-gene recurrence score in node-negative and node-positive postmenopausal patients with breast cancer treated with anastrozole or tamoxifen: a TransATAC study. J Clin Oncol. 2010;28:1829–1834. doi: 10.1200/JCO.2009.24.4798. [DOI] [PubMed] [Google Scholar]
- Dowsett M, Sestak I, Lopez-Knowles E, Sidhu K, Dunbier AK, Cowens JW, Ferree S, Storhoff J, Schaper C, Cuzick J. Comparison of PAM50 Risk of Recurrence Score with oncotype DX and IHC4 for predicting risk of distant recurrence after endocrine therapy. J Clin Oncol. 2013;31:2783–2790. doi: 10.1200/JCO.2012.46.1558. [DOI] [PubMed] [Google Scholar]
- Drukker CA, Bueno-de–Mesquita JM, Retel VP, Harten WH, Tinteren H, Wesseling J, Roumen RMH, Knauer M, Veer LJ, Sonke GS. A prospective evaluation of a breast cancer prognosis signature in the observational RASTER study. Int J Cancer. 2013;133 (4:929–936. doi: 10.1002/ijc.28082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Early Breast Cancer Trialists' Collaborative Group (EBCTCG) Effects of chemotherapy and hormonal therapy for early breast cancer on recurrence and 15-year survival: an overview of the randomised trials. Lancet. 2005;365:1687–1717. doi: 10.1016/S0140-6736(05)66544-0. [DOI] [PubMed] [Google Scholar]
- Filipits M, Rudas M, Jakesz R, Dubsky P, Fitzal F, Singer CF, Dietze O, Greil R, Jelen A, Sevelda P. A new molecular predictor of distant recurrence in ER-positive, HER2-negative breast cancer adds independent information to conventional clinical risk factors. Clin Cancer Res. 2011;17:6012–6020. doi: 10.1158/1078-0432.CCR-11-0926. [DOI] [PubMed] [Google Scholar]
- Freidlin B, McShane LM, Korn EL. Randomized clinical trials with biomarkers: design issues. J Natl Cancer Inst. 2010;102:152–160. doi: 10.1093/jnci/djp477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gianni L, Zambetti M, Clark K, Baker J, Cronin M, Wu J, Mariani G, Rodriguez J, Carcangiu M, Watson D. Gene expression profiles in paraffin-embedded core biopsy tissue predict response to chemotherapy in women with locally advanced breast cancer. J Clin Oncol. 2005;23:7265–7277. doi: 10.1200/JCO.2005.02.0818. [DOI] [PubMed] [Google Scholar]
- Mandrekar SJ, Sargent DJ. Clinical trial designs for predictive biomarker validation: theoretical considerations and practical challenges. J Clin Oncol. 2009;27:4027–4034. doi: 10.1200/JCO.2009.22.3701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mina L, Soule SE, Badve S, Baehner FL, Baker J, Cronin M, Watson D, Liu ML, Sledge GW, Jr, Shak S. Predicting response to primary chemotherapy: gene expression profiling of paraffin-embedded core biopsy tissue. Breast Cancer Res Treat. 2007;103:197–208. doi: 10.1007/s10549-006-9366-x. [DOI] [PubMed] [Google Scholar]
- Paik S, Shak S, Tang G, Kim C, Baker J, Cronin M, Baehner FL, Walker MG, Watson D, Park T. A multigene assay to predict recurrence of tamoxifen-treated, node-negative breast cancer. N Engl J Med. 2004;351:2817–2826. doi: 10.1056/NEJMoa041588. [DOI] [PubMed] [Google Scholar]
- Paik S, Tang G, Shak S, Kim C, Baker J, Kim W, Cronin M, Baehner FL, Watson D, Bryant J. Gene expression and benefit of chemotherapy in women with node-negative, estrogen receptor–positive breast cancer. J Clin Oncol. 2006;24:3726–3734. doi: 10.1200/JCO.2005.04.7985. [DOI] [PubMed] [Google Scholar]
- Parker JS, Mullins M, Cheang MC, Leung S, Voduc D, Vickery T, Davies S, Fauron C, He X, Hu Z. Supervised risk predictor of breast cancer based on intrinsic subtypes. J Clin Oncol. 2009;27:1160–1167. doi: 10.1200/JCO.2008.18.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perou CM, Sorlie T, Eisen MB, van de Rijn M, Jeffrey SS, Rees CA, Pollack JR, Ross DT, Johnsen H, Akslen LA. Molecular portraits of human breast tumours. Nature. 2000;406:747–752. doi: 10.1038/35021093. [DOI] [PubMed] [Google Scholar]
- Ring BZ, Seitz RS, Beck R, Shasteen WJ, Tarr SM, Cheang MC, Yoder BJ, Budd GT, Nielsen TO, Hicks DG. Novel prognostic immunohistochemical biomarker panel for estrogen receptor–positive breast cancer. J Clin Oncol. 2006;24:3039–3047. doi: 10.1200/JCO.2006.05.6564. [DOI] [PubMed] [Google Scholar]
- Rousson V, Seifert B. A mixed approach for proving non-inferiority in clinical trials with binary endpoints. Biom J. 2008;50:190–204. doi: 10.1002/bimj.200710410. [DOI] [PubMed] [Google Scholar]
- Sargent DJ, Conley BA, Allegra C, Collette L. Clinical trial designs for predictive marker validation in cancer treatment trials. J Clin Oncol. 2005;23:2020–2027. doi: 10.1200/JCO.2005.01.112. [DOI] [PubMed] [Google Scholar]
- Simon R. Clinical trial designs for evaluating the medical utility of prognostic and predictive biomarkers in oncology. Per Med. 2010;7:33–47. doi: 10.2217/pme.09.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorlie T, Perou CM, Tibshirani R, Aas T, Geisler S, Johnsen H, Hastie T, Eisen MB, van de Rijn M, Jeffrey SS. Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proc Natl Acad Sci USA. 2001;98:10869–10874. doi: 10.1073/pnas.191367098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van De Vijver MJ, He YD, van't Veer LJ, Dai H, Hart AA, Voskuil DW, Schreiber GJ, Peterse JL, Roberts C, Marton MJ. A gene-expression signature as a predictor of survival in breast cancer. N Engl J Med. 2002;347:1999–2009. doi: 10.1056/NEJMoa021967. [DOI] [PubMed] [Google Scholar]
- Zhou X, Liu S, Kim ES, Herbst RS, Lee JJ. Bayesian adaptive design for targeted therapy development in lung cancer–a step toward personalized medicine. Clin Trials. 2008;5:181–193. doi: 10.1177/1740774508091815. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.