From a structural average to the conformational ensemble of a DNA bulge

Significance

Obtaining the conformational ensembles of biological macromolecules, beyond average structures, is extremely challenging but necessary for a complete understanding of their folding and functions. Such insights may also lead to the rational design of therapeutics that can target less-ordered macromolecules and may advance the design of nanostructures and nanomachines from nucleic acids. We have applied X-ray interferometry to estimate the conformational ensemble of a small-model macromolecule, a DNA bulge, representative of helix–junction–helix building blocks of natural RNAs and designed DNA nanostructures. The measured ensemble, in combination with molecular dynamics simulations, provides testable atomic-level models. X-ray interferometry is extremely sensitive and can detect changes in the ensemble arising from different bulge sequences and solution salt conditions.

Abstract

Direct experimental measurements of conformational ensembles are critical for understanding macromolecular function, but traditional biophysical methods do not directly report the solution ensemble of a macromolecule. Small-angle X-ray scattering interferometry has the potential to overcome this limitation by providing the instantaneous distance distribution between pairs of gold-nanocrystal probes conjugated to a macromolecule in solution. Our X-ray interferometry experiments reveal an increasing bend angle of DNA duplexes with bulges of one, three, and five adenosine residues, consistent with previous FRET measurements, and further reveal an increasingly broad conformational ensemble with increasing bulge length. The distance distributions for the AAA bulge duplex (3A-DNA) with six different Au-Au pairs provide strong evidence against a simple elastic model in which fluctuations occur about a single conformational state. Instead, the measured distance distributions suggest a 3A-DNA ensemble with multiple conformational states predominantly across a region of conformational space with bend angles between 24 and 85 degrees and characteristic bend directions and helical twists and displacements. Additional X-ray interferometry experiments revealed perturbations to the ensemble from changes in ionic conditions and the bulge sequence, effects that can be understood in terms of electrostatic and stacking contributions to the ensemble and that demonstrate the sensitivity of X-ray interferometry. Combining X-ray interferometry ensemble data with molecular dynamics simulations gave atomic-level models of representative conformational states and of the molecular interactions that may shape the ensemble, and fluorescence measurements with 2-aminopurine-substituted 3A-DNA provided initial tests of these atomistic models. More generally, X-ray interferometry will provide powerful benchmarks for testing and developing computational methods.

A grand challenge in biology is to understand the complex free-energy landscape of macromolecules and to decipher the resulting conformational ensembles. To perform their biological functions, macromolecules must adopt a multiplicity of conformations. Balancing and controlling different conformational states is central to biological processes including protein folding, allostery and signaling, and the stepwise assembly and function of macromolecular machines. To understand these complex molecules requires characterization of their free-energy landscapes—i.e., their equilibrium conformational ensembles. Precise measurements of conformational ensembles could allow quantitative modeling of the folding and function of biological macromolecules, would provide valuable experimental data to test current computational models and assumptions, and might facilitate the rational design of specifically acting inhibitors (1, 2).

Techniques including NMR and EPR relaxation have been developed to incisively probe motions in the ensemble on different time scales, ranging from picoseconds to milliseconds (3, 4). Nonetheless, such dynamic information represents an average of the dynamics of the molecules across the conformational ensemble. In special cases, where the ensemble contains slow exchanging conformational states, these states can be separately detected [e.g., relaxation dispersion approaches can detect conformational states interconverting at tens of microseconds to hundreds of milliseconds, and single-molecule FRET (smFRET) can characterize conformational transitions at millisecond or slower time scales (5, 6)]. However, again, each of these states is an average of a more complex local conformational ensemble.

To date, successes in reconstructing equilibrium ensembles have mostly relied on experimental measurement of NMR residual dipolar couplings (RDCs) (7, 8). Compared with other NMR techniques, RDCs provide long-range angular structure information that helps to generate equilibrium ensemble models (9). In combination with molecular dynamic simulations, RDCs have been used to generate ensemble models for small disordered proteins (7, 10), DNA duplexes (11), and a RNA bulge motif (12–14). In addition to RDCs, relaxation dispersion and paramagnetic relaxation enhancement have been used to detect and characterize conformational states that are in low abundance in an ensemble (5). Although powerful, these NMR-based methods, like all approaches, have limitations. For example, RDCs have difficulty distinguishing between conformations with similar angular orientations but different translational displacements (15, 16). Additional methods are needed to construct ensembles that can test and complement these current methods.

To meet this challenge, we continue to develop, test, and apply the capabilities of a solution X-ray interferometry technique (17, 18). X-ray interferometry can be used to determine site-to-site distance distributions instantaneously because it relies on atomic scattering (17, 19–24). Standard small-angle X-ray scattering (SAXS) measures the sum of the scattering and scattering interference from all atoms in a macromolecule (25). As it would not be possible to decompose this sum and distinguish contributions from specific atoms or atom pairs, standard SAXS provides no site-specific information and is limited to determining the overall size and shape of macromolecules (25). X-ray interferometry overcomes this limitation through the introduction of a pair of site-specifically labeled gold nanocrystal probes and isolation of the scattering interference from this strongly scattering probe pair. This scattering interference can be directly converted into a distance distribution through a Fourier transformation, without the complications of a nonlinear mapping (26). Multiple pairs of gold nanocrystal probes, in different site-specific locations, provide matched-set distance information and increase the information content of the technique (e.g., refs. 17 and 18).

Unlike standard ensemble-averaged methods such as FRET that give a single average value for the distance between each probe pair, X-ray interferometry naturally yields a distance distribution between each probe pair. Strategies measuring the time dependence of fluorescence energy transfer (27) or spin echo intensity [double electron–electron resonance (DEER)] (28) are powerful but are limited in their ability to determine an ensemble by the complex relationships between the measured values and the desired probe–probe distances. These complications amplify the uncertainty of determining an average value and introduce even greater uncertainty in determining a distance distribution and the underlying conformational ensemble.

Prior results using the DNA double helix as a model experimental system (18) indicate that detailed and quantitative information about solution ensembles can be obtained. For the DNA helix, X-ray interferometry distance distributions were found to quantitatively agree with consensus elastic parameters of DNA (18). Nevertheless, the ensemble of a DNA double helix is simpler than that for most macromolecules and could be well described by broadening from a single conformation using an elastic potential. The ensembles of most biological macromolecules are likely to contain substantial anharmonicities and multiple local free-energy minima.

To further test X-ray interferometry as a general method for probing macromolecule equilibrium ensembles and to determine fundamental properties of basic nucleic acid structures, we have applied X-ray interferometry to a nucleic acid helix–junction–helix (HJH) motif, the DNA bulge. DNA bulges can provide a model for the RNA bulges that are more commonly encoded in biology and can be used to engineer nanostructures (29, 30). We chose the A-bulge DNA system for this study to allow comparison with a prior smFRET study that provided models for the average structures of these DNAs (31).

Results and Discussion

Bulges Bend DNA Helices and Broaden Their Conformational Ensembles.

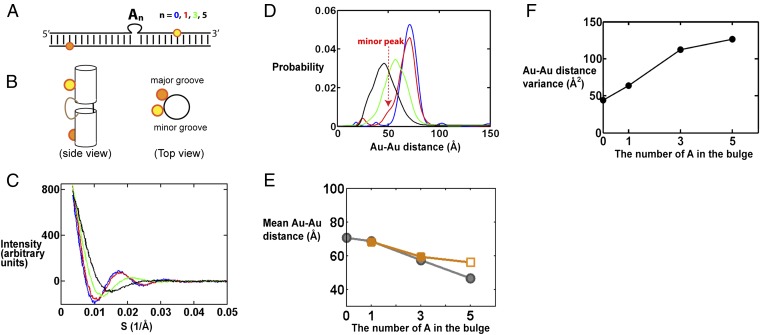
We first studied a series of bulged DNA helix constructs, with the bulge consisting of an increasing number of adenosine residues [0, 1, 3, and 5 adenosine residues (31)]. To use X-ray interferometry to investigate the ensemble of the bulge series, gold-nanocrystal probes were introduced site-specifically through amino-modified thymine using an N-Succinimidyl 3-[2-pyridyldithio]-propionate (SPDP)-based linker, following our prior procedures (17, 18). To facilitate comparison of the different bulge constructs, the gold-nanocrystal probe pairs spanned the bulge and were placed at the same positions for each of the bulge constructs (Fig. 1A). The Au-Au scattering interference pattern for each construct was measured (Fig. 1C), and the resulting interference patterns were converted into distance distributions (Fig. 1D), again following previously published procedures (17, 18).

Fig. 1.

X-ray interferometry measurement of DNA bulges with different numbers of adenosines. (A) Schematic depiction of bulged DNA constructs labeled with a pair of Au probes (yellow and orange spheres). The top (yellow) and bottom (orange) Au probes are labeled on T residues 7 and 11 base steps from the bulge site, respectively. (SI Appendix, Table S1, gives the sequences used.) Results for the 0-nt bulge construct (i.e., duplex DNA) are from ref. 18. (B) A cartoon view of the constructs as a straight duplex. (Left) Side view from the minor groove of the bulge site. In a continuous DNA helix the bottom gold nanocrystal (orange) would be about 58° clockwise of the top gold nanocrystal (yellow) when viewed from the top (Right) and is away from the viewer when viewed from the minor groove side (Left). (C) The Au-Au scattering profile for DNA constructs (A) with a bulge sequence of 0 (blue), 1 (red), 3 (green), and 5 (black) adenosines. The x axis is the scattering-angle parameter S. (D) The Au-Au center-to-center distance distributions deduced from the Au-Au scattering profiles in C, following the same color code as C. The minor peaks at the short and long distances, outside of the main distribution, are generally noise that is sample-preparation-dependent, as described in ref. 23. (E) The mean Au-Au distance values determined from X-ray interferometry (gray) and predicted from the literature average structure models generated by smFRET (orange) (30). The 5A value from the smFRET model (open symbol) is unreliable as the smFRET data for the 5A construct were poorly fit by the model, as noted by the authors (31). (F) The Au-Au distance variance in D as a function of bulge length.

As expected, the average Au-Au distance decreases with increasing bulge length (Fig. 1 D and E), consistent with increased bending. The observed decrease in distance with increasing bulge size reasonably matches the inferred distances from the literature smFRET average structures (31) (Fig. 1E). This agreement provides further support that X-ray interferometry is able to provide high-resolution average structural information, as it did in determining the average rise and twist per base of the DNA helix in solution (18). Nonetheless, the prior smFRET data (31) do not provide information on the nature of the ensemble. We found that the width of the pairwise distance distributions increases upon introduction of the bulge and further increases with increasing bulge length (Fig. 1D), as can be represented in terms of the variance of the distance distribution (Fig. 1F). This result suggests that bulged DNA has a broader ensemble than that of a continuous duplex and that this distribution broadens as the number of residues that are not restricted in motion by base-paired neighbors increases—i.e., as the number of single-stranded residues increases.

Beyond probing the extent of ensemble broadness (i.e., the variance), these distance distributions provide previously unavailable information about the ensemble. For example, the shape of the distance distribution for DNA with the 1A bulge (1A-DNA; Fig. 1D, red) is asymmetrical compared with that of a regular duplex (Fig. 1D, blue), which immediately suggests that the conformational ensemble of the 1A bulge cannot be represented by a single harmonic potential in its free-energy landscape. [An isotropic broadening around a single stable conformation would be expected to broaden the position of gold probes in all directions and result in largely symmetrical broadening of the Au-Au distance distribution, as is the case for the duplex (Fig. 1D, blue; also ref. 18).] Thus, the highly asymmetrical small shoulder for 1A-DNA (Fig. 1D, dashed arrow) strongly suggests the presence of at least one minor conformer family. The position of the minor peak also provides information on the nature of this family. Its smaller probe–probe distances compared with that of a straight helix can in principle arise from bending, such that the top helix bends toward the bottom helix, or twisting, such that the top helix twists clockwise to bring the two probes closer (clockwise rotation of the yellow sphere in Fig. 1B, Right). We can rule out the twist-only model as twisting could only reduce the mean probe–probe distance from 70.7 Å (for the straight duplex) to about 67 Å (for a twist sufficient to align the nanocrystals directly above and below one another), and not to the observed distance of around 50 Å (Fig. 1D, dashed arrow).

Although this single probe pair provides information about the conformational ensemble, the information has major limitations. Using the above discussion as an example, a bend-only model can account for the minor peak, but so can a family of models with successively less bending and more twisting. The minor peak with a mean Au-Au distance of 50 Å (Fig. 1D) could arise from bending alone with an angle of 58°, from a smaller bend of 53° together with a twist of 58°, or from a continuous series of intermediate bend-and-twist angle pairs. Measuring distances between additional probe pairs is needed to remove degeneracies and to obtain the molecule’s conformational ensemble. We chose to pursue DNA with the 3A bulge (3A-DNA) because it has a broader and potentially more complex conformational ensemble than the 1A bulge (Fig. 1 D and F).

Estimating the 3A-Bulge DNA Conformational Ensemble.

Construct design and experimental results.

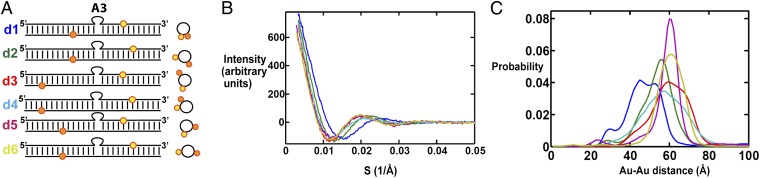
To estimate the conformational ensemble of 3A-bulge DNA (3A-DNA), we labeled the flanking helices with six different pairs of gold nanocrystals (Fig. 2A). Six scattering interference patterns were measured; one for each gold pair (Fig. 2B). As noted above, each scattering profile contains interference intensities across the range of measured scattering angles (s) and not just a single intensity (Fig. 2B). Each profile has a range of Au-Au distances (Fig. 2C), which correspond to the full distribution of pairwise distances from each member of the ensemble. This experimental ensemble information is then used to weight a large set of potential bulge conformations, generated through simple geometric modeling, to obtain an ensemble model for 3A-DNA, as described in the following sections and in SI Appendix, SI Methods.

Fig. 2.

X-ray interferometry measurement of 3A-DNA. (A) Schematic of the 3A-DNA constructs labeled with six pairs of Au nanocrystals (yellow and orange spheres). (SI Appendix, Table S1, gives the sequences of constructs d1 through d6.) Cartoon views of the constructs show the Au nanocrystal positions (Right) analogously to Fig. 1B. (B) The Au-Au scattering profiles for constructs d1 to d6, color coded as in A. (C) The Au-Au center-to-center distance distributions deduced from the Au-Au scattering profiles in B, color coded as in A and B.

Testing the null model: are multiple states required to account for the conformational ensemble of 3A-DNA?

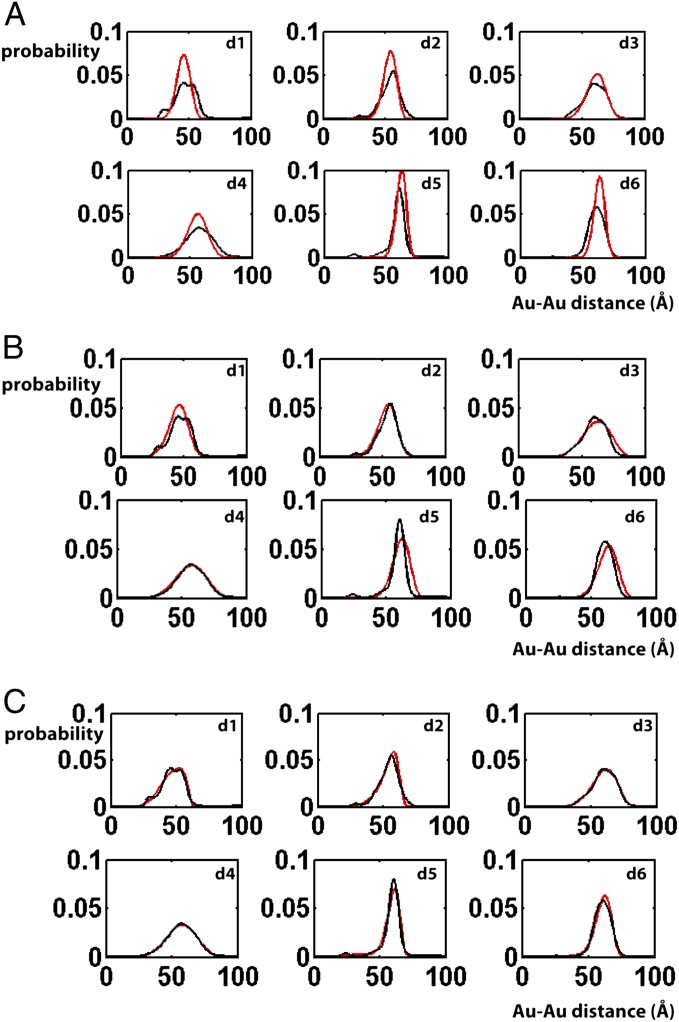
We first determined if the interference data can be accounted for by a single conformational family, with a single energy minimum and a simple elastic free-energy potential akin to that for a simple DNA duplex (18). We generated a pool of ∼5 × 10⁴ geometrically allowed conformations to extensively sample the allowed conformational space (A Procedure for Building the Ensemble and SI Appendix, SI Methods provide details). Each conformation corresponds to a unique position of the top helix relative to the bottom helix (Fig. 1B), described by a set of rotational (α, β, γ) and translational (x, y, z) parameters. [A bulge conformation (α, β, γ, x, y, z) is generated by first rotating the top helix by (α, β, γ), followed by a translation of (x, y, z). We use the zyz Euler convention (32), in which the order of rotation is as follows: a clockwise rotation of α along the z axis when viewed from above; a bend of β toward the negative x axis (i.e., clockwise rotation around the y axis); and finally a clockwise rotation of γ around the z axis, with γ = 0°, 90°, 180° and 270° corresponding to the x−, y+, x+, and y− directions, respectively. A slightly different definition of the six-dimensional conformational space of HJH was previously used by Bailor et al. (33); SI Appendix, SI Methods, provides details.] The data were fit with a single bulge conformation in the allowed space (Fig. 3A and SI Appendix, Fig. S1A, χ² = 12, where n = 1,898 is the total number of measured data points combined over all six probe pairs) and with an elastic expansion from this single bulge conformation (Fig. 3B and SI Appendix, Fig. S1B, χ² = 4.9), with the (α, β, γ, x, y, z) of the ensemble conformations normally distributed around the values of (α, β, γ, x, y, z) of the single best-fit conformation. The dispersion of the six parameters, (α, β, γ, x, y, z), were changed independently. These fits, constrained to a single state, gave a nearly twofold larger χ² compared with the unconstrained fit described below (Fig. 3C and SI Appendix, Fig. S1C, χ² = 2.6 for a nonconstrained model allowing multiple states), suggesting that the 3A-DNA ensemble is not well described by a single free-energy minimum.

Fig. 3.

Fitting of Au-Au distance distributions with a series of physical models. Experimental Au-Au center-to-center distance distributions (black lines) are plotted together with the best-fit model prediction (red lines) using a one-state approximation (A and B) or a nonconstrained multiple-state ensemble model (C). In the one-state approximation models the ensemble is assumed to only contain a single conformation (A) or elastic fluctuations around a single conformation (B). In the nonconstrained multiple-state model (C), there is no prior assumption of the ensemble (A Procedure for Building the Ensemble provides details).

To explore the information content of the data beyond a single state, we fit the data with an increasing number of discrete conformations. As expected, the fitting improved as the number of discrete conformations allowed in an ensemble was increased. The improvement in fitting becomes negligible beyond about five conformations (SI Appendix, Fig. S2). In other words, the distance distributions contain enough information to distinguish about five discrete types of conformations in an ensemble. We emphasize that an ensemble of a few discrete conformations is not a physically realistic model, as it assumes no motion of the bulge around each discrete conformer. Similar to NMR-based ensemble methods, a realistic but underdetermined ensemble model can be generated by refining computationally generated ensemble models with the X-ray interferometry data, as described in the next section (7). We envision that a combination of multiple techniques will improve the confidence in the ensemble models generated in the future.

A procedure for building the ensemble.

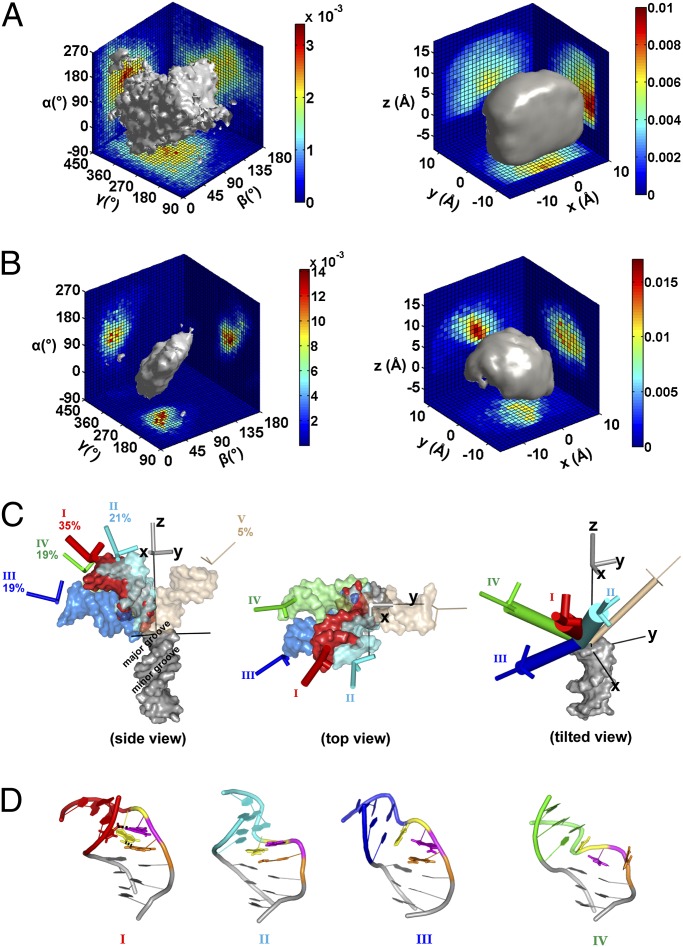
We briefly outline the procedure we used to build an ensemble for the 3A-DNA here and provide a more detailed description in SI Appendix, SI Methods. We first generated an allowed space, as alluded to above, using simple geometric modeling. molecular dynamics (MD) simulations were used to set boundary conditions but were not directly involved in the modeling (SI Appendix, SI Methods, provides details). We systematically sampled the six-dimensional conformational space (α, β, γ, x, y, z) to generate an initial pool of about 1.8 × 10⁶ conformations and then eliminated conformations that result in steric clashes of the top and bottom helices and conformations with unreasonably long distances between the connections of the two helices, leaving a total of ∼5 × 10⁴ conformations, representing our basis set of the geometrically allowed conformational space of the bulge [Fig. 4A (34, 35)].

Fig. 4.

Model for the 3A-DNA ensemble derived from X-ray interferometry data. (A) The geometrically allowed conformational space of the 3A-DNA helices (also SI Appendix, SI Methods). The gray surface encloses 80% of the total population. The sharp edge on the Rght is the result of limiting the allowed space within a cube, which was defined by a set of MD conformations to estimate limiting x, y, and z values and then extending this by 1 Å to provide a more conservative limit (SI Appendix, SI Methods, provides details; also see SI Appendix, Fig. S22). (B) The estimated conformational ensemble of 3A-DNA obtained by reweighting the allowed space ensemble in A using the X-ray interferometry data (Materials and Methods provides details). The gray surface encloses 80% of the total population. (C) A 3D view of representative conformers of each of the five groups of conformations (SI Appendix, Fig. S10). The conformer shown for each group is the one that is closest to the mean of the group in terms of (α, β, γ, x, y, z) (SI Appendix, Table S3). (D) Atomistic models of the representative bulge conformations for groups I to IV. The three adenosine residues in the bulge are colored in orange, magenta and yellow, in the order from the 5′ to 3′ end of that DNA strand.

The allowed space represents a prior model of the ensemble where all conformations in the allowed space have equal probability. An ensemble model is a specific set of probabilities of the allowed space conformations. The experimental scattering profile of an ensemble model, I(S), can be predicted from the weighted sum of the expected scattering profile of individual bulge conformations: . The probability that a given ensemble model is the actual ensemble would then be related to the level of agreement between the predicted and measured scattering profiles, I_exp(S). The most probable ensemble model, or the optimum set of w_i weights of the basis set conformations, was estimated using a simplified Bayesian method (36, 37) (Materials and Methods and SI Appendix, SI Methods, provide details). The procedure sums over different ensemble models weighted by their likelihood given the experimental data, which was calculated from χ² statistics. This weighted summation combines reasonable individual ensemble solutions to provide an estimate of the overall ensemble.

Using the procedure described above, a good fit to the data were obtained (Fig. 3C and SI Appendix, Fig. S1C; χ² = 2.6), and the corresponding conformational ensemble is illustrated in Fig. 4B. As a test of this ensemble model and the bulge not being disturbed by Au labeling, we used the estimated ensemble to predict (38) the SAXS profile of the unlabeled bulge constructs and determine if it agrees with the measured profile. Good agreement was found between the predicted and measured profiles (SI Appendix, Fig. S20, χ² = 0.8). We further carried out a cross-validation test of our ensemble model and our fitting procedure, where each of the sets of five distance distributions were used to predict the sixth distribution. The six predicted distributions strongly resembled the corresponding experimental distributions (SI Appendix, Fig. S4), and the six conformational ensembles generated using each of the sets of five of the six distance distributions closely resemble that of the conformation ensemble obtained using all six distance distributions (SI Appendix, Figs. S5 and S6). This agreement suggests a relatively high confidence in the regions of the conformational space that are populated by the 3A-DNA. The SD of these six ensembles also provides a crude estimate of the error of our 3A-DNA conformational ensemble model (SI Appendix, Fig. S6C).

The 3A-DNA Conformational Ensemble.

The conformational ensemble of the 3A-DNA, estimated via the approach described in the previous section, is shown in Euler space (Fig. 4B, Left) and in translational space (Fig. 4B, Right). This ensemble populates a much restricted space compared with the allowed space (Fig. 4A). It will be of great interest to determine the variation in conformational restrictions for different HJH elements, relative to the maximum covalently and geometrically allowed space, to determine how large this contribution is to folding and how variable it is between junction motifs.

To describe the ensemble, we divided the ensemble into five groups of conformations, labeled I to V, based on the experimentally measureable properties of the conformations —i.e., their Au-Au distance profiles (SI Appendix, Fig. S10 and Table S3). To better visualize the ensemble, representative conformers from the five clusters are shown in Fig. 4C. The four dominant groups of the 3A-DNA ensemble (I to IV, 95%) all bend toward the major groove side of the bottom helix (Fig. 4C, Left), mostly within the +x/−y quadrant (Fig. 4C, Middle), with 90% of the bending angles between 24 and 85° (Fig. 4C, Left, and SI Appendix, Fig. S10B). More detailed descriptions of the ensemble are presented in SI Appendix, SI Text.

To explore the potential molecular interactions that could be responsible for stabilizing different bulge conformers and shaping the ensemble, we used MD to generate atomistic models of the bulge conformations that are consistent with the conformations obtained from the X-ray interferometry-generated ensemble (Fig. 4D). The MD atomistic model for the most abundant region of the ensemble was found to be consistent with results from a 2-aminopurine fluorescence assay (Fig. 5; SI Appendix, SI Text, provides details).

Fig. 5.

The 2-aminopurine fluorescence to test the atomic-level models for 3A-DNA. (A) The relative position of the two flanking guanines (green) and the 5′ (orange) and 3′ (yellow) bulge adenine in the experimental conformer I (Left) and the most stable MD conformer (Right). The central A is magenta and not rendered space filling (also see SI Appendix, Table S4). (B) The 2-aminopurine intensity for DNA constructs with 5′ (orange bar) or 3′ (yellow bar) bulge adenine replaced with 2-aminopurine. Materials and Methods gives experimental conditions. The 3′-A (yellow) is less quenched than the 5′-A (orange) in the bulged duplex, and the 3′-A is less quenched in the bulge than in a single strand, consistent with model I (A, Left) and not expected for the structure corresponding to the MD model in which there is extensive stacking of both A residues (B, Right). See also SI Appendix, SI Text, and Table S4.

X-Ray Interferometry to Probe the Effects of Bulge Sequence and Ionic Conditions on the Bulge-DNA Ensemble.

To probe the sensitivity of a HJH ensemble to ionic conditions and junction sequence and to further probe the ability of X-ray interferometry to distinguish conformational ensembles, we tested the effect of adding Mg²⁺ and of changing the bulge sequence from 3A to 3T. In particular, we assessed their effects on the small population of extremely bent conformers (β > 90°) that is part of group III.

The 3A-DNA ensemble obtained from the interferometry data exhibits limited bending compared with the allowed space: conformers with bends (β) of greater than 90° made up 29% of our allowed space (Fig. 4A and SI Appendix, Fig. S9A), but these conformers populate only 4% of the actual ensemble (Fig. 4B). Two simple factors could contribute to the limited bending in 3A-DNA. Stacking in the bulge and electrostatic repulsion between the helices in the highly bent conformations would tend to favor a roughly continuous arrangement of the helices. If base stacking were important in limiting bending, then the reduced stacking with the 3A bulge replaced with 3T would be expected to increase occupancy in the extremely bent region (β > 90°). If electrostatic repulsion were important, screening by added Mg²⁺ would reduce this repulsion and likewise be expected to increase occupancy of this region.

We tested these models using the d4 gold labeling pair (Figs. 2A and 6A), as this labeling pair is highly sensitive to bending (Fig. 6C and SI Appendix, Fig. S13). Fig. 6C shows the bending angles for all conformers that share the same d4 distance. As d4 distance gets smaller, the values of β becomes larger, and distances of <27 Å require that β be greater than 90° (Fig. 6C, dotted line). Thus, populations of strongly bent conformations can be probed by the population at small d4 distances (Fig. 6C and SI Appendix, Fig. S13).

Fig. 6.

Effect of sequence composition and ionic conditions on the bulge-DNA ensemble. (A) Schematic of the constructs used with bulges of 3A or 3T and Au probe pair d4 as defined in Fig. 2A, the position that is most sensitive to bending. (B) The measured Au-Au center-to-center distance distribution for 3A-DNA with probe pair d4 (black, also in Fig. 2C) and the individual contributions from the five conformational groups [I to V, colored dashed lines (Fig. 4C and SI Appendix, Fig. S10)]. (C) The relationship between d4 Au-Au distances and the possible range of bending angles, β, in the allowed space. Each dot corresponds to a conformation in the allowed space (SI Appendix, Fig. S13, provides a density map); the x axis is the mean distance of the d4 Au-Au center-to-center distance distribution of each allowed space conformation. The minimum bending angle at the same d4 Au-Au distance is labeled as a brown line. (D) Comparison of the d4 Au-Au center-to-center distance distributions for 3A-DNA bulge without (solid line) and with (dashed line) 4 mM Mg²⁺ in the background of 160 mM Na⁺. (E) Comparison of the d4 Au-Au center-to-center distance distributions for 3A-DNA (black) and 3T-DNA (magenta). (F) Comparison of the d4 Au-Au center-to-center distance distributions for 3T-DNA without (solid line) and with (dashed line) 4 mM Mg²⁺ in the background of 160 mM Na⁺.

Addition of 4 mM Mg²⁺ had no significant effect on Au-Au distance distributions of the DNA helix lacking bulged residues (SI Appendix, Fig. S14) but did alter the distribution for 3A-DNA (Fig. 6D, solid vs. dashed lines). Upon addition of Mg²⁺ there is a small but measureable increase in conformers with d4 distances of about 33 Å (Fig. 6D, arrow). This distance corresponds to strongly bent conformations with β values of 80° or greater (Fig. 6C, brown line). The modest magnitude of this change is consistent with Poisson–Boltzmann (PB) model predictions. We estimated that an addition of 4 mM Mg²⁺ would preferentially stabilize the strongly bent (β > 90°) over the less bent (β = 30–90°) bulge conformations by about 0.2–0.5 kcal/mol (SI Appendix, Fig. S15, and SI Methods), which would correspond to stabilization and enrichment of the strongly bent conformations by about 30–110%. PB tends to underestimate the effects of divalent cation screening (39–41), and the observed ∼twofold effect (Fig. 6D) is at the upper end of the predicted range.

Changing the base sequence from 3A to 3T led to a new d4 distance peak at 23 Å (Fig. 6E, magenta line and arrow), consistent with increased bending, which could arise via a reduction of stacking, different hydrogen bonding patterns, and/or a reduction of steric constraints from the purine bases. Conformers that give rise to a peak at 23 Å require β values of >100° (Fig. 6C, brown line). We also added 4 mM Mg²⁺ with the 3T bulge to additionally test electrostatic factors and observed an increase in populations with small d4 distances (<50 Å, Fig. 6F), as expected from enhanced electrostatic screening, although not an increase of the small fraction of the most bent conformers.

The effects from changing the bulge sequence and increasing electrostatic screening are small, but they are readily detected by appropriately placed gold nanocrystals, providing support for the above noted models and the sensitivity of X-ray interferometry. Future experiments, in conjunction with atomic level models, will be required to dissect the origins of these effects in greater detail.

It is of interest to compare our results on DNA bulge and literature results on the average bending of RNA bulges. Transient electric birefringence (TEB) and gel mobility results (42) suggest that a 3U-RNA bulge is slightly less bent than a 3A-RNA bulge. Our data, although revealing an increase in a strongly bent subpopulation, are consist with a slightly less bent average conformation, as the major peak (Fig. 6E, larger peak on the right) of 3T-bulge DNA (Fig. 6E, magenta line) is slightly shifted to longer distance compared with the 3A-bulge DNA (Fig. 6E, black line). Conversely, Zacharias and Hagerman (42) observed a decrease in bending for 3U-RNA with an increase in Mg²⁺ concentration, whereas our data suggest that 3T-DNA is slightly more bent in the presence of Mg²⁺. This difference could result from specific metal binding to the RNA but not DNA bulge or from stacking or other differences between this DNA and RNA (43, 44). The ability of X-ray interferometry to probe beyond structure averages should render this technique particularly valuable in determining the origin of such differences.

Conclusions and Implications

Determining a molecule’s conformational ensemble, beyond that of an average structure, is a major and necessary step toward a predictive and quantitative understanding of macromolecule structure, folding, and function. This task is extremely challenging even for simple HJH motifs, which represent the building blocks of complex nucleic acids structure and an ideal starting point for developing such approaches (13, 45). The average structural information from single-molecule FRET experiments with bulged DNAs (31) was reproduced by X-ray interferometry (Fig. 1 and SI Appendix, Fig. S16) and extended to provide incisive information about the ensemble of conformers present that could not be obtained from FRET.

We obtained information about the conformational ensembles of HJH motifs with increasing numbers of A residues, and we estimated the 3A-DNA conformational ensemble. The 3A-DNA ensemble populates a limited region of its geometrically allowed conformational space. Predominant in the ensemble are conformers with bend angles ranging between 24 and 85° and with characteristic bending directions and helical twists as well as helical displacements. X-ray interferometry also revealed changes to the conformational ensemble from perturbations in ionic conditions and the bulge sequence, and our results suggest that stacking and electrostatics limit bending in 3A-DNA.

X-ray interferometry instantaneously assays distances and allows a direct transformation from interference pattern to distance. Thus, X-ray interferometry can be readily predicted from MD simulations and should therefore be valuable in testing and refining MD-based models. A community-wide competition for predicting flexible nucleic acids structures using X-ray interferometry as experimental benchmark would be a powerful addition to the current RNA CASP (46), which currently predicts only folded RNA structures; obtaining the correct weighting of an ensemble of structures is a more stringent test than the correct prediction of a single most-stable structure and is necessary to understand and effectively predict thermodynamics and kinetics.

X-ray interferometry provides elusive ensemble information of macromolecules and complements existing NMR-based approaches. X-ray interferometry readily provides information about translational displacements, which are difficult to assess with RDC measurements (47), as well as angular movements, and it is more straightforward to extend to larger structures (22, 24) and other classes of macromolecules. However, X-ray interferometry is limited in detecting rare conformers (17, 18, 23) so that techniques that can trap or assess rare excursions, such as NMR relaxation dispersion (48), paramagnetic relaxation enhancement (49), hydrogen/deuterium exchange (50), and cyclization (51), are powerful complements to X-ray interferometry. Full atomic-level resolution of conformational ensembles and free-energy landscapes of macromolecules will require continued synergy between the development of X-ray interferometry, RDC measurements, and other experimental techniques as well as MD and other computations approaches.

Materials and Methods

Materials.

Au-labeled DNA oligonucleotides were prepared following procedures described previously (17, 18). Briefly, the DNA oligonucleotides were synthesized using Applied Biosystems 394 DNA synthesizer and purified by Poly-Pak (Glen research) followed by anionic exchange HPLC. Internal thiol groups were introduced through derivatization at amino-allyl dT (Glen Research) using succinimidyl 3-(2-pyridyldithio)propionate (SPDP, Pierce), followed by DTT reduction and desalting. The thiolated DNA oligonucleotides were coupled to thioglucose-passivated gold nanocrystals (17) for 2 h at pH 9.0, purified by anion exchange HPLC, and desalted by centrifugal buffer exchange with water. Complementary strands were annealed at room temperature for 30 min, then purified and desalted as above. 2-Aminopurine-modified DNA oligonucleotides were synthesized as above and purified by anionic exchange HPLC.

SAXS Measurements and Data Processing.

Small-angle X-ray scattering measurements were carried out at Stanford Synchrotron Radiation Lightsource (SSRL) Laboratory (beamline 4-2) using a sample to detector distance of 1.7 m. The buffer conditions for all experiments are 150 mM NaCl, 70 mM Tris⋅HCl, pH 8.0, with 10 mM sodium ascorbate. Data were acquired and analyzed following procedures described previously (18, 23).

Predicting the Au-Au Distance Distribution and Scattering Profile for a Bulge Conformation.

Each bulge conformation was identified by a set of (α, β, γ, x, y, z), and the equivalent matrix M. The rotation and translation indicated by (α, β, γ, x, y, z) is equivalent to applying the rotational and translational matrix M to the top helix at (0, 0, 0, 0, 0, 0), a standard duplex. At (0, 0, 0, 0, 0, 0), the position of the gold probe on either the bottom or the top helix is not a point but a point cloud, due to internal conformational fluctuation of the DNA duplex (18). For a pair of gold probes j, one on the bottom helix and one on the top helix, we generated the two probe position clouds at (0, 0, 0, 0, 0, 0) based on our prior DNA double-helix model (18). For a bulge conformation i, the bottom helix gold position cloud is unchanged, and the top helix cloud can be calculated by applying the rotational and translational matrix Mi to the top helix cloud at (0, 0, 0, 0, 0, 0). The pairwise distance distribution between the bottom and top helix gold clouds gives rise to the Au-Au distance distribution for gold pair j and conformer i. A Au-Au distance distribution ij can be transformed back to its equivalent Au-Au scattering interference profile, Ii,j(S), as previously described (18, 23).

Estimating the Conformational Ensemble.

The conformational ensemble is determined using a procedure simplified from a published Bayes approach (37). A detailed description of the procedure is included in SI Appendix, SI Methods. Briefly, the optimum weight for i = 1 to N conformers in the allowed space was calculated as

where the weights for conformer i in each ensemble solution E, w_i,E, were averaged over all E and weighted by f(m|E), the probability of obtaining data m with ensemble solution E, which can be determined using χ² statistics. Here data m is I(S), the scattering-angle dependence in scattering intensity.

Due to the complexity of the ensemble solution space, Eq. 1 cannot be solved by directly sampling the entire ensemble solution space as in ref. 37. Instead, we simplified by sampling the ensemble solution space in hierarchical stages and used a method similar to empirical Bayes approximation (36) in which a smaller subensemble solution space is represented only by its maximum likelihood solution. Specifically, we first divided the ensemble space into smaller subensemble spaces. We randomly select 100 conformers out of the 50,000 allowed conformational space to be allowed to have nonzero weights. These 100 conformers can have different weight vectors and in itself is a subensemble solution space. We then approximated this subensemble solution space with its maximum likelihood solution, the set of optimum weights that maximize f(m|E), which was determined using the lsqnonneg function of Matlab. The above sampling procedure was repeated by randomly selecting different 100 conformers from the 50,000 allowed conformational space. Convergence was found among five separate 200,000-step samplings. The five 200,000-step samplings were combined to calculate the final weight vector using Eq. 1, where each randomly selected subensemble space E is weighted by f(m|E).

Molecular Dynamics Modeling of the Bulge.

MD simulations were used to generate a library of plausible bulge conformations and provide a MD estimate of the bulge ensemble. Simulations were performed using Gromacs 4.5.5 (52) and the AMBER99 force field (53). The simulated construct included three bulged A’s flanked by three base pairs at each end of the helix. Distance restraints were used to fix the secondary structure of each closing base pair and to enforce the helicity of the adjacent bases in the nonbulge strand. The TIP3P explicit solvent model was used to model water. Particle mesh Ewald was used to calculate electrostatic forces. Simulations were performed in a cubic box of length 55.9 Å. The box contained DNA with 13 backbone phosphates, 5,600 water molecules, 29 sodium ions, and 16 chloride ions. Multiple simulations were performed at 288 K with the temperature controlled by a Langevin integrator. A total of ∼2 μs of simulation was performed; conformations were saved every 100 ps, leading to a total of ∼200,000 conformations in the resulting bulge conformation library.

For each MD bulge conformer, the corresponding (α, β, γ, x, y, z) was determined as described in SI Appendix, SI Methods. The d1 to d6 (Fig. 2A) Au-Au distances were then predicted as described above (Predicting the Au-Au Distance Distribution and Scattering Profile for a Bulge Conformation). For each representative X-ray interferometry conformer (Fig. 4C), the closest matched MD conformer was found as the MD conformer with the smallest d1 to d6 RMSD from the X-ray interferometry conformer. This MD conformer then provides an atomistic structure model for an X-ray interferometry conformer (Fig. 4D).

Fluorescence Measurement

Steady-state fluorescence intensity of 2-aminopurine-modified DNA was measured using a Fluorolog-3 spectrometer (Horiba) with excitation and emission wavelengths set to 320 and 380 nm, respectively. Fluorescence lifetimes were measured using an Easylife fluorometer (OBB). All measurements were carried out with 150 mM NaCl and 20 mM Tris⋅HCl, pH 8.0, at 20 °C (steady state) or room temperature (time-resolved).