Understanding the mechanism of proteasome 20S core particle gating

Significance

The proteasome plays a critical role in regulating cellular homeostasis by degrading target protein substrates. Gating residues that are part of the barrel-like proteasome structure provide a barrier to prevent inadvertent proteolysis. With NMR spectroscopy, the mechanism by which the gates interconvert between open and closed states is studied. We show that collisions with water molecules provide a driving force for gate interconversion and that the process takes place via many small steps that involve protein segments smaller than 4 Å. The effect of cellular lysate on proteasome gating is explored, establishing that gating equilibria and kinetics are not perturbed relative to buffer solutions under conditions of similar viscosity.

Abstract

The 20S core particle proteasome is a molecular machine playing an important role in cellular function by degrading protein substrates that no longer are required or that have become damaged. Regulation of proteasome activity occurs, in part, through a gating mechanism controlling the sizes of pores at the top and bottom ends of the symmetric proteasome barrel and restricting access to catalytic sites sequestered in the lumen of the structure. Although atomic resolution models of both open and closed states of the proteasome have been elucidated, the mechanism by which gates exchange between these states remains to be understood. Here, this is investigated by using magnetization transfer NMR spectroscopy focusing on the 20S proteasome core particle from Thermoplasma acidophilum. We show from viscosity-dependent proteasome gating kinetics that frictional forces originating from random solvent motions are critical for driving the gating process. Notably, a small effective hydrodynamic radius (EHR; <4Å) is obtained, providing a picture in which gate exchange proceeds through many steps involving only very small segment sizes. A small EHR further suggests that the kinetics of gate interconversion will not be affected appreciably by large viscogens, such as macromolecules found in the cell, so long as they are inert. Indeed, measurements in cell lysate reveal that the gate interconversion rate decreases only slightly, demonstrating that controlled studies in vitro provide an excellent starting point for understanding regulation of 20S core particle function in complex, biologically relevant environments.

The 20S proteasome core particle (20S CP) is responsible for most of the nonlysosomal protein degradation in the cell, thereby ensuring protein homeostasis (1–4). Regulated protein hydrolysis is critical for cell viability through removal of potentially toxic misfolded or otherwise damaged proteins before they accumulate to levels leading to aggregation. This important molecular machine also plays a critical role in regulating the cell cycle by controlling the concentrations of key proteins in a time-dependent manner and in the immune response by producing antigenic peptides. Not surprisingly, it has emerged as a major drug target in the fight against certain types of cancer (5).

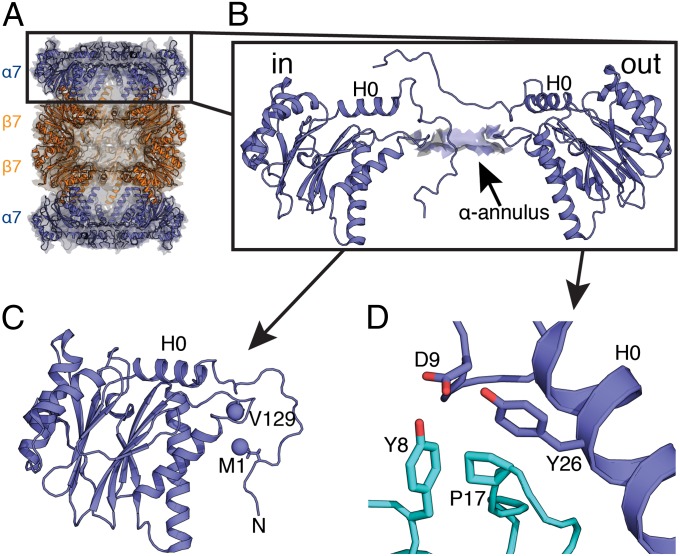
To ensure that the proteasome does not inadvertently proteolyze proteins in the cell, the 20S CP assumes a barrel-like architecture composed of four stacked heptameric rings (6, 7), as shown in Fig. 1A. The two outer rings are composed of α-subunits (α₇), with catalytic sites localized to the inner β₇-rings and facing the lumen of the barrel. Access to the β-subunit catalytic sites is blocked by the first 12 amino acids of the α-subunit, which form a gate that occludes entry of substrate through the narrow pore in the α-ring, called the α-annulus, Fig. 1B (1, 6, 8). Substrate entry into the catalytic chamber of the proteasome is controlled further through the binding of regulatory particles (RPs) to each of the barrel ends. These include the 19S RP that recognizes ubiquitin-tagged proteins that are earmarked for degradation (3) and other protein systems that function in an ATP-independent manner, including proteasome activator 200 kDa (PA200) and PA28 (eukaryotic 20S CPs), as well as AAA protein complexes such as PAN and VAT (archaeal 20S CPs) (1, 7, 9–12).

Fig. 1.

Architecture of the N-terminal gating residues of the T. acidophilum proteasome. (A) Cross-sectional side view of the 20S CP proteasome (α₇β₇β₇α₇) showing the barrel-like structure of the CP [Protein Data Bank (PDB) ID code 1YA7] (52). Two subunits have been removed from each of the rings so that the antechambers (α₇-β₇) and catalytic chamber (β₇-β₇) are visible. (B) α₇-ring highlighting gating residues in the in (closed) and out (open) states. The α-annulus is shown in a space-filling representation, with helix H0 labeled for reference (PDB ID code 2KU1) (17). (C) Stabilizing interactions between M1 and V129 in the in state, as established from NOE experiments recorded on a 20S CP sample. (D) The reverse-turn interaction formed between conserved residues, Y8, D9, P17, and Y26, from adjacent α-subunits (teal and blue) in the out state (52).

The role of the ubiquitin-dependent protein degradation pathway, and hence the significance of the 19S–20S proteasome complex in eukaryotic organisms, is well established (3, 4, 10). Recent studies further clarified that the naked 20S CP also may play a significant role in in vivo protein lysis, particularly that involving intrinsically disordered proteins or folded proteins with regions of significant disorder (13, 14). It is estimated that up to 20% of all cellular proteins may serve as substrates for the 20S CP proteasome, with the gating residues assuming a critical role in controlling proteolysis (15). The importance of gating is emphasized further by studies of yeast cells with gateless proteasomes, showing very low survival rates under conditions of prolonged starvation, in contrast to their counterparts with wild-type 20S CPs (16).

The significance of gating to proteasome function has led us to study how gating termini control access to the 20S CP, by using proteasomes from the archaea Thermoplasma acidophilum as a model system. We previously showed by solution NMR spectroscopy that although the gating residues of the T. acidophilum 20S CP are disordered, they can assume distinct conformations in which the gate is either localized outside the lumen and above the annulus (the “out” position) or inside the lumen (the “in” position) (Fig. 1B) (17). These in and out termini exchange stochastically on the seconds timescale, with a population of two in and five out, on average, for the wild-type protein. Gating termini that penetrate the α-annulus decrease the surface area available for substrate entry, leading to decreased rates of hydrolysis (17).

Paramagnetic relaxation enhancement NMR studies establish that in the in state, there are large numbers of transient interactions between gating residues and the lumen of the antechamber (17). Furthermore, methyl-NOESY spectra show a clear contact between M1 of the gate and V129 of the antechamber (Fig. 1C). In addition, X-ray studies indicate that the out state is stabilized by a reverse-turn interaction between four highly conserved residues (Y8, D9, P17, and Y26) in pairs of adjacent α-subunits (Fig. 1D) (18). Thus, although structural details about the end points of the gate exchange reaction have been elucidated and the importance of the exchange between multiple gating conformations for regulating substrate entry into the archaeal 20S CP is clear, the mechanism of gate exchange remains to be discovered. For example, is this process driven through interactions with solvent, or are there significant internal (intraproteasome) frictional forces in play? A second question relating to the mechanism of gating concerns the average size of the structural units that take part in the transition leading to the interconversion between in and out states. Does the exchange process occur in a series of only a few steps involving large pieces of the protein, or are many smaller steps and correspondingly smaller protein segments involved? Answers to these basic questions have important implications for understanding how the rate of gate exchange might vary in vivo as a function of cellular protein concentration, for example.

To address these mechanistic aspects of proteasome gating, we have used magnetization exchange NMR spectroscopy to measure the rate of gate exchange as a function of viscogen concentration, using a pair of viscogens of different sizes. The rate vs. viscogen profiles so obtained have been analyzed using the Kramers rate equation valid in the high-friction limit (19, 20), establishing that water plays a critical role in driving gate exchange and that the process proceeds through very small step sizes, smaller than an amino acid. Rates of proteasome gating also have been measured in an archeal lysate from the thermophile Thermus thermophilus. Despite the large number of potential proteasome interacting partners, exchange kinetics are little changed and populations of in and out states remain unaltered relative to buffer. Measured viscosity values as a function of probe size in cellular lysate have been used to construct a molecular ruler for estimating how rates of reactions quantified in solutions of buffer, in general, translate to in-cell. For processes driven by solvent and occurring via small protein segments, the ruler predicts only small rate decreases in lysate so long as it is inert (≤30% for a lysate protein concentration of 100 g/L), consistent with the changes in kinetics observed here for α₇ gating.

Results

Characterizing the α-Ring Gate Transition.

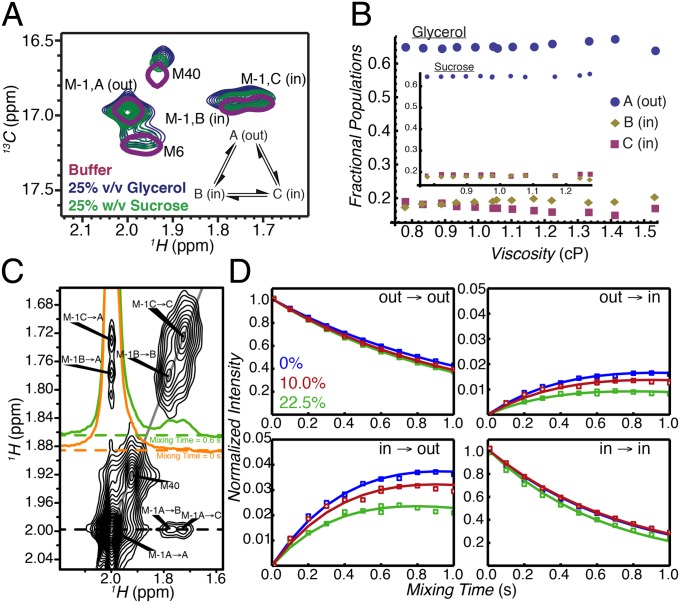
In a previous NMR study, we showed that the 180-kDa single α₇-ring is an excellent model for understanding the interconversion of gating residues in the full 670-kDa 20S CP (17). For example, ¹³C-¹H spectra of a highly deuterated ¹³CH₃-M sample of α₇ (²H, ¹³CH₃-M, α₇) showed correlation peaks for the five Met residues in each of the identical α-subunits with positions that are essentially superimposable with those observed in either an α₇α₇–double-ring structure or the full 20S CP (17). More extensive studies involving Ile, Leu, and Val methyl-labeled proteins further established that the α-subunits in the single ring are essentially identical to their counterparts in the intact proteasome (21). In what follows here, therefore, we will continue to work with the α₇ single ring, because its relatively small size offers advantages in quantitative NMR studies. Fortunately for studies of proteasome gating, several methionine residues are localized to the gate region, including M-1, which was introduced at the N-terminal end of the protein (17), providing probes of structure and dynamics in this critical area. However, the partial overlap between the M-1 and M1 cross-peaks does complicate the accurate quantification of peak intensities that is required here. As a result, we constructed an M1I mutant that has been used in all experiments described below. Fig. 2A shows a ¹³C-¹H heteronuclear single quantum coherence (HSQC) spectrum of ²H, ¹³CH₃-M, M1I α₇, 14.0 T, 45 °C. As before, three correlations are observed for M-1, labeled A, B and C, that correspond to the gate-out (A) and gate-in (B and C) conformations, and no changes are observed in the positions of these peaks relative to the spectrum of the wild-type protein (17). These conformers interconvert on the seconds time scale, according to the triangle model indicated in Fig. 2A, Inset (17).

Fig. 2.

Probing the kinetics of in/out α₇ gate interconversion by magnetization exchange NMR spectroscopy. (A) Selected regions of ¹³C,¹H HSQC spectra of ²H, ¹³CH₃-M, M1I α₇, 14.0 T, 45 °C dissolved in buffer (single magenta contour), in buffer + 25% (vol/vol) glycerol (blue contours), and in buffer + 25% (wt/vol) sucrose (green contours). (B) Fractional populations of the M-1A (out), M-1B (in), and M-1C (in) α₇ gate conformations as a function of viscosity during the course of glycerol (sucrose, Inset) titrations. (C) Two-dimensional ¹H,¹H plane from a ¹³C-edited magnetization exchange experiment (17) recorded in 22.5% (vol/vol) glycerol with a mixing time of 0.6 s. Cross-peaks arise because of slow conformational exchange between out (M-1A) and in (M-1B and M-1C) states. Correlations connecting states B and C are not resolved because of the significant line broadening due to the high viscosity of the sample. The orange and green 1D traces through the M-1A resonance highlight the absence of exchange cross-peaks when the mixing time is zero (orange) and their presence (green) for nonzero mixing times. (D) Normalized auto- and cross-peak intensities vs. mixing time at 0% (blue), 10.0% (red), and 22.5% (vol/vol) (green) glycerol concentrations. 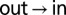The auto- and cross-peaks were normalized by the intensity at time 0 of the 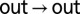auto-peak, whereas the 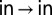auto- and 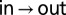cross-peaks were normalized by the intensity at time 0 of the 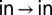auto-peak. Solid curves are from fits to a two-site exchange model, described in Supporting Information. Error bars denoting uncertainties in peak intensities were calculated from duplicate measurements at two mixing times and are smaller than the symbols used to denote the intensity values.

Kinetic processes, such as the interconversion of the α₇ gates, can be modeled as a diffusive search across a simplified 1D energy landscape (20, 22, 23). The rate constant for the transition from state m to n, 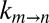is given by Kramers’ theory in the strong friction limit modified to include contributions from both solvent and internal friction (19, 20, 22, 24),

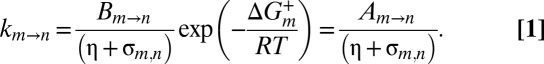In Eq. 1, 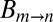is a constant that is independent of viscosity but that depends on, among other things, the curvature of the energy landscape at state m and the transition state (+), and 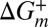is the free energy difference between m and +, which is assumed to be independent of viscosity (see below). The rate 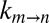is inversely related to the friction along the landscape, which is expressed in terms of the sum of viscosity contributions from the solvent η and interactions that are internal to the protein (σ). Thus, by monitoring the rate of exchange vs. η, the value of σ can be determined, providing a measure of the relative contributions from solvent and internal (intra-α₇) degrees of freedom to the overall gate exchange process.

An important prerequisite in the choice of viscogen(s) used to increase η is that it does not change the average free energies of states along the landscape (25). Although it is difficult to prove that the landscape remains completely unaltered, it nevertheless is possible to perform several tests that provide a high degree of confidence that the viscogen is inert. In this regard, the exquisite sensitivity of NMR chemical shifts to even very low-affinity (millimolar) interactions may be exploited to show that the viscogens do not bind to the interconverting conformers. Fig. 2A superimposes spectra of α₇ recorded in buffer (no viscogen, single contours), in 25% (vol/vol) glycerol (blue), and in 25% (wt/vol) sucrose (green), with the chemical shifts of methionine methyl groups only very slightly perturbed, providing strong evidence that the structural properties of the gating states remain unchanged. A more comprehensive study in which all the Ile residues in the protein were labeled (¹³CHD₂-δ1) confirmed that only very minimal changes to the spectra are produced by the addition of viscogen (average rmsd of 0.012 and 0.078 ppm in ¹H and ¹³C dimensions, respectively), consistent with a lack of binding (Fig. S1). As a second control, the populations of each of the three states were measured from intensities of cross-peaks in ¹³C-¹H HSQC spectra recorded as a function of viscogen concentration (Fig. 2B). Average fractional populations of 64.8 ± 1.0% (64.0 ± 0.4%), 16.8 ± 1.1% (18.3 ± 0.3%), and 18.5 ±1.0% (17.3 ± 0.6%) were obtained for states A, B, and C, respectively, across the glycerol (sucrose) titration, consistent with a free energy landscape that is not affected by the addition of these viscogens.

Having established that glycerol acts as a “good” viscogen, we next quantified gate exchange rates as a function of 13 glycerol concentrations ranging from 0% to 25% (vol/vol) (SI Materials and Methods). Rates were recorded using a ¹³C-edited magnetization exchange experiment described previously (17), whereby a series of 2D spectra are generated as a function of a parametrically varied mixing time during which chemical exchange is allowed to occur. Fig. 2C shows one such spectrum, recorded with a glycerol concentration of 22.5% (vol/vol) and a mixing time of 600 ms. Diagonal peaks are on the black line y = x and derive from magnetization not transferred between states during the mixing period. In contrast, cross-peaks connecting the diagonal correlations result from magnetization transferred between conformers during this interval. Notably, the exchange cross-peaks connecting states B and C could not be separated from the diagonal peaks in experiments recorded on samples with viscogen (Fig. 2C) because of increased linewidths, preventing quantitation of the rates of exchange between the two in-gate conformations. The kinetic data therefore have been analyzed by using a simplified model of exchange in which all signal intensities derived from states B and C have been combined, effectively reducing the analysis to a two-site interconversion between in and out states, 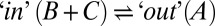. As we show in Supporting Information, such a simplification is reasonable for the kinetic parameters and populations that are germane here, with accurate values of exchange rates, 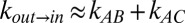, 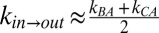and σ values extracted from the fits (Fig. S2). Fig. 2D illustrates the quality of fits obtained from a two-state analysis for several different glycerol concentrations. As predicted from Eq. 1, exchange rates decrease as a function of increasing solvent viscosity. Remarkably, rates as low as 0.04 s⁻¹ are measured at the high-viscogen end, which are more than an order of magnitude slower than methyl ¹H spin lattice relaxation (R₁) rates that describe the overall decay of longitudinal magnetization.

Small Internal Friction for the α-Ring Gate In–Out Transition.

As is evident from Eq. 1, values of σ can be estimated readily by fitting 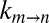vs. η profiles generated by measuring reaction rates as a function of solvent viscosity (20). In a first set of experiments, the solvent viscosity was increased through the addition of glycerol, which we have shown does not perturb the energy landscape (see above) and thus functions as a good (inert) viscogen, a requirement in studies of the sort presented here. A critical advantage of using a viscogen such as glycerol is its small hydrodynamic radius, R_H,v (2.6 Å). The effective viscosity of the solvent, which in turn is used as a proxy for the solvent contribution to the viscosity along the reaction coordinate (η in Eq. 1), is essentially independent of the probe used to measure it in the case in which R_H,v is small, because all probes have hydrodynamic radii on the order of or larger than R_H,v (Figs. S3 and S4); that is, the viscosity as measured by any probe is the macroscopic solution viscosity (26).

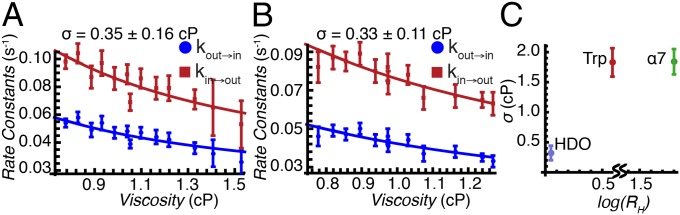
Fig. 3A shows the viscosity dependencies of the exchange rates measured using the viscogen glycerol, with the viscosity η obtained by measuring the diffusion of the residual water (HDO) signal in the sample via NMR (Supporting Information; Figs. S5 and S6). Independent fits of 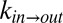or 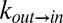vs. η to Eq. 1 produced σ values that were within error of each other, with a value of σ = 0.4 ± 0.2 cP calculated from a simultaneous fit involving both rates. Slightly larger values of σ = 0.8 ± 0.3 cP and 0.5 ± 0.2 cP were fitted when η was estimated from the diffusion of tryptophan and α₇ probes, respectively, that essentially are within the range obtained from HDO.

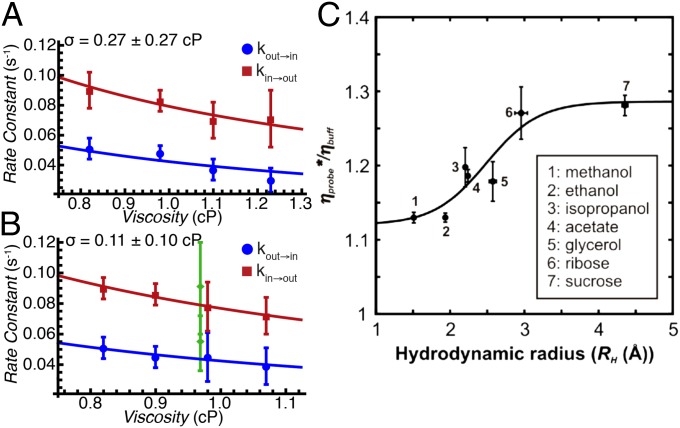
Fig. 3.

Deciphering the mechanism of gate exchange. (A and B) Exchange rate constants, 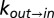(blue) and 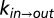(red), measured as a function of solution viscosity, by using viscogens glycerol (A) and sucrose (B). Viscosity values were obtained from the measured diffusion constant of water, as described in Supporting Information. Fits of Eq. 1 to 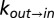and 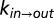provide an estimate of σ (upper left-hand corners). (C) Overestimation of solvent contributions to the viscosity along the energy landscape results in values of σ that are too large, as observed in the case in which η values in solutions of the viscogen sucrose are estimated using the diffusion of tryptophan and α₇ probes (see text).

Interestingly, the σ values are on the order of or smaller than the viscosity of ²H₂O at 45 °C (∼0.76 cP). Thus, the contribution to the kinetics of proteasome gating from internal friction is no more than that from water, and collisions with water thus are critical for driving the gating process, consistent with the “slaving model” for protein dynamics (27, 28).

Determining the Effective Hydrodynamic Radius for the In–Out Transition.

As a next step, we were interested in quantifying the effective hydrodynamic radius (EHR) for the gating process (22). By “EHR,” we refer to the average size of the protein unit that undergoes conformational changes in each step of the reaction. For example, if the exchange between in and out gating states occurs in a single step, then this would involve a large EHR with an approximate size on the order of the length of the N-terminal 10–12 residues that comprise a proteasome gate. By contrast, if multiple steps were required to traverse between in and out states, with each step involving just a single side chain, the EHR would be on the order of 3–4 Å. Thus, the EHR provides an important metric for understanding the mechanism by which a reaction proceeds.

To estimate the EHR, the dependence of 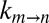on viscosity must be measured for at least a pair of viscogens. We have examined a significant number of potential viscogens, including the small molecules ethylene glycol, 1,2-propanediol, 2-methyl-2,4-pentanediol, glucose, sorbitol, and trehalose, as well as the proteins lysozyme and BSA and the polymer Ficoll. In all cases, populations of the in and out α₇ gating states were perturbed relative to what was quantified in a pure buffer solution. In contrast, sucrose did not perturb populations (Fig. 2B, Inset), nor were the chemical shifts of M-1 correlations affected in ¹³C,¹H HSQC spectra (Fig. 2A and Fig. S1). The kinetics of gate exchange, therefore, were quantified as a function of the viscosity of samples prepared with varying amounts of sucrose. Importantly, the use of a viscogen larger than glycerol (R_H,v = 4.5 Å for sucrose vs. 2.6 Å for glycerol) provides an avenue for estimating the length scale of gate exchange, so long as the value of σ is already known. The approach used here exploits the fact that σ must be viscogen independent and equal to ∼0.5 cP, which is obtained from fits of 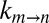vs. η using the viscogen glycerol and η values based on measurements using any of the water, tryptophan, or α₇ probes of viscosity (see above). In contrast to the diffusion of probes in glycerol, diffusion values vary considerably in the case of sucrose solutions (Fig. S4). Thus, if the EHR of gating is on the order of the size of a water molecule, then η in Eq. 1 would be well approximated by the viscosity estimated from the diffusion of a water probe, and the value of σ obtained from fits of the resulting 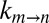vs. η profiles measured in solutions of sucrose would coincide with that measured using glycerol. In a similar manner, if the EHR is larger, on the order of the size of a single amino acid side chain, then η would be well approximated by the viscosity estimated from the diffusion of a tryptophan probe, with the correct value of σ obtained. Where solvent contributions to the viscosity along the free energy landscape are not estimated correctly, erroneous values of σ and A_i are fit. For example, overestimation of η leads to a compensating increase in both σ and A_i in fits of 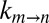vs. η (see Eq. 1), with an opposite scenario occurring when η is underestimated.

Fig. 3B plots 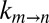vs. η (sucrose viscogen), where η is the solution viscosity measured from the diffusion of water. The value of σ = 0.3 ± 0.1 cP obtained from a fit of the data to Eq. 1 agrees well with the σ value calculated using glycerol as a viscogen (0.4 ± 0.2 cP), indicating that the viscosity of water is a good proxy for the viscosity along the gate exchange reaction coordinate. In contrast, a significantly larger (and overestimated) value of σ, 1.8 ± 0.2 cP, was obtained from fits of 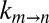vs. η by using viscosity values measured from tryptophan, with an identical value of 1.8 cP obtained when η was estimated from the diffusion of α₇ (Fig. 3C). The similar values of σ obtained with tryptophan and α₇ reflect the fact that both probes measure the macroscopic solution viscosity, which is the case when the probe size is on the order of or larger than the size of the viscogen. The macroscopic viscosity, in this case, is not the viscosity along the reaction coordinate. Importantly, a value of σ = 1.8 cP obtained using viscosity measured with the tryptophan probe (3.5 Å) indicates that the free amino acid “feels” a higher viscosity in the sucrose solution than does the gating reaction, which in turn is consistent only with an EHR value less than that of the hydrodynamic radius of tryptophan. Thus, the gating process involves a series of small steps that, on average, may be described by an EHR <3.5Å, rather than one or two transitions of a large length scale. Further, a small EHR implies that the kinetics of gate interchange will be affected only marginally by the presence of macromolecular viscogens, such as those found in heterogeneous cellular environments (so long as they are inert), because these cannot couple effectively to the exchange reaction. That this is the case is illustrated below.

Characterizing the Effect of Cell Lysate on the α₇ Gate Interconversion.

It is of interest to extend the measurements described above from viscogen–buffer solutions to cell lysates, which of course are a more relevant milieu for biomolecules. Initially, we prepared solutions of only the small molecule fraction of T. thermophilus lysate (<3 kDa in molecular mass; SI Materials and Methods) and verified that the fractional population of each of the gating states was not perturbed. The obtained 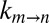vs. η profiles (Fig. 4A) subsequently were fit to Eq. 1, and the value of σ = 0.3 ± 0.3 cP so obtained is in good agreement with estimates from measurements in either glycerol or sucrose solutions. Values of 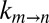also were measured in samples prepared with various concentrations of macromolecules extracted from cell lysate (≥6 kDa in molecular mass; SI Materials and Methods) and the rate vs. viscosity profile plotted in Fig. 4B, where η is estimated from the diffusion of HDO. Again, the extracted σ value is within the expected range (0.1 ± 0.1 cP). Notably, σ increases to 5.0 ± 0.5 cP when η is taken to be the viscosity as measured from the diffusion of α₇. As before, this reflects the fact that the viscosity along the reaction coordinate is overestimated by the diffusion of α₇ in the solution, a result expected for an EHR <3.5 Å, which is much smaller than the dimensions of the macromolecular viscogens that have been used. It also is of interest to measure 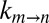values in total lysate solutions (i.e., including both small molecules and macromolecular components). Although the resulting signal to noise of spectra is compromised in lysate, we could obtain approximate rate constants for gate exchange in a sample in which the lysate protein concentration was 100 g/L. As with the experiments recorded on either lysate small molecule or macromolecule fractions, peak positions and fractional populations were the same as in buffer (Fig. S7). Exchange rates are plotted in green in Fig. 4B, with the viscosity estimated by the diffusion of HDO. To within error, the measured rates fall on the expected 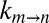vs. η profiles.

Fig. 4.

Gating studies in T. thermophilus cell lysate. (A and B) Exchange rate constants (see legend to Fig 3) as a function of viscosity, manipulated through the addition of the small molecule lysate component (<3 kDa) (A) or larger macromolecule fraction, >6 kDa (B). Solid lines are from a global fit to Eq. 1, with the resulting σ values in the upper left corner. Green points in B are exchange rate constants obtained from α₇ in 100 g/L complete lysate. (C) A molecular ruler of viscosity as a function of probe size (R_H), as measured in 100 g/L T. thermophilus cell lysate. The probe-dependent viscosity in lysate (η_probe*) was determined from NMR-based translational diffusion measurements as detailed in Supporting Information and is normalized to the viscosity of the probe in buffer (η_buff). The solid line is used to guide the eye.

Discussion

The importance of gating residues in regulating the function of the 20S CP proteasome has become increasingly appreciated with the realization that the naked CP plays a significant role in ubiquitin-independent protein hydrolysis involving intrinsically disordered proteins or proteins with regions of disorder (13–15, 29). Although structural studies have been reported for the open form of the 20S CP, in which the gates extend outward from the proteasome lumen (9, 18), or the closed form, in which the annulus is blocked by the gates (17, 30, 31), the mechanism by which the gates interconvert between in and out conformations has not been elucidated. Here, we have used magnetization exchange NMR spectroscopy, focusing on the gating termini of the α-subunits of the 20S CP proteasome from T. acidophilum to address this issue. Fits of Kramers’ equation in the high friction limit (19) to the rates of gate interconversion vs. viscosity provide the relative contributions from internal and solvent friction to the reaction (20, 22, 24). The results of the present study using glycerol, sucrose, the small molecule fraction of T. thermophilus lysate, and the macromolecule components of the lysate as viscogens establish that collisions with water are a dominant force for gate interchange. The importance of water dynamics in driving protein conformational changes, in general, is becoming increasingly evident. Examples include the global two-state folding/unfolding of small modular domains, such as the IgG binding domain of protein L (32) and CspB (33, 34); the relaxation of a photoperturbed PDZ domain (35); the collapse of amino and carboxyl folding units in the α-subunit of tryptophan synthase (36); and the folding of an on-pathway intermediate of the four-helix bundle FF domain (37). On the other hand, protein frictional forces are thought to be important in the reorganization of collapsed conformations of fast-folding proteins (25, 38–40) and, intriguingly, in the rate-limiting helix-docking step of the R16 and R17 α-spectrin domains (41, 42). The importance that protein friction may assume is emphasized further in a seminal report on CO dissociation from myoglobin (20).

In the present study, we exploited the size differences of glycerol and sucrose to ascertain that the EHR for the gate exchange reaction is less than 3.5 Å, consistent with a process involving small segments of protein and many small steps, rather than a large-scale, highly cooperative transition between states. Notably, a small EHR also was obtained for the folding of the FF domain from a compact intermediate (43).

The importance of water friction and the size of the EHR are based on the analyses of rate vs. viscosity profiles, which in turn presuppose that the viscogens used do not perturb the free energy landscape. Here, we have shown that neither the populations nor the chemical shifts of each of the interconverting α₇ conformers change upon addition of the four viscogens indicated above. Moreover, the fact that similar σ values are obtained for the viscogens further validates that they are inert. For example, an assumption inherent to our use of Eq. 1 is that 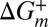is independent of viscogen [i.e., there is no interaction with the transition state ensemble (TSE)]. It is noteworthy that if the viscogens were to perturb reaction rates through interactions with the TSE, then different σ values would be expected because it is unlikely that structurally distinct viscogens (e.g., compare glycerol vs. lysate macromolecules) would affect the TSE the same way in each case (37). Thus, the obtained σ values support parsing Eq. 1 into a viscosity-dependent prefactor and a viscosity-independent exponential, as has been done here and in other studies (20, 40, 41).

We also have extended our analysis from the test tube to an environment that is cell-like. Of interest is how such a complex, heterogeneous mixture such as that found in a cell, forming the natural milieu for the proteasome, affects the α₇ gate exchange process. Generally, it has been shown that a high macromolecule concentration leads to protein compaction because of excluded volume effects (44), which potentially might change the equilibrium distribution of in and out states from what is observed in vitro. Moreover, the kinetics and thermodynamics of the interchange might well be affected by interactions with peptides and proteins in the cell. We have chosen to work with lysate as opposed to intact cells, because this eliminates the worry that the recorded signal derives from extracellular rather than intracellular α₇, which would result in the case of leakage from dead or damaged cells (45). Moreover, the use of lysate permits higher concentrations of α₇ than would be possible in intact cells, an important consideration for quantitative NMR studies. At the same time, it is straightforward to manipulate the sample composition to include, for example, only small molecule components or cellular macromolecules. Notably, the relative populations of gate conformers do not change in the lysate, measured gate exchange rates are decreased only slightly from buffer solution by an amount that is in keeping with the increased viscosity of the milieu (as quantified by water diffusion), and ¹³C-¹H correlation spectra of U-²H, ¹³CHD₂-M, ¹³CHD₂-I(δ1) α₇ show little change relative to those recorded in buffer (Fig. S7). Taken together, the results establish that, at least in terms of the gating reaction, the molecules of the lysate have little influence on kinetics and thermodynamics, so they function as inert viscogens. Additionally, as it is very likely that a variety of proteasome substrates are present in the lysate, the fact that the rates of gate interconversion are similar to those predicted in buffer with a viscosity corresponding to that of the lysate is consistent both with water remaining a major factor in driving gate opening and with a negligible influence of substrates on gate exchange in the more complex lysate environment.

The study in cell lysate discussed above has focused on a single kinetic process, that of gate exchange in the proteasome, but it is of interest to ascertain more generally how other kinetic events might be affected by the cellular environment. To address this question, we prepared a molecular ruler that relates the relative increase of viscosity in lysate (100 g/L in protein) over that in buffer to the probe size, with the size varying from 1.5 to 4.5 Å (Fig. 4C and Fig. S8). This is a length scale that is germane for processes with small effective hydrodynamic radii, such as has been measured for the exchange between in and out gate conformations considered here. Notably, rate decreases in cell lysate of no more than 30% are predicted for processes with EHR values <5 Å, assuming that the solutes in the lysate function as inert viscogens. This is in agreement with what is measured for the α₇ gates (Fig. 4B, green), but more generally allows one to predict how rates will scale for any small EHR. Of interest, a similarly moderate decrease in rate constants (25–30% compared with buffer) for a biomolecular protein-binding reaction was observed by Schreiber and coworkers (46) using in-cell fluorescence measurements. This result later was shown to be consistent with a theory for association reactions that incorporates the length-scale–dependent viscosity resulting from the heterogeneous cellular environment (47, 48).

With the development of new approaches for studies of molecular dynamics, including NMR (17, 49), single-molecule–based spectroscopy (40, 50), and long–time-scale molecular dynamics simulations (51), it is becoming possible to understand not only the end points of conformational exchange processes, but also the intervening steps in atomic detail. Ultimately, this might lead to the ability to manipulate these processes, leading, in the case of the 20S CP, to the potential development of new drugs to control function.

Materials and Methods

U-²H, ¹³CH₃-M, M1I α₇ (Δ97–103) was expressed and purified as previously described (17). Isotopic labeling of M^ε-¹³CH₃ groups in a highly deuterated background was achieved by expressing α₇ in M9 minimal media, 99% (vol/vol) ²H₂O/1% ¹H₂O with ¹²C,²H-glucose and ¹⁵NH₄Cl as the sole carbon and nitrogen sources, respectively, and adding 75 mg/L M^ε-¹³CH₃ (CDLM-8885; Cambridge Isotope Laboratories) 1 h before induction. After purification, NMR samples were buffer exchanged into 25 mM potassium phosphate (pH 6.8), 50 mM NaCl, 1 mM EDTA, 0.02% (wt/vol) NaN₃ in 99% ²H₂O by using a 10-kDa molecular weight cutoff Amicon centrifugal concentrator. All NMR samples ranged between 2.2 mM and 2.5 mM in monomer concentration. Further experimental details, including an analysis of magnetization exchange data, may be found in SI Material and Methods.