Observing (non)linear lattice dynamics in graphite by ultrafast Kikuchi diffraction

Significance

Mechanical, electrical, and thermal properties of materials are governed by the nature of constituent atoms and their motions. Mapping atomic motions in the nonequilibrium regime, and thus the linear and nonlinear responses to stimuli, is nontrivial to achieve. Here, we report the methodology of ultrafast electron diffraction, enabling visualization of the atoms in motion. By using a special variant called Kikuchi diffraction, we map out the response of the lattice of nanoscale graphite. Following an impulsive excitation, two types of motions are resolved, one involving the reflections of strain between the two surfaces and the other involving planes of atoms in the transverse direction. The approach presented here has the potential for a wide range of applications.

Abstract

In materials, the nature of the strain–stress relationship, which is fundamental to their properties, is determined by both the linear and nonlinear elastic responses. Whereas the linear response can be measured by various techniques, the nonlinear behavior is nontrivial to probe and to reveal its nature. Here, we report the methodology of time-resolved Kikuchi diffraction for mapping the (non)linear elastic response of nanoscale graphite following an ultrafast, impulsive strain excitation. It is found that the longitudinal wave propagating along the c-axis exhibits echoes with a frequency of 9.1 GHz, which indicates the reflections of strain between the two surfaces of the material with a speed of ∼4 km/s. Because Kikuchi diffraction enables the probing of strain in the transverse direction, we also observed a higher-frequency mode at 75.5 GHz, which has a relatively long lifetime, on the order of milliseconds. The fluence dependence and the polarization properties of this nonlinear mode are entirely different from those of the linear, longitudinal mode, and here we suggest a localized breather motion in the a-b plane as the origin of the nonlinear shear dynamics. The approach presented in this contribution has the potential for a wide range of applications because most crystalline materials exhibit Kikuchi diffraction.

Materials of graphite-type structure are prototype models for studies in solid-state physics (1–3), mainly because of their highly anisotropic bonding characteristics and their consequential unique properties (4, 5). Although the elastic properties of graphite and other carbon allotropes have been investigated for decades (6), a comprehensive and complete picture (7–9) still is lacking, especially when describing the nonlinear elastic properties, whose measurement requires homogeneous and large specimens (8).

Using parallel-beam X-ray or electron illumination, the atomic structure of materials can be determined by measuring the position and intensity of Bragg spots. Time-resolved Bragg diffraction has been incorporated successfully to study longitudinal elastic motion, which involves compression/expansion of the unit cell along the direction perpendicular to the specimen’s surface. In graphite, which has an anisotropic thermal expansion, both longitudinal acoustic waves (10) and shear (transverse) waves may be generated as a result of the breaking of the translational symmetry at the level of thermoelastic forces (11).

With convergent electron beam illumination, time-integrated Kikuchi diffraction provides a sensitive and precise measure of static lattice plane orientation (12). When time resolved, the evolution of Kikuchi diffraction patterns makes possible the investigation of both the longitudinal and transverse dynamics of the strain and associated lattice deformations (13, 14). This is because Kikuchi diffraction results from the scattering of electrons in the material and a large cone of wave vectors permits reflections that fulfill Bragg condition from different lattice planes; hence, it is possible to monitor the dynamics as the planes tilt and the lattice changes transversely. In contrast, these types of motions will not change the position (only the intensity) of Bragg spots in conventional diffraction experiments; for an illustration, see figure 2 in ref. 13.

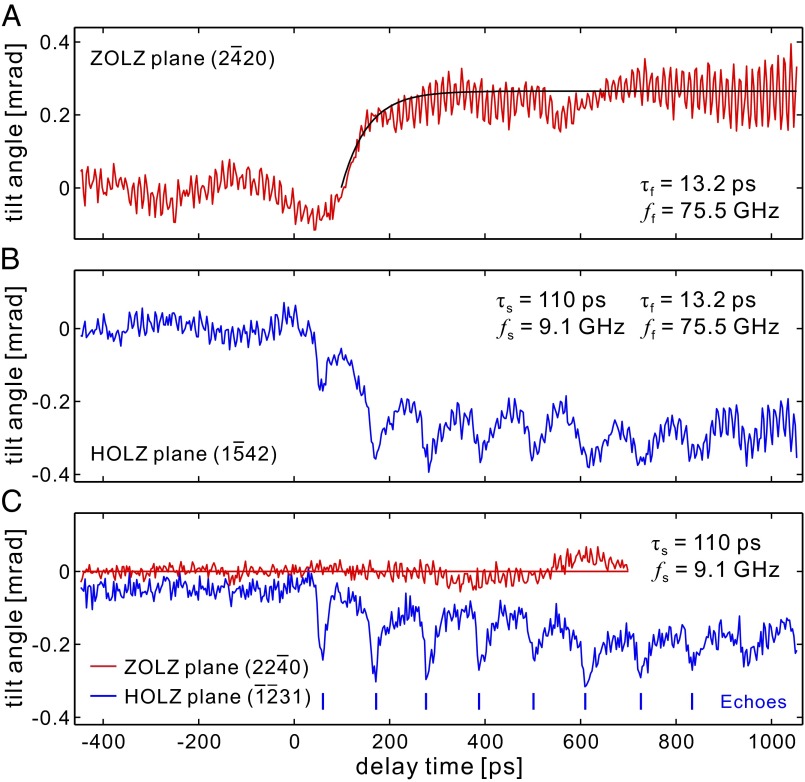
Fig. 2.

Kikuchi diffraction dynamics. (A) Oscillation dynamics of the ZOLZ plane (2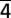20): a single 75.5-GHz mode is detected. The black solid line is a monoexponential fit to mimic the incoherent thermal stress buildup. Note that the behavior in the negative time is a result of the long lifetime (milliseconds) of the 75.5-GHz mode (see text for details). (B) Oscillation dynamics of the HOLZ plane (142): a 9.1-GHz mode superimposed on the 75.5-GHz mode is detected. (C) Oscillation dynamics of the ZOLZ plane (22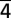0) and the HOLZ plane (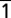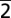31): echoes at 9.1-GHz frequency were observed for the HOLZ plane (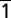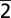31) (data are shifted by −0.05 mrad for clarity). For the ZOLZ plane (22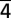0), no transients were observed, as discussed in the text.

Here, we use the Kikuchi diffraction approach in a convergent-beam ultrafast electron crystallography (CB-UEC) setup to investigate the acoustic wave dynamics of single crystals of graphite. By monitoring the temporal evolution of the Kikuchi pattern, it was possible to separate the longitudinal and transverse atomic motions. We observe longitudinal acoustic echoes propagating along the c-axis of the graphite unit cell, which represent the linear response and out-of-plane motion of the graphite lattice. The transverse lattice motion is observed as a higher-frequency mode at 75.5 GHz, and this mode exhibits a relatively long lifetime, on the order of milliseconds, and a polarization direction that rotates with the excitation fluence. The mode is an in-plane shear deformation of the graphite unit cell, and we suggest a localized breather motion in the a-b plane as its origin. In this work, the specimen was obtained from a natural graphite single crystal (naturally graphite) by mechanical cleavage (see Fig. 1B), and the thickness used is 220 nm.

Fig. 1.

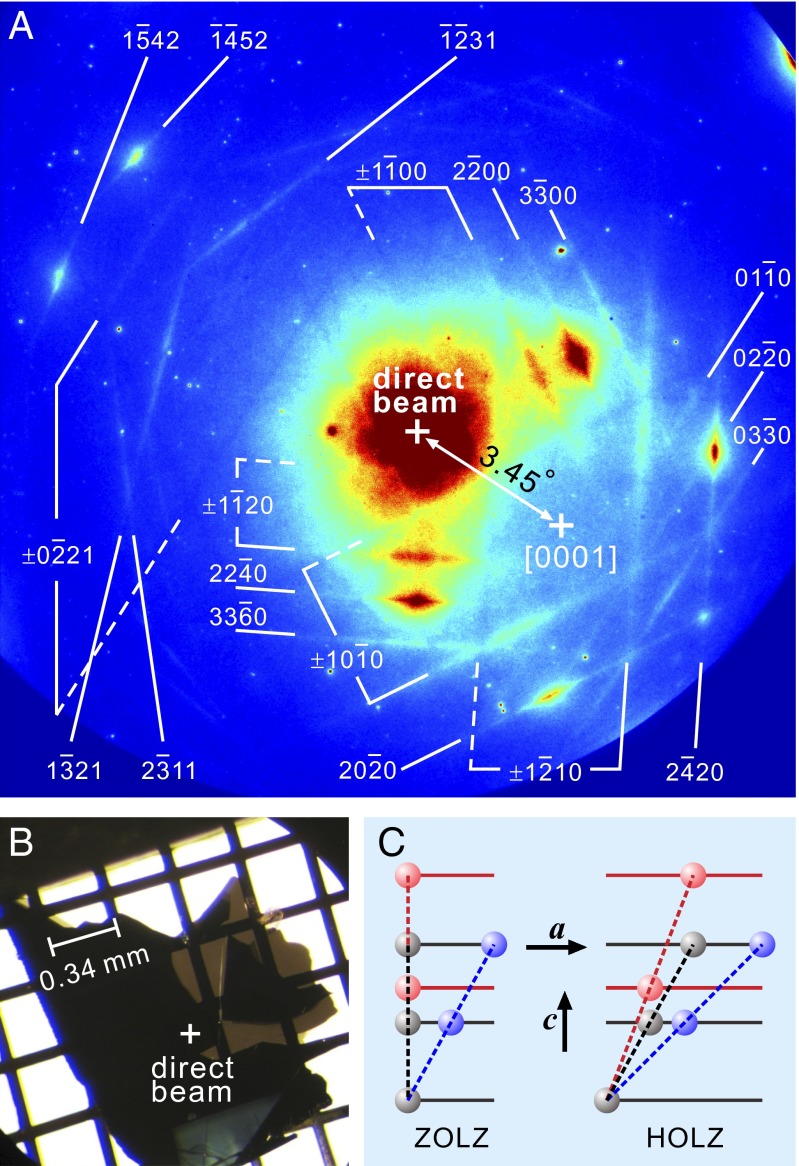
Kikuchi diffraction of graphite. (A) A representative pattern together with the indexed Kikuchi lines. Dashed and solid lines represent “deficiency” and “excess” lines (12), respectively. (B) Free-standing single crystalline graphite sample on a TEM grid. The white + marks the probed position. (C) Gray and colored dashed lines denote, respectively, lattice planes at equilibrium and when lattice deformation occurs. The blue lines represent the tilting of a ZOLZ plane (Left) and of a HOLZ plane (Right) as induced by an in-plane shear motion along the a-axis. The red lines represent the effect of a longitudinal motion along the c-axis; only for the HOLZ plane (Right) is there an effective tilting.

The CB-UEC experiments were performed in a transmission geometry (15, 16), and the electron beam was focused down to a micrometer-length scale with a convergent angle of ∼3 mrad. Fig. 1A shows the measured CB diffraction pattern together with the indexed Kikuchi lines for graphite (17). The electron beam direction was set to 3.45° off the [0001] zone axis (Fig. 1A) to minimize the background from multiple electron scatterings.

As a function of time, the shift of the Kikuchi line position with respect to the electron beam is proportional to the tilting of the corresponding lattice plane in the specimen; thus, lattice motion may be correlated directly with changes in the measured CB pattern. Lattice planes with different orientations respond differently to a certain lattice modulation (14). For instance, a lattice plane belonging to the zero-order Laue zone (ZOLZ), which is parallel to the c-axis, is sensitive to any tilt or shear motion developing in the a-b plane, whereas it is completely unaffected by motion along the c-axis (see schematics in Fig. 1C, Left). This is not the case for a lattice plane in high-order Laue zones (HOLZs) intersecting with the c-axis, which turns out to also be tilted by a lattice expansion/contraction along the c-axis (see schematics in Fig. 1C, Right).

The experimental setup and the methodology for ultrafast dynamics measurements are detailed elsewhere (18–20). Briefly, structural dynamics are initiated by femtosecond laser pulses (120 fs, 800 nm, 45° incidence, p-polarized, 1.1 × 1.6-mm² spot size, 1 kHz) and probed by ultrashort electron pulses with kinetic energy of 30 keV, at different delay times between the arrival time of the excitation laser pulse and the electron pulse at the sample. The dynamics were recorded with time steps of 1 ps, or longer if needed. For each delay time, more than 50 patterns, each averaged over 10⁴ electron pulses, were recorded to achieve a high signal-to-noise level. It is worth noting that the use of the pump laser and the pulsed electron probe with a repetition rate of 1 kHz enables us to follow the dynamics under investigation up to 1 ms from time zero, which is defined as the moment at which the dynamics are initiated and both the optical and electron pulses overlap in space and time. This is possible to establish by monitoring the temporal response at the negative delay times (19). By using active cavity length control of the femtosecond laser oscillator, the repetition rate is synchronized to an external clock, yielding a frequency stability better than 1 Hz with a synchronization jitter below 1 ps.

After determining the position of all Kikuchi lines (Supporting Information), we construct the temporal evolution of the tilting motion for each corresponding lattice plane by monitoring the change in position as a function of the delay time. Representative dynamics for the ZOLZ planes (2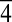 20) and (22 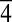0) and the HOLZ planes (1 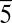42) and (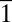 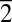31) are shown in Fig. 2, with time steps of 3 ps. Positive values of the tilt indicate that the lattice plane is inclining outward relative to the direct electron beam, whereas negative values indicate an inward inclination. Noted in Fig. 2A is the exponential fit (black solid curve), which describe the average incoherent thermal stress buildup (14). Experiments performed at the same sample position with a parallel electron beam illumination in a [0001]-zone axis result in a diffraction pattern that exhibits sharp Bragg spots, and the intensity of the spots is altered as the result of thermal-induced changes of the lattice, i.e., no oscillations are observed.

Besides the thermal stress buildup, two major oscillations with distinct envelopes are observed in the Kikuchi pattern: a fast oscillation with a period of ∼13 ps and a slower one superimposed on the fast oscillation with a period of ∼110 ps. The amplitude of the fast oscillation is sensitive to the particular crystallographic direction (see Fig. 2 A and C for an example), whereas the slow one remains nearly the same for all associated lattice planes (Fig. 2 B and C).

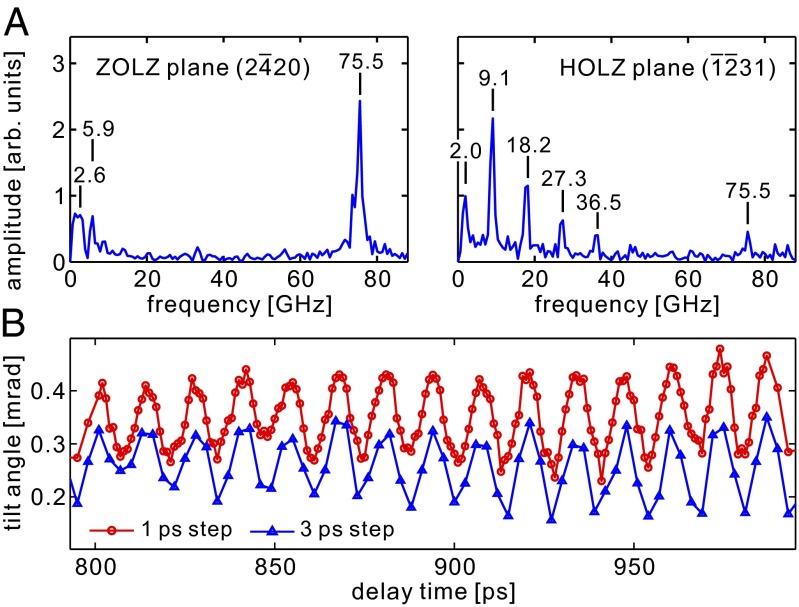
From fast Fourier transform (FFT) analysis, we determine the frequencies to be 75.5 GHz and 9.1 GHz, as displayed in Fig. 3A.* To visualize the lattice motion from the measured Kikuchi pattern, we use the method of Fourier maps introduced by Yurtsever and Zewail (13). This method permits us to follow changes in both the amplitude and phase as a function of time. For each pixel of the diffraction pattern, we determine the amplitude and the phase in the Fourier spectra at the resonance frequencies of 9.1 GHz and 75.5 GHz. The images for the phase change are presented in Fig. 4 for both frequencies and for the three investigated excitation fluences. They clearly show the relative shift of the Kikuchi lines, from which details of the lattice motion can be deduced. From these Fourier maps, it is evident that the mode at 9.1 GHz involves only Kikuchi lines associated with the HOLZ planes, whereas the mode at 75.5 GHz affects the whole pattern, although with different amplitudes for the different planes. It also is clear from the maps that the polarization of the 75.5-GHz mode lies close to the direction [1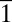 00] and exhibits a clear rotation with the excitation fluence. A more quantitative evaluation of these observations will be discussed below.

Fig. 3.

FFT spectra and oscillation period. (A) FFT spectra of the dynamics after time zero for the ZOLZ plane (2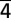20) (Left) and for the HOLZ plane (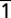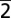31) (Right). The spectral resolution of the FFT is 0.65 GHz. (B) Close view of the oscillations at 75.5 GHz from the ZOLZ plane (2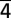20), measured with time steps of 1 ps (red) and 3 ps (blue). Both profiles exhibit the same sinusoidal behavior with identical periods and matching phase (see text).

Fig. 4.

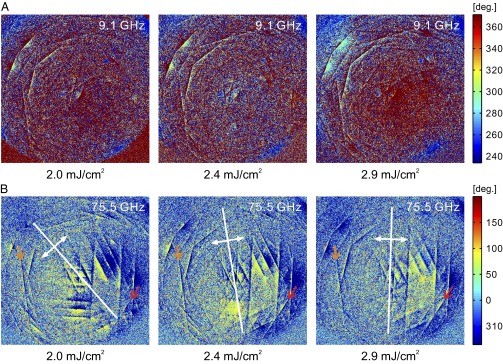
Fourier maps for the phases at the indicated resonance frequency. Shown are the phase images at 9.1 GHz (A) and 75.5 GHz (B) for the three investigated fluences, as obtained by Fourier transform of the time-resolved Kikuchi patterns. It is evident that the mode at 9.1 GHz involves only Kikuchi lines associated with HOLZ planes, whereas the mode at 75.5 GHz affects the whole pattern, with different amplitudes for different planes. The orange and red arrows in B are shown to follow the evolution of the Kikuchi lines (2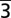11) and (03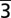0), respectively. The yellowish region in B close to each Kikuchi line is a qualitative measure of the relative change. As the fluence increases, this region evolves preferentially toward the right part of the diffraction pattern and, hence, the direction of polarization, as shown by the white double arrows; a more quantitative evaluation of the amplitude is given in Fig. 5. The scale bar is in degrees.

Careful control experiments were performed to verify the intrinsic origin of the 75.5-GHz mode. First, we compared the transients obtained using 3-ps steps with those recorded with smaller time steps of 1 ps, but at the same acquisition time per point. For both cases, we obtained the same 13.2-ps period with a precise phase matching (as shown in Fig. 3B). This rules out the effect of external periodic artifacts because the period, although the same in “real time,” must change in the “pump–probe” recording when the step duration changes; a more detailed discussion is presented in Supporting Information. Second, for the same diffraction pattern, the mode amplitude depends on the planes involved, i.e., the modulation is not the same across the entire pattern, as shown in Fig. 2. Third, the oscillations were absent when the excitation laser was blocked. Finally, to further verify the robustness of the mode across the specimen, we carried out the same measurements at another position on the graphite surface (with a thickness of 100 nm instead of 220 nm) and more than 1 mm away from the current one. We obtained the same oscillation dynamics with the identical frequency of 75.5 GHz.

It follows that the weak-intensity oscillations observed in the negative delay-time region (Fig. 2) are a result of the long-lived 75.5-GHz mode, which survives until a new excitation from a following pump pulse (in a millisecond) resets the lattice in motion. When examining the phase of oscillations, we found no correlation between the phase observed before (small amplitude) and after (large amplitude) time zero, thus excluding the possibility of a one-frequency artifact oscillation. It is worth mentioning that direct monitoring of the output of our amplified laser shows no additional pulse between the pump pulses separated by 1 ms at a sensitivity level greater than 1%.

In contrast to the long-lived mode, the 9.1-GHz mode and its higher-order harmonics (observed at 18.2, 27.3, and 36.5 GHz; Fig. 3A, Right) vanish at long delay times; the decay time is a few nanoseconds, typical of heat dissipation in solid systems. The observation that only the HOLZ planes exhibit the 9.1-GHz mode indicates that this mode is that of a wave with polarization and propagation direction along the c-axis, a direction that does not induce orientational modulation of the ZOLZ planes. This is supported further by the close resemblance of the temporal lineshape for this mode to the successive acoustic echoes created by an impulsively excited picosecond acoustic wave traveling between the two boundaries of a metal thin film along its normal (21–23).

In this picture, a traveling sound wave is created, and its frequency fulfills the relation f = v/2l, where v is the speed of sound and l is the film thickness. With the measured thickness of l = 220 nm, which we determined from electron energy-loss spectroscopy, and knowing the frequency f = 9.1 GHz from FFT plots, we obtained the sound velocity of 4.0 km/s, which is in very good agreement with the value reported for the sound velocity of longitudinal acoustic waves propagating along the c-axis in graphite [v_LA[001] = 4.14 km/s (8)]. The behavior of this traveling longitudinal wave along the [0001] direction reflects the linear response of the lattice to the impulsive excitation, and a linear chain model (24) can describe the atomic motions involved.

The lattice strain created by the excitation is within a region of the absorption length [33 nm at λ = 800 nm in graphite (25)] close to the front surface. From this point, this lattice deformation begins to propagate as a sound wave into the depth of the sample along the c-axis and undergoes multiple reflections by the front and back surfaces of the graphite plate. Because of the inhomogeneous excitation, this wave induces large surface displacement and considerable energy dissipation every time it reaches the boundaries.^† Because the laser absorption length initially makes the longitudinal spatial extension smaller than the sample thickness, the sound wave at the boundaries approaches a delta-like functional behavior, which results in several high-order harmonics in the FFT spectra.

For both types of modes, we investigated the fluence dependence of the amplitude. This dependence can be visualized directly in the Fourier maps shown in Fig. 4. Whereas the amplitude of the 9.1-GHz mode exhibits a linear dependence on the excitation fluence, the mode at 75.5 GHz shows a much different behavior. For instance, the amplitude of the HOLZ plane (2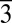 11) shows no discernable change as a function of the fluence in the range of 2.0–2.9 mJ/cm², whereas for the ZOLZ plane (03 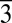0), the amplitude exhibits a definite nonlinear trend (at 2.0 mJ/cm², the mode is barely visible, whereas at 2.4 mJ/cm² and 2.9 mJ/cm², it has a well-defined amplitude).

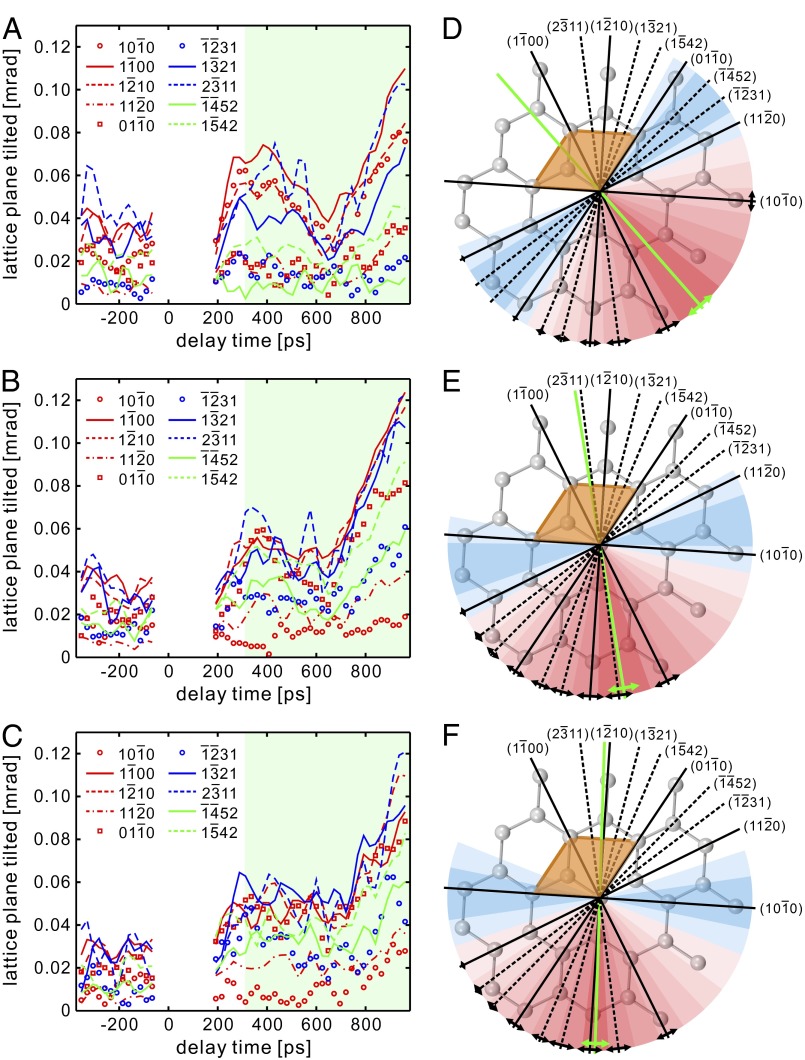
From these fluence-dependence experiments, it was possible to systematically monitor the oscillation amplitude along different directions of the Brillouin zone, represented in Fig. 5 for the excitation fluence of 2.0 mJ/cm² (Fig. 5 A and D), 2.4 mJ/cm² (Fig. 5 B and E), and 2.9 mJ/cm² (Fig. 5 C and F). The oscillation amplitude exhibits the same temporal evolution, within the time scale of 1 ns from the initial excitation, for all Kikuchi lines with a well-defined frequency of 75.5 GHz. Moreover, the maximum value remains approximately constant, within the measurement sensitivity, to 0.10 mrad for all fluences. By performing a temporal average of the amplitude profiles for each plane, we could determine the amplitude distribution along different crystallographic directions projected on the a-b plane of the graphite unit cell (Fig. 5 D–F).

Fig. 5.

Temporal evolution and plane-specific projection of amplitude. (A–C) Temporal evolutions of the amplitudes at excitation fluences of 2.0 mJ/cm², 2.4 mJ/cm², and 2.9 mJ/cm², respectively, for the 75.5-GHz mode. Light green regions mark the time interval over which the oscillation amplitude has been averaged. (D–F) The average amplitudes derived from the temporal profiles shown in A–C are plotted along different crystallographic directions in the a-b plane of the graphite lattice. The intensity of the oscillation amplitude is represented by a shade modulation from red (intense) to blue (weak), and quantitatively described by the length of the black double-way arrows. The plane perpendicular to the deduced polarization is denoted by a green solid line. The orange lozenge in each panel outlines the graphite unit cell in the a-b plane.

The direction of polarization can be obtained from the distribution of amplitudes. This is because lattice planes perpendicular to the polarization direction have strong oscillation amplitudes, whereas those lying close to the polarization direction have weak amplitudes. As evident from Fig. 5 A–C, both the ZOLZ and the HOLZ planes exhibit a synchronous temporal evolution with similar amplitudes, suggesting that the 75.5-GHz mode is a shear motion with a polarization direction preferentially lying in the a-b plane, as schematically depicted in Fig. 1C (blue colored).^‡ We note that an out-of-plane component would introduce a different temporal behavior for the ZOLZ and HOLZ planes, especially for those close to the polarization direction. We also note that as the excitation fluence increases, the 75.5-GHz mode changes its polarization direction rather than its total amplitude (Figs. 4 and 5).

The above studies of ultrafast Kikuchi diffraction, dependence on the fluence, and the polarization properties provide the following picture for lattice dynamics. The linear mode at 9.1 GHz has its origin in a longitudinal wave, and the atomic motions can be understood simply by considering a linear chain of atoms, each of which represents a plane perpendicular to the c-axis. Because the absorption length of the optical pulse is smaller than the sample thickness, a delta function-like stress excitation is created, and in this regime, the presence of higher harmonics is expected, as observed experimentally and is evident in the FFT spectra.

The nonlinear mode at 75.5 GHz is an in-plane shear deformation, as discussed above, created by lateral strain confinement (27) (see also Supporting Information). At a microscopic level, several authors (28–30) theoretically showed that elastically deformed carbon structures can support the existence of high-frequency and long-lived nonlinear localized modes in the form of breathers (31). These nonlinear modes are robust to local perturbations of the lattice and for a graphene sheet, are represented by the out-of-phase oscillation of neighboring atoms that are polarized within the a-b plane (32). Given the observed period of 13.2 ps and using the shear “speed” of ∼14.66 km/s (8), the length scale is ∼200 nm. The long lifetime of the breathers is a result of the fact that their frequency lies inside the gap of the phonon spectrum (29, 32); thus, their decay to other modes essentially is forbidden. The excitation of breathers has been reported experimentally in several systems, such as spin waves (33), optical lattices (34), and micromechanical cantilever arrays (35), and they also are expected for atomic systems because of the discreteness of the lattice structure, the presence of lattice defects, and the nonlinearity of the interaction between atoms.

In conclusion, with CB ultrafast Kikuchi diffraction, it is shown that both the longitudinal and transverse (shear) elastic dynamics of the material can be observed and separated by following changes of selective diffraction reflections. The longitudinal motion along the c-axis is the result of a linear acoustic wave propagation, whereas the transverse motion in the a-b planes is associated with a nonlinear shear deformation. From knowledge of the fluence dependence, the polarization properties, and the long lifetime, we suggest a motion involving a localized breather on a length scale of a few hundred nanometers. The reported Fourier maps at the frequency of an individual mode display the atomic planes involved in the motion, and this feature is unique to Kikuchi diffraction dynamics. It is the basis for the potential use of the approach in a wide range of applications.