Robust Spectral Analysis of Thoraco-Abdominal Motion and Oxymetry in Obstructive Sleep Apnea

Abstract

Standard PSG montage involves the use of nasal-oral airflow sensors to visualize cyclic episodes of upper airflow interruption, which are considered diagnostic of sleep apnea. Given the high-cost and discomfort associated with in-laboratory PSG, there is an emergent need for novel technology that simplifies OSA screening and diagnosis with less expensive methods. The main goal of this project was to identify novel OSA signatures based on the spectral analysis of thoraco-abdominal motion channels. Our main hypothesis was that proper spectral analysis can detect OSA cycles in adults using simultaneous recording of SaO2 and either, chest or abdominal motion. The impact of this new approach is that it may allow the design of more comfortable and reliable portable devices for screening, diagnosis and monitoring of OSA, functioning only with oximetry and airflow-independent (abdominal or chest) breathing sensors.

I. Introduction

Obstructive sleep apnea (OSA) is an important condition that affects approximately 4–5 percent of adults and is linked to life-threatening cardiovascular disorders such as stroke and myocardial infarction [1, 2]. The diagnosis of OSA relies on polysomnography (PSG), a multidimensional overnight biosignal recording that is typically conducted in sleep laboratories. Standard in-laboratory PSG montage involves the use of nasal-oral airflow sensors to visualize cyclic episodes of upper airflow interruption, which are considered diagnostic of sleep apnea [3]. Given the high-cost and discomfort associated with in-laboratory PSG, there is an emergent need for novel technology that streamline OSA screening and diagnosis with less expensive methods [4]. In this regard, simplified systems have been proposed to identify the cyclical pattern of OSA using spectral analysis of PSG biosignals [5–7]. Indeed, previous studies have reported that the low frequency component of the PSG power spectrum contains crucial information on the periodic nature of OSA events. For instance, frequency and time-frequency spectral analysis of pulse, blood pressure and heart rate variability (HRV) demonstrate oscillations in the low frequency range (i.e. 0.01 - 0.1 Hz) that correlate with the presence of OSA [5–7]. Moreover, Alvarez et al. have recently reported that the magnitude squared coherence (MSC) analysis of simultaneously recorded airflow and oxymetry signals also displays OSA-related oscillations in the low frequency band of the PSG spectrogram [8]. The latter information supports the notion that the presence of low-frequency oscillations in the spectral analysis of PSG biosignals is an important diagnostic signature of OSA that maybe used to develop simplified tools to detect this condition.

The development of simplified OSA-diagnostic tools based on spectral analysis is hampered by the sensors required to acquire airflow signals. Airflow sensors often cause facial discomfort and signal artifacts due to dislodgment of nasal-oral transducers during sleep [9], an issue that affects the feasibility of unattended home sleep studies. OSA detection relies on airflow sensors because the absence or reduction of nasal-oral airflow is considered a sign of upper airway obstruction [3]. Interestingly, although upper airway obstruction is also manifested as changes in thoracic pressures and thoraco-abdominal motion [10], these airflow-independent parameters are not used as primary indicators of OSA in standard PSG [3]. Accordingly, the main goal of this project was to identify novel OSA signatures based on the spectral analysis of thoraco-abdominal motion channels. To this end, we applied spectral signal processing to PSG data and compute the MSC between chest-abdominal respiratory signals and oxygen saturation (SaO2) to elucidate airflow-independent diagnostic features of OSA. Our main hypothesis was that MSC analysis can detect OSA cycles in adults using simultaneous recording of SaO2 and either, chest or abdominal motion. The impact of this new approach is that it may allow the design of more comfortable and reliable portable devices for screening, diagnosis and monitoring of OSA, functioning only with oximetry and airflow-independent (abdominal or chest) breathing sensors.

II. Methodology

A. Study Sample, Signal Acqusition and Polysomonography (PSG) Protocol

PSG data from 35 adult subjects with OSA (n = 15) or without OSA (n = 20) that underwent routine sleep study at Penn State Sleep Research and Treatment Center (Hershey, PA, U.S.A.) were used for signal processing and spectral analysis. Adult subjects (older than 18 years of age) of both genders were included. Table I shows demographic and PSG scoring data of the study subjects. This project was approved by the Institutional Review Board of Penn State College of Medicine.

TABLE I.

Study Sample Characteristics¹

	Total (n=35)	No OSA (n=20)	OSA (n=15)	P-value
Age: yrs (SE)	48.6 (2.1)	46.3(2.8)	51.7(3)	NS
Male gender: n(%)	21(60%)	13(65%)	8(53.3%)	NS
BMI: kg/m2 (SE)	32.4(1.3)	30.1(1.7)	35.5(2)	0.04**
Waist: cm (SE)	106.5(2.5)	102.4(2.7)	112(4.6)	NS
OAHI: (e/hr)	18(3.6)	2(0.4)	39(4.5)	< 0.01**

¹Demographic and polysomnographic profile of subjects.

Data are presented as mean ± standard error (SE).

BMI: body mass index; OAHI: obstructive apnea-hypopnea index.

Standard PSG montage was performed on all subjects according to American Academy of Sleep Medicine (AASM) guidelines [3]. During an 8–10 hr period, sleep was continuously recorded to a computerized system (Twin PSG software; Grass Technologies. Inc., West Warwick, RI). All signals were sampled at 200 Hz. PSG signals included in this study were thoracic chest and abdominal abd wall motion (respiratory inductance plethysmography), pulse oximetry SaO2 (with 2-sec averaging time) and combined nasal/oral thermistor CTC (model TCT R, Grass Technologies. Inc., West Warwick, RI). PSG was scored manually in 30-sec epochs using AASM standardized criteria. Calculation of obstructive apnea-hypopnea index (OAHI) included the sum of obstructive apneas, hypopneas, and mixed apneas divided by total sleep time and expressed as events/hour (e/h).

B. Robust Coherence Spectrum Analysis

The magnitude squared coherence (MSC) spectrum of two signals x(n), y(n) is related to the cross-correlation between the signals, i.e R_xy, and brings information about the rate at which one signal influences the other [11]. By definition, the MSC is the ratio

$${\gamma }_{xy}^2(f)=\frac{{|S_{xy}(f)|}^2}{S_x(f)S_y(f)}\le 1,$$

where |S_xy (f)|² = ℱ {R_xy} is the cross-spectrum density between x(n) and y(n), and |S_x (f)|² = ℱ {R_x} and |S_y (f)|² = ℱ {R_y} are the power spectrum density functions of x(n) and y(n) respectively. The operator ℱ {·} denotes a Discrete-Time Fourier Transform, and R_x, R_y correspond each to the autocorrelation functions of x(n) and y(n). The rationale behind the use of the MSC to study SaO2 in combination with certain body signals, such as CTC, is straightforward and stems from the direct physiological influence between airflow and oxygen saturation. Previous studies on the subject have confirmed this relationship, identifying a band of interest between 0 and 0.5 Hz [8]. However, some airflow-independent signals such as those coming from motion sensors located in chest and abdomen are also greatly influenced by breathing events (including the breathing rate), therefore those signals should also have a relationship with oxygen saturation. Such is the hypothesis being tested in this study. The calculation of the Coherence Spectrum between SaO2 and signals from airflow (CTC), chest or abdomen was performed by adapting a robust low-rank decomposition method, such as the one described in [12]. From each pair of signals, for example SaO2 and CTC, data is first divided into overlapping windows, an estimate of the MSC is computed at every windowed segment, and the result is then averaged over all windows. In order to prevent masking of low-frequency components, particularly due to spectral leakage coming from the large D.C component of SaO2, the signals were always treated as zero-mean signals. In this case, for a pair of data windows of equal length L, the zero-mean real vectors x(n), y(n) are formed by substracting their respective mean values. The cross-correlation matrix is then defined as

$${\mathbf{R}}_{\mathbf{x}\mathbf{y}}(l_1,l_2)=\left(\begin{array}{ccc}\hfill E\{x_n{y}_n\}\hfill & \hfill \cdots \hfill & \hfill E\{x_n{y}_{n-L+1}\}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill E\{x_{n-L+1}{y}_n\}\hfill & \hfill \cdots \hfill & \hfill E\{x_n{y}_n\}\hfill \end{array}\right)$$

where E{x_n−l1 y_n−l2} is the expectation between the value of signal x at time n − l₁ and the signal y at time n − l₂, with l₁, l₂ ∈ [0, L − 1]. Assuming ergodicity, an estimate of R_xy may be obtained with time averages of each matrix entry. In similar fashion, the auto-correlation matrices R_x, R_y may be defined and estimated. The coherence matrix Γ_xy is then defined as

$${\mathbf{\Gamma }}_{\mathbf{x}\mathbf{y}}={\mathbf{R}}_{\mathbf{x}}^{-\mathbf{1}/\mathbf{2}}{\mathbf{R}}_{\mathbf{x}\mathbf{y}}{\mathbf{R}}_{\mathbf{y}}^{-\mathbf{1}/\mathbf{2}}.$$ (1)

A numerical estimate of the MSC function, i.e ${\gamma }_{xy}^2(f)$, is achieved by first defining the Discrete Fourier Transform vector $\mathbf{F}(f)={[1\dots e^{-j2\pi f(L-1)}]}^H·\frac{1}{\sqrt{L}},f\in [0,0.5]$, and then computing

$${\gamma }_{xy}^2(f)={|\mathbf{F}{(f)}^H{\mathbf{\Gamma }}_{\mathbf{x}\mathbf{y}}\mathbf{F}(f)|}^2.$$ (2)

By SVD theory, the matrix Γ_xy may be decomposed as the product Γ_xy = UΛV^T, where the matrices U, V are unitary, and Λ is a diagonal matrix with all the singular values of Γ_xy. A more robust, low-rank estimate is then achieved by selecting the subspace associated with the largest coherence components, which spans those components with highest correlation and is less affected by estimation errors, for example errors due to finite sample effects, measurement noise, etc. More interestingly, by using a subspace spanned by large coherence components in airflow-independent signals the aim is also to avoid artifacts coming from non-breathing events, such as those commonly caused by body motion. For this low-rank decomposition only the k < L largest singular values and their corresponding columns in the matrices U, V are kept in the modified matrices Û, Λ̂, V̂. Defining

$${\mathbf{\Gamma ̂}}_{\mathbf{x}\mathbf{y}}=\mathbf{Û}\mathbf{\Lambda ̂}{\mathbf{V̂}}^{\mathbf{T}},$$ (3)

the robust MSC estimate of a pair of data windows is then

$${\mathrm{\gamma ̂}}_{xy}^2(f)={|\mathbf{F}{(f)}^H{\mathbf{\Gamma ̂}}_{\mathbf{x}\mathbf{y}}\mathbf{F}(f)|}^2.$$ (4)

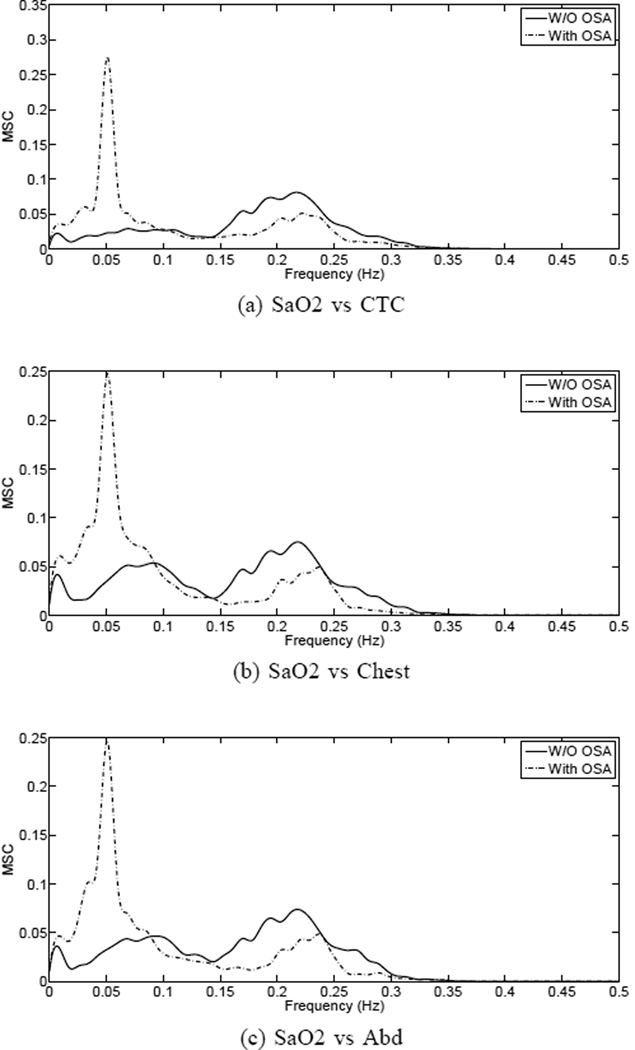
In the study, a window length L = 120, Bartlett windowing with 50 percent overlap and a low-rank decomposition with k = 2 were selected. In order to achieve the best possible resolution in the frequency band from 0 to 0.5 Hz, the signals were sharply filtered and downsampled to 1 Hz. Also, in a previous step, a zero-order interpolation was used to filter the SaO2 signal from any artifacts coming from loose sensors during acquisition. Frequency samples of γ̂²(f_j) were estimated at equally spaced points $f_j=\frac{j}{L},j=0,1,\dots ,\frac{L}{2}$. The results are shown in Fig. 1(a)–(c). By looking at the average MSC functions of SaO2 vs chest and abdomen, it is apparent a peak in the higher frequencies (0.1–0.5 Hz), suggesting a relationship between airflow-independent signals and oxygen saturation. The same peak appears in the MSC of SaO2 vs CTC, which corresponds to the normal breathing cycle. Also in Fig. 1, since results are discriminated by subjects with and without OSA, it is readily apparent a spectral difference in the lower frequency band, approximately between 0.01 and 0.10 Hz, with increased energy in the OSA cases. For comparison purposes, the same MSC plots are included for SaO2 vs airflow (Fig. 1(a)).

Fig. 1.

Robust MSC estimates of oxygen saturation vs airflow(a) and airflow-independent signals(b),(c). Results are discriminated in groups of patients with and without OSA.

C. Statistical Analysis

Data were analyzed using the software SAS version 9.2 or later (SAS Institute Inc., Cary, NC). For pair-wise relationships, two-sample t-test or non-parametric testing was used to compare the value of continuous outcomes and chi-square test was used to compare the proportion of positive signals for binary outcomes. Multivariate regression contrasted the peak amplitude (PA) in the power spectrum at the low-frequency (LF) band (0.01-0.1 Hz) from different MSC models (i.e. SaO2 vs. CTC, chest or abd) in subjects with and without OSA while adjusting for demographic and anthropometric variables. Pearson correlation coefficient (r) was used to evaluate the linear relationships between airflow (CTC) and airflow-independent (chest or abd) signals after MSC analysis. OSA parameters from spectral analysis (i.e. PA at LF band) were also correlated (r) with standard PSG scoring (i.e. OAHI). Significance level was taken at p < 0.05.

III. Results and Discussion

To test the hypothesis that the low-frequency component (0.01-0.1 Hz) of the spectral coherence PSG analysis contains OSA diagnostic features, we first used data obtained from airflow signals (CTC) and simultaneous oxymetry (SaO2) recording. As illustrated in Fig. 1(a) there were two distinctive PA identified by MSC analysis of CTC-SaO2 signals, one at low-frequency (LF-PA= 0.01-0.1 Hz) and another at high-frequency (HF-PA= 0.15-0.3 Hz). Given that normal sleep respiratory cycles are approximately 10–20 breaths per min, we concluded that the HF-PA corresponded to normal respiratory oscillations, which were not significantly different in subjects with or without OSA (Fig. 1(a)). In contrast, the LF-PA was significantly higher in subjects with OSA indicating that the LF-PA contained information on the periodic nature of OSA cycles (Fig. 1(a)). These findings are in general agreement with prior studies using cardiovascular PSG signals (i.e. HRV in ECG), blood pressure and airflow channels to detect OSA [5–7].

Given that airflow sensors are poorly tolerated due to its nasal-oral placement [9], we next investigated whether the OSA-related LF-PA was also detectable using MCS analysis derived from airflow-independent respiratory PSG channels (chest and abd motion) and simultaneous SaO2 recording. Figs. 1(b),(c) illustrate that LF-PA is a distinctive trait of subjects with OSA seen in airflow-independent channels, which is independent of body mass index (BMI), abdominal circumference, age and gender (Table. II). Collectively, these findings demonstrate that the spectral analysis of thoraco-abdominal motion and oxymetry identifies OSA diagnostic signatures that are independent of airflow.

TABLE II.

Multivariate Analysis of Spectral Features and Clinical Variables¹

	LF-PA Chest	P-value	LF-PA Abd	P-value
OSA	0.079 (0.02)	<0.01**	0.093 (0.03)	<0.01**
Age(yrs)		0.682		0.443
Gender		0.978		0.865
BMI(kg/m2)		0.565		0.777
Waist(cm)		0.121		0.407

¹Regression coefficients ± standard error (SE) of chest and abdominal spectral features discriminated by OSA status and adjusted by covariates.

LF-PA: low-frequency band peak amplitude in magnitude squared coherence analysis with SaO2.

OSA is caused by upper airway obstruction, which in turn alters nasal-oral airflow and thoraco-abdominal pressure and motion [10]. Standard PSG analysis relies on airflow abnormalities for OSA detection. We postulate that the airflow abnormalities caused by OSA have correspondent changes in thoraco-abdominal motion that can be detected by spectral PSG analysis. To address this hypothesis, we examined the linear correlation between the LF-PA values obtained in MCS analysis derived from chest-SaO2 or abd-SaO2 (airflow-independent signals) with LF-PA values obtained by airflow spectral parameters (CTC-SaO2) or standard PSG visual OSA severity scoring (OAHI= events/hr). Table III illustrates significant linear relationships between LF-PA values obtained by chest-SaO2 and either, LF-PA from CTC-SaO2 signals (r = 0.83, p < 0.01) or OAHI from PSG visual severity scoring (r = 0.73, p < 0.01). Similar linear relationships were seen in correlations between abd-SaO2 and airflow or visual scoring data (Table III).

TABLE III.

Correlation of Chest and Abdominal Motion With Airflow Parameters and OSA Severity Index¹

	r-value	p-value
Chest and Abdominal Motion with Airflow
MSC Chest-SaO2 vs. MSC CTC-SaO2	0.83	<0.01**
MSC Abd-SaO2 vs. MSC CTC-SaO2	0.79	<0.01**
Chest and Abdominal Motion with OAHI
MSC Chest-SaO2 vs. OAHI	0.73	<0.01**
MSC Abd-SaO2 vs. OAHI	0.67	<0.01**

¹Linear correlations of magnitude squared coherence (MSC) parameters.

CTC: Airflow signal; OAHI: obstructive apnea-hypopnea index; r-value: Pearson correlation coefficient.

IV. Conclusions and Future Directions

The most important finding of this study was that the use of robust magnitude squared coherence (MSC) analysis of thoraco-abdominal signals and oxymetry successfully identified a sleep-apnea spectral signature. The main feature consists on a sharp Low-Frequency Peak of Amplitude (LF-PA), indicative of OSA cycles. Moreover, this spectral parameter identified by MSC analysis of thoraco-abdominal signals correlated with airflow parameters (CTC-SaO2 analysis) and OSA severity (OAHI) in standard PSG visual scoring. This spectral OSA feature is airflow independent, which is important for the design of novel devices to detect OSA, given that nasal-oral airflow sensors are often uncomfortable and prone to signal artifacts. Conversely, thoraco-abdominal motion sensors are usually well-tolerated and are part of standard cardio-respiratory monitoring in ambulatory and in-hospital settings. Further research should aim to implement the present findings in the design of simplified tools for screening, diagnosis and monitoring of OSA, based only on oximetry and abdominal or chest motion sensors.