BAYESIAN WAVELET-BASED CURVE CLASSIFICATION VIA DISCRIMINANT ANALYSIS WITH MARKOV RANDOM TREE PRIORS

Abstract

Discriminant analysis is an effective tool for the classification of experimental units into groups. When the number of variables is much larger than the number of observations it is necessary to include a dimension reduction procedure into the inferential process. Here we present a typical example from chemometrics that deals with the classification of different types of food into species via near infrared spectroscopy. We take a nonparametric approach by modeling the functional predictors via wavelet transforms and then apply discriminant analysis in the wavelet domain. We consider a Bayesian conjugate normal discriminant model, either linear or quadratic, that avoids independence assumptions among the wavelet coefficients. We introduce latent binary indicators for the selection of the discriminatory wavelet coefficients and propose prior formulations that use Markov random tree (MRT) priors to map scale-location connections among wavelets coefficients. We conduct posterior inference via MCMC methods, we show performances on our case study on food authenticity and compare results to several other procedures..

1. Introduction

Discriminant analysis, sometimes called supervised pattern recognition, is a statistical technique used to classify observations into groups. For each case in a given training set a p×1 vector of observations, x_i, and a known assignment to one of G possible groups are available. Let the group indicators be stored in a n × 1 vector y. On the basis of the X and y data we wish to derive a classification rule that assigns future cases to their correct groups. When the distribution of X, conditional on the group membership, is assumed to be a multivariate normal then this statistical methodology is know as discriminant analysis. Here we focus in particular on situations in which the number of observed variables is considerably large, often larger than the number of samples. We present a typical example from chemometrics that deals with the classification of different types of food into species via near infrared spectral data, i.e., curve predictors.

Different approaches can cope with the high dimensionality of a data matrix. One approach is to reduce the dimensionality of the data by using a dimension reduction technique, for example principal component analysis, and then using only the first k components to classify units into groups via linear or quadratic discriminant analysis, see for example Jolliffe (1986). Another approach is to first select a subset of the variables, essentially removing noisy ones, and then perform discriminant analysis using only the selected variables. This, for example, is the approach taken by Fearn, Brown and Besbeas (2002) who developed a Bayesian decision theory approach to linear discriminant analysis that balances costs of variables against a loss due to classification errors. Also, more recently, Murphy, Dean and Raftery (2010) proposed a frequentist model-based approach to discriminant analysis in which variable selection is achieved by imposing constraints on the form of the covariance matrices. These authors use a specifically designed search algorithm that compares models using BIC approximations of log Bayes factors.

In this paper we take a dimension reduction approach and model the functional predictors in a nonparametric way by means of wavelet series representations. Wavelets can accurately describe local features of curves in a parsimonious way i.e., via a small number of coefficients. Because of this compression ability, selecting the important wavelet coefficients, rather than original variables, may be expected to lead to improved classification performances. We therefore apply wavelet transforms, reducing curves to wavelet coefficients, and then perform discriminant analysis in the wavelet domain while simultaneously employing a selection scheme of the relevant wavelet coefficients. We consider a Bayesian conjugate normal discriminant model, either linear or quadratic, and introduce latent binary indicators for the selection of the discriminatory coefficients. Unlike current literature on wavelet-based modeling, where models are fit one wavelet coefficient at a time, our model formulation avoids independence assumptions among the wavelet coefficients. We go one step further and, additionally, propose a prior model formulation that includes Markov random tree (MRT) priors to map scale-location connections among wavelet coefficients. We achieve dimension reduction by building a stochastic search variable selection procedure for posterior inference. We investigate performances of the proposed method on our case study on food authenticity and compare results to several other procedures.

Our approach to selection builds upon the extensive literature on Bayesian methods for variable selection. For example, we introduce a latent binary vector γ for the identification of the discriminating variables (wavelet coefficients) and use stochastic search MCMC techniques to explore the space of variable subsets. This is also the approach taken by George and McCulloch (1993,1997), among many others, for linear regression models, and by Brown, Fearn and Vannucci (2001), in a wavelet approach to curve regression. However, unlike linear settings, where γ is used to induce mixture priors on the regression coefficients of the model, in mixture models, like the one we work with, the elements of the matrix X are viewed as random variables and γ is used to index the contribution of the different variables to the likelihood term of the model, Tadesse, Sha and Vannucci (2005). The method for variable selection we adopt here can be used either for linear discriminant analysis, where all groups share the same covariance matrix, or for quadratic discriminant analysis, where different groups are allowed to have different covariance matrices. We illustrate the model for the quadratic discriminant analysis case and report the modification needed to perform linear discriminant analysis in the Appendix.

The rest of the paper is organized as follows: we complete this introductory Section by providing a brief review of wavelet series representations and wavelet transforms. We also introduce the concept of zero-tree wavelet structures that map wavelet coefficients with the same spatial locations but at different resolution scales. In Section 2 we describe how to perform discriminant analysis under the Bayesian paradigm and how to re-parameterize the model in the wavelet domain. We also discuss likelihood and prior distributions that allow us to implement a variable selection mechanism in the wavelet domain. We then describe how to incorporate into the prior model information about the connections among wavelet coefficients at same spatial locations. We present the MCMC algorithm for posterior inference in Section 3, where we also address the case of having samples with missing labels. Finally, in Section 4, we apply our method to the NIR spectral data for food classification and compare results to several other competing procedures.

1.1 Wavelet Representations of Curves

The basic idea behind wavelets is to represent a general function in terms of simpler functions (building blocks), defined as scaled and translated versions of an oscillatory function, describing local features in a parsimonious way. The existence of fast and efficient transformations to calculate coefficients of wavelet expansions have made wavelets a simple tool that can be used for a great variety of possible applications. Indeed, wavelets have been extremely successful in a variety of fields, for example in the compression or denoising of signals and images, see for example Antoniadis, Bigot and Sapatinas (2001) and Gonzalez and Woods (2002) and references therein.

In L²(IR), for example, an orthonormal wavelet basis is obtained as translations and dilations of a “mother” wavelet ψ as ψ_j,k(x) = 2^j/2ψ(2jx – k) with j, k integers. A function f is then represented by a wavelet series as

$$f\left(x\right)=\sum _{j,k\in \mathbb{Z}}{d}_{j,k}{\psi }_{j,k}\left(x\right),$$ (1.1)

with wavelet coefficients $d_{j,k}=\int f\left(x\right){\psi }_{j,k}\left(x\right)dx$ describing features of the function f at spatial locations indexed by k and scales indexed by j. Because of their localization properties, i.e. fast decay in both the time and the frequency domains, wavelets have the ability to represent many classes of functions in a sparse form by describing important features with a relatively small number of coefficients.

Wavelets have been extremely successful as a tool for the analysis and synthesis of discrete data. Let x = (x₁, . . . , x_p)^T be a sample of the function f(·) at equally spaced points and let p be a power of 2, i.e. p = 2^J. This vector of observations can be viewed as an approximation of f at scale J. A fast algorithm exists, known as the Discrete Wavelet Transform (DWT), that permits decomposition of x into a set of wavelet coefficients, Mallat (1989). This algorithm operates in practice by means of linear recursive filters, however, for illustration purposes, it is useful to write the DWT in matrix form as

$$\mathbf{z}=Wx,$$ (1.2)

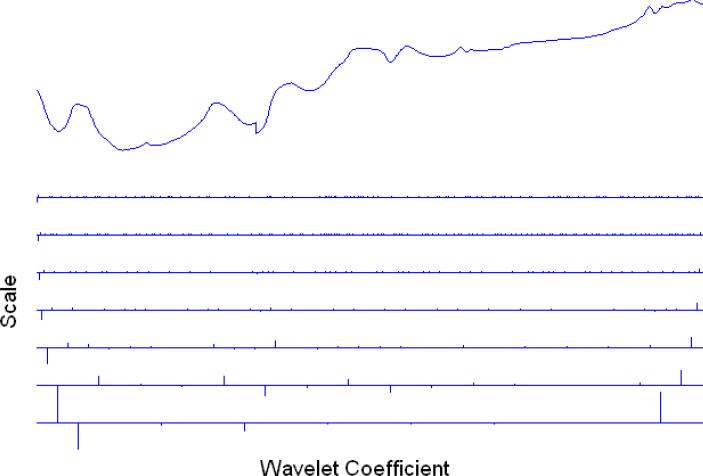
with W an orthogonal matrix corresponding to the discrete wavelet transform and z a vector of wavelet coefficients describing features of the function at scales from the fine J–1 to a coarser one, say J–r. As an example, Figure 1.1 illustrates the wavelet decomposition of one of the near infrared curves analyzed in Section 4. The NIR curve is shown at the top of the figure and the wavelet coefficients at the individual scales are depicted below, from coarsest to finest. An algorithm for the inverse construction, the Inverse Wavelet Transform (IWT), also exists.

Figure 1.1.

Discrete wavelet transform of one of the NIR curves analyzed in Section 4. The NIR curve is shown at the top of the figure and the wavelet coefficients at the individual scales are depicted below, from finest to coarsest.

In this paper we use Daubechies wavelets which have compact support and maximum number of vanishing moments for any given smoothness. Daubechies wavelets are extensively used in statistical applications. A detailed description of the construction of these wavelets, together with a general exposition of the wavelet theory, can be found in Daubechies (1992). Some of the early applications of wavelets in statistics are described in Vidakovic (1999).

1.2 The Zero-tree Wavelet Structure

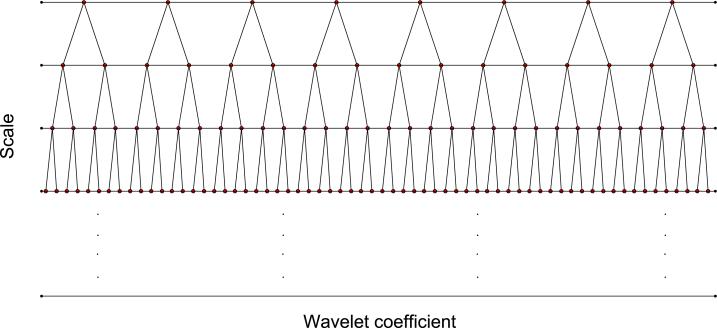
Because of the recursive nature of the DWT, the resulting wavelet coefficients tend to share certain properties. This is true, in particular, for coefficients that map to the same spatial locations but at different scales. When a decimation is performed at every iterative step of the DWT, the transform naturally leads to a tree structure in which each coefficient at a given scale serves as “parent” for up to two “children” nodes at the finer scale. The wavelet coefficients of the coarsest scale compose the “root node” and those at the finest scale the “leaf nodes”. Figure 1.2 provides a schematic representation of the wavelet tree structure.

Figure 1.2.

Schematic representation of the wavelet tree structure, where each coefficient serves as “parent” for up to two “children” nodes.

In general, for most signals and images, if a coefficient at a particular scale is negligible (or large) then its children will likely tend to be negligible (or large) as well. This simple intuition has led to the construction of “zero-tree” structures for signal and image compression, where coefficients belonging to sub-trees are all considered negligible, see Shapiro (1993). Many commercial software packages for image coding and compression routinely incorporate zero-tree structures in their algorithms, like for example JPEG2000. In statistical modeling, He and Carin (2009) have used zero-tree structures in a Bayesian approach to compressive sensing for signals and images that are sparse in the wavelet domain.

2. Wavelet-based Bayesian Discriminant Analysis

We start by first describing the model for discriminant analysis. We assume that each observation comes from one of the G possible groups, each with distribution N(μ_g, Σ_g). We represent the data from each group by the n_g × p matrix

$${\mathbf{X}}_g-1_{n_g}{\mu }_g^T\sim \mathcal{N}(\mathbf{I},{\Sigma }_g),$$ (2.1)

with g = 1, . . . , G and where the vector μ_g and the matrix Σ_g are the mean and the covariance matrix of the g-th group, respectively. Here the notation $\mathbf{V}-\mathbf{M}\sim \mathcal{N}(\mathbf{A},\mathbf{B})$ indicates a matrix normal variate V with matrix mean M and with variance matrices b_iiA for its generic i-th column and a_jjB for its generic j-th row. This notation was proposed by Dawid (1981) and has the advantage of preserving the matrix structure instead of reshaping V as a vector. It also makes for much easier formal Bayesian manipulation and has become quite standard in the Bayesian literature.

Model (2.1) is completed by imposing a conjugate multivariate normal distribution on μ_g and an Inverse-Wishart prior on the covariance matrix Σ_g, that is

$$\begin{array}{c}\hfill {\mu }_g\sim N({\mathbf{m}}_g,h_g{\Sigma }_g)\hfill \\ \hfill {\Sigma }_g\sim IW({\delta }_g,{\Omega }_g),\hfill \end{array}$$ (2.2)

where Ω_g is a scale matrix and δ_g a shape parameter.

In discriminant analysis the predictive distribution of a new observation x^f (1 × p) is used to classify the new sample into one of the G possible groups. This distribution is a multivariate T-student, see Brown (1993) among others,

$${\mathbf{x}}^f-{\tilde{\mu }}_g\sim \mathcal{T}({\delta }_g^{\ast },a_g,{\Omega }_g^{\ast }),$$ (2.3)

where ${\tilde{\mu }}_g={\pi }_g{\mathbf{m}}_g+(1-{\pi }_g){\stackrel{‒}{\mathbf{x}}}_g$, ${\delta }_g^{\ast }={\delta }_g+n_g$, a_g = 1 + (1/h_g + n_g)^– and ${\Omega }_g^{\ast }={\Omega }_g+{\mathbf{S}}_g+{(h_g+1∕n_g)}^{-1}{({\stackrel{‒}{\mathbf{x}}}_g-{\mathbf{m}}_g)}^T({\stackrel{‒}{\mathbf{x}}}_g-{\mathbf{m}}_g)$ with π_g = (1 + h_gn_g)^–1 and ${\mathbf{S}}_g={({\mathbf{X}}_g-1n_g{\stackrel{‒}{\mathbf{x}}}_g^T)}^T({\mathbf{X}}_g-1_{n_g}{\stackrel{‒}{\mathbf{x}}}_g^T)$. The probability that a future observation, given the observed data, belongs to the group g is then given by

$${\pi }_g(y^f\mid \mathbf{X})=p(y^f=g\mid {\mathbf{x}}^f,\mathbf{X}),$$

where y^f is the group indicator of the new observation. By estimating the probability that one observation comes from group g as ${\widehat{\pi }}_g=n_g∕n$ the previous distribution can be written in closed form as

$${\pi }_g(y^f\mid \mathbf{X})=\frac{p_g\left({\mathbf{x}}^f\right){\widehat{\pi }}_g}{\sum _{i=1}^G{p}_i\left({\mathbf{x}}^f\right){\widehat{\pi }}_i},$$ (2.4)

where p_g(x^f) indicates the predictive distribution defined in equation (2.3). The underling assumption of exchangeability of the training data with the future data is required, i.e. we assume that observations from training and validation set arise in the same proportions from the groups, see also Fearn, Brown and Besbeas (2002). A new observation is then assigned to the group with the highest posterior probability.

2.1 Model in the Wavelet Domain

We approach dimension reduction by transforming curves into wavelet coefficients. Because of the compression ability of wavelets, selecting the important wavelet coefficients, rather than original variables, is expected to lead to improved classification performances. Our wavelet-based approach incorporates both selection and synthesis of the data.

We next show how to apply wavelet transforms to the data. We have n curves and want to apply the same wavelet transform to them all. In matrix form, a DWT can be applied to multiple curves as Z_g = X_gW^T, with W the orthogonal matrix representing the discrete wavelet transform, see Brown, Fearn and Vannucci (2001). We therefore rewrite model (2.1) as

$${\mathbf{Z}}_g-1_{n_g}{\tilde{\mu }}_g^T\sim \mathcal{N}(\mathbf{I},{\tilde{\Sigma }}_g),$$

where ${\tilde{\Sigma }}_g=\mathbf{W}{\Sigma }_g{\mathbf{W}}^T$ and ${\tilde{\mu }}_g^T={\mu }_g^T{\mathbf{W}}^T$. The prior model on ${\tilde{\Sigma }}_g$ transforms into

$${\tilde{\Sigma }}_g\sim IW({\delta }_g,{\tilde{\Omega }}_g)$$

with $\tilde{\Omega }=\mathbf{W}{\Omega }_g{\mathbf{W}}^T$. Vannucci and Corradi (1999) have derived an algorithm to compute variance and covariance matrices like ${\tilde{\Sigma }}_g$ and ${\tilde{\Omega }}_g$ that makes use of the recursive filters of the DWT and avoids multiplications by the matrix W. In the sequel we drop the tilde notation and simply refer to Σ_g, Ω_g and μ_g.

It is worth noticing that our model formulation avoids any independence assumption among the wavelet coefficients of a given curve. Such assumptions are often made in the current literature on wavelet-based Bayesian modeling, as a convenient working model that allows to fit models one wavelet coefficient at a time, and heuristically justified by the whitening properties of the wavelet transforms, see for example Morris and Carroll (2006) and Ray and Mallick (2006).

2.2 A Prior Model for Variable Selection

In the wavelet domain we now achieve dimension reduction by selecting the discriminating wavelet coefficients. We do this by extending to the discriminant analysis framework an approach to variable selection proposed by Tadesse, Sha and Vannucci (2005) for model-based clustering. As done by these authors, we introduce a (p × 1) latent binary vector γ to index the selected variables, i.e. wavelet coefficients, meaning that γ_j = 1 if the jth wavelet coefficient contributes to the classification of the n units into the corresponding groups, and γ_j = 0 otherwise. We then use the latent vector γ to index the contribution of the different wavelet coefficients to the likelihood term of the model. Unlike Tadesse, Sha and Vannucci (2005) we avoid independence assumptions among the variables by defining a likelihood that allows separation of the discriminating coefficients from the noisy ones as follows:

$$L(\mathbf{Z},\mathbf{y};\cdot )=\prod _{i=1}^{n}p({\mathbf{z}}_{i\left({\gamma }^c\right)}\mid {\mathbf{z}}_{i\left(\gamma \right)})\prod _{g=1}^G{w}_g^{n_g}\prod _{i=1}^{n_g}{p}_g\left({\mathbf{z}}_{i\left(\gamma \right)}\right),$$ (2.5)

where w_g is the prior probability that unit i belongs to group g, z_i(γ^c) is the |γ^c| × 1 vector of the non selected wavelet coefficients and z_i(γc) is the |γ| × 1 vector of the selected ones, for the i-th subject. The first factor of the likelihood refers to the non important variables, while the second is formed by variables able to classify observations into the correct groups. Under the assumption of normality of the data the likelihood becomes:

$$\prod _{i=1}^n{N}_{\mid {\gamma }^c\mid }({\mathbf{z}}_{i\left({\gamma }^c\right)}-{Bz}_{i\left(\gamma \right)};{\mu }_{0\left({\gamma }^c\right)},{\Sigma }_{0\left({\gamma }^c\right)})\prod _{g=1}^G{w}_g^{n_g}\prod _{i=1}^{n_g}{N}_{\mid \gamma \mid }({\mathbf{z}}_{i\left(\gamma \right)};{\mu }_{g\left(\gamma \right)},{\Sigma }_{g\left(\gamma \right)})$$ (2.6)

where B is a matrix of regression coefficients resulting from the linearity assumption on the expected value of the conditional distribution p(z_i(γ^c)|z_i(γ)), and where μ_0(γ^c) and Σ_0(γ^c) are the mean and covariance matrix, respectively, of z_i(γ^c) – Bz_i(γ). Note that all parameters of the distribution of the non discriminatory variables are assumed independent of the cluster indicators and that the (conditional) distribution of the non discriminatory variables z_i(γ^c) is therefore not a mixture-type. This assumption also implies that the covariance between z_i(γ) and z_i(γ^c) is not group dependent. These choices reflect our intention of having a likelihood that factorizes into two parts, the first one with group specific parameters and the second one with parameters that are common to all the non discriminatory variables. Murphy, Dean and Raftery (2010) use a similar likelihood formulation in a frequentist approach to variable selection in discriminant analysis.

For the parameters corresponding to the non-selected wavelet coefficients we again choose conjugate priors:

$$\begin{array}{cc}\hfill {\mu }_{0\left({\gamma }^c\right)}\mid {\Sigma }_{0\left({\gamma }^c\right)}\sim & N({\mathbf{m}}_{0\left({\gamma }^c\right)},h_0{\Sigma }_{0\left({\gamma }^c\right)}\hfill \\ \hfill \mathbf{B}-{\mathbf{B}}_0\mid {\Sigma }_{0\left({\gamma }^c\right)}\sim & \mathcal{N}({\mathbf{H}}_{\gamma },{\Sigma }_{0\left({\gamma }^c\right)})\hfill \\ \hfill {\Sigma }_{0\left({\gamma }^c\right)}\sim & IW({\delta }_c,{\Omega }_{0\left({\gamma }^c\right)}).\hfill \end{array}$$ (2.7)

This parametrization, besides being the standard setting in the Bayesian approach, allows us to create a computationally efficient variable selection algorithm, as shown in Section 3 below. We also assume Ω_0(γ^c) = k₀I_|γ^c|, a specification implying shrinkage towards the case of no correlation between non-selected variables, which is also adopted by Tadesse, Sha and Vannucci (2005), in model-based clustering, and Dobra, Jones, Hans, Nevins and West (2004) for graphical model settings.

We complete the prior model by specifying an improper non-informative prior on the vector w = (w₁, . . . , w_G) using a Dirichlet distribution, w ~ Dirichlet(0, . . . , 0). With this prior, marginalizing over w in the predictive distribution π_g(y^f|Z), with the integration done over the posterior distribution w ~ Dirichlet(n₁, . . . , n_G), is equivalent to estimating ${\widehat{\pi }}_g=n_g∕n$, as we have done in (2.4). Note that, with the inclusion of the variable selection mechanism, the predictive distribution does not change because it depends only on the selected variables. We discuss prior models for γ in the Section below.

2.3 Markov Random Tree Priors for Zero-tree Structures

Although our model allows for dependencies among variables through the choice of the priors (2.2) and (2.7), it is not straightforward to specify dependence structures known a priori on the prior covariance matrices. We take a different approach and show how available information can be incorporated into the model via the prior distribution on γ.

In defining our prior construction we follow the original idea of Shapiro (1993) and use a zero-tree structure to specify a dependence network among wavelet coefficients. In this network, given the wavelet decomposition of a signal, an individual wavelet coefficient at a given scale is directly “linked” to the two coefficients at the next finer scale that correspond to the same spatial location. We encode this network structure into our model via a Markov random tree (MRT) prior on γ. This is a type of Markov random field (MRF), i.e., a graphical model in which the distribution of a set of random variables follows Markov properties that can be described by an undirected graph. In a MRF variables are represented by nodes and relations between them by edges. In our context, the nodes are the wavelet coefficients and the edges represent the relations encoded in the zero-tree structure.

We adopt the parametrization suggested by Li and Zhang (2010) for the global MRF distribution for γ,

$$p(\gamma \mid \mathbf{d},\mathbf{E})\propto \exp ({\mathbf{d}}^T\gamma +{\gamma }^T\mathbf{E}\gamma ),$$ (2.8)

where d = d1_p, with 1_p the unit vector of dimension p, and where E is a matrix with elements {e_ij} usually set to a constant e for the connected nodes and to 0 for the non connected ones. Note that the connections among wavelet coefficients on the MRT prior are a characteristic of the data by definition of the wavelet transform. This feature implies that there is no uncertainty on the links of the MRT.

The parameter d in (2.8) represents the expected prior number of significant wavelet coefficients and controls the sparsity of the model, while e affects the probability of selecting a variable according to its neighbor values. This is more evident by noting that the conditional probability

$$P({\gamma }_j\mid d,e,{\gamma }_k,k\in N_j)=\frac{\exp \left({\gamma }_j(d+e{\sum }_{k\in N_j}{\gamma }_k)\right)}{1+\exp (d+e{\sum }_{k\in N_j}{\gamma }_k)},$$ (2.9)

with N_j the set of direct neighbors of variable j in the MRF, increases as a function of the number of selected neighbors. Note that if a variable does not have any neighbor, then its prior distribution reduces to an independent Bernoulli with parameter p = exp(d)/[1 + exp(d)], which is a logistic transformation of d.

Although the parametrization above is somewhat arbitrary, some care is needed in deciding whether to put a prior distribution on e. First, allowing e to vary can lead to the phase transition phenomenon, that is, the expected number of variables equal to 1 can increase massively for small increments of e. This problem can happen because equation (2.9) can only increase as a function of the number of z_j's equal to 1. A clear description of the phase transition phenomenon is given by Li and Zhang (2010). In brief, Ising models undergo transitions between an ordered and a disordered underlying state, i.e. from a model with most of the variables equal to 1 to a model with most of the variables equal to 0, at or near the phase transition boundary, which depends on the parameter specifications. Phase transition leads to various dramatic consequences, such as the loss of model sparsity and consequently a critical slow down of the MCMC. In Bayesian variable selection with large p, the phase transition phenomenon leads to a drastic change in the proportion of included variables, for example, from < 5% to > 90%, near the phase transition boundary.

The most effective way to obtain an empirical estimate of the phase transition value is to sample from (2.8) using the algorithm proposed by Propp and Wilson (1996) and obtain an estimate of the expected model size for different values of d, over a range of values for e. The value of e for which the expected model size shows a dramatic increase can be considered a good estimate of the phase transition point. However, even if an estimate of the phase transition value is obtained, inference on the parameters d and e would require special techniques in order to handle non tractable priors of type (2.8), which are known only up to its normalizing constant, and would substantially increase the computational complexity of our model. In this paper we have therefore opted for fixing the parameters d and e. Similar choices have been made by Li and Zhang (2010). We provide some guidelines for choosing these parameters in the application section, where we also perform a sensitivity analysis.

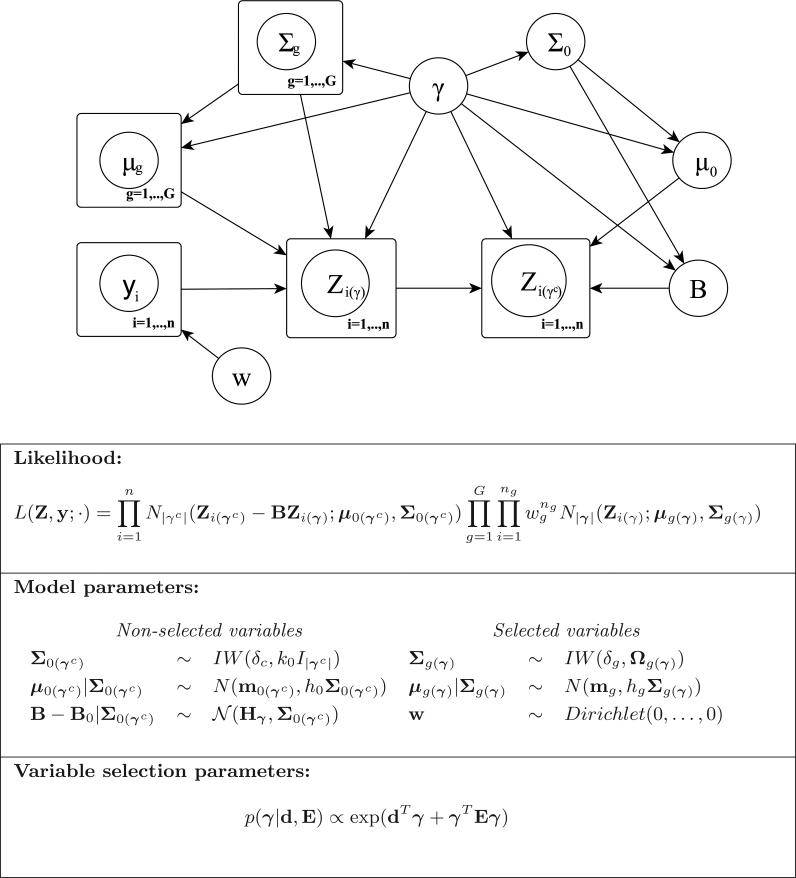
Figure 2.3 provides a graphical representation of our proposed model, illustrating the probabilistic dependencies among the observed variables and the model parameters. The different layers of the proposed hierarchical model are also summarized.

Figure 2.3.

Graphical model representation and hierarchical formulation of the proposed probabilistic model.

3. MCMC for Posterior Inference

We perform posterior inference by concentrating on the posterior distribution on γ, which allows us to achieve variable selection. This distribution cannot be obtained in closed form and an MCMC is required. We illustrate here the procedure for the quadratic discriminant analysis case and report the modification needed to perform linear discriminant analysis in the Appendix.

The inferential procedure can be greatly simplified by integrating out the parameters w_g, B, Σ₀, μ₀, μ_g and Σ_g. In the MCMC procedure we describe below a single variable is added and/or removed at every iteration. Therefore, without loss of generality, one can simplify the prior parametrization by assuming that the set of non-selected variables is formed by only one variable, so that the matrix Σ_0(γ^c) reduces to a scalar σ² and the |γ^c| × |γ| matrix B to a |γ| × 1 vector β, that is to the row of B corresponding to the regression coefficients between the selected variables and the variable prosed to be added or removed. Our priors therefore reduce to σ² ~ Inv-Gamma(δ_c/2, k₀/2) and β ~ N(β₀, σ²H_γ). Integrating out the parameters w_g, β, σ², μ₀, μ_g and Σ_g leads to the following marginal likelihood:

$$\begin{array}{cc}\hfill p(\mathbf{Z}\mid \mathbf{y},\gamma )\propto & {(k_0+\left({\mathbf{z}}_{{\gamma }^c}\right)-1_{p_{\gamma }}{m}_{0\left({\gamma }^c\right)}-{\mathbf{Z}}_{\left(\gamma \right)}{\beta }_0)}^T\hfill \\ \hfill & {({\mathbf{I}}_n+h_0{1}_n{1}_n^T+{\mathbf{Z}}_{\left(\gamma \right)}{\mathbf{H}}_{\gamma }{\mathbf{Z}}_{\left(\gamma \right)}^T)}^{-1}\hfill \\ \hfill & {({\mathbf{z}}_{\left({\gamma }^c\right)}-1_{p_{\gamma }}{m}_{0\left({\gamma }^c\right)}-{\mathbf{Z}}_{\left(\gamma \right)}{\beta }_0))}^{-\frac{n+6}{2}}\hfill \\ \hfill & \prod _{g=1}^G{\mathbf{K}}_{g\left(\gamma \right)}{\mid {\Omega }_{g\left(\gamma \right)}\mid }^{(d+p_{\gamma }-1)∕2}{\mid {\Omega }_{g\left(\gamma \right)}+{\mathbf{S}}_{g\left(\gamma \right)}\mid }^{-(n_g+\delta +p_{\gamma }-1)∕2},\hfill \end{array}$$ (3.1)

where

$$\begin{array}{cc}\hfill {\mathbf{K}}_{g\left(\gamma \right)}=& {(h_1{n}_g+1)}^{-p_{\gamma }∕2}\prod _{j=1}^{p_{\gamma }}\Gamma \left(\frac{1}{2}(n_g+\delta +p_{\gamma }-j)\right)∕\Gamma \left(\frac{1}{2}(\delta +p_{\gamma }-j)\right),\hfill \\ \hfill {\mathbf{S}}_{g\left(\gamma \right)}=& \sum _{i\mid {\gamma }_i=1}({\mathbf{z}}_{i\left(\gamma \right)}-{\stackrel{‒}{\mathbf{z}}}_{g\left(\gamma \right)}){({\mathbf{z}}_{i\left(\gamma \right)}-{\stackrel{‒}{\mathbf{z}}}_{g\left(\gamma \right)})}^T+\frac{n_g}{h_0{n}_g+1}({\mathbf{m}}_{0\left(\gamma \right)}-{\stackrel{‒}{\mathbf{z}}}_{g\left(\gamma \right)}){({\mathbf{m}}_{0\left(\gamma \right)}-{\stackrel{‒}{\mathbf{z}}}_{g\left(\gamma \right)})}^T,\hfill \end{array}$$

with p_γ being the number of selected variables. We implement a Stochastic Search Variable Selection (SSVS) algorithm that has been used successfully and extensively in the variable selection literature, see Madigan and York (1995) for graphical models, Sha, Vannucci, Tadesse, Brown, Dragoni, Davies, Roberts, Contestabile, Salmon, Buckley and Falciani (2004) for classification settings and Tadesse, Sha and Vannucci (2005) for clustering, among others. This is a Metropolis type of algorithm that uses two different moves as follows:

• with probability ϕ, we add or delete one variable by choosing at random one component in the current γ and changing its value;

• with probability 1 – ϕ, we swap two variables by choosing independently at random a 0 and a 1 in the current γ and changing their values.

The proposed γ^new is then accepted with a probability that is the ratio of the relative posterior probabilities of the new versus the current model:

$$\min \left[\frac{p(\mathbf{Z}\mid \mathbf{y},{\gamma }^{new})\pi \left({\gamma }^{new}\right)}{p(\mathbf{Z}\mid \mathbf{y},{\gamma }^{old})\pi \left({\gamma }^{old}\right)},1\right].$$ (3.2)

Because these moves are symmetric, the proposal distribution does not appear in the previous ratio. Here we also simplify the computation of the acceptance probability using a factorization of the marginal likelihood adopted by Murphy, Dean and Raftery (2010) in their calculation of the ratio between the BIC statistics of two nested models, i.e.,

$$p({\mathbf{Z}}_{\left({\gamma }^c\right)}\mid \mathbf{y},{\mathbf{Z}}_{\left(\gamma \right)},{\mathbf{Z}}_{\left(prop\right)})p({\mathbf{Z}}_{\left(\gamma \right)},{\mathbf{Z}}_{\left(prop\right)}\mid \mathbf{y}),$$

where Z_(prop) represents the variable, for an add/delete move, or the two variables, for a swap move, whose indicator element(s) have been proposed to change. The first factor of this marginal likelihood simplifies when calculating the ratio of equation (3.2), while the second one can assume either the form of the joint marginal distribution of the selected variable(s) or it can be written as equation (3.1) where the set γ^c is formed by only the proposed variable(s). In details, the acceptance probability of the Metropolis step is given by:

• min $[\frac{p_m(\mathbf{Z}\mid {\gamma }^{p-})p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{new})\pi \left({\gamma }^{new}\right)}{p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{old})\pi \left({\gamma }^{old}\right)},1]$, for a remove move;

• min $[\frac{p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{new})\pi \left({\gamma }^{new}\right)}{p_m(\mathbf{Z}\mid {\gamma }^{p+})p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{old})\pi \left({\gamma }^{old}\right)},1]$, for an add move;

• min $\frac{[\frac{p_m(\mathbf{Z}\mid {\gamma }^{p-})p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{new})\pi \left({\gamma }^{new}\right)}{p_m(\mathbf{Z}\mid {\gamma }^{p+})p_m(\mathbf{Z}\mid \mathbf{y},{\gamma }^{old})\pi \left({\gamma }^{new}\right)},1]}{}$, for a swap move; where p_m(Z|γ^p–) is the marginal likelihood of the variable selected to be removed from the set of significant variables while p_m(Z|γ^p+) is the marginal likelihood of the variable selected to be added to the set of significant variables. Note that in all of the possible moves the part of the marginal likelihood that involves the non significant variables is one-dimensional.

The MCMC procedure results in a list of visited models, γ⁽⁰⁾, . . . , γ^(T) and their corresponding posterior probabilities. Variable selection can then be achieved either by looking at the γ vectors with largest joint posterior probabilities among the visited models or, marginally, by calculating frequencies of inclusion for each γ_j and then choosing those γ_j's with frequencies exceeding a given cut-off value. Finally, new observations are assigned to one of the G groups according to formula (2.4).

3.1 Handling Missing Labels

Murphy, Dean and Raftery (2010) show how to handle unlabeled data, i.e. situations where the group information for some of the samples is missing, using an EM algorithm within their frequentist approach to discriminant analysis. Although we do not have unlabeled samples in our case study data, for completeness we show how to adapt our Bayesian method to handle such situations.

In Section 2 we have implicity defined the distribution of y as P(y_i = g) = w_g, and then performed all inference conditioning upon the observed group indicators. Within this framework, missing labels can be handled by considering latent variables that we can sample via an additional MCMC step. Let {y_k, k ∈ S} indicate the set of unlabeled observations. To simplify the sampling of the y_k's we do not integrate the mixture weights w_g's but sample them from their full conditional distribution, that can be derived in closed form as w|y ~ Dirichlet(n₁, . . . , n_G). Note that the n_g's now depend on the sampled values of the missing y_i's. As a consequence of not having integrated w out, equation (3.1) also changes. In particular, P(Z|y, γ, w) is obtained as in (3.1) by replacing K_g(γ) with

$${\mathbf{K}}_{g\left(\gamma \right)}^{\prime }=w_g^{n_g}{(h_1{n}_g+1)}^{-p_{\gamma }∕2}\prod _{j=1}^{p_{\gamma }}\Gamma \left(\frac{1}{2}(n_g+\delta +p_{\gamma }-j)\right)∕\Gamma \left(\frac{1}{2}(\delta +p_{\gamma }-j)\right).$$

Given the sampled w_g's, the full conditional distribution of y_i|y_–i, Z, γ is exactly equal to the predictive distribution (2.4) with the only difference that we replace ${\widehat{\pi }}_g$ with the sampled value for w_g. This step is equivalent to sample from a multinomial distribution with probabilities that depend on the selected variables and the group indicators, both observed and sampled.

4. An Application to NIR Spectral Data

Discriminant analysis is frequently used to classify units into groups based on near infrared (NIR) spectra, see for example Fearn, Brown and Besbeas (2002) and Dean, Murphy and Downey (2006) for approaches that incorporate variable selection. Food authenticity studies are concerned with establishing whether foods are authentic or not. NIR spectroscopy provides a quick and efficient method of collecting the data, see Downey (1996). Correct identification of food via analysis of NIR spectroscopy data is important in order to avoid potential fraud like supplying cheaper unauthentic food instead of the more expensive original products. Food producers, regulators, retailers and consumers need to be assured of the authenticity of food products.

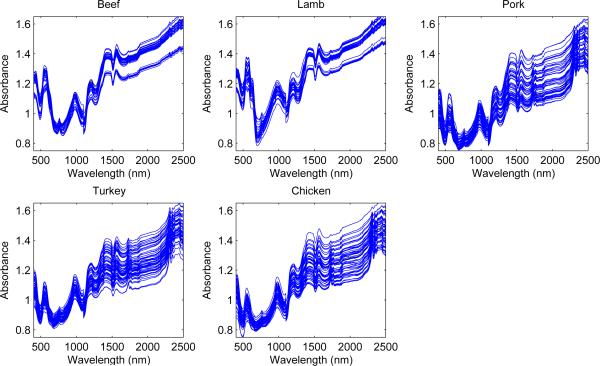
We analyze a data set which consists of combined visible and near-infrared spectroscopic measurements from 231 homogenized samples of five different species of meat (Beef, Chicken, Lamb, Pork and Turkey). The NIR data were collected in reflectance mode using a NIRSystems 6500 instrument over the range 400-2498nm at intervals of 2nm. These are shown in Figure 4.4. These data have been analyzed by Dean, Murphy and Downey (2006) and recently by Murphy, Dean and Raftery (2010). A two-step approach was adopted by Dean, Murphy and Downey (2006), who first applied the standard wavelet thresholding of Donoho and Johnstone (1994) and then performed discriminant analysis on selected subsets of wavelet coefficients. Murphy, Dean and Raftery (2010) also reported results on other standard techniques, such as Transductive Support Vector Machine (SVM), Random Forest, AdaBoost, Bayesian Multinomial Regression, Factorial Discriminant Analysis (FDA), k-nearest neighbors, discriminant partial least squares (PLS) regression and soft independent modeling of class analogy (SIMCA).

Figure 4.4.

NIR spectral data from 231 food samples of five different species of meat.

We removed the first 27 wavelengths to obtain curves observed at 1,024 equispaced points (in nm). We transformed the curves into wavelet coefficients using DWT and Daubechies wavelets with 3 vanishing moments. This gave us 8 scaling coefficients and 1,016 wavelet coefficients for each curve. Because the scaling coefficients carry information on the global features of the data we decided to discard them and performed our selection only on the standardized wavelet coefficients. Previous experience with wavelet-based modeling of NIR spectra has confirmed the intuition that the important predictive information of the data is represented by local features and therefore captured by the wavelet coefficients, see Brown, Fearn and Vannucci (2001).

We randomly split the data into a training set of 117 observations (16 samples of Beef, 28 of Chicken, 17 of Lamb, 28 of Pork and 28 of Turkey) and a validation set of 114 observations (16 samples of Beef, 27 of Chicken, 17 of Lamb, 27 of Pork and 27 of Turkey). We assumed δ₁ = . . . = δ_G = δ_c = δ and set δ = 3, the minimum value such that the expectation of Σ exists. We set each element of m_g and m₀ to the corresponding interval midpoint of the observed wavelet coefficients. We let β₀ = 0, a pretty standard choice when no additional information is available. As suggested by Tadesse, Sha and Vannucci (2005), we specified h₁ = 100, h₀ = 1000 and H_γ = 100·I_|γ|. A good rule of thumb for these values is to set them in the range 10 to 1, 000 to obtain fairly flat priors over the region where the data are defined. A diagonal specification for H_γ still allows posterior dependence among regressions coefficients, mostly depending on the covariance structure of the selected wavelet coefficients. Alternative specifications are also possible. For example, Brown, Fearn and Vannucci (2001) adopted a first-order autoregressive structure in the data domain and then transformed the variance-covariance matrix via the wavelet transform, similarly to what done in Section 2.1 to define ${\tilde{\Sigma }}_g$ and ${\tilde{\Omega }}_g$. Because of the decorrelation properties of the wavelet transform, their transformed matrix has a nearly block-diagonal form.

Some care is needed in the choice of Ω_g and k₀, since the posterior inference is sensitive to the setting of these parameters. This was originally noted in Kim, Tadesse and Vannucci (2006), where guidelines for the specification of these parameters are provided. In general, these parameters need to be specified in the range of variability of the data. A data-based specification, in particular, ensures that the prior distributions overlap with the likelihood, resulting in well-behaved posterior densities. Other authors have reported that noninformative or diffuse priors produce undesirable posterior behavior in finite mixture models, see for example Richardson and Green (1997) and Wasserman (2000), among others, and Kass and Wasserman (1996) for a nice discussion on prior specifications and their effects on the posterior inference. In our application we set Ω_g = kI_|γ| with k = 3^–1, a value close to the standard deviation of the means of the columns of Z. We also specified k₀ = 10^–1, a value in the same scale of magnitude of Ω_g.

The hyperparameters of the MRT were set to d = –2.5 and e = 0.3. The choice of d reflects our prior expectation about the number of significant variables, in this case equal to 7.5%, while a moderate value was chosen for e to avoid the phase transition problem. In general, any value of e below the phase transition point can be considered a reasonable choice. However, a value close to the phase transition point would result in a high prior probability of selection for those nodes whose neighbors are already selected, particulary in a sparse network. Consequently the data would play a much less important role in the selection of the wavelet coefficients. The approach we adopt considers also that the prior probability of a wavelet coefficient should not enormously vary according to the selection of its neighbors. Specifically we set e so that the prior probability of inclusion of a wavelet coefficient with all its three neighbors already selected is roughly twice the prior probability of a coefficient that does not have any of its neighbors selected.

We assumed unequal covariance matrices across the groups. We ran MCMCs by setting ϕ = 0.5, therefore giving equal probability to the add/delete and the swap moves. We used two chains, one that started from a model with two randomly-selected variables, the other one from a model with 10 included variables. We ran the chains for 200,000 iterations, using the first 1,000 as burn-in. We observed fast convergence, therefore selecting a relative short burn-in. The stochastic searches mostly explored models with 16-18 wavelet coefficients and then quickly settled down to models with similar numbers of variables. In our Matlab implementation, the MCMC algorithm needs only a few minutes to run.

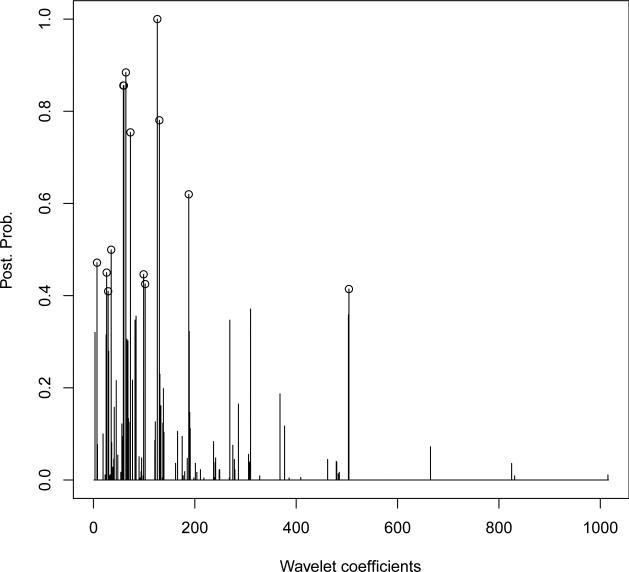
The results we report here were obtained by pooling together the output of the two chains. Figure 4.5 shows the marginal probability of inclusion of the individual wavelet coefficients. A threshold of 0.4 on these probabilities selected a subset of 14 wavelet coefficients. This threshold corresponds to an expected false discovery rate (Bayesian FDR) of 36.7%, which we calculated according to the formulation suggested by Newton, Noueiry, Sarkar and Ahlquist (2004). As we expected, the selected wavelet coefficients belonged to the intermediate scales, with 12 out of 14 belonging to scales 5-6-7 (in our decompositions wavelet coefficients ranged from scale 3, the coarsest, to scale 9, the finest). Additionally, we found that 4 of these 12 coefficients were directly connected in the prior tree structure. Increasing the threshold to 0.5 selected 7 wavelet coefficients, corresponding to a Bayesian FDR of 17.9%.

Figure 4.5.

Marginal posterior probabilities of inclusion for single wavelet coefficients.

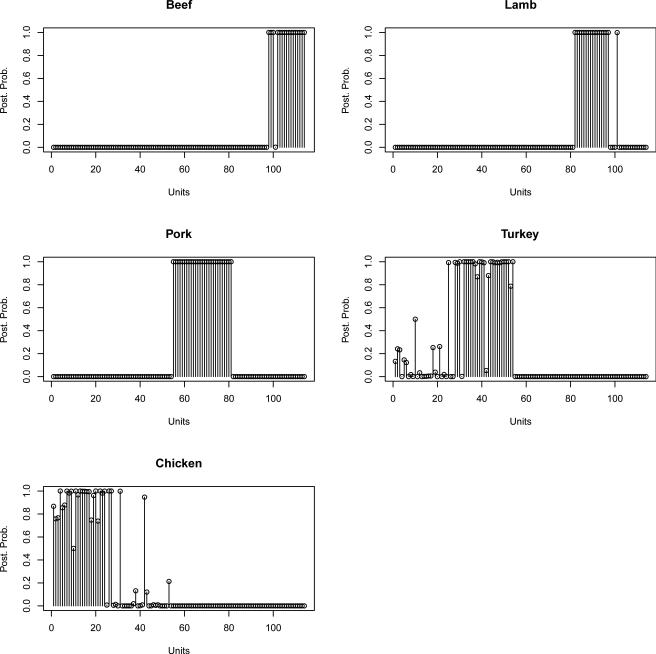
Figure 4.6 shows the posterior probabilities of class memberships for the 114 observations of the validation set, calculated based on the selected 14 wavelet coefficients, and Table 4.1 summarizes the classification results according to these probabilities and a threshold of 0.4. Overall, the model is able to classify 110 of the 114 food samples of the validation set. Predictions worsen to 102 out of 114 by using the 7 wavelet coefficients selected with the 0.5 threshold on the marginal probabilities of inclusion.

Figure 4.6.

Posterior probabilities of group memberships for the 114 observations in the validation set.

Table 4.1.

Validation set: Classification results for the five different species of meat using a threshold of 0.4 for the posterior of inclusion.

	Predicted
Truth	Beef	Lamb	Pork	Turkey	Chicken
Beef	100.0	0.0	0.0	0.0	0.0
Lamb	5.9 (1)	94.1	0.0	0.0	0.0
Pork	0.0	0.0	100.0	0.0	0.0
Turkey	0.0	0.0	0.0	92.6	7.4 (2)
Chicken	0.0	0.0	0.0	3.7 (1)	96.3

The number of misclassified units is reported in parentheses.

We also looked into comparisons of our results with alternative procedures. A standard approach in Chemometrics is to apply linear or quadratic discriminant analysis on selected principal components. We therefore calculated the principal components of our NIR curves, i.e., in the original domain of the data, and computed classical LDA and QDA by selecting different numbers of principal components. We found best results in terms of misclassification rate by using 13-14 principal components with LDA, achieving a total misclassification rate of 5.3%, and 11-13 components with QDA, achieving a total misclassification rate of 6.1%. With a total misclassification rate of 3.4% our method compares favorably to these more standard techniques. Our method also outperforms the results reported by Murphy, Dean and Raftery (2010) obtained with their proposed method and those obtained with various other competing alternatives as reported by these authors. It needs to be pointed out, however, that the authors perform variable selection by fitting their model to all the 231 samples and eliminating at random half of the labels, which they predict. This procedure is repeated 50 times and an average misclassification rate is then reported. With respect to their results, our method, in particular, obtains a consistently better separation between Turkey and Chicken samples.

We conclude this Section by briefly commenting on additional analyses we performed to understand the sensitivity of the model to the specification of the parameters d and e. In particular, we re-analyzed the NIR data using values of d in the range –3 to –2 (implying a proportion of expected significant wavelet coefficients from 5% to 12%) and values of e in the range 0.6 to 1. A value e = 0.6 implies that the prior probability of selecting a wavelet coefficient with all its three neighbors already selected is roughly 4 times the prior probability of a wavelet coefficient that does not have any of its neighbors selected, while with e = 1 this ratio is almost 10 when d = –3 and between 6 and 7 when d = –2. Our method performed well in all the four settings. With a threshold of 0.4 for the posterior probabilities our method correctly classified on average 110 of the 114 samples in the validation set. The best predictive power was achieved with e = 1 and d = –2, with 112 correctly classified samples. The number of selected wavelet coefficients was pretty stable among the different scenarios, with 14 to 17 selected coefficients that mostly overlapped, except for some coefficients that represented the same feature of the data at closed locations. As a general behavior, we noticed that, while different settings of the parameters slightly affect the magnitude of the posterior probabilities of inclusion of the wavelet coefficients, their ordering tends to remain largely unaffected.

5. Conclusion

We have put forward a wavelet-based approach to discriminant analysis for curve classification. We have employed wavelet transforms as an effective tool for dimension reduction that reduces curves into wavelet coefficients. We have illustrated how to perform variable selection in the wavelet domain within a Bayesian paradigm for discriminant analysis. We have considered linear and quadratic discriminant analysis and have constructed Markov random field priors that map scale-location connections among wavelet coefficients. Unlike current literature on Bayesian wavelet-based modeling, our model formulation avoids any independence assumption among wavelet coefficients. For posterior inference we have achieved dimension reduction using a stochastic search variable selection procedure that selects the discriminatory wavelet coefficients. We have presented a typical example from chemometrics that deals with the classification of different types of food into species via near infrared spectroscopy. Our method has performed well in comparison with several alternative procedures. As already noticed by Tadesse, Sha and Vannucci (2005) in real data applications a careful setting of Ω_g and k₀ is needed, due to the sensitivity of the model to these hyperparameters.

A possible extension of the model we have presented is to allow for a third group of variables in the likelihood factorization (2.5) formed by variables that are marginally independents of the significant ones. The factor of the marginal likelihood corresponding to this third group of variables simplifies in the Metropolis-Hasting steps proposed in Section 3, while new moves that allow variables to be assigned to or removed from this third set are needed. We have implemented this approach but did not see any significant difference in the selection of the wavelet coefficients and in the corresponding predictions.

The assumption of Gaussianity is commonly made in applications with the type of spectral datasets we have considered in this paper, see Dean, Murphy and Downey (2006) and Oliveri, Di Egidio, Woodcock and Downey (2011), among many others. However, readers may wonder whether the performances of our method depend on the Gaussianity of the observations. In order to investigate this aspect we designed a small simulation study with non-Gaussian data. First we selected one curve x^B at random among the observed data analyzed in Section 4 and generated a set of n observations belonging to two groups using the following steps: (1) For each data point x_ij we added some uniform noise as $x_{ij}=x_j^B+u$, with u ~ Uniform(–c, c), i = 1, . . . , n, j = 1, . . . , p. This implies that the distribution at each data point x_ij is uniform in the original data domain. (2) We applied the DTW, using Daubechies wavelets with 3 vanishing moments, to the generated curves. (3) We randomly selected three wavelet coefficients belonging to intermediate scales. For samples belonging to group 1 we added a constant c_w to these three coefficients, while we subtracted the same constant c_w for samples belonging to group 2. (4) For samples belonging to group 1 we added a constant c_n to all neighbors of the three wavelet coefficients selected at point 3. We subtracted the same constant c_n for samples belonging to group 2. Since each of the wavelet coefficients selected at point 3 had three neighbors in the MRT, there were 12 wavelet coefficients that had discriminatory power among the two groups. We considered three different scenarios. In the first scenario we set (c, c_w, c_n) = (0.02, 0.06, 0.03), in the second (c, c_w, c_n) = (0.015, 0.02, 0.04) and in the third (c, c_w, c_n) = (0.05, 0.08, 0.04). The small values for (c, c_w, c_n) we considered did not alter the original shape of the observed curve x^B. Note that the first two scenarios result in c_n < 2c < c_w, while the third one is more challenging, with c_n < c_w < 2c. With the same hyperparameter settings adopted in Section 4 for the analysis of the NIR spectral data, in the first scenario a threshold of 0.5 on the marginal posterior probabilities resulted in the selection of all the 12 significant wavelet coefficients without any false positive. In the second scenario the same threshold led to the selection of 11 significant wavelet coefficients without any false positive. In the third scenario 8 coefficient were correctly select without any false positive. We therefore conclude that our method performs well even in the case of non-Gaussian data.

Appendix. Linear Discriminant Analysis

If all G groups share the same covariance matrix Σ then the most appropriate technique is linear discriminant analysis (LDA). Using an Inverse-Wishart prior on this matrix, i.e., Σ ~ IW (δ, Ω), and leaving all the other settings unchanged, the marginal likelihood used in the MCMC algorithm, corresponding to equation (3.1) for the quadratic case, becomes:

$$p(\mathbf{Z}\mid \mathbf{y},\gamma )\propto {(k_0+{({\mathbf{Z}}_{\left({\gamma }^c\right)}-1_{p_{\gamma }}{m}_{0\left({\gamma }^c\right)}-{\mathbf{Z}}_{\left(\gamma \right)}\beta )}^T{({\mathbf{I}}_n+h_0{1}_n{1}_n^T+{\mathbf{Z}}_{\left(\gamma \right)}{\mathbf{H}}_{\gamma }{\mathbf{Z}}_{\left(\gamma \right)}^T)}^{-1}({\mathbf{Z}}_{\left({\gamma }^c\right)}-1_{p_{\gamma }}{m}_{0\left({\gamma }^c\right)}-{\mathbf{Z}}_{\left(\gamma \right)}\beta ))}^{-\frac{n+\delta }{2}}{\mathbf{K}}_{\left(\gamma \right)}{\mid {\Omega }_{\left(\gamma \right)}\mid }^{(\delta +p_{\gamma }-1)∕2}{\mid {\Omega }_{\left(\gamma \right)}+\sum _{g=1}^G{\mathbf{S}}_{g\left(\gamma \right)}\mid }^{-(n+\delta +p_{\gamma }-1)∕2},$$

with

$${\mathbf{K}}_{\left(\gamma \right)}=\left[\prod _{g=1}^G{(h_1{n}_g+1)}^{-p_{\gamma }∕2}\right]\prod _{j=1}^{p_{\gamma }}\Gamma \left(\frac{1}{2}(n_g+\delta +p_{\gamma }-j)\right)∕\Gamma (\frac{1}{2}(\delta +p_{\gamma }-j)$$

and S_g(γ) defined as in Section 3. The predictive distribution for the LDA case is a multivariate T-student, see Brown (1993):

$${\mathbf{z}}^{\mathbf{f}}-{\tilde{\mu }}_g\sim \mathcal{T}({\delta }^{\ast },a_g,{\Omega }^{\ast }),$$

where ${\tilde{\mu }}_g={\pi }_g{\mathbf{m}}_g+(1-{\pi }_g){\stackrel{‒}{\mathbf{z}}}_g$, δ* = δ + n, a_g = 1 + (1/h_g + n_g)^–1 and Ω* = Ω + S + (h_g + 1/n_g)^–1(Z̄ – M)^T(Z̄ – M) with π_g = (1 + h_gn_g)^–1 and S = (Z – JZ̄)^T (Z – JZ̄); J consists of G dummy vectors identifying the group of origin of the observation, Z̄ is the G × p matrix of the sample group means and M = (m₁, . . . , m_G)^T. Note that the part relative to the non selected variables does not change compared to equation (3.1). When handling units with missing label K_(γ) can be written as:

$${\mathbf{K}}_{\left(\gamma \right)}=\left[\prod _{g=1}^G{w}_g^{n_g}{(h_1{n}_g+1)}^{-p_{\gamma }∕2}\right]\prod _{j=1}^{p_{\gamma }}\Gamma \left(\frac{1}{2}(n_g+\delta +p_{\gamma }-j)\right)∕\Gamma (\frac{1}{2}(\delta +p_{\gamma }-j),$$

while the predictive distribution remains unchanged after having assigned unlabeled units to groups.