Facilitating Neuronal Connectivity Analysis of Evoked Responses by Exposing Local Activity with Principal Component Analysis Preprocessing: Simulation of Evoked MEG

Abstract

When connectivity analysis is carried out for event related EEG and MEG, the presence of strong spatial correlations from spontaneous activity in background may mask the local neuronal evoked activity and lead to spurious connections. In this paper, we hypothesized PCA decomposition could be used to diminish the background activity and further improve the performance of connectivity analysis in event related experiments. The idea was tested using simulation, where we found that for the 306-channel Elekta Neuromag system, the first 4 PCs represent the dominant background activity, and the source connectivity pattern after preprocessing is consistent with the true connectivity pattern designed in the simulation. Improving signal to noise of the evoked responses by discarding the first few PCs demonstrates increased coherences at major physiological frequency bands when removing the first few PCs. Furthermore, the evoked information was maintained after PCA preprocessing. In conclusion, it is demonstrated that the first few PCs represent background activity, and PCA decomposition can be employed to remove it to expose the evoked activity for the channels under investigation. Therefore, PCA can be applied as a preprocessing approach to improve neuronal connectivity analysis for event related data.

1. INTRODUCTION

The brain's fundamental purpose is to perform both functional integration and functional specialization (Horwitz 2003), where the integration within and among specialized areas is mediated by effective connectivity (Friston 2011). The brain with its complex neuronal connections can be viewed as an amazing information processing device that integrates specialized information conveyed by the activity of functionally segregated areas and neuronal groups into a unified coherent whole. This function of integration is facilitated by synchronization of activity within and between neuronal networks in the brain, and is currently the focus of intense neuroimaging research efforts (Friston 2011; Sakkalis 2011). In fact, the functional role played by any component (e.g. cortical area, subarea or neuronal population) of the brain is largely defined by its connections. Therefore, studying neuronal networks is fundamental to both neuroscience and clinical applications. Among all the neuroimaging tools, MEG and EEG are the only approaches that provide whole-head coverage and excellent temporal resolution on the order of milliseconds; furthermore, MEG provides good spatial resolution. Thus, MEG is a preferred technique to study brain activity on the time scale of cognitive processes (~1ms).

In neuroscience studies, the event-related experiment is a fundamental method to activate certain brain areas connected by underlying neuronal networks. Different stimulation paradigms are often employed to activate specific neuronal networks. The activated network is characterized by the evoked data in epochs, which is mixed with on-going spontaneous activity. This on-going spontaneous activity represents the basic neuronal networks in the brain, and generally has much larger amplitude than the evoked responses, thereby masking the activity of the evoked cortical networks (Kuriki et al. 1994; Sekihara et al. 1992; Sekihara et al. 1994; Kobayashi and Kuriki 1999). In addition to the spontaneous signals, external noise, also contributes to the background activity, which makes it difficult to interpret connectivity analysis at the sensor level. Furthermore, field spread (caused by volume conduction and spatial blurring due to the scalp for EEG and spatially distributed lead fields for MEG) also complicates the interpretation of cortical connectivity patterns at the sensor level (Schoffelen and Gross 2009; Nolte et al. 2004). Therefore, it is still a challenging task using MEG/EEG recordings to estimate connectivity between brain regions.

Carrying out connectivity analysis in source space is the best choice to disentangle the above problems (Schoffelen and Gross 2009). Source localization provides direct estimation of the interaction between neuronal sources, attenuating the effect of background activity differently. However, source localization itself suffers from many issues. Among them the major one is that there is no unique solution for the inverse problem (Sarvas 1987; Nolte et al. 2004). Therefore, in order to solve the problem, assumptions must be made. Depending on the assumptions, they may influence connectivity determined in source space. In addition, some background activity may be misinterpreted as event-related connectivity. Thus it is critical to know how to remove the background activity in the exploration of the connectivity between different locations represented by evoked activity.

In order to solve the issue of the background activity, there are a variety of approaches for MEG preprocessing. Signal Space Projection (SSP) method is widely used to identify and remove eye-blink artifacts, cardiac artifacts and characterize the local oscillatory content of spontaneous cortical activity during mental imagery (Huotilainen et al. 1993; Jousmaki and Hari 1996; Taulu and Kajola 2005; Tesche et al. 1995a; Tesche et al. 1995b; Salmelin et al. 1995; Uusitalo and Ilmoniemi 1997). A linear integration of multiple channels for extracting individual components without making any spatial modeling assumptions was also proposed to remove eye-motion artifacts, and extract strong evoked responses (Parra et al. 2005). The imaginary part of coherency is a measure to identify true brain interaction from MEG/EEG data for its robustness to volume conduction (Gomez-Herrero et al. 2008; Nolte et al. 2004; Nolte et al. 2008; Schoffelen and Gross 2009; Stam et al. 2007). Besides the external noise and volume conduction, the background activity also includes the spontaneous brain activity, which may produce substantial misinterpretations of cortical connectivity results (Schoffelen and Gross 2009; Nolte et al. 2004). According to the analysis above, most preprocessing approaches emphasize the elimination of external noise and volume conduction, however, the consideration of the effect of spontaneous brain activity on the evoked response is limited in connectivity studies.

On the other hand, the covariance stationarity of the data is the fundamental requirement to analyze connectivity in single trial data (Seth 2010), while most MEG/EEG recordings are non-stationary. Using a windowing approach to obtain stationarity (Seth 2010), may limit the ability to track rapid changes in connectivity. Therefore, it is a significant issue to extract the stationary part from the non-stationary signal with minimum loss of connectivity. Cui et al. (2008) developed a method to subtract the phase locked response from event related signals, and found the remaining residuals were mostly stationary and still maintained the connectivity information (Cui et al. 2008). In practice, a widely used method is to difference the data as many times as necessary until stationarity is achieved. However, differencing causes loss of valuable information in the data, in addition to the difficulty in interpreting the results.

Principal Component Analysis (PCA) is usually applied in preprocessing multi-channel data to improve the Signal to Noise Ratio (SNR) by keeping the first few PCs while discarding the residuals (Lagerlund et al. 1997). An opposite use of the PCA, namely Principal Component Elimination Method (PCEM), was previously proposed to remove the spontaneous potential, which is considered as noise in the analysis of evoked data, and enhances the SNR for evoked MEG measurement by eliminating the 1st Principal Component (PC) (Kobayashi et al. 1999). In a typical event-related experiment, the evoked responses are often detected only by a small number of the available sensors in a multi-channel MEG system. Compared with the ubiquitous background activity in MEG measurements, the evoked responses behave in some neural evoked sources with relatively local distribution (Kobayashi and Kuriki 1999; Nolte et al. 2004). The applications of PCA provide a possible method for eliminating the background activity, especially the spontaneous activity, for connectivity analysis of the evoked response.

In this paper, we hypothesized that the evoked responses are orthogonal to the dominant background activity, thus the PCA can be applied to separate them from each other. This indicates that the dominant components of the background activity may be captured by the major PCs after PCA, while the evoked activity is expected to remain in the residuals after discarding the projection of the first few PCs because of the focal nature of evoked responses. Different from the PCEM study by Kobayashi and Kuriki (1999), we developed our approach to quantify the PCs representing the dominant background activity based on Global Field Power (GFP) and average coherence. Here, the dominant PCs originate from spontaneous activity. Hence, characterizing the neuronal connections from evoked activity can be improved by analyzing the residuals with less background activity. In this paper, we test our approach with a well-established realistic simulation to test source connectivity of the evoked signals. Thus, we test the proposed approach using results from simulated human MEG data, which could facilitate the analysis of evoked neuronal connectivity in MEG/EEG fields.

2. MATERIALS AND METHODS

2.1 Methods

2.1.1 Principal Component Analysis

The multi-channel evoked signal model is described by Eq. 1.

$$S=S_{\mathit{spont}}+S_{\mathit{evoked}}+S_{\mathit{external}}+S_n$$ (1)

Where the data detected by the MEG system are composed of the spontaneous activity S_spont, evoked response S_evoked, the external interferences S_external, and the normally distributed white noise S_n individually. Firstly, the recording from each channel is normalized by its standard deviation (SD) over the time interval, after subtracting the mean value S_mean, for connectivity analysis to set the same weight for all sensors before applying PCA decomposition:

$$\stackrel{‒}{S}=(S-S_{\mathit{mean}})∕SD$$ (2)

The normalization ensures that only the globally distributed temporal patterns in the data can be represented by the first few PCs. We then check how many of the largest PCs represent the background activity. The details are in 2.1.4. These largest PCs capture spontaneous activity S_spont, and also external interference S_external since interference from distant sources appears more or less in all channels. After discarding the back projection of the first few largest PCs, the background activity across sensors is eliminated, and the residual is named as $\overline{S_{\mathit{res}}}$ by Eq. 3.

$$\overline{S_{\mathit{res}}}=S_{\mathrm{spont}\_\mathrm{ref}}+S_{\mathit{evoked}}+S_{\mathrm{external}\_\mathrm{res}}+S_n$$ (3)

S_{spont _ res} and S_{external _ res} are the residuals after discarding the largest PCs. We took the data after PCA preprocessing as our input data for further connectivity analysis by utilizing the conventional connectivity methods, which are available as a free toolbox (Seth 2010).

2.1.2 Global Field Power (GFP)

GFP is used to quantify the activity at each time point in the field for the average data from all recording channels simultaneously (Lehmann and Skrandies 1980; Lehmann and Skrandies 1984). GFP at a specific time point can be calculated as follows:

$$\mathit{GFP}=\frac{\sum _{n=1}^N{A}_n^2}{N}$$ (4)

Wherein A is the average for each channel at that time point. N is the number of all channels. MEG/EEG data across multiple channels can be integrated using the GFP (Skrandies 1990).

2.1.3 Coherence for merged data

Coherency between two MEG/EEG channels is a measure of the linear relationship between the two channels at a specific frequency (Nunez et al. 1997). Suppose x_i(f) and x_j(f) be the Fourier transforms of the time series of channel i and j, respectively. Then the cross-spectrum is defined as

$$S_{ij}\left(f\right)\equiv \langle x_i\left(f\right)x_j^{\ast }\left(f\right)\rangle$$ (5)

Where * means complex conjugation and < > means expectation value. Generally, the expectation value can only be estimated as an average over a sufficiently large number of epochs. Coherency is now defined as the normalized cross-spectrum as follows.

$$C_{ij}\left(f\right)\equiv \frac{S_{ij}\left(f\right)}{{\left(S_{ii}\right(f\left)S_{jj}\right(f\left)\right)}^{1∕2}}$$ (6)

Then coherence is defined as the absolute value of coherency:

$${\mathit{Coh}}_{ij}\left(f\right)\equiv \mid C_{ij}\left(f\right)\mid$$ (7)

In our approach, we made a change to the conventional coherence method. After visually discarding the noisy epochs and zeroing the mean of the remaining signal, we merged all selected epochs together as if they were continuously recorded. We then carried out the coherence analysis for this merged data, which allowed us to achieve a higher frequency resolution, if desired. Potentially, the pitfall of this merging method is that a fake coherence peak corresponding to the reversal of the epoch period (1/T) might exist. This problem can be eliminated by padding each epoch with pseudo-white noise at both the beginning and end to an epoch length, such that the frequency of the modified period is outside the frequency range of interest.

2.1.4 Determination on the number of largest PCs to be removed by GFP and coherence

We recognize that different numbers of sources of background activity may be present in the MEG data thereby making it necessary to develop a method to determine the number of PCs to eliminate for each dataset.

First, a k-means clustering was performed to determine the channels with evoked response for each t-by-n data matrix including signals from n sensors during t distinct time instants in an epoch (Gourevitch and Le Bouquin-Jeannes 2003). PCA was applied firstly to initialize the first two centers of the classes, with the two signals having the highest and lowest covariances with the first component of each data matrix respectively (Gourevitch and Le Bouquin-Jeannes 2003). Then, we assigned each signal to the class with the nearest center. After allocating all the signals, the two centers were updated at each step as the first component of the matrix to reflect the changes in both classes, and the clustering was reiterated until all class members had fixed membership. Then the times for each electrode belonging to the class with the best electrodes were computed for all epochs. The first derivative of this curve provides a threshold to finally determine the channels with evoked response (Gourevitch and Le Bouquin-Jeannes 2003).

We selected electrodes with evoked signal to focus on the evoked cortical areas. The GFP for the selected electrodes was calculated after sequentially removing the largest PCs, and a t-test was performed between the GFP for the original data and the residuals after PCA preprocessing during the time period when the evoked responses happened, which helped ensure that the evoked information was maintained after PCA preprocessing. If the first few PCs represent the background activity, we propose an assumption that the average coherence between all channels might be decreased while the coherence between the selected channels with evoked response will increase during the elimination of PCs. Therefore, the number of the removed PCs was judged by increasing average coherence between evoked channels with discarding PCs while maintaining the evoked response by t-test results.

2.1.5 KPSS stationarity test

Application of Granger causality connectivity analysis requires that each time series is covariance stationary. The KPSS (Kwiatkowski, Phillips, Schmidt, and Shin) test is adopted as a stationarity test in the Granger Causality Connectivity Analysis toolbox (Kwiatkowski et al. 1992; Seth 2010). The KPSS test uses the hypothesis that the time series is stationary. For the test result H, 0 means `reject the hypothesis' and 1 means `do not reject the hypothesis'.

2.1.6 Minimum Norm Estimation (MNE)

The MEG and the current source strengths can be described as follows:

$$Y=AX+N$$ (8)

Where Y is an n-by-t matrix including signals from n sensors during t distinct time instants, and X is a 3m-by-t matrix demonstrating the time-dependent amplitudes of the three components of m current sources, A is the gain matrix denoting the mapping of the source currents to the MEG sensors, and N is the noise in the measured data. Assume that N is a Gaussian distribution with a spatial covariance matrix C, and the source amplitudes have a Gaussian distribution with a covariance matrix R, the MNE solution is:

$$X^{\mathit{MNE}}=R{A}^T{({\mathit{ARA}}^T+{\lambda }^{2}C)}^{-1}Y$$ (9)

Where λ² is a regularization parameter to avoid magnification of errors in data in the current solution, and the superscript T indicates the matrix transpose. For this study, we projected the data with and without PCA preprocessing into source space for comparison by MNE toolbox (Lin et al. 2006). Prior to source analysis with MNE the SD scaling that was applied prior to PCA was reversed (each channel was multiplied by its SD) to restore the physiological amplitudes to all channels.

2.1.7 Granger causality connectivity

Granger causality is a linear regression modeling approach where x₂ `Granger causes' x₁ if the inclusion of past observations of x₂ reduces the prediction error of x₁, compared with the inclusion of only previous observations of x₁. Suppose that the two stationary time series x₁(t) and x₂(t) are expressed by the autoregressive model as follows:

$$x_1\left(t\right)=\sum _{i=1}^T{a}_{11,i}{x}_1(t-i)+\sum _{i=1}^T{a}_{12,i}{x}_2(t-i)+{\xi }_1\left(t\right)$$ (10)

$$x_2\left(t\right)=\sum _{i=1}^T{a}_{21,i}{x}_1(t-i)+\sum _{i=1}^T{a}_{22,i}{x}_2(t-i)+{\xi }_2\left(t\right)$$ (11)

Where a is the coefficient, ξ₁ and ξ₂ are the prediction errors for x₁ and x₂ respectively, and T is the number of past observations. x₂ `causes' x₁ when variance of ξ₁ reduces with the inclusion of x₂. The interaction gc is quantified by the log ratio of the prediction error variance between the model omitting the other variable and the full model.

$$g{c}_{2\to 1}=\ln \frac{\text{var}\left({\xi }_{o,1}\right)}{\text{var}\left({\xi }_1\right)}$$ (12)

Where ξ_o,1 is derived from the model omitting the a_12,i in the Eq. 10 and ξ₁ is from the full model. The Granger causality analysis can be expanded to multivariate models for the connectivity analysis between more than two interested regions. In the paper, we used the Granger Causality toolbox with the source data of original and residuals for assessment of connectivity (Seth 2010). The Granger causality connectivity was also calculated based on the merged data similar to the calculation of average coherence in 2.1.3.

2.2 Simulation

To evaluate the feasibility of the approach, we applied our basic method to simulated data. The work made use of realistic simulated datasets with the Elekta Neuromag Vectorview (306 channels) MEG array configuration. These simulated datasets are available to researchers worldwide via the website http://portal.mind.unm.edu/megsim and are described in Aine et al. (2011). Based on our hypothesis that the local information carried by a subset of channels remains in the residuals after removing the first few PCs, and the evoked responses are only locally distributed, we compared the averaged results on all channels, and GFP and average coherence results on the channels carrying evoked information with and without PCA preprocessing to remove the background activity in order to evaluate the feasibility of the approach proposed here for realistic MEG experiments. We also applied source connectivity results for the evoked epochs with and without discarding the first few PCs to determine if the new method improves the results. Additionally, we performed spectral analysis on the selected and non-selected channels with and without our preprocessing to further explore the components of the removed PCs and the effect of our approach.

Of the available simulation data, we selected the realistic simulated visual datasets developed from 100 averaged noise trials in which the sources of activity, with the addition of oscillatory activity, reflected functional connectivity of different cortical areas. Source activity embedded within 100 single trials of noise were jittered about their mean latency and amplitude. The cortical patch current strengths were initially assigned values similar to the values in visual working memory studies, and were then randomly jittered about the values by up to +/− 50% across the single trials. Peak latencies were also jittered across each trial by a randomly selected value up to +/− the full width at half maximum divided by 2. Each trial lasted 1250 ms with a sampling frequency of 1000 Hz. We removed the 60 Hz powerline noise and bandpass filtered the data offline within 1–100 Hz (Zhang and Okada 2005). As in previous working memory studies, the late activity, i.e., 400–600ms, was synchronous across four cortical sites: 1) primary visual cortex (V1); 2) inferior lateral occipital gyrus (I.LOG); 3) intraparietal sulcus (IPS); 4) dorsolateral prefrontal cortex (DLPFC) (Stephen et al. 2002; Aine et al. 2006; Sanfratello et al. 2010). V1, I.LOG and IPS oscillate in Gamma band (30–60HZ), while IPS and DLPFC oscillate in Beta band (13–30Hz). Hence, there is significant connectivity between V1 and I.LOG, V1 and IPS, I.LOG and IPS in Gamma band, IPS and DLPFC in Beta band. The MEG data were generated via a realistic head model derived from MRI, which was used to localize the source data with MNE toolbox in our study. The details for source connectivity are in the reference (Aine et al. 2011).

3. RESULTS

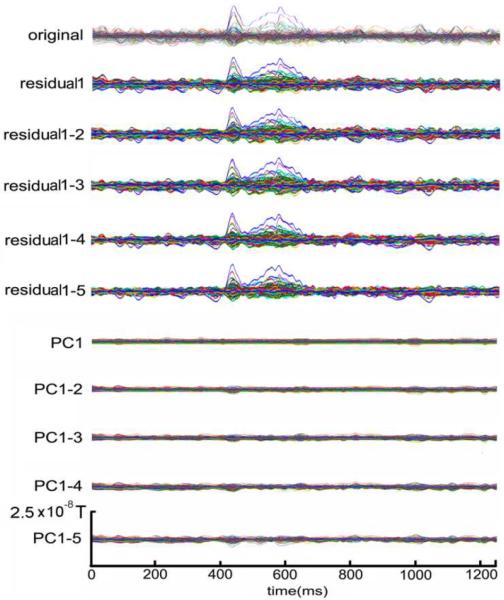
The averages with and without discarding the first PCs are shown in Fig.1. The top plot of Fig.1 illustrates the conventional average of the 100 epochs and serves as a baseline. We removed first few PCs from 1 to 5, and then averaged the residuals, as shown in the next five plots in Fig.1. The averages of the discarded components, i.e., 1–5 PCs, were plotted in the last five plots in Fig.1. The averages of the removed PCs look more like non-phase locking activity in the background. This provides some evidence that the evoked response is orthogonal to some background activity.

Fig.1.

Averaged original simulated data, residuals after removing first 1–5 PCs, and corresponding removed PCs. `original' indicates the average without any processing. `residual1', `residual1-2', `residual1-3', `residual1-4' and `residual1-5' indicate the average after removing first 1–5 PCs, and `PC1', `PC1-2', `PC1-3', `PC1-4', and `PC1-5' present the average of the corresponding removed PCs

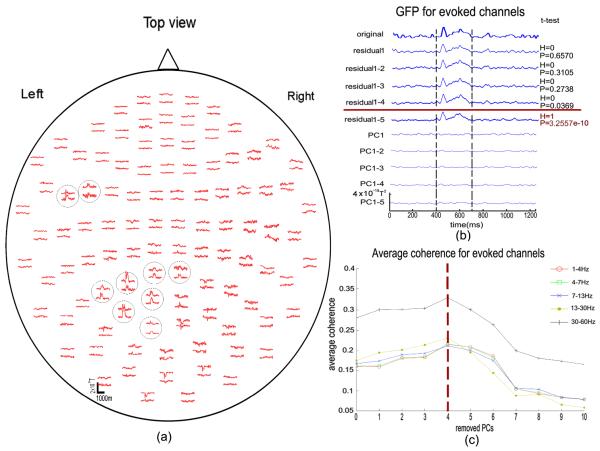
Next the number of removed PCs was determined as described in methods 2.1.4. Note that we used the planar gradiometers for analysis in our study. We selected eighteen channels with evoked activity here by K-means clustering method (Gourevitch and Le Bouquin-Jeannes 2003). As shown in Fig.2(a), the evoked response is recognizable for the selected channels compared with the non-selected channels. The GFP of original data, residuals after removing the first 1–5 PCs and the corresponding removed PCs for the channels with evoked signals is shown in Fig.2(b). The number of PCs containing global signals must be determined without losing the information of interest. Thus, we performed a t-test on the GFP across the epoch with evoked responses (400–700 ms in the simulated dataset) for the evoked channels with and without PCA, i.e. removing the 1–5 PCs respectively, to determine if the evoked activity was retained after PCA removal. The results demonstrate (see p-values in Fig.2(b)) that the GFP is statistically equivalent to the original signal when removing up to the first four PCs, while it cannot be considered to be equal after discarding the top five PCs. Then we calculated the average coherence in the major physiological frequency bands, i.e., 1–4Hz, 4–7Hz, 7–14Hz, 14–30Hz, and 30–60Hz between selected channels which carry the evoked responses for both the original signal and the residuals after removing the first one to ten PCs. The results were plotted in Fig.2(c). Note that the x-axis denotes the number of removed PCs. It starts from zero, indicating that the first point stands for the averaged coherence of the original data without discarding any components. The first coherence value is a baseline to evaluate the method applied here. We can clearly see the trend that, after removing the first few PCs, the average coherence for selected channels firstly increases to a peak value in all frequency bands, then gradually decreases. This change in coherence with number of PCs discarded should reflect an increase in the evoked information ratio carried by the corresponding channels. When this increase reaches a peak, the evoked information ratio can no longer be improved upon, which indicates the limit of the method. For this particular simulation, it is enough to discard the first four PCs to achieve the best connectivity index as indicated in Beta and Gamma band, which is consistent with the analysis with GFP.

Fig.2.

(a) Spatial distribution of MEG averages. In each sensor unit, the traces illustrate signals recorded by two orthogonal gradiometers. The selected channels with evoked response are circled. (b) GFP for original data, residuals after removing first 1–5 PCs, and corresponding removed PCs for the channels with evoked signal. `original' indicates the GFP without any processing. `residual1', `residual1-2', `residual1-3', `residual1-4' and `residual1-5' indicate the GFP after removing first 1–5 PCs, and `PC1', `PC1-2', `PC1-3', `PC1-4', and `PC1-5' stand for the GFP of corresponding removed PCs. The t-test was performed between original GFP and GFP of residuals after discarding one to five PCs, respectively, from 400ms to 700ms, when the evoked signal appears. The right column is the t-test results for the residuals, respectively. The hypothesis is that GFP of original data and residuals comes from distribution with equal means. H=0 indicates the null hypothesis (“means are equal”) cannot be rejected at the 5% significance level. H=1 indicates the null hypothesis can be rejected at 5% level. P value is the probability of observing the given result, or one more extreme, by chance if the null hypothesis is true. (c) Average coherence for selected evoked channels with PCs discarded at the physiological frequency bands in 1–4Hz (Delta band), 4–7Hz (Theta band), 7–13Hz (Alpha band), 13–30Hz (Beta band), and 30–60Hz (Gamma band), individually

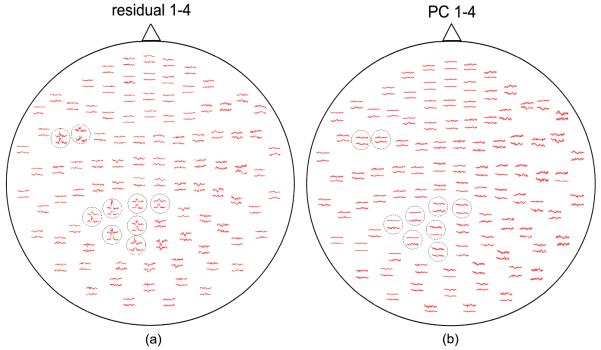
The spatial distribution of the averages for the residuals after removing first four PCs is illustrated in Fig.3(a), while the discarded first four PCs are shown in Fig.3(b). By comparison of average data between the residuals and first four PCs, we found that the evoked information is almost completely preserved, and the removed PCs after averaging look like the non-phase locking activity in the background.

Fig.3.

(a) Spatial distribution of MEG averages of the residuals after removing first four PCs; (b) Spatial distribution of MEG averages of first four PCs. The selected channels with evoked response are encircled

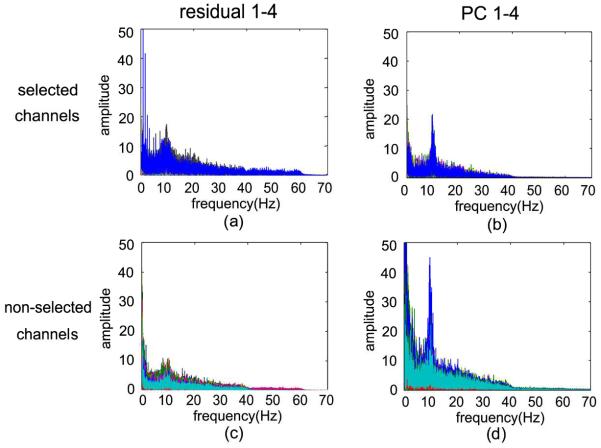
Before eliminating the first four PCs for connectivity analysis, the residuals and the first four PCs to be discarded were characterized with spectral analysis. The frequency spectrum of selected channels and non-selected channels for the residuals and the first four PCs is shown in Fig.4, and the resulting value is plotted as amplitude versus frequency. Regarding the selected channels, the residuals in Fig.4(a) fall into 0–60 Hz, which indicates that the connectivity information in Gamma band was almost preserved. The amplitude of the discarded PCs for the selected channels in Fig.4(b) is much smaller compared with the non-selected channels by comparison between Fig.4(b) and Fig.4(d), while there is also a peak in Alpha band in Fig.3(b). The results of the residuals and the first four PCs of the non-selected channels in Fig.4(c) and Fig.4(d) fall into physiological frequency band in 0–40 Hz, while the first PCs show a high peak in the Alpha band, and the residuals represent less information than first four PCs. Thus, the first four PCs are not simply artifacts, but mainly represent background neural activity. The results show the evoked information almost remains in the residuals, while much of the spontaneous activity is discarded by the first four PCs.

Fig.4.

The frequency spectrum for the residuals and removed PCs of the selected channels (a, b) and non-selected channels (c, d), respectively

Application of Granger causality to explore effective connectivity in neuronal networks requires the time series to be covariance stationary. We show here that, after removing the first four PCs, the evoked data in single trial become stationary. After merging all trials into one long epoch, the stationary results using the KPSS test for all channels of data with and without preprocessing are illustrated in Fig.5. The bar plot in Fig.5 demonstrates that by removing the first four PCs, the time series for all channels are stationary, while the evoked information is still preserved as we demonstrated earlier; whereas 54% of channels in the original recordings were non-stationary.

Fig.5.

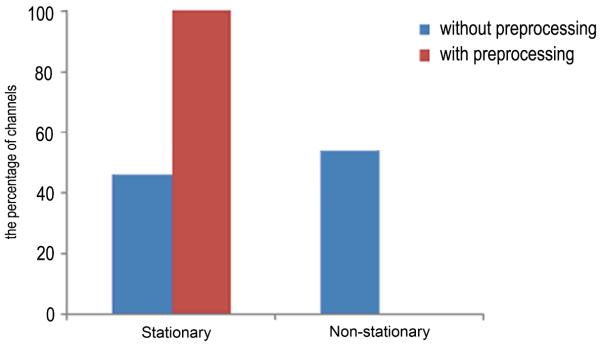
Stationarity comparison of data with and without discarding the first four PCs. Before applying our method, there are 54% non-stationary channels. In contrast, after applying our procedure, all the channels present the stationarity

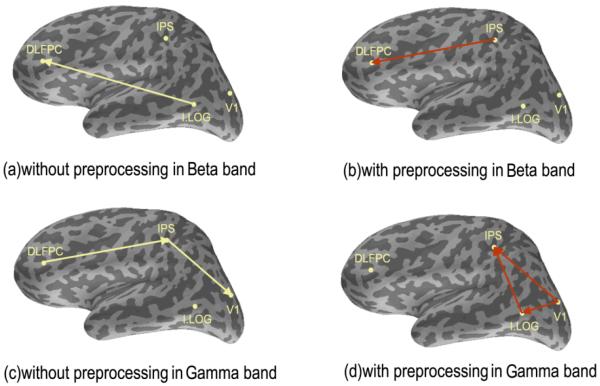
Based on the known source locations of the simulated data, the evoked data were projected to the four source locations using MNE (Lin et al. 2006). We applied the connectivity analysis to single trial data for the source data without preprocessing and the source data after removing the first four PCs. We studied the connectivity in the Beta and Gamma band, respectively. The simulation was designed with synchronous activity in the Beta band between DLPFC and IPS, and synchronous activity in the Gamma band between the following three areas (V1 -IPS, IPS-I.LOG, V1-I.LOG). Therefore, we calculated the largest connectivity in the Beta band and the three largest in the Gamma band by Granger Causality Analysis. In Fig.6(a) and (c), we can see that the results without preprocessing using our method give false connectivity, and do not reveal the true connectivity as included in the simulated dataset. In contrast, the connectivity results with the PCA preprocessed data as shown in Fig.6(b) and (d) are consistent with the source connectivity pattern generated in the simulated dataset. After our preprocessing, the connectivity value calculated by Eq. 13 is 0.4545 (DLPFC-IPS) in Beta band, 0.3007(V1-IPS), 0.1913 (IPS-I.LOG), and 0.1546 (V1-I.LOG) in Gamma band. The largest connectivity value in other frequency bands is 0.1219 in Alpha band. Compared with the connectivity value in other frequency bands, we could infer that the connectivity in Beta and Gamma band is stronger even if the connectivity in Beta and Gamma band is unknown before in our study. In contrast, the connectivity value was not stronger in Beta and Gamma band compared with other frequency bands without the PCA preprocessing.

Fig.6.

Connectivity of simulated data with and without removing first four PCs in Beta (a, b) and Gamma band (c, d), respectively

4. DISCUSSIONS AND CONCLUSIONS

In typical event related recordings, the evoked response is generally, at least one order of magnitude smaller than the on-going spontaneous activity. In other words, in each epoch the evoked response is masked by the spontaneous activity, therefore, the exploration of the underlying neuronal network of the evoked responses may be masked. Besides the spontaneous activity, the background activity from the external noise, the field effects between coils and cortex, and the overlap of the sensitivity area of different coils also result in relatively large extracranial coherence even when the underlying brain sources are uncorrelated (Srinivasan et al. 1999; Winter et al. 2007; Malmivuo and Plonsey 1995).

In this paper, we found that applying PCA decomposition is critical for capturing the dominant background activity, especially spontaneous activity, by the first few PCs for evoked response connectivity analysis. We demonstrated in MEG simulated data that the dominant components of the background activity can be removed by applying our approach for evoked responses. This new approach of PCA preprocessing improves the evoked information carried by individual channels, and also improves the connectivity analysis of the true neuronal interactions between cortical areas with event-related data. Hence, PCA can be employed to expose the evoked activity, and further applied as a preprocessing approach to improve neuronal connectivity analysis for event related data.

In the application of our approach, a major issue is to determine the number of PCs to be discarded. Many factors are expected to influence this choice, such as the strength of the spontaneous activity, external noise and the number of channels in the measurement system, to name a few, in addition to the actual event-related experiment. In our system, we need variable number of channels for the same purpose. Generally speaking, the number of the largest PCs for the background activity should not necessarily be constant for different subjects. In our studies, we also proposed a novel way to quantify the background signal in PCA decomposition. Many kinds of preprocessing may cause the loss of the original signals. In order to check the significance of the loss of the evoked information by our preprocessing approach, we carried out the t-test on the GFP of the data before and after applying our method. The channels with evoked signal were selected to focus on the evoked cortical areas. The GFP for the selected electrodes was calculated with removing additional largest PCs, and the t-test on GFP between original data and residuals was performed to ensure that the evoked information was maintained after PCA preprocessing as in Fig.2(b). If the first few PCs represent the background activity, the average coherence between the selected channels will increase during the elimination of PCs according to our results (Fig.2(c)), while the average coherence between all channels will decrease (the results were observed in simulated data but omitted here). Based on these results, we suggest that the rule-of-thumb is to balance increasing evoked connectivity information by discarding PCs, while maintaining the evoked response. We also validated this approach with somatosensory evoked MEG data of ten subjects, and obtained consistent results, which are detailed in our next paper.

The spontaneous activity represents stronger power, and it contributes more to the measured coherence than the local neuronal sources. Thus, it could bias the coherence greatly, which reflects the real coupling between brain regions. We also know the improved SNR by removing artifacts could also lead to increased evoked components and thereby increase their similarity across sensors. In order to further explore the components discarded, we performed spectral analysis in Fig.4, and the peaks in physiological bands of removed PCs prove that the discarded PCs mainly capture physiological components rather than strictly artifacts. In that case, the paper is not about artifact rejection, but focuses on the influence of spontaneous brain activity on event-related connectivity analysis.

Coherence is a classic connectivity index in the frequency domain. Until the 1990s, many scientists and physiologists were skeptical as to whether large or even moderate extracranial coherence could be reliably associated with brain source coherence. Such skepticism was bolstered by intracranial research on patients and animals measuring the subdural coherence using 2 mm diameter electrodes which reduced to zero at all frequencies for electrode separations greater than about 2 cm (Bullock et al. 1995a; Bullock et al. 1995b). Neocortical dynamics is believed to consist of local and regional cortical and thalamocortical networks embedded in global fields of synaptic action (Nunez and Srinivasan 2006a; Nunez and Srinivasan 2006b). Previously, many efforts were made to solve this problem by developing new methods. One of them is the application of the imaginary part of coherency to identify the true interactions (Nolte et al. 2004). The fundamental principle for this method is that the imaginary part is only sensitive to coupling of two time courses time-lagged to each other. The activity across channels due to field spread does not result in time-lag. The imaginary part is small or even vanishing if the time-lag is small or difficult to detect due to noise. Thus, the imaginary part of coherency is supposed to be purely related with interdependency. However, the connections between cortical areas are complicated, and could not be easily exposed by the time-lags between each other. Hence, it is possible that this approach misses some of the true connectivity.

Neuronal connectivity, including both functional and effective connectivity, is a rapidly developing field. Functional connectivity quantifies the statistical relations between neuronal signals without directionality, while the latter quantifies it with directionality. Frequency-resolved estimates of directed interactions between cortical areas can be obtained from parametric spectral estimators with multivariate autoregressive models (MVAR-models) (Schoffelen and Gross 2009). After fitting the MVAR-model to the time courses of the estimated sources, these directed interactions can be quantified by means of the directed transfer function (DTF) or the partial directed coherence. Alternatively, the Granger causality method (Granger 1969; Ding et al. 2006; Seth 2007) defines the directional information flow between stochastic time series purely according to the temporal interdependence (Seth 2010). This is not generally available for exploring interactions between sources. A basic requirement for applying this approach is that the data must be covariance stationary (Seth 2010), such that at least the stationarity is satisfied in a windowed segment (Seth 2010), which may result in loss of rapid changes in connectivity. However, MEG data are mostly non-stationary. Therefore, how to extract the stationary part from the non-stationary signal with minimum loss of connectivity becomes a critical issue. In this regard, we compared the stationarity of the data before and after applying our method, as shown in Fig.5. The results demonstrated that the data of all channels became stationary after PCA preprocessing, while the connectivity information remained. This indicates that the Granger causality analysis is feasible after applying our preprocessing procedure. Therefore, the approach introduced in our paper provides an alternative/add-on method to deal with the non-stationarity issue caused mainly by spontaneous activity.

Finally, we tested the effectiveness of our method with connectivity analysis of source data in event-related simulation. As demonstrated in Fig.6, the results after removing the first four PCs reflect the interactions designed in the simulation. In contrast, the results without removing the first four PCs show the wrong connectivity. It reveals that the first few PCs mainly contain strong and correlated background activity, and the evoked information is largely retained in the residuals.

In conclusion, the proposed PCA approach was tested in simulated human MEG data, and the results demonstrated that the PCA approach could be applied to capture the dominant components of background activity, and expose the evoked activity for the channels under investigation. Therefore, PCA decomposition can be applied as a preprocessing approach to facilitate the analysis of the evoked neuronal connectivity in MEG/EEG data.