Abstract
A GIS-based risk index model was developed to quantify EEEV transmission risk to horses in the State of Florida. EEEV is a highly pathogenic arbovirus that is endemic along the east coast of the United States, and it is generally fatal to both horses and humans. The model evaluates EEEV transmission risk at individual raster cells in map on a continuous scale of 0 to 1. The risk index is derived based on local habitat features and the composition and configuration of surrounding land cover types associated with EEEV transmission. The model was verified and validated using the locations of documented horse cases of EEEV. These results of the verification and validation indicate that the model is able to predict locations of EEEV transmission to horses broadly across the state. The model is relatively robust to regional variation in EEEV transmission and habitat conditions in Florida, and it accurately predicted nearly all verification and validation cases in the Panhandle, North, and Central regions of the state. The model performed less accurately in the South, where relatively few cases are documented. Despite these differences, the model provides a useful way to assess EEEV risk both from a regional perspective and at more localized scales. The resulting predictive maps are designed to guide EEEV surveillance and prevention efforts by county mosquito control districts.
1 Introduction
The most pathogenic arbovirus—or arthropod-borne virus—to affect the United States is Eastern Equine Encephalitis virus (EEEV). Viral transmission of EEEV is found predominately along the east coast of the United States from Maine to Florida with cases of neuro-invasive EEE reported in 20 states (Bigler et al., 1976). EEEV circulates in a transmission cycle involving freshwater swamp mosquitoes, competent avian reservoirs, and mammals (Crans, 1962; Moncayo, Edman, & Finn, 2000; Morris, 1988). The mosquito Culiseta melanura is thought to be the primary enzootic vector for EEEV in North America, although numerous other species can carry the virus. The primary reservoir hosts are thought to be passerine songbirds for which the virus is generally non-fatal. Recent studies have also implicated reptiles as potential hosts of the virus (Bingham et al., 2012). The transmission cycle also involves bridge vectors—mosquitoes that feed on both birds and mammals—which transmit EEEV to humans, horses, and other mammals during epizootic outbreaks(Weaver, 2005).
Currently, there is no approved human vaccine or effective treatment available for those infected with EEEV. Symptoms of EEEV in humans include swelling of the brain, chills, fever, and malaise, among others. The case fatality rate of symptomatic humans can be 35% or more with surviving cases often suffering from neurological complications, including brain impairment, and resulting in million dollar health care costs (Villari, Spielman, Komar, McDowell, & Timperi, 1995). Therefore, prevention and surveillance still remain the best options for controlling the risk of infection to humans. A vaccine is available to protect horses, although horse fatalities are still common in North America. Florida has the greatest burden of EEE cases in the United States, accounting for 25% of all human fatalities since 1964 (CDC, 2010). In Florida, EEEV claims an average of 70 horse fatalities a year (P. T. Vander Kelen et al., 2012). EEEV continues to be widespread across Florida, with transmission reported in 64 of Florida's 67 counties (Lobo, Jimenez-Valverde, & Real, 2008; Zweig & Campbell, 1993). Unlike the Northeast and Central United States, which observe epizootic outbreaks of human and horse cases in August and September (Letson, Bailey, Pearson, & Tsai, 1993), EEEV transmission in Florida occurs throughout the year, with most human and horse cases occurring in June and July (Bigler, Lassing, Buff, Lewis, & Hoff, 1975).
In addition to EEEV, Florida has several other endemic mosquito borne diseases, including West Nile Virus (WNV) and St. Louis encephalitis virus (SLE). As a result, most counties in Florida maintain active surveillance and control programs aimed at reducing the threat of arboviruses. The surveillance activities undertaken by these programs involve mosquito collections to monitor increases in putative vector populations and screening of sentinel chicken flocks to monitor virus activity. These data are used to guide mosquito control activities. Florida spends approximately $150 million per year on these activities (Jaing, 2010), which represents one of the largest state expenditures in the country. Traditionally, the locations of many of the sentinel chicken flocks in Florida were determined based upon the proximity to human cases of SLE during the last major human outbreak of this virus in the 1970s (Monath & Tsai, 1987; Nelson et al., 1983). Since EEEV, SLE, and WNV do not necessarily share the same environmental risk variables (LaBeaud et al., 2008; Moncayo et al., 2000), it is important to modify existing surveillance efforts to improve public protection from multiple arboviruses.
Geographic information systems (GIS) are commonly used to map disease occurrence and predict potential high risk areas for arboviral disease transmission. For instance, a number of studies have used climate, vegetation, elevation, and other environmental variables to predict West Nile Virus (Crowder et al., 2013; Day & Shaman, 2008; LaBeaud et al., 2008; Rochlin, Turbow, Gomez, Ninivaggi, & Campbell, 2011; Ruiz et al., 2010; Yoo, 2013; Young, Tullis, & Cothren, 2013). Similar approaches have also been used to map Dengue (Dickin, Schuster-Wallace, & Elliott, 2014; Machado-Machado, 2012) and Malaria (Fuller, Troyo, Alimi, & Beier, 2014) risk, as well. While risk maps developed to predict arboviral transmission can be used to guide prevention efforts such as chemical spraying (Chu, Chan, & Jao, 2013), such a model has not previously been developed to predict EEEV in Florida. Developing a model capable of identifying EEEV foci would be very useful in assisting the county mosquito control districts in targeting their surveillance and vector control efforts to those areas most likely to support viral transmission. Such a targeted surveillance and control program would result in more efficient detection of viral activity, thereby providing increased protection to Florida's residents.
This study reports development and application of a risk index model for predicting EEEV transmission to horses in the state of Florida. This is the first reported attempt, to our knowledge, to predictively map EEEV transmission risk. The model incorporates previously published habitat risk variables derived from Florida's 2005-2010 horse cases (P. T. Vander Kelen et al., 2012). The GIS-based model is applied using publicly available land use-land cover data. The index model estimates transmission risk to horses on a continuous scale from 0 to 1. The risk index model was verified using the previously published dataset and validated with independent cases documented during 2004 and 2011. The overall goal is to develop an accurate model that can be applied to assist county mosquito control districts in their EEEV surveillance and prevention efforts.
2 Methods
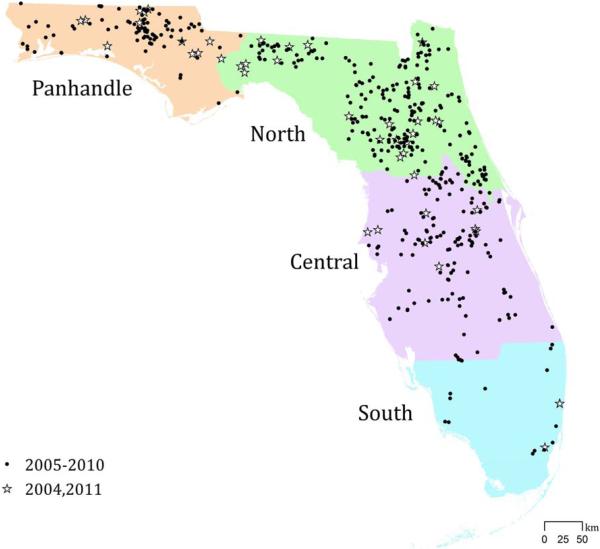
A spatially-explicit GIS-based risk index model was developed to quantify EEEV transmission risk to horses in Florida. The model inputs and parameters were derived from a recent study published by Vander Kelen et al. (2012) that quantified habitats associated EEEV horse cases in Florida (hereinafter referred to as the previous study). The previous study examined habitat composition and configuration associated with 438 horse cases of EEEV reported during 2005-2010 within four regions of the state: Panhandle, North, Central, and South (Figure 1). Development of the risk index model was consistent with that for spatially-explicit habitat suitability index (HSI) models used to evaluate habitat for wildlife, where suitability is measured on a continuous scale that ranges from 0 (unsuitable) to 1 (optimal) (Brooks, 1997; Dijak, Rittenhouse, Larson, Thompson, & Millspaugh, 2007; Downs, Gates, & Murray, 2008; Rickers, Queen, & Arthaud, 1995; Roloff & Kernohan, 1999). The risk index model assesses EEEV transmission risk for horses on a similar scale extending from 0 (minimal risk) to 1 (maximal risk), where intermediate values measure relative levels of risk. The model relies on land cover data in raster format and assesses EEEV transmission risk at each grid cell. Land cover data at a 30 m spatial resolution generated by the Florida Department of Environmental Protection's Bureau of Watershed Restoration and distributed by the state's five Water Management Districts was used in both this and the previous study. This dataset includes land use and cover classified at four levels, with Level 1 being the most generalized and Level 4 the most specific. This study utilized Level 2 descriptions, as they differentiated between various wetland types and residential classes which were necessary for the model. The forty-two Level 2 classes were aggregated into 14 classes (Table 1) relevant to the model. Coastal habitats were excluded, as the vectors for EEEV are freshwater species of mosquito. EEEV risk is quantified based on the local land cover at each cell, as well as habitat composition and configuration in the surrounding area. The developed model includes five individual risk variables—all scaled 0 to 1—which are integrated into a final index that assesses overall risk on the same scale. These risk variables include: local habitat, wetland proximity, wetland composition, tree plantation-coniferous forest proximity, and tree plantation-coniferous forest composition.
Figure 1.
Locations of documented horse cases of EEEV during 2005-2010 (Vander Kelen et al. 2012a) and 2004 and 2011 (validation sites) within four regions of Florida.
Table 1.
Risk values for local habitat (RV1) for 14 land cover types.
| Land cover type at raster cell | RV1 |
|---|---|
| Low density residential | 1.00 |
| Crop-pastureland | 1.00 |
| Tree plantations | 0.48 |
| Upland hardwood forest | 0.41 |
| Medium density residential | 0.27 |
| Commercial | 0.20 |
| High density residential | 0.14 |
| Upland coniferous forest | 0.13 |
| Wetland mixed forest | 0.11 |
| Wetland coniferous forest | 0.08 |
| Shrubland and brushland | 0.08 |
| Vegetated nonforested wetland | 0.07 |
| Wetland hardwood forest | 0.07 |
| Water | 0.04 |
| Urban | 0.03 |
| Mining | 0.02 |
| All others | 0.01 |
2.1 Risk Model Formulation
2.1.1 Risk Variable 1 (RV1): Local habitat
RV1 measures EEEV transmission risk associated with the land cover type at each cell. Values for RV1 were derived from the proportions of documented horse cases that fell within each land cover type. The highest proportions were found in low density residential (0.34) and crop-pastureland (0.21). Since these classes represent the most likely places to find horses, raster cells with those cover types were assigned maximal values of 1.0 for RV1. Values for other cover types were calculated by dividing the observed proportion of cases by 0.21, the smaller of the latter two values. This assigns risk values to the other cover types based on the relative proportion of cases found in each type. Calculated values for RV1 for all cover types are summarized in Table 1, with the next highest values including tree plantations, upland hardwood forests, and medium density residential.
2.1.2 Risk Variable 2 (RV2): Wetland proximity
RV2 measures EEEV transmission risk associated with wetland proximity. The previous study indicated that EEEV horse cases were strongly associated with close proximities to wetlands. Although there were small variations among the four regions of the state, more than half of the cases occurred within 400 m of some type of wetland, with most located within 1500 m. Additionally, cases in all regions were located closer to wetlands than expected at random. Therefore, RV2 is calculated based on the distance from the focal raster cell (i.e. the raster cell being evaluated) to the nearest wetland in meters, dw, where:
Effectively, if a cell is less than 400 m from the nearest wetland, it is assigned a risk value of 1. If it is located between 400 and 1500 m, it receives a value that extends from 0 to 1, inversely proportional to the distance away. If a cell is more than 1500 m from the nearest wetland, it is assigned a 0. Note this 1500 m threshold also coincides with the distance that many of the EEEV bridge vector mosquito species typically disperse (Estep, Burkett-Cadena, Hill, Unnasch, & Unnasch, 2010) (Morris, Larson, & Lounibos, 1991) .
2.1.3 Risk Variable 3 (RV3): Wetland composition
RV3 measures EEEV transmission risk associated with the amount of wetland surrounding each raster cell. Wetland habitats are known to be associated with EEEV, since they frequently support vectors of the virus (Moncayo et al., 2000). The previous study found that the proportion of wetlands within a 1500 m buffer—or radius—of a horse case averaged 0.18. RV3 is calculated from the proportion of wetlands within 1500 m of each focal cell, pw, where:
In other words, if the calculated proportion of wetlands in the focal area (i.e. circular window with a radius of 1500 m centered at the focal cell) is greater than 0.18, the focal cell receives a value of 1 for RV3. For values less than 0.18, the cell receives a value proportional to the amount. For example, if the calculated proportion is 0.09, the cell receives a RV3 value of 0.5. Cells not surrounded by any wetlands receive 0.0.
2.1.4 Risk Variable 4 (RV4): Tree plantation-coniferous forest proximity
RV4 measures EEEV transmission risk associated with proximity to tree plantations and other upland coniferous forests. The previous study indicated that EEEV horse cases were strongly associated with close proximities to tree plantations and other coniferous forests, which was further supported by Vander Kelen et al. (2012). Although there were variations among the four regions of the state, more than half of the cases occurred within 250 m of tree plantations or other coniferous forests; most occurred within 1500 m. Additionally, cases in northern and central Florida were located significantly closer to coniferous forests than expected at random, while median distances were about 600 and 1300 m for the panhandle and south, respectively. RV4 is calculated based on the distance from the focal raster cell to the nearest tree plantation or coniferous forest in meters, dc, where:
If a cell is less than 250 m from the nearest tree plantation or coniferous forest, it is assigned a value of 1. If it is located between 250 and 1500 m, it receives a value that extends from 0 to 1, inversely proportional to the calculated distance. If a cell is more than 1500 m away, it is assigned a 0, or minimal risk.
2.1.5 Risk Variable 5 (RV5): Tree plantation-coniferous forest composition
RV5 measures EEEV transmission risk associated with the amount of tree plantations and coniferous forest surrounding each raster cell. Other studies have identified a relationship between the abundance of tree plantations and EEEV (P. Vander Kelen, T. et al., 2012). The previous study found that the proportion of tree plantations and coniferous forests within a 1500 m buffer of a horse case averaged 0.20. RV5 is calculated from the proportion of tree plantations and coniferous forests within 1500 m of each focal cell, pc, where:
If the calculated proportion of these habitats in the focal area is greater than 0.20, the focal cell receives a value of 1 for RV5. For values less than 0.20, the cell receives a value proportional to the amount calculated.
2.1.6 Risk index model
The final risk index model assesses EEEV transmission based on the five risk variables identified above. The model consists of two parts that are multiplied together to generate a final risk index (RI) value for each grid cell, where:
The first part—simply RV1—represents the transmission risk at the grid cell based on its cover type. The reason that RV1 operates as a multiplicative factor is that the local habitat type plays a controlling role in EEEV transmission. In other words, if a cell has a cover type likely to be occupied by horses, such as low density residential, crop-pastureland, or others associated with numerous reported horse cases of EEEV, then those cells initially are assigned higher risk values. Cells with habitats unlikely to support horses, such as open water, start with very minimal risk values.
The second part of the equation calculates risk based on the surrounding habitat which also plays a role in transmission. Here, the other four risk variables calculated for each cell—RV2, RV3, RV4, and RV5—are averaged. When averaged, cells located in close proximity to an abundance of wetlands and tree plantations-coniferous forests will receive the highest risk based on surrounding habitat, since they will have high risk values for the latter four risk variables. Similarly, cells that are not located near any wetlands or tree plantations-coniferous forests will receive a low average for these four risk variables. Averaging also allows low values for some risk variables to be partially compensated by higher values in the others, generating intermediate values for the second half of the equation. Although other formulations are possible, averaging produces less restrictive output than would occur for instance by multiplying them together; in that case a zero for any risk variable would always produce a final index value of zero.
Then, the final RI value is calculated by multiplying RV1 by the resulting average of the other four RVs. Multiplying these two portions of the equation ensures that cells only receive high index values if high risk values are calculated for both parts of the equation—in other words if the calculated risk is high for both the local habitat and the surrounding landscape. For example, if the focal cell is classified as medium density residential, RV1 equals 0.27 based on Table 1. If the average of the other four risk variables equals 0.9 as calculated from the surrounding landscape, the estimated risk index value is 0.243, moderately low risk. On the other hand, if a focal cell is classified as low density residential, where RV1 equals 1, then a 0.9 calculated from the surrounding landscape would yield a final risk index of 0.9, a very high risk. The EEEV transmission risk index model was applied using a geographic information system (GIS), ArcMap v. 10.0 (ESRI, Inc), with the land cover data described in section 2.1 to produce a map of risk index values for the state of Florida (excluding the Florida Keys).
2.2 Risk Model Verification and Validation
Verification and validation procedures are commonly used to assess the accuracy of suitability and risk models (Brooks, 1997; Roloff & Kernohan, 1999). Verification involves evaluating how well the model predicts the sample data used to generate the model. In this case, locations of the 438 horse cases analysed in the previous study were used to verify the computed risk index values. The point locations for these cases were overlaid with the risk index map in the GIS, and the values at each location were extracted. Basic summary statistics were calculated. For comparison, the same statistics were generated for random points in the state (n ~ 4700). The random points were generated in proportion to the number of cases documented within each of the four regions, excluding coastal areas, such that they would mimic the overall distribution of EEEV in the state (Panhandle: 19.9%, North: 48.5%, Central: 27.9%, South: 3.7%; Figure 1). A Mann-Whitney test was used to evaluate if higher risk values were recorded at the known case locations than expected at random, which would suggest the model predicts transmission of EEEV to horses. Additionally, since the x-y spatial coordinates of the horse cases are subject to potential geo-referencing errors (GPS or geocoding errors, x-y coordinates recorded at owner's residence rather than horse's location, etc.), the analysis was repeated using a 100 m error radius for each case. Here, the maximum RI values within 100 m of the horse cases were analysed to assess if the model predicted cases when considering a relatively small amount of positional error. The maximum RI values within 100 m of the random points were used in the comparison, as well. The analysis was completed both state-wide and by region.
Validation involves testing how well a model predicts independent data. Here, documented horse cases of EEEV in Florida during 2004 and 2011, data not analysed in the previous study, were used to validate the risk index model. There were 41 cases observed during 2004 and 6 during 2011, so the sample represents cases from both high and low transmission years. Risk index values were extracted for these locations, summarized, and compared to the same values for random points in the state using the same procedures as for the verification analysis. The analysis was also repeated using the 100 m error radius around each location in the same manner, both state-wide and by region. Figure 1 illustrates both the horse cases from the previous study and the test cases within the four regions of Florida.
3. Results
3.1 Risk Model Application
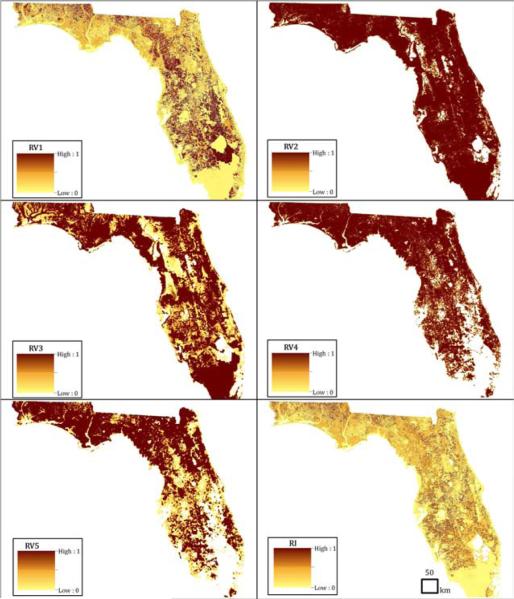
Figure 2 shows individual risk variables and the final risk index for EEEV transmission to horses across the state of Florida. The state-wide mean value for RV1, the local habitat variable, is 0.36 (s=0.37) with higher values more concentrated in rural portions of the Panhandle, North, and Central regions. RV2, which measures wetland proximity, averaged 0.28 (s=0.44), with high values distributed patchily across the state. The mean value for RV3, wetland composition, was 0.66 (s=0.41), with maximal values distributed widely across the state, including the South where the Everglades are located. Values for RV4, tree plantation-coniferous forest proximity, averaged 0.22 (s=0.39), with higher values more frequent in the Panhandle, North, and portions of the Central region. The average for RV5, tree plantation-coniferous forest composition, was 0.52 (s=0.45), with maximal values more concentrated in the Panhandle and North. Finally, risk index values computed from overlaying these five risk variable maps averaged 0.28 (s=0.29). High risk index values are patchily distributed across the state and are predominately located in the Panhandle, North, and Central regions.
Figure 2.
State-wide maps of five risk variables (RV1 through RV5) used to generate risk index (RI) values for EEEV transmission to horses in Florida.
Figure 2 only shows broad-scale patterns in the individual risk variables and the final risk index, partially obscuring variability that occurs at more localized scales. Figure 3 illustrates all five risk variables and the risk index for a small portion of the Panhandle, which are displayed at a larger cartographic scale such that individual 30 m grid cells in the maps can be discerned. The figure highlights how cells are initially assigned risk values based on the habitat classification at each cell (RV1), and those values are reduced by the average of the other four risk variables (RV2-RV5) to achieve a final risk index (RI). For example, the darkest cells in the map of RV1 with values of 1 are either low density residential or crop-pastureland. In the final map, some of those cells retain a risk index of 1 based on the composition and configuration of the surrounding landscape with respect to wetlands and tree plantations-coniferous forest, while others show drastically reduced RI values because they are not near either of those habitats. This illustrates how EEEV transmission can be assessed at a fine spatial resolution. Figure 3 also illustrates the model output relative to two validation sites, which fall in high risk areas, as described in the next section.
Figure 3.
Localized maps of five risk variables (RV1 through RV5) used to generate risk index (RI) values for EEEV transmission to horses in Florida. The starred locations indicate two horse cases used to validate the model.
3.2 Risk Model Verification and Validation
Table 2 summarizes the mean and median risk index values for the horse cases from the previous study (2005-2010) and those from 2004 and 2011 used to verify and validate the model, respectively, as compared to random locations in the state. The first three rows of the table summarize the results of the state-wide analysis. When the RI value at each location is examined, horse cases from the previous study had RI values that have a mean of 0.54 and a median of 0.48. This compares to state-wide mean and median values of 0.31 and 0.24 for random points distributed proportionally by region. When a radius of locational error is included, the horse cases have a mean of 0.72 and a median of 0.84. This compares to a mean of 0.44 and a median of 0.48 for random points. A Mann-Whitney test indicated the median RI values for the horse cases were statistically higher than the random cases for both the local cell and error radius comparison (p<0.001), verifying that the risk index predicts the cases used to generate the model.
Table 2.
EEEV transmission risk index (RI) values summarized state-wide and by region for documented horse cases during 2005-2010 (Vander Kelen et al. 2012a), documented horse cases during 2004 and 2011, and randomly distributed points recorded at the location and within a 100 m error radius.
| Value at location |
Maximum value within 100 m of location |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scale | Sample | n | min | mean | s | med | max | min | mean | s | med | max |
| State-wide | 2005-2010 cases | 438 | 0.00 | 0.54 | 0.36 | 0.48 | 1.00 | 0.00 | 0.72 | 0.31 | 0.84 | 1.00 |
| 2004,2011 cases | 47 | 0.00 | 0.56 | 0.35 | 0.54 | 1.00 | 0.00 | 0.75 | 0.30 | 0.89 | 1.00 | |
| Random locations | 4700 | 0.00 | 0.31 | 0.29 | 0.24 | 1.00 | 0.00 | 0.44 | 0.31 | 0.48 | 1.00 | |
| Panhandle | 2005-2010 cases | 87 | 0.03 | 0.55 | 0.34 | 0.48 | 1.00 | 0.03 | 0.78 | 0.31 | 0.96 | 1.00 |
| 2004,2011 cases | 11 | 0.07 | 0.44 | 0.36 | 0.40 | 1.00 | 0.27 | 0.75 | 0.29 | 0.88 | 1.00 | |
| Random locations | 934 | 0.00 | 0.36 | 0.30 | 0.38 | 1.00 | 0.00 | 0.49 | 0.31 | 0.48 | 1.00 | |
| North | 2005-2010 cases | 212 | 0.00 | 0.56 | 0.35 | 0.48 | 1.00 | 0.02 | 0.72 | 0.29 | 0.81 | 1.00 |
| 2004,2011 cases | 24 | 0.08 | 0.61 | 0.34 | 0.70 | 1.00 | 0.10 | 0.78 | 0.25 | 0.86 | 1.00 | |
| Random locations | 2275 | 0.00 | 0.32 | 0.27 | 0.30 | 1.00 | 0.00 | 0.45 | 0.29 | 0.48 | 1.00 | |
| Central | 2005-2010 cases | 122 | 0.02 | 0.53 | 0.38 | 0.64 | 1.00 | 0.02 | 0.71 | 0.32 | 0.83 | 1.00 |
| 2004,2011 cases | 9 | 0.25 | 0.73 | 0.29 | 0.90 | 1.00 | 0.26 | 0.87 | 0.24 | 0.96 | 1.00 | |
| Random locations | 1315 | 0.00 | 0.32 | 0.32 | 0.14 | 1.00 | 0.00 | 0.43 | 0.34 | 0.41 | 1.00 | |
| South | 2005-2010 cases | 16 | 0.00 | 0.49 | 0.36 | 0.64 | 1.00 | 0.00 | 0.54 | 0.39 | 0.71 | 1.00 |
| 2004,2011 cases | 3 | 0.00 | 0.13 | 0.23 | 0.00 | 0.39 | 0.00 | 0.14 | 0.25 | 0.00 | 0.43 | |
| Random locations | 176 | 0.00 | 0.11 | 0.20 | 0.04 | 0.99 | 0.00 | 0.18 | 0.26 | 0.04 | 1.00 | |
When the analysis was used to validate the model using horse case data from 2004 and 2011, the results were very similar. When the RI value at each location was examined, horse cases from the independent data set had RI values that have a state-wide mean of 0.56 and a median of 0.54, values very similar to the original cases. When the error radius was included, these test cases had a mean of 0.75 and a median of 0.89. When compared to the medians for the random points, the Mann-Whitney test also indicates that risk index values are higher at the 2004 and 2011 horse case locations than expected at random (p<0.001). This validates that the risk index model is able to predict locations of EEEV transmission risk to horses in Florida broadly across the state.
Table 2 also summarizes how the model performed in each of the four regions of the state. For the risk index values extracted directly from each location, horse cases from the previous study had similar averages across all four regions, ranging from 0.49 to 0.56. The mean for random points were similar in the Panhandle, North, and Central regions (0.32-0.36) but much lower in the South, averaging 0.11. Median risk index values for the cases were 0.64 in both the Central and South and 0.48 in the Panhandle and North. Medians for the random points varied more by region, ranging from 0.04 in the South to 0.38 in the Panhandle. Similarly, the validation cases displayed higher risk index values in the Panhandle, North, and Central regions—with means ranging from 0.44 to 0.73 and medians from 0.40 to 0.90—and lower values in the South with two of those three cases recorded as 0.0. Mann-Whitney tests indicated that the median values were higher than expected at random for cases from the previous study in all regions and the validations in both the North and Central regions (p<0.001).
The differences between the horse cases and random locations are much more pronounced when a 100 m error radius is considered. The means for cases from the previous study in the Panhandle, North, and Central regions ranged from 0.54 to 0.78, with medians from 0.71 to 0.96. The validation cases had mean values of 0.72 to 0.86 and median values of 0.75 to 0.96 for these same three regions. Mean and median values were considerably lower in the South, 0.14 and 0.00, respectively. The means and medians for random points were also higher in the upper three regions (mean values from 0.43 to 0.49) and much lower in the South, with a mean of 0.18. Mann-Whitney tests indicated that the median values were higher than expected at random for cases from the previous study. The median values were also higher than expected at random in all regions except the South.
4. Discussion and Conclusions
This research produced a state-wide risk index model that assesses EEEV transmission risk for horses in Florida based on local habitat features and the composition and configuration of surrounding land cover. The model is relatively simple to apply can be derived solely from detailed land cover. The results of the model show considerable amounts of high risk locations in the upper three regions of the state and relatively little in the South. The model is relatively robust to regional variation in EEEV transmission and habitat conditions in the state, and accurately predicted nearly all verification and validation cases in the Panhandle, North, and Central regions of the state. The model performed less accurately in the South, where relatively few cases are documented. Despite these differences, the model provides a useful way to assess EEEV risk both from a regional perspective and at more localized scales of individual farms.
In terms of local predictions, the model performed better when factoring very modest locational errors of 100 m for the documented cases. In practice, horse cases are often geo-referenced based on the owner's residence, while the animal may actually be housed on another portion of the owner's property or farm. The process of geo-coding municipal addresses in a GIS also introduces additional error (Zandbergen, 2009). These types of errors may explain why the model did not predict some of the documented horse cases, particularly two cases in the South that were not located within 1.5 km of wetlands or tree plantations-coniferous forests. One explanation for the low risk index values is that there may be some errors in the land cover data set, as habitat classification accuracy can be low for wetlands and other cover types.
Alternatively, it is possible that those horses became infected with the virus at another location, such as if the horse was transported to another farm or recreational area for some time period. In these cases, it would be more useful to geo-reference the case to the location of infection, if known. Another explanation for some lower risk values recorded for documented cases is that they were located in habitats less likely to support horses and thus received low index values due to low values associated with RV1, the local habitat risk variable. This is an important consideration if the risk map is to be used to evaluate if a particular owners’ horses are likely to be at high risk for EEEV infection in situations where they are located in a cover type assigned low RV1 values. In these cases, since horses are known to be present, the model could be modified to assign a value of 1.0 for that risk variable, with the other risk variables used to evaluate overall risk based on the surrounding habitat.
The risk model formula is flexible and allows for the possible inclusion of additional variables. For example, meteorological variables such as precipitation, water table depth, and temperature could improve the models performance. Studies in Florida have shown that hydrologic conditions can provide accurate temporal predictions for arboviral transmission (Day & Shaman, 2008; Shaman, Day, & Stieglitz, 2004). The possible inclusion these kinds of variables into this model could improve the EEEV prediction efforts by adding a temporal dimension; EEEV activity could be predicted both in space and in time. However, incorporating more dynamic variables like temperature and precipitation, both of which fluctuate day to day, may offer refinement but the model will have to be run more frequently. Further research is needed to determine the usefulness of adding more variables to the risk index model.
One of the biggest obstacles to EEEV research is determining where to direct field work, both in terms of surveillance and prevention efforts. The risk index model addresses this issue by focusing on the spatial location of risk. A state wide risk model that provides accurate local predictions of horse cases could be adapted to predict human cases of EEE. Florida accounts for 25% of all human EEE fatalities in the U.S. and the locations of these cases could be used to determine if the risk index model can accurately predict both horse and human cases, since humans and horses often reside in the same land cover types. This could provide local mosquito control districts with the opportunity for targeted surveillance. Relocating some of the chicken sentinel sites to high risk areas could be another method for validating the model while increasing the surveillance's effectiveness. The model offers an opportunity to reevaluate how surveillance for EEEV is being conducted at state and county levels as well as in individual mosquito control districts. Using a targeted approach to mosquito control could reduce the cost of operations while providing better public health prevention for Florida's residents.
Highlights.
A GIS-based risk model was developed to predict EEEV
The model was verified and validated using documented cases
The model accurately predicted horse cases in Florida
The results can be used to guide mosquito control efforts
Acknowledgements
The authors thank NIAID for financial support through grants R01AI49724 and R56AI01372.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bigler WJ, Lassing E, Buff E, Lewis AL, Hoff GL. Arbovirus surveillance in Florida: Wild vertebrate studies 1965-1974. Journal of Wildlife Diseases. 1975;11(3):348–356. doi: 10.7589/0090-3558-11.3.348. [DOI] [PubMed] [Google Scholar]
- Bigler WJ, Lassing EB, Buff EE, Prather EC, Beck EC, Hoff GL. Endemic eastern equine encephalomyelitis in Florida: a twenty-year analysis, 1955-1974. Am J Trop Med Hyg. 1976;25(6):884–890. doi: 10.4269/ajtmh.1976.25.884. [DOI] [PubMed] [Google Scholar]
- Bingham AM, Graham SP, Burkett-Cadena ND, White GS, Hassan HK, Unnasch TR. Detection of Eastern Equine Encephalomyelitis Virus RNA in North American Snakes. The American Journal of Tropical Medicine and Hygiene. 2012;87(6):1140–1144. doi: 10.4269/ajtmh.2012.12-0257. doi: 10.4269/ajtmh.2012.12-0257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks RP. Improving habitat suitability index models. Wildlife Society Bulletin. 1997;25(1):163–167. [Google Scholar]
- CDC Eastern Equine Encephalitis, Epidemiology and Geographic Distribution. 2010 from http://www.cdc.gov/easternequineencephalitis/tech/epi.html.
- Chu H-J, Chan T-C, Jao F-J. GIS-aided planning of insecticide spraying to control dengue transmission. International Journal of Health Geographics. 2013;12(1):42. doi: 10.1186/1476-072X-12-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crans WJ. Bloodmeal preference studies with New Jersey mosquitoes. Proceedings of the New Jersey Mosquito Extermination Association. 1962;49:120–126. [Google Scholar]
- Crowder DW, Dykstra EA, Brauner JM, Duffy A, Reed C, Martin E, Owen JP. West Nile Virus Prevalence across Landscapes Is Mediated by Local Effects of Agriculture on Vector and Host Communities. PLoS One. 2013;8(1):e55006. doi: 10.1371/journal.pone.0055006. doi: 10.1371/journal.pone.0055006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day JF, Shaman J. Using hydrologic conditions to forecast the risk of focal and epidemic arboviral transmission in peninsular Florida. J Med Entomol. 2008;45(3):458–465. doi: 10.1603/0022-2585(2008)45[458:uhctft]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Dickin SK, Schuster-Wallace CJ, Elliott SJ. Mosquitoes & vulnerable spaces: Mapping local knowledge of sites for dengue control in Seremban and Putrajaya Malaysia. Applied Geography. 2014;46(0):71–79. doi: http://dx.doi.org/10.1016/j.apgeog.2013.11.003. [Google Scholar]
- Dijak WD, Rittenhouse CD, Larson MA, Thompson FR, Millspaugh JJ. Landscape habitat suitability index software. Journal of Wildlife Management. 2007;71(2):668–670. doi: 10.2193/2006-341. [Google Scholar]
- Downs JA, Gates RJ, Murray AT. Estimating carrying capacity for sandhill cranes using habitat suitability and spatial optimization models. Ecological Modelling. 2008;214(2-4):284–292. doi: 10.1016/j.ecolmodel.2008.02.006. [Google Scholar]
- Estep LK, Burkett-Cadena ND, Hill GE, Unnasch RS, Unnasch TR. Estimation of Dispersal Distances of Culex erraticus in a Focus of Eastern Equine Encephalitis Virus in the Southeastern United States. Journal of Medical Entomology. 2010;47(6):977–986. doi: 10.1603/me10056. doi: 10.1603/ME10056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuller DO, Troyo A, Alimi TO, Beier JC. Participatory risk mapping of malaria vector exposure in northern South America using environmental and population data. Applied Geography. 2014;48(0):1–7. doi: 10.1016/j.apgeog.2014.01.002. doi: http://dx.doi.org/10.1016/j.apgeog.2014.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaing P. [Florida Department of Agriculture and Consumer Services, Mosquito Control] 2010 [Google Scholar]
- LaBeaud AD, Gorman AM, Koonce J, Kippes C, McLeod J, Lynch J, Mandalakas AM. Rapid GIS-based profiling of West Nile virus transmission: defining environmental factors associated with an urban-suburban outbreak in Northeast Ohio, USA. Geospat Health. 2008;2(2):215–225. doi: 10.4081/gh.2008.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letson GW, Bailey RE, Pearson J, Tsai TF. Eastern equine encephalitis (EEE): A description of the 1989 outbreak, recent epidemiologic trends, and the association of rainfall with EEE occurrence. American Journal of Tropical Medicine and Hygiene. 1993;49(6):677–685. doi: 10.4269/ajtmh.1993.49.677. [DOI] [PubMed] [Google Scholar]
- Lobo JM, Jimenez-Valverde A, Real R. AUC: a misleading measure of the performance of predictive distribution models. Global Ecology & Biogeography. 2008;17:145–151. [Google Scholar]
- Machado-Machado EA. Empirical mapping of suitability to dengue fever in Mexico using species distribution modeling. Applied Geography. 2012;33(0):82–93. doi: http://dx.doi.org/10.1016/j.apgeog.2011.06.011. [Google Scholar]
- Monath TP, Tsai TF. St. Louis encephalitis: lessons from the last decade. Am J Trop Med Hyg. 1987;37(3 Suppl):40S–59S. doi: 10.4269/ajtmh.1987.37.40s. [DOI] [PubMed] [Google Scholar]
- Moncayo AC, Edman JD, Finn JT. Application of geographic information technology in determining risk of eastern equine encephalomyelitis virus transmission. J Am Mosq Control Assoc. 2000;16(1):28–35. [PubMed] [Google Scholar]
- Morris CD. Eastern Equine Encephalomyelitis. In: Monath TP, editor. The Arboviruses: Epidemiology and Ecology. Vol. 3. CRC Press; Boca Raton, FL: 1988. pp. 1–20. [Google Scholar]
- Morris CD, Larson VL, Lounibos LP. Measuring mosquito dispersal for control programs. J Am Mosq Control Assoc. 1991;7(4):608–615. [PubMed] [Google Scholar]
- Nelson DB, Kappus KD, Janowski HT, Buff E, Wellings FM, Schneider NJ. St. Louis encephalitis--Florida 1977. Patterns of a widespread outbreak. Am J Trop Med Hyg. 1983;32(2):412–416. [PubMed] [Google Scholar]
- Rickers JR, Queen LP, Arthaud GJ. A Proximity-Based Approach to Assessing Habitat. Landscape Ecology. 1995;10(5):309–321. [Google Scholar]
- Rochlin I, Turbow D, Gomez F, Ninivaggi DV, Campbell SR. Predictive Mapping of Human Risk for West Nile Virus (WNV) Based on Environmental and Socioeconomic Factors. PLoS One. 2011;6(8):e23280. doi: 10.1371/journal.pone.0023280. doi: 10.1371/journal.pone.0023280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roloff GJ, Kernohan BJ. Evaluating reliability of habitat suitability index models. Wildlife Society Bulletin. 1999;27(4):973–985. [Google Scholar]
- Ruiz M, Chaves L, Hamer G, Sun T, Brown W, Walker E, Kitron U. Local impact of temperature and precipitation on West Nile virus infection in Culex species mosquitoes in northeast Illinois, USA. Parasites & Vectors. 2010;3(1):1–16. doi: 10.1186/1756-3305-3-19. doi: 10.1186/1756-3305-3-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaman J, Day JF, Stieglitz M. The spatial-temporal distribution of drought, wetting, and human cases of St. Louis encephalitis in southcentral Florida. Am J Trop Med Hyg. 2004;71(3):251–261. doi: 71/3/251 [pii] [PubMed] [Google Scholar]
- Vander Kelen P, T., Joni AD, Nathan DB-C, Christy LO, Kevin H, Stephen S, Thomas RU. Habitat associations of eastern equine encephalitis transmission in Walton County Florida. J Med Entomol. 2012;49(3):746–756. doi: 10.1603/me11224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vander Kelen PT, Downs JA, Stark LM, Loraamm RW, Anderson JH, Unnasch TR. Spatial epidemiology of eastern equine encephalitis in Florida. Int J Health Geogr. 2012;11:47. doi: 10.1186/1476-072X-11-47. doi: 1476-072X-11-47 [pii] 10.1186/1476-072X-11-47 [doi] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villari P, Spielman A, Komar N, McDowell M, Timperi RJ. The economic burden imposed by a residual case of eastern encephalitis. American Journal of Tropical Medicine and Hygiene. 1995;52(1):8–13. doi: 10.4269/ajtmh.1995.52.8. [DOI] [PubMed] [Google Scholar]
- Weaver SC. Host range, amplification and arboviral disease emergence. In: Peters CJ, Calisher C, editors. Infectious Diseases from Nature: Mechanisms of Viral Emergence and Persistence. Springer; Vienna: 2005. pp. 33–44. [DOI] [PubMed] [Google Scholar]
- Yoo E-H. Exploring space-time models for West Nile virus mosquito abundance data. Applied Geography. 2013;45(0):203–210. doi: http://dx.doi.org/10.1016/j.apgeog.2013.09.007. [Google Scholar]
- Young SG, Tullis JA, Cothren J. A remote sensing and GIS-assisted landscape epidemiology approach to West Nile virus. Applied Geography. 2013;45(0):241–249. doi: http://dx.doi.org/10.1016/j.apgeog.2013.09.022. [Google Scholar]
- Zandbergen PA. Geocoding Quality and Implications for Spatial Analysis. Geography Compass. 2009;3(2):647–680. doi: 10.1111/j.1749-8198.2008.00205.x. [Google Scholar]
- Zweig M, Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clinical Chemistry. 1993;39:561–577. [PubMed] [Google Scholar]