Using electronic health record data to develop inpatient mortality predictive model: Acute Laboratory Risk of Mortality Score (ALaRMS)

Abstract

Objective

Using numeric laboratory data and administrative data from hospital electronic health record (EHR) systems, to develop an inpatient mortality predictive model.

Methods

Using EHR data of 1 428 824 adult discharges from 70 hospitals in 2006–2007, we developed the Acute Laboratory Risk of Mortality Score (ALaRMS) using age, gender, and initial laboratory values on admission as candidate variables. We then added administrative variables using the Agency for Healthcare Research and Quality (AHRQ)'s clinical classification software (CCS) and comorbidity software (CS) as disease classification tools. We validated the model using 770 523 discharges in 2008.

Results

Mortality predictors with ORs >2.00 included age, deranged albumin, arterial pH, bands, blood urea nitrogen, oxygen partial pressure, platelets, pro-brain natriuretic peptide, troponin I, and white blood cell counts. The ALaRMS model c-statistic was 0.87. Adding the CCS and CS variables increased the c-statistic to 0.91. The relative contributions were 69% (ALaRMS), 25% (CCS), and 6% (CS). Furthermore, the integrated discrimination improvement statistic demonstrated a 127% (95% CI 122% to 133%) overall improvement when ALaRMS was added to CCS and CS variables. In contrast, only a 22% (CI 19% to 25%) improvement was seen when CCS and CS variables were added to ALaRMS.

Conclusions

EHR data can generate clinically plausible mortality predictive models with excellent discrimination. ALaRMS uses automated laboratory data widely available on admission, providing opportunities to aid real-time decision support. Models that incorporate laboratory and AHRQ's CCS and CS variables have utility for risk adjustment in retrospective outcome studies.

Introduction

Mortality predictive models incorporating objective clinical data enhance clinical validity. With the deployment of electronic health record (EHR) systems, clinical data, especially numeric laboratory data, are becoming widely automated. Rapid assessment of clinical severity using EHR data available at the time of admission may aid decision support and improve healthcare quality. Previous studies have demonstrated that laboratory data contribute most to predicting mortality in hospitalized patients in both disease-specific and generic models in the US patient population.^1–6 Studies from other countries have also demonstrated the high predictive value for laboratory data.^7–9

The disease-specific risk adjustment model is developed for patients with specific clinical conditions (eg, pneumonia, septicemia, heart failure, acute myocardial infarction).^4–6 Although disease-specific models are commonly used for outcome studies and hospital profiling, their application is limited to high-volume clinical conditions, while low-volume clinical conditions are less studied. Furthermore, disease specific models usually rely on discharge principal diagnosis for disease classification, which limits real-time applications because discharge diagnoses are not available until after patients are discharged from the hospital.

The generic approach generates one predictive model for all pertinent patients, such as all patients admitted to intensive care units (ICUs). For example, the Acute Physiology and Chronic Health Evaluation (APACHE IV) and Simplified Acute Physiology Score (SAPS) are developed and applied to all patients admitted to ICUs.^{1 2} A newer generic model, the Laboratory-based Acute Physiology Score (LAPS), and the COmorbidity Point Score (COPS), were developed for all patients admitted to acute-care hospitals,³ and used outpatient laboratory data from the 24 h preceding the index hospitalization and diagnosis data from the 12 months preceding the index hospitalization as predictor variables. This requires highly integrated inpatient and outpatient electronic systems, which are currently less available than inpatient data only. Furthermore, studies incorporating classification of clinical conditions as covariates in the model tend to use proprietary classification systems, which are not in the public domain.^{2–4 6}

The objectives of our study were twofold: (1) use EHR data available at the time of inpatient admission to develop an Acute Laboratory Risk of Mortality Score (ALaRMS), to serve as a potential real-time decision support tool for patients admitted to acute care hospitals; and (2) add administrative data available after patient discharge to the ALaRMS model to serve as a risk adjustment tool for retrospective inpatient outcome studies. To facilitate the standardization, reproducibility, and public access, we used the clinical classification algorithms of diagnoses in the public domain by the Agency for Healthcare Research and Quality (AHRQ).^{10 11}

Methods

Data

We used one of the clinical research databases from CareFusion (San Diego, California, USA (formerly Cardinal Health/MediQual/MedisGroups)). This database has been used for research since the late 1980s and the data collection system has been fully described elsewhere.^{4 6 12–19} We used data from the EHR systems of 70 hospitals for all consecutively hospitalized patients from 2006 through 2008. The laboratory data included numeric laboratory test results and collection times. A total of 23 numeric laboratory test results were included: serum chemistry (alphabetically ordered: albumin, aspartate transaminase, alkaline phosphatase, blood urea nitrogen (BUN), calcium, creatinine, glucose, potassium (K), sodium (Na), and total bilirubin); hematology and coagulation parameters (bands, hemoglobin, partial thromboplastin time, prothrombin time international normalized ratio (PT INR), platelets, and white blood cell count (WBC)); arterial blood gas (partial pressure of carbon dioxide (PCO2), partial pressure of oxygen (PO2), and pH value); cardiac markers (brain natriuretic peptide (BNP), creatine phosphokinase MB (CPK MB), pro-BNP, and troponin I).

The database also included imported hospital administrative data comprising demographics, discharge disposition (which identifies inpatient mortality status), principal diagnosis, and up to 24 secondary diagnosis codes from the index hospitalization. We used discharges in 2006 and 2007 as the derivation cohort and discharges in 2008 as the validation cohort. A total of 95% of patients had laboratory data on the day of admission for both cohorts. For patients with multiple laboratory assessments on the admission day, we used the first reported value.

Model development and validation

Step 1: develop and validate ALaRMS

We fit a logistic regression model using age, gender, and the first laboratory test results on the day of admission as candidate predictor variables and inpatient mortality as the outcome variable. We partitioned age into 5-year increments with age <30 years as the reference group. We partitioned each laboratory variable into multiple discretion levels based on the distribution of laboratory values and their associated mortality rates, and designated the laboratory range associated with the lowest mortality rate as the reference group. We examined mortality rates for patients with missing values for each laboratory assessment and collapsed them into the corresponding reference group because their observed mortality rate was most comparable with that of the reference group.

We converted the final laboratory model to an integer score system (ALaRMS) using a method described in the Framingham Study.²⁰ Specifically, we identified the variable with the smallest coefficient in the final multivariable model and applied it as the denominator. Then we divided each of the remaining regression coefficients in the model by this denominator and rounded the resulting quotient to the nearest whole number (integer), which formed the score weight for that variable. We then calculated each person's overall risk score by summing the points across all variables present. Converting model coefficients into a score system makes the risk adjustment model easy to understand and implement. We validated the ALaRMS using the validation cohort.

Step 2: fit ALaRMS+CCS+CS model

We summed all applicable laboratory points into a single ALaRMS value for each patient, and then fit a logistic regression model with the stepwise approach. We used the ALaRMS score as a continuous candidate variable along with candidate covariates of principal diagnosis-based clinical categories and secondary diagnosis-based comorbidity categories. We adopted AHRQ's clinical classification software (CCS)¹¹ and comorbidity software (CS)¹⁰ as standard classification tools. The CCS collapses over 14 000 ICD-9-CM diagnosis codes (International Classification of Diseases, 9th revision, Clinical Modification) into 285 clinically meaningful categories. The CS grouped selected secondary diagnosis codes into 30 comorbidity categories.

Step 3: validate ALaRMS+CCS+CS model

We validated the ALaRMS+CCS+CS model using the validation cohort. Specifically, we used the ALaRMS+CCS+CS model coefficients generated from the derivation cohort to score the validation cohort. We used the c-statistic and the Hosmer–Lemeshow statistic to evaluate the model fit.

Analysis on the relative importance of ALaRMS versus CCS and CS variables

We calculated the relative unique contributions of ALaRMS, CCS, and CS using methods described in previous research.^{2 3 6} Specifically, we calculated changes in the model fit log likelihood value when each group of variables was retained and then removed from the full model.

To further evaluate the relative importance of ALaRMS versus CCS and CS variables in the mortality predictive models, we conducted the following additional analyses: (1) we fit four individual models using age and gender alone, laboratory variables alone, CCS alone, and CS alone, and compared the c-statistics; (2) we compared the cumulative change in the c-statistics by reversing the order of ALaRMS and the CCS and CS variables; (3) and we conducted integrated discrimination improvement (IDI) analysis, which assesses the new model's ability to improve the integrated sensitivity without sacrificing the integrated specificity.²¹

Sensitivity analysis

To test whether our model could be applied to different types of patients, we conducted sensitivity analyses on model fit to different subgroups by patient age, medical versus surgical status, hospital teaching status, number of beds, and urban–rural status.

All analyses were conducted using SAS V.9.01. The study was approved by the New England Institutional Review Board/Human Subjects Research Committee (Wellesley, Massachusetts, USA) and conducted in compliance with the Health Insurance Portability and Accountability Act (HIPAA), and the Helsinki Declaration.

Results

Patient characteristics

The derivation cohort comprised 1 428 824 discharges and 34 147 deaths (2.4% mortality rate) (table 1). Median age was 63 (IQR: 45, 78), and 58.9% were women. Approximately 83.6% were white, 7.9% were black, and 8.5% were other race/ethnicity. For payers, 37.7% were Medicare, 8.7% were Medicaid, and the rest (53.6%) were private or other payers. Approximately 64.1% of discharges were from teaching (n=36) and 35.9% were from non-teaching (n=34) hospitals; 52.6% of discharges were from small and medium (bed size ≤300) and 47.4% were from large hospitals (bed size >300); 83.9% were from urban and 16.1% were from rural hospitals. The validation cohort comprised 770 523 discharges and 18 456 deaths (2.4% mortality rate), with similar patient characteristics.

Table 1.

Patient characteristics by derivation and validation cohorts

Variable	Derivation cohort (2006–2007)		Validation cohort (2008)
	Discharges, n (%)	Mortality, n (%)	Discharges, n (%)	Mortality, n (%)
Total	1 428 824	34 147 (2.4)	770 523	18 456 (2.4)
Age
Age, median (IQR)	63 (45, 78)		63 (45, 78)
Age <65	744 160 (52.1)	7961 (1.1)	405 566 (52.6)	4444 (1.1)
Age ≥65	684 664 (47.9)	26 186 (3.8)	364 957 (47.4)	14 012 (3.8)
Gender
Men	579 562 (41.2)	16 797 (2.9)	318 966 (41.6)	9282 (2.9)
Women	849 262 (58.9)	17 350 (2.0)	451 557 (58.4)	9174 (2.0)
Race/ethnicity
White	1 177 959 (83.6)	28 774 (2.4)	600 305 (78.3)	14 740 (2.5)
Black	110 565 (7.9)	2182 (2.0)	63 908 (8.3)	1191 (1.9)
Other	140 300 (8.5)	3191 (2.3)	106 310 (13.4)	2525 (2.4)
Payer
Medicare	531 347 (37.7)	19 552 (3.7)	271 342 (35.4)	9947 (3.7)
Medicaid	122 650 (8.7)	1197 (1.0)	70 193 (9.2)	715 (1.0)
Private or other	774 827 (53.6)	13 398 (1.7)	428 988 (55.5)	7794 (1.8)
Teaching status
Teaching	915 321 (64.1)	22 004 (2.4)	496 452 (64.4)	12 132 (2.4)
Non-teaching	513 503 (35.9)	12 143 (2.4)	274 071 (35.6)	6324 (2.3)
Number of beds
≤300	751 677 (52.6)	16 868 (2.2)	400 131 (51.9)	8543 (2.1)
>300	677 147 (47.4)	17 279 (2.6)	370 392 (48.1)	9913 (2.7)
Urban/rural status
Urban	1 198 334 (83.9)	28 768 (2.4)	655 528 (85.1)	15 845 (2.4)
Rural	230 490 (16.1)	5379 (2.3)	114 995 (14.9)	2611 (2.3)
Medical/surgical discharges
Medical	939 081 (65.7)	26 621 (2.8)	514 932 (66.8)	14 519 (2.8)
Surgical	489 743 (34.3)	7526 (1.5)	255 591 (33.2)	3937 (1.5)

ALaRMS model

Age was a significant mortality predictor (table 2). Compared with patients aged less than 30 years (reference age group with OR of 1.00 and risk point weight of 0), patients aged between 30 and 35 had a moderate increase in mortality risk (3 points), and patients aged between 35 and 39 old had a steep increase in mortality risk (10 points). Thereafter, the mortality risk increased 2–4 additional points consecutively for every 5-year increment.

Table 2.

Acute Laboratory Risk of Mortality Score (ALaRMS)

Age	18–29	30–34	35–39	40–44	45–49	50–54	55–59	60–64	65–69	70–74	75–79	80–84	85–89	>89
Score	0	3	10	13	17	20	23	25	27	30	32	35	38	42

Gender	Female	Male
Score	0	2
Albumin (g/dL)	≤2.4	2.5–2.7	2.8–3	3.1–3.3	>3.3
Score	14	7	4	1	0
AST (U/L)	≤30	31–40	41–60	61–100	>100
Score	0	2	4	6	9
Total bilirubin (mg/dL)	≤1.4	1.5–2	>2.0
Score	0	1	4
Calcium (mg/dL)	≤7.9	8–8.4	8.5–10.1	>10.1
Score	4	1	0	3
Creatinine (mg/dL)	≤2.0	>2.0
Score	0	1
pro-BNP (pg/dL)	≤8000	8001–18 000	>18 000
Score	0	5	10
BNP	≤1200	1201–2400	>2400
Score	0	2	4
Glucose (mg/dL)	≤70	71–135	136–165	>165
Score	7	0	2	5
K (mEq/L)	≤3.2	3.3–4.9	5–5.3	>5.3
Score	3	0	2	3
Na (mEq/L)	≤130	131–135	136–143	144–145	>145
Score	4	1	0	4	9
Alkaline phos (U/L)	≤115	116–220	221–630	>630
Score	0	2	5	8
BUN (mg/dL)	≤25	26–30	31–40	41–55	>55
Score	0	4	6	8	10
pH Arterial	≤7.2	7.21–7.3	7.31–7.35	7.36–7.48	>7.48
Score	21	13	10	0	8
PO2 Arterial (mm Hg)	≤50	50.1–55	55.1–140	>140
Score	12	9	0	12
pCO2 Arterial (mm Hg)	≤35	36–50	>50
Score	9	0	7
PTT	≤22	23–45	45.1–55	>55
Score	3	0	3	4
PT INR	≤1.1	1.11–1.4	1.41–2	2.1–5	>5
Score	0	4	7	5	8
Bands (%)	≤6	7–13	14–32	>32
Score	0	6	9	12
Hemoglobin (g/dL)	≤10	11–18	>18
Score	2	0	4
Platelets (109/L)	≤115	115.1–150	150.1–420	>420
Score	10	2	0	2
WBC (1000/mm3)	≤4.3	4.4–10.9	11–14.1	14.2–19.8	>19.8
Score	4	0	4	7	12
Troponin I (ng/mL)	≤0.04	0.05–0.1	0.11–0.2	0.21–0.3	>0.3
CPK MB (ng/mL)*	≤2	3–5	6–10	11–34	>34
Score	0	2	4	8	13

Reference range for each variable is presented in bold.

*Use troponin I when available; otherwise use CPK MB.

AST, aspartate transaminase; Alkaline phos, alkaline phosphatase; BNP, brain natriuretic peptide; BUN, blood urea nitrogen; CPK MB, creatine phosphokinase MB; PCO2, partial pressure of carbon dioxide in arterial blood; PO2, partial pressure of oxygen in arterial blood; pro-BNP, pro-brain natriuretic peptide; PTT, partial thromboplastin time; PT INR, prothrombin time international normalized ratio; WBC, white blood cell count.

The laboratory covariates with the highest mortality impact (risk scores ≥10; approximate ORs ≥2) were albumin ≤2.4 g/dL, pro-BNP >18 000 pg/mL, BUN >55 mg/dL, arterial pH ≤7.2, arterial pH 7.21–7.30, arterial pH 7.31–7.35, PO2 ≤50 mm Hg, PO2 >140 mm Hg, bands >32%, platelets ≤115 000 cells/mm³, WBC >19 800 cells/mm³, and troponin I >0.3 ng/mL or CPK MB >34 ng/mL (table 2). Detailed ALaRMS model parameters with 95% CIs are presented in online supplementary appendix A. The ALaRMS model c-statistic was 0.87 with good model calibration (figure 1A). The predicted probability of mortality risk ranged from 0.004% to 99.3%. Mean ALaRMS score was 36 (SD 21); median was 36 (IQR 22, 49). The results for the validation cohort were similar (figure 1A).

Figure 1.

Hosmer–Lemeshow calibration plot for: (A) the ALaRMS model; (B) the ALaRMS+CCS+CS model. ALaRMS, Acute Laboratory Risk of Mortality Score; CCS, clinical classification system; CS, comorbidity software.

ALaRMS+CCS and CS model

In addition to the ALaRMS variables, the logistic regression model yielded 35 CCS and 9 CS significant covariates (table 3). Every point increase in ALaRMS score resulted in an approximately 6% increase in mortality risk (OR 1.057; 95% CI 1.056 to 1.058). The principal diagnosis-based CCS variables with ORs >2.00 included cardiovascular disease, major organ, hematologic, or metastatic cancers, brain or multiple traumas, and severe infectious diseases (eg, septicemia, HIV). Only one secondary diagnosis-based comorbidity variable (metastatic cancer) in the CS had an OR >2.00. Adding CCS and CS variables increased the model c-statistic from 0.87 to 0.91. When the ALaRMS+CCS and CS model coefficients were applied to the 2008 validation cohort, the model c-statistic was 0.90. The model exhibited good calibration for both the derivation and validation cohorts (figure 1B).

Table 3.

ALaRMS+CCS+CS model

Variable		Discharge, n (%) (n=1 428 824)	Unadjusted mortality, n (%) (n=34 147)	Multivariable adjusted OR (95% CI)
ALaRMS score, continuous variable (per 1 point increment)				1.06 (1.06 to 1.06)
Clinical classification software (CCS) variables
CCS100	Acute myocardial infarction	35 421 (2.5)	2213 (6.2)	2.58 (2.44 to 2.71)
CCS102	Non-specific chest pain	39 691 (2.8)	15 (0.0)	0.07 (0.04 to 0.12)
CCS103	Pulmonary heart disease	8818 (0.6)	275 (3.1)	1.93 (1.70 to 2.19)
CCS108	Congestive heart failure; non-hypertensive	58 501 (4.1)	1852 (3.2)	1.58 (1.50 to 1.67)
CCS109	Acute cerebrovascular disease	25 956 (1.8)	2334 (9.0)	8.41 (8.00 to 8.84)
CCS114	Peripheral and visceral atherosclerosis	9632 (0.7)	367 (3.8)	2.63 (2.35 to 2.95)
CCS115	Aortic, peripheral, and visceral artery aneurysms	5636 (0.4)	476 (8.4)	4.81 (4.32 to 5.34)
CCS12	Cancer of esophagus	811 (0.1)	72 (8.9)	5.52 (4.26 to 7.16)
CCS122	Pneumonia (except that caused by tuberculosis or sexually transmitted disease)	44 365 (3.1)	1680 (3.8)	1.64 (1.55 to 1.73)
CCS129	Aspiration pneumonitis; food/vomitus	10 372 (0.7)	1186 (11.4)	3.15 (2.93 to 3.38)
CCS13	Cancer of stomach	1277 (0.1)	93 (7.3)	3.47 (2.76 to 4.36)
CCS131	Respiratory failure; insufficiency; arrest (adult)	17 462 (1.2)	3140 (18.0)	3.24 (3.08 to 3.41)
CCS133	Other lower respiratory disease	5579 (0.4)	217 (3.9)	2.85 (2.47 to 3.29)
CCS14	Cancer of colon	5723 (0.4)	211 (3.7)	2.03 (1.76 to 2.36)
CCS145	Intestinal obstruction without hernia	15 040 (1.1)	396 (2.6)	1.98 (1.78 to 2.20)
CCS159	Urinary tract infections	21 548 (1.5)	217 (1.0)	0.55 (0.48 to 0.63)
CCS16	Cancer of liver and intrahepatic bile duct	966 (0.1)	101 (10.5)	2.99 (2.39 to 3.75)
CCS17	Cancer of pancreas	1948 (0.1)	164 (8.4)	2.46 (2.07 to 2.93)
CCS19	Cancer of bronchus; lung	7968 (0.6)	849 (10.7)	6.70 (6.19 to 7.26)
CCS2	Septicemia (except in labor)	31 452 (2.2)	4917 (15.6)	2.82 (2.70 to 2.95)
CCS203	Osteoarthritis	43 389 (3.0)	42 (0.1)	0.18 (0.13 to 0.24)
CCS205	Spondylosis; intervertebral disc disorders; other back problems	35 984 (2.5)	48 (0.1)	0.27 (0.20 to 0.36)
CCS233	Intracranial injury	8882 (0.6)	703 (7.9)	7.13 (6.53 to 7.78)
CCS234	Crushing injury or internal injury	4062 (0.3)	179 (4.4)	2.93 (2.48 to 3.47)
CCS249	Shock	133 (0.0)	46 (34.6)	6.11 (3.99 to 9.38)
CCS27	Cancer of ovary	831 (0.1)	53 (6.4)	6.26 (4.65 to 8.42)
CCS35	Cancer of brain and nervous system	1650 (0.1)	61 (3.7)	5.05 (3.88 to 6.57)
CCS38	Non-Hodgkin lymphoma	2626 (0.2)	215 (8.2)	5.47 (4.70 to 6.37)
CCS39	Leukemia	1784 (0.1)	262 (14.7)	6.45 (5.57 to 7.47)
CCS40	Multiple myeloma	857 (0.1)	73 (8.5)	5.10 (3.94 to 6.60)
CCS42	Secondary malignancies	13 815 (1.0)	1140 (8.3)	4.97 (4.64 to 5.33)
CCS43	Malignant neoplasm without specification of site	184 (0.0)	31 (16.8)	10.86 (7.1 to 16.6)
CCS5	HIV infection	1255 (0.1)	102 (8.1)	6.44 (5.13 to 8.08)
CCS50	Diabetes mellitus with complications	19 795 (1.4)	172 (0.9)	0.47 (0.41 to 0.55)
CCS85	Coma; stupor; and brain damage	829 (0.1)	87 (10.5)	5.76 (4.43 to 7.48)
Comorbidity software (CS) variables
	Congestive heart failure	117 594 (8.2)	9271 (7.9)	1.48 (1.44 to 1.53)
	Depression	150 995 (10.6)	3018 (2.0)	0.80 (0.77 to 0.83)
	Hypertension	677 039 (47.4)	18 104 (2.7)	0.75 (0.74 to 0.77)
	Metastatic cancer	33 342 (2.3)	2751 (8.3)	2.16 (2.06 to 2.26)
	Other neurological disorders	94 647 (6.6)	4386 (4.6)	1.37 (1.32 to 1.42)
	Pulmonary circulation disease	25 575 (1.8)	2234 (8.7)	1.46 (1.39 to 1.54)
	Renal failure	135 725 (9.5)	8127 (6.0)	1.18 (1.14 to 1.22)
	Solid tumor without metastasis	28 198 (2.0)	1506 (5.3)	1.51 (1.43 to 1.61)
	Weight loss	35 984 (2.5)	3836 (10.7)	1.56 (1.50 to 1.63)

ALaRMS, Acute Laboratory Risk of Mortality Score.

Analysis on the relative importance of ALaRMS versus CCS and CS variables

The relative contributions to the model predictive ability were 69% for ALaRMS, 25% for CCS, and 6% for CS. The c-statistics were 0.704 for model with age and gender variables alone, 0.843 for laboratory variables alone, 0.776 for CCS variables alone, and 0.713 for CS variables alone.

The c-statistic improved from 0.838 to 0.907 when ALaRMS was added to the CCS and CS model (table 4). In contrast, the c-statistic improved from 0.868 to 0.907 when CCS and CS variables added to ALaRMS.

Table 4.

Integrated discrimination improvement (IDI)

Model	c-Statistic	IDI
		Died in hospital (n=34 147)		Live discharge (n=1 394 677)		Discrimination slope	IDI (95% CI)
		Integrated sensitivity (IS)	Standard deviation (IS)	Integrated 1-specificity (IP)	Standard deviation (IP)
Adding ALaRMS to CCS and CS
CCS and CS	0.838	0.0910	0.0974	0.0223	0.0398	0.0688
CCS and CS+ALaRMS	0.907	0.1766	0.197	0.0202	0.0515	0.1564
Difference		0.0855	0.1759	−0.0021	0.0398	0.0876	0.0876 (0.0858 to 0.0895)
% Improvement by adding ALaRMS (95% CI)		94%		9%		127% (122%, 133%)
Adding CCS and CS to ALaRMS
ALaRMS	0.868	0.1496	0.1894	0.0208	0.046	0.1287
ALaRMS+CCS and CS	0.907	0.1766	0.197	0.0202	0.0515	0.1564
Difference		0.027	0.0944	−0.0007	0.0276	0.0277	0.0277 (0.0267 to 0.0287)
% Improvement by adding CCS and CS (95% CI)		18%		3%		22% (19%, 25%)

Calculation of % of improvement:

Adding ALaRMS to CCS&CS:

DS_CCS&CS=IS_CCS&CS−IP_CCS&CS=0.0910−0.0223=0.0688

DS_{CCS&CS+ALaRMS}=IS_{CCS&CS+ALaRMS}−IP_{CCS&CS+ALaRMS}=0.1766−0.0202=0.1564

IDI of adding ALaRMS=DS_{CCS&CS+ALaRMS}−DS_CCS&CS=0.1564−0.0688=0.0876

% of improvement by adding ALaRMS=IDI/DS_CCS&CS=0.0876/0.0688=127%

Adding CCS&CS to ALaRMS:

DS_ALaRMS=IS_ALaRMS−IP_ALaRMS=0.1496−0.0208=0.1287

DS_{ALaRMS+CCS&CS}=IS_{ALaRMS+CCS&CS}−IP_{ALaRMS+CCS&CS}=0.1766−0.0202=0.1564

IDI of adding CCS&CS=DS_{ALaRMS+CCS&CS}−DS_ALaRMS=0.1564−0.1287=0.0277

% improvement of adding CCS&CS=IDI/DS_ALaRMS=0.0277/0.1287=22%

ALaRMS, Acute Laboratory Risk of Mortality Score; CCS, clinical classification system; CS, comorbidity software; IS, integrated sensitivity=mean predicted probability of mortality in the group of patients died in hospital; IP, integrated 1-specificity=mean predicted probability of mortality in the group of patients discharged live; Discrimination slope, IS−IP; IDI, integrated discrimination improvement=(IS [new]−IS [old])−(IP [new]−IP [old]).

The IDI analysis revealed that adding ALaRMS on top of CCS and CS variables improved the IDI by 127% (95% CI 122% to 133%) (table 4). In contrast, adding CCS and CS variables on top of ALaRMS only improved the IDI by 22% (95% CI 19% to 25%).

Sensitivity analyses on model applicability to subgroups of patients

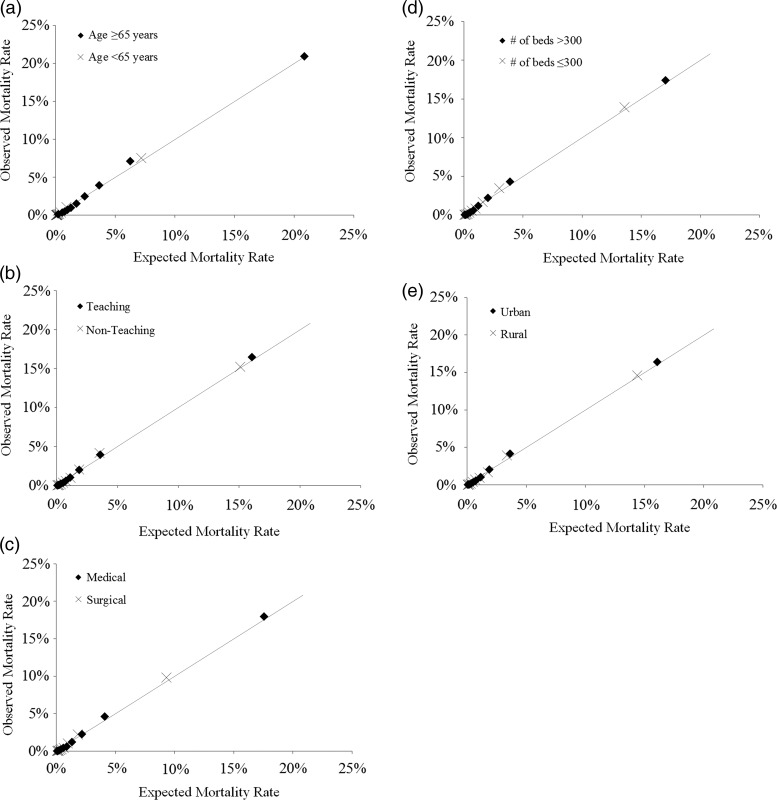
The ALaRMS+CCS+CS model exhibited excellent discrimination for age, teaching status, size (number of beds), location, and medical versus surgical subgroups (table 5). The c-statistic for all subgroup analyses ranged from 0.86 to 0.94 and the calibrations were good (figure 2).

Table 5.

Sensitivity analysis: model discrimination for subgroups

Variable	Derivation cohort		Validation cohort
	Number of discharges	Model c-statistic	Number of discharges	Model c-statistic
Total	1 428 824	0.907	770 523	0.903
Age
Age <65	744 160	0.939	405 566	0.935
Age ≥65	684 664	0.863	364 957	0.856
Teaching status
Teaching	915 321	0.903	496 452	0.900
Non-teaching	513 503	0.910	274 071	0.904
Number of beds
≤300	751 677	0.909	400 131	0.903
>300	677 147	0.907	370 392	0.903
Urban/rural status
Urban	1 198 334	0.908	655 528	0.903
Rural	230 490	0.905	114 995	0.900
Medical/surgical discharges
Medical	939 081	0.903	514 932	0.897
Surgical	489 743	0.910	255 591	0.910

Figure 2.

Hosmer–Lemeshow calibration plot for subgroup patients: (A) age 65 or older versus age younger than 65; (B) discharges from teaching versus non-teaching hospitals; (C) medical versus surgical discharges; (D) discharges from large (>300 beds) versus small/medium-sized (≤300 beds) hospitals; (E) discharges from urban versus rural hospitals.

Discussion

Using over 2 million discharges from the EHR systems with numeric laboratory results, we demonstrated that the laboratory results obtained first on the day of admission can generate a clinically valid mortality predictive model with excellent predictive ability (the c-statistic of 0.87). ALaRMS may have utility for real-time decision support because it uses only EHR data available at the time of admission. The large sample size enabled precise parameter estimates as indicated by narrow CIs. We further demonstrated that AHRQ's standard principal diagnosis-based classification (CCS) and secondary diagnosis-based comorbidity (CS) can be incorporated and further improve model c-statistic from 0.87 to 0.91. The model that incorporated CCS and CS may be useful for retrospective outcome studies where post-discharge administrative data are available.

Value of numeric laboratory data

Laboratory results obtained at admission provide the data for objective assessment of patients with acute clinical presentation. ALaRMS used only age, gender, and the initial laboratory test results, which are most widely automated and commonly available at the time of admission. This enables near real-time risk stratification that may be useful in aiding disease management. Patients who present with severely deranged laboratory results have higher ALaRMS scores, indicating higher mortality risk. Conversely, patients who present without abnormal laboratory results have lower ALaRMS scores, indicating lower mortality risk. Hence, ALaRMS can provide a near real-time aggregated assessment of severity in acute-care settings when discharge diagnosis data are not yet available. The potential utility in real-time settings needs to be validated in future prospective studies.

For retrospective outcome studies and benchmarking, a valid risk adjustment model enhances clinical validity. The ALaRMS plus CCS and CS model minimizes potentially unfair risk adjustment due to up-, under-, or mis-coding. Since the ALaRMS score carries the largest proportion of the total weight in the risk adjustment model, which is consistently demonstrated in c-statistic, log likelihood, and IDI analysis, it would be desirable to incorporate it into the risk adjustment strategies. This would represent another meaningful use of information technology in the healthcare settings.

Laboratory data are quantitative, providing more precise and graded information on clinical severity. The graded relationship between degree of abnormality of the laboratory measures and risk of mortality is not captured with diagnosis code-based dichotomous variables, even when these diagnosis codes are coded accurately. This explains in part the robust finding that the laboratory and physiology data contribute most to the predictive ability of the model in disease-specific and generic mortality predictive models among inpatient and ICU patient populations.^{2–4 6}

Laboratory results are parsimonious and potentially cost-efficient as relatively few laboratory test results (23 in our ALaRMS model) are needed to assess the major organ/system functions that keep patients alive. The objective, quantitative, and parsimonious nature of numeric laboratory data exhibited high predictive ability as shown in the ALaRMS model. Although not directly comparable, the ALaRMS model's c-statistic of 0.87 represents higher model discrimination than the c-statistics of 0.70, 0.71, and 0.72 achieved by the congestive heart failure, acute myocardial infarction, and pneumonia models derived from administrative claims that are currently used by the Centers for Medicare and Medicaid Services (CMS) in the USA for the Hospital Compare website.^22–24 Nevertheless, it should be emphasized that our model predicted inpatient mortality and the CMS models predicted 30-day mortality, hence the absolute c-statistic is not directly comparable. Our full model (ALaRMS+CCS and CS) achieved a c-statistic of 0.91, which is slightly higher than the c-statistic of 0.88 previously reported in a risk adjustment model using pre-admission laboratory and administrative data for inpatient population.³

Value of using standard clinical classification system in the public domain

Adopting a standard clinical condition classification system is critical because it allows for public access, enables future validations using different datasets, and offers opportunities to further improve the risk adjustment model through refinement of the laboratory score algorithms and code-based clinical condition classification system. The AHRQ's CCS has undergone multiple revisions and is updated annually to reflect ICD-9-CM updates,¹¹ and is perhaps the most feasible clinical classification system available to the public.

Principal diagnosis-based groups are especially important for a generic risk adjustment model because general patient populations are heterogeneous. As in our model, patients with principal diagnoses (primary reason for the index hospitalization) of major acute clinical conditions of vital organs/systems (eg, cardiovascular or neurologic systems, cancers of major organs/systems, dissimilated cancers) have high mortality risk. In contrast, clinical conditions involving less-vital organs/systems (eg, joint and muscular system) or less-acute diagnosis (eg, unspecific chest pain) have lower mortality risk. These results are valid clinically and are consistent with the mortality statistics reported by the National Center for Health Statistics.²⁵

Among secondary diagnosis-based comorbidity variables, metastatic cancer carried the highest independent risk of mortality. Other comorbid conditions tended to be either statistically insignificant or carry less independent weight because they are likely accounted for by ALaRMS physiology parameters. The less-prominent contributions of secondary diagnosis-based comorbid conditions are consistent with previous risk adjustment models that incorporated physiology data.^{1–4 6}

Limitations

Our study has limitations. First, although our dataset comprised over 2 million discharges from 70 hospitals from the northeast region, it is not geographically representative of the US patient population. Further validation of this model is needed when data from a more representative patient population become available in the future. Second, we did not include vital sign and altered mental status data in the physiology risk score because our goal was to develop a model using only data that are currently widely available in hospital EHR systems. Inclusion of vital signs and mental status requires incorporating nursing notes or other more complex electronic medical records systems, which are not as widely available as numeric laboratory data in acute-care hospital settings. At the time when vital sign and mental status data are widely captured electronically across hospitals, it would be important to incorporate them into the physiology score because of their clinical face validity. Third, we did not incorporate AHRQ's procedure groups in our model because many of the procedures are diagnostic in nature. For procedure groups indicating treatment, it is not possible to distinguish whether a treatment procedure was implemented early at admission as planned or at a later hospital stay after patients possibly developed complications. The latter should not be included as a risk adjustor because it would give credit (higher expected mortality rates) to hospitals with potentially substandard care if they have more potential complications requiring procedural treatments after admission. On the other hand, omitting procedure categories is unlikely to have a large impact on the model predictive ability because planned treatment procedures would likely be correlated with principal diagnosis categories. For example, patients receiving cardiac operations would likely have cardiac disease diagnoses, which have already been included in the model. Their acute clinical presentation and severity would have been largely taken into account with ALaRMS. As further evidence, the high c-statistic of our model (ranged from 0.90 to 0.91, nearly identical for medical and surgical patients) indicated excellent predictive ability for both medical and surgical patients in our sensitivity analysis.

Significance of the study

The data derived from an EHR typically covers many broad domains. Numeric laboratory data are objective and quantitative in nature, which are desirable features in predictive modeling. The objective nature ensures the data reliability and reproducibility. The quantitative nature enables precise estimation of the graded relationship of the degree of physiologic derangement and the risk of inpatient mortality. Furthermore, numeric laboratory data are perhaps most scalable among all EHR domains due to the objective and quantitative nature. While the health informatics field has devoted considerable effort to extract data from free text reports or expensive but infrequently used tests, it is worthwhile to examine the utility of the most commonly measured, most scalable, and perhaps the least expensive data domains. This is particularly true in regard to real-time decision support and outcome studies, which often require a large scale implementation at a low cost.

Conclusions

Admission laboratory physiologic data captured in the hospital EHR systems provide objective, precise, and parsimonious assessment of acute clinical severity and are highly predictive of inpatient mortality risk in hospitalized adult patients. Relying only on data available at the time of admission, ALaRMS may have utility in aiding real-time disease management. Incorporating AHRQ's standardized clinical classification systems (CCS and CS) further improves model predictive power and facilitates public access to the risk adjustment algorithms. Using a completely automated EHR dataset available on admission, ALaRMS can be implemented for real-time decision support. The full model incorporating CCS and CS may be cost-efficient to implement for large-scale retrospective studies on inpatient outcomes. These would represent meaningful use of health information technology.