Dynamic permeability of the lacunar–canalicular system in human cortical bone

Abstract

A new method for the experimental determination of the permeability of a small sample of a fluid-saturated hierarchically structured porous material is described and applied to the determination of the lacunar–canalicular permeability (K_LC) in bone. The interest in the permeability of the lacunar–canalicular pore system (LCS) is due to the fact that the LCS is considered to be the site of bone mechanotransduction due to the loading-driven fluid flow over cellular structures. The permeability of this space has been estimated to be anywhere from 10⁻¹⁷ to 10⁻²⁵ m². However, the vascular pore system and LCS are intertwined, rendering the permeability of the much smaller-dimensioned LCS challenging to measure. In this study, we report a combined experimental and analytical approach that allowed the accurate determination of the K_LC to be on the order of 10⁻²² m² for human osteonal bone. It was found that the K_LC has a linear dependence on loading frequency, decreasing at a rate of 2 × 10⁻²⁴ m²/Hz from 1 to 100 Hz, and using the proposed model, the porosity alone was able to explain 86 % of the K_LC variability.

1 Introduction

Almost two decades ago, it was first proposed that the amplification of the mineralized tissue strain levels needed for osteocyte mechanosensation occurs when interstitial fluid flow is enhanced by the time-varying mechanical loads applied to bone (Weinbaum et al. 1994; You et al. 2001). Bone interstitial fluid flows through different discrete levels of porosity that coexist in cortical bone, which are nested hierarchically one inside another as a set of Russian dolls in microcirculatory pathways (Cowin et al. 2009). The largest pore size (~25 μm radius) is associated with the vascular porosity, which consists of the volume of all the tunnels in bone that contains blood vessels, nerves, and bone interstitial fluid and includes all the osteonal canals (primary and secondary) as well as transverse (Volkmann) canals (Malachanne et al. 2008; Li et al. 1987; Wen et al. 2010). The lacunar–canalicular porosity contains the osteocytes and bone fluid and consists of the volumes of all the osteocyte lacunae (~3–10 μm radius) and the canaliculi channels (~0.15–0.55 μm diameter) (Marotti 1990). The space between the osteocyte and the lacunar–canalicular wall is filled by the osteocyte’s glycocalyx and interstitial fluid. The smallest pore size in bone (<1 nm) is found in the collagen–apatite porosity, where most of the water is bound to ionic crystals in bone (Neuman et al. 1953; Wehrli and Fernandez-Seara 2005). A detailed review of interstitial fluid flow and mechanotransduction in bone was recently presented by Fritton and Weinbaum (2009).

The permeability (inverse of flow resistivity) of the lacunar–canalicular system (LCS) is a critical determinant of interstitial bone fluid flow, which is considered as the main mechanism to stimulate osteocyte cell processes in the LCS and initiate bone mechanotransduction. Accordingly, changes in the lacunar–canalicular permeability may play a key role in bone mechanotransduction as well as in the ability of bone to adapt its local tissue mass and architecture to its mechanical environment (Weinbaum et al. 1994; Cowin et al. 2009; Fritton and Weinbaum 2009). The permeability of the vascular system (K_V) has been estimated from the vascular pore architecture (Johnson 1984; Dillaman 1984; Zhang et al. 1998; Swan et al. 2003) and has been experimentally measured using a traditional technique based on Darcy’s law (Rouhana et al. 1981; Li et al. 1987; Wen et al. 2010). This technique consists of measuring the volume of fluid flow per unit area and per unit time across a porous layer, which is then divided by the pore pressure gradient across the layer. Reported estimates and measurements of permeability associated with the vascular porosity span several orders of magnitude (10⁻¹¹ to 10⁻¹⁷ m²). Unfortunately, Darcy permeability measurements are experimentally unfeasible for assessing the LCS permeability (K_LC). The LCS permeability has been derived from theoretical analysis of the fluid flow in the pore architecture of the LCS and from combined experimental–numerical–analytical approaches using bone tissue from animal models. Theoretical estimates of K_LC reported in the literature span several orders of magnitude, ranging from 10⁻¹⁷ to 10⁻²⁰ m², while experimental studies have reported a different range of LCS permeability, from 10⁻²² to 10⁻²⁵m². This wide range of values and the difference between theoretical and measured LCS permeability suggests that the permeability of the lacunar–canalicular system has not been determined with sufficient accuracy to date.

Measurements of the intrinsic lacunar–canalicular permeability of human cortical bone are scarce, and the effect of loading frequency on the dynamic permeability of the lacunar–canalicular system is practically unknown (Cardoso et al. 2013). In order to eliminate the influence of the vascular permeability in experimental measurements of the lacunar–canalicular permeability, Gailani and Cowin (2008) proposed to perform the permeability measurement in samples containing the lacunar–canalicular porosity only, such as a single osteon. An analytical solution of a saturated compressible poroelastic annular cylinder under an unconfined stress relaxation test was developed, and predictions from this model were compared to experimental stress relaxation measurements made on isolated osteons in vitro, i.e., considering zero blood pressure (Gailani et al. 2009; Gailani and Cowin 2008, 2011). Recently, a frequency-dependent analytical model of a fluid-saturated porous annular cylinder subjected to an axial cyclic strain loading was developed by Benalla et al. (2012). Formulas for the loss tangent, tan[δ(ω̄)], representing the frequency-dependent time-delay between the sinusoidal stress and strain in the LCS, were obtained as a function of the lacunar–canalicular permeability in the radial direction and loading frequency. In the present study, this frequency-dependent analytical model (Benalla et al. 2012) and measurements of loss tangent on isolated human osteons under harmonic loading are used (1) to determine the intrinsic lacunar–canalicular permeability in the radial direction of fresh osteonal samples, (2) to assess the effect of time post-isolation of osteons on lacunar–canalicular permeability measurements, (3) to evaluate the effect of loading frequency on the dynamic permeability of the lacunar–canalicular system, and (4) to investigate the relationship between porosity and permeability in the LCS.

2 Materials and methods

2.1 Formulation of the loss tangent with respect to frequency

The analytical model developed in Benalla et al. (2012) considers a transverse segment of an isolated osteon whose annular region (LCS) between the Haversian canal and cement line is subjected to an axial cyclic loading between two smooth, parallel, and impermeable plates. The contact between the specimen and the plates is assumed to be frictionless, and the applied load is considered to be uniformly distributed on the loaded surface. For boundary conditions, free flow is assumed between the LCS and the vascular pore system (VS) and zero flow is considered at the cement line boundary. The axial loading in the form of an applied strain is

$$\epsilon (t)={\epsilon }_o{\mathrm{e}}^{i\omega t},$$ (1)

where ε_o and ω are the amplitude and frequency, respectively. Under the same assumptions (Cowin et al. 2009) but for zero blood pressure, the governing equation of the pore pressure that leads to a permeability and frequency-dependent relationship between stress and strain was found to be (Benalla et al. 2012)

$${\sigma }^{\ast }(t)=C^{\ast }(\overline{\omega })\epsilon (t),$$ (2)

where ω̄ is the dimensionless frequency (Table 2 in Benalla et al. 2012) and the complex-valued modulus, C^*(ω̄), is given by

$$\begin{array}{l}{C}^{\ast }(\overline{\omega })=C_{zz}^d+\frac{c_1-c_2{K}_{rr}}{c_3{K}_{rr}+c_4}-\frac{c_5}{K_{rr}},\\ C^{\ast }(\overline{\omega })=C_o{\mathrm{e}}^{-i\delta (\overline{\omega })}\text{and}{C}_o=\frac{{\sigma }_o}{{\epsilon }_o}.\end{array}$$ (3)

The magnitude and phase of C^*(ω̄) depend on the c_i (i = 1 – 5), $C_{zz}^d$ is the axial elastic normal stress constant, Krr is the lacunar–canalicular permeability in the radial direction (also simply referred to as K_LC), and σ_o is the magnitude of the average resultant stress in the osteon, while δ(ω̄) is the phase angle between the applied strain and the resultant stress. Based on Euler’s formula, the dynamic modulus C^*(ω̄) can be written as

$$\begin{array}{l}{C}^{\ast }(\overline{\omega })=C_o{\mathrm{e}}^{i\delta (\overline{\omega })}=C_{o}cos[\delta (\overline{\omega })]+i{C}_{o}sin[\delta (\overline{\omega })]\\ =C^{\prime }(\overline{\omega })+i{C}^{″}(\overline{\omega }),\end{array}$$ (4)

where C′(ω̄) is known as the storage modulus and C″(ω̄) as the loss modulus of the cyclically loaded osteon. From Eq. (4), the expression of the loss tangent is

$$tan[\delta (\overline{\omega })]=\frac{C^{″}(\overline{\omega })}{C^{\prime }(\overline{\omega })}=\frac{sin[\delta (\overline{\omega })]}{cos[\delta (\overline{\omega })]}.$$ (5)

Formulas for the storage modulus, loss modulus and tan[δ(ω̄)] are presented in equations (29) and (30), respectively, in Benalla et al. (2012).

2.2 Formulation of the K_LC with respect to loss tangent and frequency

In order to express the K_LC with respect to tan[δ(ω̄)] and frequency, Eq. (3) is reformulated as

$$K_{rr}^2(C_{zz}^d{c}_3-c_2-C^{\ast }{c}_3)+K_{rr}(C_{zz}^d{c}_4-C^{\ast }{c}_4-c_5{c}_3)-c_5{c}_4=0.$$ (6)

Separating Eq. (6) into real and imaginary parts gives

$${\beta }_1{K}_{rr}^2(\omega )+{\beta }_2{K}_{rr}(\omega )+{\beta }_3+i\left({\alpha }_1{K}_{rr}^2(\omega )+{\alpha }_2{K}_{rr}(\omega )+{\alpha }_3\right)=0,$$ (7)

where β_n and α_n(n = 1, 3) are the coefficients of the two quadratic expressions in Eq. (7). Solutions of the quadratic expressions provide values of the K_LC with respect to specified frequency values: C^*(ω̄) is a component of the coefficients in the quadratic Eq. (6). Using Eqs. (4) and (5), C^*(ω̄) is expressed with respect to tan[δ(ω̄)] as

$$C^{\ast }(\overline{\omega })=\frac{C_o}{\sqrt{{tan}^2[\delta (\overline{\omega })]+1}}1+itan[\delta (\overline{\omega })].$$ (8)

Equation (8) permits the computation of complex modulus C^*(ω̄) based on the experimental data of tan[δ(ω̄)] at different loading frequencies.

2.3 Sample preparation

Approximately one hundred osteons were extracted from the mid-diaphysis of fresh frozen femurs from three human female donors provided by the National Disease Resource Center. The ages of the donors were 53, 62, and 75 years old, and their medical history excluded any metabolic bone diseases or skeletal cancer. Femurs were kept at −80°C prior to cutting a 10-mm-length segment from the mid-diaphysis. Cortical segments were thawed, cleaned of soft tissue and bone marrow. Then 0.5-mm-thick cross-sections were machined from each segment using a low-speed diamond saw to obtain smooth and parallel surfaces. Each 0.5-mm-thick section was placed on the stage of an inverted biological microscope equipped with a small drilling machine and a diamond drill bit that was aligned with the center of the microscope field of view. An osteon with a circular or near circular shape was identified using the microscope and carefully isolated.

2.4 Micromechanical loading

A small uniaxial cyclic loading apparatus was developed to measure the stress produced in a single osteon undergoing harmonic strain. The experimental device works under displacement control using a digital controller connected in a closed loop to a piezoelectric linear actuator (P-841.10, Physik Instrumente, Auburn, MA). The linear actuator has a maximal push/pull force of 5 N and a minimal displacement increment of 3 nm. The piezoelectric actuator is vertically aligned to a 10 g load cell (Transducer Techniques, Temecula, CA). The osteon is placed over a stainless steel platen at the top of the load cell, immersed in PBS solution, preloaded, and cyclically strained with the piezoelectric actuator under frequencies ranging from 1 to 100 Hz. The cyclic strains applied by the piezoelectric actuator as well as the resultant stresses acquired from the load cell were collected with Lab-View and analyzed in MATLAB to determine the phase angle δ

Experiment 1. Effect of osteon’s storage time on the loss tangent measurements

The change in mechanical properties of post-mortem fresh frozen tissue due to the time elapsed after being thawed for experimental testing was investigated. For this purpose, two subsets of osteon specimens were cyclically loaded with a magnitude of 1,000 μ ε and 1 Hz frequency. The first set (9 osteons) was loaded five times every 60 min, hereafter designated as the hourly group. The second set (9 osteons) was loaded every 24 h for 5 days, and is henceforth named the daily group. Samples in the daily group were stored in PBS at −20°C and thawed before testing every day. Data from these tests determined the maximal time between the isolation and mechanical loading of the osteons in which changes in properties of the tissue are small, defining a time window to perform the experimental tests.

Experiment 2. Measurement of osteon’s loss tangent and K_LC at different frequencies

A second experiment was performed to determine tan [δ(ω̄)] and K_rr as a function of frequency in a larger set of samples. At twelve different frequencies (1, 2, 3, 5, 8, 10, 15, 20, 30, 50, 70, 100 Hz), cyclic strain was applied to all osteons, and the related tan[δ(ω̄)] was measured individually. The loss tangent was measured based on the slope between the applied strain and the resultant stress that determines the phase angle. Then, the K_LC of each osteon was obtained based on curve fitting loss tangent experimental data to the analytical model over the range of loading frequencies. Prior to curve fitting of data into the model, the lacunar–canalicular porosity (φ_LC), Haversian canal radius, cement line radius, and mineralized tissue elastic modulus were obtained for each osteon based on high-resolution μCT images, light microscope images of the osteons, and a structural model of the LCS morphology, as described in the following sections.

2.5 μCT scanning

After micromechanical testing, osteons were scanned using a high-resolution μCT system (1172 SkyScan, Belgium). X-ray projections were generated from the sample every 0.3°, obtaining 680 consecutive views with 2.1-μm resolution (Nrecon, V.1.6.9, Skyscan, Belgium). Images were density calibrated in Hounsfield Units (HU) and mineral density, ρ_HA, using a calibration scan containing air, water, and two density phantoms (0.25 and 0.75 g/cm³ of hydroxyapatite). Cortical bone was segmented using a global thresholding procedure to exclude the volumes corresponding to the lacunae and the Haversian canal. Segmented cortical bone images were used to calculate the average tissue mineral density (TMD) in the tissue matrix of each osteon. In addition to the TMD, the total number of lacunae, the volume of the lacunae, and the dimensions of each osteon were determined. Also, μCT images were used to determine the alignment of the Haversian canal at the center of the sample and the absence of cracks or inhomogeneities (i.e., resorption areas) that might increase the sample’s permeability. Osteons that did not meet these requirements were discarded. A total of 18 osteons were retained for experiment 1 and 60 osteons for experiment 2.

2.6 Measurement of lacunar–canalicular porosity (φ_LC)

The lacunar–canalicular porosity was estimated for each tested osteon as the sum of the lacunar porosity, φ_Lac (%), and the canalicular porosity, φ_Can (%). The lacunar porosity was assessed by automated 3D counting of closed porosities within the osteon specimen (CTAn, V.1.13, SkyScan, Belgium). The canalicular porosity was estimated using a structural model that used five parameters either taken from the literature or measured from the analyzed osteons. The volume of the osteonal specimen, V_s (mm³), the lacunar density, N_Lac/mm³, and the inner and outer diameter of the osteon, r_i and r_o (μm), were derived from μCT and light microscopy images, while the average distance between two neighboring lacunae was evaluated using a parallelepiped periodic unit cell (PPUC) that surrounded a lacuna. The side dimension, L (μm), of the PPUC represents the center-to-center distance between two neighboring lacunae (Beno et al. 2006).

$$L={(V_{\mathrm{s}}/N_{\text{Lac}})}^{1/3}.$$ (9)

Based on Eq. (9), the average canaliculi length is

$$L_{\text{Can}}=L-2r_{\text{Lac}}.$$ (10)

where r_Lac is the average radius of lacunae in the radial direction, estimated to be approximately r_Lac = 2.5 μm (Beno et al. 2006). Finally, we use the diameter of the canaliculi reported in the literature as 259 ± 129 nm (You et al. 2004), and the number of canaliculi emanating from each lacuna as 62, based on the average of measurements reported in Beno et al. (2006) using the slicing method. The final formula for the canalicular porosity, φ_Can, is then

$${\phi }_{\text{Can}}=\frac{62{(129.5)}^2\pi L_{\text{Can}}}{V_{\mathrm{s}}}.$$ (11)

2.7 Tissue mineral density and elastic constants

In order to estimate the Young’s elastic modulus of each osteon, the ρ_HA was obtained from μCT density-calibrated VOIs. Using the relationship between ρ_HA and $E_r^m$ from Wagner et al. (2011)

$${log}_{10}{E}_r^m=-8.58+4.05{log}_{10}\frac{400}{1+(504/{\rho }_{\text{HA}})},$$ (12)

where ρ_HA is the TMD obtained from the μCT, and the Young’s modulus of the matrix material in the radial direction, $E_r^m$, was evaluated. The Young’s modulus in the axial direction, $E_z^m$, was calculated based on the symmetry of the fourth-order transversely isotropic elasticity tensor,

$$\frac{E_r^m}{{\nu }_{rz}^m}=\frac{E_z^m}{{\nu }_{zr}^m},$$ (13)

where the Poisson’s ratios were ${\nu }_{zr}^m=0.312$ and ${\nu }_{rz}^m=0.255$ (Weinbaum et al. 1994).

2.8 Determination of the lacunar–canalicular permeability (K_LC)

The lacunar–canalicular permeability was first determined from curve fitting of the analytical model (Benalla et al. 2012) against experimental data of tan[δ(ω̄)] measured in the 1–100 Hz frequency range. The curve fitting was performed in MATLAB using a least-squares algorithm with a single free parameter, K_LC. Then, the lacunar–canalicular permeability was also obtained using Eq. (6), which represents the inverse solution for K_LC from the analytical poroelasticity model of the osteon under cyclic loading.

2.9 Statistical analysis

Descriptive statistics were obtained for the lacunar density (N_Lac/mm³, #/mm³), lacunar porosity (φ_Lac, %), canalicular porosity (φ_Can, %), lacunar–canalicular porosity (φ_LC, %), tissue mineral density (TMD, gHA/cm³), Young’s moduli in the radial, and axial directions ( $E_r^m$ and $E_z^m$, GPa). Repeated measures ANOVA and Tukey’s multiple comparison tests were performed to identify differences in tan[δ(ω̄)] and K_rr measured at different time points, as well as at different frequencies. Prior to performing statistical tests, normality was verified by the Kolmogorov–Smirnov test. All tests were performed using Prism statistics software (V.5.03, GraphPad, La Jolla, CA, USA) with a significance level of p < 0.05.

3 Results

3.1 Material properties and microstructure of isolated osteons

The mean ± SD values of the inner and outer radius for the sixty isolated human osteons were 41.5 ± 19.0 and 76.0 ± 32.5 μm, respectively. The volumetric lacunar density, N_Lac/mm³, was found to be (36.85 ± 9.99) × 10³ lacunae per mm³. The average lacunar porosity, φ_Lac, estimated from μCT scans was 1.69 ± 0.50 %, and using the structural model described by Eq. (9), the average canalicular porosity, φ_Can, was found to be 2.79 ± 0.91 % (Table 1). These two porosities lead to an estimated lacunar–canalicular porosity, φ_LC, of 4.51 ± 2.01 %. The average tissue mineral density, TMD, or volumetric hydroxyapatite density, ρ_HA/cm³, from μCT measurements was found to be 0.91 ± 0.06 g_HA/cm³, which is used in Eqs. (12–13) to yield Young’s moduli (Wagner et al. 2011) estimates of $E_r^m=15.29\pm 1.31$ GPa in the radial direction and $E_z^m=18.72\pm 1.61$ GPa in the axial direction.

Table 1.

Measurements and estimates of micro/nanoarchitecture of the lacunar–canalicular network (updated from Cardoso et al. 2013)

Reference	Method	Tissue	Lacunar porosity (%)
Schneider et al. (2007)	SR-μ CT	Mouse (B6) femoral mid-diaphysis	1.3
Tommasini et al. (2012)	SR-μ CT	Rat femoral diaphysis	1.5
Palacio-Mancheno et al. (2013)	μ CT	Rat tibial cortical metaphysis	1.5 ± 0.44
Present study	μ CT	Human femoral diaphysis	1.69 ± 0.50
Reference	Method	Tissue	Canalicular porosity (%)
Schneider et al. (2011)	FIB/SEM	Mouse (B6) femoral mid-diaphysis	0.70
Sharma et al. (2012)	CLSM	Rat tibial cortical metaphysis	14 (overestimated due to partial volume effects)
Present study	μ CT	Human femoral diaphysis	2.79 ± 0.91
Reference	Method	Tissue	Lacuna per unit volume (#/mm3)
Hannah et al. (2010)	SR-μ CT	Human femur	40–90 (×103)
Tommasini et al. (2012)	SR-μ CT	Rat femoral diaphysis	56.5 (×103)
Sharma et al. (2012)	CLSM	Rat tibial cortical metaphysis	67.3 ± 14.0 (×103)
Carter et al. (2013)	SR-μ CT	Human femur	26–37 (×103)
Palacio-Mancheno et al. (2013)	μ CT	Rat tibial cortical metaphysis	68.8 ± 13.2 (×103)
Present study	μ CT	Human femoral diaphysis	36.85 ± 9.99 (×103)
Reference	Method	Tissue	Lacunar volume (μ m3)
McCreadie et al. (2004)	CLSM	Human hip	455 ± 200
Hannah et al. (2010)	SR-μ CT	Human femur	290 ± 107
Sharma et al. (2012)	CLSM	Rat tibial cortical metaphysis	352 ± 30
Carter et al. (2013)	SR-μ CT	Human femur	~400
Reference	Method	Tissue	Inter-lacuna separation (μ m)
Sugawara et al. (2005)	CLSM	Chick calvaria, E16 days old	24.1 ± 2.8
Hannah et al. (2010)	SR-μ CT	Human femur	21.9 ± 6.3
Sugawara et al. (2011)	CLSM	Chick calvaria, E16 days old	23.5 ± 6.1
		Mouse calvaria (B6), E17 days old	39.6 ± 11.6
Sharma et al. (2012)	CLSM	Rat tibial cortical metaphysis	24.8 ± 1.7
Reference	Method	Tissue	Canaliculi diameter (nm)
Marotti (1990)	SEM	Human tibia	150–550
You et al. (2004)	TEM	Mouse female	259 ± 129
Sugawara et al. (2005)	CLSM	Chick calvaria, E16 days old	<500
Lin and Xu (2011)	AFM	Bovine tibia, transverse direction	426 ± 118
		Bovine tibia, radial direction	459 ± 144
		Bovine tibia, longitudinal direction	419 ± 113
Schneider et al. (2011)	FIB/SEM	Mouse (B6) femoral mid-diaphysis	95
Sharma et al. (2012)	CLSM	Rat tibia, cortical metaphysis trab. remnants	520 ± 42
		Rat tibia, cortical metaphysis lamellar region	553 ± 33
		Rat tibia, cancellous metaphysis	483 ± 24
	SEM	Rat tibia, cancellous metaphysis	335 ± 32
	TEM	Rat tibia, cancellous metaphysis	228 ± 11
Reference	Method	Tissue	# canaliculi per lacuna
Sugawara et al. (2005)	CLSM	Chick calvaria, E16 days old	52.7 ± 5.7
Beno et al. (2006)	Estimated from (Remaggi et al. 1998) light microscopy data	Chick	54
		Rabbit	60
		Bovine	85
		Horse	115
		Dog	81
		Human	41
Schneider et al. (2011)	FIB/SEM	Mouse (B6) femoral mid-diaphysis	78
Sugawara et al. (2011)	CLSM	Chick calvaria, E16 days old	52.7 ± 6.4
		Mouse calvaria (B6), E17 days old	49.7 ± 9.7
Sharma et al. (2012)	CLSM	Rat tibia, primary canaliculi	83.9 ± 14
		Rat tibia, secondary canaliculi	387 ± 34

μCT micro-computed tomography, CLSM confocal laser scanning microscopy, SR-μCT synchrotron radiation-based micro-CT, TEM transmission electron microscopy, AFM atomic force microscopy, FIB/SEM focused ion beam/scanning electron microscopy

3.2 Effect of osteon freshness on loss tangent

Changes in loss tangent measurements due to the lack of tissue freshness during the time elapsed between the isolation and loading of the sample were analyzed hourly and daily. No significant differences were found in tan[δ(ω̄)] measurements within the first three hours after isolation of osteons (Fig. 1a). However, a small (~1%) but statistically significant (p < 0.05) change in tan[δ(ω̄)] was found when measurements were taken 4 and 5 h after the samples were extracted. In addition, a clear, statistically significant decrease of tan[δ(ω̄)] was found in measurements taken every 24 h, with tan[δ(ω̄)] found to be almost 5 % lower at the fifth day of testing (Fig. 1b).

Fig. 1.

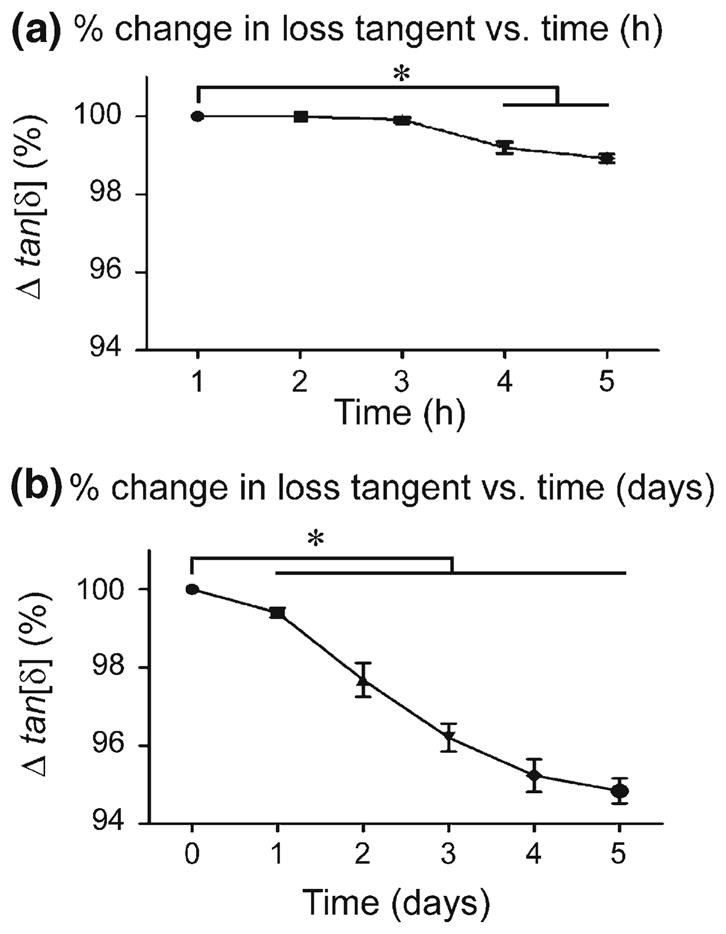
a The loss tangent (mean ± SD) versus time for a period of 5 h. b The loss tangent (mean ± SD) versus time for a duration of 5 days (* p<0.05, nine loaded osteons in each analysis)

The hourly and daily changes in tan[δ(ω̄)] (direct measurement from experiments) were also analyzed to determine whether such changes have a significant effect on K_LC (indirect estimates using analytical model). A change of 1 % in tan[δ(ω̄)] observed in the osteon samples measured hourly resulted in a change in K_LC of less than 0.1 %, while the 5 % change in tan[δ(ω̄)] from the osteon samples measured daily produced a change in K_LC of approximately 10 %. Therefore, to maintain tissue freshness, testing of osteons in the second experiment of this study was performed within 5 h of specimen cutting.

3.3 Intrinsic and dynamic permeability of human LCS

In this study, K_LC was obtained by two methods, namely the curve fitting of loss tangent data to the analytical model (Benalla et al. 2012) and by using the inverse solution of the poroelastic model (Eq. 6). In the first method, the experimental measurements of loss tangent at different loading frequencies were curve-fitted to the analytical model (Benalla et al. 2012), in which K_LC is the fitting parameter. This approach resulted in an average lacunar–canalicular permeability in the osteonal radial direction, K_rr = (2.34 ± 0.33) × 10⁻²²m² (Fig. 2). Changes in loss tangent due to frequency were not statistically significant different at frequencies below 3 Hz, but differences were significant at 5 Hz and higher frequencies when compared to the loss tangent measured at 1Hz. Also, the standard deviation of the tan[δ(ω̄)] decreased as the frequency increased. The K_LC measurements have an 11.4% coefficient of variation (CV = 100 × standard deviation/mean). In the second method, using Eq. (6), the lacunar–canalicular permeability was found to vary between (3.27± 0.45) × 10⁻²²m² and (1.68± 0.11) × 10⁻²²m² when analyzed in the 1–100 Hz range, showing a linear decrease with respect to frequency at a rate of −0.02 × 10⁻²²m²/Hz (Fig. 3). The ordinate at the origin (zero frequency) represents the intrinsic K_LC, which was found to be 3.27 × 10⁻²²m². When compared to K_LC measured at 1 Hz, the lacunar–canalicular permeability showed no significant differences below 20 Hz, but changes were significant at 30 Hz and higher frequencies.

Fig. 2.

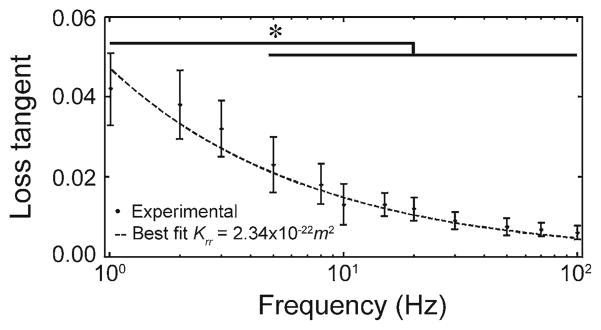
Curve fitting of the analytical model and experimental data of the loss tangent to evaluate the average lacunar–canalicular permeability, K_rr = (2.34 ± 0.33) × 10⁻²²m²(^* p < 0.05, sixty loaded osteons)

Fig. 3.

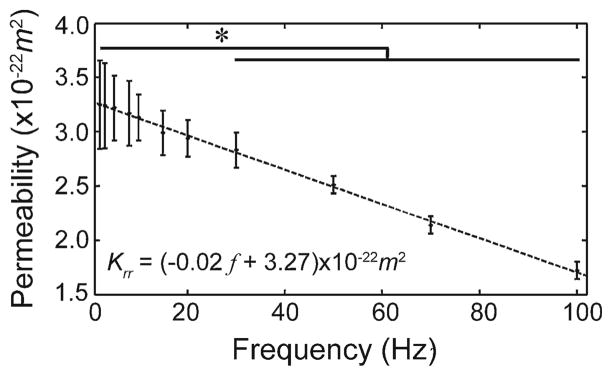
Lacunar–canalicular permeability versus frequency, K_rr = (3.27 − 0.02 f ) × 10⁻²²m²(^* p < 0.05, sixty loaded osteons) from inverse poroelastic model of K_rr

3.4 Loss tangent and K_LC as a function of the lacunar–canalicular porosity

The loss tangent versus lacunar–canalicular porosity (φ_LC) displays a linear behavior within the narrow range of porosity investigated (Fig. 4). The correlation between these two variables is r² = 0.54, and the equation of the linear fit model is tan[δ(ω̄)] = 0.003φ_LC + 0.027. Similarly, the analysis of K_LC versus φ_LC exhibits a linear behavior, K_rr = (0.27φ_LC + 1.14) × 10⁻²²m², and a strong correlation coefficient, r² = 0.86 with p < 0.05 (Fig. 5).

Fig. 4.

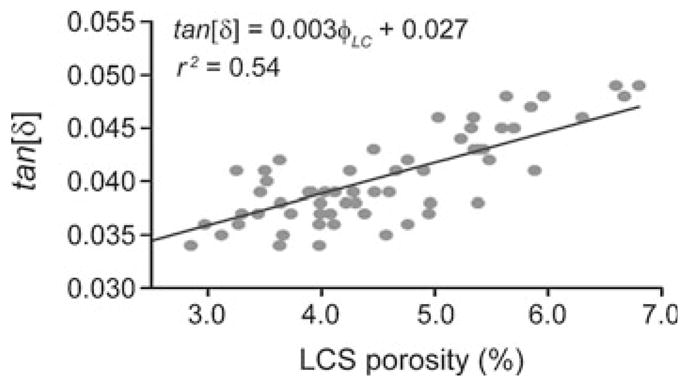
Loss tangent, tan [δ(ω = 2π)], measured at 1 Hz cyclic loading of isolated human osteons versus lacunar–canalicular porosity, φ_LC (sixty loaded osteons)

Fig. 5.

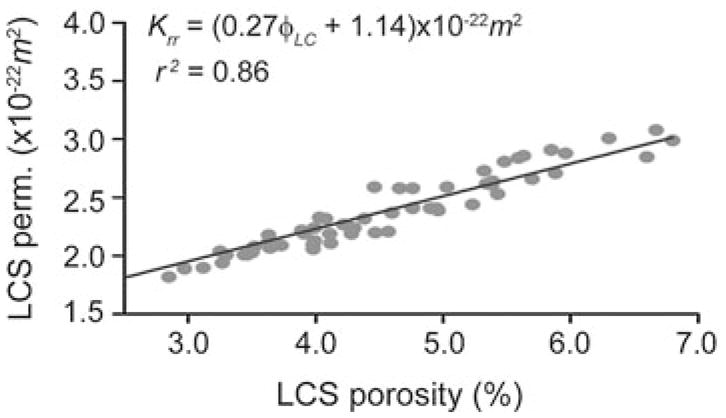
Lacunar–canalicular permeability in the radial direction of isolated human osteons, K_rr, versus lacunar–canalicular porosity, φ_LC (sixty loaded osteons)

4 Discussion

4.1 Material properties and microstructure of isolated osteons

There are not many measurements of the lacunar–canalicular porosity (φ_LC) reported to date; however, recent advances in 3D imaging have lead to measurement of several microarchitectural parameters of the lacunar–canalicular system, from where φ_LC can be estimated. The lacunar–canalicular microarchitecture includes the volumetric lacunar density, which represents the number of osteocyte lacuna measured per unit volume (#/mm³), lacunar volume, inter-lacuna separation, canaliculi diameter, and number of primary and secondary (branching) canaliculi emanating from a lacuna (Table 1). The average lacunar porosity, φ_Lac, estimated from μCT scans in this study, 1.69 ± 0.50 %, using 2-μm resolution is in close agreement with the 1.3 % from Schneider et al. (2007) using 0.7-μm resolution in mice, the 1.5 % from Tommasini et al. (2012) using 0.75-μm resolution in rats, and the 1.5 ± 0.44 % lacunar porosity values reported by Palacio-Mancheno et al. (2013) using 1-μm resolution. Based on the structural model described by Eq. (9), the average canalicular porosity, φ_Can, was found to be 2.79 ± 0.91 %, which is in between the range of values, 0.7 and 14 %, reported by Schneider et al. (2011) using focused ion beam/scanning electron microscopy (FIB/SEM) and Sharma et al. (2012) using confocal laser scanning microscopy (CLSM), respectively. However, measurements of the canalicular porosity using CLSM seem to be overestimated due to partial volume effects. In our study, the addition of the lacunar and canalicular porosities lead to an estimated lacunar–canalicular porosity, φ_LC, of 4.51±2.01 %. The volumetric lacunar density (N_Lac/mm³) of 36.85 ± 9.99(×10³) lacunae per mm³ measured in this study also falls within the range of values, 26 – 90 × 10³ lacunae/mm³, in other studies using synchrotron radiation-based micro-CT (SR-μCT) (Hannah et al. 2010; Tommasini et al. 2012; Carter et al. 2013), μCT (Palacio-Mancheno et al. 2013), and CLSM (Sharma et al. 2012). Interestingly, N_Lac/mm³ seems to be significantly larger in rodents when compared to human data. Studies using CLSM and SR-μCT have found the average lacunar volume to fall in the range of 290–455 μm³ (Sharma et al. 2012; McCreadie et al. 2004; Hannah et al. 2010; Carter et al. 2013). The inter-lacunar separation has been reported to vary between 22 and 40 μm in different species in CLSM studies (Sharma et al. 2012; Sugawara et al. 2011, 2005), and using SR-μCT (Hannah et al. 2010). Canaliculi morphology measurements were reported in the early work of Marotti (1990), Marotti et al. (1995, 1985) and in several more recent studies. The average canaliculi diameter spans a range of 100–700 nm using electron microscopy (Sharma et al. 2012; Marotti 1990; You et al. 2004; Schneider et al. 2011), CLSM (Sharma et al. 2012; Sugawara et al. 2005), and atomic force microscopy (AFM) (Lin and Xu 2011). Canalicular diameter measurements are considered to be overestimated in studies using CLSM systems because of partial volume effects. Finally, an average of 41–115 primary canaliculi per lacuna was reported using CLSM measurements and estimates from light microscopy measurements (Sharma et al. 2012; Sugawara et al. 2005; Beno et al. 2006), as well as using FIB/SEM (Schneider et al. 2011). Secondary canaliculi, which may branch from the primary canaliculi directly connected to a lacuna, were found to be ~ 390 canaliculi per lacuna (Sharma et al. 2012), which is four times higher than the number of primary canaliculi reported in the same study (Table 1). The tissue mineral density from μCT measurements found in this study using 2.1-μm resolution, 0.91 ± 0.06 gHA/cm³, is in general agreement with previous reports of TMD in human samples, 0.926 ± 0.035 and 1.047 ± 0.046gHA/cm³, measured at 13.5 and 3.4-μm scanning resolution (Souzanchi et al. 2012), respectively. These TMD values from human tissue are slightly lower than TMD values reported in rodents, 1.13–1.36 gHA/cm³ (Palacio-Mancheno et al. 2013; Matsumoto et al. 2006; Martin-Badosa et al. 2003; Windahl et al. 1999).

4.2 Effect of osteon freshness on loss tangent

A main objective of this study was to determine the K_LC of fresh human bone after excluding the effect of the vascular system permeability. The freshness of the specimen is one of the most important factors for improving the accuracy in determining K_LC. Bone tissue loses some of its freshness with time and storage conditions, despite precautions that can be taken. Keeping the bone specimens hydrated with physiological solution and performing the experiment immediately after the specimen isolation are critical for acquiring ex vivo measurements that are as close as possible to the in vivo condition. Plots of tan[δ(ω̄)] obtained from loaded osteons versus time show a decline of less than 1 % for a time duration of five hours and a decline of 5 % for a period of five days. The 1 % decrease of tan[δ(ω̄)] does not significantly affect the final result of K_LC, while the 5 % decrease reduces K_LC by 10 %. In this study, we have made every effort to preserve the freshness of the osteons by storing them immersed in PBS and loading them within five hours after isolation.

4.3 Intrinsic permeability of human LCS

The estimates of lacunar–canalicular permeability in Table 2 exhibit a broad range of values, from 10⁻¹⁷ to 10⁻²⁵ m², with a noticeable 2–3 orders of magnitude difference between the average permeability value obtained from theoretical approaches (10⁻¹⁷ to 10⁻²⁰ m²) and experimental/theoretical approaches (10⁻²² to 10⁻²⁵ m²). In this study, the values of K_LC obtained by both curve fitting and inverse poroelastic model, 2.34 × 10⁻²²m² and 3.27 × 10⁻²²m², respectively, are much closer to the predicted values of K_LC by several theoretical analyses. Overall, these K_LC values lie in the middle range of values reported from theoretical and experimental studies (Table 2). Data also exhibit a small coefficient of variability (14.1 %) when compared to previous reports in the literature (Table 2), possibly due to the individual measurement of φ_LC and tissue elastic modulus for each osteon.

Table 2.

Measurements and estimates of intrinsic permeability in the vascular and lacunar–canalicular systems (updated from Cardoso et al. 2013)

Reference	Method (theoretical estimate)	Tissue	VS permeability (m2)
Johnson (1984)	Theoretical study	–	2.5×10−14
Dillaman (1984)	Theoretical study	Rat	1 × 10−13 to 1 × 10−11
Zhang et al. (1998)	Theoretical study	–	1 × 10−15 to 1 × 10−13
Swan et al. (2003)	Theoretical study	–	1.25 × 10−13 to 3 × 10−12
Reference	Method (experimental measurement)	Tissue	VS permeability (m2)
Rouhana et al. (1981)	Perfusion	Bovine	3 × 10−13
Li et al. (1987)	Perfusion	Canine	5 × 10−17 to 1 × 10−15
Malachanne et al. (2008)	Compression and FEA	Bovine, ox femurs	1.1 × 10−13
Wen et al. (2010)	Perfusion	Canine	4 × 10−17
Reference	Method (theoretical estimate)	Tissue	LCS permeability (m2)
Weinbaum et al. (1994)	Ultrastructural model	–	1.0 × 10−22 to 1.0 × 10−19
Zhang et al. (1998)	Theoretical, adapted from Weinbaum et al. (1994)	–	1.5 × 10−20
Wang et al. (1999)	Theoretical, adapted from Weinbaum et al. (1994)	–	1.0 × 10−21 to 1.3 × 10−19
Smit et al. (2002)	Finite element analysis	–	2.2 × 10−22
Gururaja et al. (2005)	Theoretical, adapted from Weinbaum et al. (1994)	–	7.5 × 10−20
Beno et al. (2006)	Adapted from Weinbaum et al. (1994)	Chick, rabbit, bovine, horse, dog, human (data from Remaggi et al. 1998)	1.0 × 10−22 to 1.0 × 10−19
Lemaire et al. (2008)	Glycocalyx fiber permeability, adapted from Weinbaum et al. (1994)	–	5.9 × 10−18 to 2.0 × 10−17
Anderson et al. (2008)	Perfusion on scaled-up models and predictive virtual and stochastic computational models	Scaled-up, rapid prototyped models of human femoral neck	2.7 × 10−18 to 8.7 × 10−18
Cowin et al. (2009)	Poroelasticity theory	–	1.5 × 10−20
Goulet et al. (2009)	Carman–Kozeny permeability model	–	1.0 × 10−18 to 1.0 × 10−20
Kameo et al. (2010)	Morphology of LCP using CLSM	Swine tibia	3.3 × 10−19 to 1.3 × 10−18
Lemaire et al. (2012)	FEM, Carman–Kozeny permeability model	–	1.0 × 10−19 to 1.0 × 10−18
Reference	Method (experimental measurement)	Tissue	LCS permeability (m2)
Oyen (2008)	Nanoindentation poroelasticity	Human	4.1 × 10−24
Galli and Oyen (2009)	Nanoindentation poroelasticity	Human	6.5 × 10−23
Zhou et al. (2008)	FRAP poroelasticity	Mice	1.0 × 10−21
Gailani et al. (2009)	Stress relaxation single osteons poroelasticity	Bovine	5.0 × 10−25 – 8.0 × 10−24
Gardinier et al. (2010)	Step loading in vivo poroelasticity	Canine	2.8 × 10−23
Present study	Harmonic loading of isolated osteons	Human femoral diaphysis	2.34 × 10−22 ± 0.33 × 10−22

There may be several reasons for the wide range of K_LC in previous studies (Cardoso et al. 2013) The first reason is related to the specimen size. A limitation associated with data from experimental studies that have used millimeter size or larger bone samples is that the resulting measurements correspond to the combination of the VS and LCS permeability due to the intermingling of the vascular and lacunar–canalicular pores. Such permeability measurements are thus dominated by the vascular pores, which are much larger than the lacunar–canalicular pores. In order to measure the K_LC only, the VS should not be included in the sample to be tested. The second reason is related to the material properties of the specimen. In most previous work, the material properties of the bone were adopted from the literature and generalized to all the samples. The adopted values may be close to the real ones; however, certain parameters, such as the φ_LC, may have a significant effect on the analytical model, which causes a significant variation in the determination of the K_LC. The sensitivity of the model parameters (Benalla et al. 2012) indicated that the φ_LC and Young’s modulus were among the most influential parameters on the measurement of K_LC. Therefore, instead of adopting a single value of φ_LC and Young’s modulus of the tissue matrix material from the literature, these parameters were determined separately for each osteon specimen. The average Young’s moduli of the matrix material in the radial (15.29 ± 1.31 GPa) and axial (18.72 ± 1.61 GPa) directions as well as the φ_LC (4.51 ± 2.01 %) were found to be in close agreement with values reported by others (Goulet et al. 2009; Orias et al. 2009; Cardoso et al. 2013). The individual determination of these parameters increased the accuracy in determining K_LC. Third, this large variability in the lacunar–canalicular permeability is likely influenced by theoretical assumptions and experimental errors associated with the measurement of a very small quantity. Performing direct measurements on samples with very small permeability and very small size (i.e., samples 100–250 μm in diameter and 0.5 mm in height) is highly sensitive to measurement errors. Fourth, the freshness of the tissue seems very important to obtain appropriate values of permeability. When the tissue is no longer fresh, or has been treated (i.e., dehydrated, resin infiltrated, and embedded), its properties change, and the lacunar–canalicular pores may be not be as open as in their natural state and result in smaller permeability estimates. Fifth, several theoretical estimates analyze the lacunar–canalicular system considering open pores at both ends of the LCS. However, the knowledge of boundary conditions of the analytical model used to estimate the lacunar–canalicular permeability is generally imprecise. Sixth, there exist hydroelectrochemical effects associated with fluid flow in canaliculi (Lemaire et al. 2012) that could significantly influence the permeability of the LCS, which are not fully elucidated to date.

4.4 Dynamic permeability of human LCS

The second goal of this study was to investigate the dependence of K_LC on loading frequency. It was found that as the frequency increases from 1 to 100 Hz, K_LC decreases linearly at a rate of −0.02 × 10⁻²² m²/Hz, from 3.25 × 10⁻²²m² to 1.82 × 10⁻²²m² (Fig. 3). The inverse relationship between K_LC and frequency is considered to be mainly related to the decrease in the loss modulus and the increase in the storage modulus in the matrix material (Figs. 3 and 4 in Benalla et al. (2012)). Because the relaxation time associated with the LCS is around 4.9 ms (Zhang et al. 1998), which corresponds to ~ 200 Hz, it is expected that the decreasing rate of K_LC will increase after 200 Hz because the LCS pore pressure will not have enough time to relax entirely. The incomplete relaxation of the LCS will cause the interstitial fluid to lower its velocity between all the lacunae and through the canaliculi, which will amplify the decreasing rate of K_LC at loading frequencies higher than 200 Hz. It was noted that the coefficients of variation of tan[δ(ω̄)] and K_LC are larger at low frequency and keep decreasing as the frequency increases (Figs. 2 and 3). This observation is explained by the fact that at high frequencies, the mechanical behavior of the osteon becomes purely elastic (Figs. 3 and 4 in Benalla et al. 2012).

4.5 Effect of φ_LC on tan[δ(ω̄)] and K_LC

The sensitivity study in Benalla et al. (2012) showed that φ_LC is one of the most influential parameters of the model inputs. Therefore, the variability of K_LC and tan[δ(ω̄)] versus φ_LC was also studied. Strong relationships were found between tan[δ(ω̄)] and φ_LC (Fig. 4) as well as between K_LC and φ_LC (Fig. 5) for the sixty loaded osteons. The high correlation, r² = 0.86 (p < 0.05), of the permeability with respect to porosity (Fig. 5) shows that there is a strong linear relation-ship between the two parameters and suggests that the variability of K_LC depends mainly on φ_LC. Thus, the equation of the linear fit model, K_rr = (0.27φ_LCS + 1.14) × 10⁻²²m², represents an empirical formula to predict the K_LC from φ_LC measurements. However, the correlation between loss tangent versus porosity, r² = 0.54 (p < 0.05), illustrates that tan[δ(ω̄)] is not dependent on the φ_LC alone and that other parameters such as the elastic constants and inner and outer osteonal radius are also involved.

4.6 Study limitations

There are several limitations in this study. First, the idealization of the osteon and the Haversian canal as pure cylinders is not fully correct. The shape of the osteon and the Haversian canal is not purely circular, and their radii may slightly change from bottom to top. However, the small height of the osteon sections, 500 μm, minimizes the inaccuracy of this assumption. Second, in the evaluation of the lacunar–canalicular porosity, the canaliculi are considered to be straight tubes relating the lacunae with each other and with the Haversian canal. In reality, some of these canaliculi, especially the ones emanating from the apices of the lacunae, radiate along the vertical axis of the lacunae before they bend horizontally following the radial direction Marotti (1996). Nonetheless, only few canaliculi take that bent shape, which reduces their effect. The third limitation is related to the assumption of considering the outer boundary of the osteon to be impermeable. However, interstitial fluid flow across the cement line, if it exists, should be negligible compared to fluid flow at the surface of the Haversian canal. Finally, the φ_Lac was estimated using μCT scans with a 2.1-μm resolution. A more accurate estimate of φ_Lac could be obtained with a nanoCT system.