Dynamic contrast-enhanced magnetic resonance imaging: fundamentals and application to the evaluation of the peripheral perfusion

Abstract

Introduction

The ability to ascertain information pertaining to peripheral perfusion through the analysis of tissues’ temporal reaction to the inflow of contrast agent (CA) was first recognized in the early 1990’s. Similar to other functional magnetic resonance imaging (MRI) techniques such as arterial spin labeling (ASL) and blood oxygen level-dependent (BOLD) MRI, dynamic contrast-enhanced MRI (DCE-MRI) was at first restricted to studies of the brain. Over the last two decades the spectrum of ailments, which have been studied with DCE-MRI, has been extensively broadened and has come to include pathologies of the heart notably infarction, stroke and further cerebral afflictions, a wide range of neoplasms with an emphasis on antiangiogenic treatment and early detection, as well as investigations of the peripheral vascular and musculoskeletal systems.

Applications to peripheral perfusion

DCE-MRI possesses an unparalleled capacity to quantitatively measure not only perfusion but also other diverse microvascular parameters such as vessel permeability and fluid volume fractions. More over the method is capable of not only assessing blood flowing through an organ, but in contrast to other noninvasive methods, the actual tissue perfusion. These unique features have recently found growing application in the study of the peripheral vascular system and most notably in the diagnosis and treatment of peripheral arterial occlusive disease (PAOD).

Review outline

The first part of this review will elucidate the fundamentals of data acquisition and interpretation of DCE-MRI, two areas that often remain baffling to the clinical and investigating physician because of their complexity. The second part will discuss developments and exciting perspectives of DCE-MRI regarding the assessment of perfusion in the extremities. Emerging clinical applications of DCE-MRI will be reviewed with a special focus on investigation of physiology and pathophysiology of the microvascular and vascular systems of the extremities.

Introduction

Dynamic magnetic resonance imaging (MRI) has been applied for over a decade to extract functional information regarding the peripheral vascular system (1-4). Two frequently used techniques, blood oxygen level-dependent (BOLD) MRI and arterial spin labeling (ASL), are limited to the measurement of energy consumption and perfusion but are unable to ascertain information regarding vessel permeability or volume fractions (5-8).

DCE-MRI however, provides the possibility for multiple and quantifiable parameters pertaining to tissue perfusion and microvascular status (9,10). Since its initial presentation the approach has mainly been applied in studies of the myocardium (11), the brain (12-15) and oncological research (11,16-21). Lately, DCE-MRI has also been adopted to examine the peripheral vascular and muscular system.

The first part of this review will elucidate the fundamentals of data acquisition and interpretation of DCE-MRI, two areas that often remain baffling to the clinical and investigating physician because of their complexity. Basic fundamentals will be explained including the physical and physiological concepts behind DCE-MRI. The second part will discuss developments and exciting perspectives of DCE-MRI regarding the assessment of perfusion in the extremities. Emerging clinical applications of DCE-MRI will be reviewed with a special focus on investigation of physiology and pathophysiology of the microvascular and vascular systems of the extremities.

Fundamentals

Origin of the DCE-MRI signal and technical principles

As suggested by its name, DCE-MRI analyzes the temporal enhancement pattern of a tissue following the introduction of a paramagnetic contrast agent (CA) into the vascular system. This is achieved by the acquisition of baseline images without contrast enhancement, followed by a series of images acquired over time (usually over a few minutes) during and after the arrival of the CA in the tissue of interest.

The acquired signal is used to generate a so-called time intensity curve (TIC, Figure 1) for the tissue, which mirrors the tissue’s response to the arrival of CA in enhancement values. It is by the analysis of this curve that those certain physiological properties that are related to the microvascular blood flow, such as vessel permeability, vessel surface area product and tissue volume fractions, can be derived.

Figure 1.

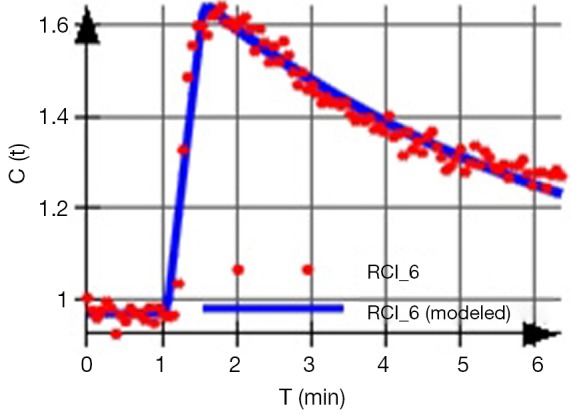
Exemplary time intensity curve acquired from a tumor metastasis.

The underlying principal of all variations of DCE-MRI studies is rather simple: as a paramagnetic particle enters and disperses through the tissue, it alters the MR signal intensity (SI) of the tissue depending on its local concentration (though, as opposed to computed tomography, this relationship is not linear).

In a selected region of interest (ROI) MR images are acquired every few seconds before, during, and after a CA is intravenously injected. Each image acquired corresponds to one time point, and each pixel in each set of images generates its own curve of intensity values. Since the induced variation in SI (correlating to the CA concentration in the tissue) at every time point after injection depends on tissue vascularization, the permeability of the vessels, the vessels’ surface area product, extraction fraction, blood flow, etc., parametric maps of specific microvascular biomarkers can be derived. Moreover, absolute values of these parameters can be extracted using appropriate mathematical models. These parameters reflect the two-compartment pharmacokinetics exhibited by CAs, which are distributed between the intravascular and extravascular spaces.

DCE-MRI currently defines two techniques depending on the origin of the measured signal and its registration.

Underlying the high sensitivity of MRI to small concentrations of paramagnetic materials, passing through a tissue, are two different physical-chemical properties.

Relaxation effect

Diffusible CA reduces the tissue relaxation times T1 and T2. This effect is used to generate positive enhanced T1-weighted images. Studies assessing this effect are commonly termed Dynamic Contrast Enhanced (DCE)-MRI, T1-W DCE or Dynamic Relaxivity MRI.

Susceptibility effect

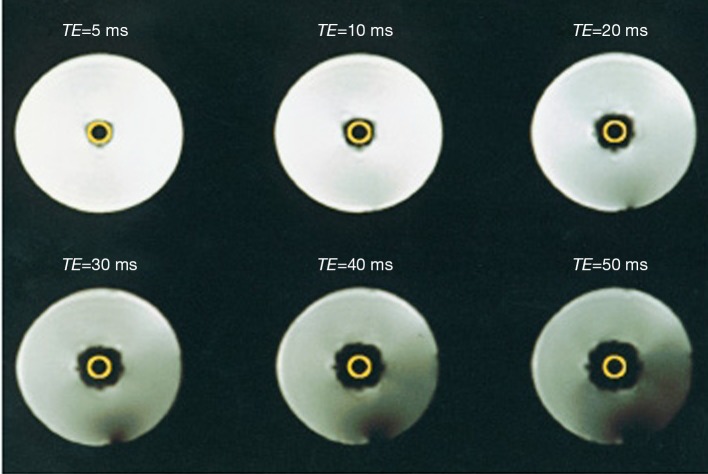
It is known from conventional MRI, that on the boundaries between structures that differ in their magnetic susceptibility, local magnetic inhomogeneities arise. These inhomogeneities lead to signal reduction on T2*-W gradient echo sequences. The same effect occurs when a paramagnetic CA resides in the intravascular space of a tissue. If the magnetic susceptibility of the CA is much higher than that of the surrounding tissue water, local magnetic inhomogeneities will form between the intra and extravascular space (Figure 2). The formation of these transient magnetic field inhomogeneities during the passage of a paramagnetic CA through the capillaries is used to produce negative enhanced T2 or T2* weighted images. Studies relying on this effect are referred to as Dynamic Susceptibility Contrast (DSC)-MRI or T2*-W DCE (22).

Figure 2.

Susceptibility effect: a tube containing a Gd-DTPA solution enclosed within a water phantom. As the echo times are prolonged the signal reduction effect increases on T2*-W images. From Themen [1997]. This material is reproduced with permission of Springer from Brix et al., Methodische Ansätze zur quantitativen Beurteilung der Mikrozirkulation im Gewebe mit der dynamischen Magnetresonanztomographie, Radiologe, 1997.

It becomes evident that this imaging modus can only be applied in tissues where specific vascular barriers prevent a fast passage of the CA into the interstitial space such as brain, retina, and testes. Alternatively, intravascular (blood pool) CA can be administered as those CA leave the vessels at a much slower rate.

The two techniques will be discussed separately as not only the origin of their signal but also other aspects, such as data acquisition and analytical interpretation, are quite different.

Image acquisition

The number of measurements required for data acquisition is dependent on the quantification method one wishes to apply. These measurements include:

1. Recording a map of pre-contrast native T1 values (T1₀ map): this map is necessary for the calculation of CA concentrations (23).

2. Acquisition of heavily T1-weighted images prior and following CA introduction: at a reasonably high temporal resolution in order to be able to characterize the kinetics of the CA entry and exit out of the tissue (22,24).

3. Acquiring the arterial input function (AIF): estimation of the CA concentration in the blood plasma of a feeding artery as a function of time. Obtaining the AIF is essential for nearly all quantitative analysis methods and remains technically the most challenging part in the process of data acquisition.

For simple semi-quantitative analysis of SI curves measurement (I) will suffice. For additional CA-concentration values measurement (II) must also be included. For quantitative pharmacokinetic analysis, which is able to yield absolute metrics, all three measurements are necessary.

The arterial input function (AIF)

When calculating the various vascular parameters, mathematical pharmacokinetic models assume that the CA arrives in a vessel entering the tissue in the form of an ultra-narrow bolus (i.e., impulse input of tracer also known as the residue or residual response) (22). Only this curve can be used to extract quantitative information pertaining intrinsic tissue properties. In reality however, the concentration time course of the CA in a vessel entering the tissue (the AIF) differs substantially from the ideal form, therefore the residual function cannot be measured directly (Figure 3). To solve this problem concentration time courses of both the tissue and a feeding artery (AIF) are measured whereupon these two curves can be used to reconstruct the sought after residual function, (The mathematical process of reconstructing an underlying unknown original function, in our case the residual function, that has been modified by a second function (the AIF) to subsequently produce a third function (tissue concentration time course) is called deconvolution, a term which often surfaces in publications discussing DCE-MRI). The above description represents a simplified view of a rather complicated mathematical process. The interested reader is referred to reference (25).

Figure 3.

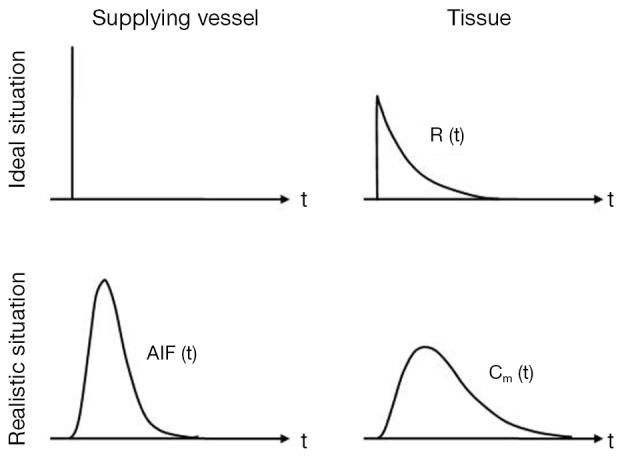
The AIF: mathematical pharmacokinetic models assume that the CA arrives in a supplying vessel in the form of an ultra-narrow bolus. The tissues response (and therefore the measured signal) is then the sought after residual function from which quantitative information can be extracted. De facto, the bolus form in a feeding artery (the AIF) differs considerably from this ideal form. The tissues response is consequently not the residual function but rather a dispersed time concentration curve. AIF, arterial input function; CA, contrast agent.

Three main approaches have been developed for AIF estimation (I-III) and two further approaches (IV,V) eliminate the requirement for its measurement: (I) invasive (26); (II) assuming an average AIF for all subjects; (III) acquiring the AIF from the DCE-MRI data sets (1,27,28); (IV) reference region models (29-31) and the (V) step input method (2,32).

DCE-MRI data analysis

The arrival of CA and thus the enhancement pattern of the tissue depend on a wide variety of factors including vascularity, capillary permeability, perfused capillary surface area, volume and composition of extracellular fluid, renal clearance and perfusion. The analysis of DCE data can provide valuable information concerning the vascular status and perfusion. Analysis of the data can be performed using either: simple semi-quantitative methods, analysis of curve morphology or quantitative methods.

Semi-quantitative analysis

Simple semi-quantitative metrics are derived directly from the SI curve alone. They are easy to calculate and do not have any rigorous requirements in terms of data acquisition (33). Frequently used metrics are listed in Table 1.

Table 1. Semi-quantitative metrics of DCE-MRI.

Parameter	Definition	Unit
Initial area under the curve (iAUC)	Calculates the area under tissue concentration time curve until a stipulated time point that includes a major portion of the tissues’ response*
Maximum (relative) enhancement	Defined as maximum signal difference (MSD)/signal baseline (SB), where MSD is the difference between the signal intensity at its maximum (SImax) and SB	In %
Time to maximum signal intensity	Time elapsed between the arterial peak enhancement and	In sec
Time to peak enhancement	Time elapsed between the arterial peak enhancement and the end of the steepest portion of enhancement (Figure 4)	In sec
Rate of peak enhancement	[(SIend – SIprior/(SIbase × T)] ×100	In %/min
Rate of enhancement	[(SImax–Slbase)/(SIbsae × Tmax)] ×100**	In %/min
T90	Measurement of the time taken for the tissue to attain 90% of its subsequent maximal enhancement***	In sec
Maximum rate of change of enhancement (MITR)	Maximal intensity change per time interval ratio***	in %/min

*, iAUC can be normalized by the corresponding area under the AIF time concentration curve. It can then be used as an approximate index of the CA distribution volume in the tissue. In oncological studies, iAUC_norm is demonstrative of the combined volumes of v_ρ and v_e (see Table 2) and several studies have shown its usefulness as a potential biomarker in antiangiogenic drug trials (34); **, The slope of the TCC can be normalized as well by dividing it with the arterial TIC slope. This parameter is termed perfusion index (PI) and has been used both in studies of skeletal muscle and the myocardium (1,3,11); ***, Parameters 9 and 10 are designed to minimize physiological patient variables, variations in contrast dose and injection technique as well as scanning protocols and different scanner types (35). DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging; CA, contrast agent; MITR, maximum intensity time ratio.

Semi-quantitative analysis has several advantages: it obviates the need for the measurement of the AIF, it is robust, and several parameters such as AUC are relatively independent of injection protocols (36). One challenging aspect, however, is the fact that semi-quantitative parameters do not necessarily have any obvious physiological correlates. Since they represent a mixture of microcirculatory and tissue properties, the degree to which each of these physiological parameters contributes to the MR-signal, remains unknown (37). A further limitation is that most Model-free parameter extraction methods remain sensitive to variations between different acquisition protocols. Parameter metrics will depend on factors such as sequence parameters, hardware settings, scan duration, amount of administered CA (38), CA properties, injection protocol and so on. This will occur even if identical sequences are used since the baseline signal for any given tissue, using a particular sequence, will differ by the choice of imager (36). As a consequence, comparison of semi-quantitative studies is difficult at best.

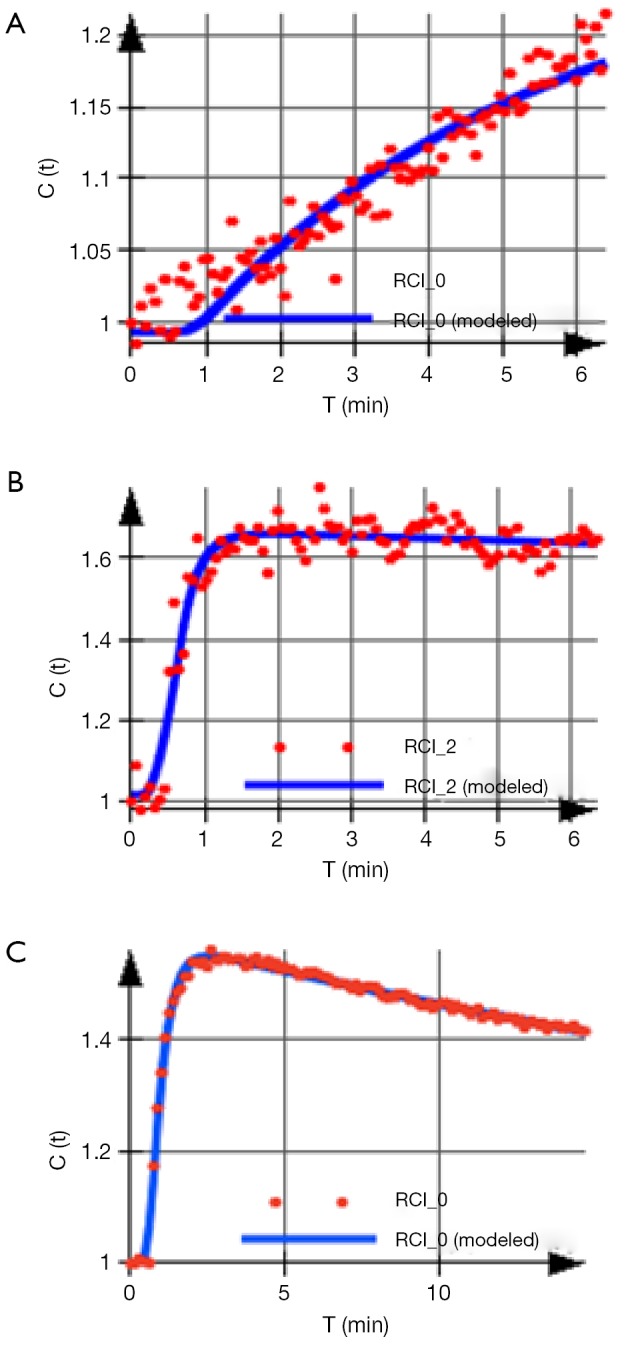
This having been said, semi-quantitative parameters do mirror physiological mechanisms and qualitative signal based analysis is very useful, especially when measurements of relative changes in an individual or a group of patients is required. Semi-quantitative analysis has demonstrated clear diagnostic value in a number of areas. For instance, in oncological studies (16-21) including the assessment of tumor angiogenesis (39) but also in studies of rheumatoid illnesses (40,41), the heart (11) and of musculoskeletal perfusion evaluation (Figure 4).

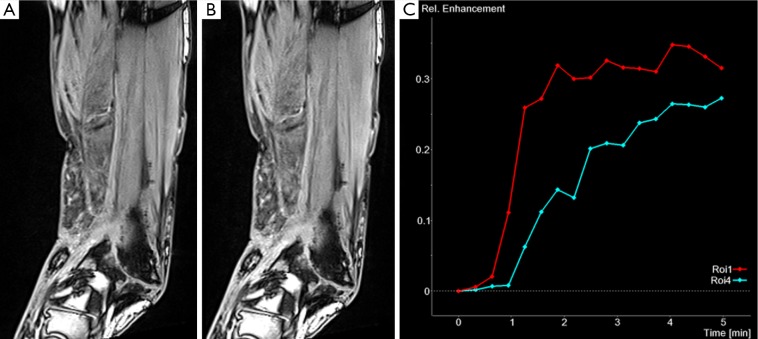
Figure 4.

DCE-MRI in a patient with fracture non-union (two early phases shown in A and B) and (C) corresponding signal intensity curves for regions of interest in the non-union (Roi 1) and adjacent muscle (Roi 4). Due to the more intense contrast agent uptake in the non-union compared to adjacent muscle this can be classified as vascularised non-union associated with improved outcome. DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging.

Semi-quantitative analysis can also be applied using the so-called first-pass methods. First-pass methods assume that the dynamic enhancement pattern observed early during the first pass (the increment slope) will represent primarily the kinetics of the CA within the blood vessels (whereas the peak of the TIC will reflect the enhancement created by the CA in both the intravascular and extravascular extracellular space). These methods are easily implemented in clinical settings with relatively low scanning time and have been applied most extensively in studies of myocardial perfusion (42) including ischemic conditions (43), cardiac Syndrome-X (11), to some extent in the skeletal muscle (see below) and also in oncological studies (21,44).

Morphologic analysis

Investigators who explore this method define distinctive TIC curve patterns (Figure 5) and attempt to assign them to physiological or pathological findings (45). The method has been branded “curve-ology” by Yankeelov et al. (23). Though not quantitative, this approach offers some appealing advantages: (I) it is less sensitive to variations in sequence parameters and scanner calibrations; (II) it is not computationally demanding as fitting is not involved; (III) it does not rely on any assumptions (some more, some less physiological) as model based methods do (38).

Figure 5.

Common distinctive curve patterns: (A) referred to as type 2, slow enhancement; (B) referred to as type 3, fast enhancement followed by plateau phase; (C) referred to as type 4, fast enhancement followed by washout phase.

For example, in the skeletal muscle a rapid SI increase followed by a narrow peak and consequent washout is evident of an adequate vascular reserve. But if the TIC displays a shallow increment, a delayed peak and only a weak or absent washout after exercise, this indicates a limited vascular reserve (4) (Figure 6).

Figure 6.

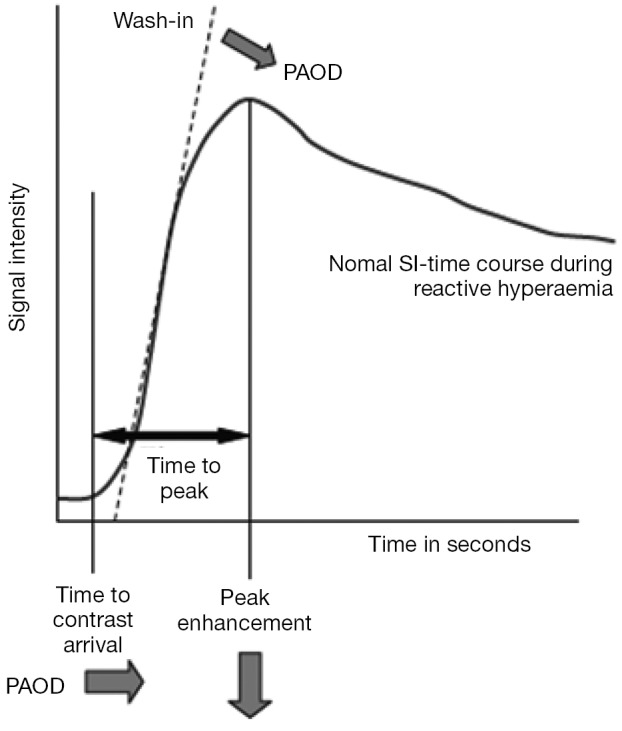
Diagram of a TIC illustrating the CA dependent signal intensity of a tissue over time: the perfusion reserve of patients can be assessed by measuring the reactive hyperemia, following post occlusive or exercise protocols and comparing them with age-matched controls. In case of peripheral arterial occlusive disease (PAOD), the TIC displays a shallow increment (i.e., a delayed peak), a lower peak enhancement (arrows) and only a weak or absent washout after exercise, this indicates a limited vascular reserve. A rapid signal intensity increase followed by a narrow peak and consequent washout is evident of an adequate vascular reserve. This material is reproduced with permission of Springer from Weber et al., Quantitative evaluation of muscle perfusion with CEUS and with MR, European Radiology, 2007. TIC, time intensity curve; CA, contrast agent.

Quantitative analysis

DCE-MRIs’ greatest appeal is its ability to produce parameters, directly related to the physiological (and pathophysiological) properties of the vascular environment and the surrounding tissue, in absolute terms. The crucial advantage of absolute numbers is their comparability. Ordinarily, this is facilitated by means of model based pharmacokinetic analysis.

Compartmental pharmacokinetic modeling

To recapitulate, for quantitative analysis the following steps are needed:

1. Measurement of baseline T1 before gadolinium injection in order to transform the signal TIC into a time-concentration curve (TCC);

2. Measurement of SI changes in the tissue, before and after CA application, and optionally the AIF (complex pharmacokinetic models require identification of the AIF);

3. Conversion of SI data to CA concentrations;

4. Once the computed TCCs are obtained they are analyzed by tracer kinetic models using curve-fitting techniques.

In order to describe and analyze the temporal and physical distribution of an inert tracer the classical pharmacokinetics usually utilizes linear compartmental models. A compartment is defined as a distinguishable tracer distribution space (anatomic, functional or fictive) within a biological system. Inside this space, the tracer spreads rapidly whereas the transport between adjacent compartments is hindered in some way, resulting in individual time concentration courses of the tracer in the different compartments. As CAs distribute at different rates in blood and tissue, a two-compartment model considers the intravascular-extracellular volume fraction (blood plasma) to be the central compartment (v_ρ), and the extravascular-extracellular volume fraction (v_e) as the peripheral compartment. The fundamental physiological variables governing CA movement across the vascular endothelium include vessel wall permeability, vessel surface area, blood flow (i.e., perfusion), ratios of the CA concentrations across the endothelium as well as intravascular and extracellular-extravascular volume fractions.

The purpose of the model is to describe the underlying physiological phenomenon in mathematical terms in order to enable the estimation of specific tissue parameters from the measured signal. Sacrificing biological specificity, these models must make very simplified assumptions and approximations about the behavior of the biological system they choose to describe and the kinetics of the CA accordingly. The available analytical models differ in the degree of physiological specificity that they seek to provide. Though, it must be stated that as the number of biological details incorporated in the model increase its accuracy decreases.

The bulk of quantitative analyses techniques rely on mathematical curve-fitting methods to yield estimates of the desired parametric values. Each model is an equation containing a number of adjustable (free fitting) parameters—the more complex the model (and thus more “physiologic”) the more parameters are included. Assuming a model is adequate, it will describe the tissues’ response to a CA bolus (the TCC). By applying mathematical algorithms, the values of the adjustable parameters in those equations are varied and a parameter combination that best fits the TCC is obtained. It becomes immediately clear that this routine will perform less reliably as the number of free fitting parameters increases since the equations are less constrained.

Overview of main existing models

Over the course of the 1990s a variety of pharmacokinetic models were developed. In an attempt to handle the growing nomenclature of model parameters and to enable the comparison and combination of results from different models, Tofts and other leading experts in the field defined a standardized language and a corresponding set of symbols (46) (Tables 2,3). Although perhaps confusing and slightly overwhelming at first, it is extremely worthwhile to get acquainted with these symbols before attempting to explore the literature. A short glimpse at the tables will also reveal two important facts:

Table 2. Parameters used in DCE-MRI models.

Symbol	Parameter	Unit
Ca	Tracer concentration in arterial whole blood	mM = mmol/L
Ce	Tracer concentration in EES	mM
Cp	Tracer concentration in arterial blood plasma	mM
Ct	Tracer concentration in tissue	mM
Cv	Tracer concentration in venous whole blood	mM
Vb	Total whole blood volume*	mL
Ve	Total EES volume*	mL
Vp	Total blood plasma volume*	mL
Vt	Total tissue volume*	mL
vb	Whole blood volume per unit volume of tissue*	None (%)
vp	Blood plasma volume per unit volume of tissue	None (%)
CLd	Distribution clearance	mL·min–1
E	Initial extraction ratio (fractional reduction in capillary blood concentration of a CA as it passes through tissue)	None (%)
Hct	Hematocrit	None
F	Perfusion (or flow) of whole blood per unit mass of tissue	mL·g–1·min–1
P	Total permeability of capillary wall	cm·min–1
PS	Permeability surface area product per unit mass of tissue	mL·min–1·g–1
S	Surface area per unit mass of tissue	cm2·g–1
λ	Tissue blood partition coefficient	mL·g–1
ρ	Density of tissue	g·mL–1

*V_b = v_bV_t; V_e = v_eV_t; V_ρ = v_ρV_t = (1–Hct) V_b. Subscript letters: a, arterial blood; e, extravascular extracellular space; p, plasma; t, tissue; v, venous. C, concentrations (mM); V, total volumes (mL); v, fractional volumes (%); DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging; EES, extravascular extracellular space; CA, contrast agent.

Table 3. Fundamental parameters of DCE-MRI.

Symbol	Parameter	Unit
Ktrans	Volume transfer constant (or coefficient) between blood plasma and extravascular extracellular space (EES)	min–1
ve	Volume of EES per unit volume of tissue	None (%)
keρ**	Rate constant between EES and blood plasma (backflux exchange rate)	min–1

k_eρ** = K^trans/v_e; DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging.

1. There is a vast amount of useful information that DCE-studies are able to produce;

2. DCE does not merely measure the flow of blood through a tissue but rather the actual perfusion on a microscopic level.

As a rule, model based analysis enables the calculation of three relevant microcirculatory parameters:

1. CA exchange rates between the capillaries and the interstitial tissue (capillary permeability);

2. Regional blood volumes (rBVs) and;

3. Regional blood flow (rBF).

The calculation of the physiologic parameters is based in all models on the assumption that an estimate of the concentration of CA in both the tissue and the plasma compartment (the AIF) can be obtained with reasonable accuracy.

The most widely used models in clinical studies are the conventional (assuming instantaneous dispersion of the CA) two-compartment models independently proposed by Brix and Tofts (9,10,46).

(I) The model by Brix et al. (9) describes three parameters: the amplitude A (proportional to the distribution volume of the CA in the tissue of interest; A ~ v_eρ), the exchange rate constant k_eρ (which he termed k₂₁, describes the leakage of contrast from the extravascular [_e] to the vascular compartment [_ρ]) and the elimination rate constant kel (Figure 7). k_eρ is a mass for the endothelial permeability, whereas k_el is a systemic property of the organism. Interestingly enough none of the three is dependent on the form of C_ρ (47,48).

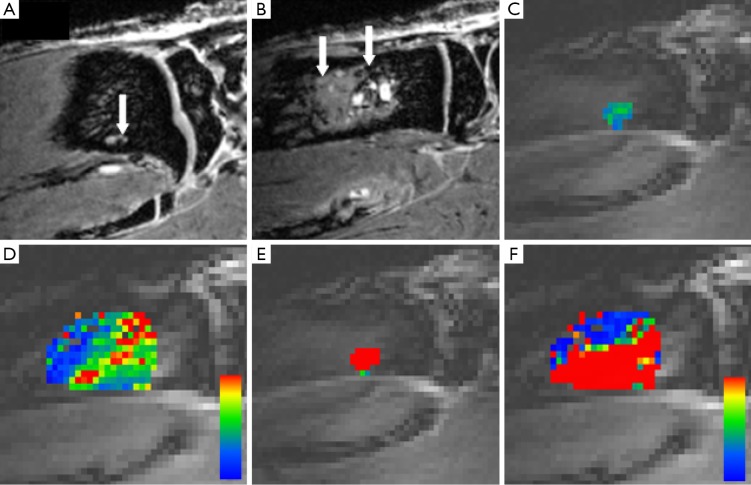
Figure 7.

Comparison of treated experimental breast cancer bone metastases-bearing rats at day 20 after tumor cell injection; T1-weighted MRI after contrast agent application (A), DCE-MRI-derived color coded maps for amplitude A (C) and exchange rate constant k_eρ (E) with sham-treated rats; T1-weighted MRI after contrast agent application (B), DCE-MRI-derived color-coded maps for amplitude A (D) and exchange rate constant k_eρ (F). Arrows point to soft tissue parts of bone metastases. DCE-MRI color code; red color indicates higher values and blue color depicts lower values for amplitude A (D) and exchange rate constant k_eρ (F). DCE-MRI, dynamic contrast-enhanced magnetic resonance imaging.

(II) The Tofts model calculates the parameters K^trans (bulk transfer coefficient which governs the leakage of contrast from the vascular to the extravascular compartment) and v_e (fractional volume of the extravascular extracellular distribution space) (10).

Both the original Brix and Tofts models ignore the intravascular portion of the CA in the tissue and, in contrast to novel models which measure the AIF, both models approximate the AIF inducing uncertainty in the quantification (49).

Please take a moment to observe once more the definition of the transfer constant: K^trans = E·F·ρ (1– Hct). It is evident that the constant is a composite and reflects a combination of microcirculatory flow, microvessel permeability, and surface area. In other words, K^trans reflects both flow and permeability. The interpretation of K^trans will depend on the contribution made by each of these. This, in turn, is determined by the physiological conditions and the molecular mass (or size) of the MR CA used. While some groups directly report K^trans as an index of perfusion, others report an estimate of total perfusion, F, which can be computed from the equation F = K^trans/E. The issue of K^transs’ multiple facets can be resolved in various ways: (I) models which can separately measure these two phenomena, such as the adiabatic model proposed by St Lawrence et al. and the Brix model from 2004 (24,50) (discussed below); (II) the use of first passage methods (51) which assume that the concentration of CA in the interstitium is negligible; (III) utilizing intravascular (blood pool) CAs.

(III) In 1990 Larsson et al. also independently proposed a two compartment model which they originally developed to study multiple sclerosis (52). Though the model is relatively seldom used, Larsson further developed the model to describe myocardium perfusion in 1994 (53). This model has been employed more extensively and is able describe skeletal muscle perfusion as well.

(IV) The Generalized Kinetic model (GKM). Besides proposing a unified vocabulary for DCE-MRI, in 1999 Tofts et al. also introduced a general quantitative model for the estimation of tissue parameters under three different transport conditions (46): flow-limited, permeability-limited and mixed conditions.

The great advantage of the GK model is its simplicity and currently it is perhaps the most extensively used model for DCE MRI data analysis (36,54). However, like its predecessors, the GKM neglects the contribution of the concentration of the plasma space v_ρ. An extended model, introduced by Tofts in 1997, accounts for the vascular plasma space v_ρ (55).

Advanced models: (V) in 1998 Lawrence et al. introduced a new distributed parameter model (assumes concentration gradients within compartments) commonly known as the adiabatic approximation to the tissue homogeneity (AATH) model, or the adiabatic model (50). The adiabatic model allows for separate estimates of blood flow (F), capillary permeability surface (PS) area product, proportional intravascular blood volume (BV) (v_ρ) and the proportional volume of the extravascular extracellular distribution space (v_e). Moreover, it compensates for intravascular contrast.

Although this degree of biological accuracy is tempting, as with all complex models the main problem lies in the use of an increased number of free parameters. The model also relies on the use of curve fitting algorithms which perform less reliably as the number of free fitting parameters rises. This produces increasing uncertainty in the derived measurements and considerably increasing demands on the quality of the data.

(VI) An additional model which enables perfusion and permeability to be measured separately is the two-compartment model presented by Brix in 2004 (24). Similar to the adiabatic model, the simulation of the underlying physiology is more accurate, but the increased complexity makes model-fitting more problematic.

Dynamic susceptibility contrast MRI (DSC-MRI)

In dynamic susceptibility contrast MRI (DSC-MRI) a bolus of CA is rapidly injected intravenously resulting in transient T2* reductions which are tracked during the first passage of the CA through the capillary bed. The rapid loss of MR signal on T2* weighted images is measured and subsequently used to calculate the change in CA concentration for each voxel. This is possible owing to the relationship between local intravascular CA concentration and changes in the transverse relaxation rate (1/T2*). The conversion of TICs into TCCs is performed in order to calculate estimates of local BV and local blood flow. In other words, the transient signal reduction is proportional to local BV and local blood flow.

The most extensive clinical applications of DSC are studies of perfusion pathologies of the brain, including cerebrovascular insufficiency (12,13), stroke (14,15) and brain tumors (56,57) where DSC is capable of detecting under-perfused as well as over-perfused tissues. It has also been used on occasion to measure perfusion in animal experiments (58,59).

Image acquisition

Typically DSC makes use of single or multishot echo planar imaging (EPI) techniques (either spin echo or gradient echo sequences). While spin echo sequences minimize the signal contribution from large vessels, gradient echo sequences maximize T2* weighting. These fast imaging techniques enable a temporal resolution of about 2 seconds and up to 15 slices can be acquired (35). In order to estimate the SI baseline, a set of at least five pre-contrast images should be collected prior to the passage of the bolus.

Special care should be taken with the injection technique. The protocol should be well standardized and a saline flush, delivered at the same rate as the bolus, should follow in order to ensure that the entering bolus is as coherent as possible.

DSC-MRI quantification

DSC uses the first-passage of the contrast bolus to measure tissue perfusion. Basing the analysis purely on first pass data ensures a short acquisition time. The main objective of DSC-MRI is the measurement of:

1. rBV—defined as the volume (mL) of blood perfused vessels in a voxel divided by the tissue mass in the voxel (g);

2. Mean transit time (MTT)—average transit time of a tracer particle through the capillary bed;

3. rBF, i.e., perfusion (milliliters per minute).

The standard approach to estimate absolute blood flow from the obtained data is comprised of four steps:

1. The time-concentration data from each individual voxel is deconvolved with the AIF, derived from a major feeding vessel (48). If only relative comparison of the BVs in the different areas of the tissue is sought, one can forego the measurement of the AIF. In this case calculation of the area under the concentration time curve will suffice;

2. The area under the contrast concentration curve is used for an analytical calculation to estimate the BV within the pixel;

3. The MTT is then approximated using some form of a standardized relationship between the height and the surface of the TCC;

4. Using the central volume theorem {rBF = rBV/MTT [mL·min^–1·g^–1)]} blood flow is calculated.

In addition to flow related parameters, DSC can also produce other useful parameters such as time to peak (TTP) concentration and time of arrival (the time it takes the contrast to reach the voxel).

DCE- and DSC-MRI combination methods

The Dual-echo DSC-MRI methods can simultaneously measure DCE-MRI kinetic parameters (related to extravasation) besides conventional blood flow and BV metrics. The feasibility of separately measuring T1- and T2*-induced signal changes, using dual-echo pulse sequences was first demonstrated in studies of brain tumors (60-62). When combined with a pre-contrast T1 map, dual-echo DSC-MRI protocols are able to reliably determine K^trans and v_e. These parameters exhibited in turn a high degree of correlation with the DSC-MRI-derived parameters (63).

Assessment of perfusion in the extremities

Early studies regarding musculoskeletal lesions

Early investigational DCE studies focused on assessing the potential of the technique in distinguishing between malignant and benign MSK lesions (64-66). Applying semi-quantitative slope values, different reports found significant differences between benign compared to malignant tissues. Lavini et al. also investigated a large palette of MSK afflictions (Figure 5) using the semi quantitative curve shape analysis method (discussed above) (38). Although the shape maps they obtained revealed a significant heterogeneity of TIC patterns within the lesions, a finding they suggested might lead to an appropriate selection of a quantification model for different lesions, they did not report the ability of the method to differentiate reliably between malignant and benign lesions. Bäuerle and coworkers conducted many successful exams to test the ability of DCE-MRI to detect the vascular response of MSK metastasis from breast carcinoma as primary to different therapies (67-69). Equally important, they managed to significantly correlate their results with histopathological findings and by doing so further validated the technique.

Developments regarding the vascular system

Following the initial DCE-MRI studies, which mainly dealt with neoplasms, further studies investigated the potential of DCE-MRI regarding the evaluation of the extremities vascular system. Validation studies utilized the arterial ligation animal model to successfully correlate DCE perfusion analysis with radionuclide-labeled microsphere blood flow measurements (70) (considered as a validation standard for perfusion studies) as well as high-spatial-resolution contrast-enhanced MR angiography (MRA) (71). Further relevant in the aforementioned correlation is the fact that although MRA is able to depict growth of sub-millimeter sized collateral arteries, it remains a purely morphological type of imaging technique and does not include functional microcirculatory information. Therefore correlations with other imaging techniques evaluating the microcirculatory network in quantitative terms might be of considerable benefit (5-8).

Other investigators applied diverse DCE methods to study the physiology and pathophysiology of peripheral perfusion. Faranesh et al. conducted experiments in the resting hind limb of rabbits (72) were they were able to use the extended Tofts model [1997] combined with the CA Gadomer (a blood pool CA) to demonstrate significantly higher values for K^trans and v_ρ in the soleus muscle (type I “slow-twitching”) compared with the tibialis anterior muscle (type II, “fast-twitching”), consistent with their physiological differences. An Israeli group successfully combined the use of Biotin-BSA-Gd-DTPA (blood pool CA) and DCE to monitor angiogenesis in mice following femoral arterial ligation (73). They observed that physical-functional parameters (such as regaining the ability to step on the limb and the color and shape of the toes), correlated with reduced vessel permeability, known to be associated with formation of mature vessels, as shown by MRI analysis and histopathology. Thus hinting the method could be applied to monitor angiogenic and/or conventional treatment of peripheral arterial occlusive disease (PAOD). In order to investigate the hypothesis that blood flow influences vascular growth and may contribute to arteriogenesis, Rissanen et al. applied DSC-MRI and the SPIO Resovist^® to study rabbits that underwent femoral artery ligation (58). Vectored by an adenovirus, the animals received vascular endothelial growth factor (VEGF) gene therapy to the hind limb and perfusion parameters between the operated and non-operated limb were compared. Their experiments showed a strong increase in perfusion to the AdVEGF treated unlegated muscle, whereas the response in the operated limbs was attenuated. These findings, coupled with supporting evidence from histological studies performed on the same animals, strongly affirmed their hypothesis regarding the crucial role of blood flow in capillary arterialization and collateral vessel growth and once more displayed the potential of the method to monitor angiogenic therapy.

The earliest report on human skeletal muscle perfusion during rest and exercise was performed by Nygren et al. (74). Similar to muscle BOLD MRI (5-8), DCE studies also make use of the post occlusive reactive hyperemia and exercise paradigms to investigate muscle perfusion. Nygren compared DCE measurements to the calf of healthy young adults performing a plantar flexion exercise at different workloads, with measurements of blood flow in the popliteal artery using ultrasonography. Maximal SI, upslope and downslope of the bolus, MTT and integrated curve areas were measured semi-quantitatively bilaterally within regions of interest. All the MRI parameters they collected were able to visually separate the muscles into exercising and non-exercising. However, the increase in SI they measured was much smaller compared to the increase in blood flow values acquired from ultrasonography and the correlation between the two measurements was limited to a small range (depending on the muscle chosen, 0.85< R <0.95). The group attributed the discrepancy to a number of possible reasons, namely: poor temporal resolution, increased water content in the muscle and nonlinear peak response to the CA. In conclusion, though the semi-quantitative method they used made it possible to delineate resting from exercising muscle, the SI curve grossly did not (overall) quantitatively reflect perfusion.

A further inquiry applied a post occlusion reactive hyperemia paradigm in order to investigate first pass perfusion in the calf muscle of 20 healthy volunteers (75). TICs were analyzed descriptively and quantitatively by the general Tofts model (46) (the AIF was calculated from the artery exhibiting the maximum relative signal increase in the corresponding leg) and results were then compared to corresponding measurements from segmental volume plethysmography. Though the estimated DCE perfusion values did not correlate with the initial reperfusion rates measured by plethysmography, results showed highly significant changes in calf muscle signal dynamics in the hyperemic leg vs. those in the contralateral leg at rest, both in semiquantitative and quantitative analysis. Furthermore, flow extraction fraction products [E·F·ρ (1- Hct)= K^trans] within the non-compressed-leg were in agreement with published resting perfusion values.

In 2005 a new method was described to quantitatively measure skeletal muscle blood flow during postischemic reactive hyperemia, without the requirement of deconvolution (56). Thompsons’ first pass method termed step-input, utilizes a rapid release of an occlusive thigh cuff to deliver a step-input of CA that was injected after cuff inflation. As a result, the arrival of the CA coincides with the onset of reactive hyperemia. The simple input function only requires a slight modification of Larsson’s model (53) to extract K^trans and v_e. The authors listed several advantages of the step-input method over conventional bolus methods for the purpose of quantitative analysis: (I) the simple input shape eliminates the need for deconvolution of tissue and arterial TICs thus drastically simplifying the analysis; (II) the steady-state SI is proportional to v_e and (III) bolus recirculation effects are eliminated. Thompson compared the results of the protocol to bulk blood flow studies with the same volunteers using phase-contrast velocimetry (PCV) obtained from the popliteal artery. The results found for the distribution volume (v_e) were in good agreement with values reported in the literature and correlated significantly with the PVC blood flow studies with the same volunteers.

Recently an extensive investigation was conducted concerning the effect of CA size on the quality of DCE analysis in skeletal muscle (33) comparing two CAs: Gd-DTPA (a small CA) with Gadomer (medium sized CA). Additionally, different pharmacokinetic models and the model-free parameter area-under-curve were examined to see if fitting each CA to an appropriate model would improve parameter sensitivity. The authors concluded that for optimal results, both model-based and model free analysis should be adapted to the pharmacokinetic properties of the CA. For medium CA, the optimal model should include K^trans and v_ρ, whereas for the small CA, K^trans and v_e should be incorporated. Both CAs administered demonstrated equal performance in detecting microvascular differences in the calf muscles with the medium CA having a slight edge due to better spatial resolution.

Peripheral artery occlusive disease (PAOD)

One of the earliest accounts of DCE being used to describe blood flow in PAOD patients dates back to 2004 (4). Blood flow to the lower leg muscles was quantified at rest and after individually adjusted plantarflexion muscular exercise in five individuals: a patient with PAOD (Fontaine IIb) before and after percutaneous transluminal angioplasty (PTA) of a femoral artery stenosis, a patient with coronary heart disease without clinical signs of a PAOD, a healthy volunteer and two professional athletes. The applied semi-quantitative analysis showed distinctive exercise induced changes of the upslope, wash-in, peak and washout of the TIC in the different muscles of the calf in all subjects. The magnitude of the changes induced, also seemed to be dependent on the individual fitness of these subjects. In particular, the shortened time-to-peak and increased mean-intensity to time ratio, both indicating an improved blood flow reserve mobilization, were very prominent among the athletes. Notably, the PAOD patient demonstrated a steeper SI-curve after exercise following interventional treatment. These results were rather descriptive due to the small number of individuals and no statistical significance was reached.

In 2007 a new sequence was developed to allow for simultaneous acquisition of the AIF and tissue perfusion images (1). The method uses a saturation recovery GRE sequence for the estimation of the AIF, interlaced with an inversion-recovery GRE sequence for the measurement of tissue perfusion. Though model-based analysis was not performed, a normalized PI was defined as the slope of the TIC of the tissue divided by the arterial TIC slope. First pass imaging was adopted for PI measurements in 11 patients with mild to moderate symptomatic PAOD and 22 normal subjects directly after peak exercise using a MR-compatible pedal ergometer. Although in the PAOD group, the ankle-brachial index (ABI) failed to correlate with PI and neither ABI nor the PI correlated with the workloads achieved, peak-exercise measurements were able to distinguish PAOD patients from normal subjects.

The group further used their method to determine the utility and reproducibility of rest, exercise, and perfusion reserve (PR) as measured by DCE-MRI in both normal subjects and PAOD patients (3). Measuring tissue perfusion and arterial input both at rest and peak exercise, the calves of 11 PAOD patients with claudication and 16 age-matched controls were imaged. TICs were generated for the muscle group with the greatest SI and both PI as well as the PR (ratio of exercise to rest blood flow) were calculated. Though highly reproducible, rest perfusion parameters were too variable and too low in the muscle to distinguish between controls and PAOD patients. Naturally this also affected the PR which was reproducible but highly variable as well. This result could also be explained by previous animal experiments which indicated that save for a short time period directly following femoral artery ligation, rest perfusion values return rapidly to normal values (73). As in their previous experiment, the exercise parameters could distinguish between the two groups.

Lately Versluis et al. tested the ability of different quantitative MRI imaging methods, including DCE, to reproducibly assess morphologic and functional peripheral vascular status, as well as vascular adaptations over time in patients with PAOD (2). The methods assessed were: MRA, phase contrast angiography flow measurements in the popliteal artery, dynamic BOLD imaging and DCE. Versluis used the first pass step-input method (32) (see above). Like Thompson he also applied Larsson’s model (53) to extract the influx constant K_i (K_i is defined as E·F) but in addition he calculated the AUC up to 90 seconds after contrast arrival (AUC90). Moreover, inter-scan and inter-reader reproducibility were determined. A total of 20 subjects, 10 patients with verified symptomatic PAOD with proven extensive collateral artery formation, and 10 healthy volunteers were examined using an ischemia cuff paradigm. The groups’ results showed that quantification of the number of arteries and artery diameter as well as macrovascular blood flow measurements were highly reproducible in both PAOD patients and healthy controls. However, reproducibility of both methods used to measure microvascular function, DCE and BOLD, was poor in patients due to large inter-scan variations. The authors argued that since T1 values, which were determined during the pre-contrast T1 mapping, showed high inter-scan reproducibility in both patients and healthy volunteers, the problem does not lie in the technique itself but rather in the physiologic process that was studied (i.e., the microvascualr parameters undergo large physiologic fluctuations).

The group repeated their experiment, this time using Gadofosveset, a blood pool CA which binds to human serum albumin (76). Other than changing the pharmacokinetic parameters to account for the use of an intravascular CA, most other aspects of the study remained unchanged. Determined were the hyperemic fractional microvascular blood plasma volume v_ρ (%), rate constant k (min^–1) describing the speed of muscle enhancement after cuff deflation and AUC90. Versluis hypothesized that the maximum microvascular dilatation can be assessed by determining v_ρ and that a decreased v_ρ in PAOD patients can perhaps be explained by impaired microvascular dilatation capacity, which is the result of endothelial dysfunction in these patients. He further postulated that v_ρ might be a superior parameter to K^trans in the assessment of the severity of microvascular disease, since K^trans reflects a combination of the rate of microvascular reactivity and permeability, both of which may be impaired in patients with PAOD. Moreover, K^trans undergoes a physiological decrease with age. In this instance the group obtained significant results for the pharmacokinetic parameters v_ρ and k, both of which were significantly lower for all muscle groups in PAOD patients as compared to healthy control subjects, establishing the capability of the method to objectively distinguish healthy from afflicted subjects.

Finally, we would like to draw attention to the possibility of studying plaque neovascularization in animals and patients with atherosclerosis (77-80). Plaque angiogenesis is an attractive target to attempt the identification of asymptomatic yet high-risk atherosclerotic lesions. Although to the best of our knowledge studies in peripheral vessels (carotid arteries excluded) have as yet not been carried out, one can envision the relevance of the theme in clinical applications.

Conclusions

Functional microvascular parameter determination using DCE-MRI may contribute considerably to objective evaluation of many vascular diseases. The unparalleled potential of the method to non-invasively and simultaneously measure multiple relevant parameters, to subsequently study disease pathophysiology, objectively assess illness severity as well as the efficacy of new therapeutic strategies in absolute terms, is highly promising.

Alas, although the technique exists for over 20 years it is still being viewed as an immature technology. This is partly due to considerable variations from study to study in both data analysis and acquisition protocols as the field remains in an ongoing state of investigation and development, and to date no optimal model or method exists. Moreover, pharmacokinetic analysis and interpretation of dynamic data is complex and computationally demanding. It is complicated by the availability of a plethora of analysis algorithms and by the fact that some calculated parameters may represent different biological phenomena depending on the model applied. Nevertheless, though quantitative parameters are more difficult to extract, a comparison of the robustness of compartmental modeling to semi-quantitative analysis concluded that model-based methods should be preferred as they provide more insight into physiology without a loss in power—at a cost in terms of complexity and time (81). Furthermore, they are potentially independent of the type of scanner, of the scanning technique and individual patient variations.

DCE has been applied successfully in countless studies first and foremost in oncology (66,82-90), including antiangiogenic drug assessment (34,91,92), perfusion studies of the heart (93-95), but also rheumatic illnesses (96,97) and increasingly in the evaluation of peripheral perfusion.

Though many publications in the past have made detailed inquiries as to the theoretical aspects of the technique, its application to the peripheral vascular and muscular system in clinical settings has been relatively modest despite its unique abilities. Assessment of PAOD is emerging as the most promising clinical application of DCE-MRI in the assessment of peripheral perfusion. On its way into clinical practice DCE-MRI will require higher standardization, further validation and more reproducibility experiments as well as reduced measurement times.