Rotation of Electromagnetic Fields and the Nature of Optical Angular Momentum

Abstract

The association of spin and orbital angular momenta of light with its polarization and helical phase fronts is now well established. The problems in linking this with electromagnetic theory, as expressed in Maxwell's equations, are rather less well known. We present a simple analysis of the problems involved in defining spin and orbital angular momenta for electromagnetic fields and discuss some of the remaining challenges. Crucial to our investigation is the duplex symmetry between the electric and magnetic fields.

1. Introduction

The suggestion that Laguerre–Gaussian laser modes carry orbital angular momentum about the beam axis [1] led to rapid and sustained growth of interest in this previously neglected mechanical property of light [2]. These modes have characteristic helical phase fronts and a phase vortex on the beam axis such that a circuit around the beam axis introduces a 2ℓ change in the phase of the field. There is an orbital angular momentum along the beam axis associated with this of lħ per photon. This angular momentum is quite distinct from and separate from the ±ħ of spin angular momentum associated with the two possible circular polarizations. The description of orbital and spin angular momenta for light becomes more difficult if we go beyond the paraxial approximation [3,4]. Here the larger values taken by the electric and magnetic fields in the direction of propagation make it difficult to separate the angular momentum into orbital and spin components.

Light is fundamentally an electromagnetic phenomenon and it should be possible to understand its properties by reference to those of the electromagnetic field, as described by Maxwell's equations. It has long been known how to write the energy, momentum and total angular momentum for the electromagnetic field [5]. It is also possible to split the angular momentum into spin-like and orbit-like parts [6], but there has been much confusion as to whether this separation is physically meaningful [7–11]. The situation was greatly clarified in the seminal work of van Enk and Nienhuis [12,13] who showed that the separation is indeed physical but, remarkably, that neither of the constituent parts is a true angular momentum.

In this paper we recover the startling result of van Enk and Nienhuis from a slightly different starting point by asking how we might rotate the electric and magnetic fields. We follow this with an investigation into the problem of defining sensible local spin and orbital properties for the electromagnetic field to match the familiar densities of energy and linear momentum. We find that the obvious quantities derived from the separation of the total angular momentum into spin and orbital parts are not satisfactory.

2. Spin and orbital parts of the electromagnetic angular momentum

Let us begin by reviewing the usual forms for the mechanical properties of light and for extracting spin and orbital parts from the total angular momentum. We work throughout with the electromagnetic field in vacuum so as to describe freely propagating light. The electric and magnetic fields (E and B) satisfy the familiar Maxwell equations

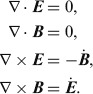(1)

Here we work in the natural system of units in which the pemittivity, permeability and speed of light are all unity (ε₀, μ₀, c = 1). Note that the first two equations mean that both the electric and magnetic fields are purely transverse, that is that for each plane wave component the directions of both the electric and magnetic fields are perpendicular to the wavevector.

It will be useful to express the electric fields in terms of a vector potential, A, which we also take to be transverse (∇ · A = 0), so that our electric and magnetic fields have the form.

(2)

It is important to realise that although the vector potential is subject to gauge transformations, its transverse part is gauge invariant. This means that we can express physically meaningful quantities in terms of the transverse part of the vector potential, which is our A.

It is straightforward to find the energy density for the electromagnetic field, w, and from this to determine the densities of linear momentum, g and angular momentum, j [5]:

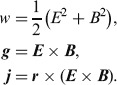(3)

From these we can obtain the total energy, momentum and angular momentum by integrating over all space. The total angular momentum, in particular, is

(4)

If we substitute for B in terms of the transverse vector potential A and then perform some elementary vector calculus we find that we can rewrite this total angular momentum in the form [11]

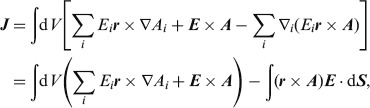(5)

where we have used Gauss's theorem to obtain the final integral over the surface of the volume. If the fields fall off quickly enough or if the volume is large enough then this surface integral will be zero and we are left with the highly suggestive form

(6)

It is entirely natural, if only by analogy with quantum theory, to associate the first integral (L) with the orbital angular momentum of the field and the second (S) with its spin angular momentum, and this is usually what is done. It is these quantities that have given rise to the controversy and that were shown, by van Enk and Nienhuis, not to be true angular momenta because their quantised forms do not satisfy the required commutation relations [12,13].

For monochromatic fields it is sometimes appropriate to cycle-average the total angular momentum and also the quantities L and S and to rewrite these in terms of the components of a complex electric field [14]:

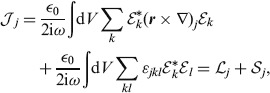(7)

where ω is the angular frequency of the light and ε_jkl is the usual permutation symbol. This is a familiar starting point in describing the angular-momentum properties, in particular, of paraxial laser fields. Let us emphasise, however, that no such restriction applies to expression (6) and hence our analysis applies both to paraxial and non-paraxial fields and there is no restriction placed on the spectrum of the light.

3. The problem of rotation of electric and magnetic fields

It is a fundamental, even defining, property of angular momentum that it is the generator of rotations [15]. It is reasonable, therefore, to begin a study of optical angular momentum by considering the rotation of the electric and magnetic fields. It is natural to associate the spin angular momentum with the vector nature of the electromagnetic field and the orbital part with the spatial dependence. If these two parts are distinct angular momenta then the spin angular momentum should rotate the direction of E and B and the orbital angular momentum should rotate the fields in space and leave their directions unchanged. We show, however, that such separate rotations are not possible without violating Maxwell's equations.

It suffices to consider only small (formally infinitesimal) rotations and to this end we introduce the vector θ the direction of which corresponds to the axis of the rotation and the magnitude of which (|θ| « 1) is the angle of rotation. Let us consider first a rotation of the coordinates but not the direction of the electric field to produce

(8)

For this to be an allowed field it must satisfy Maxwell's equations and, in particular, for the first equation, it is straightforward to show, however, that this is not the case

(9)

This is not, in general zero and so the rotation violates the first Maxwell equation.

The same problem occurs, naturally enough, for rotations only of the direction of E:

(10)

This field also violates the first Maxwell equation:

(11)

It is clear that it is not possible, in general to rotate independently the direction of the electric field or to parallel transport the field by rotating the coordinates but leaving the direction of the field unchanged. Clearly the same problem arises for the magnetic field, for which we find

(12)

Note that there is no problem, of course, if we rotate both the field distribution and its direction:

(13)

This rotated field is clearly transverse and satisfies Maxwell's equations. This is an indication, of course, that there is a well-behaved total angular momentum for the electomagnetic field. We can take the impossibility of rotating just the field distribution or just the direction of the field as a demonstration of the absence of well-defined orbital and spin angular momenta.

It is reasonable to ask what is the effect on the electric and magnetic fields of the spin (S) and orbital (L) parts of the angular momentum, obtained in the previous section. We could proceed within the framework of either classical or quantum electrodynamics, but for definiteness we choose the quantum description which requires us to introduce the canonical (equal-time) commutation relation

(14)

where

(15)

is the transverse delta function [16,17]. It will be recalled that the transverse delta function extracts the transverse, or divergenceless, part of a vector field:

(16)

There is also a longitudinal delta function

(17)

the action of which extracts the longitudinal or curl-less part of a vector field:

(18)

We consider the effect, on the electric and magnetic fields, of unitary transformations generated by the operators S and L. For the effect of the spin part on the electric field we find

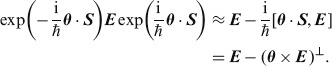(19)

Similarly, we find for the magnetic field that

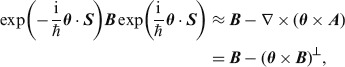(20)

where we have used the fact that

(21)

the first term of which is clearly longitudinal and the second is clearly transverse. It is clear, when written in this way, that the spin part of the angular momentum generates the closest approximation to the desired rotation of the directions of E and B that is consistent with the requirements of transversality [12,13]. We note that there is much experimental evidence to support the idea that, at least for a paraxial beam of light [2], the components of spin and orbital angular momenta in the direction of propagation of the beam are well defined. We can see at least an indication of why this is so in these expressions, as for such beams the components of E and B (and also of A) in the direction of propagation are very small and it follows that these expressions for the rotated fields, (19) and (20), are close to the ideal ones, (8) and its magnetic counterpart. We can see, clearly, that this is true by considering the identity (21) in which the missing longitudinal part of θ × B (which is ∇(θ · A)) is proportional to the gradient of the component of the vector potential in the direction of propagation. For rotations not in the direction of propagation, no such simplification is possible; it is only the component of angular momentum parallel to the direction of propagation which simplifies in this way in the paraxial approximation.

Naturally enough, the orbital part of the angular momentum generates the closest approximation to rotation leaving the directions of the fields unchanged:

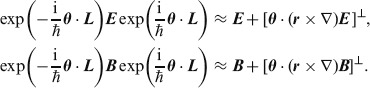(22)

We can understand the fact that the spin and orbital parts of the angular momentum are not themselves angular momenta as a consequence of the impossibility of performing, independently, the rotation of the direction of the fields or a rotation of the field leaving the orientations of E and B unchanged.

4. Electric-magnetic symmetry

We have seen that it is not possible to rotate, for example, the orientations of the electric and magnetic fields whilst leaving the spatial distribution of the fields unchanged. It is possible to separate the total angular momentum into spin and orbital parts and, although neither of these is a true angular momentum, they are the generators of the closest physically allowed approximation to the desired independent rotations. There is a remaining difficulty, however, with the spin and orbital parts as we have identified them. To see this we need to invoke a subtle symmetry of Maxwell's equations (1).

It was noted by Heaviside and by Larmor (although it is not easy to find in their writings) [18,19] that these equations are unchanged on interchanging the electric and magnetic fields (E → · B, B · –E).¹ More generally, we see that their form is unchanged if we make the duplex transformation [5]

(23)

for any angle θ. It is also manifestly the case that the densities of energy, linear momentum and angular momentum (3) are all invariant under this transformation. Given these observations, it would indeed be bizarre if the spin and orbital components of the optical angular momentum did not also respect the symmetry.

Let us consider the spin part of the angular momentum. It is tempting to infer from the total spin part, S, a spin density

(24)

In order to determine whether or not this is acceptable, we need to extend the symmetry (23) to the potentials. We can do this by introducing a new potential C in analogy with the usual vector potential A [20]. Like the usual vector potential it is transverse (∇ · C=0) and it is related to the electric and magnetic fields by the equations

(25)

Note that in contrast to (2) it is the electric field that is represented as a curl and the magnetic field that is a time derivative. These definitions will be compatible with our Heaviside–Larmor symmetry (23) if we require invariance of physically important quantities under the analogous transformation

(26)

It is now clear that the proposed density for the spin component of the angular momentum that it does not respect the Heaviside–Larmor symmetry. For this reason we can reject the form (24) as the density for the spin component of the angular momentum.

At this stage we should question whether the spin part of the total angular momentum, S, is a physically acceptable quantity. To see that it is, we note that we can use integration by parts to rewrite it in the form

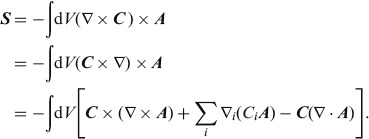(27)

Integration of the penultimate term is zero (by Gauss's theorem) and the last term is zero because the vector potential is transverse. It follows that

(28)

Clearly, we can combine this expression with our original form in terms of E and A to write the total spin part in the form

(29)

which clearly respects the Heaviside–Larmor symmetry. Hence, the expression for the total spin angular momentum is a physically acceptable one in that S respects the Heaviside–Larmor symmetry. We can infer, however, that the seemingly natural guess for the density of spin, given in (24), is not because it does not.

Similar considerations show that 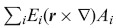is not the physically relevant density of the orbital part of the angular momentum, but that the total orbital part, L, is acceptable, at least in the sense that it respects the Heaviside–Larmor symmetry.

5. Discussion

We have traced the problem in obtaining satisfactory spin and orbital angular momenta for the electromagnetic field to the impossibility of performing, independently, a rotation of the directions of the field vectors and a rotation of the spatial dependence without changing the directions of the fields. It is possible to break the field into spin and orbital parts [6], but neither of these is a true angular momentum [12,13], although they do generate the closest allowed transformation to independent rotations.

The question of identifying densities for the spin and angular parts of the angular momentum remains a problem. We have seen that the Heaviside-Larmor symmetry is sufficient to argue that the ‘obvious’ candidate for a density of spin, E × A, is not acceptable. It is true that we can overcome this objection by adopting instead 1/2(E × A + B × C), but merely satisfying the symmetry seems to be an insufficient justification for identifying this as the density for the spin part of the angular momentum.

It is well known that the Dirac equation does not conserve, separately, the spin and angular momenta of an electron [21]. There is, nevertheless, an important limit in which well-defined and separately conserved spin and orbital angular momenta arise, and this is the non-relativistic limit. It is possible that similar ideas might determine the necessary conditions for well-behaved, approximate, spin and orbital angular momenta of light to arise. We shall return to this idea elsewhere.