On deriving the dose–effect relation of an unknown second component: An example using buprenorphine preclinical data

Abstract

Buprenorphine, like many other drugs, displays a biphasic dose–response relation (‘hormesis’), viz., its antinociceptive effect in some preclinical models increases up to some dose level (often achieving 100% effect) and decreases at high-doses. A decreasing component was evident in the tail-flick tests described here, occurring in both the mouse and the rat. While the mechanism of dose-related decline in antinociceptive effect, when observed, might be related to nociceptin/orphanin-FQ, the precise mechanism remains unknown. Regardless of the mechanism, the values of this dose-related decline yield data that can be used to calculate the dose–effect relation of the decreasing (unknown second) component. The calculation, which uses the same concept of dose equivalence that underlies additivity in isobolographic analysis, was employed here from tail-flick data obtained in mouse and rat. The derived dose–effect curves of the second component, though differing in efficacy between mouse and rat, displayed a very notable similarity. This novel technique offers possible insight into the dual low-dose (analgesic), high-dose (addiction medication) uses of buprenorphine.

1. Introduction

Buprenorphine, first synthesized in the late 1960s, is a centrally-acting analgesic that is gaining prominence due to its approved use in opioid addiction treatment. It is an analog of the poppy-derived alkaloid the baine and possesses high binding affinity for opioid receptors (Villiger and Taylor, 1981; Rothman et al., 1995; Huang et al., 2001; Lutfy and Cowan, 2004). Buprenorphine shares certain preclinical and clinical attributes of standard opioid analgesics such as morphine and fentanyl, but differs by having slow receptor dissociation kinetics, less respiratory depression and immune suppression, and a biphasic (‘bell’- or ‘inverted U’-shaped) dose–response relation in certain animal models such as the hot water-immersion tail-flick test (reviewed in Cowan and Lewis, 1995 and Budd and Raffa, 2005). Such a biphasic dose–response curve (‘hormesis’) is actually more common than generally recognized (Calabrese, 2008). This was strikingly evident in a recent study in mouse (Raffa and Ding, 2007), which showed that the dose–effect curve reached 100% maximum possible effect, but was biphasic, increasing at doses below 10 mg/kg and decreasing at doses above 10 mg/kg. While the precise molecular mechanism responsible for the biphasic response in this test is still debated, it has been speculated that it may be due to activation of the nociceptin/orphanin-FQ (NOP; ORL1, opioid receptor like) receptor which compromises buprenorphine’s antinociceptive effect (reviewed in Cowan and Lewis, 1995 and Budd and Raffa, 2005). Part of the support for this view is that nociceptin/orphanin-FQ, the endogenous ligand for the NOP (ORL1) receptor, is pronociceptive in some pain models following i.c.v. (intracerebroventricular) dosing (Meunier et al., 1995; Reinscheid et al., 1995; Hara et al., 1997).

Regardless of the underlying molecular mechanism of the high-dose-related decline in buprenorphine effect, there is clearly a second component that antagonizes its antinociceptive action in some (but by no means all (Christoph et al., 2005)) preclinical tests (Ding and Raffa, 2009). It would be important to determine at least if the descending portion is similar in mammalian species. Such a demonstration would be consistent with the use of low-doses of buprenorphine for one clinical endpoint (analgesia) (Benedetti et al., 1998; Oifa et al., 2009) and high-doses for a different clinical endpoint (addiction medication (Boothby and Doering, 2007). Our aim here was to apply a novel approach to answer this question. Toward that end we here analyze data on mouse tail immersion from Raffa and Ding (2007), as well as new data (Cowan, unpublished results) in the rat, in a calculation that uses the concept of dose equivalence, the same principle that underlies additivity in isobolographic analysis.

2. Materials and methods

2.1. Experimental

The tail immersion/flick test data in mice reported in Raffa and Ding (2007) were used in the analysis. Briefly stated, the mice were placed into restraining holders and the distal portion of their tail was lowered into a temperature-controlled water bath (48 °C). The time interval between tail immersion and removal (‘flick’) of the tail was recorded as tail-flick latency. The cut-off time (to avoid injury) was 40 s. A baseline control latency value was obtained for each mouse before s.c. buprenorphine administration. After drug administration, the procedure was repeated and reaction times were compared to pre-drug reaction times. A similar procedure was followed in the rat tail immersion test, except that the water temperature was 50 °C and the cut-off time was 20 s.

2.2. Isobolographic analysis

The concept of dose equivalence is most familiar from isobolographic analysis of a combination of two drugs (reviewed in Tallarida, 2000, 2006, 2007) as briefly summarized here for two agonist drugs that exhibit a constant potency ratio. This means that for every level of effect the dose a of drug A alone, and the dose b of drug B alone, it follows that a/b = R, a constant. Most often the effect level analyzed is 50% of the maximum, from which it follows that A₅₀/B₅₀ = R, where A₅₀ and B₅₀ are the unitary doses that give half-maximal effect. An arbitrary dose a that is less than A₅₀ will require a dose b of B such that their sum= B₅₀. To calculate the quantity b, dose a is first converted to its B-equivalent, which is a/R. Thus, b + a/R = B₅₀, which can be rearranged to b/B₅₀ + a/RB₅₀ = 1 and, since RB₅₀ = A₅₀, can be written in the more familiar form.

$$\frac{b}{B_{50}}+\frac{a}{A_{50}}=1$$

The above equation, when plotted on an a−b Cartesian plot, is a straight line with intercepts A₅₀ and B₅₀. All a−b combinations on this line, the isobole, represent pairs that are expected to yield the 50% effect. Because the dose-equivalent of drug A is added to dose b the condition derived is termed ‘additive’ and would demonstrate that there is no interaction between the agonist drugs. The concept of dose equivalence described here is employed, as shown in Section 3, in the analysis of the buprenorphine curve that arose from hot water tail immersion tests in the mouse (Raffa and Ding, 2007) and in the rat (Cowan, unpublished results).

3. Results

3.1. Theory

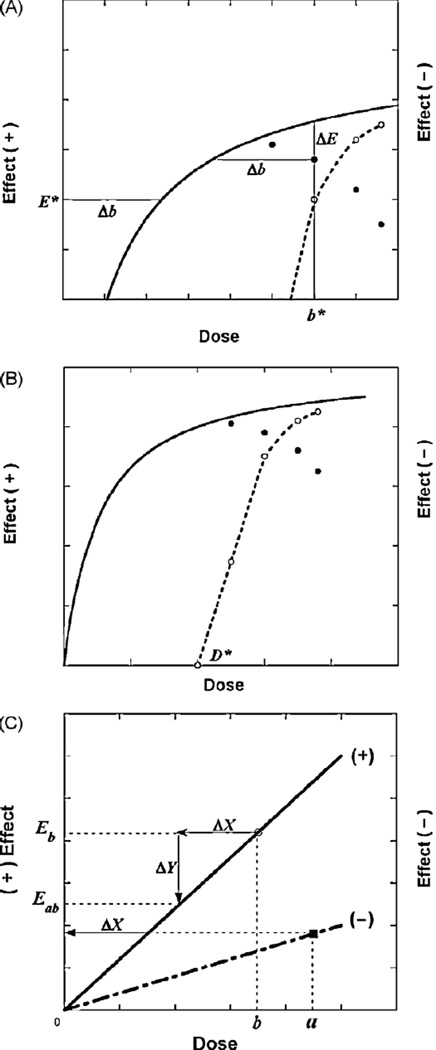
The concept of dose equivalence, described above, is used here in the analysis of the high-dose decreased effect that arises from the second component, when present, of buprenorphine’s dose–effect curve. As illustrated in Fig. 1A, we see at some agonist dose b* there is a decrease (ΔE) from the fitted curve. This decrease is associated with a decrease in agonist dose, Δb, a value that occurs at effect level E* on the agonist’s fitted curve. Thus (b*, E*) is a point on the dose–effect curve of the second component. In other words, b* represents a dose at which the second component effectively nullifies a quantity (Δb) of the agonist’s positive action that is sufficient to reduce its effect by the observed amount ΔE. Fig. 1B illustrates the result of analyzing the decreases in effect that constitute the inverted-U as described above. It is seen that this procedure allows the construction of the second component as a dose–effect relation in cases in which the interaction is additive.

Fig. 1.

(A) Illustration. A representative drop from the smooth curve (solid line), denoted ΔE, is equivalent to a decrease in agonist dose = Δb, a dose value on the smooth curve at effect E* and, therefore, locates the point (b*, E*) for the (decreasing) second component of action (dotted line). (B) Illustration. A dose–effect curve (solid line) for doses up to dose D* ismonotone increasing, whereas for doses greater than D* the effect decreases due to a second component of action. The dotted line, whose effect magnitudes are indicated on the right ordinate scale, represents decreasing effects for doses above D* due to the second component of the drug’s action. The combination of the decreasing and increasing components of action would yield the observed inverted-U values. (C) Illustration of two drugs that exert opposite effects. The upper line is an illustration of the dose–effect curve (not necessarily linear) of a drug whose effect is in a positive direction, whereas the lower line represents a drug that produces the opposite effect. The latter is plotted on the same coordinate system and, thus, its ordinate position denotes the magnitude of the negative effect.

A further illustration of the analysis for opposite effects is provided in Fig. 1C. A dose b of the ‘+’ drug would produce the effect denoted E_b. The presence of the second drug in dose a produces an opposite (‘−’) effect and is equivalent to a dose reduction ΔX of the first drug. Accordingly the quantity ΔX is subtracted, thereby reducing its effect by amount ΔY and bringing it to the effect labeled E_ab. This process assumes that there is no interaction between the two drugs, i.e., that the combination is simply additive. In this case the additivity is algebraic, i.e., one subtracts the equivalent from dose b. Additivity is the basis for the usual linear isobole that is produced by two drugs with overtly similar effects.

3.2. Mouse tail immersion

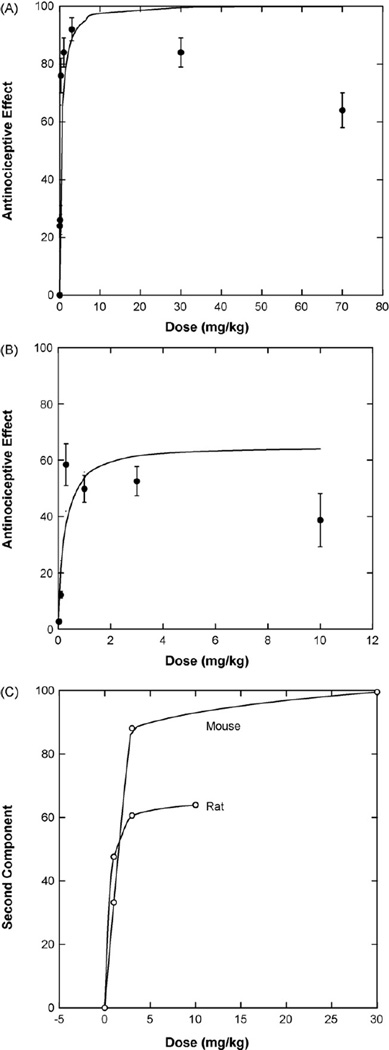
Data obtained from Raffa and Ding (2007) in the mouse are shown in the plot of Fig. 2A and in which the reported ED₅₀ = 0.21 ± 0.04 mg/kg, as determined by linear regression on log dose. This ED₅₀ is consistent with prior publications (e.g., Lutfy and Cowan, 2004). Nonlinear regression applied to doses up to 3 mg/kg yielded an ED₅₀ value rather close to the above, viz., 0.16 ± 0.04 mg/kg and produced the smooth curve shown. The buprenorphine dose–effect values are seen to be biphasic in this test so that the decreased effects could be estimated from the fitted curve. The dose–effect curve is seen to increase for doses up to 10 mg/kg and decrease at doses above 10 mg/kg. At some dose above 10 mg/kg the decrease, due to the second (antagonistic) component, becomes evident. This antagonistic component of action is likely operative at lower doses, so for this reason, the observed values were compared to the smooth curve values at 1, 3, 30 and 70 mg/kg and yielded (%) drops = 1, 3, 15 and 36, respectively. These values were used in determining the dose–effect curve of the second component, such as that calculated and illustrated as point (b*, E*) in Fig. 1A.

Fig. 2.

(A) Buprenorphine in the 48 °C water tail-flick test in mice gave the values plotted (Raffa and Ding, 2007) and show decreasing effects at the higher doses. Doses up to 3 mg/kg were used in fitting the ascending smooth curve from which drops (decreased effects) at 1, 3, 30 and 70 mg/kg were estimated to be of magnitude 1, 3, 15 and 36, respectively. The drops allow an estimation of the second component shown in panel C. (B) Buprenorphine in the 50 °C water tail-flick test in rats (Cowan, unpublished results). Drops (decreased effects) at doses 1, 3 and 10 mg/kg were 5.94, 9.09, 25.24, and led to estimations of the second component as shown in panel C. (C) The second component from analysis of both the mouse and rat data are plotted against the buprenorphine dose.

3.3. Rat tail immersion

A second data set (Cowan, unpublished results) was analyzed. In this the rat tail in water at 50 °C was used with the cut-off set at 20 s; the dose–effect graph (with linear dose scale) is shown in Fig. 2B. It is again seen that the curve shows a decrease at higher drug doses; however this decrease is evident at doses much lower than those seen in the mouse test data previously described. Further, the maximum effect (approximately 65%) is far short of the 100% observed in the mouse. The fitted curve is based on doses up to and including 3.0 mg/kg and leads to a half-maximal value (ED₅₀) = 0.17 ± 0.09 mg/kg, a value virtually identical to that in the mouse. When the observed values were compared with the smooth curve, we estimated decreases at 1, 3 and 10 mg/kg and from these the dose–effect curve of the second component was determined as shown in Fig. 2C which shows the dose–effect curve of the second component for both animal tests.

4. Discussion

It is common, but not widely recognized, that many drugs display a biphasic dose–response curve (‘hormesis’) (see comprehensive reviews by Calabrese, e.g., Calabrese, 2008). Since the hormetic effect is observed for so many different types of drugs and for so many diverse clinical endpoints (including models of drug abuse and addiction), it has been proposed that the hormetic dose–response curve is adaptive in nature (Calabrese, 2008).

In some preclinical tests of antinociception in rodents buprenorphine produces a bell-shaped (inverted-U) dose–effect curve, depending on the nature and intensity of the noxious stimulus. The observation of such a curve in some preclinical tests has led to projection, speculation, or prediction about the clinical implications. The history and inappropriateness of such assertions have been reviewed (Raffa and Ding, 2007). The focus here was on the development and application of a novel method of examining the question.

The molecular mechanism of the second component, in the situations in which it is observed, has been the subject of much interest and investigation (reviewed in Cowan and Lewis, 1995 and Budd and Raffa, 2005). The most commonly held view is that the second component is mediated through an orphanin/nociceptin-FQ pathway (NOP/ORL1 receptors). However, the exact mechanism is not known. Nevertheless, a mechanism distinct from that of the first component would be consistent with the use of much higher doses of buprenorphine to treat opioid dependence than pain. The analgesic dose, whether measured as an AD₅₀ (Benedetti et al., 1998) in postoperative nociceptive and neuropathic pain or the amount used in patient-controlled analgesia (Oifa et al., 2009), is in the range of 0.2–0.6 mg, whereas the recommended target dose for the treatment of opioid dependence is at least 10-fold greater (Boothby and Doering, 2007).

Toward the end of defining the dose–response relation of the unknown second (high-dose) component, we used the same principle of dose equivalence that underlies the isobolographic method for two drugs (reviewed in Tallarida, 2000, 2006, 2007). In that analysis the main idea is that a dose of one of the drugs is equivalent to some dose of the other drug – either in producing similar (e.g., positive) effects or opposite effects. In the former case the dose and its equivalent add, hence called ‘additive’, whereas in cases of opposing effects the dose and equivalent subtract (which is an algebraic addition), hence called ‘subadditive’. The latter applied here and we used the method to extract the opposing effect of buprenorphine that appears in the high-dose range. The antinociceptive results differ in the mouse and the rat (possibly due to the different antinociceptive dose–effect curves produced in the two species or the slightly different water temperatures). However, the derived curves reveal a difference in efficacy that is consistent with their respective antinociceptive efficacy, yet they display a very notable similarity.

The results of this novel analysis – which is generally applicable to all drugs that display a hermetic dose–effect curve, but is here applied to buprenorphine – suggest that the same mechanisms underlie the descending portion (when present) of buprenorphine’s antinociceptive dose–effect curve in mice and rats. This should provide a complementary approach to, and contribute to, understanding the clinically distinct low-dose (treatment of pain) and high-dose (treatment of opioid dependence) uses of buprenorphine.