Control of cell growth, division and death: information processing in living cells

Abstract

By way of surface receptor molecules and internal surveillance mechanisms, the living cell receives information about its external environment and internal state. In light of this information, the cell must determine its most appropriate course of action under the circumstances and initiate the relevant response pathways. Typical responses include growth and division, sexual reproduction, movement, differentiation and programmed cell death. Similar to a digital computer that uses bistable electrical switches to store and process information, the living cell uses bistable biochemical switches to implement its decision-making capabilities. In this review article, we describe some of the lines of thought that led, over the last 50 years, to our current understanding of cellular information processing, particularly related to cell growth, division and death.

1. Introduction

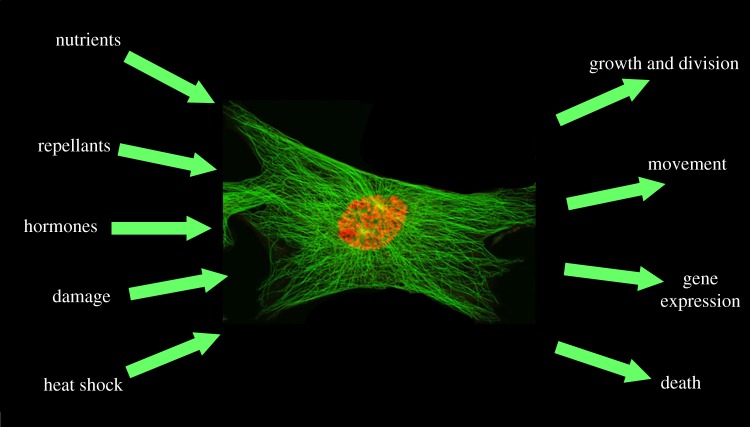
The living cell is an information-processing system, receiving information from its environment and making decisions about what responses are most appropriate under the circumstances (figure 1). It may grow and divide, move towards an attractant, differentiate into a specialized cell; it may even commit suicide. A chief goal of cell biologists is to understand the molecular mechanisms that govern these decisions.

Figure 1.

The cell is an information-processing system. Input signals (left) are picked up by surface receptors and internal surveillance mechanisms and processed by a cell (centre) to determine its most appropriate course of action under the circumstances. The cell's decisions are then carried out by the relevant response pathways (right).

To illustrate the information-processing abilities of living cells, consider skin tissue. An epithelial cell of the skin has receptors on its surface that are sensitive to signals in the cell's environment. Growth factors are soluble molecules that bind to receptors on the epithelial cell and give it ‘permission’ to grow and divide. In addition, an epithelial cell has receptors that bind to the extracellular collagen matrix in which the cells are embedded. Thirdly, these cells have surface receptors that bind to neighbouring cells to provide information about the integrity of the epithelial layer. The rule for epithelial cell growth and division is this: if cell–cell contacts are broken because of a wound to the skin, and if the epithelial cell is attached to the extracellular matrix, and if the cell is stimulated by growth factors, then the cell may grow and divide and close the wound. When the wound is closed and the cell is now in contact with other epithelial cells on all sides, then the cell stops proliferating.

Cancer cells break the rules [1]. For instance, a melanoma cell may start growing and dividing, even though it is surrounded by normal cells and is not stimulated by growth factor. If it breaks away from the epithelial matrix and invades another tissue, where it continues to grow and divide, it is called a malignant melanoma. The job of killer T cells is to pick out these cancer cells and shower them with ‘death’ factors, which induce the targeted cells to commit suicide. Many cancer cells comply, but if they have lost the death-response pathway, then they are very dangerous indeed.

These are some of the basic rules by which living cells process information, make decisions and implement responses that foster the survival and reproduction of the organism. When the decision-making machinery malfunctions, the whole organism suffers, perhaps fatally. As scientists, our job is to understand how this machinery works and how to fix it when it is broken.

2. Information processing in computers and cells

Maybe we can get some hints about how cells process information by considering digital computers [2]. The information-processing system of a computer consists of a complex network of ‘bistable’ electrical switches that implement Boolean logic functions. Each switch has two stable steady states separated by an unstable state (figure 2). The lower voltage state corresponds to a binary ‘0’ and the high-voltage state to a binary ‘1’. To flip the switch from 0 to 1, the circuit is perturbed with a biasing voltage in one direction and to flip it back from 1 to 0 with a biasing voltage in the other direction.

Figure 2.

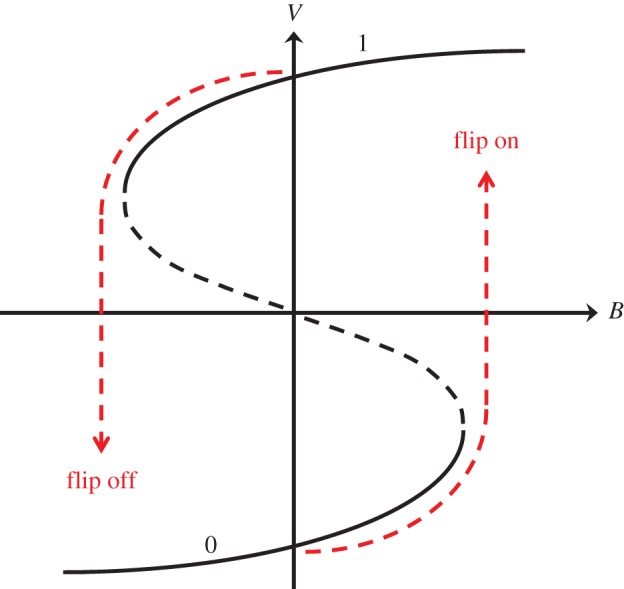
Digital computers process information using bistable electrical switches. The central processing unit of a digital computer consists of thousands of flip–flop circuits. Each switch has two stable steady states (solid lines 0 and 1) separated by an unstable steady state (dashed line). The switch can be flipped from 0 to 1 by a biasing voltage in one direction and back to 0 by a biasing voltage in the other direction.

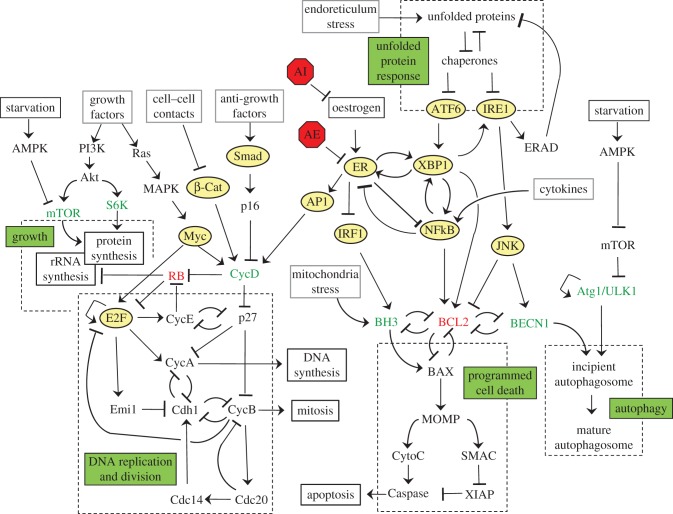
If we look inside a living cell, we find something completely different (figure 3). We can easily identify input signals and output responses, but in between we see a jumble of biochemical reactions involving genes, mRNAs, proteins and metabolites. These chemical reactions must represent the information-processing system, but where are the bistable switches? Indeed, are there any switches in the biochemistry of the cell? Or does the living cell process information by completely different principles?

Figure 3.

The molecular signalling network in breast epithelial cells. The information-processing system of a typical mammalian cell is implemented in terms of hundreds of interacting genes, mRNAs, proteins and metabolites. Does the living cell process information by biochemical flip–flop circuits or by completely different principles? (Online version in colour.)

3. Lessons from thermodynamics

How might the living cell use chemistry to process information and make life-or-death decisions? Immediately upon asking this question, a chemist will be perplexed by the second law of thermodynamics. The second law implies—and all chemical experience confirms—that a chemical reaction occurring in a beaker on the laboratory bench proceeds ultimately and inexorably to equilibrium, a state in which all chemical concentrations are uniform in space and unchanging in time. From the point of view of a cell, chemical equilibrium is death not life. Information processing requires that the chemical reactions in a cell are continually changing, retracing their steps, switching back and forth from one characteristic state to another, sending and receiving signals. How can a cell maintain this state of chemical mayhem in the face of the second law of thermodynamics, which is continually trying to drive the cell to chemical equilibrium?

This fundamental question was addressed by Ilya Prigogine and his colleagues at the Free University of Brussels in the 1960s [3]. They showed that an ‘open’ chemical system can be maintained far from equilibrium by a continual flux of matter and energy through the system. The living cell is certainly an open system in this regard. For example, a metabolically active yeast cell continually ingests high-energy glucose molecules and excretes ethanol, CO₂ and heat. The Prigogine School showed that an open chemical reaction system operating far from equilibrium, provided it is endowed with certain feedback properties, especially autocatalysis, can exhibit ‘dissipative structures’, which are patterns of chemical concentrations that are non-uniform in space and/or time. Examples of dissipative structures are spontaneous chemical oscillations, travelling waves and spatial patterns. They are called dissipative structures because they are behaviours that are non-uniform, i.e. structured in space and/or time, and these structures are maintained, from a thermodynamic point of view, by a continuous dissipation of free energy (e.g. the fermentation of glucose to ethanol + CO₂). The dissipative nature of the system is evidenced by the heat that is given off to the environment, increasing the entropy of the universe.

A particularly important paper by Prigogine & Lefever [4] introduced a deceptively simple chemical reaction system known now as the ‘Brusselator’

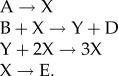The overall reactions, A → E and B → D, are imagined to be maintained far from equilibrium by holding the concentrations of the reactants (A and B) and products (D and E) at constant concentrations (i.e. the system is open to a flow of matter from A and B to D and E). The intermediates, X and Y, are allowed to change in time and space as governed by the classical laws of reaction kinetics and diffusion. Under these conditions, Prigogine and Lefever showed that this little reaction mechanism can exhibit temporal oscillations and surprising spatial patterns that sweep back and forth across an unstirred reaction vessel. Essential to the exotic behaviour of the Brusselator is the autocatalytic reaction step, Y + 2X → 3X.

Although the Brusselator was a purely hypothetical reaction mechanism, introduced by chemical physicists for illustrative purposes, some remarkable experimental discoveries were being made at about the same time. Spontaneous oscillations and travelling waves were being observed and documented during glycolysis in yeast cells (for review: [5,6], ch. 2), cyclic AMP signalling in slime mould cells ([6,7], ch. 5) and—most notably for chemists—in a simple chemical reaction mixture discovered by Belousov [8] and studied in detail by Zhabotinsky [9].

The recipe for the Belousov–Zhabotinsky (BZ) reaction is quite simple [10], involving a few chemical reactants that can be found in any well-stocked chemical laboratory. When they are mixed together in a beaker and the solution is stirred vigorously, the reaction mixture exhibits repetitive oscillations of oxidation and reduction, as indicated by the periodic colour change from red to blue to red to blue. When the reactants are dispersed in a thin layer at the bottom of a Petri dish, an even more surprising behaviour is observed: waves of oxidation that travel periodically through the medium. Such behaviour had never before been observed in a chemical reaction system, but it was in perfect accord with the theoretical predictions of the Brusselator.

These remarkable properties of the BZ reaction are observed in a reaction vessel that is closed to material flux and thus it should be—and indeed it is—proceeding inexorably to a state of chemical equilibrium. But on the way to equilibrium, one can observe all these surprising behaviours that are so reminiscent of the oscillations and spatial patterns observed in living cells. When the BZ reaction is carried out under open conditions—in continuous flow reactors—it can maintain the temporal and spatial dissipative structures indefinitely and it also exhibits (under appropriate conditions) the behaviour of a bistable switch [11,12].

4. Lessons from molecular biology

As intriguing and suggestive as the BZ reaction may be, it is a bunch of simple chemicals reacting in a beaker—nothing like the genes and proteins that constitute a living cell. While the chemistry and thermodynamics of dissipative structures was being sorted out in the 1960s and early 1970s, another equally important line of research was being pursued in nascent molecular biology laboratories of Europe and the USA. Of particular importance was the seminal work of Jacob & Monod [13] on the lac operon in bacteria. They uncovered the molecular basis of gene regulation by transcription factors, and their ideas about positive and negative feedback in bacterial operons were translated into the mathematical language of chemical reaction kinetics by Griffith [14,15], who showed that positive feedback loops had a propensity to behave like bistable switches and negative feedback loops had a propensity to oscillate.

A few years later, the molecular basis of metabolic control by allosteric enzymes was worked out by Monod et al. [16] in France and Koshland et al. [17] in California. Their theory of allosteric regulation was implemented in a mathematical model of glycolytic oscillations by Goldbeter & Lefever [18], who attributed the oscillations to the allosteric activation of an enzyme (phosphofructokinase) by its end product (ADP). End-product activation is a form of autocatalysis, which is crucial to destabilizing the time-independent steady state of glycolysis and generating a time-dependent oscillation. Despite the complicated theory of allosteric regulation in the Goldbeter–Lefever model, it was evident that the oscillations arise from a very Brusselator-like mechanism.

5. Lessons from genetics and biochemistry

As a postdoctoral researcher in Murdoch Mitchison's cell biology laboratory at the University of Edinburgh, UK, in the 1970s, Paul Nurse was looking for genes that regulate the cell-division cycle of fission yeast. He was using a genetic screen developed by Leland Hartwell [19] to isolate cell cycle genes in budding yeast. The idea is to randomly mutagenize yeast cells and look for rare mutants that get stuck uniformly in a particular phase of the cell-division cycle (G1, S, G2 or M). Hartwell had discovered dozens of such cdc genes in budding yeast [20], and Nurse was looking for similar genes in fission yeast. Nurse and Mitchison added another condition to the cdc phenotype: the mutant cells, though arrested in the DNA replication–division cycle, should continue to grow. Nurse discovered three genes of particular interest—cdc2, cdc9 and cdc25 [21,22]. Actually, cdc9 was misnamed, because it does not display the classic cdc phenotype; cdc9-mutant cells grow and divide but at an unusually small size, so the gene was renamed wee1 to properly reflect its phenotype [23].

These genes encode three proteins: Cdc2, Wee1 and Cdc25. From genetic evidence, Nurse reasoned that Cdc2 was responsible for driving mitosis and division in fission yeast cells. The cyclic nature of the process seemed to be due to switching Cdc2 between an active and an inactive state. The switching was carried out somehow by Wee1 (which inactivates Cdc2) and Cdc25 (which activates Cdc2). Small cells have lots of Wee1 activity, so Cdc2 is inactive and the cells cannot divide. Large cells have lots of Cdc25 activity, which activates Cdc2 and drives the cell into mitosis and cell division.

A few years later, Nurse's group showed that Cdc2 is a protein kinase, i.e. an enzyme that phosphorylates target proteins and thereby triggers the basic events of the cell cycle. Cdc2, in turn, is regulated by phosphorylation. Wee1 is the enzyme (a protein kinase) that phosphorylates and inactivates Cdc2, and Cdc25 is the enzyme (a protein phosphatase) that removes the inactivating phosphate group (for review, see [24,25]).

At the same time, Marc Kirschner and his colleagues were studying the biochemistry of ‘mitosis-promoting factor’ (MPF) in frog eggs. MPF activity fluctuates during the division cycles of a fertilized frog egg: it is high in mitosis and low in interphase (the period between mitoses, when the egg is replicating its DNA) [26,27]. The activity of MPF was somehow related to another protein called cyclin [28]. Cyclin accumulates during interphase and is destroyed as cells exit mitosis and divide [29,30]. Kirschner and co-workers [31] showed that cyclin somehow activates MPF, and Karsenti's group showed that MPF stimulates the degradation of cyclin as the cell exits mitosis and returns to interphase [32]. Furthermore, Masui's laboratory [33] and Kirschner's laboratory [27] showed that activation of MPF is autocatalytic: when a small amount of MPF is removed from an M-phase arrested mature oocyte and injected into a G2-phase arrested immature oocyte, the recipient oocyte is driven into M-phase, to become a mature oocyte with large amount of active MPF, and this process does not require protein synthesis [34].

The final piece of the puzzle was put in place by Jim Maller, whose laboratory purified MPF from bucket-loads of frog eggs [35] and showed that MPF is a dimer of cyclin and Cdc2 [36].

6. Lessons from mathematical modelling

In 1993, we published a mathematical model of this molecular regulatory system [37]. Our model is a mathematical expression of the biochemical reactions shown in figure 4. Cyclin molecules, synthesized by the frog egg, combine with a plentiful supply of (inactive) Cdc2 subunits to form active MPF. Immediately as it is formed, MPF is inactivated by phosphorylation by Wee1. Later in the cycle, the inhibitory phosphate group is removed by Cdc25, and active MPF drives the cell into mitosis. To exit mitosis, cyclin must be destroyed, which is the job of a protein complex called the anaphase-promoting complex (APC) [30].

Figure 4.

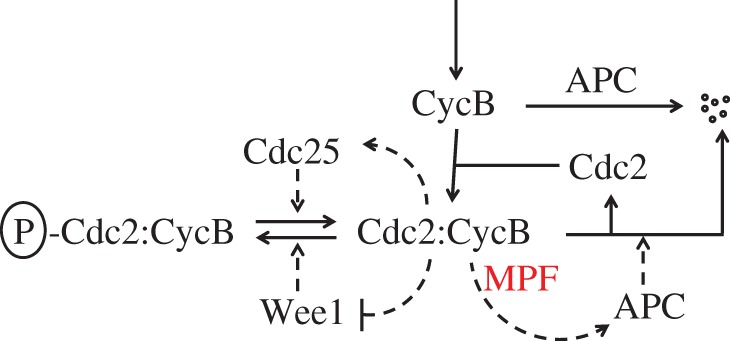
The reaction network (chemical circuit) controlling MPF activity in frog egg extracts. MPF is a heterodimeric protein, consisting of a protein kinase subunit (Cdc2) and a regulatory subunit (CycB). In intact, fertilized frog eggs and in frog egg extracts, CycB is synthesized from amino acids at a constant rate (topmost ↓ arrow) and degraded in response to the periodic activation of the APC. CycB subunits combine with Cdc2 subunits (available in excess) to form active MPF (Cdc2 : CycB), but the active dimer is rapidly phosphorylated by Wee1 (a protein kinase). The cell (or extract) enters mitosis when inactive P-Cdc2 : CycB is dephosphorylated by Cdc25 (a protein phosphatase). Note that MPF activates Cdc25 and APC and inhibits Wee1. (Online version in colour.)

The interplay of these chemical reactions is orchestrated by three feedback signals from active MPF to Wee1, Cdc25 and APC. MPF and Cdc25 are involved in a positive feedback loop: MPF activates Cdc25 and Cdc25 activates MPF. MPF and Wee1 are involved in a double-negative feedback loop (they phosphorylate and inactivate each other), which is effectively a second positive feedback loop for entry into mitosis. MPF and APC are involved in a negative feedback loop: MPF activates APC (indirectly), and APC destroys MPF activity by labelling its cyclin subunit for proteolysis.

The two positive feedback loops create a robust bistable switch for MPF activity (figure 5a). At low cyclin concentration, the network has a single steady state of low-MPF activity. But, as the cyclin concentration increases beyond a threshold, T_a, MPF is abruptly activated by the positive feedback loop. The activation of MPF drives the frog egg into mitosis, and it also activates APC, which degrades cyclin and causes MPF activity to drop (the role of the negative feedback loop). As cyclin concentration decreases, MPF activity stays high for a while, until the cyclin level drops below an inactivation threshold, T_i. At this point, MPF activity plummets and the cell returns to interphase. This sort of behaviour is called a ‘hysteresis loop’.

Figure 5.

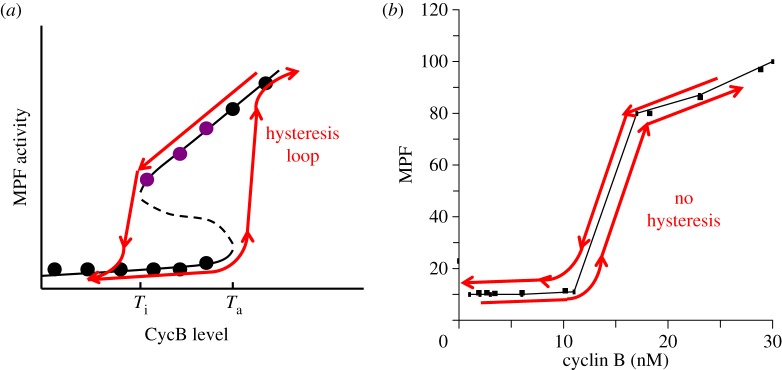
The MPF bistable switch. (a) A mathematical model of the chemical circuit in figure 4 predicts that MPF activity in a frog egg extract can function as a bistable switch. For low levels of CycB, MPF activity is very small (the ‘off’ state). When the total concentration of CycB increases above the activation threshold (T_a), MPF is abruptly activated. If the switch starts in the ‘on’ state, the concentration of CycB must be decreased below the inactivation threshold (T_i) in order to flip the switch back to the ‘off’ state. (b) In order to activate MPF in a frog egg extract, the concentration of cyclin B must be raised above a threshold level of approximately 12 nM. (Data from Solomon et al. [31].) What would happen if we start the extract in the high-MPF state and decrease the concentration of cyclin B? Would MPF activity drop in a reversible fashion (no hysteresis), as in panel (b), or in an irreversible fashion (hysteresis), as predicted by the model in panel a?

We were delighted by what we considered to be the evident success of the model. In trying to understand the molecular regulation of a central aspect of cell physiology with significant consequences for human health and technology, we were confronted by a bewildering array of facts about how the cell cycle is regulated in frog eggs, fission yeast cells, budding yeast cells and mammalian cells. A full understanding of cell cycle regulation seemed to require the synthesis of information and ideas from many different disciplines (physical chemistry, cell biology, molecular genetics and biochemistry). To our minds, what held everything together was the mathematical model. The model allowed us to think consistently about the complex and contrary interactions of the control system and to make reliable deductions about how the control system works under a variety of conditions, both real and imagined. The model proved to give an accurate description of a wide variety of known facts about cell cycle regulation in frog eggs and in fission yeast cells [37,38]. Nonetheless, the acid test of a model is whether it makes unexpected, counterintuitive predictions that are confirmed by experiments.

7. Hysteresis in frog egg extracts

The novel idea of our theory is the hysteresis loop in figure 5a. Three years before our theory was published, the cyclin threshold for MPF activation, T_a, had already been observed by Mark Solomon in Kirschner's laboratory [31]. Solomon found that if he added cyclin protein to a frog egg extract, at first he saw no MPF activity, but if he added cyclin in excess of a threshold the extract showed lots of MPF activity (figure 5b). Our model is perfectly consistent with this behaviour and attributes the threshold for MPF activation to bistability in the control system. Furthermore, our model makes the novel and counterintuitive prediction that, if we start in the high-MPF activity state and reduce cyclin concentration, the extract will stay in mitosis until cyclin is reduced below a lower inactivation threshold, T_i.

It is not obvious that there are two different thresholds. In fact, the simplest, most intuitive expectation is that, as cyclin concentration decreases, MPF activity drops along the same path as it rises (figure 5b). This observation suggests a clear test of our theory: does the activation and inactivation of MPF in frog egg extracts exhibit hysteresis or not?

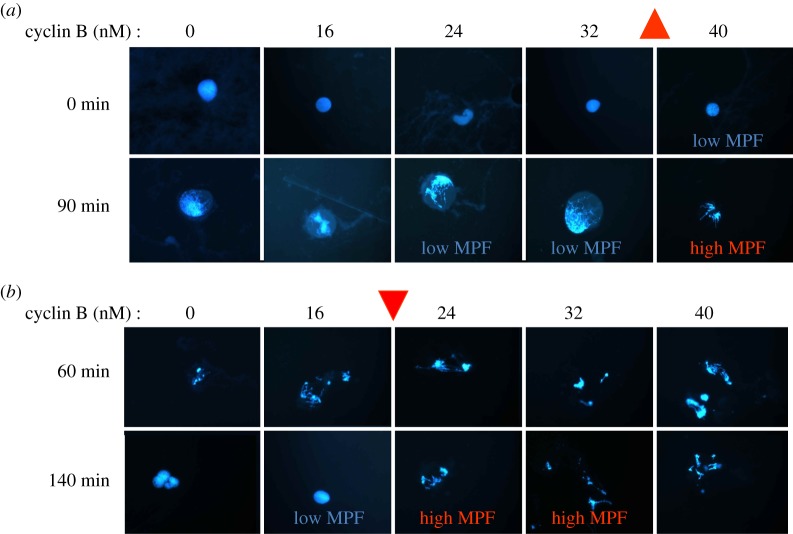
Although this prediction was made in 1993, it was 10 years before it was tested and confirmed by Wei Sha in Jill Sible's laboratory at Virginia Tech [39]. Her definitive experiment is reproduced in figure 6. In the first phase of the experiment, Sha started with extracts in the low-MPF state, as evidenced by the nuclei with dispersed DNA. She added increasing amounts of cyclin and asked how much does it take to induce the nuclei to enter mitosis. Cyclin concentrations of 16, 24 and 32 nM were not enough; she needed to add at least 40 nM cyclin to activate MPF. This is just a repeat of Solomon's experiment, to demonstrate that the cyclin threshold for activation of MPF is between 32 and 40 nM in Sha's experimental preparation. In the second phase of the experiment, Sha started out with an extract in the high-MPF state, as evidenced by the nuclei being in mitosis with condensed DNA molecules. She then asked, what is the minimal concentration of cyclin necessary to keep the nuclei in mitosis? Either 24 or 32 nM cyclin is enough to keep the nuclei in mitosis. Cyclin concentration needed to be reduced to 16 nM before the nuclei return to the low-MPF state, exactly as predicted by the Novak–Tyson model. Note that the control system is clearly bistable: for cyclin concentrations of 24 or 32 nM, the control system may persist stably in either the low or high activity state.

Figure 6.

Hysteresis in the activation and inactivation of MPF in frog egg extracts. (Data from Sha et al. [39].) (a) Frog egg extracts, treated with cycloheximide (a drug that blocks synthesis of cyclin B), arrest in interphase as evidenced by the morphology of sperm nuclei in the extract (dispersed chromatin, stained blue by DAPI, and intact nuclear membrane, visible in the phase contrast image). At t = 0 min, non-degradable cyclin B is added to separate aliquots in increasing amounts from 0 to 40 nM. By t = 90 min, nuclei in the 40 nM aliquot have entered mitosis (condensed chromatin and dispersed nuclear membrane), but nuclei in the other aliquots are still in interphase. The cyclin threshold for MPF activation in this experiment is approximately 35 nM. (b) Frog egg extracts are allowed to enter mitosis at t = 60 min, when separate aliquots are treated with cycloheximide (to block any further synthesis of cyclin B) and supplemented with increasing concentrations of non-degradable cyclin B. By t = 140 min, nuclei in the 16 nM aliquot have returned to interphase, but nuclei in the 24 nM aliquot are still in mitosis. The cyclin threshold for MPF inactivation in this experiment is approximately 20 nM. For [cyclin B] = 24 and 32 nM, the extract can persist stably in the low-MPF steady state (a) or in the high-MPF steady state (b), confirming the prediction of bistability and hysteresis in the MPF control system.

Similar experimental results were obtained by Joe Pomerening in Jim Ferrell's laboratory in Stanford, CA, and published simultaneously [40]. It is reassuring that two laboratories independently confirmed the existence of hysteresis in the MPF control system of frog eggs. In fact, Jonathan Moore, working at Duke University, NC, was the first person to confirm the prediction of hysteresis, but his preliminary results were never published separately from the Sha et al. paper.

8. Hysteresis in the mammalian cell cycle control system

Let us return to our original description of how skin cells control growth and division at the site of a wound. They are permitted to grow and divide if they are attached to the collagen matrix, if they are at a wound site and if they are exposed to systemic growth factors. This decision to proliferate is now known to be controlled by a bistable switch involving three proteins: RB, E2F and cyclin E (figure 7). In mammalian cells, cyclin E, in combination with a kinase subunit (Cdk2), sets off the programme of DNA synthesis, mitosis and cell division. The production of cyclin E is controlled by a transcription factor called E2F. In the resting (non-proliferating) cell, E2F is kept inactive by a binding partner called RB (the retinoblastoma protein). The cell cannot proliferate until it gets a signal from the ‘starter’ enzyme, cyclin D-dependent kinase, which phosphorylates RB and lowers RB's activity. Note that cyclin E-dependent kinase can also phosphorylate and inactivate RB. Hence, RB, E2F and cyclin E are involved in a positive feedback loop: RB --| E2F → cyclin E --| RB, two ‘negative’ interactions = ‘positive’ effect on cyclin E accumulation. The double-negative feedback loop creates a bistable switch on cyclin E-dependent kinase activity, and the state of the switch (cyclin E-kinase high or low) is controlled by the activity of cyclin D-dependent kinase [41]. The activity of cyclin D is determined by the input signals to the information-processing system. Growth factors and cell-matrix contacts promote the activity of cyclin D and favour cell proliferation. Cell–cell contacts, on the other hand, produce a powerful inhibitor of cyclin D. Loss of cyclin D-dependent kinase activity causes the control system to switch back to the non-proliferative state. This is how the cell-proliferation rules are implemented in chemistry.

Figure 7.

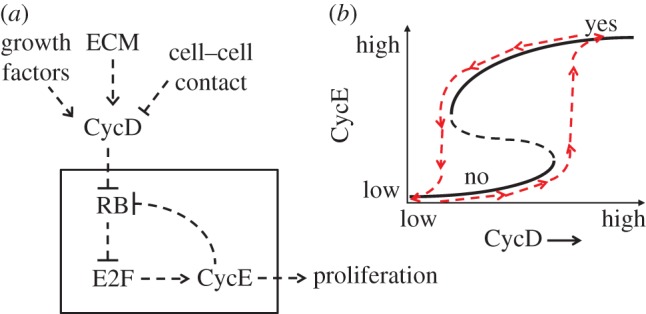
Hysteresis in the proliferation switch in mammalian cells. (From Yao et al. [41].) (a) The three proteins RB, E2F and CycE are involved in a positive feedback loop (−+−), which creates a bistable switch for the activity of CycE-dependent kinase (the signal that starts a sequence of events leading to DNA synthesis and mitosis in mammalian cells). (b) The level of CycD in the cell determines whether CycE-dependent kinase activity is low (non-proliferating state) or high (proliferating state). CycD concentration responds to external signals from growth factors, extracellular matrix attachments and cell–cell contacts. (Online version in colour.)

9. Commitment to programmed cell death

The decision to die is implemented in a very similar way (figure 8a). The cell-death programme (‘apoptosis’) is triggered by a protein called BAX, which is regulated by two other proteins, BCL and BH3. BH3 activates BAX, so it is a pro-death protein. BCL binds to and inhibits both BH3 and BAX, so BCL is a pro-survival protein. The double-negative feedback loops in the circuit create a bistable switch controlled by the ratio of BH3 to BCL proteins (figure 8b) [42]. This ratio is determined by upstream signals. Survival factors upregulate BCL proteins and downregulate BH3 proteins, promoting cell survival. Under these conditions, the control system is maintained at a stable steady state of low BAX activity. Killer cells and internal damage pathways upregulate BH3 proteins, causing the BH3-to-BCL ratio to increase, thereby flipping the switch to the cell-death state. Once the cell has decided to commit suicide, the decision cannot be revoked even if the death signals are withdrawn.

Figure 8.

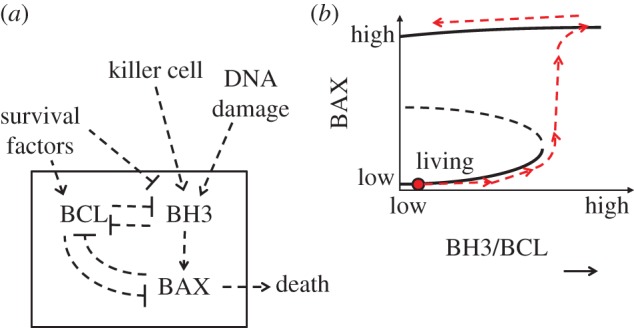
Potential bistability in the programmed cell-death decision. (From Zhang et al. [42].) (a) Programmed cell death is triggered by activation of BAX proteins in the mitochondrial outer membrane. BAX is activated by BH3 proteins and inhibited by BCL proteins. (b) The balance between BH3 and BCL protein concentrations determines the activity of BAX. The mathematical model suggests that the BAX response exhibits bistability. In the model, the switch from living to dying is one-way. (Online version in colour.)

This picture of the cell-death decision as a one-way bistable switch is still speculative; there is no firm experimental evidence—either pro or con—that the signalling pathway for apoptosis has two stable steady states (‘living’ and ‘dying’). However, it appears that the pathway has a stable ‘off’ state, because living cells do not spontaneously commit suicide in response to inevitable small fluctuations of the regulatory proteins (BAX, BH3, etc.). Furthermore, the commitment to apoptosis (flipping to the ‘on’ state) appears to be a point of no return, because cells do not revert to the ‘living’ state if the death signals are later withdrawn. Although a one-way bistable switch seems to be the simplest explanation of these properties of programmed cell death, there are other possibilities [43].

10. Role of serendipity

Serendipity—the accidental discovery of something of great importance—played a major role in working out the molecular controls of the cell-division cycle. The accidental discovery of cyclin by Tim Hunt during a laboratory exercise on gel electrophoresis for summer school students at Woods Hole, MA, is a well-known story [44]. Less often told is the accidental discovery of the wee1 gene by Paul Nurse, which was the crucial clue to unravelling the mystery of cell cycle regulation in eukaryotes [45].

In the 1970s, Hartwell and later Nurse were looking for temperature-sensitive cdc genes, i.e. genes that when mutated are conditionally lethal. At room temperature, the cells grow and divide more or less normally, but at elevated temperature (say, 35°C) the cells grow but do not divide. At high temperature, these mutant cells cannot form colonies and eventually die. The cdc phenotype is very nice for isolating mutants. Using replica plates, one looks for mutant yeast cells that form colonies at 25°C but not at 35°C. Next, it is essential to take a sample of the presumptive cdc^ts mutant cells from the 25°C plate, culture them at 35°C for a few hours and then examine the cells microscopically. By definition of the cdc phenotype, the mutant cells at 35°C do not divide but continue to grow until they die. Secondly, by definition of the cdc phenotype, the mutant cells must arrest uniformly at one particular phase of the cell cycle, say in G1 (with unreplicated DNA) or in G2 (with replicated DNA) or in mitosis (with chromosomes aligned on the mitotic spindle).

The problem with the cdc phenotype is that it does not distinguish between ‘regulatory’ and ‘nuts-and-bolts’ genes. Suppose we find a cdc^ts gene that blocks cells in late G1 or early S phase. This gene might have something to do with the decision to enter S phase, but more likely it is a defect in the nuts and bolts of DNA synthesis, say a mutation in DNA polymerase, topoisomerase or ribonucleotide reductase. If we are interested in the regulation of cell cycle events, how are we to pick out the regulatory genes from the presumably more common nuts and bolts of cell cycle progression?

What makes wee1 unusual is that, although it was first identified in a cdc screen, wee1^ts is not a cdc gene! At higher temperature, the wee1^ts strain is viable: it makes a colony. Paul Nurse should not have been looking at it! But as he was scanning his Petri dishes under the microscope, something strange caught his eye: cells that were unusually small, about half the size of normal fission yeast cells. Remember, he was looking for really big cells that are growing and not dividing. But he recognized the significance of these small cells. This could not be a nuts-and-bolts mutation because the cells are growing and dividing just fine; it must be a mutation in the control system because the cells are midgets.

Suppose you are part of a team trying to understand why the lecture hall is always 23°C in the winter even though it is very cold outside. While most of the team is down in the basement hammering on the furnace, pipes and ducts, you are snooping around in a corner of the lecture hall. They find plenty of ‘mutations’ that cause the lecture hall to cool down to the ambient outside temperature, but you find a little box with a lever. When you push the lever in one direction, the room cools down to 20°C and when you push it in the other direction, the room warms up to 26°C. They found the nuts and bolts of the heating system; you found the thermostat.

With his discovery of wee1, Paul Nurse had found part of the ‘thermostat’ of the cell cycle. By looking for genes that interact genetically with wee1, he quickly determined that cdc2 and cdc25 were encoding other parts of the thermostat. Twenty-five years later, he received a Nobel Prize for this remarkable bit of serendipity.

It is also relevant to point out that Paul Nurse's project was the sort that grant reviewers would call ‘unimaginative’, ‘derivative’, ‘unlikely to yield anything new’. He was simply repeating with fission yeast a genetic screen that had been devised and brilliantly applied by Lee Hartwell with budding yeast. But the crucial discovery of wee1 seemed to require a different set of eyes and a different organism (a twofold difference in cell volume is much easier to spot in rod-shaped fission yeast cells than in spherical budding yeast cells).

Perhaps this story will help the tax-paying public to understand why it is so crucial to support curiosity-driven basic research of little obvious, immediate utility to society. It is just this sort of research that leads to the rare serendipitous discoveries that change the course of science. Without wee1, molecular biologists might still be in the basement banging on the pipes of the cell cycle. The discovery of wee1 drew their attention directly to the control system, and subsequent research (including our serendipitous discovery of hysteresis in MPF activation) has created a body of knowledge about cell cycle regulation that has changed forever the way we think about cell growth and division in normal cells and in cancer cells.

Funding statement

Preparation of this article was supported in part by the National Institutes of Health (USA) grant no. 5R01 GM078989-07 to J.J.T. and by the European Community's Seventh Framework grant no. MitoSys/241548 to B.N.