Occam's Razor in sensorimotor learning

Abstract

A large number of recent studies suggest that the sensorimotor system uses probabilistic models to predict its environment and makes inferences about unobserved variables in line with Bayesian statistics. One of the important features of Bayesian statistics is Occam's Razor—an inbuilt preference for simpler models when comparing competing models that explain some observed data equally well. Here, we test directly for Occam's Razor in sensorimotor control. We designed a sensorimotor task in which participants had to draw lines through clouds of noisy samples of an unobserved curve generated by one of two possible probabilistic models—a simple model with a large length scale, leading to smooth curves, and a complex model with a short length scale, leading to more wiggly curves. In training trials, participants were informed about the model that generated the stimulus so that they could learn the statistics of each model. In probe trials, participants were then exposed to ambiguous stimuli. In probe trials where the ambiguous stimulus could be fitted equally well by both models, we found that participants showed a clear preference for the simpler model. Moreover, we found that participants’ choice behaviour was quantitatively consistent with Bayesian Occam's Razor. We also show that participants’ drawn trajectories were similar to samples from the Bayesian predictive distribution over trajectories and significantly different from two non-probabilistic heuristics. In two control experiments, we show that the preference of the simpler model cannot be simply explained by a difference in physical effort or by a preference for curve smoothness. Our results suggest that Occam's Razor is a general behavioural principle already present during sensorimotor processing.

1. Introduction

Prediction is a ubiquitous phenomenon in biological systems ranging from basic motor control in animals to scientific hypothesis formation in humans [1–6]. A fundamental problem of such predictive systems is how to choose between multiple competing hypotheses that explain observed data equally well, but make different predictions. A principled way to address this problem is Occam's Razor, suggesting that one should accept the simplest explanation requiring the fewest assumptions. Mathematically, Occam's Razor can be formalized within the framework of Bayesian inference—known as Bayesian Occam's Razor [7,8]. In Bayesian inference, the simplicity or complexity of a model can be illustrated by the distribution over different datasets the model can explain (figure 1a). A simple model predicts only a small number of specific datasets, whereas a more flexible complex model can explain a wider range of data. If a particular dataset can be explained by both models, the more complex model has to assign lower probability to this dataset than the simpler model, because it has to spread its probability mass over many different datasets. This naturally embodies Occam's Razor.

Figure 1.

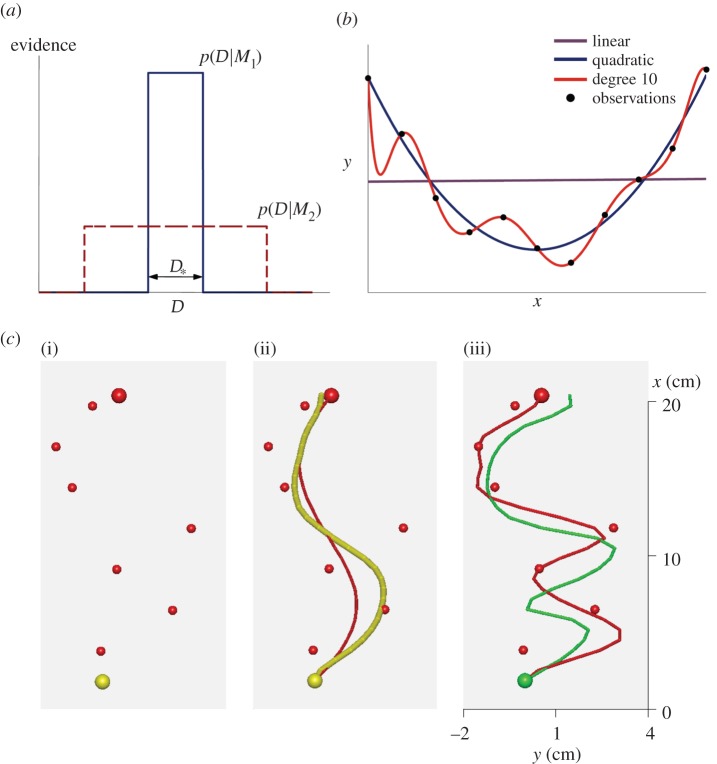
Bayesian Occam's Razor. (a) Schematic plot of evidence for a simple model M₁ (blue, solid line) and a complex model M₂ (red, dashed line) for different data 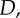such as different random trajectories. Because both models have to spread unit probability mass over all compatible observations, the simpler model M₁ has a higher evidence in the overlapping region 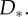(b) Exemplary polynomials of different degrees fitted to noisy observations (black dots) by minimizing mean-squared error. The linear model (purple line) is not flexible enough to capture the underlying function and results in a large fitting error. The most complex model (red line) is too flexible and passes exactly through each data point, thus achieving a fitting error of zero. A reasonable fit should trade off the complexity of the model against the goodness of fit. In this example, this is achieved by the quadratic model (blue line). (c) Standard trials. (i) Noisy observations are shown to the participant as small red spheres. Start position (yellow sphere) and end position (larger red sphere) are noise-free. The yellow colour of the start sphere indicates that the underlying trajectory was drawn from M₁ with the long length scale. (ii) After completion of a standard trial, the underlying trajectory (red) is revealed and shown along with the participants trajectory (yellow). (iii) Example of a standard trial where the short-length-scale model M₂ was the generating model, as indicated by the green colour of the start position and participants trajectory. Note that the noisy observations are exactly the same in all three panels and the drawn trajectories were recorded from the same participant.

A generic example of Occam's Razor is depicted in figure 1b. The black dots represent a number of observed data points and the coloured curves represent potential underlying processes. This generic depiction could show the flight path of another animal obscured from vision or a scientist trying to find a law underlying a few noisy measurements. When trying to fit the observed data points with a curve, the difficulty lies in trading off the fitting error against the complexity of the hypothesis [9]. A linear model might be simple, for example, but will potentially incur large fitting errors. By contrast, a very flexible complex model will achieve low or even zero fitting error, but carries the danger of overfitting, which will ultimately lead to poor prediction and generalization. This trade-off between model fit and complexity is considered automatically by Bayesian inference, because determining the likelihood of a model requires consideration of not only the best-fitting parameter setting of each model—as this would virtually always lead to the preference of the more flexible model—but the average goodness of fit over all possible parameter settings of the model. A too complex model that implies many badly fitting parameter settings will therefore be disfavoured. Well-known approximations of this Bayesian complexity trade-off include counting the number of model parameters, as in the case of the Akaike or the Bayesian information criterion [10,11], but this simplification does not hold generally [8].

The goal of our study is to test whether Occam's Razor can be found in human sensorimotor control. This question is especially compelling, as recent studies have found evidence that the sensorimotor system integrates prior knowledge with new incoming information to make inferences about unobserved latent variables in a way that is consistent with Bayesian statistics [12–21]. We designed a sensorimotor task similar to the problem depicted in figure 1b, where participants were exposed to noisy observations similar to the black dots and had to guess and draw the curve they believed to be underlying the observations. Participants were trained on two different models: a simple model M₁ generating smooth trajectories and a complex model M₂ that could also explain more wiggly trajectories. They were then exposed to ambiguous stimuli to see whether they showed a preference for the simpler model.

2. Methods overview

In our virtual reality experiment, participants were shown noisy observation stimuli on a head-mounted display and could draw regression trajectories through these observation clouds with a manipulandum to indicate the presumed noiseless trajectory as shown in figure 1c. In standard training trials, participants were informed by a colour cue about the model (M₁ or M₂) that generated the observation stimulus so that they could learn the statistics of each model. Figure 1c(ii) shows an example of a simple model M₁ trajectory, where the red curve shows the underlying function the participant is supposed to guess, and the yellow curve shows the participant's actually drawn trajectory. Figure 1c(iii) shows an example of a complex model M₂ trajectory that could explain the same observations. Participants were instructed to try and match the underlying functions as closely as possible. In standard training trials, the underlying curve (red) was revealed to participants after they had drawn their guessed trajectory. In probe trials, subjects were exposed to a stimulus of noisy observations sampled from one of the two models, but without giving them any additional cues or feedback about the model class or underlying curve. Participants were instructed that the observations were generated by one of the two models that they experienced during the standard training trials and that they should match the underlying curve as closely as possible, even though it was never revealed to them in probe trials.

To synthetically generate M₁ and M₂ trajectories, we used Gaussian Process (GP) models [22] that allow manipulating the trajectory smoothness with a single length-scale parameter. Simple M₁ trajectories could therefore be characterized by a long length scale λ₁, and complex M₂ trajectories could be characterized by a short length scale λ₂. To illustrate the complexity of the two models, we generated artificial observation datasets and ordered them according to the probability of the datasets under model M₁ (see [8] for a discussion on how to illustrate the hypothetical plot on real data). In the simulation results shown in electronic supplementary material, figure S1, it can be seen that the simpler model M₁ concentrates its probability mass on a smaller subset of data than model M₂, which corresponds in essence to the schematic plot in figure 1a. Another advantage of using GP models (with a Gaussian likelihood model) is that the log-probability of the model under uninformative prior can be expressed in closed form as

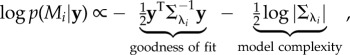2.1

where 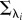is a covariance matrix associated with model i and y are the noisy observations. The first term is a data-driven goodness-of-fit error term. The second term is a data-independent complexity penalization and instantiates Occam's Razor. A more complex model, which is a model with shorter length scale λ and therefore more flexibility, is always associated with a higher complexity penalization. In physics, the complexity term is a log partition function that measures the effective number of possible states, which can also be interpreted in terms of the complexity of decision-making processes [23,24]. The complexity penalization term also has an information-theoretic interpretation within the framework of minimum description length [25] that specifies the minimum amount of information needed in a message that encodes the recorded data. The total message length 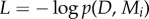can be decomposed into message length needed to record the data under a given model M_i and the message length required to specify the model itself. Complex models can encode data efficiently (low L_D), but require detailed model specifications (high L_M). Bayesian Occam's Razor consists in finding the model M_i with the shortest total message length . It is important to note that the strength of the Razor crucially depends on the available class of models. For further details on the methods, see the electronic supplementary material.

3. Results

(a). Standard trials

Two example trajectories drawn by participants in standard trials can be seen in figure 1c. In both examples, the participant was shown the same noisy stimulus, but they drew different trajectories corresponding to the colour cue that informed them about the model (i.e. whether to expect a smooth or wiggly trajectory). To have a model-independent check of whether participants were able to distinguish the two model classes, we performed a Fourier analysis of their trajectories and found that in model M₂ trials trajectories had significantly increased higher-frequency components in their spectrum compared with model M₁ trials (cf. electronic supplementary material, figure S2). To further assess how well participants were able to learn the two model classes, we compared participants’ trajectories with three different generation mechanisms: (i) samples from the posterior predictive GP with the correct length scale conditioned on the actual observations, (ii) a straight line connecting the first and last sample, and (iii) a connect-all trajectory that simply connects all the shown samples with straight lines. In particular, we computed the length scales of participants’ trajectories by maximizing the marginal likelihood of the predictive distribution and compared these fitted length scales against the true model length scales. We found that the length scales inferred from participants’ trajectories roughly match the true length scale, especially in the later part of the experiment, but, importantly, none of the non-probabilistic strategies—the straight-line (ii) or connect-all strategy (iii)—could generate length scales that were compatible with both trajectory types (cf. electronic supplementary material, figure S4). The fact that some of the estimated length scales were slightly lower than the length scales of the stimuli, especially in the early part of the experiment, does not necessarily imply that participants actually underestimated the length scale systematically, but could also be a consequence of a slight estimation bias towards lower length scales resulting from samples with mixed length scales (both too high and too low) (cf. electronic supplementary material, figure S5).

(b). Model choice in equal-error probe trials

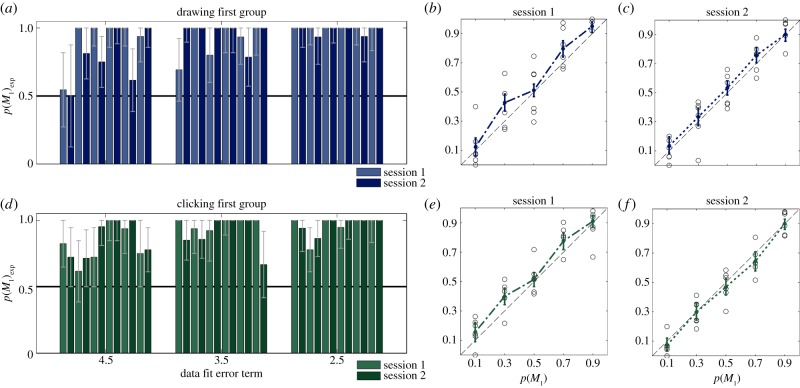
To test for Occam's Razor directly, we introduced equal-error probe trials where the presented stimulus was ambiguous and could be explained by both models equally well. In these trials, the goodness-of-fit values in equation (2.1) were equal under both models. Importantly, in these trials, a decision-maker who does not care about model complexity would choose between the two models with 50 : 50 probability. We tested ambiguous stimuli with three different goodness-of-fit values (small, medium, large). Figure 2a shows subjects’ actual choice behaviour in these trials. Subjects’ choice probabilities were obtained by classifying their drawn trajectories into the two model classes. For all three error levels, we found that subjects significantly preferred the simpler model M₁ (p < 0.001, sign test against median of 0.5).

Figure 2.

(a,d) Occam's Razor observed in the experiment. The plots show the choice probability for the simple model M₁ when presented with a stimulus that has equal goodness of fit for both models. Each bar corresponds to the choice behaviour of one participant in a particular error condition—error bars show the 95% CI. (a) Results for the group that performed the drawing session first and then the clicking session. (d) Results for the clicking first, then drawing group. Both groups show a clear bias towards the simpler model M₁. (b,c,e,f) Pooled group choice probabilities. Circles represent individual participants median choice probability, the thick line (dash-dotted in the first session and dotted in the second session) shows the median using pooled data of all participants along with 95% CIs. The dashed black line illustrates the ideal case, where theoretical choice probabilities and observed choice behaviour match exactly. (b,c) Results for the group that performed the drawing session first. (e,f) Results for the group that performed the clicking session first. The individually fitted choice probabilities are shown in the electronic supplementary material, figure S6.

An alternative explanation for the preference for the simpler model could be the lower physical effort of drawing a smooth trajectory as opposed to a wiggly one. To control for this effect, we designed a control experiment in which participants did not draw the trajectory, but they clicked mouse buttons to indicate the model class. We randomly assigned subjects into two groups, one of them performing the drawing session before the clicking session—and the second one performing the two sessions in reverse order. In terms of the observed choice behaviour in ambiguous trials, we found no systematic difference between the two groups (figure 2d).

(c). Model choice in general probe trials

While ambiguous stimulus trials directly demonstrate Occam's Razor, the framework of Bayesian modelling allows for more general quantitative predictions. In particular, Bayesian models weight goodness of fit and model complexity for arbitrary stimuli, including the ambiguous ones just described. The comparison between the experimentally observed choice probabilities and the fitted theoretical choice probabilities for all probe trials is shown in figure 2b,c,e,f using the pooled data across all subjects both for drawing and clicking trials. Theoretical and empirical choice probabilities are in good agreement, as the 95% CIs mostly overlap with the identity line. The corresponding comparison of theoretical and empirical choice behaviour of individual participants can be seen in the electronic supplementary material, figure S6. To obtain the theoretical choice probabilities, we fitted psychometric sigmoid functions to subjects’ model choice in probe trials, where we used the difference in model log-evidence from equation (2.1) as the discrimination variable [26]. The psychometric sigmoid function has a single parameter α to tune the sensitivity of the decision boundary. The α-values were fitted by maximizing the likelihood and are shown in the electronic supplementary material, table S1. The experimental choice probabilities for different stimuli were obtained by first discretizing the theoretical choice probabilities into five equidistant bins, and then determining the choice frequency of model M₁ for all five bins. To quantitatively assess the explanatory power of the individual fits, we performed linear regression on the individually observed choice patterns. For all participants and all conditions, the ideal slope of 1 lies within the 95% CIs of the fitted slope. The ideal intercept of 0 lies within the 95% CIs for all subjects, except for subject 2 in the first session (cf. electronic supplementary material, figure S7).

(d). Control experiment: spatial frequency

Finally, we tested for trajectory smoothness as a confounding variable. In the choice trials considered so far, the simple model was always the model with less spatial frequency. To test whether subjects really cared about model complexity rather than spatial frequency, we designed a control experiment where the simpler model had a higher spatial frequency than the more complex model. This unusual scenario can be created by modulating the noise and signal variability of the two models. If model M₂ generates wiggly trajectories that are highly reproducible across trials (i.e. with low variability), it constitutes a simple model, because it cannot explain many different datasets. If, by contrast, model M₁ generates smooth trajectories with low spatial frequency, but with high noise and signal variability, it might be able to explain more datasets than the wiggly model. To test whether the critical variable was indeed trajectory smoothness or model complexity, we therefore trained a group of participants on these two models and exposed them to probe trials in which the goodness-of-fit values were equal under both models (see the electronic supplementary material for details). If participants cared about smoothness, they should prefer the more complex model M₁ in these trials. If, however, participants cared about model complexity as the critical variable, they should prefer the simpler, but more wiggly model M₂. Participants’ choice probabilities can be seen in figure 3a. For all three error levels, we found that subjects significantly preferred the simpler model M₁ (p < 0.001, sign test against median of 0.5). Compared with figure 2a,d, it can be seen that the choice probabilities indicate a more stochastic choice behaviour, because the discrimination in the probe trials was more difficult owing to the different noise and signal variances of the two models. This is also reflected in more shallow psychometric curves in the probe trials and the associated lower α-values quantifying their reduced steepness (cf. electronic supplementary material, table S2). The choice probabilities in all probe trials are shown in figure 3b. To quantitatively assess the fitted choice probabilities, we performed linear regression on the individually observed choice patterns (cf. electronic supplementary material, figure S8). For all participants and all conditions, the ideal slope of 1 lies within the 95% CIs of the fitted slope. The ideal intercept of 0 lies within the 95% CIs for 5 out of 10 subjects (cf. electronic supplementary material, figure S9). While these results cannot completely rule out a weak smoothness bias, they clearly show that participants’ choices are modulated by Bayesian model complexity, and that participants tend to prefer the simpler model and not the smoother model when both fit the observations equally well (cf. figure 3a).

Figure 3.

Control experiment where the simpler model M₂ had a higher spatial frequency. (a) Occam's Razor observed in the control experiment. The plots show the choice probability for the more complex model M₁ when presented with a stimulus with equal goodness of fit for both models. A bias towards the simpler but higher-spatial-frequency model M₂ can be seen. (b) Pooled group choice probabilities in the control experiment. Circles represent individual participants’ median choice probability and the purple line shows the median using pooled data of all participants. The dashed black line illustrates the ideal case, where theoretical choice probabilities and observed choice behaviour match exactly. Error bars show the 95% CI. The individually fitted choice probabilities are shown in electronic supplementary material, figure S8.

4. Discussion

To test whether Occam's Razor plays a role in human sensorimotor learning, we designed a visuomotor experiment where participants had to produce a regression trajectory from noisy observations generated by one of two possible models with different complexity. Participants were trained on both generative models and were then presented with ambiguous stimuli where both models were able to explain the observed data equally well. We considered five different hypotheses: (1) subjects prefer the simpler model (Occam's Razor); (2) subjects are indifferent between the two models; (3) subjects ignore both models and either follow a straight-line or connect-all strategy; (4) subjects decide based on physical effort; and (5) subjects decide based on trajectory smoothness (spatial frequency). In accordance with Occam's Razor, we found that participants showed preference for the simpler model in ambiguous trials. Over all trials, we found that their behaviour was quantitatively consistent with Bayesian Occam's Razor trading off goodness of fit and model complexity. To control for the influence of physical effort required for drawing regression trajectories, we designed a control experiment where the indication of either model required the same physical effort. We found that subjects’ preferences were essentially unaltered, suggesting that the difference in effort required for drawing the two different trajectory types was negligible and that their choices were indeed affected by the underlying trajectory complexity. We also designed a control experiment where the simpler model implied underlying curves with a high spatial frequency but low variability across trials, and found that participants’ choices were mainly governed by model complexity and not trajectory smoothness.

In our study, we made a number of simplifying modelling assumptions that might limit the generalizability of our results: we assumed that trajectories can be well described by a Gaussian Process (GP) model, we assumed a squared exponential kernel for the GP, and we assumed a fixed observation noise set by the experimenter. First, the reasons for choosing a GP model in our experiment include their mathematical tractability, their clear distinction between model complexity and data complexity, they allow modelling very general smooth trajectories since GPs are non-parametric, and they have been previously shown to adequately capture human motion [27]. Second, we assumed that trajectories generated with a squared exponential kernel can be adequately mimicked by human motion. Our assumption is based on the close relationship between squared exponential kernels and radial basis function networks that have been previously suggested for modelling human sensorimotor processing [28]. To test the appropriateness of this modelling assumption, we also fitted a neural network kernel [22,29] to participants’ motion trajectories and found that the squared exponential kernel provided a better explanation for all subjects in all conditions (cf. electronic supplementary material, figure S10). The reason for this could simply be that the synthetic trajectories were generated from the squared exponential kernel and that participants were able to learn this.

Third, in our fits we assumed that subjects learned the variance of the observation noise that enters as an additive constant on the diagonal of the covariance matrix 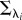in equation (2.1). This assumption was motivated by the fact that the observation noise stayed the same throughout the experiment and was set by the experimenter. The magnitude of this observation noise was on the order of centimetres, and thus far larger than perceptual noise owing to natural limitations of visual acuity. We also evaluated the predictive likelihood of a range of length scales and observation noise values for participants’ movement trajectories, and found that the likelihoods were sharply peaked within the neighbourhoods of the experimentally induced values, suggesting that our assumption regarding the observation noise was reasonable (cf. electronic supplementary material, figure S11).

The problem of disambiguating competing explanatory hypotheses when faced with ambiguous stimuli has been previously investigated. In fact, the human sensorimotor system is frequently confronted with such decision-making situations, for instance when perceiving a visual or motion illusion [30,31]. Interestingly, the emergence of many illusions can be explained within the Bayesian framework by using priors that reflect environmental statistics [32–35], including priors for light-from-above illumination in object perception [36,37], priors for low number of categories in object categorization [38] and priors for lower speed in motion perception [30,39]. Deciding for a particular hypothesis can also be thought of as choosing the simpler explanation, which highlights the important role of the prior in defining what is simple or difficult. As the prior is subjective, it can encode information about the statistics of the stimulus, but also subject-specific features like cognitive difficulty.

The problem of model selection has been recently addressed in a number of studies. Körding et al. [40] investigated integration versus segregation of audio-visual stimuli in human subjects, which can be cast as selecting between two different models: in one model, there was only one source explaining both stimuli (auditory and visual), and in the other model there were two different sources at different locations explaining both stimuli. When subjects reported their perception of unity [41], they were effectively doing inference over the two different models. Another recent study [42] introduced a sensorimotor paradigm for Bayesian model selection. In their task, subjects had to point to one of two targets (representing two models) after observing a cursor shift (representing the model parameter) drawn from one of two possible distributions (the prior over the model parameters given either model). When facing ambiguous visual feedback of the shift parameter, participants had to ‘integrate out’ the compatible range of parameter values. It was found that their choice behaviour was consistent with Bayesian model selection. In motor control, selecting between different models is relevant in the context of structure learning [43–49], where abstract invariants form structures or abstract models that are applicable to a range of motor tasks.

In contrast to these previous studies on model selection, our current study explicitly investigates the trade-off between fitting error and model complexity. We therefore designed a sensorimotor regression task based on GP models that allowed for an analytic expression of the model complexity, which we could exploit for the design of ambiguous probe trials. Thus, we could perform a quantitative analysis of the preference for simpler models in probe trials and compare against human behaviour. The main contribution of this study is the illustration of Occam's Razor as it is depicted in figure 1a in the human sensorimotor system. Constructing tasks that allow this interpretation of model complexity is not trivial [8]. Our study thus adds a new angle to the growing number of psychophysical experiments where participants’ behaviour was successfully modelled within a Bayesian framework.

The study was approved by the local ethics committee, and all participants were naive and gave informed consent.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Data accessibility

The primary data for the study are publicly available at Dryad doi:10.5061/dryad.94jt2.

Funding statement

This study was supported by the DFG, Emmy Noether grant no. BR4164/1-1.