Power of the Classical Twin Design Revisited: II Detection of Common Environmental Variance

Abstract

We expand our previous deterministic power calculations by calculating the required sample size to detect C in ACE models. The theoretical expected value of the maximum log-likelihood for the AE model was derived using two optimisation methods and these gave near-identical results. Theoretical predictions were verified by computer simulation and the results agreed very well. We have developed a user-friendly web-based tool, TwinPower, to perform power calculations to detect either A or C for the classical twin design. This new tool can be found at http://genepi.qimr.edu.au/cgi-bin/twinpower.cgi

The classical twin design, in which phenotypic measurements are available for monozygotic (MZ) twin pairs raised together and dizygotic (DZ) twin pairs raised together, has been used for decades to disentangle genetic and nongenetic sources of resemblance between relatives. The design is simple and balanced (two observations per family), the sufficient statistics are four mean squares (between and within MZ pairs and DZ pairs) and, in addition to the total (phenotypic) variance, only two variance components can be estimated. It is remarkable therefore, that, to our knowledge, no simple deterministic equations exist in the literature to calculate either the sampling variance of the parameter estimates of interest, or the power to detect genetic or non-genetic sources of variance. Martin et al. (1978) provided a comprehensive theoretical analysis of the power of the classical twin design using weighted-least-squares to estimate variance components and a goodness-of-fit test to reject ‘false’ models. We recently presented derivations to calculate power for the additive genetic component of variance from the comparison of ACE and CE models when using maximum likelihood (Visscher, 2004). Here we extend those derivations to the common environmental component of variance by comparing ACE and AE models. We have incorporated all deterministic power predictions in a user-friendly web-based program TwinPower (http://genepi.qimr.edu.au/cgi-bin/twinpower.cgi).

Methods

The notation follows Visscher, (2004). The objective of this note is to compare ACE versus AE models, rather than ACE versus CE models as was dealt with previously. As before, we will first deal with the simple case of least squares estimation, and then use an approximation to (RE)ML estimation.

Least Squares

Consider the between-pair (B) and within-pair (W) observed mean squares (MS) in the standard ANOVA table for n pairs, where the pairs can be either dizygotic (DZ) or monozygotic (MZ),

	df	MS	E(MS)
between pairs	n−1	B	2σb2 + σw2
within pair	n	W	σw2

The expected mean squares and between and within pair variances for the ACE model, when scaled by the phenotypic variance, are

	E(B)	E(W)	σb2	σw2
MZ pairs	2(h2+c2) + (1−h2−c2)	(1−h2−c2)	h2+c2	(1−h2−c2)
DZ pairs	2(½h2+c2) + (1−½h2−c2)	(1−½h2−c2)	½h2+c2	(1−½h2−c2)

The variance of the observed mean squares (MS) are

$$var(\text{MS})=2\mathrm{E}{(\text{MS})}^2/df,$$

with df the degrees of freedom. Hence the variance of the estimate of the between-pair component is,

$$\begin{array}{l}var({\widehat{\mathrm{\sigma }}}_b^2)=var((B-W)/2)\\ =\frac{1}{4}(\frac{2E{(B)}^2}{n-1}+\frac{2E{(W)}^2}{n})\\ \approx \frac{1}{2n}(E{(B)}^2+E{(W)}^2)\end{array}$$

From the ANOVA, the estimate of the intra-class correlation is calculated as

$$\widehat{t}=[(\mathrm{B}-\mathrm{W})/2]/[(\mathrm{B}-\mathrm{W})/2+\mathrm{W}]=(\mathrm{B}-\mathrm{W})/(\mathrm{B}+\mathrm{W})$$

Applying this formula for m MZ pairs and n DZ pairs gives t̂_MZ and t̂_DZ. A first order approximation of the variance of these correlations is

$$\begin{array}{l}var({\widehat{t}}_{\text{MZ}})\approx {(1-{\mathrm{t}}_{\text{MZ}})}^2{(1+{\mathrm{t}}_{\text{MZ}})}^2/\mathrm{m}={(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2/\mathrm{m}\\ var({\widehat{t}}_{\text{DZ}})\approx {(1-{\mathrm{t}}_{\text{DZ}})}^2{(1+{\mathrm{t}}_{\text{DZ}})}^2/\mathrm{n}={(1-{{\mathrm{t}}_{\text{DZ}}}^2)}^2/\mathrm{n}\end{array}$$

Estimates of the common environmental component and its approximate variance are:

$$\begin{array}{l}{\widehat{c}}^2=2{\widehat{t}}_{\text{DZ}}-{\widehat{t}}_{\text{MZ}}\text{and}\\ var({\widehat{c}}^2)=4var({\widehat{t}}_{\text{DZ}})+var({\widehat{t}}_{\text{MZ}})=4{(1-{{\mathrm{t}}_{\text{DZ}}}^2)}^2/\mathrm{n}+{(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2/\mathrm{m}\end{array}$$ [1]

Power and Sample Size

For large samples, the quantity λ = (c²/SE(ĉ²)) is the expected mean test statistic of a normal test to detect C. Its square is approximately equal to the non-centrality parameter (NCP) of a chi-square test statistic. The NCP per total number of pairs (N) is, from Equation [1], with p_MZ defined as the proportion of MZ twin pairs in the sample of all twin pairs,

$${\text{NCP}}_{\text{LS}}/N={(2{\mathrm{t}}_{\text{DZ}}-{\mathrm{t}}_{\text{MZ}})}^2/[{(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2/{\mathrm{p}}_{\text{MZ}}+4{(1-{{\mathrm{t}}_{\text{DZ}}}^2)}^2/(1-{\mathrm{p}}_{\text{MZ}})]$$ [2]

For a statistical test we assume that under the null hypothesis of c² = 0 (λ = 0)

$$\mathrm{T}={\widehat{c}}^2/\text{SE}({\widehat{c}}^2)~N(0,1)$$

Under the alternative hypothesis, T ~ N(λ,1). This allows a simple prediction of power. If z_1−α is the one-sided (upper tail) threshold from a standard normal distribution corresponding to a type-I error rate of α, and β the type-II error rate, then, for a one-sided test

$$\text{Power}=1-\mathrm{\beta }=\text{Prob}(\mathrm{x}>{\mathrm{z}}_{1-\mathrm{\alpha }}-\mathrm{\lambda }),$$

with x a standard N (0,1) random variable. Alternatively we can express the required power for a given value of the proportion of variance due to common environmental effects in terms of the MZ and DZ sample size,

z_β = z_1−α − λ, or, λ = z_1−β + z_1−α. Using the variance of the estimate of the heritability,

$${\mathrm{\lambda }}^2={\mathrm{c}}^4/var({\widehat{c}}^2)={({\mathrm{z}}_{1-\mathrm{\alpha }}+{\mathrm{z}}_{1-\mathrm{\beta }})}^2$$

Optimum Proportion of MZ Twins

For a given proportion of MZ twins in the sample, the required total number of twins is, from Equation [2]

$$N=4{({\mathrm{z}}_{1-\mathrm{\alpha }}+{\mathrm{z}}_{1-\mathrm{\beta }})}^2[{(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2/{\mathrm{p}}_{\text{MZ}}+4{(1-{{\mathrm{t}}_{\text{DZ}}}^2)}^2/(1-{\mathrm{p}}_{\text{MZ}})]/{\mathrm{c}}^4$$

From Equation [2] the optimum proportion of MZ pairs (p_MZ) can be derived as a function of the two twin correlations. Differentiating with respect to p_MZ, setting the result to zero, and solving for p_MZ gives:

$${\mathrm{p}}_{\text{MZ}}=[2(1-{{\mathrm{t}}_{\text{MZ}}}^2)(1-{{\mathrm{t}}_{\text{DZ}}}^2)-{(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2]/[4{(1-{{\mathrm{t}}_{\text{DZ}}}^2)}^2-{(1-{{\mathrm{t}}_{\text{MZ}}}^2)}^2]=(1-{{\mathrm{t}}_{\text{MZ}}}^2)/[(1-{{\mathrm{t}}_{\text{MZ}}}^2)+2(1-{{\mathrm{t}}_{\text{DZ}}}^2)]$$

An alternative expression is,

$$1/{\mathrm{p}}_{\text{MZ}}=1+2(1-{{\mathrm{t}}_{\text{DZ}}}^2)/(1-{{\mathrm{t}}_{\text{MZ}}}^2)$$

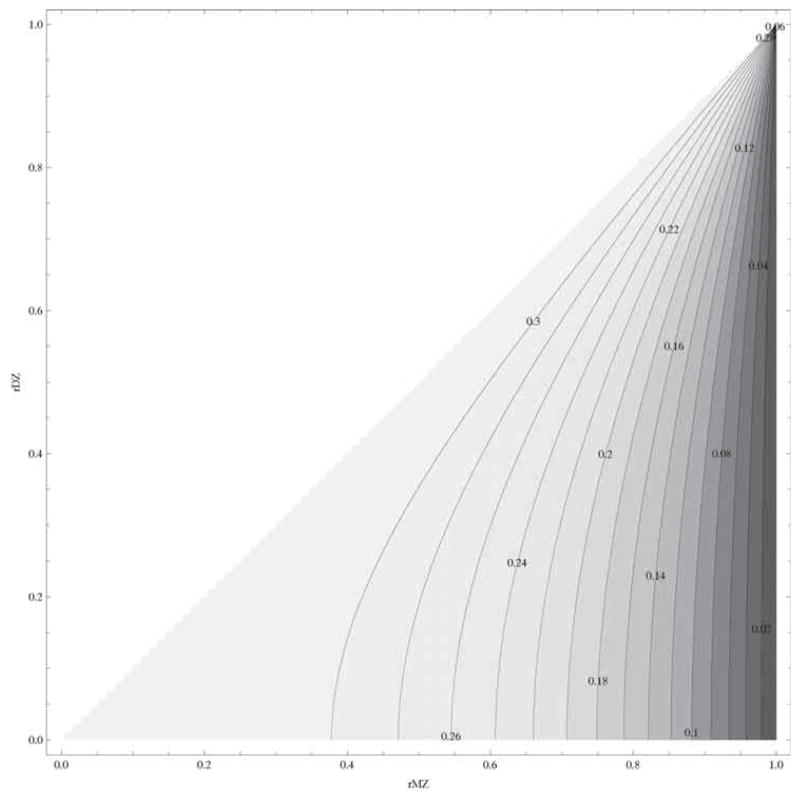
It is clear from these expressions that the optimum proportion of MZ pairs is less than one-third. In Figure 1 we give a contour plot of the optimum proportion of MZ pairs as a function of the MZ and DZ correlation coefficient. The more similar the two correlations are (when A goes to zero), the closer the ideal MZ proportion goes to one-third. For a smaller value of C (when C goes to zero), the sampling variance of the DZ correlation is proportional to 4(1 − ¼h⁴)² and the sampling variance of the MZ correlation is proportional to (1 − h⁴)². The latter is much smaller, so fewer MZ pairs are required to minimise the overall sampling variance of the estimate of C.

Figure 1.

Contour plot of the optimum number of MZ pairs (pMZ) to detect C derived from the least squares approximation.

Maximum Likelihood

Given the sufficient statistics (sums of squares within and between MZ and DZ pairs), there is a close relationship between least squares and ML estimation for balanced designs (e.g., Thompson, 1962). In Appendix A of Visscher (2004) we showed the residual maximum likelihood (REML) estimation for ACE and CE models for a mixture of two one-way designs, and gave the expected value of the likelihood-ratio test statistic per pair from the ACE and CE model. However, for the AE model there is no explicit closed form (RE)ML solution from the mean squares. We can get numerical results, however, using for an example a simple grid search over fitted values of the additive genetic and environmental variance components, and obtain the expected maximum log-likelihood value for the incorrect AE model. Asymptotically (m ≈ m−1 and n ≈ n−1), the log-likelihood function, scaled by the total number of twin pairs (N) can be written as,

$$\begin{array}{l}-2\text{lnL}/\mathrm{N}={\mathrm{p}}_{\text{MZ}}\text{ln}[\mathrm{E}({\mathrm{B}}^{\text{MZ}})]+{\mathrm{p}}_{\text{MZ}}\text{ln}[\mathrm{E}({\mathrm{W}}^{\text{MZ}})]+\\ (1-{\mathrm{p}}_{\text{MZ}})\text{ln}[\mathrm{E}({\mathrm{B}}^{\text{DZ}})]+(1-{\mathrm{p}}_{\text{MZ}})\text{ln}[\mathrm{E}({\mathrm{W}}^{\text{DZ}})]\\ +{\mathrm{p}}_{\text{MZ}}{\mathrm{B}}^{\text{MZ}}/\mathrm{E}({\mathrm{B}}^{\text{MZ}})+{\mathrm{p}}_{\text{MZ}}{\mathrm{W}}^{\text{MZ}}/\mathrm{E}({\mathrm{W}}^{\text{MZ}})+\\ +(1-{\mathrm{p}}_{\text{MZ}}){\mathrm{B}}^{\text{DZ}}/\mathrm{E}({\mathrm{B}}^{\text{DZ}})+(1-{\mathrm{p}}_{\text{MZ}}){\mathrm{W}}^{\text{DZ}}/\mathrm{E}({\mathrm{W}}^{\text{DZ}})\end{array}$$ [13]

(Appendix A of Visscher, 2004). To obtain the expected maximum likelihood value under the AE model, we use the values of B^MZ, W^MZ, B^DZ, and W^DZ expected under the true ACE model, and E(B^MZ), E(W^MZ), E(B^DZ), and E(W^DZ) under the false AE model. For example, E(B^DZ) = σ_e² + 3/2σ_a². We used a grid search for the variance components scaled by the phenotypic variance in the range of 0.01 to 1.20 and an increment of 0.01 to maximise the maximum log-likelihood function [3]. We obtained the maximum expected NCP (= twice difference in expected log-likelihood between ACE and AE models) by searching over values of p_MZ (in the range of 0.01 to 0.99, with an increment of 0.01). We constrained the estimates of the number of twin pairs by forcing a minimum of two pairs per zygosity group.

The approach to find the ML value of the AE model was verified using Mx (Neale et al., 2006), following the method outlined by Neale et al., (1994) and Hewitt et al., (1988). In essence it is a three-step procedure. First, predicted covariance matrices for MZ and DZ twin pairs are generated from the true values of the A, C, and E variance component parameters. Second, the false (AE) model is fitted to these data, using sample size proportions with the sample sizes selected. Minus two times the difference in the log-likelihood of the true (ACE) model and the false (AE) model yields a noncentrality parameter which can be used to determine statistical power. Third, using Mx’s option power = .10, 1 we obtain the power at the .05 alpha level of the 1 df test. The reason that the option requests the .10 alpha level, but the program actually delivers the .05 alpha level, is because being a variance component, the test under the null hypothesis follows a 50:50 mixture of chi-squared of zero (which would occur whenever the DZ correlation is less than half the MZ correlation) and chi-squared with one degree of freedom (which occurs whenever the DZ twin correlation is greater than half that of the MZ pairs; Dominicus et al., 2006; Self & Liang, 1987; Stram & Lee, 1994; Visscher, 2006). Note that this discrepancy was not noticed in the Neale et al. (1994) article; the alpha levels reported as .05 in that paper should be interpreted as .025. An Mx script for conducting the simulation with different proportions of MZ and DZ twin pairs, and different true values of the population A, C, and E parameters, is presented in the Appendix, and is also available on the website http://www.vcu.edu/mx in the examples section. The script uses the #loop construction to repeat the analysis for the various combinations of parameter values and MZ:DZ sample size ratio.

A simulation study was performed to validate the theoretical derivations. For each zygosity group, between and within pair mean squares were simulated from a central Wishart distribution. Residual maximum likelihood values were estimated using a hill-climbing algorithm, and likelihood-ratio test statistics were calculated from the full (ACE) and reduced (AE) models. Ten thousand replicates were run (so that the SE of the estimate of power is ~0.4%) and the proportion of test statistics that were larger than the 5% threshold under the null hypothesis (a central χ₁² value of 2.71) were counted to estimate power.

Results

The theoretical prediction of the number of pairs required to achieve 80% power, using either the REML approach or the ML approach as implemented in Mx, were extremely close (results not shown), which is not surprising because the difference between REML and ML for the models in this study only involved terms of the order of m/(m−1) and n/(n−1), which are asymptotically unity.

Table 1 gives a number of examples of the sample sizes required to achieve 80% power, for a fixed proportion of 50% MZ twins and for an optimised proportion of MZ twins. Note that these are asymptotic results. For large values of C (say, > 0.3), the AE model is such a bad fit that very few pairs are needed to reject the hypothesis that C = 0, and among those, very few MZ pairs are needed. The simulation results show that the predictions of power are very good. The one example where the power from simulations is much larger (0.86) than predicted (0.80) may be because the sample sizes are so small that the distribution of the test statistic under the null hypothesis is not a 50:50 mixture of zero and a χ₁². Indeed, when we ran simulations with h² = 0.2 and c² = 0, the mean of the test statistic was 0.23, whereas 0.50 was expected. The reason for the discrepancy is that with this small sample size (17 MZ and 17 DZ twin pairs) and a small heritability (0.2), there is a probability that there is no evidence for twin resemblance at all, let alone evidence for a larger resemblance of MZ pairs. Asymptotically, for both h² = 0 and c² = 0 we would expect the test statistic from ACE and AE models to be zero with a probability of one quarter, close to what we observe. This is analogous to testing for a QTL when there is no family resemblance (Visscher & Hopper, 2001).

Table 1.

Theoretical Total Number of Pairs Required for a Power of 80% to Reject the AE Hypothesis When it is False at a Type-I Error Rate of 0.05, and Achieved Statistical Power (in %) for that Number from Simulations

True model		Maximum likelihood pMZ
h2	c2	0.51	Optimised2
0.8	0.1	2663 / 80	1598 (0.13) / 78
0.6	0.3	262 / 82	159 (0.06) / 80
0.4	0.5	80 / 82	48 (0.04) / 79
0.2	0.7	34 / 86	20 (0.08) / 82
0.6	0.1	3425 / 79	2574 (0.25) / 80
0.4	0.3	356 / 81	252 (0.17) / 80
0.2	0.5	114 / 83	79 (0.11) / 79
0.4	0.1	4486 / 80	3617 (0.27) / 79
0.2	0.3	464 / 81	368 (0.21) / 80
0.2	0.1	5394 / 79	4701 (0.27) / 80

Note:

¹Estimate power (in %) from simulation are shown after the theoretical results.

²Lowest total number of pairs, with the proportion of MZ pairs in brackets, from a search in 0.01 step units. Estimates of power (in %) from simulation are shown after the theoretical results.

The optimum proportion of MZ twins to detect C is smaller than half, whereas the optimum proportion of MZ twins to detect A is larger than half (Visscher, 2004). Hence, we cannot have a design that is optimised to both detect A and detect C, which intuitively makes sense. A reasonable and practical compromise is to have approximately the same number of pairs of each zygosity. The same conclusions were reached by Martin et al. (1978). A comparison of our results from (RE)ML with those from Martin et et. (1978), who used weighted-least-squares and a goodness-of-fit test, shows that the required sample sizes to detect C using maximum likelihood are 30% to 50% smaller (results not shown in tables). This is most likely due to the difference in the testing approaches used: Martin et al. (1978) used a two-sided goodness-of-fit test with two degrees of freedom, whereas the likelihood-ratio-test we use is one-sided and has one degree of freedom (Visscher 2004).

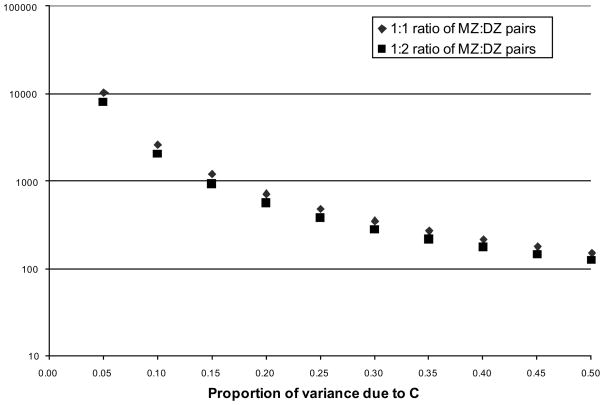
In Figure 2 we give examples of the required sample size to detect C for a fixed value of the DZ correlation of 0.5 (i.e., ½h² + c² = ½), for a proportion of MZ twins among all twin pairs of 50% and 33%. For proportions of the total variance due to C of 0.05 to 0.5, the required total sample size is 100s to 1000s, very large. Note that the y-axis is on a logarithm scale.

Figure 2.

Prediction of the required sample size to detect C with 80% power at a type-I error rate of 0.05 for a fixed value of the DZ correlation of .5.

We have incorporated the derivations from this note and from Visscher (2004) into a simple web-based tool called TwinPower (http://genepi.qimr.edu.au/cgi-bin/twinpower.cgi).

Discussion and Conclusions

We have provided simple deterministic calculations to calculate the power to detect A or C by contrasting ACE and CE or AE models, and have incorporated them in a user-friendly software tool TwinPower, (http://genepi.qimr.edu.au/cgi-bin/twinpower.cgi). Our examples show and confirm that very large sample sizes are required to detect C, even if it explains, say, 10% of the phenotypic variation. A corollary of this finding is that inference from model selection procedures starting with an ACE model will often conclude that C is not significant even if it exists. Therefore, the twin literature based upon the classical twin design and model selection procedures could be severely biased towards AE models. This bias could be reduced by having large sample sizes, so that the power to detect C when it is present is large, or by placing less emphasis on model selection procedures.

In addition to comparing AE and ACE models to test C, we revisited the power to detect A, by contrasting CE and ACE models in a simulation study. We can confirm that the predictions in Visscher (2004) are extremely accurate, because an explicit solution for the ML estimates of the variance components under the wrong CE model exists.

For arbitrary pedigrees, including, for example, extended twin designs, power calculations can be done following the same strategy we have taken in this study. That is, the approximate maximum likelihood values for the true and false models can be derived from the log-likelihood equation, using the expected value of the covariance matrix from real data. Instead of using the between and within pair mean squares, which are sufficient statistics in our study, a general pedigree approach would use the entire covariance matrix of all individuals in a pedigree. Mx can be used for such power analyses, including those where the pedigrees vary in size and structure.

Appendix A. Mx Scripts for Power Calculations

Mx Scripts for Power Calculations
! ACE Model for Power Calculations; false model AE fitted to ACE data
! #loop provides a large output to enable interpolation to find
! the optimal MZ:DZ sample size ratio. Proportions vary from 0 to 1 by
! .001 so 1000 outputs are generated per pairing of A and C variance
! components.
! A unix shell command such as
! grep ‘ .80 \| cannot \| NMZ \| ASQ \| CSQ ‘ falseAE.mxo > results.txt
! are useful to parse the output into readable form. They produce a list
! of power figures at the 80% level. Searching for CSQ or ASQ in the file
! makes it easy to find relevant sections. Note also that the cannot
! string is searched; this will detect errors.
!
! Suitable for Mx versions 1.66b and later.
!
#loop $a 1 8 1
#define r = 9 - $a
#loop $c 1 r 1
#define asq $a
#define csq $c
#define esq 10 - $c - $a
#loop $nmz 1 10001 10
#define nmz $nmz
#define ndz 10002 - nmz
! Simulate the data
#NGroups 1
G1: model parameters
Calculation
Begin Matrices;
A Lower 1 1 Fixed ! genetic structure
C Lower 1 1 Fixed ! common environmental structure
E Lower 1 1 Fixed ! specific environmental structure
H Full 1 1
Z full 1 2
End Matrices;
Matrix A asq
Matrix C csq
Matrix E esq
matrix Z nmz ndz
Matrix H .5
Begin Algebra;
M = A+C+E | A+C _
A+C | A+C+E /
D = A+C+E | H@A+C _
H@A+C | A+C+E /
End Algebra;
Options MXM = /tmp/mzsim.cov
Options MXD=/tmp/dzsim.cov
End
! Fit the wrong model to the simulated data
G1: model parameters
Calculation Ngroups=3
Begin Matrices;
X Lower 1 1 Free ! genetic structure
Y Lower 1 1 Fixed ! common environmental structure
Z Lower 1 1 Free ! specific environmental structure
End Matrices;
Matrix X 2.2360
Matrix Z 2.2360
Begin Algebra;
A= X*X′ ;
C= Y*Y′ ;
E= Z*Z′ ;
End Algebra;
Option no
End
G2: MZ twin pairs
Data NInput_vars=2 NObservations= nmz
CMatrix Full File=/tmp/mzsim.cov
Matrices= Group 1
Covariances A+C+E | A+C _
A+C | A+C+E /
Option No
End
G3: DZ twin pairs
Data NInput_vars=2 NObservations= ndz
CMatrix Full File=/tmp/dzsim.cov
Matrices= Group 1
H Full 1 1
Covariances A+C+E | H@A+C _
H@A+C | A+C+E /
Matrix H .5
Start .5 All
OPtion nO
Option Power= .10,1 ! .05 significance level & 1 df
End
#end loop
#end loop
#end loop