Differential Growth Trajectories for Achievement Among Children Retained in First Grade: A Growth Mixture Model

Abstract

The authors investigated the differential effect of retention on the development of academic achievement from grade one to five on children retained in first grade over six years. Growth Mixture Model (GMM) analyses supported the existence of two distinct trajectory groups of retained children for both reading and math among 125 ethnically and linguistically diverse retained children. For each achievement domain, a low intercept/higher growth group (Class 1) and a high intercept/slower growth group (Class 2) were identified. Furthermore, Class 1 children were found to score lower on several measures of learning related skills (LRS) variables and were characterized by having poorer self-regulation and less prosocial behaviors, compared to the other group. Findings suggest that some children appear to benefit more from retention, in terms of higher reading and math growth, than others. Study findings have implications for selecting children into retention intervention and early intervention.

1. Introduction

Grade retention is a common educational practice in US schools, despite a body of empirical evidence that offers limited evidence that repeating a grade improves the academic achievement of low-achieving children (Allen, Chen, Wilson, & Hughes, 2009; Jimerson, 2001, Wu, West, & Hughes, 2008a; Moser, West, & Hughes, 2012). Whereas earlier studies on the effects of grade retention compared the achievement of retained and comparably low-achieving, promoted children at specific points in time post-retention (e.g., Reynolds, 1992; Pierson & Connell, 1992), recent studies analyze latent achievement growth trajectories of retained children (Moser et al., 2012; Hong & Raudenbush, 2005; Wu et al., 2008a). Analysis of growth trajectories has the advantage of examining patterns of growth in the years following the retention intervention, permitting the identification of differential short-term and longer-term growth in achievement for groups of retained and promoted children (Wu et al., 2008a). However, the modeling techniques adopted in studies analyzing growth trajectories of retained and promoted children are based on the assumption that all the retained children had homogeneous developmental patterns over time and follow one single average developmental trajectory. The current study tests this assumption by answering two sets of research questions: 1) are there latent subgroups of retained children following distinct developmental trajectories for reading and math achievement? If so, how many subgroups are there among the retained children? 2) If latent trajectory subgroups are identified, do certain child and family variables differ between the subgroups? The identification of a group of retained children whose rate of academic achievement growth following retention is faster, relative to that of other retained children, would have implications for selecting children into this intervention.

To the best of the authors’ knowledge, no published study identifies classes of retained children who evince different achievement growth trajectories. However, extant empirical findings and theoretical perspectives suggest that there might be latent groups among the retained children, with some responding positively to the retention process and some not. Specifically, several lines of evidence, reviewed in a subsequent section, support the proposition that, among retained children, those with poor learning related skills (e.g., attention, behavioral and emotional self-regulation, social skills) may increase in achievement at a faster rate subsequent to retention than children with better learning related skills. In the following section, learning related skills are defined and their role in early school achievement is described.

1.1 Learning Related Skills

Learning related skills (LRS), sometimes referred to as learning approaches, refer to a cluster of self-regulatory skills (e.g., ability to attend, persist in the face of challenges, plan, cooperate with others, inhibit impulsive responses, and respond with flexibility to changes in one’s environment) that facilitate efficient engagement in learning (Fantuzzo, Bulotscky-Sheare, Fusco, & McWayne, 2005; Matthews, Kizzie, Rowley, & Cortina, 2010). LRS are thought to reflect differences in the temperamental construct of effortful control and involve the ability to voluntarily direct and manage one’s behavior and attention in learning situations and to respond flexibly and appropriately (Blair & Razza, 2007). Next, key dimensions of LRS are defined and described.

1.1.1 Effortful control

Effortful control, defined as the ability or capacity to voluntarily inhibit a dominant response to activate a subdominant response, allows for the development from more reactive to more self-regulative behavior (Rueda, Posner, & Rothbart, 2005). Children high in effortful control voluntarily control their attention and behavior as needed, including focusing and shifting attention, persisting on tasks in the face of challenges, and delaying gratification. Thus they achieve higher accuracy on paper and pencil tasks requiring attention to detail and monitoring one’s performance against a criterion (Kochanska, Murray, and Harlan, 2000). Inhibitory control and task accuracy reflect good effortful control. Individual differences in the ability to effortfully control or regulate behavior are hypothesized to reflect biologically based, temperamental variation among children (Posner & Rothbart, 1998). However, experience also affects development of these skills; poor and minority children perform more poorly than middle-class and white children on measures of effortful control and self-regulation (Blair 2010; Matthews et al., 2010). The development of effortful control occurs most rapidly during the preschool years (Kochanska & Knaack, 2003), although children continue to show rapid development in effortful control and related self-regulatory skills throughout the early school years (Kochanska et al., 2000).

1.1.2 Hyperactivity

Children with hyperactivity also demonstrate poor behavioral inhibition and regulation (Barkley, 1997). Hyperactivity includes motor restlessness and fidgeting, difficulty staying in one’s seat, difficulty remaining still or playing quietly, and appearing to always be “on the go.” Higher levels of hyperactivity have been linked to lower level of school readiness (Fantuzzo et al., 2005) and lower level of academic achievement (Blair & Razza, 2007; Matthews et al., 2010; McClelland, Cameron, Connor, Farris, Jewkes, & Morrision, 2007).

1.1.3 Ego resiliency

The psychological construct of ego resiliency captures the flexible, adaptive aspect of LRS (Block & Block, 1980). For example, a child with high ego-resiliency could easily adapt and be flexible with unexpected or uncontrollable changes in the classroom schedule, whereas a child with low ego-resiliency might become flustered and “fall apart” under similar circumstances. A child who adapts and “bounces back” after challenges is more likely to persist or persevere than a child who “falls apart” and gives up on long-term and challenging goals. Ego-resiliency is associated with psychosocial adjustment and academic achievement in childhood (Dreke, 2009; Kwok, Hughes, & Luo, 2007; Shonk & Cicchetti, 2001).

1.1.4 Conscientiousness

The psychological construct of conscientiousness is also thought to reflect differences in children’s temperament (Graziano & Ward, 1992; John, Caspi, Robins, Moffitt, & Stouthamer-Loeber, 1994). Conscientiousness is the child’s dependability, task interest, will to achieve, impulse control, constraint, control, and work persistence (Digman, 1989; John & Srivastava, 1999). Children who are high in conscientiousness are more likely to cope with classroom stressors better, persist in the face of challenges, and achieve more in school (Digman, 1989: Barbaranelli, Capara, Rabasca, & Pastorelli, 2003; Kwok et al., 2007).

1.1.5 Prosocial skills

Both effortful control and ego-resiliency are associated with peer acceptance and positive social behaviors (Block & Block, 1980; van Aken, van Lieshout, Scholte, & Haselager, 2002), presumably because children who can delay gratification, inhibit impulsive response (e.g., wait their turn), and respond adaptively to changing social situations (e.g., work cooperatively with others) have better social skills. Furthermore, children who are rated by teachers or peers as high on prosocial skills achieve more than do children rated lower on these skills (Wentzel, 1991, 1993). Importantly, when measures of prosocial and antisocial engagement in the classroom are considered together, only prosocial engagement uniquely predicts gains in achievement, suggesting the unique role of prosocial engagement in children’s learning (Hughes, Luo, Kwok, & Loyd, 2008).

1.2 Correlates of LRS in the Early Grades

In preschool and elementary grades, a number of demographic variables are associated with LRS. Boys score lower than girls on measures of effortful control, including attention, inhibitory control, and behavioral regulation, and on measures of prosocial skills (Birch & Ladd, 1998; Matthews, Ponitz, & Morrison, 2009). African American and poor children also score lower on measures of effortful control and prosocial skills than do non-African American and children from more advantaged home environments (Hamre & Pianta, 2001; Meehan, Hughes, & Cavell, 2003). The association between poverty and poor effortful control is thought to be a result, in part, of the deleterious effects of poverty-related stress on aspects of brain development and functions that promote or impede the development of self-regulation (Blair, 2010).

Gender and racial group differences in LRS are thought to contribute to gender and ethnic group differences in achievement in the elementary grades. In a study with a national dataset, LRS explained, to a large extent, the achievement gaps between African American boys and their White and female counterparts at school entrance and in growth in achievement across the elementary grades (Matthews et al., 2010).

1.3 Relation between LRS and Achievement in the Early Grades

In preschool and early elementary grades, LRS predict growth in achievement, above IQ and family adversity. In a coordinated analysis of six longitudinal data sets, Duncan and colleagues (2007) found that kindergarteners’ attention-related skills (e.g., task persistence, attention control, and cooperative participation in the classroom) predicted their reading and math achievement at 3^rd grade, above measures of externalizing behaviors. In a sample of 379 kindergarten and first grade children from low SES backgrounds, LRS (i.e., works independently, seeks challenges, accepts responsibility, tunes in to classroom activity) predicted literacy gains, even with prior literacy skills held constant (Stipek, Newton, & Chudgar, 2010). McClelland and colleagues (2007) found that measures of behavioral self-regulation (inhibitory control, attention, and working memory) were significantly associated with early math and literacy skills, above cognitive ability. Furthermore, gains in behavioral self-regulation predicted gains in emergent literacy above family background variables. Matthews et al. (2010) found LRS had the strongest effect on achievement in kindergarten and for achievement development through 5^th grade, in comparison to other social and behavioral variables. The authors concluded that LRS are more proximal influences on the achievement of African American boys than are behavioral variables such as externalizing problems. Overall, the strength of these associations/effects is small to moderate.

Several processes may explain why children with poor LRS show lower achievement growth. Children who have poor LRS may benefit less from instructional supports than children with good LRS. For example, early reading places a premium on effortful control because early readers must attend to individual phoneme patterns and have patience to self-monitor and correct miscues as well as to work independently despite feeling angry or frustrated or the presence of distractions (Li-Grining, Votruba-Drzal, Maldonado-Carreño, & Haas, 2010). Because self-regulated learners and prosocial children elicit more supportive and responsive instruction from their teachers (Birch & Ladd, 1997) and are viewed by their classmates as more capable and socially preferred (Realmuto, August, Sieler, & Pessoa-Brandao, 1997), they may develop more positive perceptions of their academic competence, leading to more active engagement in learning (Liew, Barrois, McTigue, and Hughes, 2008).

1.4 Learning Related Skills and Grade Retention

Research on LRS and grade retention is sparse. Interviews with elementary teachers reveal that the large majority of teachers believe that retention in the early grades is effective for “immature” children (Tomchin & Impara, 1992). Although immaturity was not defined in this study, the term is often used by educators to refer to poor learning-related behaviors such as impulsivity, inattentiveness, and poor social skills. Self-regulatory skills such as attention and inhibitory control continue to develop in the primary grades (Posner & Rothbart, 2000; Kochanska et al., 2000). For children with delayed self-regulatory skills, the extra year of maturation that retention in first grade affords may allow these children to benefit more from instruction the following year, thereby gaining the foundation necessary for future learning. The importance of mastery of the first grade curriculum to one’s achievement throughout the elementary grades was demonstrated by Pianta, Belsky, Vandergrift, Houts, and Morrison (2008). Using data from the NICHD Early Child Care and Youth Development study, these researchers reported that 93% of the growth in reading and 76% of the growth in math between kindergarten and fifth grade takes place by the end of first grade. Other researchers also report that lagging behind one’s classmates as one leaves first grade forecasts long-term poor achievement (Alexander, Entwisle, & Horsey, 1997; Stipek, 2001). The extra year of maturation that grade retention affords may be a more appropriate intervention for low achieving first grade children who lag behind their classmates than for low achieving children with better developed LRS.

Some empirical support for the view that a group of children with poor LRS may show faster growth following retention, compared to children with better LRS, comes from a study investigating moderators of the effects of being retained in first grade on subsequent growth in achievement (Wu, West, & Hughes, 2008b). Using samples of children either retained or promoted in first grade that were matched on their propensity to be retained, Wu et al. investigated several possible moderators of the impact of retention in first grade on reading and math achievement trajectories over the following 3 years. Retention was more beneficial for children who had poorer behavioral self-regulation (defined in terms of teacher-rated conduct problems) than for children with better self-regulation. The researchers reasoned that children with poor behavioral self-regulation lacked the LRS necessary to successfully meet the challenges of encountering a more advanced curriculum, if promoted. Although the Wu et al. study suggests that retention may be more beneficial than promotion to children with poor behavioral self-regulation, her study did not address heterogeneity in achievement trajectories among the retained group.

2. The Current Study

The first purpose of the current study was to determine if subsets of children retained in first grade exist whose achievement growth trajectories over six years deviate from the overall growth trajectory of retained children. The second purpose is to test whether there are systematic differences in LRS between growth trajectory classes among grade-retained children. Specifically, we expect differences in LRS will be associated with differential patterns of growth in reading and math, such that a trajectory class with faster growth will evince poorer LRS and achievement at baseline, relative to other trajectory classes. The predicted negative relation between rate of growth in achievement and LRS in Year 1 is contrary to the positive relations between these variables among samples comprised primarily of promoted students (Li-Grining et al., 2010; Matthews et al., 2010). Our expectation is based on the reasoning that among children retained in first grade, those children with the poorest learning related skills will benefit the most (or be harmed the least) from the additional year of growth in learning related skills that repeating a grade entails. Differences between achievement trajectory classes on selected demographic variables (family SES, child’s ethnicity, and gender) will also be investigated, based on research finding an association between these variables and measures of LRS. Although we expect these variables will be correlated with LRS at Time 1 (i.e., when children were in first grade for the first time), we make no predictions regarding their association with membership in different growth classes.

We apply growth mixture modeling with unknown groups (Muthén, 2004) to concurrently model individual and possibly group-related trajectories of math and reading development over six years, beginning when children were in first grade for the first time. Thus the growth trajectories cover the elementary school years (1^st grade to 5^th grade). The decision to model reading and math trajectories separately rather than using a composite measure of achievement was based on previous research using longitudinal data from a large, national study of elementary children that found support for two latent trajectory classes for reading but only one latent trajectory class for math (Pianta, et al., 2008).

3. Method

3.1 Participants

Participants were 125 (61% male) first-grade children attending one of three school districts (1 urban, 2 small city) in southeast and central Texas, selected from a sample of 784 children participating in a longitudinal study examining the impact of grade retention on academic achievement. Participants were recruited across two sequential cohorts in first grade during the fall of 2001 and 2002. The composition of first grade classrooms in these three school districts was 42% Caucasian, 25% African American, 27% Hispanic, and 5% Other; 44% were eligible for free or reduced lunch, and 53 % were male. Children were eligible to participate in the larger longitudinal study if they scored below the median score for their school district on a state approved, district-administered measure of literacy, spoke either English or Spanish, were not receiving special education services, and had not been previously retained in first grade (i.e., were in 1^st grade for the first time at the beginning of the study). School records identified 1,374 children as eligible to participate. Parent permission to participate was obtained for 784 of the eligible children. Analyses on a broad array of demographic variables, scores on a district-administered measure of early literacy, and school context variables did not indicate any difference between the 784 children with consent and the 590 children without consent.

Of these 784 participants, 165 were retained in first grade, of whom 125 (76%) met the following additional criteria for participation in the current study: (1) had at least one wave of data on Woodcock–Johnson III Broad Reading and Broad Mathematics tests (Woodcock, McGrew, & Mather, 2001), and (2) were still active in the study at Year 6. These 125 children did not differ from the 40 children who did not meet inclusion criteria on any demographic variables, scores on a district-administered test of literacy, or study variables at baseline (Year 1). At entrance to first grade (Year 1), these children’s mean age was 6.47 (SD = 0.27) years. The ethnic composition for these 125 children was 44 African American, 34 Hispanic, 44 Caucasian, and 3 other. Participants’ age-standard scores on the Woodcock–Johnson III Broad Reading and Broad Mathematics tests (Woodcock et al., 2001) at Year 1 were 87.39 (SD = 15.68) and 96.74 (SD = 14.00), respectively. On the basis of family income, 70.1% of participants were eligible for free or reduced lunch. At Year 1, these 125 children were nested within 68 classrooms and 29 schools.

3.2 Data Collection

Measures of math and reading achievement were individually administered at school annually for six years, beginning when participants were in first grade for the first time (Year 1). A minimum of 8 months separated each annual assessment. At Year 1, classmates reported on children’s externalizing behaviors, children were individually administered performance measures of effortful control (i.e., inhibitory control and task accuracy), and teachers reported on children’ externalizing behaviors, ego resiliency, prosocial behaviors, and conscientiousness. Teachers received $25.00 for completing and returning each student questionnaire.

If children or their parents spoke any Spanish in Year 1, children were individually administered the Woodcock-Munoz Language Test (Woodcock & Munoz-Sandoval, 1993) by bilingual (English/Spanish) examiners to determine the child’s baseline academic language proficiency in English and Spanish. All measures were administered in the language in which the child demonstrated greater language proficiency. If the child demonstrated equal or greater academic language proficiency in English for three consecutive years, subsequent tests were administered in English. Among the 125 children, four were tested in Spanish initially and three shifted to English later.

3.3 Measures of Academic Achievement

The WJ-III Tests of Achievement (Woodcock et al., 2001) is an individually administered measure of academic achievement for individuals ages 2 to adulthood. The WJ-III Broad Reading W Scores (Letter-Word Identification, Reading Fluency, Passage Comprehension subtests) and the WJ-III Broad Math W Scores (Calculations, Math Fluency, and Math Calculation Skills subtests) were used. The Reading and Math W scores are based on the Rasch measurement model, yielding an equal interval scale, which facilitates modeling growth in underlying latent achievement (Khoo, West, Wu, & Kwok, 2005). The reliability and construct validity of the WJ-III and its predecessors are well established (Woodcock & Johnson, 1989; Woodcock, et al., 2001).

Children tested as more proficient in Spanish than in English were administered the Batería Woodcock-Muñoz: Pruebas de aprovechamiento – Revisada (Woodcock & Munoz-Sandoval, 1996), which is the comparable Spanish version of the Woodcock-Johnson Tests of Achievement—Revised (WJ-R; Woodcock & Johnson, 1989). The Woodcock Compuscore (Woodcock & Muñoz-Sandoval, 1996) program yields scores for the Batería-R that are comparable to scores on the WJ-R. The Broad Reading and Broad Mathematics W Scores were used in this study.

3.4 Measures of Learning Related Skills

3.4.1 Teacher report of hyperactivity

Teachers completed the Strengths and Difficulties Questionnaire (SDQ; Goodman, 1997), a 25-item screening measure for psychopathology. Each item is rated on a 0–2 scale (i.e., not true, somewhat true, certainly true). The SDQ yields five scales comprised of 5 items (conduct problems, emotional symptoms, hyperactivity, peer problems, and prosocial behaviors). Scores on the SDQ have demonstrated good construct and predictive validity (Goodman, 2001; Hill & Hughes, 2007). Only the Hyperactivity and Prosocial scales were used in the current study. The Hyperactivity scale assesses children’s impulsive, inattentive, and hyperactive behaviors. For our sample, the coefficient alpha for Hyperactivity was .89.

3.4.2 Peer nomination of hyperactivity

Peers’ perceptions of classmates’ hyperactivity were obtained in individual interviews using peer nominations procedures (Realmuto et al., 1997). After reading all classamates’ names, the interviewer asked the child to nominate as few or as many classmates as they wished who fit each descriptor. The hyperactivity item reads: “Some kids do strange things and make a lot of noise. They bother people who are trying to work.” The number of nominations received was standardized within classrooms. Written parent consent was obtained for each child who participated in the sociometric interview. However, all children in a classroom were eligible to be rated or nominated. The mean rate of classmate participation in the sociometric administrations was .65 (range .40 to .95). Children as young as first grade are reliable reporters of classmates’ behavioral traits (Hughes, Zhang, & Hill, 2006).

3.4.3 Teacher-rated ego resiliency

The 7-item measure of ego resiliency is adapted from California Child Q-Set (Block & Block, 1980). On a 1–5 scale, teachers rated children’s adaptability, resourceful, stress resistance, and confidence (Kwok et al., 2007). The resulting alpha for this 7-item scale for the study sample was .85.

3.4.4 Teacher-rated prosocial behaviors

Teachers completed the 5-item prosocial scale of the Strengths and Difficulties Questionnaire (Goodman, 1997, described above). Example items include “Considerate of other people’s feelings” and “Shares readily with other children, for example, toys, treats, and pencils.” The alpha for the scale for the current sample was .93.

3.4.5 Teacher-rated conscientiousness

Teachers completed the 8-item conscientious scale of the Big Five Inventory (BFI; John & Srivastava, 1999). Scales on the BFI have demonstrated good internal consistency and both factorial and predictive validity (John & Srivastava, 1999). Teachers indicate their agreement or disagreement to each item on a 5-point Likert-type scale. Example items include “Does a thorough job”, “Is a reliable worker”, and “tends to be disorganized” (reverse scored). The alpha for the sample was .94.

3.4.6 Effortful control: Inhibitory control and task accuracy

To assess two aspects of effortful control (i.e., inhibitory control and task accuracy), trained research assistants individually administered four tasks from a behavioral battery designed to assess effortful control (Murray & Kochanska, 2002). Children’s responses on each task were observed first without, and then with instructions to voluntarily slow or inhibit their behaviors, with the former considered baseline responses. The four tasks were Walk-a-Line, Star, Telephone Poles, and Circle. In Walk-a-Line, children were asked to walk along a (12 ft long by 2.5 in wide) ribbon that was taped onto the floor. In Star, Circle, and Telephone Poles, children were asked to trace geometric figures using a pencil without going outside the lines of the figures (i.e., Star and Circle) or to draw a line connecting two dots (i.e., Telephone Poles).

Scores for inhibitory control were represented by the duration (in seconds) that it took children to complete the tasks when they were told to do them as slowly as possible, after taking into account children’s baseline duration. Scores for task accuracy were represented by the reversed score of the number of times children traced outside the lines on the Star and/or Circle (i.e., reversed score of number of errors committed on tasks) under instructions to go slow, taking into account the number of errors on the baseline (for scoring details, see Liew, Chen, & Hughes, 2010).

3.5 Demographic variables

Information about children’s gender, and ethnicity were obtained from the participating schools. SES was defined as the standardized mean (based on the 784 sample) of the highest adult occupational level (coded as 1- 9) and highest occupational code (coded 1–9) of any adult in the home, as reported by parents.

3.6 Analyses Overview

Data analyses proceeded in three steps. First, descriptive statistics were conducted. Second, unconditional growth mixture models (GMM) were fitted to explore the latent classes. Lastly, we examined if there were differences on learning related skills and selected demographic variables among the extracted latent classes. Because children are nested within classrooms and schools, we investigated the design effect, which indicates how much the standard errors are underestimated in a single level analysis (Kish, 1965). The design effects for reading at the classroom and school levels are 1.12 and 1.33 while the design effects for math at the classroom and school levels are 1.92 and 1.06, respectively. Therefore, the GMM analyses we have conducted were likely to be unbiased (Muthén & Satorra, 1995).

3.6.1 Growth Mixture Modeling

As a person-centered statistical approach, GMM can be used to address the unobserved heterogeneity within data by extracting the number of latent classes and calculating the posterior probability of class membership for each individual (Muthén & Muthén, 2000). The number of latent classes is determined by utilizing a combination of both statistical and substantive model checking routines (Muthén, 2003). As indicated by Nylund and colleagues (2007) as well as Tofighi and Enders (2008), the two most recommended model selection statistics for GMM are: (1) the information-based criteria, including: Akaike’s information criterion (AIC; Akaike, 1987), Bayesian information criterion (BIC; Schwartz, 1978), and sample size adjusted BIC (SABIC; Sclove, 1987), and (2) the nested model likelihood ratio tests, including: the Vuong-Lo-Mendell-Rubin likelihood ratio test (VLMR; Lo, Mendell, & Rubin, 2001), the adjusted Lo-Mendell-Rubin likelihood-ratio test (ALMR; Lo et al., 2001), and the bootstrap likelihood ratio test (BLRT; McLachlan & Peel, 2000).

As suggested by Petras and Masyn (2010) and Ram and Grimm (2009), we conducted growth mixture model analyses in four steps, repeated for reading and for math. First we examined individual growth trajectories for the presence of outliers. Second, we fitted a single-class latent growth curve model to determine whether growth was best described by linear or nonlinear models. Third, we identified the optimal number of latent trajectory classes that best described heterogeneity of growth trajectories. Fourth, we examined the type and extent of differences between and within the latent groups. All analyses conducted in this study employed Mplus 6.1 (Muthén & Muthén, 1998–2010). Overall 9.6% of the data were shown to have properties in line with the missing completely at random (MCAR) condition according to the attrition analyses. To address the missingness, we analyzed the model using the full information maximum likelihood (FIML) with robust standard errors method under Mplus.

4. Results

4.1 Descriptive and correlational results

Descriptive statistics of WJ-III reading and math achievement scores are presented in Table 1. The variables were screened for normality and outliers. All variables were within the normal range according to the cutoff values of 2 for skewness and 7 for kurtosis (West, Finch, & Curran, 1995). As shown in the table, both reading and math achievement scores increased from Year 1 to Year 6. Correlation analyses indicated that the one year stability for both reading and math scores was high, ranging from .77 to .94, and .76 to .88 respectively. The within-wave correlations between reading and math scores were moderate, ranging from .49 to .74.

Table 1.

Descriptive Statistics for Academic Achievement

Variable	Year	M	SD	Minimum	Maximum
Reading	1	418.79	23.99	370.00	476.00
Reading	2	440.71	21.48	402.00	488.00
Reading	3	461.05	21.95	393.00	504.00
Reading	4	475.57	19.59	409.00	510.00
Reading	5	486.77	20.40	414.00	532.00
Reading	6	496.56	23.06	414.00	568.00
Math	1	459.49	12.90	426.00	492.00
Math	2	468.97	10.99	429.00	497.00
Math	3	477.53	10.39	444.00	503.00
Math	4	488.32	10.94	443.00	510.00
Math	5	497.63	11.28	447.00	523.00
Math	6	504.74	12.49	458.00	534.00

Note. N = 125, M and SD based on full information maximum likelihood estimates; Minimum and Maximum based on actual data.

Table 2 shows the descriptive statistics and correlations of all Year 1 Learning Related Skills (LRS) variables, demographic variables and Year 1 reading and math scores. Overall, the pattern of correlations shows that African American status, lower family SES, more peer-rated hyperactivity (for math only), lower inhibitory control, lower ego resiliency, lower conscientiousness at work, and lower prosocial behaviors were associated with lower reading and math achievement. A positive association between LRS variables and academic achievement is consistent with prior research conducted with non-select community samples of children. In addition, between the demographic and LRS variables, boys were more hyperactive, less conscientious at work, and less prosocial. Compared to their peers, African American kids had lower family SES, were more hyperactive according to their peers, and were lower on inhibitory control, task accuracy, ego resiliency, conscientiousness at work, and prosocial behaviors. Additionally, children’s family SES was positively correlated with inhibitory control.

Table 2.

Descriptive Statistics and Correlation Matrix of Year 1 Academic Achievement, Learning Related Skills Variables, and Demographic Variables.

Variable	1	2	3	4	5	6	7	8	9	10	11	12
1 Read 1
2 Math 1	0.75 ***
3 Gender	0.11	0.10
4 African American	−0.26 **	−0.41 ***	−0.01
5 Family SES	0.27 **	0.25 **	−0.07	−0.21 *
6 P-Hyperactive	−0.07	−0.20 *	0.34 ***	0.18 †	0.04
7 T-Hyperactive	−0.10	−0.11	0.42 ***	0.10	0.00	0.47 ***
8 O-Inhibitory Control	0.18 *	0.27 **	0.14	−0.18 *	0.21 *	0.01	0.02
9 O-Task Accuracy	0.01	0.07	0.00	−0.22 **	0.13	0.06	0.05	0.19 *
10 T-Ego Resiliency	0.35 ***	0.31 ***	−0.06	−0.30 ***	−0.02	−0.19 †	−0.42 ***	0.20 *	0.12
11 T-Conscientiousness	0.16 †	0.19 *	−0.32 ***	−0.16 †	−0.09	−0.31 ***	−0.71 ***	0.08	0.07	0.61 ***
12 T-Prosocial	0.35 ***	0.34 ***	−0.26 **	−0.35 ***	0.00	−0.44 ***	−0.49 ***	0.04	0.13	0.63 ***	0.48 ***
M	418.79	459.83	0.61	0.35	−0.21	0.21	1.02	−1.17	−0.01	3.39	2.79	1.32
SD	23.78	12.61			0.83	1.05	0.59	15.66	1.46	0.82	1.01	0.55

Note. N = 125, based on full information maximum likelihood estimates;

^†p < .10,

^*p < .05,

^**p < .01,

^***p < .001;

P- = Peer-rated, T- = Teacher-rated, O- = Observed; African American (1 = African American, 0 = non-African American); Gender (0=female, 1=male).

Within the LRS variables, peer-rated and teacher-rated hyperactivity were moderately correlated, and both variables were negatively associated with children’s ego resiliency, conscientiousness at work, and prosocial behaviors. Inhibitory control and task accuracy were positively correlated, and inhibitory control was positively correlated with ego resiliency. Ego resiliency, conscientiousness at work, and prosocial behaviors were positively correlated with each other. The pattern of correlations among the measures of LRS assessed using multiple sources provides support for the construct validity of the measures.

4.2 Identifying the number of latent classes

Growth mixture models (GMM) were fitted to reading and math achievement scores separately to examine the developmental patterns of each outcome for the retained children. We first screened the data by plotting the observed reading and math scores and identified 4 and 2 outlier children¹ for reading and math, respectively, which were excluded for the following analyses. The sample size for reading and math GMM were 121 and 123, respectively.

We then plotted the achievement trajectories for both reading and math. As was true for the larger longitudinal sample (Wu et al., 2008a), the developmental trajectories for the retained sample were nonlinear. To approximate the nonlinear growth trajectories, we freely estimated the time-specific factor loadings of waves² 3 to 6 as this is a relatively simpler alternative method of approximating a nonlinear growth trajectory compared to the approach of estimating a quadratic term (Kwok, Luo & West, 2010; McArdle, 1988; Meredith & Tisak, 1990).

Four different class solutions have been examined and the corresponding model fit statistics are presented in Table 3. Both IC indices and LRTs suggested that the 2-class solution fit the data better than the other solutions³.

Table 3.

Model Fit Information for Class Enumeration of Reading and Math GMM Models.

	Model	Parameter#	Log likelihood	AIC	BIC	SABIC	VLMR	ALMR	BLRT	Entropy	Class size
Read	1 class	14	−2534.03	5096.06	5135.20	5090.94	NA	NA		NA	121
	2 class	17	−2510.06	5054.12	5101.65	5047.90	0.01	0.01	<.001	0.68	58, 63
	3 class	20	−2505.73	5051.45	5107.37	5044.14	0.18	0.20	0.12	0.61	46, 24, 51
	4 class	23	−2504.74	5055.48	5119.78	5047.06	0.59	0.60	1.00	0.59	24, 9, 50, 38
Math	1 class	14	−2239.44	4506.88	4546.25	4501.98	NA	NA		NA	123
	2 class	17	−2229.38	4492.76	4540.56	4486.81	0.01	0.02	<.001	0.57	38, 85
	3 class	20	−2225.74	4491.49	4547.73	4484.49	0.21	0.23	0.18	0.69	39, 2, 82
	4 class	23	−2224.80	4495.60	4560.28	4487.55	0.76	0.77	0.67	0.70	2, 5, 39, 77

Note. N_read = 121, N_math = 123.

4.3 Description of the two latent classes

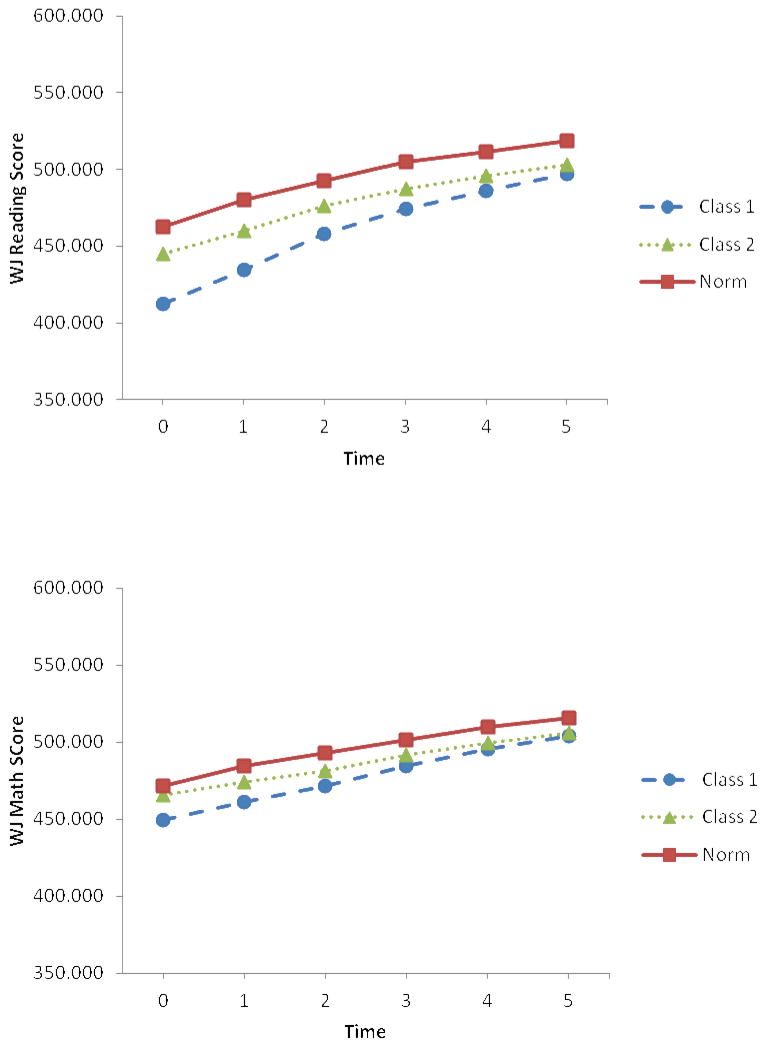
Table 4 presents the parameter estimates for two latent classes for reading and math achievement respectively. In addition, Figures 1a and 1b shows the estimated mean trajectories⁴ for Class 1, Class 2, as well as the age-equivalent average WJ score based on the standardization sample for the WJ (Woodcock et al., 2001). The age equivalent norm scores are included merely as a point of reference for interpreting the growth trajectories for the two classes of retained children. For both reading and math, Class 1 has lower intercept and faster growth (I_read = 412.22, S_read=22.24; I_math = 449.58, S_read = 11.40), whereas Class 2 has higher intercept and slower growth (I_read = 444.97, S_read=15.26; I_math = 465.54, S_read = 8.41). More children belonged to Class 1 for reading than for math.

Table 4.

Parameter Estimates for Two-Class Growth Mixture Model (GMM) for Reading and Math Growth

	Reading (N = 121)		Math (N = 123)
	Class 1	Class 2	Class 1	Class 2
Latent class membership
N	87	34	41	82
Proportion	0.72	0.28	0.33	0.67
Latent variable means
Intercept mean	412.22 ***	444.97 ***	449.58 ***	465.54 ***
Slope mean	22.24 ***	15.26 ***	11.40 ***	8.41 ***
Slope loadings
Wave 1	0.00	0.00	0.00	0.00
Wave 2	1.00	1.00	1.00	1.00
Wave 3	2.07	2.07	1.91	1.91
Wave 4	2.79	2.79	3.08	3.08
Wave 5	3.33	3.33	4.06	4.06
Wave 6	3.82	3.82	4.79	4.79
Latent variable covariances
Intercept variance	304.96 ***	84.32 **	35.68 ***	35.68 ***
Slope variance	20.72 ***	0.00	0.95	0.95
Intercept-slope covariance	−35.83 **	0.00	3.32 *	3.32 *

Note. Based on full information maximum likelihood estimates;

^*p < .05,

^**p < .01,

^***p < .001, the WJ-III Broad Reading W Scores and the WJ-III Broad Math W Scores were used.

Figure 1.

Figure 1a. Estimated mean trajectories of latent classes for reading compared with the age equivalent average WJ scores from national norm.

Figure 1b. Estimated mean trajectories of latent classes for math compared with the age equivalent average WJ scores from national norm.

The estimated slope loadings for reading from Years 3 to 6 were 2.07, 2.79, 3.33, and 3.82 respectively. Specifically, the estimated time 4 (2.79), time 5 (3.33) and time 6 (3.82) loadings were all smaller than the hypothesized time loadings (i.e., 3, 4, and 5 respectively) for a linear growth model, meaning that the real change or gain in the reading achievement from time 3 became smaller than expected (or hypothesized) which resulted in a nonlinear (decelerated) growth trend as presented in Figure 1a.

Similarly, the estimated slope loadings for math from Years 3 to 6 also revealed the nonlinear growth trajectories. Specifically, there is a noticeable reduction in the magnitude of the time-specific loadings at Year 6 (i.e., 4.79), indicating a deceleration of the change in math scores between Years 5 and 6 (see Figure 1b). In other words, the real change or gain in math scores is smaller than the expected gain in math score between Years 5 and 6.

The variances of intercepts for both latent classes for both reading and math were significantly different from zero. Only the slope variance for Class 1 for reading is significantly different from zero (S_var = 20.72, Z = 4.956, p < .001). The Intercept-Slope covariance for Class 1 for reading is negative and significantly different from zero (I-S_cov = −35.83, Z = −2.781, p = .005), indicating that for Class 1, higher beginning reading scores were associated with lower growth. The Intercept-Slope covariances for Class 1 and Class 2 for math are the same and are positive and significantly different from zero, (I-S_cov = 3.32, Z = 2.018, p = .04), indicating that higher beginning math scores were associated with faster growth within each latent class.

The association of membership for reading and math was significant (χ²(1) = 6.31, p = .012). The estimated odds of being in math Class 1 for children belonging to reading Class 1 is 3.611 times the estimated odds for children belonging to reading Class 2. In other words, the estimated odds of being in math class 1 were 261% higher for the reading class 1 children.

4.4 Class Differences on LRS

The class membership of the children for reading and math scores were saved and 20 logistic regression analyses were conducted to see if the LRS variables and demographic variables predict the membership. In order to reduce the probability of Type II error due to small sample size, one-tailed tests were used to test our a priori directional hypotheses on LRS variables. Following Thompson’s (2006) recommendation, we also report the effect size statistic (i.e., Cohen’s d converted from odds ratio based on Chinn’s (2000) method) for each significant test result to show the magnitude of difference between the two latent classes. We also adopted the Benjamini-Hocbberg (BH) correction (Benjamini & Hochberg, 1995) as recommended by the WWC (2008) to control for the potential inflated type I error rate mainly due to the multiple comparisons. Based on the WWC’s (2008) recommendation, we report: (1) comparisons that are statistically significant after the BH correction, and (2) effects that are greater than .25 but not statistically significant as “substantively important” (p. 23). The test results indicate that six out of eight significant effects remain significant after applying BH correction; furthermore, all effect sizes are larger than 0.25 except for African American status, indicating substantive importance of these effects.

In Table 5, we reported the p values from the logistic regression analyses and the Cohen’s d when a significant difference was found, as well as the means and standard deviations for the two latent classes for each academic achievement. The test results for LRS were all in the expected direction of the effects (i.e., Class 1/Lower Start Faster Growth, relative to Class 2/Higher Start Slower Growth, was expected to be composed of children with lower LRS). As shown in Table 5, for reading, children with lower ego-resiliency (B = 0.55, Z = 1.91, p_1-tail = .028, Odds Ratio = 1.74) and conscientiousness (B = 0.93, Z = 2.08, p_1-tail = .019, Odds Ratio = 2.52) had higher odds of belonging to Class 1 than Class 2. For math, children with more peer-reported hyperactive behaviors (B = −0.44, Z = −1.93, p_1-tail = .027, Odds Ratio = 0.64, Cohen’s d = 0.36), lower inhibitory control (B = 0.04, Z = 1.88, p_1-tail = .030, Odds Ratio = 1.04, Cohen’s d = 0.57), lower teacher reported ego resiliency (B = 0.50, Z = 1.98, p_1-tail = .024, Odds Ratio = 1.64, Cohen’s d = 0.90), and lower teacher-reported prosocial behaviors (B = 0.60, Z = 1.66, p_1-tail = .049, Odds Ratio = 1.83, Cohen’s d = 1.01) had higher odds of belonging to Class 1 than Class 2. The resulting effect size ranged from medium (0.36) to large (1.39), indicating practical significance of class differences on LRS.

Table 5.

Descriptive Statistics of LRS and Demographic Variables for Two Latent Classes and Logistic Regression Results

		Reading						Math
Variable		Class 1 (87)		Class 2 (34)		Logistic		Class 1 (41)		Class 2 (82)		Logistic
		M	SD	M	SD	p	E.S.	M	SD	M	SD	p	E.S.
Demographic	Gender	0.55		0.71		.12		0.59		0.62		.70
	African American	0.34		0.32		.82		0.59		0.23		<.001†	0.12
	Family SES	−0.24	0.81	−0.04	0.89	.35		−0.46	0.76	−0.09	0.84	.049†	0.95
Learning Related Skills	P-Hyperactive	0.23	1.10	0.20	0.92	.45		0.61	1.28	0.07	0.90	.027	0.36
	T-Hyperactive	1.06	0.59	0.88	0.58	.07		1.12	0.54	0.96	0.61	.07
	O-Inhibitory Control	−1.70	16.81	1.18	12.77	.22		−5.34	13.68	1.03	16.19	.030	0.57
	O-Task Accuracy	−0.01	1.55	0.07	1.21	.43		−0.30	1.68	0.15	1.32	.09
	T-Ego Resiliency	3.31	0.82	3.66	0.72	.028†	0.96	3.16	0.74	3.50	0.83	.024†	0.90
	T-Conscientiousness	2.75	1.03	2.95	0.94	.21		2.63	0.93	2.88	1.04	.13
	T-Prosocial	1.27	0.57	1.53	0.45	.019†	1.39	1.20	0.58	1.40	0.52	.049†	1.01

Note. Based on full information maximum likelihood estimates; p values are 2-tailed for demographic variables, and 1-tailed for LRS variables; numbers in bold when there is a significant effect (i.e., p < .05),

^† indicates a significant effect after the Benjamini-Hocbberg (BH) correction. P- = Peer-rated, T- = Teacher-rated, O- = Student-self-reported; African American (1 = African American, 0 = non-African American); Gender (0 = female, 1 = male); Class 1: Lower Start Faster Growth, Class 2: Higher Start Slower Growth; Logistic = Logistic Regression; E.S. = Effect Size; numbers in brackets are the number of children belonging to that class.

The two latent classes did not differ significantly on demographic variables, except for children with lower family SES (B = 0.55, Z = 1.97, p = .049, Odds Ratio = 1.73, Cohen’s d = 0.95) and African American status (B = −1.54, Z = −3.76, p < .001, Odds Ratio = 0.21, Cohen’s d = 0.12) had higher odds of belonging to Math Class 1 than Math Class 2.

5. Discussion

Latent class trajectory analyses supported the existence of two distinct trajectory groups for both reading and math. For each achievement domain, a low intercept/higher growth group (Class 1) and a high intercept/slower growth group (Class 2) were identified. The overlap in class membership across achievement domains was statistically significant, with the expected odds of being in math Class 1 for reading Class 1 children 3.611 times higher than for reading class 2 children. The finding of similar growth classes for reading and for math and the overlap in class membership across reading and math suggest that among retained children, some children appear to benefit more, in terms of higher reading and math growth, than others.

5.1 LRS and Class Membership

As expected, the faster growth groups for reading and for math scored lower on several measures of LRS. The direction of effect was in the expected direction for all 7 measures of LRS, for both reading and math. Statistically significant effects were found for only 2 of the 7 measures for reading (i.e., teacher-reported resiliency and prosocial behavior), compared to 4 of 7 measures for math (i.e., the same two measures as for reading plus peer-rated hyperactive and observed inhibitory control). The Cohen’s d for these effects falls in the moderate (.36) to large (1.39) range.

All children retained in first grade are expected to improve in LRS and academic competencies over the course of their repeat year. Thus they are expected to improve their standing on these competencies, relative to their new, younger, classmates during their repeat year. In a study on the effects of retention in first grade on performance on measures of social and academic competencies during the post-retention year that was conducted with this same longitudinal sample (Wu, West & Hughes, 2010), repeaters, but not low-achieving promoted peers, made substantial gains relative to their (younger) classmates in their repeat year of first grade on teacher-report and peer-report measures of social and academic competence. For example, whereas retained and subsequently promoted children were equally low in peer-rated academic competence during their first year of first grade (with scores of retained and promoted children surpassing 40.1 and 38.6 percent of their classmates in year 1, respectively), during their second year of first grade, retained children’ peer-rated academic competence scores surpassed 61.4 percent of their classmates, whereas promoted peers’ scores surpassed only 42.5 percent of their classmates). Teacher-rated classroom achievement and engagement showed similar benefits of retention, with retained children improving by more than 1 standard deviation, whereas promoted children’ scores stayed virtually the same.

Although short-term academic and social benefits of grade retention diminish over time for the “average” retained child (Wu et al., 2008a; Wu et al., 2010; Moser et al., 2012), the current study suggests the existence of a class of retained children for whom the short-term benefits of retention may be more durable. Specifically, those children with the poorest LRS and academic achievement in their first time in first grade may have the most to gain by repeating first grade, both academically and socially. The opportunity for children most poorly prepared for the academic and social challenges of first grade to repeat the grade puts these children on a more equal footing with their (younger) classmates, academically and socially. Their quite low performance on measures of LRS in Year 1 may have hampered their ability to benefit from instruction; however, with a year’s growth in LRS they were better prepared to attain the foundational skills needed for success in the future, as reflected in their more rapid rate of growth over the next 5 years.

5.2 Reading and Math Differences in LRS

The finding of more consistent effects of LRS on math class membership than reading class membership may be due to differences in reading and math instruction in the early grades. Much more time is spent in reading than in math in the primary grades (NICHD EERC 2002; Pianta et al., 2008). Furthermore, teacher emotional quality and support to children is a stronger predictor of reading growth than of math growth in the elementary grades (Pianta et al., 2008). Some researchers have reported that reading instruction involves more teacher-student interaction and small group instruction than math instruction (Chorzempa & Graham, 2006; Mason & Good, 1993). If this is true, self-regulated learning skills may be more important to math than to reading achievement in the early grades.

5.3 Demographic Differences on LRS

In this sample of retained children, being male was associated with poorer LRS but not with lower achievement, whereas low SES was associated with lower achievement, but generally not with lower LRS. On the other hand, African American status was associated with both poor LRS and low achievement at time 1. These group differences at baseline are reflected in statistically significant differences in class membership for math, with African American status and low SES associated with membership in the low intercept/high growth class for math.

5.4 Study Limitations

Although our assessment of LRS included more sources of assessment information (teacher, peers, observed) than most other researchers, our assessment was still limited in scope. It is possible that a more complete assessment of LRS including, for example, observations of children’ approaches to learning in the classroom, would have resulted in stronger prediction of class membership. Additionally, because our assessment of LRS occurred only at baseline, we were not able to determine if growth in LRS variables predicted class membership.

We only examined child characteristics as predictors of growth trajectories. It is important to note that retention effects likely differ based on how this policy is implemented in schools. For example, effects may differ in schools that implement progress monitoring and early intervention to children who struggle than in schools with fewer supports. Most retained children are exposed to the same material and instructional resources as used in the previous year (Peterson & Hughes, 2011; Stone & Engel, 2007). However, retained children who are provided supplemental, individualized resources and supports during the repeat year increase more in achievement than do children not provided such supports (Karweit, 1999; Stone & Engel, 2007). Such intensive interventions may begin to prepare retained children to meet the academic challenges beyond the repeat year, regardless of their LRS, when they encounter novel material.

The study sample was small, with as few as 34 children in some trajectory classes. Thus the study had insufficient power to detect small effects even using one-tail significance tests, introducing the possibility of Type II errors. Because the sample was drawn from a larger sample of children who scored below their school district’s median on a measure of literacy at the end of kindergarten or at the beginning of first grade, children who were retained for reasons other than low literacy performance (e.g., boys being retained for purposes of greater athletic prowess in later grades), were not included, and results cannot generalize to these children. Despite these limitations, the study offers the first examination of heterogeneity in growth trajectories of retained children and the characteristics that are associated with differential growth patterns, among retained children.

5.5 Implications

5.5.1 Selecting children into retention

Because class membership and Year 1 reading and math are confounded, one is not able to identify a unique effect of LRS on differential growth in the two classes of retained children. That is, the differential growth rate observed between the two classes could be a result solely of differences in their baseline reading and math skills or to their LRS. Given prior research demonstrating that LRS predict reading and math in the early grades, it is not surprising that among a sample of children who were retained in first grade, those children with the poorest LRS also had the lowest reading and math scores. These results suggest that grade retention is likely to be more beneficial (or less harmful) to children with the lowest academic achievement and LRS.

Because the current study did not include a sample of children promoted to first grade who were matched to the retained children on probability of being selected for retention, one cannot conclude from these findings that the children in the low intercept/faster growth group benefitted from retention, relative to promotion. Questions of the effect of retention have been addressed in previously published studies with the larger sample of children retained or promoted after their first year in first grade. These studies used propensity matching procedures to control for pre-retention differences between retained and promoted children and same-grade comparisons and found that retention had a short-term positive impact on children’s achievement that dissipated by grade 5 (Wu et al., 2008a; Moser et al., 2012). Those studies assumed a single trajectory characterized the growth of retained children. The current findings show that within the retained children a subgroup characterized by low baseline LRS and low achievement had faster growth subsequent to retention, relative to a somewhat larger subgroup of children. Thus, the typically found positive association with LRS and growth in achievement does not hold for children retained in first grade. The inclusion in Figures 1a and 1b of the average reading and math scores for the standardization sample for the Woodcock Johnson III at the same average age as participants in the current study shows that the low intercept/faster growth class were more successful than the high intercept/slower growth group at narrowing the gap in achievement, relative to the normative sample, by Year 6.

5.5.2 Early intervention

Race differences in baseline LRS variables and achievement found among the current sample of retained children and in studies of representative samples of kindergarten children have implications for early intervention. The effects of poverty on the development of emerging self-regulation, effects that are both mediated and moderated by disrupted parent-child interactions and low stimulation, are well established (Blair, 2010). Also amply documented are the beneficial effects of early parenting and compensatory education programs on children’s cognitive development (Bogard & Takanishi, 2005; Masse & Barnett, 2002; Reynolds, Ou, & Topitzes, 2004). For poor African American children, access to such programs would be expected to buffer children from the negative effects of poorly resourced communities on both cognitive and self-regulatory skills, thereby decreasing race-based achievement disparities that are present at school entrance (Matthews et al., 2010).

Interventions that support elementary school teachers in creating a positive social-emotional classroom context may also improve children’s LRS and buffer poorly regulated children from low achievement. For example, close and supportive teacher-student relationships buffer children with poor inhibitory control from low gains in achievement from grade 1 to grade 2 (Liew et al., 2010). Also, the positive effect of a supportive teacher-student relationship on gains in achievement are mediated by the effect of the teacher-student relationship on gains in children’s engagement in classroom learning activities and positive academic self-views (Hughes et al., 2008; Hughes & Chen, 2011). Recent studies of teacher professional development interventions and classroom curricula designed to improve teacher-student relationships and the social-emotional climate of the classroom have found positive effects on children’ social and behavioral skills associated with achievement (Capella, Hamre, Kim, Henry, Frazier, Atkins, & Schoenwald, 2012; Domitrovich, Cortes, & Greenberg, 2007; Freiberg, Huzinec, & Templeton, 2009). In a randomized control design, Raver and colleagues (2009, 2011) evaluated effects of a teacher-directed training in classroom management and emotional regulation strategies in Head Start classrooms. Intervention effects were found for classroom management and social-emotional climate as well as for children’s executive functioning skills (i.e., attention and inhibitory control) and academic skills. Importantly, intervention effects on children’s executive functioning skills largely accounted for intervention effects on achievement.

6. Conclusion

Whereas prior studies of the effect of grade retention on children’ growth in achievement have assumed that children retained in grade are drawn from a single population with a common set of growth parameters, results of the current study challenge that assumption. Among children retained in first grade, two growth trajectory classes across six years were identified for both reading and math. The trajectory class with faster growth across the six years of elementary school had poorer academic skills and learning related skills during their first year in first grade. Grade retention may be a more appropriate intervention for children with the poorest academic and learning related skills than for children whose deficits in first grade are less severe.