Modeling Time-Dependent Association in Longitudinal Data: A Lag as Moderator Approach

Abstract

We describe a straightforward, yet novel, approach to examine time-dependent association between variables. The approach relies on a measurement-lag research design in conjunction with statistical interaction models. We base arguments in favor of this approach on the potential for better understanding the associations between variables by describing how the association changes with time. We introduce a number of different functional forms for describing these lag-moderated associations, each with a different substantive meaning. Finally, we use empirical data to demonstrate methods for exploring functional forms and model fitting based on this approach.

Whenever variables are measured at different times, it is possible to examine how individual differences on a variable measured at one occasion are related to individual differences on another variable (or perhaps the same variable) measured at a later occasion. Such examinations are at the heart of longitudinal studies utilizing panel designs (Little, Preacher, Selig & Card, 2007; Little, in press). The magnitude of a relationship between variables measured at different occasions will often depend upon the amount of time that elapses between measurement occasions (i.e., the lag between occasions). Our goal is to promote an approach to analyzing longitudinal data that focuses on change in the degree of association between two variables as a function of the time between measurement occasions. In this approach, a time-dependent association is modeled using a regression model with a statistical interaction term describing how association changes as a function of the lag between occasions.

We refer to such functional relationships as time-dependent associations; to illustrate, consider the following multiple regression equation:

$${\widehat{Y}}_i=b_0+b_1{X}_i+b_2{\mathit{Lag}}_i+b_3{\mathit{Lag}}_i\times X_i.$$ (1)

In this equation the variables X and Lag, and the product of X and Lag, are used to predict Y. Lag represents the amount of time that passes between the first and second measurement occasions. Both X and Lag are free to vary between persons. The regression coefficients can be interpreted as: b₀ is the expected value for Y when both X and Lag equal zero; b₁ is the expected change in Y for a one unit change in X when Lag = 0; b₂ is the expected change in Y for a one unit change in Lag when X = 0; and b₃ is the expected change in the linear relationship between X and Y for a one unit change of Lag. If there is theory supporting a particular lag as being important, the Lag variable can be centered so that the b₁ coefficient can be interpreted as expected change in Y for a one unit change in X at that lag.

This regression model (Equation 1) and the other models we present to illustrate the lag as moderator (LAM) approach fall under the broad heading of longitudinal regression models. For simplicity, we focus on two variables measured at two occasions. Our goal is to illustrate a novel approach to modeling time-dependent associations. The research design necessary for these models assumes the amount of time passing between occasions of measurement varies between persons. We will refer to this as a variable-lag design and contrast it with the fixed-lag design, in which the amount of time that elapses between occasions of measurement is the same for all participants. The LAM approach carries the same assumptions as longitudinal panel models, which focus on the analysis of individual differences. Among the assumptions required for these models are that the lag moderation of any associations is constant for all persons.

We believe the LAM approach is a useful tool for describing how the strength of an association changes as a function of lag. In this regard, the LAM approach is mute about the causal influence of one variable on another and how that causal influence may change over time. The assumptions needed for causal inference and the possibility of using the LAM approach in this context will be addressed briefly in the discussion.

Previous Relevant Work

The idea of studying time-dependent association, or lag moderated associations between two or more variables, rests on the assumption that an association changes as a function of the time between measurements. Such lag dependent associations have long been of interest to methodologists. Early descriptions of panel models (both path and structural models) address the importance of lag choice (Heise, 1970; Shingles, 1985; Wright, 1960). Pelz and Lew (1970) report a simulation showing that the estimated effect of one variable on another fluctuates with the choice of time lag. In one example, they show that not only will the magnitude of an effect vary with choice of time lag, but the estimated direction of influence can also vary such that an effect that is simulated to be positive will be estimated as a negative effect for some time lags. Gollob and Reichardt (1987, 1991; Reichardt & Gollob, 1986) examine this issue as it relates to causal models and mediation models. Gollob and Reichardt emphasize the importance of choosing a particular lag and how this choice can affect one’s results. Cohen (1991) highlights this issue by noting that poorly choosing a lag for an important covariate in a study could serve to bias estimates of other focal parameters in a model. Collins and Graham (2002) provide a description of the effects of the choice of time lag in the context of a study on alcohol and drug use. Cole and Maxwell (2003; Maxwell & Cole, 2007) offer a thorough description of the importance of lag choice in studies of mediation. More recently, the importance of choosing lags has been re-emphasized in planning longitudinal studies to detect the relation between risk factors and outcomes (Cole & Maxwell, 2009) and when either cross-sectional data, or longitudinal data collected at an incorrect lag are used to model a longitudinal mediation process (Maxwell, Cole, & Mitchell, 2011; Reichardt, 2011).

The most common response to the issue of lag dependent association has been the recommendation that investigators carefully choose lags when designing a study – lag choice should be informed by theory and prior findings. Others have moved beyond these admonitions, however, and pursued paths closer to those we will endorse (e.g., use of variable lag designs, or explicitly modeling change in effects that are due to lag). McArdle and Woodcock (1997) used a variable lag design in the context of latent growth modeling to model trajectories of change using only two data points from each participant. Econometricians sometimes address the issue of time-dependent covariation by using the Distributed Lag Model (see, e.g., Hsiao, 1986). This model uses time series data to examine change in the effect of one variable on another across different lag lengths. Finally, Wang, Zhang, and Estabrook (2010) describe an approach that uses fixed lag panel data and an assumption of stationary effects to examine changing effects over time. Our unique proposal is to use longitudinal regression models in conjunction with variable lag panel data to explicitly model how an association changes with increasing time between measurements.

LAM Perspective

Studies describing the potential for lag dependent associations usually alert researchers to the possibility that a poor choice of lag may lead to biased results. This bias is based on an assumption that some true effect exists at a particular lag and using a lag other than the one associated with the true effect will result in an incorrect estimate of the effect. Analyses based on the LAM approach could be used to better choose an optimal lag for a study using fixed lags; however, such use of the LAM approach rests on the assumptions that the model is properly specified both in terms of the variables included and the chosen functional form.

When there is no support for the assumptions required for causal inference, we believe there remains much to be learned from adopting the LAM approach in a descriptive fashion. For example, if the goal is to understand how and when variables are related, the idea of bias due to choosing the wrong lag is not as useful. Instead, any estimated association may be a useful description of the association at a particular lag. Gollob and Reichardt (1987, p. 82) constructively argue that, “Because different time lags have different effects, one must study many different lags to understand causal effects fully.” Reichardt (2011, p. 850) further argues against the idea of “correct or incorrect time lags for estimating effects.” Explicitly modeling the lag-dependency of longitudinal associations is a means to better understand them. Although the LAM approach alone cannot insure proper causal inference, examining how a bivariate relation changes as a function of the lag between measurements may offer new insight into how one variable covaries with another—an insight that could not be gained using a single fixed lag.

Models Utilizing the LAM Approach

We introduced a multiple regression model (Equation 1) as a first illustration of the LAM approach. Such a model, of course, will not be useful for many longitudinal studies in which multiple predictors and criteria are measured, but it serves here as an introduction. In general, the LAM approach can be adapted for use in any statistical model that can accommodate a moderator variable. A key difference between the proposed model and many other models for the analysis of panel data is that lags are free to vary between persons and not fixed to a value that is assumed to be the same for each individual.

When treating lag as a variable, the possible values for lag can range from very small values that indicate only a short amount of time passed after the initial assessment, to a value that is equal to the total duration of the study. By necessity the researcher will choose lower and upper bounds for the lag variable, but in principle all values within those bounds can be used. For practical purposes and due to the potential difficulty of collecting data from individuals at any possible lag between the beginning and end of a study, it may be necessary to use a limited set of such lag values that well represents the range of possible lags, but limits data collection to a reasonable number of occasions. In many instances, randomly assigning lags to participants will be advantageous. Here, the bounds for the longest and shortest possible lags are controlled and the probability of receiving any particular lag is the same across all participants. This strategy would minimize a correlation between lag and the focal predictor or potential confounding lag length with other background characteristics.

Functional Forms for Lag Moderation

Thus far we have focused on linear change in the X→Y relationship; however, many associations may change in a nonlinear fashion. For example, Wright (1960, p. 423) hypothesized that the effect of one variable on another is not static and such an effect “…in most cases rises gradually to a peak and then gradually falls off…” Analysis of changing effects from specific types of models for panel data by Cole and Maxwell (2003) and Pelz and Lew (1970) also suggest that nonlinear forms may be expected when modeling change in effects due to lag. Many authors have used graphics to illustrate hypothetical patterns of change in effects over time, which are often nonlinear in nature (e.g., Kelly & McGrath, 1988; Mitchell & James, 2001). Despite the fact that these nonlinear forms were based on conjecture or the analysis of hypothetical models, it is clear that nonlinear forms are expected. Of course many nonlinear forms can be well approximated by straight lines when the span of lags is small.

Given that nonlinear moderation is possible, it would be useful to find models capable of describing such moderation. Our goal in the following section is to begin an examination of different statistical models that could be used to represent such patterns of changing associations. Nonlinear change can be modeled using polynomial regression models such as:

$${\widehat{Y}}_i=b_0+b_1{X}_i+b_2{\mathit{Lag}}_i+b_3{\mathit{Lag}}_i^2+b_4{\mathit{Lag}}_i\times X_i+b_5{\mathit{Lag}}_i^2\times X_i.$$ (2)

The moderating effect of Lag in this model may be best understood by rearranging the equation to highlight the simple effect of X on Y. Equation 3 is arranged to show two compound coefficients representing the simple intercept and simple slope for the X→Y relationship.

$${\widehat{Y}}_i=\left[b_0+b_2{\mathit{Lag}}_i+b_3{\mathit{Lag}}_i^2\right]+\left[b_1+b_4{\mathit{Lag}}_i+b_5{\mathit{Lag}}_i^2\right]X_i.$$ (3)

The three simple coefficients composing the compound simple slope can be interpreted as: b₁ is the expected relation between X and Y when Lag is zero; b₄ describes the expected linear change in the effect of X on Y for a one-unit increase in Lag where Lag = 0; and b₅ describes the expected quadratic change in the effect of X on Y for a one-unit increase in Lag. Additional polynomial regression models could be used to describe even more complex functional forms for moderation by lag. In practice, however, the number of estimated parameters and the interpretability of those parameters become problematic. Cudeck and du Toit (2002) discuss the potential difficulty of interpreting parameters from the quadratic model and suggest an alternative parameterization that has more interpretable parameters:

$${\widehat{Y}}_i={\alpha }_Y-({\alpha }_Y-{\alpha }_0){\left(\frac{X_i}{{\alpha }_X}-1\right)}^2.$$ (4)

In this model, α₀ represents the value of Y_i when X_i is 0, α_X represents the value of X_i at which Y_i reaches its maximum (or minimum, depending upon the particular quadratic form), and α_Y represents the maximum (minimum) value of Y_i. Through substitution into a simple regression model, the moderating effect of lag can be expressed using this reparameterized model. For example, if we describe the simple relationship between X and Y as:

$${\widehat{Y}}_i=b_0+b_1{X}_i,$$ (5)

the dependence of the b₁ coefficient on values of Lag_i can be expressed with the following adaptation of Cudeck and du Toit’s model:

$$b_1={\alpha }_{Y•X}-({\alpha }_{Y•X}-{\alpha }_0){\left(\frac{{\mathit{Lag}}_i}{{\alpha }_{\mathit{Lag}}}-1\right)}^2.$$ (6)

Now α₀ is the expected effect of X_i on Y_i when Lag_i is 0, α_Lag is the value of Lag_i at which the maximum (or minimum) effect of X_i on Y_i is obtained, and α_Y•X is the maximum (minimum) effect of X_i on Y_i. The changes in subscripts are meant to highlight the fact that the quadratic model is now used to describe the effect of Lag on the complex simple slope rather the effect of X on Y. By substituting Equation 6 into Equation 5 we have:

$${\widehat{Y}}_i=b_0+\left[{\alpha }_{Y•X}-({\alpha }_{Y•X}-{\alpha }_0){\left(\frac{{\mathit{Lag}}_i}{{\alpha }_{\mathit{Lag}}}-1\right)}^2\right]X_i.$$ (7)

As pointed out by Cudeck and du Toit (2002), this form of the quadratic model is nonlinear in its parameters and must be estimated using nonlinear regression methods, which are readily available in most standard software suites (e.g., SPSS, SAS, and R).

A possible limitation of a quadratic model is that it implies that an effect will either increase to a maximum and then decline, or decrease to a minimum then increase. For some applications this functional form may not be reasonable. For example, if we examine the effect of years of education on future earnings, it could make sense to have the effect increase with the passage of time, meaning that the earnings gap between those with more education and those with less education widens with time. It would be odd if, with the passage of sufficient time, this gap reached a maximum and then began to close. In such situations, an exponential function, that increases or decreases to an asymptote, may be profitably used. The previous method of substitution to create a model where lag moderates the focal relationship can also be used for the exponential model. This model could be based on an exponential function like the following described by Sit and Poulin-Costello (1994):

$$Y={ae}^{bX}.$$ (8)

In this expression, a is the effect of X on Y when X = 0, and b describes the shape of the exponential relationship between X and Y. When b > 0, the curve approaches the horizontal asymptote as X decreases, and when b < 0, the curve approaches the horizontal asymptote as X increases. The horizontal asymptote occurs when Y = 0. The functional form in Equation 8 may be introduced into a nonlinear regression model by defining b₁, the effect of X on Y from a simple regression model, to be a function of lag, so that:

$$b_1={ae}^{{\mathit{bLag}}_i}.$$ (9)

By substitution, the regression model for Y_i would be:

$$\widehat{Y}=b_0+({ae}^{{\mathit{bLag}}_i})X.$$ (10)

Although the parameters of the LAM exponential model are not as readily interpretable as those from Cudeck and du Toit’s (2002) quadratic model, this model may be preferred if it describes the moderating effect of lag better than the quadratic model.

Other functional forms

The four LAM regression models in equations 1, 2, 7, and 10 allow the effect of X on Y to change in a variety of ways. These models are not meant to constitute an exhaustive list. The context of lag-moderated associations and future investigations of the performance of different models for lag moderation should determine the most appropriate model. For example, the effect of an intervention on an outcome may follow an S-shaped or sigmoidal functional form, such that the intervention effect is minimal at very short lags and increases to a maximum value as lag increases. Such a form could be captured by expressing the b₁ coefficient from Equation 5 as function of lag using either a logistic or Gompertz function. We can assume that the effect of some interventions may fade even within the window of observation of a particular study; therefore, functional forms that increase to a maximum and then decrease could be useful. Ratkowsky (1990) and Sit and Poulin-Costello (1994) describe several such models. The goals of selecting a functional form would be first to find one or more models that best describe the theoretically expected, or empirically explored, change in a lag association and then to choose a model whose parameters are most meaningful.

Choosing a functional form

When possible, theory and previous findings should guide the choice of a functional form. The idea of explicitly modeling change in an association will be new to many areas of research. In such cases, an exploratory approach to describing the change in association may be desirable. One potentially informative approach is to create conditional scatter plots, also called conditioning plots or co-plots (Cleveland & Devlin, 1988), showing the relation between X and Y at different ranges of the moderator. These co-plots can give a clear picture of whether lag moderates a focal effect. The number of plots to inspect, however, is based on an arbitrary division of the entire range of the continuous moderator into segments. As a result, the pattern of change can look different depending upon the number of co-plots created.

LAM Approach Analyses

Next we present applications of the LAM approach using empirical data. We note that these examples use observational data and lags were not randomly assigned. For this reason, we are very circumspect in our interpretations of the results and emphasize that results cannot be interpreted as causal effects. Our goal is to use these data examples as a means to exemplify the LAM approach. Although these are exploratory analyses, the results have the potential to further our understanding of the associations among the variables.

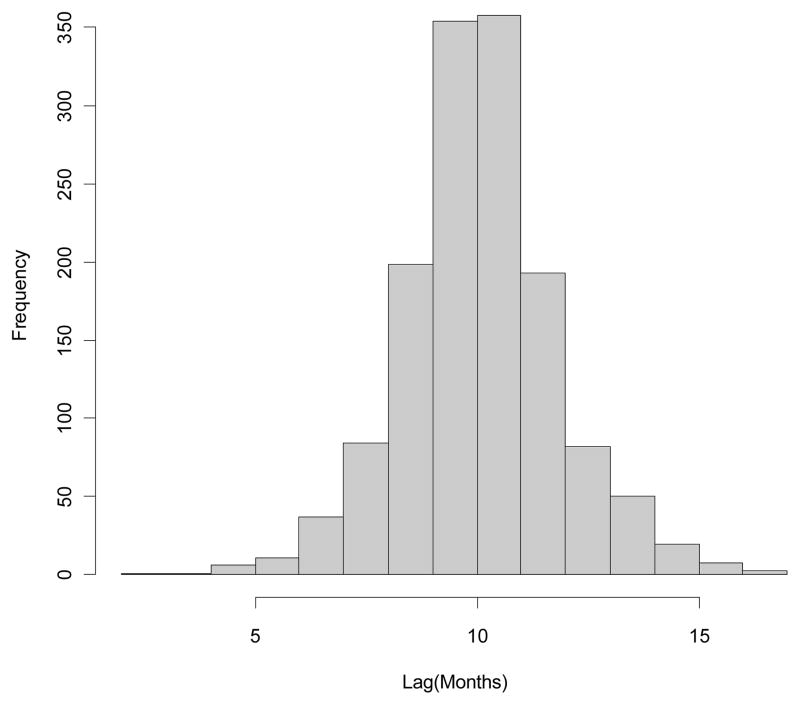
We first examine the functional forms of the relationships using conditional scatter plots and then use the results and analytical expectations to choose and fit LAM regression models. For all analyses, we used data from a large, multi-site, longitudinal study in which lags were planned to be the same for each individual, but varied considerably due to practical issues related to collecting data on a fixed-lag schedule (the Early Head Start Research and Evaluation study; Department of Health and Human Services: Administration for Children and Families, 1996–2001; found at Inter-university Consortium for Political and Social Research website: http://www.icpsr.org/). The intent of this study was to examine the impact of the Early Head Start Program on young children and their families. We used two waves of data timed to coincide with the age of the focal child in each family (14 and 24 months of age). The actual age ranges of the children at the two waves of data collection were, respectively: 11 to 22 months and 20 to 32 months. Figure 1 shows a histogram of the observed lag values in months for the first data example. It is clear that there is considerable variation in lag values, however, the average lag (10.26 m) is close to the intended fixed lag (10 m). Lag values range from 5.90 to 16.98 months, but 50% of values fall between 9.21 and 11.08 months. There were 3,001 families in the study. Of these, 1,260 had complete data for the variables used in the first example and 1,440 had complete data for the variables used in the second analysis. We used listwise deletion to simplify the analyses. We used SPSS for the linear and non-linear regression analyses.

Figure 1.

Histogram of lag values in months.

Measures and Variables

Home Observation for the Measurement of the Environment (HOME)

The HOME (Caldwell & Bradley, 1984) is a semi-structured observational instrument that assesses the quality of stimulation provided to a child in his/her home. The HOME has a total score assessing the overall quality of stimulation in the home, as well as subscales designed to assess specific aspects of the home environment. For the present analyses, only the total HOME score was used.

Bayley Scales of Infant Development – Mental Development Index (MDI)

The MDI (Bayley, 1969) measures the cognitive, language, and social development of children under the age of 42 months. Standardized scores, computed based on the child’s age, are used in all of the following analyses. The Bayley was administered to children at approximately 14 and 24 months of age.

Analyses

MDI at 14 months predicting MDI at 24 months

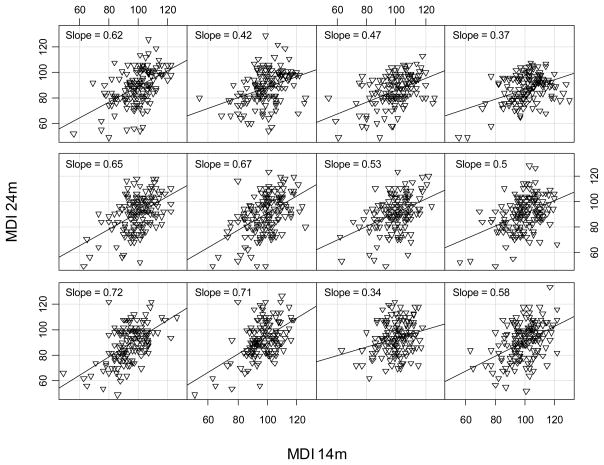
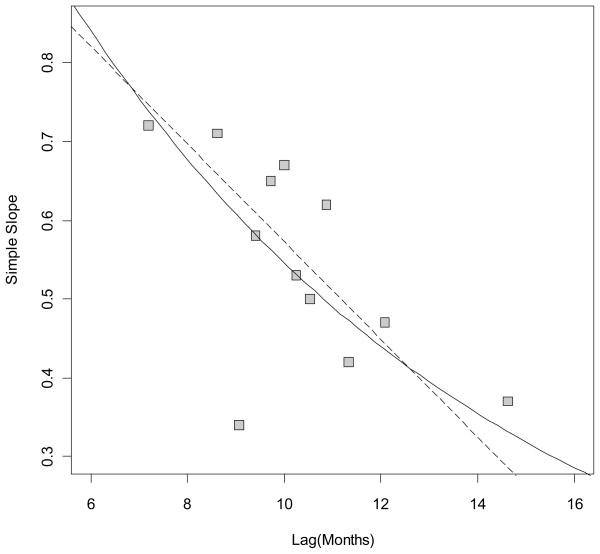
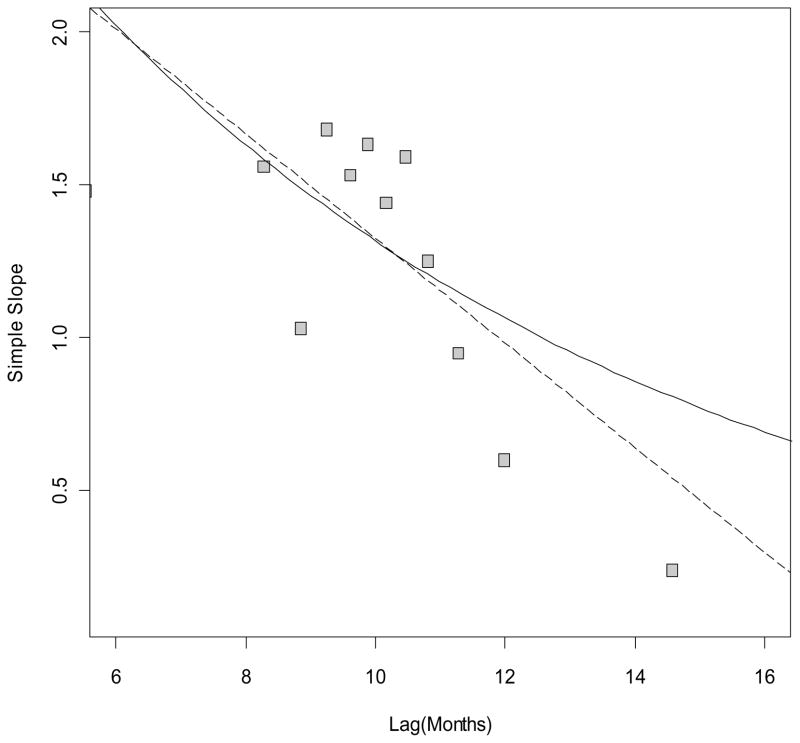
We first examined an autoregressive association between the MDI at 14 months and the MDI at 24 months. As a first step to visualizing possible lag moderation, we examined conditional scatter plots of the 24 month MDI scores plotted against the 14 month MDI scores. Plots were created in the R software package using the coplot function. When using this function, the user chooses: two variables for the scatterplots; a conditioning (moderator) variable used to define the groups represented by each plot; the number of conditional plots to generate; and the degree of overlap in group membership. We examined several sets of conditional plots. For illustration, Figure 2 shows 12 of these scatter plots. For each of the 12 plots, 14 month MDI scores are on the horizontal axis and 24 month MDI scores are on the vertical axis. The plot on the bottom left of the panel contains points for the participants with the shortest lag values. Lag values of the 12 groups increase from left to right and from top to bottom with the group having the highest lag values being in the top right panel. The membership of consecutive groups overlaps by approximately 25%. The slope of the fitted regression line is displayed in the top left corner of each plot. A general pattern can be seen such that the regression slopes begin higher and decrease for groups with longer lags. This pattern suggests moderation by lag, however, it is difficult to assess the possible functional form. As an extension, we recorded each of the 12 regression slopes at the conditional values of lag. We plotted these slopes against each corresponding group’s mean lag to create a visual representation of the relation between lag and the slope. The gray squares in Figure 3 show these slopes for the twelve groups.

Figure 2.

Conditional scatter plots for the Mental Development Index measured at 14m predicting the Mental Development Index measured at 24m for 12 groups defined by average lag. Average lags increase from left to right and from bottom to top. Average lag (months) for each plot: 7.20, 8.62, 9.07, 9.41, 9.72, 10.00, 10.25, 10.52, 10.87, 11.33, 12.08, and 14.62.

Figure 3.

Linear (dashed-line) and exponential (solid-line) regression lines for Mental Development Index measured at 14m predicting the Mental Development Index measured at 24m. Squares are the slopes from the co-plots in Figure 2.

Based on the empirical evidence and our expectation that an autoregressive association may show a nonlinear decline with increasing lag, we chose to fit the linear and exponential models to these data. The results from both models, shown in Table 2, indicated significant lag moderation. The regression lines from both models are shown in Figure 3. In terms of substantive interpretations, from Figure 3 we see that these two models result in similar predicted values.

HOME at 14 months predicting MDI at 24 months

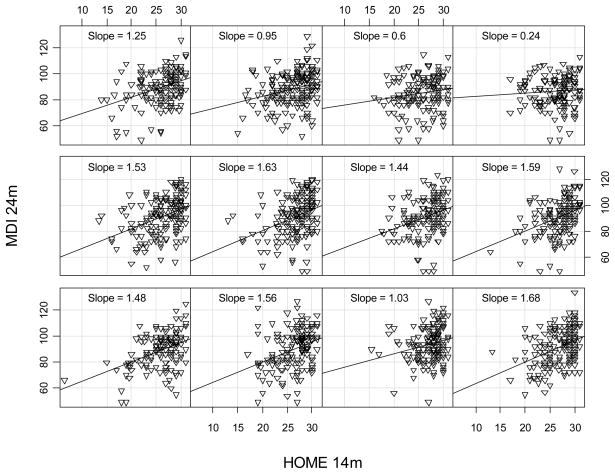
To complement the results from the previous autoregressive analysis, we next examined the cross-lagged association between the HOME at 14 months on the MDI at 24 months. As before, we first examined conditional scatter plots. Figure 4 shows 12 such scatter plots. The gray squares in Figure 5 show these 12 slopes plotted against mean lag for each group. While there is some fluctuation of the slopes with increasing lags, it is clear that there is an overall pattern of decline in the slope. Based on the empirical evidence and the previous analytical results showing that cross-lagged associations could show non-linear decline, we again fit the linear and exponential models to these data. The results from these two models are shown in the bottom half of Table 2. Both the linear and exponential models showed statistically significant lag moderation. The regression lines from these two models are shown in Figure 5. In contrast to the previous results, the substantive implications of the two models are different in that the linear model implies steady decline in the slope that will eventually become negative, whereas the exponential model implies decay that will asymptote near a slope of zero.

Figure 4.

Conditional scatter plots for the Home Observation for the Measurement of the Environment measured at 14m predicting the Mental Development Index measured at 24m for 12 groups defined by average lag. Average lags increase from left to right and from bottom to top. Average lag (months) for each plot: 5.52, 8.28, 8.85, 9.25, 9.61, 9.89, 10.16, 10.46, 10.80, 11.28, 11.98, and 14.57.

Figure 5.

Linear (dashed-line) and exponential (solid-line) regression lines for the Home Observation for the Measurement of the Environment measured at 14m predicting the Mental Development Index measured at 24m. Squares are the slopes from the plots in Figure 4.

Table 2.

Results from Analyses of MDI 14 Predicting MDI 24 and HOME 14 Predicting MDI 24

Linear Model Estimates		Exponential Model Estimates
MDI 14 Predicting MDI 24:
b0	102.519	b0	89.672
b1	1.193	b1	1.607
b2	−1.253	b2	−0.108
b3	−0.062
;SSResid.	184806.031	SSResid.	189972.448
HOME 14 predicting MDI 24:
b0	96.454	b0	89.366
b1	3.036	b1	3.837
b2	−0.704	b2	−0.107
b3	−0.171
SSResid.	236641.031	SSResid.	238968.956

Note: All p < .05

Overall, the results from these two sets of analyses support lag moderation. The first analyses showed a clear pattern of decline in an autoregressive association, which is consistent with a study by Thorndike (1933), who found a similar decline in test-retest correlations for intelligence tests. Also similar to Thorndike, we found that a linear model adequately described the interaction. The second set of analyses showed systematic decline in a cross-lagged association. These results suggest a positive association between stimulation in the home and child development that diminishes over time. Although stimulation in the home was measured only once, it is likely to be stable and continuing over time. The present results are consistent with a situation in which proximal stimulation is the most important predictor and as lags increase, the association with more distal stimulation declines.

Discussion

Our goal has been to present a new perspective on modeling time-dependent covariation by employing a LAM approach. In contrast to fixed-lag approaches for modeling longitudinal data, the LAM perspective is designed to emphasize the lag-dependent nature of longitudinal associations and explicitly model change in associations as a function of lag. This approach is useful in addressing the perennial issue of the importance of lags in the analysis of panel data. This approach is also consistent with our view that there is not a single correct lag for examining a longitudinal association and the complementary view that lag choice is a fundamental issue in the generalizability of results. To further elaborate the LAM approach, we demonstrated a few functional forms using empirical data that are potentially useful for lag moderation models and suggested methods for exploring functional forms.

Limitations and Future Directions

In general, the LAM approach has great potential for exploring and better understanding longitudinal relations. Limitations include increases in model complexity and the need for larger sample sizes. Additionally, it is most useful when the functional form of the interaction is properly specified. These limitations are not so much flaws of the approach as they are coincident with the fact that the approach involves modeling statistical interactions. Another potential limitation of this approach is that results are best understood when an independent variable occurs only once, such as in a time-delimited intervention. Although the models presented can be used to model time-dependent associations of predictors that continue beyond an occasion of measurement, the interpretations of them is less straightforward.

Causal Inference

As we noted in the introduction, the LAM approach should not be used to examine how the causal influence on one variable on another changes with lag unless several assumptions are supported. In simplest form, a regression model incorporating the LAM approach would have three independent variables: a focal predictor (x), the lag variable (Lag), and the product of the focal predictor and the lag variable that predict a dependent variable (y). Here we assume the goal is to accurately estimate a causal effect of the focal predictor on the outcome. Proper inference in this situation requires that the model be properly specified both in terms of the predictors included and in terms of the functional relationships between the predictors and the criterion.

Using the LAM approach to estimate a causal effect assumes all the important predictors have been included in the model. Similar to any regression analysis, a LAM analysis can yield biased estimates of an effect if, for example, an omitted predictor (z) causes y and is correlated with x. Complications can also arise when the Lag variable serves as a proxy for an omitted predictor as this too could obscure the effect of x on y. One way to address some of these difficulties is to randomly assign lags to participants. Such random assignment should insure that the Lag variable is independent of the focal predictor and does not serve as a proxy for an important omitted predictor. However, random assignment of lags cannot insure that the focal variable, and not some other correlated variable, has a causal influence on y.

A LAM based analysis also complicates the issue of properly specifying the functional form of the relationship between the predictors and the criterion because the analyst must specify the functional form of the lag by focal variable interaction. Based on our experience, there is often little to support the a priori specification of this functional form. In addition, the ability to accurately detect a non-linear functional form may be hindered by the quality and characteristics of the data.

When causal inference is needed, the LAM approach may have some utility in examining how causal effects evolve over time, given that all the proper design elements are in place and assumptions hold outside the model. The LAM approach is by no means a special tool to enhance causal inference. In contrast, many features of the LAM approach (e.g., making every treatment effect a conditional effect and the need to make additional assumptions about a covariate) can make the difficult task of causal inference even harder.

Functional Forms

Another key issue in the use of the LAM approach is the choice of functional form for the interaction. Beyond the previous analytical descriptions of changing effects over time and a handful of empirical investigations such as that by Thorndike (1933), there is very little to suggest appropriate forms. Much work needs to be done in this area to learn about the best methods for exploring time-moderated associations.

Once a functional form is chosen, one must decide how best to assign lags in a variable-lag design. McClelland and Judd (1993) discuss how sampling affects the ability to detect a moderation effect when the functional form of the moderation is known beforehand. They suggest that an efficient way to find significant linear moderation effects is to oversample extreme values of the interacting variables. Following this guideline, the LAM approach may benefit from disproportionately assigning very long and very short lags to participants in order to enhance the ability to detect moderation by lag. However, curvilinear effects of Lag on the X→Y relationship will require a different design to maximize efficiency for detecting interactions (McClelland, 1997). Therefore, further work must be done to identify lag-sampling strategies that would maximize the probability of detecting an interaction while also maximizing the ability to accurately describe a nonlinear interaction.

Inter- vs. intra-individual effects

Finally, the regression models we’ve used are focused exclusively on interindividual variability. Change is modeled by examining covariation of individual standing on variables at different occasions. In this way, it is similar to many other applications of regression models for longitudinal data. Critics of such models argue that when researchers use models based on individual differences, the true goal is often to draw inference about within-person change. Strong arguments have been presented showing that results from interindividual models do not readily generalize to intraindividual variation (Molenaar, 2004; Molenaar & Campbell, 2009).

Regression models following the LAM approach may be particularly open to this criticism because the time-dependent effects modeled are often best understood as within-person effects. Even the thought experiments used by authors to illustrate time dependent effects in individual differences models are often based on within-person change. Gollob and Reichardt’s (1987) aspirin example, in which time-varying effects are illustrated by the example of the effect of taking an aspirin on headache pain, is a good case in point as the models in that article are based on inter-individual differences yet the illustration describes how the effect of an aspirin on headache pain will vary for an individual depending on the time elapsed since taking the medicine. There is good reason to be skeptical of using inter-individual models to draw inference about intra-individual change. Models of between-person variation cannot yield definitive answers regarding within-person processes. It is premature to suggest, however, that models of inter-individual differences cannot contribute to our understanding of change.

Summary and Conclusions

The analyses presented here provide evidence of time-dependent associations. The fact that we were able to demonstrate lag moderation using data from a study not designed to capture such effects supports the potential utility of the LAM approach. The findings are limited because the data are observational and lags were not randomly assigned or uniformly distributed. Therefore, it is unlikely that all important predictors were used in the model, and it is possible that lag may be confounded with some other important variables for which we are unable to control. Clearly, more work is needed using studies designed to utilize a variable lag approach in order to draw sound conclusions about LAM associations.

The purpose of this work was to promote an approach for addressing the important role of time lags in models for longitudinal data. The LAM approach offers a useful strategy for addressing the perennial problem of choosing lags for a longitudinal study. The LAM approach could be used for many existing data sets in which lags vary to some degree and the lag variable can be constructed (i.e., if the dates of data collection are recorded, lags can be computed). Such secondary analyses may show that previous conclusions regarding relationships were either incorrect or incomplete. These secondary analyses could potentially form the foundation for a growing body of knowledge regarding the characteristic ways in which associations change with lag.

The true appeal of the LAM approach, however, is that it provides a straightforward means of extending and enhancing our current understanding of associations in the social sciences. A LAM analysis can provide a useful description of lag dependent association that cannot be seen from a fixed-lag analysis.

Table 1.

Descriptive Statistics for Variables Used in Example 1_a and Example 2_b.

Variable	N	Min.	Mean	Max.	SD
MDI 14ma	1260	49.00	98.79	130.00	11.11
MDI 24ma	1260	49.00	89.83	134.00	13.68
Lag 14m–24ma	1260	5.90	10.26	16.98	1.61
HOME 14mb	1404	6.46	26.24	31.00	3.44
MDI 24mb	1404	49.00	89.72	134.00	13.87
Lag 14m–24mb	1404	2.95	10.08	16.98	1.74