Statistical modeling approach to quantitative analysis of inter-observer variability in breast contouring

Abstract

Purpose

To develop a new approach for inter-observer variability analysis.

Methods and Materials

Eight radiation oncologists specializing in breast cancer radiotherapy delineated a patient’s left breast from scratch and from a template that was generated using deformable image registration. Three of the radiation oncologists had previously received training in RTOG consensus contouring for breast cancer atlas. The simultaneous truth and performance level estimation algorithm was applied to the eight contours delineated from scratch to produce a group-consensus contour. Individual Jaccard scores were fitted to a beta distribution model. We also applied this analysis to two more patients which were contoured by nine breast radiation oncologists from eight institutions.

Results

The beta distribution model had a mean of 86.2%, standard deviation of 5.9%, skewness of −0.7, and excess kurtosis of 0.55, exemplifying broad inter-observer variability. The three RTOG-trained physicians had higher agreement scores than average, indicating that their contours were close to the group-consensus contour. One physician had high sensitivity but lower specificity than the others, which implies that he/she tended to contour a structure larger than others. Two other physicians had low sensitivity but similar specificity as others, which implies that they tended to contour a structure smaller than others. With this information, they could adjust their contouring practice to be more consistent with others if desired. When contouring from the template, the beta distribution model had a mean of 92.3%, standard deviation of 3.4%, skewness of −0.79, and excess kurtosis of 0.83, which indicated a much better consistency among individual contours. Similar results were obtained for the analysis of two additional patients.

Conclusions

The proposed statistical approach was able to measure inter-observer variability quantitatively and to identify individuals who tend to contour differently from the others. The information could be useful as feedback to improve contouring consistency.

Introduction

In breast cancer radiotherapy, intensity-modulated radiation therapy (IMRT) is able to deliver a more conformal radiation dose than the traditional opposed tangential field technique (1, 2). Delineation of the whole breast is an important step for the breast IMRT (3). However, several studies have shown large intra- and inter-observer variability in contouring the whole breast, even for experienced radiation oncologists (4–6). This variability was taken into account in the National Surgical Adjuvant Breast and Bowel Project (NSABP) protocol B-39/Radiation Therapy Oncology Group (RTOG) protocol 0413 randomized study. Although RTOG has established consensus contouring for breast cancer atlas (7), intra- or inter-observer variability still exists because of differences in training, clinical experience, and quality of computed tomography (CT) images on which the contours are drawn.

Quantitative approaches have been proposed to demonstrate the existence of inter-observer variability in previous studies (3–6); however, these studies have not been able to gain insight into the causes of this variability or to suggest a feasible solution to improve consistency in contouring. Moreover, previous studies measured inter-observer variability by computing the distance/difference between the individual contour and the average contour of all observers (4, 6). This measurement is prone to the impact of outliers. If one observer draws the contour significantly different from the others, whose contours are similar, the one outlier will exaggerate the inter-observer variability. Therefore, a new quantitative approach is needed to overcome this deficiency.

The goals of this study were to develop a new quantitative approach to analyze inter-observer variations and recommend a learning experience from the result of the quantitative analysis. We applied this method to two independent studies on contouring the whole breast. We generated a group-consensus contour from a set of individual contours delineated by different physicians. The agreement between individual contour and the group-consensus contour was measured and used as the score of agreement. These scores were then fitted into a mathematical model for quantitative analysis. With this model, we were able to come up with possible solutions to improve the contouring consistency. We also compared two contouring methods, contouring from scratch and contouring from a template, to explore the potential benefits of using a template to improve contouring consistency.

Methods and Materials

Patient data

This retrospective study has been approved by the institutional review board of MD Anderson Cancer Center (Approval number: RCR03-0400). A template patient who underwent consecutive treatment to the left breast was identified from our institutional database. A team consisting of radiation oncologists, a breast surgical oncologist, and a radiologist collectively defined the whole breast clinical target volume (CTVwb) on the CT image of this template patient on a Pinnacle Treatment Planning System (Philips Medical Systems, Fitchburg, WI). A test patient with left breast treatment was also identified who underwent CT simulation in the same position as the template patient. Eight radiation oncologists, including seven breast cancer radiation oncologists and one senior medical resident, delineated the CTVwb on the CT image of the test patient using the following two methods: contouring from scratch and contouring from the template, as described below in details. Three of these eight radiation oncologists had previously received training in RTOG consensus contouring for breast cancer atlas prior to this study.

Contouring from scratch was performed on the Pinnacle Treatment Planning System too. The external skin contour was first automatically generated, and then each physician used editing tools to further contour the CTVwb individually. When contouring from the template, we first performed deformable image registration between the template patient and the test patient using an accelerated “demons” algorithm (8) and then mapped the CTVwb contour from the template patient to the test patient using the deformation field that resulted from the deformable image registration (9). Each physician individually modified this autosegmented contour as necessary.

Group-consensus contours

We introduced group-consensus contours to quantify the inter-observer variability. The group-consensus contour is defined as the best agreement of a group of individual contours. The difference between each individual contour and the group-consensus contour was measured and used as the agreement score for the individual contour. Let G denote the volume enclosed by the group-consensus contour and D denote the volume enclosed by one individual contour. We computed the sensitivity and specificity as the score of agreement for the individual contour D (10). Sensitivity and specificity were defined as follows:

$$\mathit{Sensitivity}=\frac{D\cap G}{G},\mathit{Specificity}=\frac{\overline{D}\cap \overline{G}}{\overline{G}},$$ (1)

where D̄ and Ḡ denote the space outside the volumes D and G, respectively. Sensitivity was the true-positive rate when comparing the individual contour against the group-consensus contour, while specificity described the true-negative rate. The combination of sensitivity and specificity quantifies the inter-observer variability.

The group-consensus contour representing the best agreement of a group of contours can be obtained by maximizing the sensitivity and specificity between each individual contour and the group-consensus contour. The simultaneous truth and performance level estimation (STAPLE) algorithm (11) was used to achieve this goal (see Appendix eI for details). The STAPLE algorithm takes into account the spaces both inside (sensitivity) and outside (specificity) the region of interest for a maximum likelihood estimation. In order to balance the weights of sensitivity and specificity in the estimation, we selected a small region enclosing all observer contours and forced the space outside the region of interest to be roughly equivalent to the volume inside the region of interest, i.e., G≅Ḡ. With this constraint, the sensitivity and specificity were in the same scale and the estimated group-consensus contour best approximated the underlying true segmentation (9).

Statistical modeling to quantitative analysis

The agreement score composed of the sensitivity and the specificity may also be described using the union overlap, i.e., the Jaccard coefficient (12), between an individual contour and the group-consensus contour. The Jaccard coefficient is defined as:

$$\mathit{Jaccard}=\frac{D\cap G}{D\cup G}.$$ (2)

It has a value between 0 and 1, with 1 indicating perfect agreement and 0 indicating no overlap. The Jaccard coefficients for a group of contours have been shown to follow a beta distribution (13). We fitted the Jaccard coefficients to a beta distribution model with a probability density function as follows:

$$f(y\mid \alpha ,\beta )=\frac{1}{B(\alpha ,\beta )}{y}^{\alpha -1}{(1-y)}^{\beta -1},$$ (3)

where y is a variable of the Jaccard coefficient, α> 0 and β>0 are unknown parameters characterizing the model, and $B(\alpha ,\beta )={\int }_0^1{t}^{\alpha -1}{(1-t)}^{\beta -1}dt$ is the beta function used as the normalization constant. The parameters α and β were the maximum likelihood estimates from the measured Jaccard coefficients (14). This model can be graphically displayed with a curve, which intuitively illustrates the inter-observer variability (13).

The mean (M), standard deviation (SD), skewness (SK), and excess kurtosis (EK) of the beta distribution model were used to quantitatively evaluate the inter-observer variability (15):

$$\begin{array}{l}M=\frac{\alpha }{\alpha +\beta },SD=\sqrt{\frac{\alpha \beta }{{(\alpha +\beta )}^2(\alpha +\beta +1)}},SK=\frac{2(\beta -\alpha )\sqrt{\alpha +\beta +1}}{\alpha +\beta +2\sqrt{\alpha \beta }},\\ EK=\frac{6\left[{(\alpha -\beta )}^2(\alpha +\beta +1)-\alpha \beta (\alpha +\beta +2)\right]}{\alpha \beta (\alpha +\beta +2)·(\alpha +\beta +3)}.\end{array}$$ (4)

The mean value represents the average agreement of all individual contours from the group-consensus contour; the larger the mean value, the smaller the inter-observer variability. Standard deviation denotes the distribution of agreement scores; the smaller the standard deviation, the smaller the inter-observer variability. Skewness represents the symmetry of the beta distribution. Skewness less than 0 means the distribution curve spread toward the left side, with higher possibility of agreement scores less than the mean value, thus tending to a larger inter-observer variability. Kurtosis is a measure of the peakedness of the beta distribution model. The larger the kurtosis, the less distribution of the scores to the two ends, thus tending to a smaller inter-observer variability. The tools that generated the group-consensus contours and the beta distribution models for quantitative analysis were developed in-house.

Contouring from scratch versus contouring from the template

We analyzed and quantitatively compared the inter-observer variability for two contouring methods: contouring from scratch and contouring from the template. The group-consensus contours were generated first for these two methods. The Jaccard coefficients between individual contours and the group-consensus contour were computed, and then the beta distribution models were built from the Jaccard coefficients. The beta distribution models for both methods were plotted in one coordinate system for comparison and their mean, standard deviation, skewness, and excess kurtosis values were computed for quantitative comparison.

More examples

Additional analysis was performed on two breast cancer patients from an independent source with their contours delineated by nine radiation oncologists specializing in breast radiotherapy from eight institutions (5). Patient A had Stage I (T1c, N0, M0) left breast cancer and Patient B had Stage IIIA (T2, N2, M0) right breast cancer. CT images of both patients were acquired with various external metallic markers. Nine oncologists delineated the left breast volume for Patient A and the right breast volume for Patient B. They were instructed to delineate these structures using their own segmentation tools with a window/level setting of 600/40 for soft tissue. No specific guideline was provided as how to delineate the breast volume. We applied our method to quantitatively analyze the inter-observer variability in contouring these two patients. The sensitivity, specificity, and Jaccard coefficient were recorded for analysis. The beta distribution models were built for both patients to graphically demonstrate the inter-observer variability.

Results

Group-consensus contours

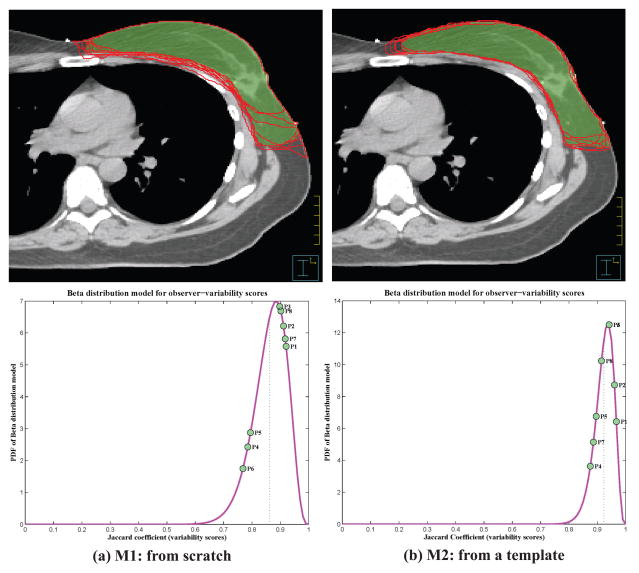
Group-consensus contours were generated for both contouring from scratch and contouring from the template. The physicians’ individual contours and the group-consensus contour were plotted overlaid on the CT image, as shown in Figure 1. The inter-observer variability can be visualized from this figure, mostly existing in the medial and lateral borders of the breast. Figure 1 suggests that contouring from the template may have had less inter-observer variability than contouring from scratch. When generating the group-consensus contour, the sensitivity and specificity between individual contour and the group-consensus contour were also measured at the same time for each observer, as listed in Table 1. These values are the maximum likelihood estimates from the STAPLE algorithm and best evaluate the inter-observer variability among the group of eight observers who drew the contours.

Figure 1.

Top row: The individual contours by eight physicians (red solid lines) and the group-consensus contour (green colorwash) for the left whole breast plotted overlaid on the CT image. Bottom row: Visualization of beta distribution models (as probability density function [PDF]) with individual agreement score on the curve. (For interpretation of the references to color, the reader is referred to the web version of this article.)

Table 1.

The agreement scores between individual contours and group-consensus contours for eight observers in both contouring from scratch and contouring from the template. The boldface numbers indicate the observers have lower sensitivity or specificity than others.

Observer	Contouring from scratch			Contouring from template
	Sensitivity	Specificity	Jaccard	Sensitivity	Specificity	Jaccard
1	96.6%	95.8%	92.1%	97.2%	99.2%	96.7%
2	96.8%	94.7%	91.2%	98.5%	97.4%	96.1%
3	98.3%	92.0%	89.8%	99.0%	95.3%	94.2%
4	86.9%	92.0%	78.5%	90.7%	96.6%	87.6%
5	95.4%	83.6%	79.5%	95.9%	94.0%	89.6%
6	81.8%	95.6%	76.8%	97.4%	96.7%	94.2%
7	95.2%	96.5%	91.8%	93.7%	95.2%	88.6%
8	93.3%	97.4%	90.2%	94.2%	97.5%	91.5%

Statistical modeling to quantitative analysis

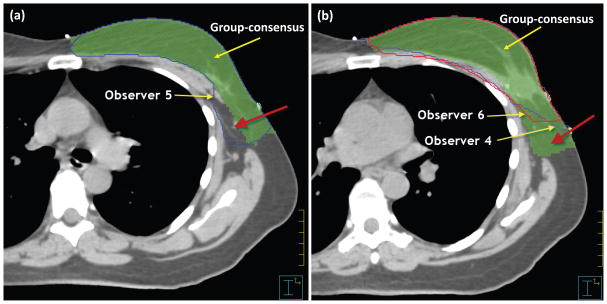
The Jaccard coefficients shown in Table 1 were calculated using Equation (2) for every individual contour. For each contouring method, the Jaccard coefficients were fitted into the beta distribution model to obtain the distribution of observer agreement scores. The distribution models were plotted with each individual’s agreement score indicated on the curve (Figure 1). The distribution model showed that the possible scores ranged between 60% and 100% for contouring from scratch, and between 80% and 100% for contouring from the template. Observers 1, 2, and 3 had received training in RTOG consensus contouring for breast cancer atlas. Their scores distributed to the right side of the curve toward a perfect agreement, representing relatively high agreement scores, which means that their contours were close to the group-consensus contour. This implies that the RTOG training may improve consensus contouring. In addition, Table 1 shows that observer 5 had consistent high sensitivity but lower specificity than others, which implies that this observer tended to contour this structure larger than others. On the other hand, observers 4 and 6 had low sensitivity but specificity similar to the others, which implies that these observers tended to contour this structure smaller than others. This was validated by comparing the individual contours with the group-consensus contour. The contour drawn by observer 5 was mostly larger than the group-consensus contour [Figure 2(a)] and the contours drawn by observers 4 and 6 were mostly smaller than the group-consensus contour [Figure 2(b)]. Therefore, our quantitative analysis could be used to instruct a particular physician to adjust his/her contouring practice to be more consistent with others. If an observer has consistently lower specificity than others, he/she may need to contour small when in doubt; on the other hand, if an observer has consistently lower sensitivity than others, he/she may need to contour large when in doubt.

Figure 2.

(a) Contour drawn by Observer 5 showed larger than the group-consensus contour; while (b) contours drawn by Observers 4 and 6 showed smaller than the group-consensus contour.

Contouring from scratch versus contouring from the template

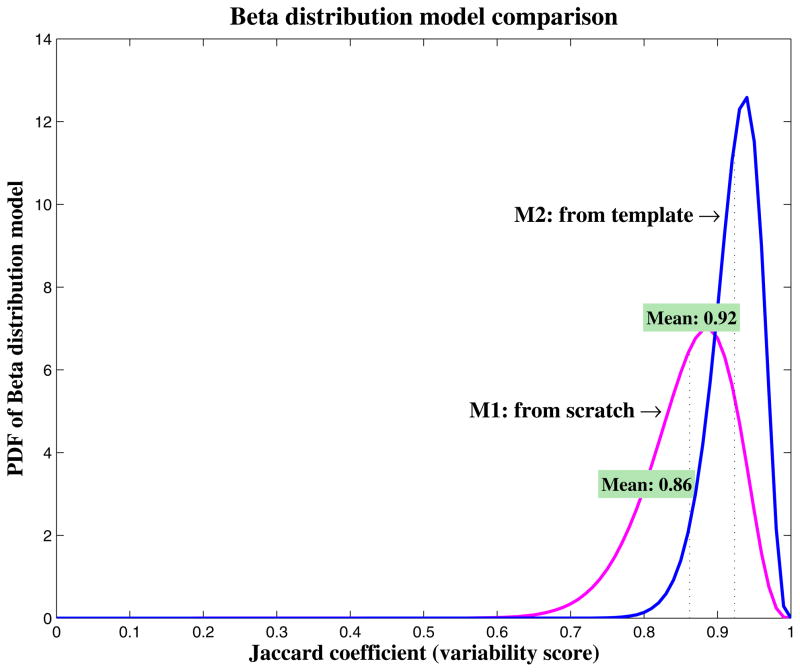
We compared the inter-observer variability quantitatively for contouring from scratch and contouring from the template. The beta distribution models were plotted in one coordinate system for comparison (Figure 3). Furthermore, we computed the mean, standard deviation, skewness, and excess kurtosis for these two distribution models. Contouring from scratch had a mean score of 86.2%, standard deviation of 5.9%, skewness of −0.70, and excess kurtosis of 0.55, with the possible scores distributing from 60% to 100%, representing a broad inter-observer variability. However, contouring from the template had a mean score of 92.3%, standard deviation of 3.4%, skewness of −0.79, and excess kurtosis of 0.83, with the possible scores distributing from 80% to 100%, which shows a much-improved consistency among individual contours. This improvement can also be observed from the individual evaluations in Table 1. Observer 6 contoured much more consistently with others when using the template than from scratch, with a change in agreement score from 76.8% to 94.2%. This demonstrates that contouring from a template improved the contouring consistency among the individual observers.

Figure 3.

Comparison of beta distribution models (as probability density function [PDF]) for contouring from scratch and contouring from the template. The higher, narrower, and sharper the curve, the smaller the inter-observer variability. Contouring from the template showed a smaller inter-observer variability than contouring from scratch.

More examples

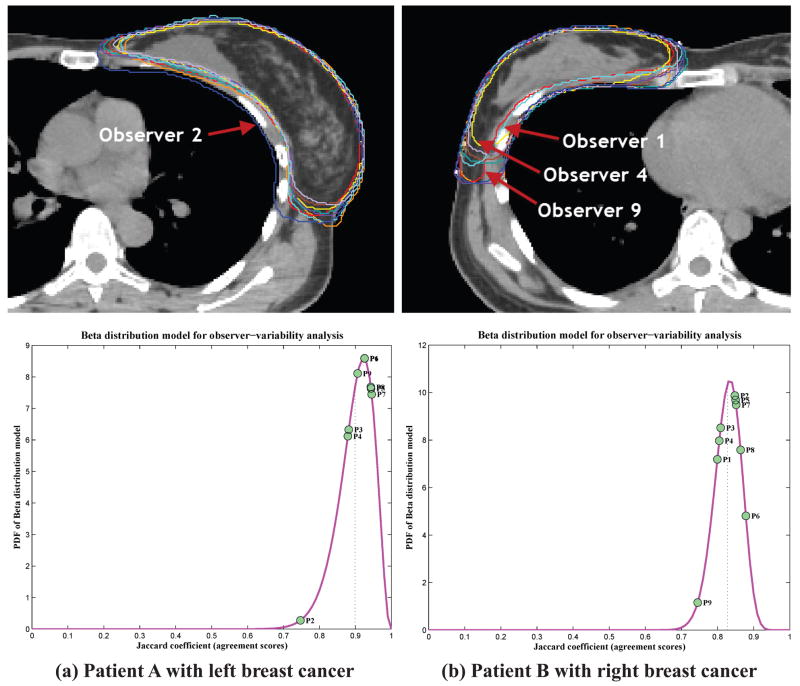
The sensitivity, specificity, and Jaccard coefficient between individual contour and the group-consensus contour were shown in Table 2 for both patients. We noticed that, when contouring the left breast of Patient A, Observer 2 had a much lower specificity than others, indicating he contoured much larger than others, which was verified by his contour shown in Figure 4. On the other hand, Observers 1, 4, and 9 had a lower sensitivity when contouring the right breast of Patient B, indicating they contoured smaller than others, which was also validated by their contours in Figure 4. In addition, Figure 4 showed that Observers 1 and 2 had their scores distributing to the left of the curve in contouring one patient, but to the right of the curve in contouring the other patient. This demonstrated the intra-observer variability for them in contouring these two patients. On the other hand, for Observers 3, 4, and 9 who had their scores distributing to the left of the curve in both patients, they had consistent low sensitivity or specificity. With this information, they might adjust their practice to be more consistent with others if necessary.

Table 2.

The agreement scores between individual contours and group-consensus contours for nine observers in contouring the left breast for Patient A and the right breast for Patient B.

Observer	Patient A with left breast cancer			Patient B with right breast cancer
	Sensitivity	Specificity	Jaccard	Sensitivity	Specificity	Jaccard
1	97.6%	95.9%	92.6%	80.7%	98.8%	80.0%
2	97.8%	76.4%	74.7%	93.6%	90.1%	84.8%
3	95.5%	93.5%	88.2%	97.4%	80.9%	80.9%
4	91.8%	96.7%	87.9%	81.9%	98.0%	80.5%
5	99.0%	96.3%	94.4%	96.0%	87.7%	85.0%
6	99.0%	94.7%	92.5%	97.3%	90.1%	87.8%
7	96.0%	98.9%	94.5%	97.6%	86.2%	85.2%
8	95.3%	99.1%	94.3%	88.9%	97.2%	86.4%
9	92.0%	98.8%	90.6%	75.7%	98.0%	74.5%

Figure 4.

Top row: Variability in contouring the breast volumes. Observer 2 contoured much larger than others on Patient A with left breast cancer, while Observers 1, 4, and 9 contoured much smaller than others on Patient B with right breast cancer. Bottom row: Visualization of beta distribution models (as probability density function [PDF]) with individual agreement score on the curve.

Discussion

We proposed a quantitative approach to analyzing inter-observer variability in contouring and demonstrated this method in breast cancer radiotherapy. To our knowledge, it is the first time to integrate the STAPLE algorithm and a beta distribution model for such analysis. Through statistical modeling, we were able to graphically visualize the quantified inter-observer variability. This method also facilitated the comparison of inter-observer variability for different contouring methods. In addition, our approach suggested ways to potentially improve an individual’s contouring practice when a consensus contour is agreed upon. Although this method was demonstrated in the scope of breast contouring, it is also applicable to other delineation tasks.

Our approach was based on the volume overlap indices and did not contain spatial or shape information of contouring structures. Although our approach can instruct a particular physician when her contouring practice varies from that of colleagues, it cannot tell specifically where to adjust the contour. On the other hand, it worth mentioning that each observer was a radiation oncology breast specialist diligently contouring using their standard clinical approach, and the test patients are common cases in clinic; therefore, each observer’s practice is very likely to reproduce when contouring other similar patients, although intra-observer variability may exist. Feedback from our approach may serve as a guideline for individuals to improve contouring consistency if desirable.

Our approach generated a group-consensus contour as the basis for quantitative analysis. Unlike the average contour used in many previous studies (4, 6), the group-consensus contour is not subject to the impact of outliers when it is used for inter-observer variability analysis. The group-consensus contour is generated by the maximum likelihood estimate from the STAPLE algorithm. Because an outlier contour does not agree with others, the STAPLE algorithm, to achieve the maximum likelihood estimate, will assign a small weight to the outlier contour automatically when estimating the group-consensus contour, thus minimizing the impact from the outlier contour. Furthermore, the group-consensus contour is the best estimation of the underlying ground truth of structure segmentation. This originates from the nature of the STAPLE algorithm and has been validated by several previous studies in multi-atlas auto-segmentation (9, 16–18).

Our study compared contouring from scratch and contouring from a template and demonstrated that contouring from the template improved contouring consistency. This conclusion is consistent with those of previous studies (6, 19, 20). Furthermore, contouring from a template required substantially less time and effort than contouring from scratch, especially for structures with low contrast and unclear anatomic boundaries on the CT images (21–23). In addition, we should also note that there are other approaches to facilitating contouring the breast, such as determining the breast boundaries using wires at the time of CT imaging (2), which we have not included in our analysis.

Contouring consistency continues to be an important aspect of radiotherapy. Variation in contouring of course contributes to variation in dose-volume histogram (DVH) reporting and evaluation. Significantly reducing it will improve the accuracy of DVH toxicity and local control correlations in volume based planning. Concerted efforts have been made to improve contouring consistency, such as the RTOG consensus contouring guideline (7) and ASTRO eContouring Learning Lab (24). Our findings verify that RTOG guideline improved contouring consistency and suggest an effective way to improve contouring consistency through consensus contouring training. Our findings also suggest using a well-defined template as the starting point for contouring to improve consistency. Furthermore, our approach is able to identify individuals whose practice tends to contouring larger or smaller than others. Bearing this information in mind, those individuals are able to adjust their practice to be more consistent with others, if consistency is desired.

Summary.

We developed a statistical modeling approach to evaluate inter-observer variability in contouring the whole breast for radiotherapy treatment planning. This approach verified that training based on RTOG consensus contouring guideline improved contouring consistency. In addition, the method could recommend ways to improve an individual’s contouring practice. The study also demonstrated that the use of a well-defined template as the starting point for contouring will improve contouring consistency.