Activation of a water molecule using a mononuclear Mn complex: from Mn-aquo, to Mn-hydroxo, to Mn-oxyl via charge compensation

Abstract

Activation of a water molecule by the electrochemical oxidation of a Mn-aquo complex accompanied by the loss of protons is reported. The sequential (2 × 1 electron/1 proton) and direct (2 electron/2 proton) proton-coupled electrochemical oxidation of a non-porphyrinic six-coordinated Mn(II)OH₂ complex into a mononuclear Mn(O) complex is described. The intermediate Mn(III)OH₂ and Mn(III)OH complexes are electrochemically prepared and analysed. Complete deprotonation of the coordinated water molecule in the Mn(O) complex is confirmed by electrochemical data while the analysis of EXAFS data reveals a gradual shortening of an Mn–O bond upon oxidation from Mn(II)OH₂ to Mn(III)OH and Mn(O). Reactivity experiments, DFT calculations and XANES pre-edge features provide strong evidence that the bonding in Mn(O) is best characterized by a Mn(III)-oxyl description. Such oxyl species could play a crucial role in natural and artificial water splitting reactions. We provide here a synthetic example for such species, obtained by electrochemical activation of a water ligand.

Introduction

Manganese complexes play critical roles in the metabolism of dioxygen in many biological systems. Arguably, one of the most important reactions involving O₂ is the photo-induced oxidation of water by plants, algae and cyanobacteria.¹ Mechanistic issues concerning this four-electron oxidation process are still a matter of debate.² This reaction takes place at the lumenal side of a transmembrane protein complex, called photosystem II (PS II).³ The reaction center's active site for water oxidation is formed by an Mn₄Ca cluster, called the oxygen evolving complex (OEC), and structural models for this cluster have been deduced by X-ray diffraction,^4–6 X-ray absorption experiments,⁷ and other spectroscopic techniques, as well as from theoretical studies.^8–11 The absorption of photons and the subsequent charge separation events in PS II lead to the accumulation of four oxidizing equivalents in the OEC during the four electron/four proton water oxidation reaction. The five different states by which the OEC cycles through are called S_n-states and are numbered with regard to the charge accumulated on the cluster (S₀ to S₄).¹² The release of oxygen occurs during the S₄ to S₀ transition, whereas the release of protons occurs along the Kok cycle (starting from S₀) with a 1 : 0 : 1 : 2 periodicity.¹³ Unquestionably, the release of protons is essential to keep the oxidation potential of the OEC low enough for the next oxidation event to occur.¹⁴ Three principal mechanisms have been proposed for the formation of the O–O bond, (i) a nucleophilic attack of H₂O/HO^– on an electrophilic Mn-oxo species in the S₄ state of the Kok cycle, (ii) a coupling of two oxo or hydroxo groups in the S₃ state, or (iii) formation of a peroxidic intermediate between a bridging/terminal oxygen radical and a water (HO^–/H₂O) molecule bound to Ca and/or Mn ion.^15–20 Among the many proposed mechanisms, one of them suggests that the substrate water molecule(s) are terminally coordinated to at least one Mn ion of the Mn₄Ca cluster^15,21 and sequentially converted into hydroxo and eventually oxo ligands that are involved in the O–O bond formation during the (S₄) transition state. The final intermediates that are present in the S₃ and S₄ states and lead to the formation of molecular dioxygen are not known yet, but putative species such as Mn(IV)=O, Mn(V)≡O,^17,22 or oxyl radicals^8,16,23–26 have been proposed. An oxyl radical is also an important ingredient in the mechanism proposed by Siegbahn on the basis of detailed quantum chemical calculations.⁸ To date, synthetic systems modeling these types of intermediates have been mostly limited to manganese(IV/V)-oxo porphyrinoids.^27–32 Other systems involving tetraanionic,³³ trianionic³⁴ and salen-like ligands³⁵ have also been reported. Recent studies of the XAS pre-edge features of some of the above mentioned manganese(V)oxo complexes have resulted in experimental benchmarks to study whether a Mn(V)-oxo unit is involved in the final intermediate state before the evolution of O₂.^36,37 In a similar way, X-ray absorption studies of Mn(IV)-oxo complexes will help identify the reactive intermediates in the higher S-states of the cycle. Despite being recently discussed,³⁸ the formation of Mn-oxo species by water activation has not been studied in detail yet. Thus the study of manganese model compounds is necessary to understand the O–O bond formation in natural and artificial systems.

We and others have shown in the past that the electrochemical oxidation of Mn(II) complexes bearing neutral N-ligands leads to the formation of dinuclear mixed-valence di-μ-oxo bridged Mn(III)Mn(IV) complexes.^39–44 Appropriate modification of the charge of the ligand and atom donor set allows us to selectively form mononuclear^45–47 or mono-μ-oxo bridged dinuclear complexes.^47,48 More specifically we have previously reported on the formation of a dinuclear mono-μ-oxo bridged Mn(III)Mn(IV) complex by electrochemical oxidation of a mononuclear Mn(II) complex using a pentadentate [N₄O] ligand (HL_e in Scheme 1).⁴⁸

Scheme 1.

[N₄O^–] propane (HL) and ethane (HLe) bridged ligands

In the present work, we show that the use of a similar ligand in which the ethane bridge is been replaced by a propane bridge (HL in Scheme 1) allows us to access mononuclear species. We describe the preparation of the hexacoordinated mononuclear complex [LMn(O)]⁺, which will be abbreviated as [3(O)]⁺, by electrochemical oxidation of the [LMn(OH₂)]⁺ complex, [1(OH₂)]⁺, concomitant with the deprotonation of the coordinated water molecule (Scheme 2). In [1(OH₂)]⁺, the manganese ion is in the divalent state whereas it is formally tetravalent in [3(O)]⁺. The best electronic structure description of this latter species will be developed in some detail below. Two different pathways for the preparation of the final [LMn(O)]⁺ species are reported. We describe the step-wise 1 electron/1 proton pathway, together with the characterisation of the [LMn(OH₂)]²⁺ (featuring trivalent manganese) [2(OH₂)]²⁺ and [LMn(OH)]⁺ (abbreviated as [2(OH)]⁺) intermediate species (also containing manganese in the oxidation state +3). We present the direct 2 electron/2 proton oxidation process in the supplementary information.^† Finally we show that the hexacoordinated [3(O)]⁺ complex described here exhibit features that are different from other Mn(IV) complexes described in the literature.

Scheme 2.

Simplified scheme for the electrochemical stepwise and direct generation of [3(O)]⁺ from [1OH₂]⁺.

Results

Synthesis and Characterisation of [LMn(II)(OH₂)ClO₄, [1(OH₂)]⁺(ClO₄)

Synthesis

Ligand LH was prepared according to a modified procedure described in the literature for the ethylene analogue L_eH.⁴⁶ The reaction of one equivalent of LH in the presence of one equivalent of triethylamine with manganese(II) perchlorate (Mn(II)(ClO₄)₂, nH₂O) leads to the formation of [LMn(OH₂)]-ClO₄, [1(OH₂)]ClO₄ as a white precipitate with reasonable yields (60–70%).

X-Ray diffraction study

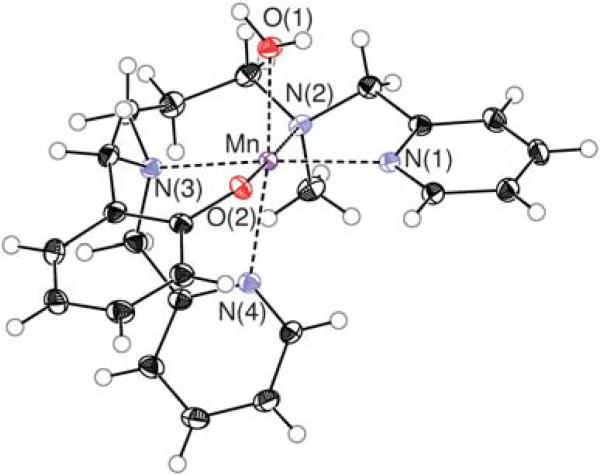
Diffusion of ether in an acetonitrile–water (9 : 1) solution of [1(OH₂)]ClO₄ under anaerobic conditions produces large colourless single crystals suitable for X-ray diffraction. It consists of a mononuclear complex with a water molecule coordinated in cis position with regard to the phenolate ligand (Fig. 1). A pyridine ligand is trans to the water molecule and the amines from the propanamine backbone are trans to a pyridine (N₃) and to the phenolate (N₂) (Table 1). The Mn–water (d = 2.163 Å) and phenolate (d = 2.099 Å) bonds are very close to those reported by Burdette et al. for a manganese complex in a very similar N₄O^– environment, where a water molecule is coordinated cis to the phenolate.⁴⁹ The longest Mn–N bond is observed for the amine (N₂, d = 2.327 Å) that is trans to the phenolate group. The angle formed by the two tertiary amines N₂ and N₃ and the manganese ion is close to a right angle (88.7°). A similar value (91.1°) is also observed for the angle formed by the water and phenolate ligands and the manganese ion. The O₁–Mn–N₄ angle is 170.4°. These bond distances and angles indicate a slightly disordered octahedral structure for [1(OH₂]²⁺ in the solid state. The second coordination sphere shows a dinuclear arrangement through an intermolecular H–bonding network between a proton of a coordinated water molecule and an oxygen atom of the phenolate group of another monomeric unit. This type of second sphere interaction has already been observed for Mn(III)-aquo complexes.^50,51 The formation of the water coordinated mononuclear complex in the presence of water indicates the higher affinity of water for manganese compared to acetonitrile.

Fig. 1.

ORTEP drawing of [1(OH₂)]⁺. Ellipsoids are drawn at the 50% probability level. The (ClO₄)^– ion is omitted for the sake of clarity.

Table 1.

Selected bond lengths (Å) and angles (°) for [1(OH₂)]ClO₄ from X-ray diffraction

Mn–N(1)	2.246(1)
Mn–N(2)	2.327(1)
Mn–N(3)	2.278(1)
Mn–N(4)	2.293(1)
Mn–O(1)	2.163(1)
Mn–O(2)	2.099(1)
N(3)–Mn–N(2)	88.78
O(1)–Mn–O(2)	91.18
O(1)–Mn–N(4)	170.44

Solution studies of [1(OH₂)]ClO₄

The X-band EPR spectrum of an acetonitrile–water (98 : 2) mixture shows an intense transition centered at 330 mT (g = 2) (Figure S1^†). This feature is consistent with a mononuclear Mn(II) complex, for which the Zeeman effect dominates the zero-field splitting interaction.^41,52

The cyclic voltammetry trace at room temperature presents a quasi-reversible anodic process at $E_1^{1∕2}=0.43$ V vs. SCE (ΔEp = 100 mV), which is attributed to the [1(OH₂)]⁺/[2(OH₂)]²⁺ redox couple (wave 1/1′ in Fig. 2A). An additional weak anodic signal is detected at Epa₂ = 1.05 V vs. SCE (peak 2), which is attributed to an oxidative process involving [2(OH)]⁺ species (vide infra). When repeating the experiment under various conditions, we observed that the intensity of this signal is very sensitive to the quality of the electrode surface, as reported in the literature for proton-coupled electron transfer reactions in the case of oxo-bridged Mn complexes.^53,54

Fig. 2.

Cyclic voltammograms of [1(OH₂)]ClO₄ in MeCN–H₂O (98 : 2) mixture at 20 °C, before (A) and after exhaustive electrolysis at +0.6 V vs. SCE (electrogeneration of [2(OH)₂]²⁺, the arrow (↓) indicates the electrolysis potential) (B). Cyclic voltammetry at T = –40 °C of the electrogenerated [2(OH)₂]²⁺ (dotted line) and of [2(OH)]⁺ formed by deprotonation of [2(OH)₂]²⁺ (solid line) (C) and after exhaustive electrolysis at +1.1 V vs. SCE (electrogeneration of [2(OH)₂]²⁺ the arrow (↓) indicates the electrolysis potential) (D). For all voltammograms: v = 0.1 V s^–1, working electrode = glassy carbon, auxiliary electrode = Pt, 2 mM, C = 0.2 M in NBu₄ClO₄.

Electrochemical oxidation of [1(OH₂)]⁺ into [2(OH₂)]²⁺ (1 electron reaction, Scheme 3)

Scheme 3.

Various Mn complexes encountered in the present study starting from the electrochemical oxidation of [1(OH₂)]⁺. Species that have been spectroscopically characterized are indicated in black traces.

An oxidative bulk electrolysis was performed at +0.6 V vs. SCE at room temperature on a MeCN–H₂O (98 : 2) solution of [1(OH₂)]⁺. During the course of the electrolysis, the colourless solution turned lawn green. After completion of the electrolysis, coulometry indicates a one electron per manganese ion process and cyclic voltammetry (Fig. 2B) only shows a cathodic process at $E_1^{1∕2}=0.43$ (wave 1/1′). The coulometry as well as the current intensity of wave 1/1′ indicate the quantitative formation of complex [2(OH₂)]²⁺. The formation of [2(OH₂)]²⁺ was monitored by UV–visible spectroscopy (Fig. 3A, Table 2). Two major bands appear at λ_max = 380 and 700 nm (ε_max = 2300 and 525 M^–1 cm^–1). Similar bands have been reported in the literature for mononuclear Mn(III)^55,56 or dinuclear Mn(III)Mn(III) complexes.^46,47 The intense band at 380 nm is attributed to a phenolato to Mn(III) charge transfer transition.^55,57–59 According to the literature, the less intense band at 700 nm can plausibly be attributed to d-d transitions of ⁵E → ⁵T₂ parentage.^60,61

Fig. 3.

UV–Vis absorption spectra recorded in the course of the electrochemical oxidation of [1(OH₂)]⁺ into [2(OH₂)]²⁺ in a MeCN–H₂O (98 : 2) mixture (glassy carbon, Pt, 2 mM, 0.2 M NBu₄ClO₄ 20 °C) (A). UV–visible monitoring of the conversion of [2(OH₂)]²⁺ into [2(OH)]⁺ upon addition of one equivalent of tert-butylamine (TBA) (B).

Table 2.

UV–Vis data for [1(OH₂)]⁺, [2(OH)₂]²⁺,[2(OH)]⁺, [3(O)]⁺,in MeCN–H₂O (98 : 2) mixture containing 0.2 M NBu₄ClO₄

	λ/nm	ε/mM–1 cm–1
[1(OH2)]+	240	10 000
	280	2420
[2(OH)2]2+	380	2700
	420	2300
	700	720
[2(OH)]+	340	2500
	500	700
	615	410
[3(O)]+	415	3400
	620	1500

The intensity of the X-band perpendicular mode EPR spectrum of the initial [1(OH₂)]²⁺ solution decreased during the course of the electrolysis. The final solution of [2(OH₂)]²⁺ resulting from the electrolysis displayed no signal, in line with a +3 oxidation state of the Mn ion. No spectrum was detected in a parallel mode EPR experiment.

Deprotonation of [2(OH₂)]²⁺ to yield [2(OH)]⁺

Access to the deprotonated form of [2(OH₂)]²⁺ was monitored by UV–vis spectroscopy. Upon addition of one equivalent of tert-butylamine (TBA, pK_a = 18.1)⁶² at room temperature, the electrochemically prepared [2(OH₂)]²⁺ solution turned from lawn green to firebrick red. The absorption spectrum monitored during the addition of base (Fig. 3B) shows a decrease at λ_max = 400 nm and 700 nm and an increase at λ_max = 500 nm and 605 nm. The presence of several isosbestic points (λ = 353, 505, 605 nm) indicates the simultaneous presence of only two absorbing species in solution, namely [2(OH₂)]²⁺ and [2(OH)]⁺ (formation of dinuclear species was ruled out on the basis of electrochemical experiments, see below). Addition of excess base did not lead to any change in the absorption spectrum. The apparent pK_a of [2(OH₂)]²⁺ was estimated to be 16.0 ± 0.5 (Scheme 4). [2(OH)]⁺ could also be prepared electrochemically by oxidizing a MeCN–H₂O (98 : 2) solution of [1(OH₂)]⁺ at +0.6 V vs. SCE in the presence of one equivalent of base (TBA).

Scheme 4.

Comparison of pK_a values for the various complexes and bases used in this study.

Cyclic voltammetry of a solution of [2(OH)]⁺ recorded at –40 °C shows a cathodic peak at Epc₄′ = –0.54 V vs. SCE which is attributed to a Mn(III) to Mn(II) reduction process (Fig. 2C). This corresponds to a downshift of 700 mV compared to the reduction potential of [2(OH₂)]²⁺ (Epc₁′ = 0.35 V) and is consistent with an increased negative charge on the complex due to the removal of a proton from the coordinated water molecule. The irreversibility of the process is explained by the high basicity of the hydroxo ligand at the Mn(II) level, leading to its protonation. When scanning towards anodic potentials, an oxidation process is observed at Epa₂ = 1.05 V (Fig. 2C), with a current intensity consistent with a one-electron oxidation. This anodic process is accompanied by two reduction peaks on the reverse scan at Epc₂′ = 0.96 V and Epc₃′ = 0.65 V (Fig. 2C). When increasing the temperature to +10 °C, the anodic wave 2/2′ loses reversibility, whereas the cathodic process at Epc₃′ = 0.65 V shifts to higher potentials (Epc₃′ = +0.80 V at +10 °C) and increases in intensity (Fig. 4A). The 2/2′ cathodic process observed at –40 °C ($E_2^{1∕2}=1.0$ V, ΔEp = 90 mV) is attributed to the redox couple [2(OH)]⁺/[3(OH)]²⁺, and the anodic peak 3′ (Epc₃′ = 0.65 V) to the reduction of the deprotonated form, namely [LMn(O)]⁺, abbreviated as [3(O)]⁺. The potential downshift observed at low temperature (310 mV) between the reduction potential of [3(OH)]²⁺ and [3(O)]⁺ is consistent with a loss of a proton from the coordinated hydroxo ligand.

Fig. 4.

Cyclic voltammograms of electrochemically generated [2(OH)]⁺ in a MeCN–H₂O (98 : 2) mixture at 0.1 V s^–1 at different temperatures (10 °C, 0 °C, –20 °C and –40 °C) (A), and at 10 °C with different scan speeds (0.1 V s^–1, 0.5 V s^–1, 1 V s^–1 and 2.5 V s^–1) (B). For all voltammograms: working electrode = glassy carbon, auxiliary electrode = Pt, C = 2 mM, 0.2 M NBu₄ClO₄. Intensity has been normalized.

Cyclic voltammograms recorded at different scan rates at +10 °C are shown in Fig. 4B. A fast scan rate has the same effect on the processes described above as low temperature: wave 2/2′ becomes reversible and peak 3′ decreases in intensity. From the high rate voltammetry experiments, we estimated the apparent reaction rate to be k_1app = 5 s^–1 (Scheme 5). We thus hypothesise that [3(OH)]²⁺ spontaneously deprotonates at +10 °C (wave 2/2′ is not reversible) to generate [3(O)]⁺ (peak 3′ has a high current intensity). When scanning at a fast scan rate, the deprotonation reaction is not fast enough to occur. Wave 2/2′ becomes reversible and peak 3′ almost disappears. At low temperature, the reaction is slowed down, and the features observed at fast scan rate at room temperature (wave 2/2′ reversible and peak 3′ very weak) are observed at low scan rate. This hypothetical electrochemical–chemical (EC) mechanism is summarised in Scheme 5.

Scheme 5.

Square scheme for the stepwise proton coupled electron transfer involved in the electrochemical formation of [3(O)]⁺.

Electrochemical oxidation of [2(OH)]⁺ into mononuclear [3(O)]⁺ (1 electron/1 proton reaction)

The mononuclear [3(O)]⁺ complex was prepared by low temperature exhaustive electrolysis (+1.1 V vs. SCE) of a solution of [2(OH)]⁺, in the presence of one equivalent of lutidine ($\mathrm{p}{K}_{\mathrm{a}}^{\mathrm{MeCN}}=14$).^63,64 The firebrick red solution turned dark green and coulometry indicated a stoichiometry of one electron per manganese. The dark green solution is stable for a few hours at –40 °C but decomposes rapidly when left at room temperature. Addition of tert-butylamine to the medium does not lead to any modification. The formation of [3(O)]⁺ was monitored by UV–visible spectroscopy (Fig. 5A). The absorption spectrum of [3(O)]⁺ displays two major bands at λ_max (ε_M) 414 nm (3.40 × 10³ mol^–1 L cm^–1) and 616 nm (1.50 × 10³ mol.^–1L cm^–1). The latter band is tentatively attributed to a phenolate to manganese LMCT transition.^{45–47,55,65} No transition was observed in the region around 1000 nm, thus discarding the possibility that a phenoxyl radical species is formed during oxidation.^35,66

Fig. 5.

UV–vis absorption spectra recorded in the course of the electrochemical oxidation of [2(OH)]⁺ into [3(O)]⁺ in a MeCN–H₂O (98 : 2) mixture (0.2 M NBu₄ClO₄) in the presence of 1 equivalent of tert-butylamine (TBA) (A). UV–vis spectrum recorded after electrochemical oxidation of [2(OH)]⁺in the absence of base () compared to a simulated spectrum obtained for a 1 : 1 mixture of [3(O)]⁺ and [2(OH₂)]²⁺ (). Spectra of [3(O)]⁺ () and [2(OH₂)]²⁺ () are also presented for comparison (B).

Perpendicular mode X-band EPR measurements were performed on the final electrolysis solution. Fig. 6 presents the spectrum and the associated simulation. The spectrum shows transitions at g_eff = 5.2, 4.2, 3.5 and 2.0 reminiscent of what is observed for S = 3/2 systems in which the zero-field splitting interaction dominates over the Zeeman effect.⁶⁷ Hyperfine lines detected at g_eff = 5.2 and 2.0, with |A| values of 72.0 × 10^–4 cm^–1 and 62.0 × 10^–4 cm^–1 respectively, are consistent with those observed for other of S = 3/2 manganese species with a formal oxidation state of +4.^34,48,68 The temperature dependence of the EPR spectrum indicates a negative D value while the experimental data can be reproduced using isotropic g = 2.0 and A = 72.0 × 10^–4 cm^–1 values and D = –0.7 cm^–1 and E/D = 0.10. The use of anisotropic g and A values also allow to well reproduce the spectrum, but the improvement versus the isotropic values is not large enough to be considered as significant. Note that attempts to improve the spectral resolution were unsuccessful and that the slight drift in the baseline of the [3(O)]⁺ spectrum precludes quantitation of the EPR signal.

Fig. 6.

Experimental X-band EPR spectrum of [3(O)]⁺ at 4 K (ν = 9.38 GHz, Mod. Ampl. 0.5 mT, microwave power = 2 mW) (A) and calculated spectrum with g = 2.0, |A| 72 × 10^–4 cm^–1, D = –0.7 cm^–1 and E/D = 0.10 (B).

Cyclic voltammograms recorded at –40 °C on the electrolyzed solution present an irreversible reduction peak at Epc₃′ = +0.65 V, which is attributed to the reduction of [3(O)]⁺ into [2(O)] and a reversible process at E^1/2 = 1.0 V, corresponding to the redox couple [2(OH)]⁺/[3(OH)]²⁺ (wave 2/2′). The irreversibility of process 3′ is due to the high basicity of the neutral complex [2(O)], which protonates as soon as it is formed upon reduction of [3(O)]⁺. The following section confirms that [3(OH)]²⁺ can be fully deprotonated.

Evidence for a ‘‘father–son’’ EC mechanism

In an attempt to generate [3(OH)]²⁺, an electrochemically prepared solution of [2(OH)]⁺ was oxidized at –40 °C, in the absence of base, at +1.1 V vs. SCE. The solution color changed from firebrick red to green and coulometry indicated a 0.5 electron per manganese ion ratio. Fig. 5B shows the UV–visible spectrum recorded at the end of the electrolysis (full-line trace). It is similar to a 1 : 1 linear combination of [2(OH₂)]²⁺ and [3(O)]⁺ spectra (see white circles line in Fig. 5B). This result, together with coulometry implies that in the absence of additional base, [2(OH)]⁺ is basic enough to capture the proton released from the transient complex [3(OH)]²⁺ generated at the electrode during the electrolysis. The resulting solution is a 1 : 1 mixture of [2(OH₂)]²⁺ (which is not oxidized at +1 V vs. SCE) and [3(O)]⁺. These data provide evidence for a so-called father–son electrochemical–chemical (EC) mechanism between [2(OH)]⁺ and [3(OH)]²⁺ (Scheme 6). The apparent rate constant k_1app estimated above from electrochemical measurements therefore characterizes a bimolecular reaction between [3(OH)]²⁺ generated at the electrode and [2(OH)]⁺ present in the bulk. The apparent rate is thus k′_1app = 2210 M^–1 s^–1, which is of the same order of magnitude as the protonation rate (k_H+ = 5440 M^–1 s^–1) reported for an oxo bridge in a di-μ-oxo bridged Mn(III)Mn(IV) complex.⁶⁹

Scheme 6.

“Father–son” EC mechanism observed for the electrochemical oxidation of [2(OH)]⁺ into [3(OH)]²⁺ in the absence of base.

The electrochemical oxidation of [2(OH)]⁺ in the absence of base confirms the hypothesis formulated above from electrochemical measurements performed on [2(OH)]⁺ at different temperatures and scan rates. The existence of a father–son EC mechanism involving a proton between [3(OH)]²⁺ and [2(OH)]⁺ demonstrates that the species generated by electrolysis of [2(OH)]⁺ in the presence of base bears a fully deprotonated water molecule.

In addition, [3(O)]⁺ was also obtained by direct electroxidation of [1(OH₂)]⁺ (2 electron/2 proton), see supplementary information.^†

Nature of the Mn–O bond

XAS studies

Mn K-edge XAS spectra were collected for the samples prepared by the step-wise (1 electron/1 proton) and the direct (2 electron/2 proton) electrochemical oxidation in order to obtain insight into the nature of the Mn–O bonds in the various species. Fig. 7A shows the XANES spectra of [1(OH₂)]⁺, [2(OH)]⁺ and [3(O)]⁺ samples obtained from the step-wise process. The XANES spectrum of [1(OH₂)]⁺ shows a feature typical of the Mn(II) oxidation state. Upon the step-wise oxidation of [1(OH₂)]⁺, the XANES edge shifts to higher energy by 2–3 eV at each step. This behaviour will be further analyzed below in the context of the electronic structure calculations. The [1(OH₂)]⁺ and [3(O)]⁺ samples obtained from the direct process (Fig. 7B) show identical XANES spectra as those from the step-wise process.

Fig. 7.

Mn K-edge XANES spectra of (A) [1(OH₂)]⁺ (blue), [2(OH)]⁺ (green), and [3(O)]⁺ (red) complexes prepared by an electrochemical step-wise and (B) [1(OH₂)]⁺ and [3(O)]⁺ complexes by direct generation. Insert shows the pre-edge region.

Fig. 8 shows the EXAFS spectra of the three compounds, [1(OH₂)]⁺, [2(OH)]⁺ and [3(O)]⁺ (in blue), with a best curve fitting result of each spectrum shown in red. The fitting parameters are reported in Table S1.^† The EXAFS data of [1(OH₂)]⁺ in MeCN–H₂O (98 : 2) solution is consistent with the XRD structure of [1(OH₂)]⁺. Upon oxidation, a shortening of the Mn–O bonds is observed. The average distance of the two Mn–O bonds in [1(OH₂)]⁺ is ~2.1 Å, while that of [2(OH)]⁺ is ~1.9 Å. Further shortening was observed in the [3(O)]⁺ state. Unfortunately, the EXAFS resolution in the current study is limited to ~0.15 Å (2.4 < k (Å^–1) < 11.7), which is not sufficient for clearly separating out two close Mn–O distances (one from Mn–O_ph and the other from Mn–O_oxo). The Mn–O one-shell fit of [3(O)]⁺ indicates an average Mn–O distance of ~1.82 Å. However, Mn–O_ph distances are typically longer than 1.84 Å.^70–72 DFT-optimized structures of the complexes (Table 3) also suggests Mn–O_ph distances to be longer than 1.82 Å for the cis and trans isomeric forms. Therefore, we carried out two-shell fits by setting one Mn–O distance to be longer than 1.84 Å. The second Mn–O distance obtained by this fitting approach was 1.79 Å, which suggests the presence of shorter Mn–O distance(s). As mentioned above the current EXAFS resolution is not sufficient to distinguish two sub-shells that differ by 0.05 Å, and therefore this distance remains ambiguous (see supplementary material^†). The second Mn–O distance obtained by the two shell fitting is much longer compared to the short 1.58 Å or 1.68 Å distances reported from EXAFS data for five-coordinated O=Mn(IV)(salen)³⁵ and O=Mn(IV)(porphyrin)³⁰ complexes, respectively. However, it is rather close to the 1.84 Å distance reported for six-coordinated O=Mn(IV)(porphyrin) complexes.³¹ Recent studies of the Mn XANES pre-edge features of synthetic Mn(V)-oxo complexes discussed the relationship between the pre-edge intensity and the Mn coordination environment.^36,37 These studies have shown that the pre-edge intensity depends largely on the symmetry of the complex. As a consequence double and triple bonded oxo species in a five-coordinated environment are expected to have significantly stronger pre-edge features because of their distorted geometry that induces extended d/p mixing. In contrast, oxo species in six-coordinated environments typically display much weaker pre-edge features. In the present case, the pre-edge intensity of [3(O)]⁺ is not noticeably intense in comparison with other Mn(IV) model compounds such as Mn(IV)(salicylate)₂(bipy).⁷³

Fig. 8.

EXAFS spectra of (A) [1(OH₂)]⁺, (B) [2(OH)]⁺, and (C) [3(O)]⁺ complexes; (left) k³-weighted EXAFS, (right) Fourier transformed EXAFS. The blue lines are the experimental data and the red lines are the curve fitting result.

Table 3.

DFT calculated bond distances (Å) for complexes [3(O)]⁺, [3(O···HLut)]²⁺ and [3(OH)]²⁺, compared with EXAFS values; “HLut” stands for lutidinium

	[3(O)]+		[3-O(···HLut)]2+			[3(OH)]2+
	cis (oxo)	trans (oxo)	trans (oxyl)	cis (oxo)	trans (oxo)	cis	trans	EXAFS
Mn–N(1)	2.08	2.10	2.22	2.07	2.09	2.12	2.25	2.08
Mn–N(2)	2.24	2.15	2.34	2.21	2.12	2.32	2.24
Mn–N(3)	2.12	2.12	2.26	2.12	2.15	2.18	2.32
Mn–N(4)	2.25	2.08	2.22	2.21	2.12	2.10	2.17
Mn–O(1)	1.66	1.68	1.72	1.69	1.72	1.82	1.81	1.79
Mn–Oph(2)	1.87	2.00	1.89	1.87	1.94	2.15	1.98	1.84

DFT calculations

Calculations at the B3LYP/TZVP level of theory were performed to gain more insight into the electronic structure of the species under study, in particular with respect to the nature of the bonding in [3(O)]⁺. Both the cis and the trans configurations were optimized, using the X-ray data of [1(OH₂)] (cis configuration) and of [2(OH)]⁺ (trans configuration) as starting points for geometry optimizations.⁷⁴ The corresponding [3(O···HLut)]²⁺ (HLut = lutidinium ion) and [3(OH)]²⁺ systems were also studied in both coordination geometries of the ligand. Selected distances for [3(O)]⁺, [3(O···HLut)]²⁺ and [3(OH)]²⁺ are summarized in Table 3 (complete coordinates are provided in Tables S5–S8).^†

Focusing first on the optimized geometries of the [3(O)]⁺ species, the cis isomer features a short Mn=O double bond at 1.66 Å, whereas this bond in the corresponding trans isomer is slightly longer (1.68 Å). Both distances are in the range typical of high-valent metal oxo-species. The Mn–O_ph distance of 1.87 Å in the cis isomer agrees very well with the EXAFS value, but in the trans isomer this bond is significantly elongated. Most importantly, however, our investigation has revealed that not only one but two distinct low-lying states exist for the trans isomer of [3(O)]⁺. Specifically, besides the expected oxo form featuring a short Mn=O bond of 1.68 Å, a more stable minimum (by 1.2 kcal mol^–1) can be located using the broken-symmetry DFT approach.⁷⁵ This species features an elongated Mn–O bond (1.72 Å) and, as we will show in the following, it can be best described as corresponding to an oxyl form of [3(O)]⁺. In terms of total energies, DFT predicts the cis-oxo isomer to be marginally lower than the trans-oxyl, by 0.8 kcal mol^–1. However, this energy difference is well below the expected error margin of the method. Hence no safe conclusions regarding the energetically preferred ligand coordination can be reached from the total energies alone. It is clear, however, from the calculations that the isomers must be very close in energy.

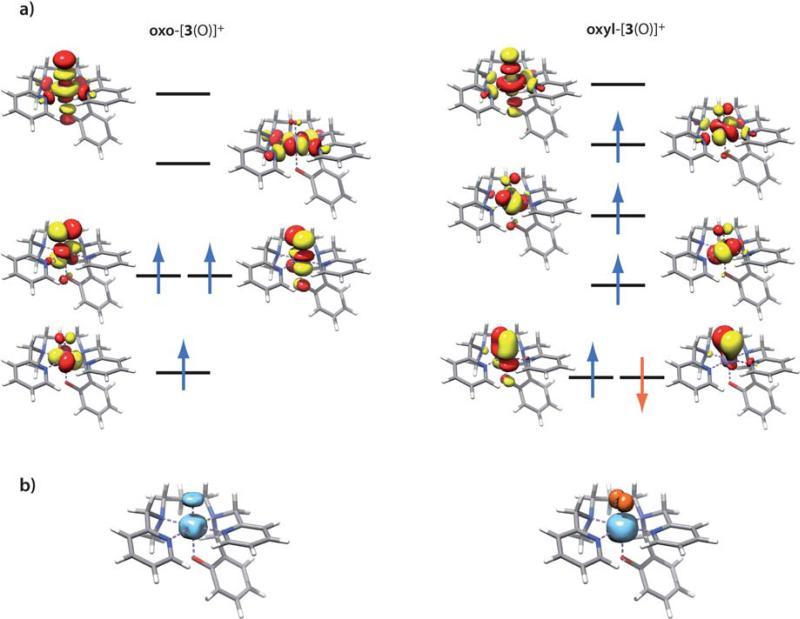
In terms of electronic structure, the differences between the oxo and oxyl species become apparent from inspection of their molecular orbitals (Fig. 9a).⁷⁶ For the oxo form of [3(O)]⁺ (Fig. 9a, left) the MOs are exactly as anticipated for a Mn(IV)=O species, with three unpaired spin-up electrons occupying the t_2g-derived orbitals. Computed spin populations are 2.59 for manganese and 0.59 for the oxo ligand. It is emphasized that the presence of positive spin density at the oxo ligand (Fig. 9b) does not imply oxyl character; it simply results from the covalency of the Mn=O bond, revealed here by the extensive mixing of metal and oxide character within the strongly antibonding Mn–O π* orbitals.⁷⁷ A related discussion is frequently found with respect to the (FeO)²⁺ core where a Fe(IV)-oxo type electronic structure is actually prevalent.^78,79 The situation is fundamentally different for the oxyl species (Fig. 9a, right). One of the Mn–O π-bonds is broken and replaced by a spin coupled pair, in which the spin-up orbital is strongly polarized towards the manganese and the spin-down orbital is strongly polarized towards the oxygen ligand (for an explanation of how to identify and interpret such spin coupled pairs see ref. 76, 80, 81). As a result of spin polarization, the spin-up electron that occupied the corresponding Mn–O π*-orbital in the oxo form now occupies the Mn–N₄ antibonding orbital. The defining characteristic of this species is therefore the antiferromagnetic coupling between a high-spin Mn(III) (S_Mn = 2) with positive spin population of 3.70 and the oxyl-radical S_O = 1/2) with negative spin population of –0.74 electrons, thus defining a leading Mn^III–O^•– type valence bond structure. The total spin state is consistent with the EPR measurements since both Mn(IV)-oxo and Mn(III)-oxyl will have a S = 3/2 ground state. Based on our calculations, the adiabatic exchange coupling constant for the Mn–O pair is –790 cm^–1, while the vertical exchange coupling constant is –1136 cm^–1. The spin density distribution of the oxyl species (Fig. 9b) nicely mirrors the electronic rearrangement, featuring a more spherical profile around Mn due to occupation of the d_x2-y2 orbital in the oxyl-species, while the minority spin density at the oxide has become distinctly asymmetric. As discussed before^81,82 the broken-symmetry spin-density is, of course, not physically sound but it nicely illustrates the effective density of unpaired electrons in the system. According to the preceding analysis, we may assign Mn–O bonding configurations as σ²π⁴π*² to the oxo species and σ²π²π*¹ to the oxyl. Using the definition of bond order as half of the difference between the number of bonding electrons and the number of antibonding electrons, we obtain formal bond orders of 2 and 1.5 for the oxo and oxyl species, respectively. This description is indeed confirmed by the computed Mayer bond orders^83–85 that are very close to the ideal values, 1.9 for the oxo and 1.4 for the energetically favorable oxyl state of [3(O)]⁺. This decrease in bond order explains the lengthening of the Mn–O bond. Importantly, the EXAFS experiments are consistent with a Mn-oxyl ground state of [3(O)]⁺ since a short (1.65 Å) Mn(IV)-oxo bond can be ruled out.

Fig. 9.

a) Electronic structures of the oxo and oxyl states of trans-[3(O)]⁺; b) spin density distribution (blue: positive, orange: negative) for the oxo and oxyl trans-[3(O)]⁺ species.

Thus, the DFT calculations and the analysis of the electronic structure suggest that [3(O)]⁺ should have extensive oxyl character. The calculations alone are not conclusive with respect to the energetic ordering of the Mn(III)-oxyl and Mn(IV)-oxo states but comparison with the EXAFS experiments clearly favors the former alternative. However, a limited deviation between the optimized Mn–O bond length for the oxyl species and the somewhat longer value derived from EXAFS still remains. To investigate probable sources of this discrepancy, the effect of interactions with lutidinium ions were considered. From Table 3, the O–lutidinium interaction is shown to induce an elongation of the Mn–O bond by 0.03 Å for the cis and 0.05 Å for the trans oxo species [3(O···HLut)]²⁺, respectively. In this case convergence to a broken-symmetry solution for the corresponding oxyl species could not be achieved (presumably, because the additional H-bond stabilizes the Mn^IV-oxo state), but a similar degree of elongation seems likely, thus bringing the predicted Mn–O bond length much closer to the EXAFS value. Finally, the possibility of protonation of [3(O)]⁺ to yield [3(OH)]²⁺ was considered. Despite the favourable Mn–O(H) bond lengths that were obtained in this case, the Mn–O_ph bond is predicted to be significantly elongated compared to [3(O)]⁺ or [3(O···HLut)]²⁺, extending to 2.15 Å for cis-[3(OH)]²⁺. Such a long Mn–O distance cannot be reconciled with the EXAFS data, therefore the possibility of a hydroxy species is unlikely.

Given the energetic proximity of the oxo and oxyl [3(O)]⁺ states, it seemed likely that more firm conclusions could be reached only on the basis of the spectroscopic features of the two species. For this purpose we compared the experimentally observed Mn XAS pre-edge features with those calculated via a recently described TDDFT approach.⁸⁶ Similar calculations were first applied by DeBeer George and co-workers to obtain insight into the bonding of manganese(V)-oxo species.³⁷ The results are presented in Fig. 10, where the experimental Mn–K-edge X-ray absorption spectra of [2(OH)]⁺ (left) and [3(O)]⁺ (right) are compared with the calculated pre-edge features of [2(OH)]⁺ and both the oxo and oxyl states of [3(O)]⁺. The main peak in all cases corresponds to the Mn-1s → Mn-3d_z2 excitation which contains Mn–O σ* character, and therefore gains electric dipole intensity through d/p mixing.⁸⁶ To allow for meaningful comparisons, the computed energies and intensities were calibrated relative to the experimental values for [2(OH)]⁺. Using the [2(OH)]⁺ pre-edge peak as reference, Fig. 10 reveals a clear correspondence between the experimentally observed energy shift (0.8 eV) and increased relative intensity of the [3(O)]⁺ peak (by a factor of 1.9) with the respective computed values for the oxyl form of [3(O)]⁺ (0.7 eV and 2.4 times, respectively). By contrast, our calculations predict that the corresponding feature for the oxo species would be shifted to higher energy by 1.9 eV with respect to [2(OH)]⁺, with a concomitant five-fold increase in intensity. Likewise, the calculations for [3(OH)]²⁺ also shown in Fig. 10 rule out the possibility of a protonated Mn(IV) species. Thus, the comparison between experimental and computed Mn–K-edge pre-edge spectra provide strong evidence that the bonding in [3(O)]⁺ is indeed best characterized by a Mn(III)-oxyl description. However, this description is not easy to reconcile with the experimental EPR parameters. Experimentally, the manganese hyperfine tensor is observed to be nearly isotropic, a feature that would be more consistent with the almost spherically symmetric (t_2g)³ subshell of a Mn(IV) ion than with a (t_2g)³(e_g)¹ configuration characteristic of Mn(III). Similarly, the zero-field splitting for a Mn(IV) species should be well below 1 cm^–1 (as observed) while that of a Mn(III) species should be much larger. It is worth noting, however, that the present EPR spectrum is highly similar to the one reported for Mn(II)-bisphenoxy⁶⁶ and Mn(III)-phenoxy³⁵ species although the latter were reproduced using strong anisotropic values. On the basis of the calculated energies no discrimination is possible as the two electronic states appear to be nearly equi-energetic. Clearly, these aspects require much more detailed spectroscopic and theoretical studies that are well outside the scope of this paper. For the time being, the present XAS and EXAFS data provide evidence for a predominant Mn(III)-oxyl description of [3(O)]⁺

Fig. 10.

Comparison of experimental (dotted lines) and calculated (solid lines) Mn pre-edge absorption spectra for [2(OH)]⁺ and [3(O)]⁺ (oxo and oxyl form and [3(OH)]⁺). Energy shifts and intensities are calibrated to [2(OH)]⁺.

Chemical reactivity

Complex [3(O)]⁺ does not show oxygen atom transfer (OAT) properties towards PPh₃, thioanisole or cyclooctene, supporting the non-electrophilic nature of the oxygen atom. However, it reacts with PMe₂Ph at 0 °C to yield the corresponding oxide with a yield close to 100%, as revealed by ³¹P NMR (Scheme S1, Fig. S4^†). The absorption spectrum of the resulting solution is characteristic of a colorless Mn(II) species, thus indicating a 2 electron reduction of [3(O)]⁺ and an OAT reaction with the phosphine. Preliminary results indicate that [3(O)]⁺ does not react with fluorene (BDE_C–H = 79.5 kcal mol^–1) but does with dihydroanthracene (DHA, BDE_C–H = 78 kcal mol^–1) at room temperature to yield anthracene (Fig. S5^†) and an unidentified mixture of green Mn(III) species (absorption spectroscopy presents several transitions in the region 500–800 nm). This hydrogen atom transfer (HAT) reaction was only observed when the temperature was raised to 20 °C. The resulting mixture of products can therefore be explained by a competition between the reaction with DHA and self-oxidation of [3(O)]⁺.

Discussion

Nuclearity

In previous papers, we reported that the mononuclear forms of the Mn(III) and Mn(IV) complexes obtained with ligand L_e^– are not stable when the exogenous ligand is a water molecule.⁴⁸ Interestingly, lengthening of the diamino-bridge by a single carbon has a dramatic effect on the reactivity of the Mn(III) and Mn(IV) species. In the case of the L_e^– ligand, the high oxidation states of the Mn ions lead to the building of oxo bridges between Mn ions, whereas using a propane diamino-bridge gives access to a mononuclear species. This is related to the formation of a 6-membered metallocycle (propane diamino-bridge) in place of a 5-membered metallocycle (ethane diamino-bridge). Such a variation of the reactivity on increasing the length of the diamino-bridge has been observed in other related Mn and Fe complexes and has been recently discussed.^41,87

Thermodynamic and kinetic aspects

Very few studies have addressed the effects of water (de)protonation on oxidation or reduction potentials of Mn–OH_x (x = 0, 1, 2) complexes. To our knowledge, there are only two studies available. They describe the effects on reduction or oxidation potentials of the (de)protonation of bridging⁸⁸ or terminal⁸⁹ water molecule(s) in dinuclear Mn(III)Mn(IV) complexes. The first report states that deprotonation of di-μ-hydroxo and μ-hydroxo bridges in dinuclear Mn(III)Mn(IV) complexes leads to a decrease in reduction potential of 400 and 700 mV, respectively. The second report shows that deprotonation of a terminal water molecule leads to a decrease in oxidation potential of 400–500 mV for the Mn(III)Mn(III) to Mn(III)Mn(IV) redox couple and about 700 mV for the Mn(IV)Mn(IV) to Mn(III)Mn(IV) redox couple.⁹⁰ The 700 mV value found for the [2(OH₂)]²⁺/[2(OH)]⁺ couple is consistent with the above mentioned values, but the 260 mV value found for the [3(OH)]²⁺/[3(O)]⁺ couple at room temperature is way below the values reported so far.

As mentioned above, the estimated proton transfer rate between [3(OH]²⁺ and [2(OH)]⁺ is of the same order of magnitude compared to the protonation rate (k = 5440 M^–1 s^–1) of a dinuclear Mn(III)Mn(IV) di-μ-oxo-bridged complex reported by Thorp and collaborators.⁶⁹ The authors suggested that such a low value might indicate that proton transfer events are rate-limiting steps in the functioning of dinuclear manganese-containing enzymes. The same could be invoked in the present work for (de)protonation of terminal water at mononuclear manganese sites.

Reactivity of [3(O)]⁺

The reactivity pattern (very low OAT and low HAT abilities) of [3(O)]⁺ has been previously reported for non-porphyrinic penta-coordinated Mn(IV)-oxo species. For these complexes, the absence of electrophilic reactivity could originate from steric hindrance and/or hydrogen bonding.³⁴ The same arguments could be invoked for the proposed [3(O···HLut)]²⁺ species. The coordination of a sixth ligand in trans position to the oxo ligand is also likely to increase the Mn–O distance^30,35 and thus decrease the oxygen atom's electrophilicity. Such trans influence has recently been rationalised in the case of Mn(V)-oxo porphyrins and shown to have an important effect on HAT reactivity (e.g. highly donating ligands trans to the oxo ligand leads to low reactivity).^77,91 Using a pentadentate ligand improves the control of the coordination sphere of the Mn ion, thus leaving only one site for the oxo ligand in contrast to the above mentioned porphyrinoid^27–32 or salen-like^33,35 ligands. Even though in the present study the unambiguous identification of the ligand in trans position to the oxo ligand (phenolate, pyridine or amine group) was not possible, DFT calculations show how it influences the nature of the Mn–O bond by regulating the amount of radical character. Thus, in [3(O)]⁺ only phenolate coordination trans to the oxide allows the development of oxyl character. Similar DFT studies on [MnO(porphyrin)(X)]⁺ (X = H₂O, OH^–, O^2–) have recently shown that both the metal coordination (five-vs. six-coordinate) and the nature of the trans ligand are crucial parameters that influence the amount of oxyl character in the Mn–O bond.^91,92

Relevance to current mechanisms for water-splitting by the OEC

The remarkable ability of the OEC to selectively oxidize water has encouraged a number of groups to explore the mechanism of O₂ evolution using numerous experimental and theoretical model studies. Theoretical analysis of the OEC^25,26 and of synthetic model complexes⁹³ performed by the group of Siegbahn (using the DFT hybrid functional B3LYP) suggest that the formation of a low-lying ligand oxygen radical precursor state is required for the formation of the O–O bond. In these studies the authors suggest that an oxygen radical on manganese reacts with a bridged oxo ligand and they emphasize the role of the electron-accepting manganese ion oriented trans to the O–O bond formation. Recently, the group of Batista investigated the catalytic cycle of water splitting and proposed that the formation of an oxyl radical is also required during the S₃ → S₄ transition by deprotonation of the substrate water molecule ligated to one of the Mn ion of the Mn₄Ca cluster.⁹⁴ Many attempts have been made to prepare chemical models of such Mn species in order to provide experimental evidence for their existence and several examples of Mn(IV)/(V)-oxo chemical models have been reported in the literature.^27–35 Recently the first terminal metal-O bond with a single bond length of 2.042(6) Å was reported in a Ru complex⁹⁵ but to our knowledge no experimental example of a Mn-oxo complex having a noticeable amount of oxyl character has yet appeared in the literature. In the current study the formation of [3(O)]⁺ was only possible using the electrochemical method that allowed the deprotonation of the initially ligated water molecule to the Mn ion. This approach appears to be more relevant to the natural system that gradually reaches high oxidation states in contrast to methods using strong chemical oxidants (oxygen atom transfer agents).^96,97 As mentioned in the Introduction, the substrate water molecules in the OEC of PSII undergo deprotonation as the valence state of the Mn₄Ca cluster increases. The protein matrix around the Mn₄Ca cluster is highly important for the coupling of proton and electron transfer reactions thus preventing high increases in oxidation potential that would occur if true charge accumulations were to occur. Recent models propose that the arginine 357 (R357) residue of the protein subunit CP43 plays an important role in the activation of substrate water.^94,98 While in the present investigation water deprotonation was facilitated by the use of an external base, future work will involve ligands bearing built-in base(s) that will trap the proton(s) released upon electrochemical oxidation of the Mn ion. The use of a base of any kind to mimic the protein environment appears necessary to avoid acid–base comproportionation reactions such as that seen for the oxidation of [2(OH)]⁺.

Conclusions

We have described the sequential (2 × 1 electron/1 proton) proton coupled electrochemical oxidation of a non-porphyrinic six-coordinated Mn(II)-aqua into a mononuclear Mn-oxo complex with a formal oxidation state of +4 (referred to below as Mn(O)²⁺) The intermediate Mn(III)-aquo and Mn(III)-hydroxo complexes were electrochemically prepared and analysed. A pK_a value of 16.5 ± 0.5 was estimated for the water molecule coordinated to the Mn(III) ion. Oxidation of the Mn(III)-hydroxo complex in the absence of base leads to an equimolar mixture of Mn(O)²⁺ and Mn(III)-aquo complexes, via a father–son EC mechanism. Formation of the final Mn(O)²⁺ complex was only possible in the presence of appropriate bases. Complete deprotonation of the coordinated water molecule in the Mn(O)²⁺ complex is confirmed by electrochemical data while the analysis of EXAFS data reveals a gradual shortening of an Mn–O bond upon oxidation from [1(OH₂)]⁺ to [2(OH)]⁺ and [3(O)]⁺. However, the Mn–O_water distance in [3(O)]⁺ can not be considered as a genuine metal–oxygen double bond.⁹⁹ Reactivity experiments, DFT calculations and XANES pre-edge features provide strong evidence that the bonding in the [3(O)]⁺ is indeed best characterized by a Mn(III)-oxyl description. This new species thus broadens the palette of formally high-valent Mn-oxo chemical models. Two points need to be emphasized: (i) a pentadentate ligand improves the control of the Mn ion coordination sphere, (ii) electrochemical oxidation allows access to several Mn species in various oxidation and protonation states that would not be possible using chemical oxidants.

Our work aims at showing that metal-oxo species can be generated in mild condition by preparative electrolysis and that cyclic voltammetry is an appropriate tool for the study of such entities. We should underline the relevance of this approach to electron/proton transfer processes happening in natural systems, compared to the commonly used “oxygen atom transfer” agents for generating metal-oxo complexes. We think this work represents an important new step towards the identification of reactive intermediates responsible for water oxidation in the OEC.

Experimental

Synthesis of ligand LH

Ligand LH was synthesized according to a published procedure,⁴⁸ ethylenediamine being replaced by propanediamine. Spectroscopic characterisations of the final ligand LH are provided here:

¹H-RMN: δ = 1.79 ppm (quint, 2H, N–CH₂–CH₂–CH₂–N); δ = 2.14 ppm (s, 3H, (Py)N–CH₃); δ = 2.38 ppm (t, 2H, N–CH₂–CH₂–CH₂–N); δ = 2.63 ppm (t, 2H, N–CH₂–CH₂–CH₂–N); δ = 3.55 ppm (s, 2H, (CH₃)N–CH₂–Py); δ 3.78 ppm (s, 2H, (Bz)N–CH₂–Py); δ 3.82 ppm (s, 2H, (Py)N–CH₂–Ph); δ = 6.71–6.86 ppm (m, 4H, H–Ph); δ = 7.03–7.72 ppm (m, 6H, H–Py(m,p)); δ = 8.49 ppm (d, 1H, H–Py(o)); δ = 8.56 ppm (d, 1H, H–Py(o))

FT-IR: ν/cm^–1 = 2900 (l, H-Oph); 1590 (f, N=C_py); 1486 (m); 1255 (f, O-Ph); 755(m)

Caution: Perchlorate salts of metal complexes with organic ligands are potentially explosive. Only small quantities of these compounds should be prepared and they should be handled behind suitable protective shields.

Synthesis of [1(OH₂)]ClO₄

500 mg (1.3 × 10^–3 mol) LH was dissolved in 5 mL of degassed acetonitrile (MeCN). 190 μL (1.3 10^–3 mol) of triethylamine was added under argon. A solution of 480 mg (1.3 10^–3 mol) of manganese perchlorate hexahydrate [Mn^II(H₂O)₆](ClO₄)₂ in degassed MeCN was added. After stirring for half an hour, a saturated, degassed aqueous solution of sodium perchlorate (NaClO₄) was added. A white solid precipitated, which was filtered in air and washed with water (73% yield). Single crystals were obtained by diffusion of ether in a MeCN–H₂O mixture (9 : 1) under inert atmosphere.

IR: ν/cm^–1 (KBr): 3501 (OH–H), 1603 (C=N), 1105 (ClO₃–O) ESI MS: m/z for [LMn^II]⁺ (%): 430.2 (100)

Anal. calcd for [LMn^II(OH₂)]ClO₄: C: 50.42 H: 5.34 N: 10.23; Found: C: 50.36 H, 5.14 N, 10.16

CCDC 691308 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

Crystal data of [1(OH₂)]ClO₄

C₂₃H₂₉ Cl₁Mn₁N₄O₆, M = 547.89, crystal dimensions = 0.28 × 0.22 × 0.16 mm³, monoclinic, space group P2₁/n (no. 14), a = 10.4540(8) Å, b = 21.4354(15) Å, c = 10.8135(8) Å, β = 100.507(2)°, V = 2382.5(3) Å3, Z = 4, ρ_c = 1.528 g cm^–3, μ(MoKα) = 0.714 mm^–1, T = 100(1) K, 2θ_max = 31.37°, 14543 reflections measured, 6592 unique (R_int = 0.0177), 5707 (I > 2σ(I)) which were used in all calculations. The final R(F2) = 0.0363 and wR(F2) = 0.0890, ρ_max = 0.838 e^– Å^–3, ρ_min = –0.784 e^– Å^–3.

The extended structure shows a dimeric arrangement of two mononuclear units, each water molecule being hydrogen-bonded tothe phenolate oxygen atom from the other unit (d(H₂O···OH₂) = 4.37 Å).

Electrochemical generation of [3(O)]⁺

A typical procedure is the following

10.7 mg (19.5 × 10^–6 mol) of [1(OH₂)]ClO₄ was dissolved in 10 mL of a mixture of distilled acetonitrile and water (98 : 2) with a 0.2 M NBu₄ClO₄ concentration. The 2 mM solution was placed in a double walled, cylindrical electrochemical cell, degassed with argon and cooled to –40 °C with an ethanol regulated cryostat (Julabo). 40 μL (2 eq) of a molar solution of 2,6-dimethylpyridine (lutidine) in distilled acetonitrile was added to the solution. A platinum grid was placed in a fritted glass compartment containing 2 mL of a 0.2 M NBu₄ClO₄–MeCN solution and used as counter electrode. A flow of argon was constantly maintained over the electrochemical solution to avoid dioxygen contamination. The potential was applied between a cylindrical glassy carbon working electrode and an Ag/AgClO₄ (in MeCN) reference electrode. After transfer of one (stepwise pathway) or two (direct pathway) electron per manganese ion, CVs were run in situ on the resulting solution. UV–visible measurements were carried out on samples taken out of the electrochemical cell. Aliquots of 100 μL were taken out of the solution, introduced in EPR tubes and immediately frozen in liquid nitrogen. Aliquots of 40 μL of solution were placed in sample holders for XAS experiments under argon flux and immediately frozen. For XAS experiments the solution concentration was 5mM.

Reactivity tests

Performed by mixing 200 μL aliquots of the electrochemical solution of [3(O)]⁺ with 5 equivalents of substrate in a UV–vis cuvette. UV–Vis spectra were recorded immediately after mixing the reactants. GC-MS (for dihydroanthracene/anthracene) and ³¹P-NMR (for PMe₂Ph/OPMe₂Ph) spectra were recorded after extraction, evaporation of the solvents and dissolution of the residues in deuterated dichloromethane (GC-MS) or chloroform (³¹P-NMR). The OAT reaction between [3(O)]⁺ and PMe₂Ph was found to be 95% (calculated from ³¹P-NMR peak area integration). No yield could be calculated for the HAT reaction between [3(O)]⁺ and dihydroanthracene, since this substrate and the reaction product (anthracene) could not be separated in the GC conditions used. Moreover, this reaction happens when the temperature is raised and therefore competes with self-degradation of the complex.

Instrumentation and physical methods

X-Ray absorption

Spectra were collected at the Stanford Synchrotron Radiation Laboratory (SSRL) on beamline 7–3 at an electron energy of 3.0 GeV with an average current of 90 mA. The radiation was monochromatized by a Si(220) double-crystal monochromator. The intensity of the incident X-ray was monitored by an N₂-filled ion chamber (I0) in front of the sample. XAS solution samples (5 mM) were filled in 40 μl Plexiglass EXAFS sample holders and kept frozen under liquid N₂ until used. The data were collected as fluorescence excitation spectra with a Ge 30-element detector (Canberra). Energy was calibrated by the pre-edge peak of KMnO₄ (6543.3 eV) for Mn XAS. The standard was placed between two N₂-filled ionization chambers (I₁ and I₂) after the sample. The X-ray flux at 6.4 to 7.1 keV was between 2 to 5.10⁷ photons s^–1 mm^–2 of the sample. Samples were kept at a temperature of 10 K in a liquid helium flow cryostat to minimize radiation damage. Prior to the XAS measurement, EPR spectrum was taken for each sample to check its chemical state.

Data reduction and analysis

Data reduction of the EXAFS spectra was performed as described earlier.¹⁰⁰ The E₀ value of 6560 eV was used to convert the energy axis to the k-space data. Curve fitting was performed using ab initio-calculated phases and amplitudes from the program FEFF 8.2.¹⁰¹ These ab initio phases and amplitudes were used in the EXAFS equation:

$$2{\left[2\left(\mathrm{OH}\right)\right]}^{+}\to {\left[3\left(\mathrm{O}\right)\right]}^{2+}+{\left[2\left({\mathrm{OH}}_2\right)\right]}^{2+}+{\mathbf{e}}^{-}$$

The neighbouring atoms to the central atom(s) are divided into j shells, with all atoms with the same atomic number and distance from the central atom grouped into a single shell. Within each shell, the coordination number N_j denotes the number of neighbouring atoms in shell j at a distance of R_j from the central atom. feff_j(π,k,R_j) is the ab initio amplitude function for shell j, and the Debye–Waller term e^–2σ_j accounts for damping due to static and thermal disorder in absorber-backscattered distances. The mean free path term $e^{-2R_j∕{\gamma }_j\left(k\right)}$ reflects losses due to inelastic scattering, where λ_j(k) is the electron mean free path. The oscillations in the EXAFS spectrum are reflected in the sinusoidal term sin(2kR_j + ϕ_ij(k)), where ϕ_ij(k) is the ab initio phase function for shell j. S₀² is an amplitude reduction factor due to shake-up/shake-off processes at the central atom(s). The EXAFS equation was used to fit the experimental data using N, R, and σ² as variable parameters. In the current analysis, the S₀² value was fixed to 0.85.¹⁰²

Curve fitting results

The best fit results for the Mn EXAFS data from complexes [1(OH₂)]⁺, [2(OH)]⁺, and [3(O)]⁺ are shown in Fig. 8 and the fitting parameters are summarized in Tables S1, S2, and S3.^† As a goodness-of-fit index, we used the R-factor (the absolute difference between theory and data), which is defined as the sum of the squares of the differences between each experimental point and the fit normalized to the sum of the squares of the experimental points.¹⁰³ For complex [1(OH₂)]⁺, the curve fitting was carried out using the distances and coordination numbers obtained from X-ray crystallography. For [2(OH)]⁺, the fitting parameters used for [1(OH₂)]²⁺ were used as initial parameters. The structural parameters obtained from the DFT calculations were taken as initial curve fitting parameters for the [3(O)]⁺ complex. Details of the curve fitting results are described in the supplementary information.^†

DFT calculations

Computational methods: full geometry optimizations were performed with the B3LYP functional^104,105 using all-electron TZVP basis sets for all atoms.^106,107 The broken-symmetry DFT formalism⁷⁵ was followed for locating the most stable form of trans-[3(O)]⁺. Calculations took advantage of the “chain of spheres” (COSX) algorithm for the Hartree–Fock exchange¹⁰⁸ and employed the def2-TZV/J auxiliary basis sets¹⁰⁹ for Coulomb fitting. All calculations were performed with ORCA¹¹⁰ using the default tight convergence criteria for SCF (10^–7 a.u. in total energy) and normal convergence for geometry optimization. To ensure that high numerical accuracy is achieved, larger than default integration grids were used (Grid4 in ORCA convention). The exchange coupling constant for the oxyl form of [3(O)]+ was calculated with Yamaguchi's formalism¹¹¹ assuming a spin Hamiltonian of the form H = –2JS₁S₂. Calculation of the Mn XAS pre-edge was carried out with the B3LYP functional using a recently described TD-DFT procedure,⁸⁶ employing the more flexible CP(PPP) basis set¹¹² and increased integration accuracy for Mn.

Elemental analyses

were carried out at the Services de Microanalyse, ICSN–CNRS, Gif-sur-Yvette, France.

Mass spectrograms

were recorded on a Finnigan MAT95S in a mixture of CH₂Cl₂–MeOH–H₂O (1 : 1 : 1) for ESI-MS mode and on a Thermo Scientific DSQ apparatus for GC-MS. In the latter case, a 15 m capillary column was used, with ammonia as vector gas and electronic impact as ionisation mode.

Gas chromatography

was performed on a GC Fisons 9000 series apparatus, using a BP1 column (length: 15 m, internal diameter: 0.32 mm, thickness: 0.25 μm, vector gas: He) and a FID detector.

FT-IR

spectra were recorded on a Fourier Transform Perkin-Elmer 883, using KBr solid pellets (1% compound in mass).

NMR spectroscopy

¹H-NMR and ³¹P-NMR spectra were recorded on a Bruker DPX 250 MHz with a ONP probe at room temperature. Solvents used are d₁-CDCl₃ (δ = 7.24 ppm) or d₆-DMSO (δ = 2.54 ppm).

EPR spectroscopy

9.4 GHz EPR (X-band) spectra were recorded on a Bruker ELEXSYS 500 spectrometer. For low temperature studies, an Oxford Instrument continuous flow liquid helium cryostat and a temperature control system were used. Solutions spectra were recorded in MeCN containing 0.2 M NBu₄ClO₄. Simulations were performed using the Xsophe software (version 4.0) developed by the department of Mathematics at the University of Queensland, Brisbane, Australia.

UV–Visible

spectra were recorded on a Varian Cary 300 Bio spectrophotometer at 20 °C with 0.1 cm quartz curvettes.

Cyclic voltammetry and bulk electrolysis

all electrochemical experiments were run under Ar atmosphere. Cyclic voltammetry and coulometry measurements were recorded on an EGG PAR potentiostat (M273 model). For cyclic voltammetry, the counter electrode used was a Pt wire and the working electrode a glassy carbon disk carefully polished before each voltammogram with a 1 μm diamond paste, sonicated in ethanol bath and then washed with ethanol. The reference electrode used was an Ag/AgClO₄ electrode (0.3 V vs. SCE electrode), isolated from the rest of the solution by a fritted bridge. For bulk electrolysis, the counter electrode used was a piece of Pt, separated from the rest of the solution with a fritted bridge. The working electrode was a cylinder of glassy carbon. The solvent used was distilled MeCN and NBu₄ClO₄ was added to obtain a 0.1 M supporting electrolyte (20 °C) or a 0.2 M supporting electrolyte (–40 °C). Low temperature regulation was ensured by a Julabo circulation cryostat.

X-Ray diffraction

data were collected on a Kappa X8 APPEX II Bruker diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å). The temperature of the crystal was maintained at the selected value (100 K) by means of a 700 series Cryostream cooling device within an accuracy of ±1 K. The data were corrected for Lorentz polarization, and absorption effects. The structures were solved by direct methods using SHELXS-97¹¹³ and refined against F² by full-matrix least-squares techniques using SHELXL-97 with anisotropic displacement parameters for all non-hydrogen atoms. Treatment on H: H atoms of the ligand were added geometrically and refined by the riding model. H atoms of water moieties were added from the difference Fourier map, and refined by DFIX instructions in which O–H distances were set 0.96(3) Å and H–H distances 1.52(3) Å according to the ideal molecular geometry of water, and with one common isotropic thermal parameter. All calculations were performed by using the Crystal Structure crystallographic software package WINGX.¹¹⁴