Probing Transient Conformational States of Proteins by Solid-State R_1ρ Relaxation-Dispersion NMR Spectroscopy

Abstract

The function of proteins depends on their ability to sample a variety of states differing in structure and free energy. Deciphering how the various thermally accessible conformations are connected, and understanding their structures and relative energies is crucial in rationalizing protein function. Many biomolecular reactions take place within microseconds to milliseconds, and this timescale is therefore of central functional importance. Here we show that R_1ρ relaxation dispersion experiments in magic-angle-spinning solid-state NMR spectroscopy make it possible to investigate the thermodynamics and kinetics of such exchange process, and gain insight into structural features of short-lived states.

Solution-state NMR spectroscopic techniques, and in particular so-called relaxation-dispersion (RD) NMR approaches, have proven very successful for studying μs–ms motion and characterizing the exchanging short-lived conformations.[1] RD NMR techniques exploit the effect of conformational-exchange processes on line broadening, that is, on the relaxation rates of nuclear spin coherence (R₂, R_1ρ). By quantifying spin relaxation rates in the presence of a variable radiofrequency (rf) field, RD approaches provide information about relative populations and exchange rates, as well as chemical shifts of short-lived conformational states, and thus about local structure.[1, 2] In the case of very large assemblies or insoluble aggregates, where solution-state NMR is severely challenged, magic-angle-spinning solid-state NMR (MAS ssNMR) is rapidly emerging as a tool for the study of structure and dynamics. However, the characterization of conformational-exchange dynamics in the solid state remains challenging. Herein, we show a ssNMR approach in which amide-¹⁵N R_1ρ RD data, that is, the rate of coherence decay under ¹⁵N spin-lock fields of variable field strengths, are quantitatively analyzed and interpreted in terms of conformational dynamics, providing insight into short-lived states in terms of chemical shifts and bond vector orientations. We investigate the robustness of this approach by studying a conformational flip in crystalline ubiquitin.

Conformational fluctuations between different states expose a given nuclear spin in a protein to different local environments, which are characterized by different bond geometries. A simple case, exchange between two states, is shown in Figure 1 a. As a result of conformational-exchange dynamics, a given spin will experience a fluctuation of its chemical shift (CS), as well as of its bond vector orientations and, thus, dipolar coupling interactions with neighboring spins and CS anisotropies (CSA). In solution-state NMR, dipolar coupling and CSA interactions are averaged to zero by Brownian movement (molecular tumbling). Consequently, only fluctuations of the isotropic CS are relevant when considering conformational dynamics on the microsecond to millisecond timescale. R_1ρ RD experiments in solution can thus only pick up conformational dynamics if they involve a change in the isotropic CS. The relevant theory is well established, and the effects of exchange can be described by the Bloch–McConnell equations.[3]

Figure 1.

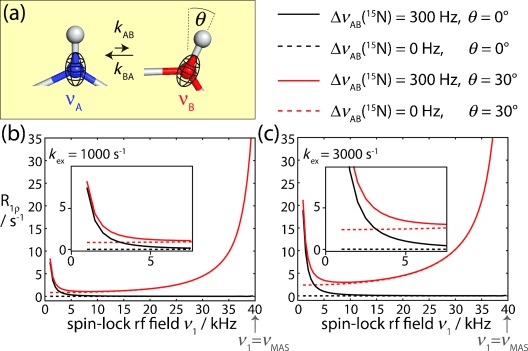
The effect of conformational exchange processes on ¹⁵N R_1ρ relaxation rates, as revealed by numerical simulations. a) Schematic representation of a two-spin N–H system that is in dynamic exchange between a minor and a major conformation, which differ in the ¹⁵N chemical shift and the orientation of the NH bond vector. The ¹⁵N CSA tensor is assumed to be collinear with the NH bond. b,c) Simulated ¹⁵N R_1ρ RD profiles obtained for this two-spin system, assuming relative populations of p_B=10 %, p_A=90 %. Different scenarios were assumed, regarding the ¹⁵N isotropic CS (solid/dotted lines), and the change of the bond angle orientation, θ, occurring during exchange (red/black), as indicated. More simulations are shown in Figure S1. The inserts in (b,c) show enlargements of the low-rf field regime.

In MAS ssNMR, where stochastic molecular tumbling is absent, anisotropic interactions (dipolar couplings and CSA) are periodically modulated by magic-angle sample spinning (MAS), and are averaged out over a sample rotation period (in the μs range). This averaging leads to the line narrowing required for high-resolution studies. However, when considering molecular dynamics and rf irradiation, as is the case in R_1ρ RD experiments, the various time-dependent processes (sample rotation, rf irradiation, and conformational exchange) may interfere, leading to different decay processes. Consequently, the situation is more complex than in solution-state NMR experiments.[4] Before considering experimental implementations of MAS ssNMR R_1ρ RD experiments, we thus investigate the properties of ¹⁵N R_1ρ decay in an exchanging system undergoing MAS by numerical simulations.

Figure 1 b,c shows simulated ¹⁵N R_1ρ RD profiles for a ¹H–¹⁵N spin pair that undergoes exchange between two states, populated to 90 % and 10 %, respectively, and which is subject to MAS and a ¹⁵N spin-lock rf field of variable amplitude. We assumed different exchange scenarios that involve either only a fluctuation of the ¹⁵N spin’s isotropic CS, or a change of the NH bond orientation within the molecular frame of reference, or both. The results of these simulations can be summarized as follows: 1) If exchange takes place between two states that differ only in their isotropic CS, but not in bond orientations, R_1ρ RD profiles can be described by the Bloch–McConnell formalism (black curves in Figure 1 b,c), as in solution-state NMR experiments.[1a] 2) If bond angle fluctuations are involved upon conformational exchange (thus reorienting the dipolar coupling and CSA interactions), the situation gets more complex. R_1ρ rate constants in this case are overall increased, because the fluctuating anisotropic interactions induce relaxation.[5] Of particular note for the present discussion is the fact that the increase of R_1ρ rates is particularly pronounced when the spin-lock field strength (ν₁) approaches the sample rotation frequency (ν_MAS), that is, close to the so-called rotary resonance conditions.[6]

Importantly, as shown in Figure 1 and Figure S1 and reported previously,[4, 5] conformational exchange broadens these rotary resonance recoupling conditions, and the R_1ρ relaxation rate in the vicinity of the rotary resonance conditions depends on the kinetics of the exchange, the relative populations of the involved states, and the jump angle between the different conformations. Taken together, these simulations demonstrate that MAS ssNMR R_1ρ RD experiments may provide rich information about conformational exchange, and that they may report not only on chemical shift fluctuations between the states (as is the case in solution-state NMR measurements), but also on the bond angles by which a short-lived “excited” state differs from the predominant “ground-state” conformation.

Exploiting this potential of MAS ssNMR R_1ρ RD experiments to quantitatively analyze conformational exchange in proteins has so far been hampered by the fact that R_1ρ decay rates in ssNMR not only contain a dynamics-related component, but also have substantial contributions from coherent decay mechanisms (i.e. dipolar dephasing). Dipolar dephasing contributes to R_1ρ decay particularly in multispin systems, such as proteins with numerous proton spins. Extracting the dynamics-related part of R_1ρ decay rates thus requires suppressing this dipolar-dephasing part. As shown recently, at high MAS frequencies of roughly 40 kHz or higher, and spin-lock fields above 15 kHz this dipolar dephasing is significantly reduced and appears negligible even in the proton-rich environment of a protein;[7] however, the requirement for high spin-lock fields eliminates the possibility of observing R_1ρ RD in the window below 5–10 kHz spin-lock field, where RD profiles are particularly sensitive to isotropic CS fluctuations.

We circumvent these limitations here by employing high degrees of sample deuteration, which strongly reduces the dipolar-dephasing contribution to ¹⁵N R_1ρ rates.[8] In highly deuterated samples, that is, samples that are fully deuterated at non-exchangeable sites, and in which the exchangeable (amide) sites are (partly) reprotonated, the proton dipolar coupling network is strongly diluted, allowing for high-resolution highly sensitive proton-detected ssNMR spectra, and long ¹⁵N coherence life times.[8, 9] Figure 2 a shows representative examples of residue-wise R_1ρ RD profiles obtained on a sample of deuterated microcrystalline ubiquitin that has been reprotonated at exchangeable sites to 50 %.

Figure 2.

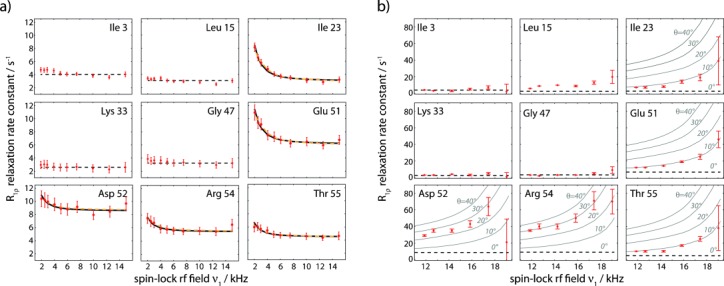
Experimental ¹⁵N RD data obtained on perdeuterated ubiquitin at 300 K, obtained from proton-detected experiments. Plotted is the on-resonance R_1ρ, that is, corrected for chemical-shift offset (see the Supporting Information). a) RD profiles obtained at 39.5 kHz MAS and low spin-lock rf field strengths of 2–15 kHz. Solid black lines show the result of a Bloch–McConnell fit of a two-state exchange model using only R_1ρ-derived data, while orange lines are derived from a fit that includes CPMG data for residues 23, 27, and 55 at 600 MHz, as reported earlier (see Figure S8). Straight dashed lines (constant R_1ρ rate) in panels (a) and (b) show the relaxation rate constant obtained at 39.5 kHz MAS and 15 kHz spin-lock field strength, which is considered as free from exchange effects. b) RD profiles obtained at 20 kHz MAS on a fully deuterated, 20 % reprotonated sample of ubiquitin. Solid lines show simulated R_1ρ RD profiles assuming an exchange rate k_ex=2900 s⁻¹ and population p_B=9.3 %. All available RD profiles, as well as experimental details are shown in the Supporting Information.

¹⁵N R_1ρ data have been measured at a MAS frequency of 39.5 kHz, and spin-lock rf field strengths of 2–15 kHz, that is, far from the n=1 rotary resonance condition (which is at 39.5 kHz). The reported rate constants are on-resonance R_1ρ, that is, the R₁ contribution in the tilted rotating frame has been eliminated (using standard formulae,[1a] see the Supporting Information).

For the vast majority of residues, for example, residues Ile 3, Leu 15, Lys 33, and Gly 47 in Figure 2 a, we find that the RD profiles are flat over the entire range of rf field strengths. This finding confirms that coherent dephasing is indeed efficiently suppressed by deuteration and fast MAS; it further suggests that nonflat R_1ρ RD profiles can safely be ascribed to motional processes. Indeed, for a few residues we observe nonflat R_1ρ RD curves, that is, increased relaxation rate constants at low spin-lock rf fields, as expected for the Bloch–McConnell regime of exchange. The residues with such nonflat ¹⁵N R_1ρ RD profiles are located in a well-defined region of ubiquitin, in the N-terminal part of the helix and a loop that is hydrogen-bonded to this helix (residues Ile 23, Lys 27, Glu 51, Asp 52, Arg 54, Thr 55; see Figure 3 and Figure S5). Conformational exchange in this region of the protein has been reported in numerous studies in solution,[10] and we have recently also reported conformational exchange in this part of the protein in microcrystals from Carr–Purcell–Meiboom–Gill (CPMG) RD and multiple-quantum relaxation experiments.[11]

Figure 3.

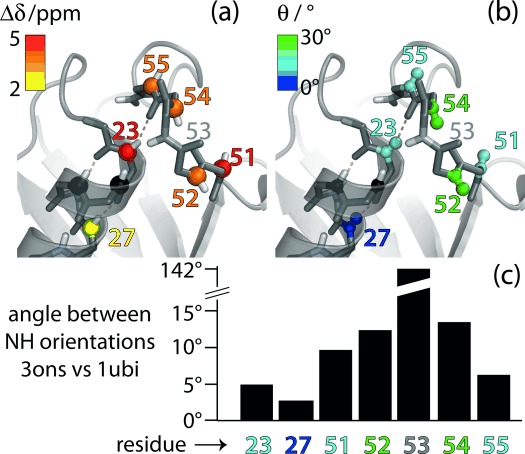
Residues involved in the conformational exchange process in ubiquitin. a) Residue-wise chemical-shift differences Δδ (obtained from data in Figure 2 a) and b) jump angles θ (obtained from Figure 2 b) are plotted onto the structure of ubiquitin crystals used in this study (PDB 3ons). Amides 24 and 25 (black spheres) are invisible in NH correlation spectra, presumably due to exchange broadening.[11] c) Residue-wise differences of the N–H orientations in the crystal structure used here (type-II β-turn) and in a structure featuring a type-I β-turn (PDB 1ubi). These angles were obtained by aligning the two structures to all secondary structure elements and extracting the direction of the respective N–H bonds.

In order to obtain quantitative insight into the exchange process occurring in this part of the protein, we have fitted an exchange model to the R_1ρ RD profiles of these residues using the Bloch–McConnell formalism. The application of this formalism is strictly speaking not correct in MAS ssNMR if bond reorientation is involved (cf. Figure 1). However, it appears justified here by the fact that the RD curves of Figure 2 were collected in a range of rf fields well outside the rotary-resonance conditions; bond angle fluctuations have only very small impact on R_1ρ RD in this regime, especially when changes in the bond vector orientations are small (cf. Figure 1). That bond angle fluctuations are indeed rather small is justified a posteriori with independent measurements (see below).We fitted a two-state exchange model to the R_1ρ-derived RD profiles of residues 23, 27, 51, 52, 54, and 55 (Figure 2 and Figure S8). Because of their close spatial proximity, we assumed that these residues are involved in the same exchange process. Consequently, the exchange rate constant, k_ex=k_AB+k_BA and minor-state population, p_B, were assumed to be identical for all these residues, and only the chemical-shift differences between the major and minor states, Δδ, which are sensitive to changes in the local environment, were assumed to be specific to individual residues. Solid lines in Figure 2 a show best-fit curves of this fit. The fit yields an exchange rate constant k_ex of 8600±1700 s⁻¹ and a minor-state population p_B of 3.1±1.2 %. Residue-wise chemical-shift differences Δδ are in the range of 2–5 ppm (all values are reported in Table S1). In order to investigate the reliability of these results, which were obtained from a single R_1ρ RD measurement, we explored the inclusion of additional, independent data sets: a first possibility, often used in solution-state NMR, would be the measurement of R_1ρ RD at additional static magnetic field strengths (requiring, however, access to another spectrometer equipped with a fast-MAS probe). As an alternative, we use here a combined fit with CPMG RD data, obtained previously under similar conditions of fast MAS and deuteration.[11] CPMG RD is sensitive to exchange processes on μs–ms timescales, making a combined fit with R_1ρ possible. Such an analysis of the present R_1ρ RD data with CPMG data, also obtained at a magnetic field strength of 14.1 T, yields values of Δδ that are very similar to those obtained from the above fit of only R_1ρ RD data (see Table S1). The obtained exchange rate k_ex is 2900±140 s⁻¹, and the population p_B is 9.3±0.6 %. Although these values slightly differ from the values obtained from fitting only a single R_1ρ RD data set (where k_ex=8600±1700 s⁻¹, p_B=3.1±1.2 %) it is noteworthy that the fit curves of the combined R_1ρ/CPMG fit, shown as orange lines in Figure 2 a, are almost indistinguishable from the fits of R_1ρ data only, which shows that the present data are in excellent agreement with independent CPMG data. The differences of the fitted parameters point to the well-known fact that it is difficult to disentangle all fit parameters from a single measurement (here, a single B₀ field strength).

The R_1ρ RD experiment has advantages over the previously proposed CPMG RD experiment:[11] In solids, even at fast MAS and high degrees of deuteration, measured R₂ rates contain a substantial amount of dipolar dephasing, in contrast to R_1ρ (see Figure S10).[7] This has two important consequences: 1) Due to the more rapid coherence decay, sensitivity in the CPMG experiment[11] is significantly lower than in the R_1ρ experiment. 2) The remaining coherent contributions to the effective R₂ rates in a CPMG experiment are almost, but not entirely independent of the CPMG frequency.[11] Thus, observed variations of the effective R₂ in the CPMG experiment may to some extent be artifactual. We note that the timescales probed by R_1ρ and CPMG RD experiments overlap but are not exactly identical, such that the approaches should be considered as complementary.

In solution, the same part of ubiquitin undergoes conformational exchange, but the process is much faster than observed here. Even at a temperature 20 K lower than what was used here, the exchange occurs much faster than here (k_ex≈12 500–25 000 s⁻¹).[10] At 298 K, a similar temperature to that used here, the R_1ρ RD profile in solution for example, for Ile 23 is flat (to within 0.5 s⁻¹),[10a] which is in stark contrast to the pronounced dispersion of R_1ρ seen in crystals in this study. This finding unequivocally establishes that the motional process in microcrystals is slower than in solution. Intermolecular contacts are at the origin of this slowdown, acting as additional energy barriers for motion in the crystal.[11]

Having thus established that R_1ρ RD experiments at high MAS frequencies can provide information about the thermodynamics and kinetics of exchange, as well as site-specific chemical-shift values of the minor states, akin to the situation in solution-state NMR experiments, we investigated whether additional structural information about the minor state may be obtained. As Figure 1 shows, ¹⁵N R_1ρ RD profiles in the vicinity of the rotary resonance condition (ν₁≈ν_MAS) are sensitive to the angle by which the NH bond (i.e. the dipolar coupling and ¹⁵N CSA) is altered upon the conformational transition. For technical reasons we refrained from performing such measurements at high MAS frequencies, because the required high spin-lock field strengths (ν₁≈ν_MAS) would challenge the integrity of hardware and sample. Instead, we performed experiments at lower MAS frequency (20 kHz), where the rotary-resonance condition is met at lower rf field. To ensure that coherent contributions to the ¹⁵N R_1ρ decay remain negligible even at slower MAS, we employed a higher degree of deuteration (20 % reprotonation of amide sites instead of 50 %); the larger volume of the sample rotor that can be used at lower MAS frequency compensates for the resulting sensitivity loss. Figure 2 b shows representative examples of ¹⁵N R_1ρ RD profiles obtained at spin-lock field strengths of 12–19 kHz. Many of the residues, such as Ile 3, Leu 15, Lys 33, and Gly 47 in Figure 2 b, show flat RD profiles over the entire range of sampled spin-lock field strengths, or only show an increase when the spin-lock field strength is within 2–3 kHz of the n=1 rotary resonance condition. Interestingly, the obtained plateau values are similar to the values obtained at fast MAS, implying that coherent contributions to R_1ρ are indeed efficiently suppressed, even at the lower MAS frequency. An increase of R_1ρ when approaching the rotary resonance condition (ν₁=ν_MAS) can be understood from partial recoupling of dipolar coupling and CSA interactions.[6] It could thus arise even in the absence of μs conformational exchange. Strikingly, however, those residues that have the strongest dependency of R_1ρ on the spin-lock field strength are the ones for which we have detected conformational exchange also through the isotropic CS mechanism, namely residues 23, 27, 51, 52, 54, and 55 (Figure 2). Based on the simulations in Figure 1, which reveal that the angle of reorientation upon exchange impacts the RD profiles, we estimated the jump angles that can explain the RD profiles of Figure 2 b. Gray curves in Figure 2 b show simulations that assume different angles. Extracted jump angles vary between the residues, and the largest angular fluctuations are observed for residues Asp 52 and Arg 54 (20–30°), while residues Ile 23, Lys 27, Glu 51, and Thr 55 show smaller reorientational motion along the exchange process, with jump angles of 10° or below. Residue Gly 53 has spectral overlap and no data are available.

It is interesting to compare these data with structural models of the exchange process. As deduced from various NMR data,[10] mutations,[12] and inspections of different crystal structures of ubiquitin, the proposed mechanism of the exchange process involves an approximately 140° flip of peptide plane D52/G53, and a rearrangement of the hydrogen bonding between this loop and the helix comprising residues 23–33. Figure 3 shows that in the microcrystal used in this study the NH bond of residue 53 points towards the helix (a so-called type-II β-turn); in most other structures deposited in the Protein Data Bank it points outward (type-I β-turn, see Figure S9). We speculate that the conformational exchange observed in our sample may be a transition between these two types of β-turns. To test this hypothesis, we extracted the angles by which the NH orientations differ in representative X-ray structures featuring type-I and type-II β-turns. The largest differences in the NH orientations are found for Asp 52 and Arg 54, which are neighboring the peptide plane of Gly 53 that is flipped. Residues 23, 27, 51, and 55 show smaller differences in their respective NH bond orientations (Figure 3 c). This is in good qualitative agreement with our data (Figure 2 b), which also reveal the largest reorientational motion for Asp 52 and Arg 54, and significantly smaller jump angles for the other residues involved in the exchange process. These data indicate that R_1ρ RD data can provide structural insight into excited states, in addition to chemical-shift data. This feature, together with the increased capabilities of relating chemical shifts to structure, may be of great value in determining the structures of short-lived conformations, including systems not suitable for atomic resolution studies by solution-state NMR spectroscopy, such as very large or insoluble proteins.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

miscellaneous_information