Abstract
In this paper, we derive interrelations of graph distance measures by means of inequalities. For this investigation we are using graph distance measures based on topological indices that have not been studied in this context. Specifically, we are using the well-known Wiener index, Randić index, eigenvalue-based quantities and graph entropies. In addition to this analysis, we present results from numerical studies exploring various properties of the measures and aspects of their quality. Our results could find application in chemoinformatics and computational biology where the structural investigation of chemical components and gene networks is currently of great interest.
Introduction
Methods to determine the structural similarity or distance between graphs have been applied in many areas of sciences. For example, in mathematics [1], [2], [3], in biology [4], [5], [6], in chemistry [7], [8] and in chemoinformatics [9]. Other application-oriented areas where graph comparison techniques have been employed can be found in [10], [11], [12]. Note that the terms ‘graph similarity’ or ‘graph distance’ are not unique and strongly depend on the underlying concept. The two main concepts which have been explored extensively are exact and inexact graph matching, see [13], [3]. Exact graph matching [2], [3] relates to match graphs based on isomorphic relations. An important example is the so-called Zelinka distance [3] which requires computing the maximum common subgraphs of two graphs with the same number of vertices. However, it is evident that this technique is computationally demanding as the subgraph graph isomorphism problem is NP-complete [14]. In contrast to this, inexact or approximative techniques for comparing graphs match graphs in an error-tolerant way, see [13]. A highlight of this development has been the well-known graph edit distance (GED) due to Bunke [15]. String-based techniques also fit into the scheme of approximative graph comparison techniques [1], [16]. This approach aims to derive string representations which capture structural information of the underlying networks. By using string alignment techniques, one is able to compute similarity scores of the derived strings instead of matching the graphs by using classical techniques. Concrete examples thereof can be found in [1], [16].
As mentioned, numerous graph similarity and distance measures have been explored. But in fact, there is still a lack of a mathematical framework to explore interrelations of these measures. Suppose let 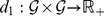 and
and 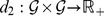 be two comparative graph measures (i.e., graph similarity or distance measures) which are defined on the graph class
be two comparative graph measures (i.e., graph similarity or distance measures) which are defined on the graph class 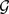 . Typical questions in this idea group would be to prove interrelations of the measures by means of inequalities such as
. Typical questions in this idea group would be to prove interrelations of the measures by means of inequalities such as 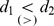 . For instance, inequalities involving graph complexity measures have been inferred by Dehmer et al. [17], [18].
. For instance, inequalities involving graph complexity measures have been inferred by Dehmer et al. [17], [18].
The main contribution of this paper is to infer interrelations of graph distance measures. To the best of our knowledge, this problem has not been tackled so far when using graph distance measures. However, interrelations of topological indices interpreted as complexity measures have been studied, see [7], [19], [20], [17], [18]. For instance, Bonchev and his co-workers investigated interrelations of branching measures by means of inequalities [7], [19], [20]. Dehmer [17] examined relations between information-theoretic measures which are based on information functionals and between classical and parametric graph entropies [18]. We here put the emphasis on graph distance measures which are based on so-called topological indices. These measures themselves have not yet been studied. Note that we only consider distance measures (without loss of generality) as they can be easily transformed into graph similarity measures [21]. In order to define these measures concrete, we employ an existing distance measure (see Eq. (6)) and the well-known Randić index [22], the Wiener index [23], eigenvalue-based measures [24], and graph entropies [17], [25]. Also, we discuss quality aspects of the measures and state conjectures evidenced by numerical results.
Methods and Results
Topological Indices and Preliminaries
In this section, we introduce the topological indices which are used in the paper. A topological index [23] is a graph invariant, defined by
| (1) |
Simple invariants are for instance the number of vertices, the number of edges, vertex degrees, degree sequences, the matching number, the chromatic number and so forth, see [26].
We emphasize that topological indices are graph invariants which characterize its topology. They have been used for examining quantitative structure-activity relationships (QSARs) extensively in which the biological activity or other properties of molecules are correlated with their chemical structures [27]. Topological graph measures have also been applied in ecology [28], biology [29] and in network physics [30], [31]. Note that various properties of topological graph measures such as their uniqueness and correlation ability have been examined too [32], [33].
Suppose 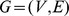 is a connected graph. The distance between the vertices
is a connected graph. The distance between the vertices  and
and  of
of 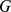 is denoted by
is denoted by  . The Wiener index of
. The Wiener index of 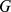 is denoted by
is denoted by 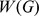 and defined by
and defined by
| (2) |
The name Wiener index or Wiener number for the quantity defined is common in the chemical literature, since Wiener [34] in 1947 seems was the first who considered it. For more results on the Wiener index of trees, we refer to [35].
In 1975, Randić [36] proposed the topological index  (
(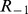 and
and 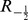 ) by using the name branching index or connectivity index, suitable for measuring the extent of branching of the carbon-atom skeleton of saturated hydrocarbons. Nowadays this index is also called the Randić index. In 1998, Bollobás and Erdös [37] generalized this index by replacing
) by using the name branching index or connectivity index, suitable for measuring the extent of branching of the carbon-atom skeleton of saturated hydrocarbons. Nowadays this index is also called the Randić index. In 1998, Bollobás and Erdös [37] generalized this index by replacing 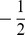 by any real number
by any real number  , which is called the general Randić index. In fact, the Randić index and the general Randić index became the most popular and most frequently employed structure descriptors used in structural chemistry [38]. For a graph
, which is called the general Randić index. In fact, the Randić index and the general Randić index became the most popular and most frequently employed structure descriptors used in structural chemistry [38]. For a graph 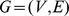 , the Randić index
, the Randić index 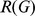 of
of 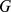 has been defined as the sum of
has been defined as the sum of 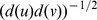 over all edges
over all edges 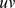 of
of 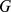 , i.e.,
, i.e.,
| (3) |
where 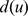 is degree of a vertex
is degree of a vertex  of
of 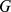 . The zeroth-order Randić index due to Kier and Hall [6] is
. The zeroth-order Randić index due to Kier and Hall [6] is
| (4) |
For more results on the Randić index and the zeroth-order Randić index, we refer to [39], [22], [38].
For a given graph 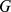 with
with  vertices,
vertices,  are the eigenvalues of
are the eigenvalues of 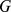 . The energy of a graph
. The energy of a graph 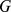 , denoted by
, denoted by 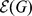 , has been defined by
, has been defined by
| (5) |
due to Gutman in 1977 [40]. For more results on the graph energy, we refer to [41], [24], [42].
Novel Graph Distance Measures
Now we define the distance measure [21]
| (6) |
which is a mapping 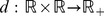 . Obviously it holds
. Obviously it holds 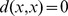 ,
, 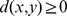 , and
, and 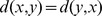 . In order to translate this concept to graphs, we employ topological indices and obtain
. In order to translate this concept to graphs, we employ topological indices and obtain
| (7) |
Further we infer a relation between the maximum value of  and the extremal values of
and the extremal values of 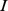 .
.
Observation 1
Let
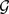 be a class of graphs.
Suppose
be a class of graphs.
Suppose
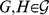 , then
, then
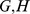 are the two graphs attaining the maximum value of
are the two graphs attaining the maximum value of
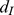 if and only if
if and only if
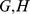 are the graphs attaining the maximum and minimum value of
are the graphs attaining the maximum and minimum value of
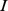 , respectively.
, respectively.
Proof. Let 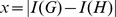 , then
, then 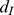 is a monotone increasing function on
is a monotone increasing function on  . Therefore, the maximum value of
. Therefore, the maximum value of 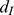 is attained if and only if the maximum value of
is attained if and only if the maximum value of 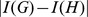 is attained.
is attained. 
From Observation 1 and some existing extremal results of topological indices, we obtain some sharp upper bounds of 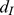 for some classes of graphs. As an example, we list some of those results for trees.
for some classes of graphs. As an example, we list some of those results for trees.
Theorem 1
Let
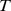 and
and
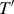 be two trees with
be two trees with
 vertices. Denote by
vertices. Denote by
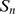 and
and
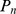 the star graph and path graph with
the star graph and path graph with
 vertices, respectively.
vertices, respectively.
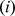 . The maximum value of
. The maximum value of 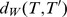 is attained when
is attained when 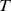 and
and 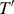 are
are 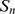 and
and 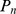 , respectively.
, respectively.
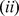 . The maximum value of
. The maximum value of 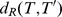 is attained when
is attained when 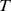 and
and  are
are 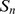 and
and 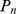 , respectively.
, respectively.
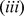 . The maximum value of
. The maximum value of 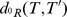 is attained when
is attained when 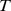 and
and 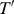 are
are 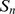 and
and 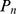 , respectively.
, respectively.
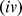 . The maximum value of
. The maximum value of  is attained when
is attained when  and
and 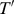 are
are 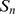 and
and 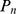 , respectively.
, respectively.
Interrelations of Graph Distance Measures
Observe that 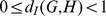 , which implies that
, which implies that 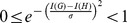 . Some trivial properties of
. Some trivial properties of 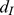 are as follows. Let
are as follows. Let 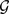 be a class of graphs and
be a class of graphs and 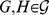 . We get
. We get
| (8) |
| (9) |
| (10) |
However, 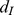 is not a metric graph distance measure, since the triangle inequality
is not a metric graph distance measure, since the triangle inequality  for
for 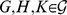 , does not hold generally. Actually, we obtain a modified version of the triangle inequality.
, does not hold generally. Actually, we obtain a modified version of the triangle inequality.
Theorem 2
Let
 be a topological index. Let
be a topological index. Let
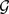 be a class of graphs and
be a class of graphs and
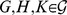 . If
. If
| (11) |
then we have 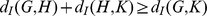 .
.
Proof. We now suppose 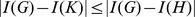 , since the proof of the other case is similar.
, since the proof of the other case is similar.
From the inequality 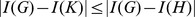 , we get
, we get
| (12) |
Since  , together with Eq. (12), we have
, together with Eq. (12), we have
| (13) |
Therefore, we have the following inequality,
| (14) |
i.e., 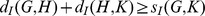 .
. 
We emphasize if the Inequalities 11 are satisfied, the modified triangle inequality holds. In practice, the triangle inequality may not be absolutely necessary (e.g., for clustering and classification problems) and is often required to prove properties of the measures.
Theorem 3
Let
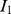 and
and
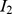 be two topological indices. Let
be two topological indices. Let
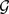 be a class of graphs and
be a class of graphs and
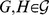 . If
. If
| (15) |
then
| (16) |
where
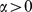 is a constant.
is a constant.
Proof. Since
| (17) |
we obtain
| (18) |
Thus
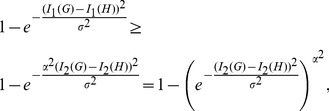 |
(19) |
i.e.,
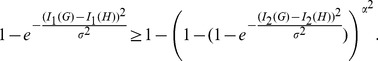 |
(20) |
Thus,
| (21) |
The proof is complete. 
Suppose 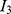 is also a topological index. Then if
is also a topological index. Then if
| (22) |
we derive similarly
| (23) |
where  is a constant. Therefore, we obtain the following theorem.
is a constant. Therefore, we obtain the following theorem.
Theorem 4
Let
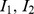 and
and
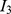 be three topological indices. Let
be three topological indices. Let
 be a class of graphs and
be a class of graphs and
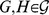 . If
. If
| (24) |
then we infer
| (25) |
where
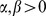 are constants.
are constants.
Theorem 5
Let
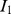 and
and
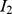 be two topological indices. Let
be two topological indices. Let
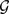 be a class of graphs and
be a class of graphs and
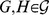 . If
. If
| (26) |
then we get
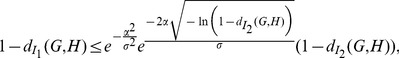 |
(27) |
where
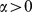 is a constant.
is a constant.
Proof. Since
| (28) |
we infer
| (29) |
And therefore,
| (30) |
| (31) |
 |
(32) |
Hence,
| (33) |
From the definition of  , i.e.,
, i.e.,
| (34) |
we obtain that
| (35) |
Finally, by substituting (35) into (33), we get the desired result. 
Suppose 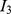 is also a topological index. Then if
is also a topological index. Then if
| (36) |
we have
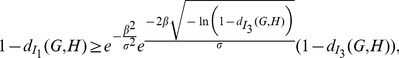 |
(37) |
where 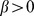 is a constant. Therefore, we obtain the following theorem.
is a constant. Therefore, we obtain the following theorem.
Theorem 6
Let
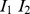 and
and
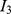 be three topological indices. Let
be three topological indices. Let
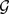 be a class of graphs and
be a class of graphs and
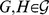 . If
. If
| (38) |
then we have
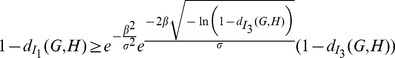 |
(39) |
and
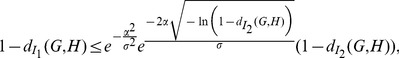 |
(40) |
where
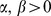 are constants.
are constants.
Theorem 7
Let
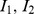 and
and
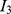 be three topological indices. Let
be three topological indices. Let
 be a class of graphs and
be a class of graphs and
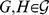 . If
. If
| (41) |
then we infer
| (42) |
Proof. Since
| (43) |
we derive
| (44) |
And therefore,
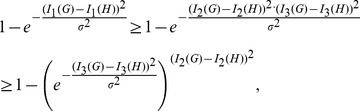 |
(45) |
i.e., 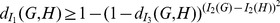 . Hence we obtain
. Hence we obtain
| (46) |
which implies that
| (47) |
By substituting (35) into (47), we easily obtain the assertion of the theorem. 
By performing a similar proof as in Theorem 7, we obtain a more general result.
Theorem 8
Let
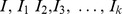 be topological indices. Let
be topological indices. Let 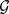 be a class of graphs and
be a class of graphs and
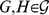 . If
. If
| (48) |
we infer
| (49) |
Theorem 9
Let
 and
and
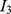 be three topological indices. Let
be three topological indices. Let
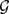 be a class of graphs and
be a class of graphs and
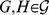 . If
. If
| (50) |
where 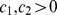 , then we get
, then we get
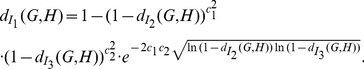 |
(51) |
Proof. Since
| (52) |
we derive
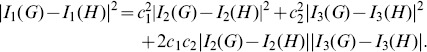 |
(53) |
Therefore,
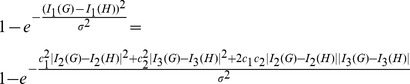 |
(54) |
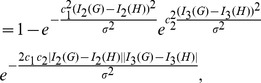 |
(55) |
which implies
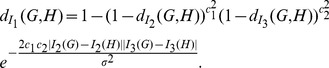 |
(56) |
By applying the substitutions
| (57) |
and
| (58) |
into (56), we obtain the final result. 
By performing a similar proof as in Theorem 9, we obtain a more general result again.
Theorem 10
Let
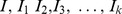 be topological indices. Let
be topological indices. Let
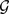 be a class of graphs and
be a class of graphs and
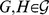 . If
. If
| (59) |
where
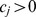 for
for
 , then we infer
, then we infer
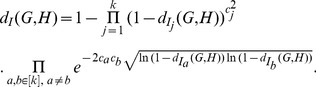 |
(60) |
Graph Distance Measures Based on Randić Index
In this section, we consider the values of the graph distance measure based on the Randić index and other topological indices for some classes of graphs. Denote by 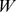 and
and 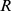 the Wiener index and Randić index, respectively.
the Wiener index and Randić index, respectively.
Theorem 11
Let
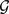 be a class of regular graphs with
be a class of regular graphs with
 vertices and
vertices and
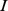 is an arbitrary topological index. For two graphs
is an arbitrary topological index. For two graphs
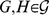 , we infer
, we infer
| (61) |
Proof. Let 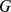 and
and 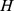 be two regular graphs of order
be two regular graphs of order  . By the definition of the Randić index, we obtain that
. By the definition of the Randić index, we obtain that 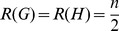 , which implies that
, which implies that  . Therefore, we infer
. Therefore, we infer 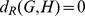 . Since
. Since 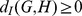 for any topological index, then we obtain the desired inequality.
for any topological index, then we obtain the desired inequality.
By using the definition of the zeroth-order Randić index for two graphs with the same degree sequences, we obtain that 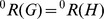 . Therefore, we get the following theorem.
. Therefore, we get the following theorem.
Theorem 12
Let
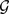 be a class of graphs with the same degree sequences and
be a class of graphs with the same degree sequences and
 is an arbitrary topological index. Then for two graphs
is an arbitrary topological index. Then for two graphs
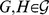 , we infer
, we infer
| (62) |
For a given graph 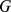 of order
of order  , we get
, we get 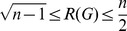 (see [39]). Thus,
(see [39]). Thus,
| (63) |
From (63), we infer an upper bound for 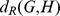 .
.
Theorem 13
Let
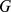 and
and
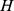 be two connected graphs of order
be two connected graphs of order
 . Then we get
. Then we get
| (64) |
The equality holds if and only if
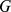 and
and
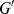 are
are
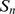 and a regular graph, respectively.
and a regular graph, respectively.
A path 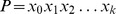 is pendent if
is pendent if 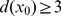 ,
, 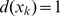 and
and 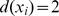 for all
for all 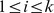 . Especially, a vertex
. Especially, a vertex  is pendent if
is pendent if 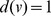 . Suppose
. Suppose  and
and  are two pendent vertices, and
are two pendent vertices, and 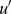 the unique neighbor of
the unique neighbor of  . We define an operation as follows: deleting the edge
. We define an operation as follows: deleting the edge 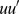 and adding the edge
and adding the edge 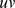 . We call this operation “transfer
. We call this operation “transfer  to
to  ”.
”.
Theorem 14
Let
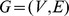 be a graph with
be a graph with
 vertices. Denote by
vertices. Denote by
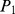 and
and
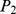 the two pendent paths attaching to the same vertex such that
the two pendent paths attaching to the same vertex such that
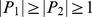 . Denote by
. Denote by
 the graph obtained by transferring the pendent vertex of
the graph obtained by transferring the pendent vertex of
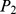 to the pendent vertex of
to the pendent vertex of
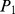 . Then we have
. Then we have
| (65) |
Proof. Let 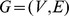 be a graph with
be a graph with  vertices. Suppose
vertices. Suppose 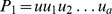 and
and 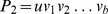 with
with 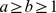 . Since
. Since 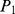 and
and  are two pendent paths attaching to the same vertex, then we get
are two pendent paths attaching to the same vertex, then we get
| (66) |
By using the definition of 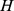 , we infer
, we infer 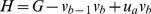 . By using the definition of
. By using the definition of  , we only need to show
, we only need to show
| (67) |
Observe that 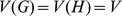 . We will discuss the difference of the distances between two vertices in
. We will discuss the difference of the distances between two vertices in 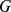 and
and 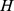 . Let
. Let  and
and 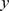 be two vertices of
be two vertices of 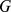 . If
. If 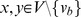 , then we have
, then we have 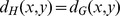 . Now we suppose
. Now we suppose 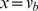 . If
. If 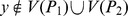 , then
, then
| (68) |
Observe that
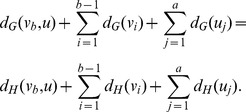 |
(69) |
Therefore, we have
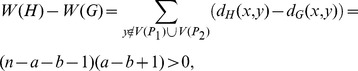 |
(70) |
i.e,
| (71) |
For 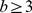 , it is easy to verify
, it is easy to verify 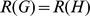 . Therefore
. Therefore 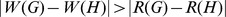 holds.
holds.
For 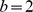 , from (66), we have
, from (66), we have 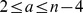 and
and 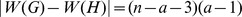 . By performing some elementary calculations, we get
. By performing some elementary calculations, we get
| (72) |
i.e.,
| (73) |
for 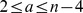 and each value of
and each value of  . Therefore, from (63), we infer
. Therefore, from (63), we infer 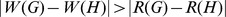 .
.
For 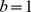 , from (66), we have
, from (66), we have 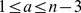 and
and  . By performing some elementary calculations, we obtain
. By performing some elementary calculations, we obtain
| (74) |
i.e.,
| (75) |
for 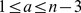 and each value of
and each value of  . Therefore, from (63), we infer
. Therefore, from (63), we infer 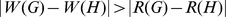 . The proof is complete.
. The proof is complete. 
This theorem can be used to compare the values of the distance measure by using trees. Let 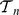 be the set of trees with
be the set of trees with  vertices and
vertices and
| (76) |
Observe that for every 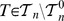 , there must be a tree
, there must be a tree 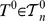 such that
such that 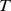 can be obtained from
can be obtained from 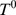 by repeatedly transferring pendent vertices. Therefore, we obtain the following corollary.
by repeatedly transferring pendent vertices. Therefore, we obtain the following corollary.
Corollary 1
Let
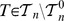 , there exists a tree
, there exists a tree
 such that
such that
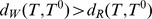 .
.
Actually, numerical experiments show that for any two trees 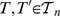 , the inequality
, the inequality 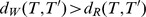 holds. We state the result as a conjecture.
holds. We state the result as a conjecture.
Conjecture 1
Let
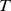 and
and
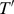 be any two trees with
be any two trees with
 vertices. Then
vertices. Then
| (77) |
holds.
As an example, we consider (all) 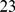 trees with 8 vertices and calculate all possible values of
trees with 8 vertices and calculate all possible values of 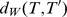 (blue) and
(blue) and 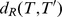 (red) as shown in Figure 1. From Figure 1, we observe that
(red) as shown in Figure 1. From Figure 1, we observe that 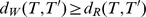 holds for each pair of trees
holds for each pair of trees 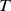 and
and 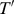 .
.
Figure 1. All the values of 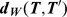 (blue) and
(blue) and  (red).
(red).
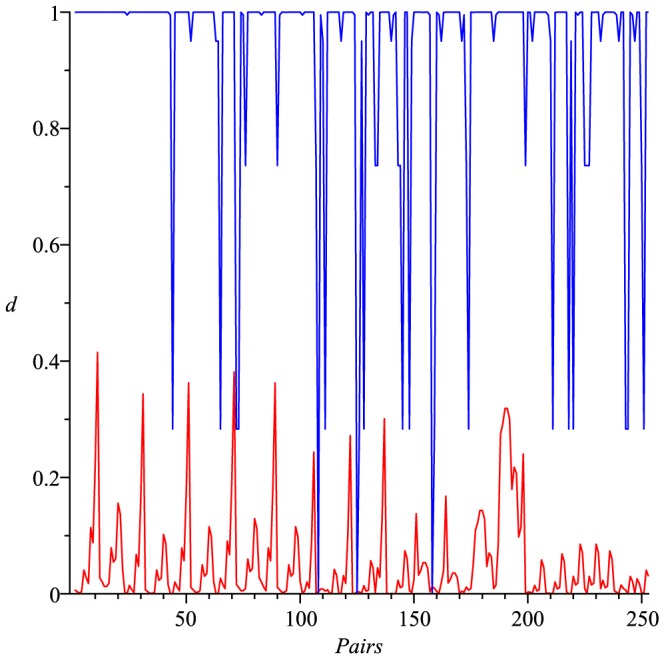
The Y-axis denotes the values of the distance measure and the X-axis denotes the graph pairs.
Graph Distance Measures Based on Graph Entropy
In this section, we consider graph distance measures which are based on graph entropy and other topological indices for some classes of graphs.
In order to start, we reproduce the definition of Shannon's entropy [43]. Let 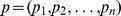 be a probability vector, namely,
be a probability vector, namely, 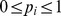 and
and 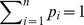 . The Shannon's entropy of
. The Shannon's entropy of 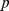 has been defined by
has been defined by
| (78) |
We denote by 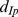 the graph distance measure based on
the graph distance measure based on 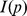 .
.
In the following, we infer an upper bound for 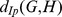 .
.
Theorem 15
Let
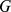 and
and
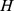 be two graphs with the same vertex set. Denote by
be two graphs with the same vertex set. Denote by
 and
and
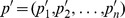 be the probability vectors of
be the probability vectors of
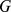 and
and
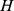 , respectively. If
, respectively. If
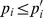 for each
for each
 , then we infer
, then we infer
| (79) |
where 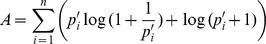 .
.
Proof. Since  for each
for each  , then we obtain
, then we obtain 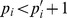 and
and 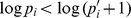 . Then we have
. Then we have
| (80) |
| (81) |
| (82) |
| (83) |
Therefore, we get the inequality,
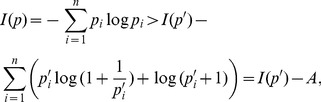 |
(84) |
i.e., 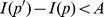 . Hence,
. Hence,
| (85) |
The desired inequality holds. 
In [25], Dehmer and Mowshowitz generalized the definition of graph entropy by using information functionals. Let 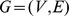 be a connected graph. For a vertex
be a connected graph. For a vertex  , we define
, we define
| (86) |
where 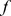 represents an arbitrary information functional. By substituting
represents an arbitrary information functional. By substituting 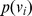 to (78), we have
to (78), we have
 |
(87) |
We denote by 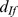 the graph distance measure based on
the graph distance measure based on 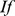 .
.
Relations between 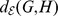 and
and 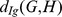
Denote by 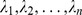 the eigenvalues of a graph
the eigenvalues of a graph 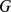 . By setting
. By setting 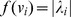 in (87), we obtain a new expression of the graph entropy namely
in (87), we obtain a new expression of the graph entropy namely
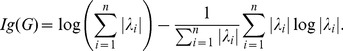 |
(88) |
Recall that the energy of 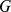 is defined as
is defined as 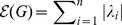 . Then we infer
. Then we infer
| (89) |
From the definition of 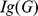 , it is interesting to investigate the relation between the graph distance measures
, it is interesting to investigate the relation between the graph distance measures  and
and 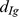 .
.
Theorem 16
Let
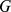 and
and
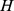 be two graphs of order
be two graphs of order
 with
with
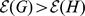 . Denote by
. Denote by
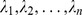 and
and
 the eigenvalues of
the eigenvalues of
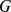 and
and
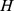 , respectively. Let
, respectively. Let
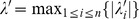 and
and
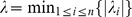 . Then we get
. Then we get
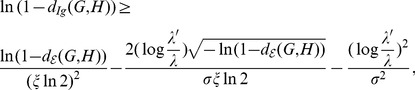 |
(90) |
where
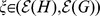 is a constant.
is a constant.
Proof. Let 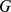 and
and 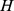 be two graphs of order
be two graphs of order  . Let
. Let 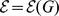 and
and 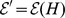 with
with 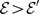 . Then we get
. Then we get
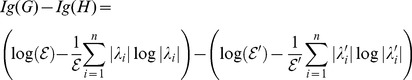 |
(91) |
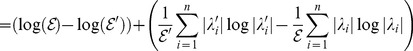 |
(92) |
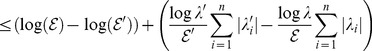 |
(93) |
| (94) |
where 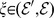 . Thus,
. Thus,
| (95) |
| (96) |
| (97) |
| (98) |
i.e.,
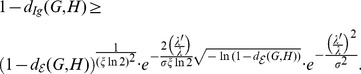 |
(99) |
Taking logarithm for the two sides of the above inequality, we have
 |
(100) |
The required inequality holds. 
Actually, numerical experiments show that for any two distinct trees 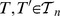 ,
, 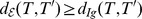 holds. See Figure 2 as an example, in which we consider (all)
holds. See Figure 2 as an example, in which we consider (all) 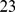 trees with 8 vertices and calculate all possible values of
trees with 8 vertices and calculate all possible values of  (red) and
(red) and  (blue). We state this observation as a conjecture.
(blue). We state this observation as a conjecture.
Figure 2. Values of 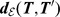 (red) and
(red) and 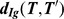 (blue).
(blue).
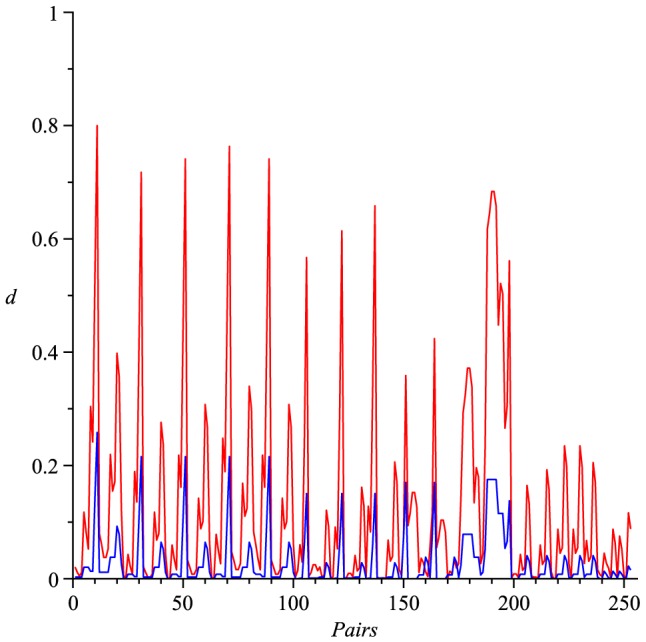
The Y-axis denotes the values of the distance measure and the X-axis denotes the graph pairs.
Conjecture 2
Let
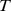 and
and
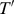 be any two distinct trees with
be any two distinct trees with
 vertices. Then
vertices. Then
| (101) |
holds.
Using a similar proof method of Theorem 16, we can obtain a generalization for the distance measure based on  (see Eq. (87)). Let
(see Eq. (87)). Let 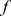 be an arbitrary information functional and
be an arbitrary information functional and 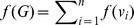 be a topological index.
be a topological index.
Theorem 17
Let
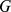 and
and
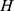 be two graphs of order
be two graphs of order
 with
with
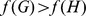 . Let
. Let
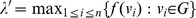 and
and
 . Then we have
. Then we have
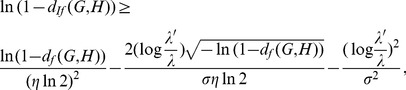 |
(102) |
where
 is a constant.
is a constant.
Dehmer and Mowshowitz [44] introduced a new class of measures (called here generalized measures) that derive from functions such as those defined by Rényi's entropy and Daròczy's entropy. Let 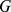 be a graph of order
be a graph of order  . Then
. Then
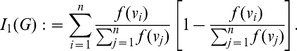 |
(103) |
If we let 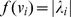 , then we can obtain the new generalized entropy based on eigenvalues. We denote the entropy by
, then we can obtain the new generalized entropy based on eigenvalues. We denote the entropy by
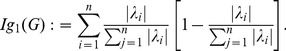 |
(104) |
For a given graph 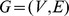 with
with  vertices, denote by
vertices, denote by 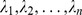 the eigenvalues of
the eigenvalues of 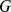 . By substituting
. By substituting 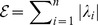 into equality (104), we have
into equality (104), we have
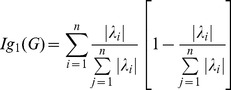 |
(105) |
| (106) |
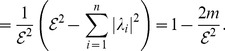 |
(107) |
The last equality holds since 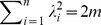 . By the following theorem, we study the relation between
. By the following theorem, we study the relation between 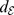 and
and 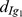 .
.
Theorem 18
Let
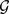 be a class of graphs with
be a class of graphs with
 vertices and
vertices and
 edges. For two graphs
edges. For two graphs
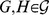 , let
, let
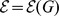 and
and
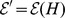 . Then we get
. Then we get
| (108) |
and
| (109) |
where
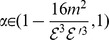 is a constant.
is a constant.
Proof. Let 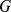 and
and 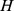 be two graphs with
be two graphs with  vertices and
vertices and  edges. Without loss of generality, we suppose
edges. Without loss of generality, we suppose 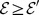 .
.
To show the first inequality, it suffices to prove
| (110) |
Then from (107), we derive
| (111) |
If we want to prove
| (112) |
we only need to show
| (113) |
From a well-known bound of energy  , we have
, we have 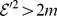 and
and 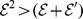 . Therefore,
. Therefore, 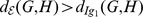 holds.
holds.
Now we show the second inequality. From (111), we have
| (114) |
| (115) |
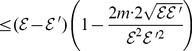 |
(116) |
| (117) |
Therefore, we have
From the definition of the distance measure, by some elementary calculations, we finally infer
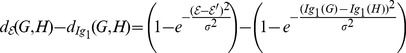 |
(118) |
| (119) |
| (120) |
| (121) |
where 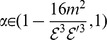 is a constant.
is a constant.
The proof is complete. 
Relations between 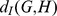 and
and 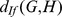
Let 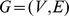 be a connected graph with
be a connected graph with  vertices,
vertices,  edges and degree sequence
edges and degree sequence  , where
, where 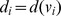 for
for 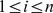 . By setting
. By setting 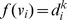 in (87), we can obtain the new entropy based on degree powers, denoted by
in (87), we can obtain the new entropy based on degree powers, denoted by 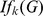
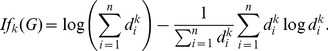 |
(122) |
For 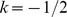 , the expression
, the expression  is just the zeroth-order Randić index
is just the zeroth-order Randić index 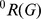 . Then by using Theorem 17, we obtain the following result.
. Then by using Theorem 17, we obtain the following result.
Theorem 19
Let
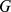 and
and
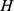 be two graphs of order
be two graphs of order
 with
with
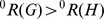 . Let
. Let
| (123) |
Then we have
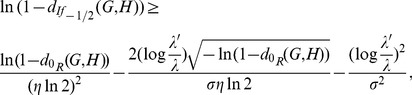 |
(124) |
where
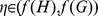 is a constant.
is a constant.
For 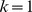 , we get
, we get
| (125) |
Furthermore, by the definition of 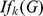 , for two graphs with the same degree sequences, we obtain that
, for two graphs with the same degree sequences, we obtain that 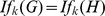 . Therefore, we get the following result.
. Therefore, we get the following result.
Theorem 20
Let
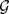 be a class of graphs with the same degree sequences and
be a class of graphs with the same degree sequences and
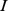 is an arbitrary topological index. Then for two graphs
is an arbitrary topological index. Then for two graphs
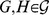 , we infer
, we infer
| (126) |
By using the similar proof method applied in Theorem 14, we obtain a weaker result.
Theorem 21
Let
 be a tree with
be a tree with
 vertices. Denote by
vertices. Denote by
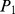 and
and
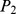 two pendent paths attaching to the same vertex such that
two pendent paths attaching to the same vertex such that
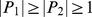 . Denote by
. Denote by
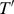 the tree obtained by transferring the pendent vertex of
the tree obtained by transferring the pendent vertex of
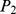 to the pendent vertex of
to the pendent vertex of
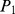 . Then we have
. Then we have
| (127) |
Proof. Let  be a tree with
be a tree with  vertices. Suppose
vertices. Suppose 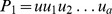 and
and 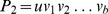 with
with  . Denote by
. Denote by  the degree of
the degree of  , i.e.,
, i.e., 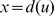 . Since
. Since 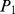 and
and 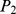 are two pendent paths attaching to the same vertex, then we have
are two pendent paths attaching to the same vertex, then we have 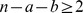 . By using the definition of
. By using the definition of 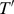 , we have
, we have 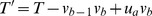 . By using the definition of
. By using the definition of  , we only need to show
, we only need to show
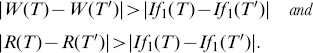 |
(128) |
For a tree 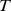 with
with  vertices, we get
vertices, we get 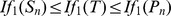 . By performing elementary calculations, we get
. By performing elementary calculations, we get
| (129) |
Observe that 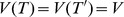 . We first discuss the difference of the distances between two vertices in
. We first discuss the difference of the distances between two vertices in 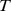 and
and 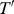 . Let
. Let  and
and 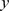 be two vertices of
be two vertices of 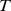 . If
. If 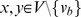 , then we have
, then we have 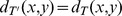 . Now we suppose
. Now we suppose 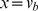 . If
. If 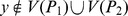 , then
, then 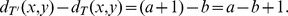 Observe that
Observe that
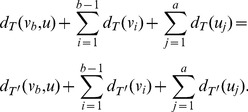 |
(130) |
Therefore, we get 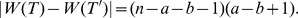
For 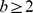 , it is easy to verify that
, it is easy to verify that 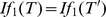 , i.e.,
, i.e., 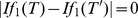 . Then,
. Then,
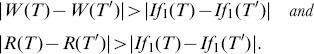 |
(131) |
In the following, we suppose 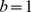 .
.
We obtain 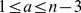 and
and 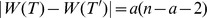 . By performing elementary calculations, we get
. By performing elementary calculations, we get
| (132) |
for 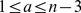 and each value of
and each value of  . Therefore,
. Therefore, 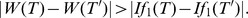
To prove the other inequality, we need more detailed discussion. By using the definition of graph entropy, we get
| (133) |
Let 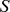 be the set of the neighbors of vertex
be the set of the neighbors of vertex  , which does not contain
, which does not contain 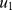 and
and 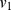 . Denote by
. Denote by 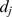 the degree of a vertex in
the degree of a vertex in 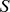 , where
, where 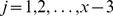 . If
. If 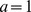 , then
, then
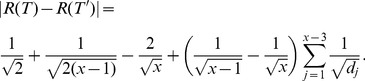 |
(134) |
By performing some calculations, we can show that for 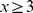 and
and  ,
,
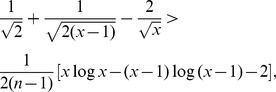 |
(135) |
i.e., 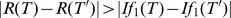 for
for  . For smaller
. For smaller  , we verify this inequality directly. If
, we verify this inequality directly. If 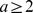 , then we have
, then we have
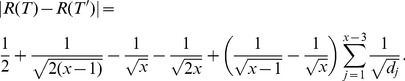 |
(136) |
We can show that for 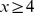 and
and 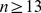 ,
,
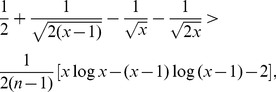 |
(137) |
i.e., 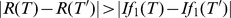 for
for 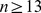 . For smaller
. For smaller  , we verify this inequality directly. Now suppose
, we verify this inequality directly. Now suppose 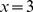 , then there is only one vertex in
, then there is only one vertex in  whose degree is at most
whose degree is at most  . Therefore by using (133) and (136), we get
. Therefore by using (133) and (136), we get
| (138) |
and
| (139) |
We can verify
| (140) |
for each  , i.e.,
, i.e., 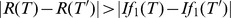 .
. 
From Theorem 14 and 21, we obtain the following corollary.
Corollary 2
Let
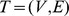 be a tree with
be a tree with
 vertices. Denote by
vertices. Denote by
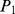 and
and
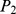 the two pendent paths attaching to the same vertex such that
the two pendent paths attaching to the same vertex such that
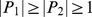 . Denote by
. Denote by
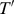 the tree obtained by transferring the pendent vertex of
the tree obtained by transferring the pendent vertex of
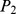 to the pendent vertex of
to the pendent vertex of
 . Then we have
. Then we have
| (141) |
Therefore, we obtain a similar result to comparing the values of distance measures of trees.
Corollary 3
Let
 , there exists a tree
, there exists a tree
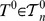 such that
such that
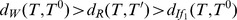 .
.
Actually, our numerical results (see section ‘Numerical Results’) show that for any two trees 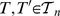 , the following inequality may hold.
, the following inequality may hold.
Conjecture 3
Let
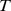 and
and
 be any two trees with
be any two trees with
 vertices. Then
vertices. Then
| (142) |
holds.
By way of example, we consider all  trees of 8 vertices and calculate all possible values of
trees of 8 vertices and calculate all possible values of 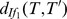 (blue) and
(blue) and 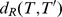 (red), respectively, as shown in Figure 3. From Figure 3, we observe that
(red), respectively, as shown in Figure 3. From Figure 3, we observe that
Figure 3. Values of 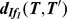 (blue) and
(blue) and 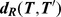 (red).
(red).
The Y-axis denotes the values of the distance measure and the X-axis denotes the graph pairs.
| (143) |
holds for each pair of trees 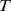 and
and 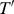 .
.
Numerical Results
In this section, we interpret the numerical results. First, we consider all trees with  vertices. The number of trees is
vertices. The number of trees is 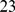 and the number of pairs is
and the number of pairs is 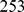 (see [45]). From the curves shown by Figure 1, we see that both measures
(see [45]). From the curves shown by Figure 1, we see that both measures 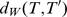 (blue) and
(blue) and 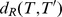 (red) satisfy the inequality Eq. (77). From the curves shown by Figure 2, we observe that both measures
(red) satisfy the inequality Eq. (77). From the curves shown by Figure 2, we observe that both measures 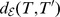 (red) and
(red) and 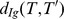 (blue) satisfy the inequality Eq. (101). From the curves shown by Figure 3, we also learn that both measures
(blue) satisfy the inequality Eq. (101). From the curves shown by Figure 3, we also learn that both measures 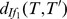 (blue) and
(blue) and 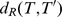 (red) fulfill the inequality Eq. (143). By using this method, several other inequalities could be generated and verified graphically.
(red) fulfill the inequality Eq. (143). By using this method, several other inequalities could be generated and verified graphically.
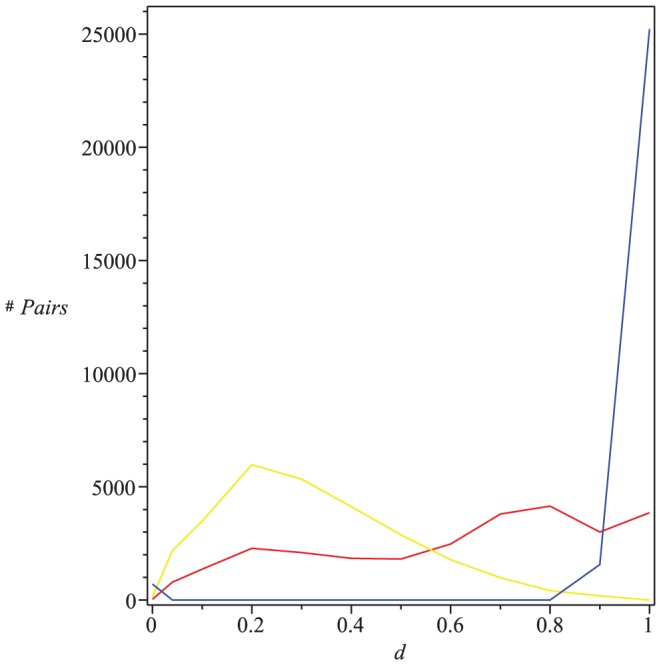
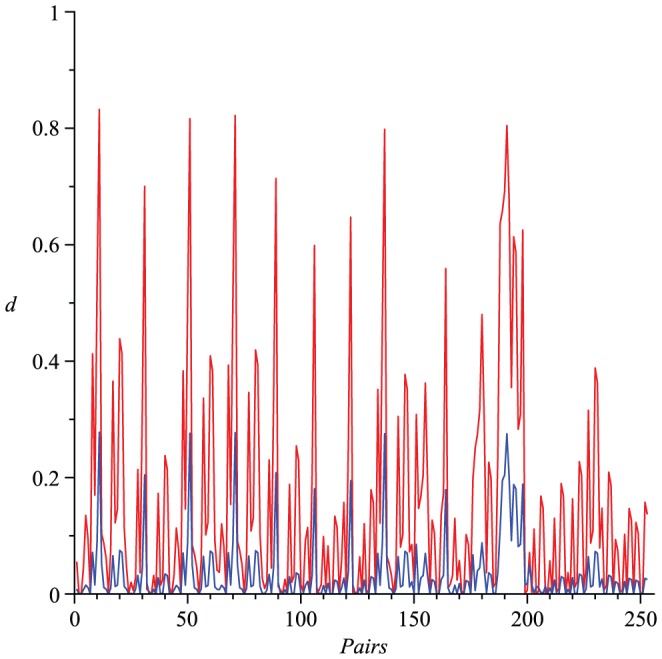
Figures 4 and 5 show the numerical results by using the graph distance measures based on graph energy 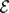 , the Wiener index
, the Wiener index 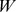 and the Randić index
and the Randić index 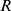 , respectively. We consider all trees with
, respectively. We consider all trees with  vertices. The number of trees is
vertices. The number of trees is 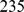 and the number of pairs is
and the number of pairs is 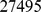 (see [45]). By Figure 4, we depict the distributions of the ranked distance values, that is,
(see [45]). By Figure 4, we depict the distributions of the ranked distance values, that is, 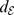 (red),
(red), 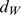 (blue), and
(blue), and 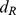 (yellow). First and foremost, we see that the measured values of all three measures cover the entire interval
(yellow). First and foremost, we see that the measured values of all three measures cover the entire interval 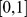 . This indicates that the measures are generally useful as they are well defined. By considering
. This indicates that the measures are generally useful as they are well defined. By considering 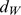 , we observe that only a relatively little number of pairs have a measured value
, we observe that only a relatively little number of pairs have a measured value  0.8. But a large number of pairs possess distance values
0.8. But a large number of pairs possess distance values  0.8. When considering
0.8. When considering 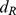 , the situation is reverse. The distance values of
, the situation is reverse. The distance values of 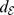 seem to slightly increase with some up- and downturns. However, Figure 4 does not comment on the ability of the graph distance measures to classify graphs efficiently. This needs to be examined in the future and would far beyond the scope of this paper.
seem to slightly increase with some up- and downturns. However, Figure 4 does not comment on the ability of the graph distance measures to classify graphs efficiently. This needs to be examined in the future and would far beyond the scope of this paper.
Figure 4. Distributions of the ranked values of the distance measure  (red),
(red), 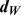 (blue),
(blue), 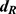 (yellow).
(yellow).
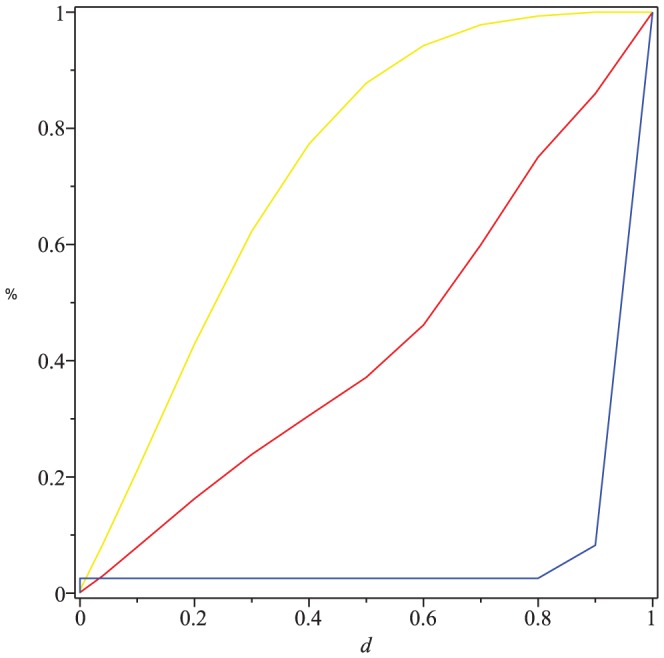
The X-axis denotes the values of the distance measure. The Y-axis denotes the number of graph pairs.
Figure 5. The X-axis denotes the values of the distance measures 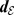 (red),
(red), 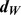 (blue),
(blue), 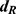 (yellow).
(yellow).
The Y-axis represents the percentage rate of all graphs studied.
Furthermore, we have computed the cumulative distributions by using the measures 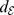 (red),
(red), 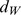 (blue),
(blue), 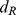 (yellow), respectively, as shown in Figure 5. In general, the computation of the cumulative distribution may serve as a preprocessing step when analyzing graphs structurally. In fact, we see how many percent of the 235 graphs have a distance value which is less or equal
(yellow), respectively, as shown in Figure 5. In general, the computation of the cumulative distribution may serve as a preprocessing step when analyzing graphs structurally. In fact, we see how many percent of the 235 graphs have a distance value which is less or equal 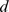 . Also, Figure 5 shows that the value distributions are quite different. From Figure 5, we see that the curve for
. Also, Figure 5 shows that the value distributions are quite different. From Figure 5, we see that the curve for 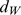 strongly differs from
strongly differs from 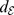 and
and 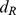 . When considering
. When considering 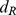 , we also observe that about 80% of the
, we also observe that about 80% of the 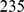 trees have a distance value approximately
trees have a distance value approximately  0.5. That means most of the trees are quite dissimilar according to
0.5. That means most of the trees are quite dissimilar according to 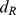 . For
. For 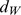 , the situation is absolutely reverse. Here 80% of the trees have a distance value approximately
, the situation is absolutely reverse. Here 80% of the trees have a distance value approximately  0.98. Finally evaluating the graph distance measure
0.98. Finally evaluating the graph distance measure 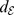 on these trees reveals that about 80% of the trees possess a distance value approximately
on these trees reveals that about 80% of the trees possess a distance value approximately  0.85. In summary, we conclude from Figure 5 that all three measures capture the distance between the graphs quite differently. But nevertheless, this does not imply that the quality of one measure may be worse than another. Again, an important issue of quality is fulfilled as the measures turned out to be well defined, see Figure 4. Another crucial issue would be evaluating the classification ability which is future work.
0.85. In summary, we conclude from Figure 5 that all three measures capture the distance between the graphs quite differently. But nevertheless, this does not imply that the quality of one measure may be worse than another. Again, an important issue of quality is fulfilled as the measures turned out to be well defined, see Figure 4. Another crucial issue would be evaluating the classification ability which is future work.
Summary and Conclusion
In this paper, we have studied interrelations of graph distance measures which are based on distinct topological indices. In order to do so, we employed the Wiener index, the Randić index, the zeroth-order Randić index, the graph energy, and certain graph entropies [25]. In particular, we have obtained inequalities involving the novel graph distance measures. Evidenced by a numerical analysis we also found three conjectures dealing with relations between the distance measures on trees.
From Theorem 1, we see that the star graph and the path graph maximize 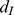 among all trees with a given number of vertices, for any topological index we considered here. Actually, this also holds for some other topological indices, such as the Hosoya index [46], [47], the Merrifield-Simmons index [48], [49], [47], the Estrada index [50], [51], [52], and the Szeged index [53], [54]. All other theorems we have proved in this paper shed light on the problem of proving interrelations of the measures. We believe that such statements help to understand the measures more thoroughly and, finally, they are useful to establish new applications employing quantitative graph theory [55]. We emphasize that the star graph and the path graph are apparently the two most dissimilar trees among all trees. Similar observations can also be obtained for unicyclic graphs or bicyclic graphs. Therefore, in the future, we would like to explore which classes of graphs have this property, i.e., identifying graphs (such as the path graph and the star graph) which maximize or minimize
among all trees with a given number of vertices, for any topological index we considered here. Actually, this also holds for some other topological indices, such as the Hosoya index [46], [47], the Merrifield-Simmons index [48], [49], [47], the Estrada index [50], [51], [52], and the Szeged index [53], [54]. All other theorems we have proved in this paper shed light on the problem of proving interrelations of the measures. We believe that such statements help to understand the measures more thoroughly and, finally, they are useful to establish new applications employing quantitative graph theory [55]. We emphasize that the star graph and the path graph are apparently the two most dissimilar trees among all trees. Similar observations can also be obtained for unicyclic graphs or bicyclic graphs. Therefore, in the future, we would like to explore which classes of graphs have this property, i.e., identifying graphs (such as the path graph and the star graph) which maximize or minimize 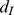 .
.
Another direction for future work is to compare the values of 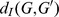 where
where 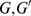 are general graphs. For example, we could assume that
are general graphs. For example, we could assume that 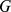 and
and 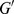 are obtained by only one graph edit operation, i.e., GED(
are obtained by only one graph edit operation, i.e., GED( ) = 1, see [15]. Then, all the graph which fulfill this equation are (by definition) similar. This construction could help to study the sensitivity of the measures thoroughly. Note that similar properties of topological indices have already been investigated, see [56]. As a conclusive remark, we mention that dynamics models on spatial graphs have been studied by Perc and Wang and other researchers, see [57], [58]. It would be interesting to study the distance measures in this mathematical framework as well.
) = 1, see [15]. Then, all the graph which fulfill this equation are (by definition) similar. This construction could help to study the sensitivity of the measures thoroughly. Note that similar properties of topological indices have already been investigated, see [56]. As a conclusive remark, we mention that dynamics models on spatial graphs have been studied by Perc and Wang and other researchers, see [57], [58]. It would be interesting to study the distance measures in this mathematical framework as well.
Supporting Information
CSV file containing descriptor values of 235 trees by using the Randić index.
(CSV)
CSV file containing descriptor values of 235 trees by using graph energy.
(CSV)
CSV file containing descriptor values of 235 trees by using the Wiener index.
(CSV)
Funding Statement
Matthias Dehmer and Yongtang Shi thank the Austrian Science Funds for supporting this work (project P26142). Yongtang Shi has also been supported by the National Science Foundation of China. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Dehmer M, Mehler A (2007) A new method of measuring similarity for a special class of directed graphs. Tatra Mountains Mathematical Publications 36: 39–59. [Google Scholar]
- 2. Sobik F (1982) Graphmetriken und klassifikation strukturierter objekte, ZKI-informationen. Akad Wiss DDR 2: 63–122. [Google Scholar]
- 3. Zelinka B (1975) On a certain distance between isomorphism classes of graphs. Časopis propest Mathematiky 100: 371–373. [Google Scholar]
- 4. Emmert-Streib F (2007) The chronic fatigue syndrome: A comparative pathway analysis. J Comput Biology 14: 961–972. [DOI] [PubMed] [Google Scholar]
- 5.Junker B, Schreiber F (2008) Analysis of Biological Networks. Wiley-Interscience. Berlin.
- 6. Kier L, Hall L (2002) The meaning of molecular connectivity: A bimolecular accessibility model. Croat Chem Acta 75: 371–382. [Google Scholar]
- 7. Bonchev D, Trinajstić N (1977) Information theory, distance matrix and molecular branching. J Chem Phys 67: 4517–4533. [Google Scholar]
- 8. Skvortsova M, Baskin I, Stankevich I, Palyulin V, Zefirov N (1998) Molecular similarity. 1. analytical description of the set of graph similarity measures. J Chem Inf Comput Sci 38: 785–790. [Google Scholar]
- 9. Varmuza K, Scsibrany H (2000) Substructure isomorphism matrix. J Chem Inf Comput Sci 40: 308–313. [DOI] [PubMed] [Google Scholar]
- 10. Mehler A, Weiβ P, Lücking A (2010) A network model of interpersonal alignment. Entropy 12: 1440–1483. [Google Scholar]
- 11. Hsieh S, Hsu C (2008) Graph-based representation for similarity retrieval of symbolic images. Data Knowl Eng 65: 401–418. [Google Scholar]
- 12. Dehmer M, Mehler A (2007) A new method of measuring similarity for a special class of directed graphs. Tatra Mountains Mathematical Publications 36: 39–59. [Google Scholar]
- 13.Bunke H (2000) Recent developments in graph matching. In: 15-th International Conference on Pattern Recognition. pp. 117–124.
- 14.Garey MR, Johnson DS (1979) Computers and Intractability: A Guide to the Theory of NP Completeness. Series of Books in the Mathematical Sciences. W. H. Freeman.
- 15. Bunke H (1983) What is the distance between graphs? Bulletin of the EATCS 20: 35–39. [Google Scholar]
- 16.Robles-Kelly A, Hancock R (2003) Edit distance from graph spectra. In: Proceedings of the IEEE International Conference on Computer Vision. pp. 234–241.
- 17. Dehmer M (2008) Information processing in complex networks: Graph entropy and information functionals. Appl Math Comput 201: 82–94. [Google Scholar]
- 18. Dehmer M, Mowshowitz A, Emmert-Streib F (2011) Connections between classical and parametric network entropies. PLoS ONE 6: e15733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Polansky OE, Bonchev D (1986) The Wiener number of graphs. I. General theory and changes due to graph operations. MATCH Communications in Mathematical and in Computer Chemistry 21: 133–186. [Google Scholar]
- 20. Polansky OE, Bonchev D (1990) Theory of the wiener number of graphs. II. Transfer graphs and some of their metric properties. MATCH Communications in Mathematical and in Computer Chemistry 25: 3–40. [Google Scholar]
- 21.Schädler C (1999) Die Ermittlung struktureller Ähnlichkeit und struktureller Merkmale bei komplexen Objekten: Ein konnektionistischer Ansatz und seine Anwendungen. Ph.D. thesis, Technische Universität Berlin.
- 22.Li X, Shi Y, Wang L (2008) An updated survey on the randić index. In: I Gutman BF, editor, Recent Results in the Theory of Randic Index, University of Kragujevac and Faculty of Science Kragujevac. pp. 9–47.
- 23.Todeschini R, Consonni V, Mannhold R (2002) Handbook of Molecular Descriptors. Wiley-VCH. Berlin.
- 24.Gutman I, Li X, Zhang J (2009) Graph energy. In: Dehmer M, Emmert-Streib F, editors, Analysis of Complex Networks. From Biology to Linguistics, Wiley–VCH. pp. 145–174. Weinheim.
- 25. Dehmer M, Mowshowitz A (2011) A history of graph entropy measures. Inform Sciences 181: 57–78. [Google Scholar]
- 26.Harary F (1969) Graph Theory. Addison Wesley Publishing Company. Reading, MA, USA.
- 27.Dehmer M, Varmuza K, Bonchev D, editors (2012) Statistical Modelling of Molecular Descriptors in QSAR/QSPR. Quantitative and Network Biology. Wiley-Blackwell.
- 28. Ulanowicz RE (2001) Information theory in ecology. Computers and Chemistry 25: 393–399. [DOI] [PubMed] [Google Scholar]
- 29. Emmert-Streib F, Dehmer M (2011) Networks for systems biology: Conceptual connection of data and function. IET Systems Biology 5: 185–207. [DOI] [PubMed] [Google Scholar]
- 30. Wilhelm T, Hollunder J (2007) Information theoretic description of networks. Physica A 388: 385–396. [Google Scholar]
- 31.Solé RV, Valverde S (2004) Information theory of complex networks: On evolution and architectural constraints. In: Lecture Notes in Physics. volume 650, pp. 189–207.
- 32. Bonchev D, Mekenyan O, Trinajstić N (1981) Isomer discrimination by topological information approach. J Comp Chem 2: 127–148. [Google Scholar]
- 33. Dehmer M, Emmert-Streib F, Tripathi S (2013) Large-scale evaluation of molecular descriptors by means of clustering. PLoS ONE 8: e83956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wiener H (1947) Structural determination of paran boiling points. J Amer Chem Soc 69: 17–20. [DOI] [PubMed] [Google Scholar]
- 35. Dobrynin A, Entringer R, Gutman I (2001) Wiener index of trees: theory and application. Acta Appl Math 66: 211–249. [Google Scholar]
- 36. Randić M (1975) On characterization of molecular branching. J Amer Chem Soc 97: 6609–6615. [Google Scholar]
- 37. Bollobás B, Erdös P (1998) Graphs of extremal weights. Ars Combin 50: 225–233. [Google Scholar]
- 38.Li X, Gutman I (2006) Mathematical Aspects of Randi'c-Type Molecular Structure Descriptors. University of Kragujevac and Faculty of Science Kragujevac.
- 39. Li X, Shi Y (2008) A survey on the randić index. MATCH Commun Math Comput Chem 59: 127–156. [Google Scholar]
- 40. Gutman I (1977) Acylclic systems with extremal hückel π-electron energy. Theor Chim Acta 45: 79–87. [Google Scholar]
- 41.Gutman I (2001) The energy of a graph: old and new results. In: Betten A, Kohnert A, Laue R, Wassermann A, editors, Algebraic Combinatorics and Applications, Springer–Verlag. pp. 196–211.
- 42.Li X, Shi Y, Gutman I (2012) Graph Energy. Springer. New York.
- 43.Shannon C, Weaver W (1949) The Mathematical Theory of Communication. University of Illinois Press. Urbana, USA.
- 44. Dehmer M, Mowshowitz A (2011) Generalized graph entropies. Complexity 17: 45–50. [Google Scholar]
- 45.Read R, Wilson R (19988) An Atlas of Graphs. Clarendon Press. Oxford.
- 46. Hosoya H (1971) Topological index. a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull Chem Soc Jpn 4: 2332–2339. [Google Scholar]
- 47. Wagner S, Gutman I (2010) Maxima and minima of the hosoya index and the merrifield-simmons index: A survey of results and techniques. Acta Appl Math 112: 323–346. [Google Scholar]
- 48. Merrifield R, Simmons H (1980) The structure of molecular topological spaces. Theor Chim Acta 55: 55–75. [Google Scholar]
- 49.Merrifield R, Simmons H (1989) Topological Methods in Chemistry. Wiley. New York.
- 50. Estrada E (2000) Characterization of 3d molecular structure. Chem Phys Lett 319: 713–718. [Google Scholar]
- 51.Deng H, Radenković S, Gutman I (2009) The estrada index. In: Cvetković D, Gutman I, editors, Applications of Graph Spectra, Math. Inst. pp. 123–140. Belgrade.
- 52.Gutman I, Deng H, Radenković S (2011) The estrada index: An updated survey. In: Cvetković D, Gutman I, editors (2011) Selected Topics on Applications of Graph Spectra, Math. Inst. pp. 155–174.
- 53. Gutman I (1994) A formula for the wiener number of trees and its extension to graphs containing cycles. Graph Theory Notes of New York 27: 9–15. [Google Scholar]
- 54. Simić S, Gutman I, Baltić V (2000) Some graphs with extremal szeged index. Math Slovaca 50: 1–15. [Google Scholar]
- 55.Dehmer M, Emmert-Streib F (2014) Quantitative Graph Theory. Theory and Applications. CRC Press. In press.
- 56. Furtula B, Gutman I, Dehmer M (2013) On structure-sensitivity of degree-based topological indices. Applied Mathematics and Computation 219: 8973–8978. [Google Scholar]
- 57. Perc M, Wang Z (2010) Heterogeneous aspirations promote cooperation in the prisoner's dilemma game. PLOS ONE 5: e15117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Jin Q, Wang L, Xia C, Wang Z (2014) Spontaneous symmetry breaking in interdependent networked game. Scientific Reports 4: 4095. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
CSV file containing descriptor values of 235 trees by using the Randić index.
(CSV)
CSV file containing descriptor values of 235 trees by using graph energy.
(CSV)
CSV file containing descriptor values of 235 trees by using the Wiener index.
(CSV)


