Commentary: A structural approach to Berkson’s fallacy and a guide to a history of opinions about it

In 1946, the physician and statistician Joseph Berkson (1899–1982) pointed out that two diseases that are independent in the general population may become ‘spuriously associated’ in hospital-based case-control studies.¹ This spurious association was later referred to, often in lively debates,^2–14 as Berkson’s fallacy, Berkson’s paradox or Berkson’s bias. Some authors restricted the interpretation of Berkson’s fallacy to disease-disease associations,^2,5,7,8 whereas others thought that the fallacy would also apply to exposure-disease associations in hospital-based case-control studies.^10–15

In this article we use directed acyclic graphs (DAGs) to describe the structure of Berkson’s fallacy, first for disease-disease associations and then for exposure-disease associations. This permits us to understand the contentious debates and strongly differing opinions about Berkson’s fallacy, and has practical implications for study design and interpretation (see Box 1).

Box 1. Practical implications of Berkson’s fallacy.

• The fallacy that became eponymous for Berkson caused controversy from its initial formulation onwards. Some held that it biased all case-control studies in hospitals; others maintained that it was only pertinent for associations between prevalent diseases, and did not exist for exposure-disease associations.

• The DAG analyses in this paper show that Berkson’s fallacy can exist when studying exposure-disease associations, be it only in an ‘indirect’ form and in exceptional circumstances: when in a hospital-based case-control study persons with a prevalent diagnosis are enrolled who were hospitalized for another disease that is associated with this exposure.

• The DAG of the problem that Berkson originally described has the same structure of all biases due to conditioning on a collider, but cannot be endowed with a causal interpretation since it was formulated and worked out as a problem of the association of prevalent diseases.

• When using incident cases in hospital-based case-control studies, Berkson’s fallacy becomes highly unlikely for exposure-disease associations, unless there are many people who have developed two different new diseases more or less at the same time and are hospitalized for the other disease, i.e. the disease that is not the subject of the case-control study.

• When incident cases in a case-control study consist only of people who have been hospitalized for that disease, Berkson’s fallacy is not possible.

• It is likely that Berkson’s fallacy has had very limited, if any, impact on the findings of epidemiological studies.

Disease-disease associations: Berkson’s fallacy

In 1946 Berkson considered the following problem.¹ Suppose a hospital wants to estimate the association between the prevalences of cholecystitis (disease 1 or D1) and diabetes mellitus (disease 2 or D2). To do so, a case-control study is conducted in which hospitalized individuals are included as cases if they have diabetes and as controls if they have ophthalmological refractive errors (disease 3 or D3). The association between cholecystitis and diabetes is then estimated by comparing the prevalence of cholecystitis D1 between cases with diabetes D2 and controls with refractive errors D3.

Berkson constructed his example so that, in the source population, the D1-D2 and D1-D3 associations were null and the probabilities of hospitalization for each of the three diseases were independent. Yet, the D1-D2 association was not null in hospitalized individuals. In the Appendix (available as Supplementary data at IJE online) we numerically work out the example Berkson used in his paper, and we discuss the strength and direction of the association in hospitalized individuals. Intuitively, this association arises because persons with two or more diseases have a higher probability of being hospitalized than persons with only one disease—even if these reasons are independent.

In the case-control study considered by Berkson, a D1-D2 association cannot generally be endowed with a causal interpretation, even in the absence of confounding and measurement error. Berkson used prevalent cases, which may lead to selection bias,¹⁵ and disregarded the timing of D1 and D2 (e.g. diabetes could predate cholecystitis), which may lead to reverse causation bias.

Because the study design does not target a causal association, we refrain from referring to the spurious association among the hospitalized as a bias. Instead, in this paper we use the term Berkson’s fallacy to refer to the wrong estimation of a prevalence difference. Most modern case-control studies attempt to use incident, rather than prevalent, cases, but there is no indication that Berkson was aware of this distinction. The use of incident cases reduces both the danger of selection bias and the potential for Berkson’s fallacy, as we explain below.

Structure

Berkson’s fallacy can be visualized by the DAG presented in Figure 1a. The nodes D1, D2 and D3 represent dichotomous variables (1: yes, 0: no) for each of the diseases described above. The node H represents a dichotomous variable (1: yes, 0 no) for hospitalization. In general, all three diseases D1, D2 and D3 may lead to hospitalization H. In Berkson’s example one might argue that refractive errors may not be a cause of hospitalization (and thus the arrow from D3 to H can be removed), without any consequences for the argument. The node S represents a dichotomous variable (1: yes, 0: no) for selection into the case-control study, either as case (i.e. D2 = 1) or as control (i.e. D3 = 1). In Berkson’s example, subjects with both D2 = 1 and D3 = 1 were included as cases.¹ For simplicity of presentation the DAG assumes, as Berkson did in his paper, that the diseases do not share any common causes and that there is no measurement error.

Figure 1.

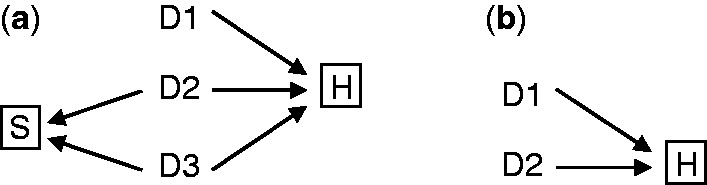
(a) DAG representing Berkson’s fallacy. D1 is the putative causal disease, D2 the case disease and D3 the control disease. S denotes selection into the study (S = 1 | D2 + D3 >0). The association between D1 and D2 is biased conditional on H (hospitalization). (b) Simplified DAG of Berkson’s fallacy. When community controls are used, H remains a collider of D1 and D2 and Berkson’s fallacy will still occur.

Two selection processes are represented in Figure 1a: the selection of hospitalized patients out of the entire population (H = 1), and the selection of patients with D2 or D3 out of the hospitalized population into the case-control study (S = 1). The box around H depicts the former; the box around S the latter. The boxes around H and S indicate that the selection depends on both H and S. Berkson’s fallacy is the result of conditioning on the collider H = 1. As easily seen by applying the d-separation rules,¹⁶ D1 and D2 are unconditionally independent but are associated conditional on H = 1.The DAG states that the selection has two components: (i) S: having one of the diseases, (ii) H: being hospitalized.

Not all components of the DAG in Figure 1a are required for Berkson’s fallacy to arise. First, as noted by Feinstein¹² and extended by Flanders,¹³ the fallacy exists even if the case-control study uses population controls (rather than controls with disease D3). Therefore, the DAG does not need to include the node D3. Second, the fallacy exists even if the case-control study is not based on a sample but involves all hospitalized individuals. Therefore, the DAG does not need to include the node S. Therefore, in the remainder of this paper we use the simplified DAG shown in Figure 1b, which has an identical structure to selection bias as described by Hernán et al.¹⁵

Berkson’s scenario assumed that the diseases D1 and D2 lead to hospitalization through independent mechanisms. This scenario can be represented by elaborating the arrows from D1 to H and from D2 to H so that they include, as an intermediate step, the disease-specific mechanisms of hospitalization H1 and H2, respectively (Figure 2).¹⁵ The mechanisms H1 and H2 are independent because there are no arrows from D1 to H2 or from D2 to H1, and because H1 and H2 do not share common causes with D2 and D1, respectively.

Figure 2.

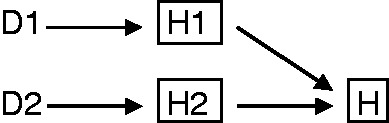
This DAG explains that spurious associations will not arise in a study outside the hospital. H1 and H2 mean disease-specific hospitalization due to D1 or D2. Conditioning on H = 0 implies conditioning on H1 = 0 and H2 = 0, which blocks the open paths between the diseases.

Under these conditions of independent mechanisms of hospitalization, one would not expect a spurious association between D1 and D2 in a study restricted to non-hospitalized patients because conditioning on H = 0 deterministically implies conditioning simultaneously on (H1 = 0, H2 = 0), which blocks all open paths between D1 and D2 via H. That is, D1 and D2 are independent conditional on H = 0. On the other hand D1 and D2 are associated in hospitalized patients because conditioning on H = 1 does not imply simultaneous conditioning on (H1 = 1, H2 = 1), i.e. individuals need only one disease to be hospitalized; this corresponds to the independence assumptions of elementary probability theory as H = 1 assumes hospitalization for either disease or for both.^15,17 Thus, the D1-D2 association in non-hospitalized patients is the same as in the source population, whereas in hospitalized patients a different association will be found. A numerical example is provided in the Appendix (available as Supplementary data at IJE online).

The null association that exists in the total population as well as in the non-hospitalized population is the mathematical consequence of the way Berkson constructed his example. In real data, there may be a non-null association in both the hospitalized and the non-hospitalized because diseases D1 and D2 may lead to hospitalization through non-independent mechanisms (e.g. presence of one disease influences the decision to be hospitalized for another disease). In that setting Figure 2 would include arrows from D1 to H2 or from D2 to H1, or common causes for H1-D2 or H2-D1, and D1 and D2 would be associated in non-hospitalized (H = 0) patients too.

Exposure-disease associations: indirect Berkson’s fallacy

After Berkson formulated his original fallacy about disease associations, a controversy arose as to whether this fallacy may also occur in studies that estimate the causal effect of an exposure on disease occurrence.^2–15 For example, suppose that hospital cases and population controls are used to estimate the effect of smoking (E) on hip arthrosis (D2), and that patients with existing hip arthrosis who had been hospitalized for a smoking-related disease, such as cardiovascular disease (CVD) (D1) were enrolled in this case-control study. Then, a smoking-arthrosis association is expected because smoking is associated with CVD and conditioning on hospitalization induces a CVD-arthrosis association.^10,13 In line with Flanders et al., we call this ‘indirect’ Berkson’s fallacy.¹³

Structure

The structure of the indirect Berkson’s fallacy is depicted in Figure 3a-c, which are variations of Figure 1b. The similarity with Figure 1b is that D2 remains the disease of interest in the study, but the difference is that D1 is not of interest in the study. Three reasons why an exposure E may be associated with a disease D1 are: E is a cause of D1 (as in the example above); D1 is a cause of E (e.g. E is a certain drug prescribed for condition D1); and E and D1 share some common causes. Because of conditioning on hospitalization, E becomes associated with D2 via D1.This situation was already hinted at by Roberts et al.¹⁰ In general, the bias induced by the indirect form will tend to be of lower magnitude than the original Berkson’s fallacy (see Appendix, available as Supplementary data at IJE online).

Figure 3.

DAGs of indirect Berkson’s fallacy in the association between exposure and disease in hospital-based studies. Exposure (E) does not directly lead to hospitalization (H), but via a disease (D1); (a) E causes D1, (b) E is a consequence of D1, or (c) E shares a common cause with D1. This disease is independent of the case disease (D2) in the study base, but become associated with those diseases conditional on hospitalization. Thus, in a hospital-based study, E can be spuriously associated with D2 via D1.

Avoiding Berkson’s fallacy

Disease-disease associations

Berkson himself indicated two rather theoretical situations in which his hospital-based case-control comparisons between prevalent diseases would not be ‘basically invalid’: (i) one of the diseases does not lead to hospitalization, i.e. H is no longer a collider; and (ii) the control disease has the same hospitalization probability as the case disease, i.e. the association between D1 and D2 via the path D1-H-D2 is exactly counterbalanced by the association via the path D1-H-D3-S-D2 (Figure 1a). This second condition only holds when patients with both diseases are excluded from the study; otherwise cases still have a slightly different hospitalization probability than controls and the association cannot completely disappear (see Appendix, available as Supplementary data at IJE online).

Indirect Berkson's fallacy

The indirect Berkson’s fallacy can be largely attenuated by using only incident cases.¹³ In our example, suppose that one enrolled only hospitalized patients with a very recent diagnosis of hip arthrosis D2. The probability of hospitalization because of another incident disease D1 like CVD after their very recent diagnosis of hip arthrosis is small. Using incident cases does not remove the potential for indirect Berkson’s fallacy, but it makes the near simultaneous occurrence of incident diseases unlikely.

The indirect Berkson’s fallacy can be completely removed if one samples as cases (and controls) only persons in whom the studied disease is also the (only) reason for hospitalization. This amounts to conditioning on H1 = 0 (Figure 4). This is a feasible strategy in any hospital-based study, and might often be applied spontaneously by researchers. The solution would also work for prevalent cases when the disease for which people are hospitalized exists already for a long time, e.g. hip arthrosis that exists for several years but the patient is hospitalized for surgery to replace the hip. This solution also assumes no interaction among mechanisms of hospitalization; that assumption would be violated if the existence of two diseases would in and by itself lead to increased hospitalization rates, for example because the management of the patient is more complex. A remaining caveat of this solution is that conditional on H1 = 0, (unmeasured) common causes of both D1 and D2 could still confound the relation between E and D2.¹⁷

Figure 4.

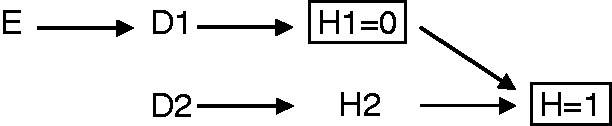
Indirect Berkson’s fallacy can be prevented by conditioning on H1 = 0 (i.e. not having a disease other than the case or control disease as reason for hospitalization).

The history of opinions about Berkson’s fallacy.

In 1955, Berkson¹⁸ explained that the original idea for his eponymous fallacy arose from an early, autopsy-based case-control study reported in 1929 by the Johns Hopkins University biologist and statistician Raymond Pearl.¹⁹ Pearl found active tuberculosis lesions in 6.6% of 816 patients who had died of cancer and in 16.3% of 816 race-sex-and age-matched autopsy records of persons who had died from causes other than cancer. As acknowledged later in that same year by Pearl himself, the inverse association between cancer and tuberculosis may have spuriously resulted from cancer killing patients before there was time for florid tuberculosis to develop.²⁰ But the flaw was not obvious. The biology and even an attempt to treat cancer using tuberculin seemed compatible with the protective effect of tuberculosis.²¹ It was Berkson who demonstrated the origin of the fallacy, 7 years after Pearl’s death (see the DAGs of Figures 1–2, in which hospitalization would be replaced by death). As in Pearl’s study, which was based on prevalences in autopsies, Berkson constructed an example with prevalent diseases.

As an aside, Berkson, who belonged to the sceptics as to the association between smoking and lung cancer, did not invoke this fallacy when arguing against the causality of that association. Rather, he argued that the observed association between smoking and many diseases other than lung cancer suggested bias rather than causation. In his 1955 paper he proposed one form of self-selection bias, which can arise in both case-control and cohort studies: see Hernán et al.¹⁵ for a causal DAG representing this bias. However, Berkson had to postulate unrealistic interactions for the bias to fully explain the magnitude of the observed association.

In 1954, Kraus² wrote that Berkson’sfallacy existed only for disease-disease associations, but not for exposure-disease associations. That opinion, which was upheld by Walter,⁵ Schlesselman⁸ and Miettinen,⁷ overlooked the indirect form of Berkson’s fallacy and the distinction between prevalent and incident conditions, which are pivotal to understanding Berkson’s reasoning—both described by Flanders et al.¹³

In 1978, Roberts et al.¹⁰ attempted to establish the existence of Berkson’s fallacy empirically, after one of their co-authors, who had invoked Berkson’s arguments at a conference, had been contradicted by other epidemiologists: ‘… that Berkson had only advanced a theoretical objection, never tested’. Roberts et al.¹⁰ used data from three household surveys about diseases, signs and symptoms of diseases, hospitalizations and uses of drugs. A spurious association, larger or smaller, was found for most of 28 disease-disease associations among those who had been hospitalized in the past 6 months, in comparison with the overall population associations. They also looked at 48 drug-disease associations, and found nine significant differences between the general population and hospitalized patients. Still, the authors found it difficult to separate Berkson’s fallacy from what they called ‘clinical selection bias’, i.e. when clinicians judge it more prudent to hospitalize a patient with two conditions ‘which occurs when patients with co-morbidity presentations are more likely to be admitted on clinical grounds such as a diabetic on oral hypoglycemics with recent chest pain’. They acknowledged that ‘… few modern studies consider a suspected causal factor which is a disease and thus a force of hospitalization in its own right.’¹⁰ They also hinted about the possibility of the indirect form of Berkson’s fallacy later described by Flanders et al.¹³ when they mentioned that ‘… one could envisage situations in which the suspected causal factor, while not subject to hospitalization when present alone, could influence the hospitalization decisions if it occurred concurrently with another disease of interest’.¹⁰

In 1979, Sackett (co-author of Roberts et al.) renamed the fallacy as ‘admission rate bias’ and stated: ‘… this bias is central to the execution of case-control studies’.¹¹ Sackett directly referred to Berkson, and used examples of disease-disease associations from Roberts et al. but not of exposure-disease associations.

In 1986, Feinstein et al. proposed that in Berkson’s fallacy, the control group needed not to be hospitalized for the fallacy to occur;¹² this is shown in our DAG in Figure 1b. Feinstein et al. wrote that ‘the assumption that exposure has no impact on hospitalization … will seldom be realistically tenable’.¹² Use of certain pharmaceutical agents, for example, ‘may lead to increased medical surveillance that can lead to the detection of ailments that might otherwise escape attention’. Furthermore, he wrote, non-pharmaceutical agents, such as smoking, ‘… may provoke a side effect that leads to increased medicalization of the patient and to detection of diseases that might be otherwise undiscovered’.¹² Such biases are of a different kind, however, and are sometimes referred to as ascertainment bias, diagnostic suspicion bias, referral bias, or clinical selection bias (as Roberts et al. named them). They result from conditioning on factors caused by disease and that affect diagnosis of the disease, as can be seen by the DAG in Figure 5, and can be prevented by specific design choices.^22,23 A few years earlier, in 1979, Feinstein had written that this type of bias ‘… is substantially different from the type of hospitalization bias that was first described by Berkson as a purely passive mathematical phenomenon. Diagnostic referral bias is an active clinical entity, in which physicians create different rates of hospitalization and/or diagnostic testing’.²⁴

Figure 5.

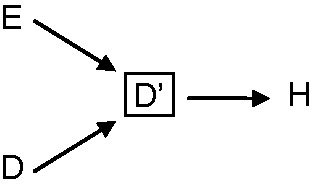
Causal DAG representing diagnostic suspicion or detection bias. E is exposure, D disease, and D’ diagnosed disease. Conditioning on factors C that affect diagnosis and are themselves affected by existing disease will create an association between exposure and diagnosed disease. Of note, this bias is not restricted to hospital-based studies.

In 2003, Schwartzbaum et al. revisited Berkson’s fallacy and described it as an overriding problem in hospital-based case-control studies.¹⁴ They approximated an idea close to the indirect form of the fallacy, but did not describe it completely when writing that it was unlikely that ‘newly diagnosed meningioma cases will occur among those admitted to the hospital for prevalent breast cancer during the relatively short time that patients are hospitalized for breast cancer’. They proposed that using controls with diseases with the same admission incidence as the cases can remedy Berkson’s fallacy. This is insufficient, as we show in the Appendix (available as Supplementary data at IJE online). Schwartzbaum et al. were commenting on a paper by Sadetzki et al.²⁵ who purported to have found Berkson’s fallacy in a hospital-based case-control study of smoking and bladder cancer. However, the bias in that study was caused by selection of hospitalized controls with diseases (e.g. lung diseases) that had the same exposure as the cases. This is again another type of bias, due to the choice of a control group that is associated with the exposure, as described in the DAG in Figure 6 (see Hernán et al.¹⁵ for further details).

Figure 6.

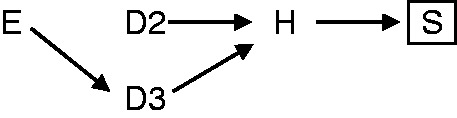
DAG of a bias in hospital-based case-control studies, that occurs when exposure (E) causes the control disease (D3). Conditioning on cases and controls selected into the case-control study (S), which is a descendent of hospitalization (H), introduces a spurious association between the exposure and the disease of the cases (D2).

Over the past years, the name ‘Berksonian bias’ has been proposed for all collider biases, both in hospital-based case-control studies and other designs.^26–28 Indeed, similarly to the fallacy originally proposed by Berkson, these biases result from conditioning on a collider. Nonetheless, these biases are not a probabilistic necessity like Berkson’s fallacy and can be avoided by specific strategies of choices of cases and controls, either in hospital-based case-control studies or in other designs.

In a recent paper, Westreich pointed to the analogy between Berkson’s fallacy, selection bias and missing data, and to the general structure of Berkson’s bias as resembling collider bias.²⁹ The DAG we present in our paper is analogous to the DAG proposed by Westreich. However, we emphasize that the original formulation by Berkson implies prevalent disease states and disease-disease associations and has little bearing on causal problems, and we add the important notion that the only type of Berkson’s fallacy that matters is the indirect form, for which we describe the potential solutions.

Interest in Berkson’s fallacy was raised in one of us (J.P.V.) during the preparation of the 2007 STROBE guidelines,³⁰ when diametrically opposed views emerged about its nature and whether it actually existed—a discussion that was similar to the one that led to the Roberts et al. paper 30 years earlier. This led to discussions with other authors (S.H.-D. and M.H.) who had published a DAG for Berkson’s fallacy with an explanation that did not pertain to Berkson’s original problem of disease-disease associations, but (in retrospect) to the indirect form of Berkson’s fallacy.¹⁵

Conclusion

We showed that the original Berkson’s fallacy is a probabilistic necessity in hospital-based case-control studies of prevalent disease-disease associations. For exposure-disease associations, an indirect form of Berkson’s fallacy in which the exposure is associated with a different disease leading to the hospitalization of the case (or control) can produce situations equivalent to Berkson’s fallacy. This indirect Berkson’s fallacy will tend to be of smaller magnitude than the direct fallacy. The fallacy is largely attenuated by limiting enrollment to incident cases (and controls when hospital-based controls are used) and is completely prevented by excluding cases (and controls) with a different disease as the reason for their hospitalization. The nature of the bias proposed by Berkson has led to repeated similar debates over a period of more than 60 years, among other reasons because of confusion with other types of selection biases.

The classical Berkson fallacy, formulated as prevalent disease-disease associations, may only rarely have been a problem in epidemiological studies directed at causes of diseases because diseases are rarely studied as causes of other diseases. The indirect form of Berksons fallacy may only have been a problem in hospital-based case-control studies with prevalent cases wherein the disease for which a person was enrolled in the case-control study was not the reason for that person’s hospitalization. Studies with prevalent cases, however, within or outside hospital, are in general a minority of case-control studies.³¹ The most common design choices in hospital-based case-control studies seem to preclude a large role of Berkson bias in epidemiology.

Funding

Miguel A Hernán: National Institutes of Health R01 HL080644; Alfredo Morabia: National Library of Medicine 1G13LM010884-01A1.

Supplementary Data

Supplementary data are available at IJE online.

Conflict of interest: None declared.