An examination of black/white differences in the rate of age-related mortality increase

Abstract

BACKGROUND

The rate of mortality increase with age among adults is typically used as a measure of the rate of functional decline associated with aging or senescence. While black and white populations differ in the level of mortality, mortality also rises less rapidly with age for blacks than for whites, leading to the well-known black/white mortality “crossover”.

OBJECTIVE

This paper investigates black/white differences in the rate of mortality increase with age for major causes of death in order to examine the factors responsible for the black/white crossover.

METHODS

The analysis considers two explanations for the crossover: selective survival and age misreporting. Mortality is modeled using a Gompertz model for 11 causes of death from ages 50–84 among blacks and whites by sex.

RESULTS

Mortality increases more rapidly with age for whites than for blacks for nearly all causes of death considered. The all-cause mortality rate of mortality increase is nearly two percentage points higher for whites. The analysis finds evidence for both selective survival and age misreporting, although age misreporting is a more prominent explanation among women.

CONCLUSIONS

The black/white mortality crossover reflects large differences in the rate of age-related mortality increase. Instead of reflecting the impact of specific causes of death, this pattern exists across many disparate disease conditions, indicating the need for a broad explanation.

1. Introduction

Human mortality rates begin to increase with advancing age starting around age 20 in most populations. Especially at older ages, age-related increases in the observed mortality rate are thought to reflect functional decline and processes associated with physiological aging. Gompertz (1825) originally noted that adult mortality increases exponentially as a function of age with remarkable consistency. That is, age-specific death rates increase at a nearly constant exponential rate for each year of age. Gompertz’ model has enjoyed success as the most heavily used model of adult mortality, and remains a quintessential tool for demographers and gerontologists. Among the many attractive characteristics of the Gompertz model is an estimate of the percentage increase in mortality for each additional year of age, the Rate of Mortality Increase (RMI). Although this measure is assumed to be a species-typical indicator of physiological aging, human population subgroups exhibit significant differences in the rate of mortality increase (Horiuchi et al. 2003). Group differences in the rate of age-related mortality increase may reflect differences in accumulated risk over the life course or in the timing of the onset of specific diseases (Carey and Liedo 1995; Horiuchi and Wilmoth 1997; Luder 1993). In examining life course trajectories of mortality, comparing group differences in the rate of increase with age can supplement our understanding of differences in the level of mortality. One important comparison is blacks and whites in the United States. Although the vast majority of research on this topic focuses on black/white differences in the level of mortality, blacks and whites also differ in the slope of age-related increase (Elo and Drevenstedt 2004; Geronimus et al. 1996; Hayward et al. 2000). This leads to categorically distinct trajectories of mortality in the adult age range.

Mortality profiles for the black and white populations in the United States differ considerably; blacks and whites experiences differences in the level and age-pattern of mortality and in the relative contribution of specific diseases. Studies examining the black mortality disadvantage throughout the life course also find that mortality increases more rapidly with age for whites than for blacks. Death rates for the two populations converge at older ages and mortality for whites begins to exceed that of blacks at the oldest ages (Manton et al. 1979). A large body of literature has examined the black/white mortality “crossover”, a process that leads to lower observed death rates among black than among whites after ages 85–90 (Dupre et al. 2006; Masters 2012). This phenomenon is unexpected because it contradicts what is known about the health and mortality disadvantage of the population throughout the life course up to this point (Hummer 1996; Williams and Jackson 2005). A considerable amount of literature has focused on the black/white crossover as a possible example of population heterogeneity and selective mortality (Manton and Stallard 1981). Alternatively, the process may be a statistical artifact, reflecting inaccurate mortality data at the oldest ages (Rosenwaike and Hill 1996).

In recent years, the widespread availability of reliable cause of death data in developed countries has greatly facilitated analysis of respective components of the mortality schedule. Cause of death analysis, the disaggregation of mortality and aging processes into specific ailments has been integral to demographic and gerontological studies of aging (Elo and Drevenstedt 2004; Finch 2009). Early research by Preston (1976) examined national differences in mortality by cause of death, which informed subsequent approaches to understanding the how components of the age pattern of mortality vary across populations (Himes 1994). Examining cause-specific mortality within rather than between populations helps to illuminate how specific diseases contribute to age-related functional decline or senescence (Carnes et al. 2006). Mortality from some causes of death rises rapidly at older ages. For instance, mortality from cardiovascular diseases is low in early adulthood and increases precipitously with age (Horiuchi et al. 2003). As a result, ischemic heart disease and stroke come to dominate mortality after age 65 (National Center for Health Statistics 2012).

The goal of this paper is to examine differences in the rate of mortality increase between non-Hispanic whites and non-Hispanic blacks in the United States. Given the large amount of literature focused on explaining the unexpected black/white mortality crossover, an understanding of how actuarial aging varies among these groups will inform future analyses of black/white disparities in old-age mortality. The analysis exploits variation among individual causes of death in order to examine several possible sources of the observed black-white difference in the rate of actuarial aging.

2. Background

There are two broad demographic perspectives for conceptualizing the rate of age-related mortality increase with respect to individual causes of death. The “bottom up” perspective essentially interprets the mortality level in a population as the sum of mortality from each cause of death (Himes 1994). This approach assumes some independence between individual diseases of aging; eliminating individual causes of death would lead to substantial reductions in age-specific mortality. In the other extreme, the “top down” perspective views the mortality rate as determined by biological risk and distributed amongst existing causes of death in a competing risks framework (Gavrilov and Gavrilova 1991). In this approach, human aging involves the cumulative senescence of bio-physiological systems that results in morbidity and mortality from various intrinsic, aging-related diseases (Carnes and Olshansky 1997). Causes of death are far from independent; on the contrary, eliminating individual causes of death will lead to only small reductions in mortality unless the underlying “top” components of the mortality schedule are substantially altered (Carnes and Olshansky 1993). Individual deaths that are prevented from specific causes of death may be filtered down to other diseases, reflecting the broad and multidimensional senescence of the body.

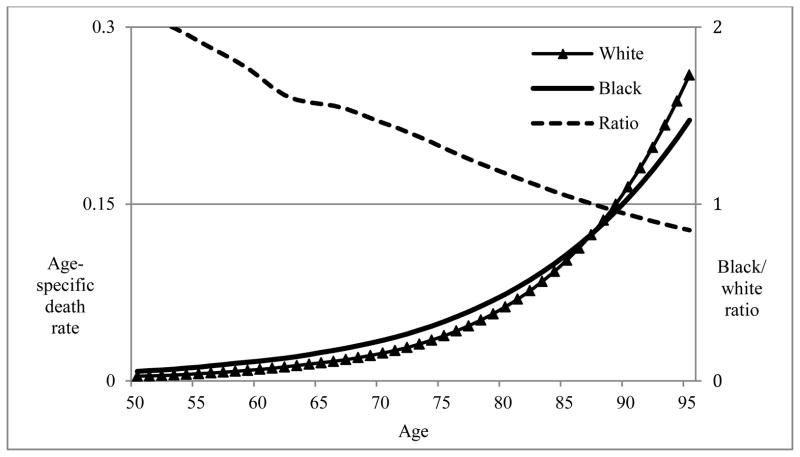
Blacks in the United States exhibit higher mortality levels than whites throughout the life course and into old age until around age 85, at which point the observed mortality rates of whites begin to exceed those of blacks (see Figure 1). Although the black/white mortality crossover has been documented using multiple sources of data and a variety of different study populations, it remains controversial (Dupre et al. 2006; Lynch et al. 2003; Masters 2012; Wing et al. 1985). It is possible that the crossover reflects differential survival to older ages of blacks and whites (Manton and Stallard 1981). Since the overall burden of mortality is higher for the black population at younger ages, the remaining survivors at older ages may be an increasingly robust subset of the population (Wing et al. 1985). The mathematical dynamics of mortality selection derive from studies assuming heterogeneity of frailty in the population (Vaupel and Yashin 1985). As cohorts age, they experience differential mortality, with the frailest members of the population dying first. The remaining members of the cohort represent a more robust subset of the original cohort, and may thus experience lower-than-expected levels of mortality (Vaupel et al. 1979). Supporters of the selective survival hypothesis claim that elevated mortality risks among blacks at younger ages single out the frailest members of the cohort, leaving a relatively healthy remaining group of individuals that experiences lower mortality risk in old age. Evidence for mortality selection comes from cohort studies documenting that death rates among whites begin to exceed those of blacks at the oldest ages (Berkman et al. 1989; Corti et al. 1999; Manton et al. 1991). Although there is very little direct evidence for the contribution of selective mortality, similar methods have been used to detect the expected consequences of differential mortality selection (Horiuchi and Wilmoth 1998; Manton and Stallard 1981).

Figure 1.

Age-specific death rates for blacks and whites aged 50–95 in 2000: Demonstrating the black/white crossover

Source: National Center for Health Statistics U.S. life tables 2000.

Notes: Age-specific death rates denote risk of death per person-year of exposure. Death rates for blacks exceed those for whites throughout the life course until age 87. The black/white mortality ratio exhibits relatively consistent monotonic decline across the adult age spectrum.

Although cohort studies purport to collect more accurate measures of the age of older individuals, they may still fail to completely eliminate the impact of age misreporting. Old-age mortality data for blacks in the United States has been plagued by a great deal of uncertainty (Preston et al. 2003). Mortality schedules of blacks and whites differ greatly, but mortality data for black Americans often exhibit substantial misreporting of ages, particularly for those born in the southern United States in the late 19^th or early 20^th centuries (Elo and Preston 1994). Although age misreporting occurs for both black and whites, there is a greater range of reported ages among older blacks, especially women (Hussey and Elo 1997). For many African-Americans over the age of 85, formal birth records are either of poor quality or unavailable completely (Preston et al. 1996). As a result, there is more noise in mortality estimates among blacks at older ages and black mortality may be biased downwards relative to whites (Hussey and Elo 1997). However, instead of reducing data quality to a level that precludes interpretation of observed mortality, previous research suggests that age misreporting leads to mortality biases with recognizable patterns (Preston et al. 1999). Some of these patterns may be indirectly observed by examining the black/white difference in the rate of mortality increase.

This paper pursues two goals with respect to the black/white difference in the rate of mortality increase with age – a lower mortality slope among blacks than among whites. The analysis refers to this slope as the Rate of Mortality Increase (RMI), interpreted as the proportional increase in the annualized death rate per year of age (Horiuchi et al. 2003). The first goal is to determine to what extent the pattern of black/white differences in cause-of-death-specific RMI reflects the two primary hypotheses explaining the black/white mortality crossover. The selective survival hypothesis suggests that RMI for blacks should be reduced relative to whites as the black population is increasingly composed of more robust individuals. Stronger mortality selection at younger ages for specific causes of death should be reflected in lower RMI for those causes of death. Thus, causes of death with larger relative black/white mortality gaps will be expected to exhibit larger gaps in the force of mortality selection, and thus in RMI. Selective survival suggests that there should be a positive association, across causes of death, between the black/white disparity in mortality at younger ages and the black/white disparity in RMI.

The age misreporting hypothesis instead argues that inaccurate ascertainment of age among older African-Americans leads to a downward bias in observed death rates. Preston and colleagues (1999) demonstrate that all forms of age misreporting (understatement, overstatement, both) lead to lower observed death rates than exist in unbiased data. However, this bias increases rapidly at the oldest ages and is relatively minor at younger adult ages. As a result, causes of death that tend to rise more rapidly with age (higher RMI) will endure larger effects. Age misreporting suggests that there should be a positive association, across causes of death between RMI level among white and the overall black/white difference in RMI. Similar methods have been used to obtain indirect evidence for age misreporting (Horiuchi and Coale 1990). These studies compare the expected unbiased age-pattern of mortality to mortality schedules of populations in which age misreporting is more prevalent. The black/white comparison is an appropriate example of this phenomenon (Preston et al. 1996). These two hypotheses will be examined using data on the 11 leading causes of intrinsic mortality among individuals over age 50.

The second goal of the analysis is to portray broad perspectives on understanding age patterns and cause-of-death distributions of mortality, and to determine whether a top down or bottom up perspective is more appropriate (Himes 1994). The black/white difference in all-cause RMI is decomposed into two components. The first component reflects black/white differences in RMI from individual causes of death. The contribution of this component implies that blacks and whites differ in the age pattern of mortality from each cause of death (top down approach). The second component reflects black/white differences in the cause of death distribution of mortality. RMI for individual causes of death varies substantially, with some causes rising rapidly with age and others rising more gradually (Horiuchi et al. 2003). This component expresses the extent to which blacks experience proportionately more deaths from causes with low RMI (bottom up approach).

3. Data and methods

3.1 Data

Data come from U.S. vital statistics from the year 2000. Death totals come from the Multiple Cause of Death (MCD) public-use files maintained by the National Center for Health Statistics. Deaths were aggregated by race, sex, age, and cause of death. Age-specific death rates were calculated using population figures from the 2000 US census (US Census Bureau 2003). Black and white populations include only individuals identifying as one race, black or white alone. Individuals of Hispanic origin (either black or white) are excluded from the analysis. In order to avoid small cell sizes for certain causes of death, death rates are aggregated to five-year age groups between 50–54 and 80–84. Although mortality data are available for more recent years, it is not clear that population estimates in non-censal years are sufficiently reliable for the analysis.

3.2 Causes of death

The cause-disaggregated analysis is useful for identifying specific disease contributions to the aging process. Additionally, it allows us to specify whether actuarial aging occurs in the same way for blacks and whites across major disease categories. The choice of the causes of death here involves two important considerations: overall contribution to mortality and presumed etiology within the physiological aging process. I examine 11 major cause-of-death categories. These causes of death have relatively well-known disease processes and are generally associated with “intrinsic mortality” (Carnes et al. 2006). They are the 11 leading causes of death (excluding external causes) among older individuals and are responsible for 75–80% of deaths between ages 50 and 84. Deaths are coded according to underlying cause of death as classified by the International Classification of Disease 10th revision (ICD 10). See Appendix Table A1 for detailed ICD codes for relevant cause of death categories. The causes of death examined here are as follows: (1) Ischemic heart disease (IHD) represents the largest cause of death in the United States and includes acute myocardial infarction and atherosclerotic heart disease. (2) Lung cancers are the most common type of cancer death in both men and women, overwhelmingly caused by cigarette smoking. (3) Stroke (cerebrovascular disease) is the second largest cause of cardiovascular death. (4) Chronic lower respiratory diseases, including chronic obstructive pulmonary disease and emphysema, are most common after age 65. (5) Breast cancer is the second largest cause of cancer death among women. (6) Diabetes mellitus is the leading endocrine disorder, and has increased steadily over the past several decades in response to the growing prevalence of obesity. (7) Colorectal cancer is a major cause of cancer death among both men and women. (8) Reproductive cancers include testicular and prostate cancer among men and ovarian, uteri, and cervical cancer among women. (9) Influenza and pneumonia represent the largest cause of infectious/parasitic disease death. (10) All other types of cancer are included in a residual “other cancer” category. This primarily includes cancers of the pancreas, stomach, and skin. (11) All other diseases of the heart, including rheumatic heart disease and hypertensive heart disease make up the “other heart diseases” category. The residual category, which comprises all causes of death not included in the 11 categories above, makes up slightly less than 20–25% of all deaths between ages 50 and 84. This category includes, among others, infectious diseases other than influenza, chronic liver disease, and external causes of death. To ensure that the results are not driven by the choice of causes of death, I perform the analysis by including the 35 largest causes of death in this age group (including external causes). The results are shown in Appendix Table A2.

3.3 Methods

It is necessary to specify mathematically what is meant by the rate of mortality increase with age. When mortality is modeled using a Gompertz function the force of mortality μ(x) is given by

$$\mu (x)=\alpha e^{\beta x}$$

with level and shape parameters α and β, respectively. Since we are interested in the proportional change in the force of mortality, we take the derivative of μ(x) divided by μ(x)

$$\mathit{RMI}=\frac{d\mu (x)}{\mu (x)dx}=\frac{\alpha \beta e^{\beta x}}{\alpha e^{\beta x}}=\beta .$$

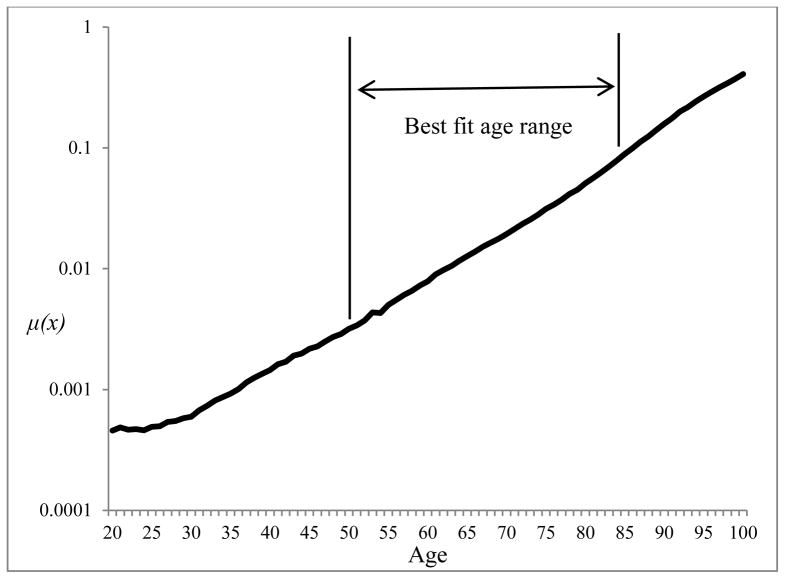
The Gompertz model fits observed mortality data extremely well in the adult ages. Figure 2 displays single-year death rates for U.S. women in 2000 between ages 20 and 100. Between ages 50 and 84, the increase is very linear and the mortality data track the Gompertz model very closely (R-squared = 0.998). This age range is the focus of the analysis and was chosen to capture the best fit for exponential mortality increase and to avoid the problematic deceleration of mortality at the oldest ages (Horiuchi and Wilmoth 1998). Other studies have used age ranges 35–64 and 65–89 and found similar fits for the model (Horiuchi et al. 2003). The model is applied to all-cause mortality as well as each cause of death. The model has the form

Figure 2.

Age-specific death rates for U.S. women: 2000

Source: Human Mortality Database (2008).

$$ln({{}_{5}M}_x^i)={\alpha }^i+{\beta }^i(x)$$

where ${{}_{5}M}_x^i$ is the death rate from cause i between ages x and x+5, and αⁱ and βⁱ are parameters estimated by least squares. βⁱ is the RMI for cause of death i. Because all causes of death sum to all-cause mortality, it is possible to express all-cause RMI as the sum of cause-specific RMIs (βⁱ) weighted by the proportionate cause of death distribution as

$$\mathit{RMI}\cong \sum _{i=1}^n{\beta }^i·{\mathrm{\Pi }}^{\mathrm{i}}$$

where βⁱ is the RMI for the total population (or population subgroup) and Πⁱ is the proportion of deaths due to cause i in the age-range 50–84 (see Appendix for more detailed derivation). The equation is an approximation due to slight cause-specific deviations from the Gompertz model, but in practice this equation gives a very similar RMI to that estimated separately by Equation 1. Kitagawa (1955) developed a method for decomposing the difference between two demographic rates which is applicable to measures that are made up of additive components, such as the mortality component and age-structural component of the crude death rate. Using this framework, the black-white difference in RMI can be decomposed into analogous components

$${}^{W}RMI-{}^{B}RMI=\sum _{i=1}^n({{}^W\beta }^i-{{}^B\beta }^i)·\left[\frac{{{}^B\mathrm{\Pi }}^{\mathrm{i}}+{{}^W\mathrm{\Pi }}^{\mathrm{i}}}{2}\right]+\sum _{i=1}^n({{}^B\mathrm{\Pi }}^{\mathrm{i}}-{{}^W\mathrm{\Pi }}^{\mathrm{i}})·\left[\frac{{{}^B\beta }^i+{{}^W\beta }^i}{2}\right]$$

In this equation, the superscripts W and B refer to the value for the white and black populations, respectively. The difference is expressed as the sum of two separate terms. The first term in the equation refers to the effect of differences in cause-specific mortality increase with age (slopes). This component denotes the extent to which mortality from individual causes of death increases more slowly with age among blacks. The second term refers to the effect of differences in the proportionate cause of death structure (distributions). This component refers to the degree to which causes of death with inherently low RMI are proportionately more common among blacks. It is possible to attribute differences in all-cause RMI between blacks and whites to these two components.

3.4 Rate of mortality increase and the black/white crossover

The black/white mortality crossover reflects differential rates of aging between blacks and whites over the adult age range, a function of the black/white difference in RMI. Finding evidence for selective survival and age misreporting depends on indirect detection of the impact of each process on the observed age pattern of mortality. Support for selective survival relies on the expectation that causes of death with higher death rates will produce greater mortality selection and lead to more rapid removal of more frail individuals (Manton et al. 1986). To the extent that the selective survival hypothesis is true, RMI for blacks should be lower for causes of death with heavy mortality selection at younger ages (Horiuchi and Wilmoth 1998). Diseases that show a larger black disadvantage at younger ages will also be expected to rise more slowly with age for blacks. Thus, the size of the black/white difference in RMI should be positively associated with the size of the black/white difference in the level of mortality.

Alternatively, indirect evidence for age misreporting relies on detectable signs of deviation in the age pattern of mortality (Horiuchi and Coale 1990). The hypothesis suggests that inaccurate ascertainment of ages biases death rates downwards among older blacks, more so than among whites (Preston et al. 2003). The extent of this bias also rises with age, leading to a greater impact of age misreporting at the very oldest ages (Coale and Kisker 1986). As long as the likelihood of misreporting ages does not vary significantly by cause of death, the relative impact of misreporting on the black/white RMI difference will be larger for causes of death that rise rapidly with age (Preston et al. 1999). That is, the downward RMI bias due to age misreporting will be more severe for causes of death that have a high RMI to begin with. Thus, to the extent that age misreporting can help to explain the crossover, there should be a positive association between the RMI level and the size of the black-white difference in RMI across the 11 causes of death considered.

4. Results

Cause of death distributions for blacks and whites by sex are shown in Table 1. There are 600,000 – 700,000 deaths each among white men and women, and close to 80,000 – 90,000 deaths among black men and women in the 50–84 age group. Ischemic heart disease (IHD) is the leading cause of death for all groups, responsible for 19%–24% of deaths between ages 50 and 84. Although blacks have higher death rates than do whites at most ages, it is important to recognize that their cause of death distributions differ little from those of whites. Notable differences occur for only three causes of death: chronic lower respiratory disease, which is more common among whites; reproductive cancers, which make up a greater portion of mortality among black men (4.6%) than white men (2.6%); and diabetes mellitus mortality, which is relatively more common among blacks (6.5% of deaths among black women, 3.5% among white women). This disparity may reflect a greater prevalence of obesity in the black population, or it may result from differences in diet more generally (Shai et al. 2006).

Table 1.

Cause of death distributions by sex and race: 2000

	Percentage of deaths between ages 50 and 84
	Men		Women
	Black1	White1	Black	White
(1) Ischemic Heart Disease	20.9%	24.4%	20.5%	18.9%
(2) Lung Cancer	9.7%	10.2%	5.9%	8.5%
(3) Stroke	6.4%	5.3%	7.9%	7.3%
(4) Chronic Lower Respiratory Disease	3.5%	6.3%	2.9%	7.2%
(5) Breast Cancer	--	--	4.2%	4.4%
(6) Diabetes Mellitus	4.1%	3.0%	6.5%	3.5%
(7) Colorectal Cancer	2.9%	2.9%	3.1%	2.9%
(8) Reproductive Cancers	4.6%	2.6%	2.7%	2.7%
(9) Influenza and Pneumonia	2.0%	2.0%	1.8%	2.2%
(10) Other Cancers	12.0%	13.8%	9.9%	11.3%
(11) Other heart diseases	8.8%	6.7%	9.9%	7.5%
All residual causes	24.9%	22.7%	25.9%	23.7%
All Causes	100%	100%	100%	100%
Total Deaths	90,405	681,246	83,221	590,326

Source: Author’s calculations from Multiple Cause of Death Public-Use file available from the National Center for Health Statistics, 2000.

¹Refers to non-Hispanic blacks and whites.

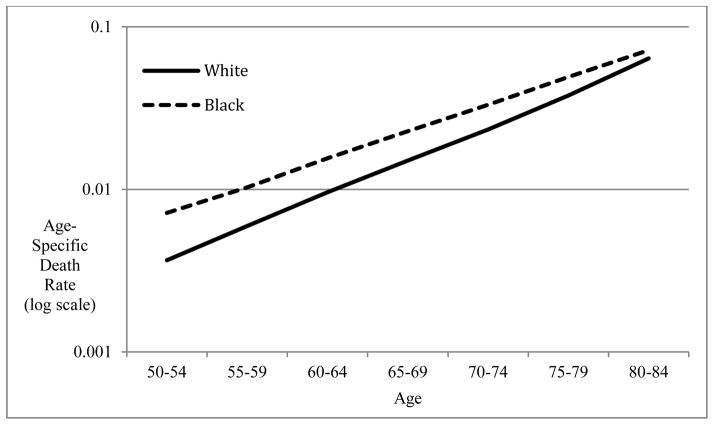
Figure 3 shows raw death rates for black and white men (results for women are very similar). Graphed on a logarithmic scale, death rates increase linearly with age. The fit of the Gompertz model is extremely good for these populations (R-squared=0.998). Above age 90 the fit becomes much more dubious as mortality increase decelerates (Horiuchi and Wilmoth 1998). Death rates for blacks are higher than those for whites between ages 50 and 84, but they converge at the oldest ages, since the slope is higher for whites. Mortality for white women increases at 9.8% per year of age compared to just 7.9% for black women. The black/white difference is nearly identical for men (9.3% versus 7.3%). This difference in the rate of increase means that, despite a substantial black disadvantage in mortality at age 50, black/white mortality rates converge and crossover at age 90 for men and age 89 for women. Mortality for black men exceeds that of white men by 6 deaths per 1,000 at age 50. Black women’s mortality is 3.5 deaths higher per 1,000. The crossover results from a less rapid increase among blacks across the entire adult age range.

Figure 3.

Age-specific death rates for U.S. black and white women ages 50–84: 2000

Notes: Age-specific death rates for 5-year age groups used to estimate RMI. Death rates are graphed on a logarithmic scale to demonstrate near linear mortality increase. Death rates for blacks and whites converge at older ages. The pattern is very similar for men.

Source: Author’s calculations from Multiple Cause-of-Death public-use files available from the National Center for Health Statistics.

Table 2 shows RMI by race, sex, and cause of death. All-cause RMI is significantly higher for whites than for blacks. There is substantial variability in RMI by cause of death. The highest RMIs are seen for influenza and pneumonia, stroke, chronic lower respiratory diseases, and reproductive cancers (among men). The lowest RMIs occur for cancers, primarily lung cancer for men (RMI = 6 – 8%), and breast and reproductive cancers for women (3 – 5%). For all groups, there is also a notable opposition in RMI between cancers and cardiovascular diseases. Cancer mortality appears to increase at a rate below the all-cause average, while other causes of death, particularly ischemic heart disease and stroke (RMI > 12% among whites), increase faster than the average. It is important to emphasize that RMI for whites exceeds that for blacks for each cause of death considered here except reproductive cancers among women. There is some variation in the size of the black-white difference by cause of death, but the pattern is tremendously consistent. The largest differences occur for stroke, chronic lower respiratory disease, and other heart diseases, each with greater than three percentage-point gaps.

Table 2.

Cause-specific RMI by sex for blacks and whites: 2000

	Yearly rate of increase between ages 50 and 84
	Men		Women
	Black	White	Black	White
All Causes	7.3%	9.3%	7.9%	9.8%
(1) Ischemic Heart Disease	7.9%	9.3%	9.6%	12.0%
(2) Lung Cancer	6.2%	7.8%	5.4%	6.7%
(3) Stroke	8.7%	12.3%	9.4%	12.6%
(4) Chronic Lower Respiratory Disease	10.5%	13.2%	8.0%	11.7%
(5) Breast Cancer	--	--	2.8%	4.2%
(6) Diabetes Mellitus	7.2%	8.5%	8.0%	8.8%
(7) Colorectal Cancer	7.5%	8.4%	7.4%	8.4%
(8) Reproductive Cancers	15.2%	15.9%	5.5%	5.2%
(9) Influenza and Pneumonia	9.9%	13.0%	10.6%	12.8%
(10) Other Cancers	5.8%	7.4%	6.9%	7.7%
(11) Other heart diseases	6.6%	9.6%	8.0%	11.2%
All residual causes	5.4%	7.5%	7.0%	8.8%
Black/white difference	1.96%		1.96%

Note: Denotes the percentage increase in the death rate from specified causes for each additional year of age between ages 50 and 84. Estimated using the regression model in Equation 1.

Source: Author’s Calculations from Multiple Cause of Death files, 2000

Before presenting the results of the decomposition, it is important to note that the high level of similarity of blacks’ and whites’ cause of death distributions indicates only a minor role for the distributions component. The results are shown in Table 3. The slopes component is responsible for 98% of the black-white difference in RMI among men and 96% among women. The results of the decomposition remain informative in that they demonstrate that the few ways in which the cause of death distributions of black and whites differ are not driving the black/white difference in RMI. For example diabetes mellitus mortality is more common among black men and women, a cause of death with relatively low RMI. Whites also exhibit a larger contribution of high-RMI chronic respiratory diseases. Despite this, the overwhelming driver of the black/white RMI gap is consistently lower RMI among blacks for each cause of death.

Table 3.

Decomposition of black-white difference in RMI into slopes and distributions components

	Difference in all-cause RMI	Portion due to slopes component1	Portion due to distributions component2
Black/white difference men	1.96%	1.91% (97.8%)	0.04% (2.2%)
Black/white difference women	1.96%	1.89% (96.1%)	0.07% (3.9%)

Notes: Decomposition component values are calculated using Equation 2. Percent contributions are shown in parentheses.

¹Portion of the all-cause difference attributable to black/white difference in RMI (slopes) for each cause of death.

²Portion of the all-cause difference attributable to black/white differences in cause-of-death distribution of mortality.

4.1 Rate of mortality increase and the black-white crossover

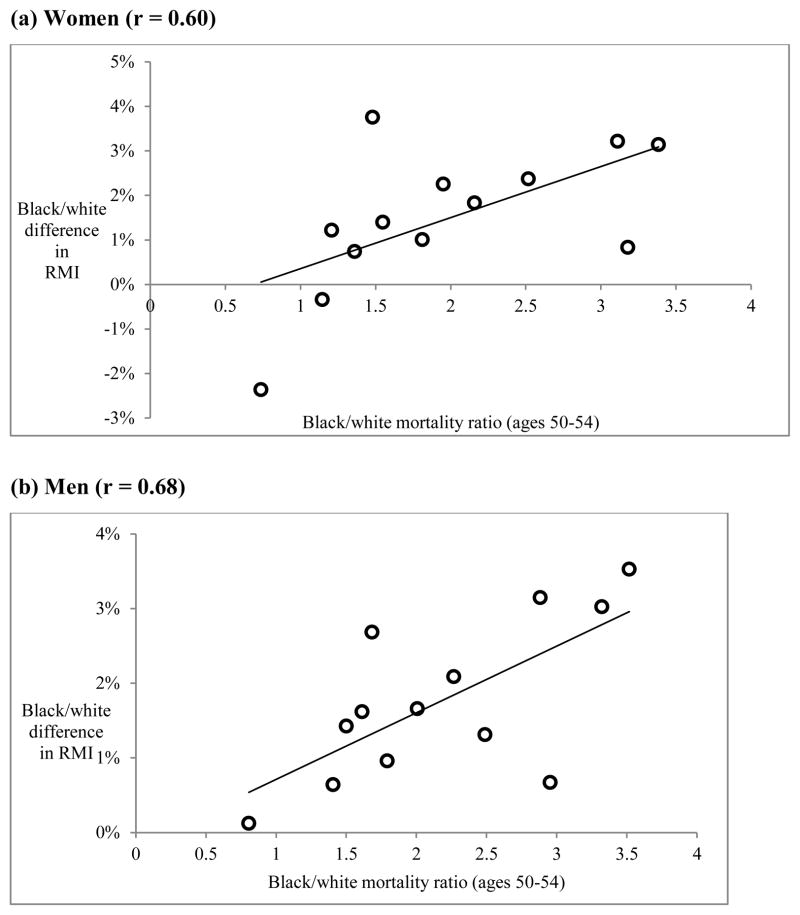
The most prominent explanation for the black-white mortality crossover is the selective survival of the most robust black individuals to older ages (Manton and Stallard 1981). As an increasingly select group of individuals remains at each successive age, mortality will rise more slowly for blacks than for whites, who are subject to weaker selection at younger ages due to lower mortality risk. The hypothesis implies that the black/white difference in RMI should thus be larger for those causes of death with stronger forces of selection: high mortality among blacks relative to whites. As a result, we would expect a positive association between the black/white disparity in cause-specific mortality level at age 50 and the difference in cause-specific RMI. Although the effects of mortality selection are likely to be complex, there is some evidence that it is contributing to the mortality crossover. Figure 4 shows a scatter plot of the black/white mortality ratio at age 50 against the black/white RMI difference. There is a relatively strong relationship (r = 0.68 for men, r = 0.60 for women), suggesting that selective survival may help to explain the black/white difference in RMI.

Figure 4.

The role of selective survival: Relationship between black-white mortality ratio at age 50 and black/white difference in RMI for each cause of death

Notes: RMI difference calculated as RMI(whites) – RMI(blacks). Mortality ratio is the age-specific death rate for blacks divided by corresponding rate for whites in the age group 50–54. Each point represents one cause of death.

Source: Author’s calculations from the 2000 Multiple Cause-of-Death public use files available from the National Center for Health Statistics.

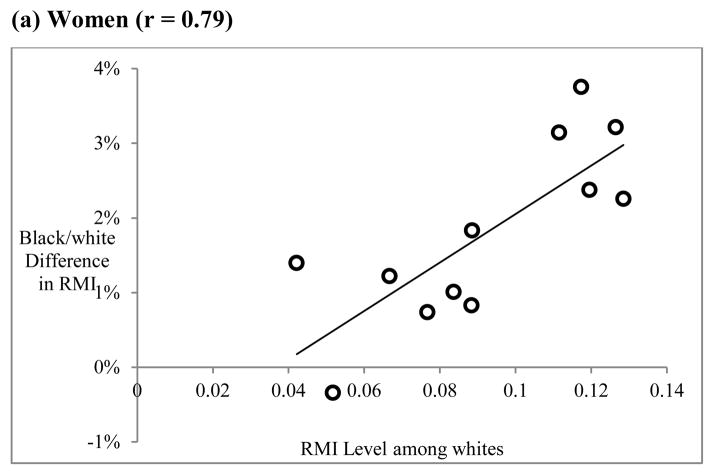
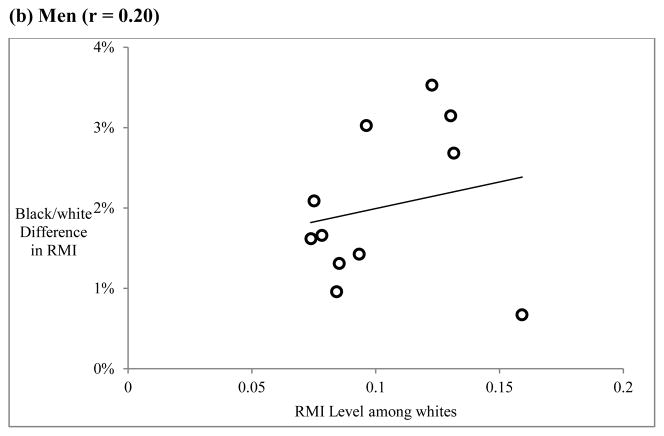
There is also some evidence of inaccurate measurement of age as an explanation of the black/white crossover. Because age-misreporting would be expected to have a greater impact on causes of death that dominate at later ages, there should be a relationship between RMI level and the size of the black/white difference in RMI. This relationship is shown in Figure 5 for women (panel a) and men (panel b). There is a strong correlation among women (r = 0.79), but a relatively weak one among men (r = 0.20). This finding suggests that age misreporting may be an important contributor to the black/white crossover, but that its impact is larger for women than for men. This is consistent with previous research indicating that age misreporting is more prevalent among older African-American women (Elo and Preston 1994; Preston et al. 2003).

Figure 5.

The role of age misreporting: Relationship between RMI level and black-white difference in RMI for each cause of death

Notes: RMI difference calculated as RMI(whites) – RMI(blacks). RMI level refers to estimated RMI for whites from Equation 1. Each point represents one cause of death

Source: Author’s calculations from the 2000 Multiple Cause-of-Death public use files available from the National Center for Health Statistics.

5. Discussion

This study examined differences between blacks and whites in the rate mortality increase with age. Previous research on the black/white mortality crossover has consistently found a lower Gompertz “slope” among blacks than among whites, and it is clear that this slope difference contributes to the crossover at the oldest ages. Although it is evident that aging-related mortality patterns among blacks were different from those of whites, previous studies provided no explanatory framework for understanding these distinctions. The current analysis employed a Gompertz model of age-related mortality increase and detailed cause of death data in order to examine the two most prominent explanations for the black/white mortality crossover: selective survival and age misreporting. The analysis finds evidence that both processes contribute to the black/white difference in the rate of age-related mortality increase, although age misreporting appears to be more important for the comparison of black and white women. The analysis also finds that lower RMI among blacks is seen across each cause of death, a finding that suggests a “top down” approach to aging-related mortality may be more appropriate.

Both selective survival and age misreporting have the potential to reduce RMI for the black population relative to the white population and thus may explain why mortality for white begins to exceed that of blacks at the oldest ages. Selective survival or heterogeneity explanations form the theoretical basis of many empirical analyses of aging-related mortality phenomena, including the deceleration and “flattening” of the mortality curve at very old ages (Vaupel and Yashin 1985; Vaupel 1997). As the more frail members of the population die at younger ages, the population is increasingly composed of robust individuals with lower underlying mortality risks. In this way, the observed mortality curve begins to diverge from the aging experiences of individuals within the population. According to selective survival explanations, the slope of the Gompertz mortality curve for the black population is reduced relative to the slope of the curve for individual risk (Strehler and Mildvan 1960). The impact of population heterogeneity on observed mortality is difficult to observe directly (Vaupel and Yashin 1985), but the current study finds indirect evidence for mortality selection. Cause of death categories with large black/white disparities in the level of mortality at younger ages, such as ischemic heart disease and stroke, are also often the causes of death that exhibit the largest black/white differences in the slope. This may indicate that higher-risk blacks die more often at younger ages, while the remaining cohort members at older ages are relatively healthy.

There is also evidence that greater rates of age misreporting among older African-Americans, particularly women, contribute to the black/white difference in the rate of mortality increase and thus the crossover. Among women, there is a strong correlation between cause-specific RMI level and the size black/white difference in cause-specific RMI. This may reflect the fact that age misreporting has a more pronounced effect on causes of death that rise rapidly with age, all else being equal. Among men, the relationship is much weaker, which is consistent with evidence that age misreporting among older African-Americans is more common among women (Elo and Preston 1994).

Although the black-white mortality crossover is not observed in the age-range considered here, we can use the estimated Gompertz model to predict that it would occur at age 90 for men and age 89 for women. Since lower RMI for blacks occurs because cause-specific RMIs are lower for blacks as well, there are corresponding mortality crossovers for individual causes of death in addition to all-cause mortality. Among men, the models predict a crossover for IHD at age 83, lung cancer at age 90, stroke at age 90, and other cancers at age 92. Only reproductive cancers and diabetes mellitus exhibit no crossover prior to age 100.

This paper also provides evidence that a “top down” approach to understanding aging-related mortality may be the appropriate perspective. The analysis used classical decomposition methods to determine that the black/white difference in RMI results from consistent RMI differences across all causes of death. That is, blacks experience lower rate of mortality increase for nearly all causes of death. Despite large differences in the level of mortality (Elo and Drevenstedt 2004), the proportionate cause of death distribution of mortality is quite similar for blacks and whites. This suggests that the underlying factors responsible for the less rapid age-related mortality increase among blacks operate across causes of death. This finding is significant on two levels. First, it provides a deeper understanding of black/white differences in adult mortality, particularly in the age-pattern of mortality among older adults, which has implications for the black/white mortality crossover. Black and white populations in the United States differ not only in the level of mortality but also in the pattern of aging. Second, it furthers our conceptual approach to studying aging-related mortality processes by cause of death. A top down approach, in which the level of all-cause mortality has a privileged position and individual causes of death are seen as outcomes of this level, may be more appropriate for analysis of cause-specific mortality (Gavrilov and Gavrilova 1991; Himes 1994). Aging-related mortality should thus be understood as reflecting the simultaneous senescence of multiple biological systems, a process that increases risk of death from many varied degenerative conditions (Bains 2000; Gavrilov and Gavrilova 2001; Laird and Sherratt 2009). Future analyses of aging-related mortality increase should not treat mortality from individual causes as independent. Explaining blacks’ and whites’ distinct patterns of aging requires a more comprehensive explanation that covers the experience of the majority of causes of death.

This study has several limitations. The first three concern the methodological strategy. Fitting a linear function to the entire age-pattern of mortality ignores deviations from exponential increase, some of which may be substantively interesting (Horiuchi and Coale 1990). Limiting the age range to ages 50–84 partially helps to resolve this problem, as the Gompertz model fits exceptionally well in this age range. Although deviations from exponential mortality increase should not be expected to be notably large, it remains unclear to what extent this simplification may mask important complexities in the age-pattern of mortality increase (Yashin et al. 1994). Second, all mortality data used in this analysis are period data, despite the fact that theories of aging and senescence implicitly refer to the experience of individuals or real cohorts (Gurven and Fenelon 2009). In periods of mortality decline, younger cohorts tend to experience larger proportional mortality than older cohorts, which may lead to inflated period RMI (Horiuchi and Wilmoth 1997). Although this simplification may affect the level of RMI, it might not impact the results of decompositions of black/white differences in RMI, since estimates for both blacks and whites would similarly be affected by period-cohort inconsistencies. Finally, this study used the age range 50–84, which may ignore important aging-related processes at younger or older ages.

Other studies have modeled mortality using a Gompertz function from ages 40–90 and have found similar levels of fit (Beltrán-Sánchez et al. 2012; Yashin et al. 2002). An expansion of the age range considered does not change the substantive interpretation of the results, although there are small deviations in the contributions of specific causes of death. This consistency suggests that black/white differences in aging-related mortality characterize a much broader age range than that considered here.

The remaining limitation concerns issues of comparability of cause of death information among blacks and whites. The analysis assumes that cause of death coding is similarly complete and accurate among both blacks and whites in the United States. Although the completeness of vital registration in the U.S. is relatively strong, there is some evidence that cause of death coding occurs differently for blacks and whites, particularly for external causes of death (Noymer, Penner, and Saperstein 2011). This may be especially true at the oldest ages, where the range of conditions to which individuals are exposed is significantly larger than at younger adult ages (Manton 1980). This limitation suggests that findings should be replicated using multiple data sources that ascertain cause of death information in various ways (e.g. Corti et al. 1999).

6. Conclusion

African-Americans have long experienced higher death rates and shorter life expectancy than whites at most ages. Substantial literature has focused on racial inequalities in health and mortality, and the reasons for these disparities have been widely examined (Elo and Drevenstedt 2004; Hayward et al. 2000). Although most research on black/white disparities in health and mortality has focused on differences in the level of mortality, studies in the 1970s and 1980s identified unique patterns of aging in the two populations (Manton et al. 1979). Differential rates of mortality increase among whites and blacks results in the mortality crossover at the oldest ages, which has generated significant interest among demographers and gerontologists (Dupre et al. 2006). Most studies on the crossover have focused exclusively on mortality at the oldest ages (Lynch et al. 2003). Given the overwhelming consistency of the rate of mortality increase with age, it may also be appropriate to consider the entire age range of adult mortality. This paper identified demographic factors responsible for differences between blacks and whites in the observed rate of actuarial aging. Blacks experience more gradual increase in mortality with age than whites, a pattern manifested across many disparate disease categories. Indeed, this pattern appears be driven by both selective survival as well as by differential age misreporting.

Although this paper supports both selective survival and age misreporting as contributors to the black/white crossover, we are left without an understanding of the proximate reasons why mortality increases more rapidly with age for whites than for blacks. One possibility concerns the relationship between the age-pattern of mortality decline over time and the rate of mortality increase with age (Hawkes et al. 2012). As the level of mortality falls, death rates are reduced first at younger ages, which provide large payoffs in terms of life expectancy gains. Once the “low-hanging fruit” of mortality decline has been exploited, future declines must come at older ages, which have smaller marginal effects on life expectancy (Keyfitz 1968; Vaupel 1986). Mortality at older ages is characterized by a greater variety of risks as functional decline occurs in individuals on many dimensions (Finch 2009; Vaupel et al. 1998). In this way, mortality at older ages is more intransigent and less responsive to medical treatment (Wilmoth 2000). Mortality after age 50 in the United States first began to fall significantly starting in the 1950s. Declines in rates of cardiovascular death first occurred at the younger adult ages 35–69, while proportional declines were much smaller at older ages (Wilmoth 2000). Because mortality declined to lower levels among whites than blacks, greater RMI among whites may reflect a faster pace of mortality decline at younger adult ages. Recently there has been some progress against mortality at the oldest ages, with evidence that death rates are declining even at the oldest ages, previously thought to be beyond the realm of medical intervention (Wilmoth 1995). As medical technology begins to make headway against diseases at very old ages (e.g. cancers, dementias), the rate of aging may decline for both blacks and whites (Goldstein and Cassidy 2012). Like the results of this paper, this explanation is also consistent with a top down approach to aging-related mortality. Future research on the mortality crossover should examine the specific diseases that exhibit large black/white differences in the rate of mortality increase with age, bearing in mind that aging-related mortality involves more than simply the sum of individual causes of death.

Appendix

The force of mortality at a given age, μ(x), can be disaggregated into n separate causes of death by

$$\mu (x)={\mu }^1(x)+{\mu }^2(x)+\cdots +{\mu }^n(x)$$

where μⁱ(x) is the force of mortality due to cause i. Since we are interested in the slope of the above function, we differentiate with respect to age

$$\frac{d}{dx}\mu (x)=\frac{d}{dx}{\mu }^1(x)+\frac{d}{dx}{\mu }^2(x)+\cdots +\frac{d}{dx}{\mu }^n(x).$$

Dividing through by μ(x) and multiplying each individual $\frac{d}{dx}{\mu }^i(x)$ term by $\frac{{\mu }^i(x)}{{\mu }^i(x)}$

$$\frac{\frac{d}{dx}\mu (x)}{\mu (x)}=\frac{\frac{d}{dx}{\mu }^1(x)}{{\mu }^1(x)}·\frac{{\mu }^1(x)}{\mu (x)}+\frac{\frac{d}{dx}{\mu }^2(x)}{{\mu }^2(x)}·\frac{{\mu }^2(x)}{\mu (x)}+\cdots +\frac{\frac{d}{dx}{\mu }^n(x)}{{\mu }^n(x)}·\frac{{\mu }^n(x)}{\mu (x)}.$$

Simplifying

$$\beta (x)=\frac{d}{dx}ln\mu (x)=\frac{d}{dx}ln{\mu }^1(x)·{\mathrm{\Pi }}^1(x)+\frac{d}{dx}ln{\mu }^2(x)·{\mathrm{\Pi }}^2(x)+\cdots +\frac{d}{dx}ln{\mu }^n(x)·{\mathrm{\Pi }}^{\mathrm{n}}(x)$$

where Πⁱ(x) is the proportion of deaths at age x due to cause i and β(x) represents the rate of mortality increase (RMI) at age x per year of age. Simplifying the above expression yields

$$\beta (x)={\sum }_{i=1}^n{\beta }^i(x)·{\mathrm{\Pi }}^i(x).$$

The rate of mortality increase at age x is equal to the sum of the rate of increase mortality due to respective causes weighted by their proportionate cause contributions to all-cause mortality. As predicted by the Gompertz model, the analysis here assumes that the rate of mortality increase remains constant from age 50 to age 84, so we can express β(x) as the sum of cause-specific slopes multiplied by the proportionate cause of death distribution

$$\beta \cong \sum _{i=1}^n{\beta }^i·{\mathrm{\Pi }}^i$$

This sum allows us to employ classical demographic decompositions methods developed by Kitagawa (1955) to separate differences between the k values of two populations into effects of cause-specific slopes and cause of death distribution respectively. To decompose the differences of rates for the black and white populations (^Bβ, ^Wβ)

$$\begin{array}{c}{}^W\beta -{}^B\beta =\sum _{i=1}^n{{}^W\beta }^i·{{}^W\mathrm{\Pi }}^{\mathrm{i}}-\sum _{i=1}^n{{}^B\beta }^i·{{}^B\mathrm{\Pi }}^{\mathrm{i}}\\ =\sum _{i=1}^n({{}^W\beta }^i-{{}^B\beta }^i)·\left[\frac{{{}^W\mathrm{\Pi }}^{\mathrm{i}}+{{}^B\mathrm{\Pi }}^{\mathrm{i}}}{2}\right]+\sum _{i=1}^n({{}^W\mathrm{\Pi }}^{\mathrm{i}}-{{}^B\mathrm{\Pi }}^{\mathrm{i}})·\left[\frac{{{}^W\beta }^i+{{}^B\beta }^i}{2}\right]\end{array}$$

The above procedure is from Preston et al. (2001, p. 28), which expresses the difference as the sum of two separate components. The first term represents the contribution of differences in cause-specific RMI (slopes) while the second term accounts for differences in cause-of-death distribution.

Table A1.

International classification of disease 10th revision codes

	ICD-10 Codes
Ischemic Heart Disease	I20–I25
Lung Cancer	C33–C34
Stroke	I60–I69
Chronic Lower Respiratory Disease	J40–J47
Breast Cancer	C50
Diabetes Mellitus	E10–E14
Colorectal Cancer	C18–C21
Reproductive Cancers	C61 (males), C53–C56 (females)
Influenza and Pneumonia	J10 – J18
Other Cancers	C00–C17, C22–CC49, C51–C52, C57–C60, C62–C97
Other heart diseases	I00–I09, I11, I13

Table A2.

Decomposition results using 35 causes of death

	Difference in all-cause RMI	Portion due to Slopes1	Portion due to cause of death distribution2
Black-white difference men	2.14%	1.89% (88.5%)	0.25% (11.5%)
Black-white difference women	2.04%	1.98% (97.1%)	0.06% (2.9%)

Notes: Decomposition component values are calculated using Equation 2. Percent contributions are shown in parentheses.

¹Portion of the difference attributable to black-white difference in RMI (slopes) for each cause of death.

²Portion of the all-cause difference attributable to black-white differences in cause-of-death distribution of mortality.