Abstract
Most implicit solvation models require the definition of a molecular surface as the interface that separates the solute in atomic detail from the solvent approximated as a continuous medium. Commonly used surface definitions include the solvent accessible surface (SAS), the solvent excluded surface (SES), and the van der Waals surface. In this study, we present an efficient numerical algorithm to compute the SES and SAS areas to facilitate the applications of finite-difference Poisson-Boltzmann methods in biomolecular simulations. Different from previous numerical approaches, our algorithm is physics-inspired and intimately coupled to the finite-difference Poisson-Boltzmann methods to fully take advantage of its existing data structures. Our analysis shows that the algorithm can achieve very good agreement with the analytical method in the calculation of the SES and SAS areas. Specifically, in our comprehensive test of 1,555 molecules, the average unsigned relative error is 0.27% in the SES area calculations and 1.05% in the SAS area calculations at the grid spacing of 1/2Å. In addition, a systematic correction analysis can be used to improve the accuracy for the coarse-grid SES area calculations, with the average unsigned relative error in the SES areas reduced to 0.13%. These validation studies indicate that the proposed algorithm can be applied to biomolecules over a broad range of sizes and structures. Finally, the numerical algorithm can also be adapted to evaluate the surface integral of either a vector field or a scalar field defined on the molecular surface for additional solvation energetics and force calculations.
Introduction
Water is crucial to the functions of biological molecules such as nucleic acids and proteins. The solute-solvent interactions can be accurately modeled by explicit solvent models in biomolecular simulations. Nevertheless extra computational cost has to be paid to handle thousands to millions of extra degrees of freedom in the explicit solvent. This is because a system of higher dimensions requires more samplings to achieve equilibrium and to cover sufficient biologically interesting conformations. Alternatively, the solvent molecules can be treated implicitly as in the implicit solvent models to capture average solvent behaviors. Most modern implicit solvent models require the definition of an interface that separates the solute in atomic detail from the solvent approximated as a continuum medium. The solvation free energy and force are both sensitively dependent on the interface location and presentation.
The interface is often based on a molecular surface definition. Well-known molecular surface definitions are the solvent accessible surface (SAS), the solvent excluded surface (SES), and the van der Waals surface (VDWS). The SAS was defined by Lee and Richards as a union of atomic spheres with radii augmented by the probe radius for a given molecule.1 The SES was introduced by Richards in 1977.2 It is more complex with two types of surfaces, the contact surface that consists of solvent exposed portions of van der Waals spheres and the reentrant surface that consists of the inward-facing surface of the solvent probe sphere as it rolls over the molecule. Finally the VDWS represents the molecular interior as the union of the atomic spheres with van der Waals radii. In contrast to the hard sphere definition of atomic volumes in the above surface definition, a smoothly varying dielectric boundary using the Gaussian(-like) density approach has also been reported.3, 4
Recent analyses have shown that the numerical Poisson-Boltzmann methods with the SES definition are reasonable in the calculation of electrostatic solvation energetics and forces with respect to explicit solvent simulations.3–7 Unfortunately the SES is not differentiable with respect to atomic positions, making it difficult to be adopted in molecular dynamics simulations.5 The SAS definition is difficult to reproduce the electrostatic energetics in the explicit solvent models due to its much enlarged atomic cavities, but the SAS definition has been used to estimate the nonpolar hydration energy with great successes.6–14 The SAS is also more efficient than the SES and differentiable with respect to atomic positions.7, 15–20 The VDWS definition is both efficient and smooth over time, making it advantageous to molecular simulations. However, it has been pointed out that the VDWS definition has the tendency to assign a much higher value to the apparent protein interior dielectric constant, as in the pKa calculations which may or may not be wanted.21–26 On the other hand, Zhou and co-workers have shown that the electrostatic free energies using the VDWS definition as the dielectric boundary are in better accord with the experimental data and the explicit solvent simulation results for a series of tests, including a single mutation to the folded protein,27 protein-protein complexes,28, 29 and protein-RNA complexes.30
Given a surface definition, an important issue is how to evaluate the surface area or surface integration for biomolecular simulations. Due to the efficiency of the SAS definition, significant prior efforts have been invested to develop analytical methods15, 16, 18, 20, 31–45 and numerical algorithms.46–51 The analytical SAS methods can be further divided into two types, exact15, 16, 18, 20, 32–38 and approximate.31, 39–45 A comprehensive review of the SAS methods can be found in Ref 45. In contrast, the SES methods are less common. The first analytical algorithm on the SES area was proposed by Connolly.32 It was implemented into AMS and later other programs such as PQMS52 and Amber/MOLSURF.53 Due to the complexity of the SES definition and the resulting self-intersecting regions of the surface, there had been no improvements on the analytical algorithm until Sanner et al.’s work in 1996.54 Sanner et al. proposed a new method to detect the self-intersecting singularities with the assistance of the reduced surface elements.54 Although the new method may successfully compute the areas for most molecules, it does encounter errors in certain molecular structures and has to be restarted with modified atomic radii.54 A different analytical approach was derived from the alpha shape theory in computational geometry.55, 56 It uses Delaunay complexes and their filtrations to describe the topological structure of a molecule, which can facilitate the computation of the surface area by removing redundant terms in the direct inclusion-exclusion method.38 In contrast, more methods exist to compute the SES area numerically.47, 57–66 Available programs include GEOPOL,47 MASKER,66 MOLSURF,65 USURF.64 Numerical methods use geometrical objects, such as dots, triangles, cubes, polyhedrons, to tessellate the surface or fill the interior volume. They are easier to circumvent the pathological singularity cases but inevitably sacrifice accuracy.
In this work we propose a numerical algorithm to compute the molecular surface area or surface integration for both the SES and SAS definitions. Different from previous numerical approaches of geometrical nature, our algorithm is physics-inspired. The algorithm is implemented as an integral part of our Poisson-Boltzmann surface area (PBSA) program.67–70 and is based upon the finite-difference Poisson-Boltzmann (FDPB) methods where a grid labeling step, i.e., mapping the molecular surface to the grid points, is necessary before computing the surface area. The pioneer work on the grid labeling was proposed by You and Bashford,71 and later improved by Rocchia et al. in efficiency.72 Our mapping strategy followed Rocchia et al.’s basic idea but tried to record additional information, such as the locations of the intersection points of the grid and the analytical surface, for the subsequent determination of dielectric constants.73 In the following, we first go over the development of our algorithm. This is followed by detailed numerical tests to validate the accuracy, convergence, and timing of the numerical algorithm.
Method
Overview of the algorithm
Our algorithm is based on the observation that a molecular surface, either in the SES definition or in the SAS definition, can be treated as a union of partial spheres of different centers and radii. The SAS is strictly a union of solvent exposed portions of extended van der Waals spheres, i.e., spheres of van der Waals radii augmented by the solvent probe radius. The SES is more complex with two types of surfaces – the contact surface that consists of solvent exposed portions of van der Waals spheres and the reentrant surface that consists of inward-facing portions of the solvent probe sphere as it rolls over the molecule. The reentrant surface can be further classified into two types according to how many atoms that the solvent probe is in contact with simultaneously: (1) saddle surfaces if two atoms are in contact with the probe and (2) spherical triangles if three atoms are in contact with the probe. A reentrant surface formed by the probe’s concurrent contact with more than three atoms can always be divided into multiple spherical triangles. Contact surfaces and reentrant spherical triangles are partial spheres, but reentrant saddle surfaces are clearly not. However the latter can be considered as consisting of small partial spheres of the solvent probe at different probe sites located on discretized solvent accessible arcs from the numerical point of view, for example in numerical surface definitions proposed for FDPB.71, 72 Apparently in the numerical surface definitions, the number of the solvent probe sites has to be finite. Therefore at each site, the probe is responsible for an area on the approximate saddle surface in the shape of a partial sphere.71, 72 Given the numerical representation of the molecular surface, if it is possible to compute the surface area/surface integration for each partial sphere, no matter how small it may be, the total surface area/surface integration is simply the sum of the contributions from all the partial spheres.
In the following we first describe the terminologies used in the finite-difference discretization. Then we validate our aforementioned assumption that the saddle surfaces in the SES definition can be numerically treated as unions of partial spheres. This is followed by how to compute the surface area with our physics-inspired strategy and its numerical implementation for the finite-difference discretization. Finally its extension to the surface integrations of both scalar and vector fields is discussed.
Finite-difference discretization
Without loss of generality, we focus on the Poisson’s equation in this study since the Boltzmann term is nonzero only outside the Stern layer, which is typically set 2Å away from the molecular surface. The partial differential equation
| (1) |
establishes a relation between the charge density (ρ) and the electrostatic potential (ϕ) given a predefined dielectric distribution function (ε) for a solvated molecule.
A commonly used numerical method to solve the Poisson’s equation is the finite-difference method where a uniform Cartesian grid is used to discretize a rectangular box containing the molecule. The grid points are numbered as (i, j, k), i = 1,…,xm, j = 1,…,ym, k = 1,…,zm, where xm, ym, and zm are the numbers of grid points along the x, y, and z axes, respectively. The spacing between two neighboring grid points is uniformly set to be h. With the finite-difference discretization, eqn (1) can be written as
| (2) |
Use of eqn (2) requires the dielectric constant ε to be defined at the grid edge centers between two neighboring grid points (denoted as grid index ±1 2 above). In this study, the dielectric constant is defined in the following way: if the grid edge center is in the solute, the dielectric constant is equal to εin; otherwise, the dielectric constant is equal to εout. It also requires mapping the point charges onto the grid points. The solution is the potentials on the grid points. More detailed implementation information specific to this study can be found in our recent publications.5, 67–70
Spherical representation of saddle surfaces
Suppose two atomic spheres of radii r1 and r2, respectively, are in contact with the solvent probe sphere of radius rp. The distance between the two atoms is d. In a typical finite-difference scheme only a finite number of solvent probe sites are used to represent the solvent accessible circle formed by the two atoms. Here the resolution of the discretized solvent accessible circle in radian is denoted by ψ. Each probe contributes a small partial sphere to the spherical representation of the saddle surface between the two atoms, and the area of each partial sphere can be computed with the following integral, provided that the centers of the two atoms are on the z axis,
| (3) |
here l is the radius of the discretized circle of probe sites and and β = (2rp + r1 + r2)(r1 − r2)/2. To evaluate the error of the above approximation of the corresponding analytical saddle surface area, we expand eqn (3) with the Taylor series at ψ = 0 and obtain
| (4) |
where the first two terms are the exact area of the saddle surface. Therefore the third term is the leading error of the spherical representation of the saddle surface. Omitting the higher-order terms in eqn (4), the relative error can be computed as
| (5) |
Eqn (5) demonstrates that the spherical representation of the saddle surface is second-order accurate. It can be shown that the relative error of the approximate saddle surface area reaches the maximum when one atom is buried in the other, and the relative error becomes
| (6) |
where m = r1/rp, n = r2/rp. In typical molecular simulations, rp = 1.4Å, r1 and r2 are between 1Å and 2Å. Since Δψ, max is monotonically increasing as either m or n increases, the maximum relative error can be estimated as
| (7) |
As the distance d increases, the saddle surface reduces to two self-intersecting parts, to which eqns (3)–(5) can no longer be applied. Here the singularity in the SES definition is not considered because it is much less common than the saddle surface. However, it can be shown that the maximum relative error of using discrete probe arcs in the singular parts is actually smaller than the error given in eqn (7).
Next we further assess the error quantitatively in the framework of the PBSA program. The density of the solvent probe sites in the PBSA program is determined by the option arcres, defined as the arc length between two neighboring probe sites. The relation of arcres and the probe site resolution ψ introduced here is
| (8) |
Provided that the self-intersecting region is not considered, l = rp = 1.4 at the upper bound of d. On the other side, as the two atoms approach each other, l decreases and reaches zero when one atom is buried in the other. To estimate the error in the spherical representation of the saddle surface in realistic situations, we further assume that the lower bound of d also gives l = rp = 1.4. This corresponds to an inter-atomic distance larger than the difference of the radii of the two atoms by at most 0.15Å. This assumption is reasonable according to the atomic radii and bond lengths in the AMBER force fields.74 The default arcres in the PBSA program is 1/16Å, and finally it can be obtained that
| (9) |
Therefore, the spherical representation of saddle surfaces is an appropriate approximation in the calculation of the molecular surface area. Note that the maximum error in eqn (9) is underestimated when a smaller probe is used because the curvature will need more grid points to resolve, which is a general problem in the finite-difference scheme.
Now that both the SAS and SES can be treated as the union of partial spheres with good accuracy, we are ready to introduce our new algorithm to compute the surface areas of partial spheres.
Field-view method
Suppose there is a point charge Q at the center of a sphere of radius R in the vacuum. The flux Φ of the electric displacement through any closed surface containing the charge is given by the integral form of the Gauss’s law, which is equal to the total free charge inside, i.e.,
| (10) |
By definition we have
| (11) |
where ε0 is the vacuum permittivity, E⃗ is the vacuum electric field, n̂ is the normal direction of the infinitesimal surface element dS. Given the central symmetry of the radial field due to a point charge at the spherical center, the flux on a spherical surface at radius R can be computed with
| (12) |
where S is the total surface area of the sphere. This is also true for a spherical surface element δS:
| (13) |
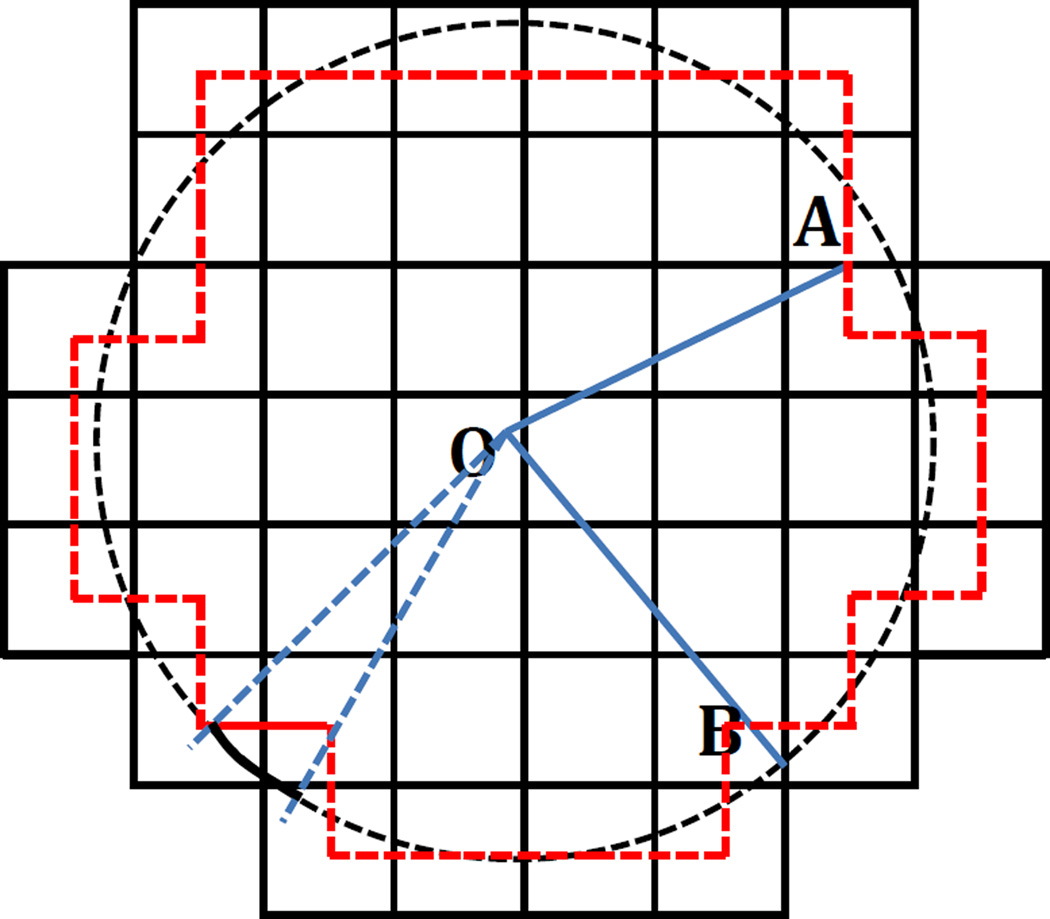
Instead of directly computing the flux through the spherical surface, we compute the flux via the finite-difference data structure by exploiting the conservation of electric flux. Figure 1 is a 2-D illustration of the finite-difference discretization of a sphere. Consider the closed surface represented by the red dash lines in Figure 1. Note that each red dash line represents a square surface element (area = h2, with h being the finite-difference spacing) located at the center of a grid edge that is intersected by the sphere. Since the square surface elements at the grid edge centers form a closed surface, the flux through the closed surface is equal to the flux through the spherical surface. And for each square surface element, there is always a spherical surface element that subtends the same solid angle, and thus they have the same flux passing through them (see Figure 1 for the two types of surfaces with the same flux: spherical surface element (black solid arc) and square surface element (red solid line)). This is the key relation that is to be exploited below to infer the surface area of the sphere or the spherical surface element.
Figure 1.
A 2-D diagram of the finite-difference discretization of a sphere (black dash circle). Black solid lines are grid edges, whose intersection points denote grid points. O is the center of the sphere, A is the center of a square surface element or a grid edge, and B is an intersection point of the sphere and a grid edge. Red dash lines denote square surface elements at grid edge centers. The red dash lines can also be viewed as the finite-difference approximation of the spherical surface. The black solid arc represents a spherical surface element and the red solid line represents a square surface element that subtends the same solid angle, so they have the same flux passing through them.
The flux through each square surface element, as well as the closed surface formed by the square surface elements, can be computed with the double integrals as follows
| (14) |
where the subscripts i, j, k are the indices in the x, y, and, z directions, respectively; δΦi, δΦj, and δΦk are the fluxes through the square surface elements at the grid edge centers in the x, y, and, z directions, respectively; Ni, Nj, Nk are the numbers of the square surface elements in the x, y, and, z directions, respectively; E⃗i, E⃗j, E⃗k are the electrical fields at the grid edge centers (or the centers of the square surface elements) in the x, y, and, z directions, respectively; n̂i, n̂j, n̂k are the unit normal vectors of the square surface elements in the x, y, and, z directions, respectively. Finally θi is the angle between E⃗i and n̂i, θj is the angle between E⃗j and n̂j, θk is the angle between E⃗k and n̂k.
On the ith square surface element in the x direction, angle θi between the direction of the radial electric field and the normal direction of the square surface element can be computed with
| (15) |
where xi is the x coordinate of the center of the ith square surface element in the x direction, and ri is the distance between the center of the square surface element and the center of the sphere (see the blue solid line OA in Figure 1, given the center of the sphere at the origin). Similarly in the y, z directions, we have
| (16) |
Thus the electric flux through the ith square surface element in the x direction at (xi, yi, zi) is
| (17) |
Applying the Taylor series expansion to eqn (17) at the center of the square surface element, i.e., (xi, yi, zi), leads to
| (18) |
where . All of the odd functions in the expansion in eqn (18) disappear due to the symmetry of the integral interval. The double integrals in the y, z directions in eqn (14) can be expanded in the same way. Thus
| (19) |
| (20) |
Substitution of eqn (18), (19) and (20) into eqn (14) and omission of fourth or higher order terms give
| (21) |
where , and are the coefficients of the second-order terms. Comparison between eqns. (12)/(13) and (21) shows that the spherical surface element areas and the total surface area of the sphere can be written as
| (22) |
Since the SES and the SAS are both composed of partial spheres (the SAS is the union of atomic spheres and the SES consists of atomic spheres and probe spheres), the above algorithm can be directly used to evaluate the SES and SAS areas numerically. In molecular applications, eqn (22) becomes,
| (23) |
where xi, yj, and zk are the relative coordinates of the ith, jth and kth square surface element centers (or the grid edge centers) in the x, y, and z directions, respectively; and Ri, Rj, and Rk are the radii of the atomic/probe spheres that intersect the ith, jth and kth grid edges in the x, y, and z directions, respectively. All relative coordinates are with respect to the atomic/probe sphere centers. We term the algorithm the field-view method in this study.
The second-order terms in eqn (23) shows that the zeroth-order truncation is second-order accurate and converges quadratically. In theory, inclusion of the second-order terms results in convergence of fourth order, but actually it is not guaranteed to achieve more accurate result in the reentrant region at coarse grid spacings. This is because at coarse grid spacings, the leading error comes from the spherical representation of saddle surfaces, which will be shown in the results and discussion.
Surface Integration
Given the spherical surface element areas in eqn (23), it is straightforward to evaluate a surface integral on the SES or SAS numerically. With the field-view method, the surface integral of any vector field A⃗ defined on the surface can be written as
| (24) |
where δSi, δSj, δSk are the spherical surface element areas introduced in the field-view method; Ai, Aj, Ak are the field magnitudes on the spherical surface elements, δSi, δSj, δSk, respectively; γi, γj, γk are the angles between the vector field A⃗ and the normal directions of the spherical surface elements, δSi, δSj, δSk, respectively. For any scalar field A defined on the surface, eqn (24) becomes
| (25) |
For example, if the finite-difference method is used to solve the Poisson’s equation or the Poisson-Boltzmann equation, eqn (24) and (25) can be used to compute the hydrophobic solvation free energy that is often modeled as being linearly proportional to the surface area.
Computational Details
The field-view method was implemented into the Amber/PBSA program.53, 67, 69 Implicit solvent models under the finite-difference scheme require the molecular surface be mapped to the grid points using a grid labeling algorithm.73 After mapping, the dielectric constant was set to be 1 in the solute region and 80 in the solvent region. On the dielectric boundary, the dielectric constant was set to be either 1 or 80 depending on whether the grid edge center was in the solute or solvent. The solvent probe was set to be 1.4Å.
All the molecules in our tests come from the PBSA test set, which includes 579 proteins,53 364 nucleic acids70 and 622 protein-protein complexes (see Appendix). However, ten of them have been left out due to the failures in the reference surface area program, Amber/MOLSURF.53 The MOLSURF program was implemented by Beroza according to Connolly’s analytical algorithm.32 When possible, the orientation and the origin of the finite-difference grid were randomized 100 times for each finite-difference run to reduce the numerical uncertainty of reported values.
Results and Discussion
Simple geometries: Agreement with exact analytical solutions
To assess the accuracy of the proposed algorithm, we first used a single sphere, double spheres, and triple spheres as test cases because their analytical surface areas can be readily calculated. The algorithm was tested at five different grid spacings, 1/2Å, 1/4Å, 1/8Å, 1/16Å, and 1/32Å, respectively, to study its convergence behavior. The arcres option (the arc length between two neighboring probe sites) was set to be as fine as 0.01Å to reduce the error introduced by limited resolution of solvent accessible arcs.
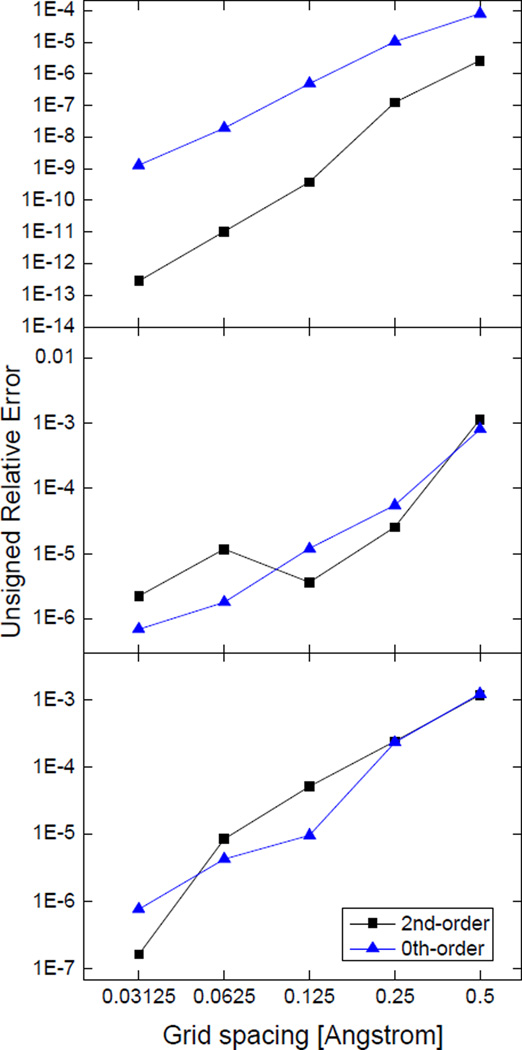
Figure 2 shows the unsigned relative errors of the numerical SES areas. It can be seen that at the finest grid spacing, the relative errors of the numerical SES areas reach as low as 10−9 for the zeroth-order truncation and 10−13 for the second-order truncation in the test case of the single sphere, but the relative errors only reach 10−6 ~ 10−7 in the test cases of the double spheres and triple spheres. This is due to the finite resolution of the numerical representation of the reentrant regions as spherical surface elements. For example, eqn (5) can be used to estimate the unsigned relative error of the reentrant region in the double spheres, which is 4.33×10−6 and consistent with the numerical analysis. The standard deviations in the numerical SES areas (not shown in the plot) are larger than or comparable with the errors of the means at all grid spacings in these simple test cases.
Figure 2.
Unsigned relative errors of numerical SES areas of simple geometries at successively fine grid spacings. Top: a single sphere, the radius of the sphere is 1.5Å; Middle: double spheres, the radii of the two spheres are both 1.5Å, the distance between the centers of the two spheres is 4Å; Bottom: triple spheres, the radii of the three spheres are all 1.5Å, the distance between one pair of spherical centers is 4Å, the distances between the other two pairs of spherical centers are both 3.606Å. The results are obtained from 100 area calculations with randomized grid orientations.
It is also interesting to note that the second-order truncation exhibits better accuracy at the tested grid spacing (1/2Å) in the single sphere case only. The reason is that there are not many square surface elements in the reentrant region at coarse grid spacings (such as the tested 1/2Å), and therefore only a fraction of solvent probe sites are employed even if a very high resolution is used in the discretized solvent accessible arcs. As a consequence, the error due to the spherical representation of saddle surfaces is dominant. For example, the number of square surface elements in the reentrant region of the double-sphere test case is ~60, much smaller than the number of available solvent probe sites, about 1,300, at the default computation setting in the Amber/PBSA program. In general, the more square surface elements exist in a saddle surface, the more solvent probe sites can be used. This is because a solvent probe contributes to the approximate saddle surface via a spherical surface element that shares the same flux as a square surface element and the square surface element is exclusively assigned to the solvent probe at a certain site. According to eqn (7), when the area of the reentrant region reaches its maximum (the radii of the two atoms are both 2Å, the distance is about 4.4Å) and at the same time the number of square surface elements reaches its maximum (about 150), the lowest possible error is about 0.06%. In contrast, the truncation error of each surface element is about 1~2% for the zeroth-order truncation and about 0.04%~0.06% for the second-order truncation. These error estimations were obtained by comparison between the truncated Taylor series and the exact analytical expression for a surface element area (eqn (17)). Although the truncation error of each surface element at the zeroth truncation level (1~2%) is larger than the error in the spherical representation of saddle surfaces (can be as low as 0.06%), the errors in the sum of the surface elements tend to cancel each other and lead to a much smaller overall error. As shown in Figure 2 (top), the overall error in the surface area of a single sphere is ~0.01% at the grid spacing of 1/2Å (the error cancellation may not be so dramatic where there is no central symmetry). As a result, the error in the spherical representation of saddle surfaces becomes the leading error term.
Thus at the grid spacing of 1/2Å, numerical surface areas computed by the zeroth-order truncation are similarly accurate as those computed by higher-order truncations. For example, in the double-sphere model (Figure 2 (middle)), the error of the zeroth-order truncation is similar as the second-order truncation (~0.1%). Therefore, the leading error shown here is actually from the spherical representation of saddle surfaces. Thus in the following tests, only the zeroth-order truncation was used to compute surface areas.
At fine grid spacings when there are abundant square surface elements in the reentrant region, more solvent probe sites can be utilized to resolve the reentrant surface. Under this circumstance, the zeroth-order truncation may have larger error than the spherical representation of saddle surfaces. For example, at the grid spacing of 1/8Å, the number of square surface elements in the saddle surface of the double spheres increases to more than 1,000, compared to ~60 at the grid spacing of 1/2Å. Consequently, at the grid spacing of 1/8Å, the second-order truncation performs better than the zeroth-order truncation in the double sphere test case (see Figure 2 (middle)). In this case, the higher-order terms generally help improve the accuracy of surface areas. Therefore, we suggest that higher-order truncations be used at fine grid spacings for better accuracy, and the resolution of solvent probe sites be dependent on grid spacings for the best performance and efficiency.
Convergence tests on realistic biomolecules
Next we analyzed the convergence behavior of the numerical algorithm with two realistic but small biomolecules: 1BRV (268 atoms) and 1FN2 (348 atoms). Both the SES and SAS areas were computed at successively fine grid spacings and the results are shown in Figure 3 and Figure 4, respectively. The arcres option was set to be 1/16Å in this test and only the zeroth-order truncation was used. The surface areas computed by the Amber/MOLSURF program that implements Connolly’s algorithm were used as reference.32, 53
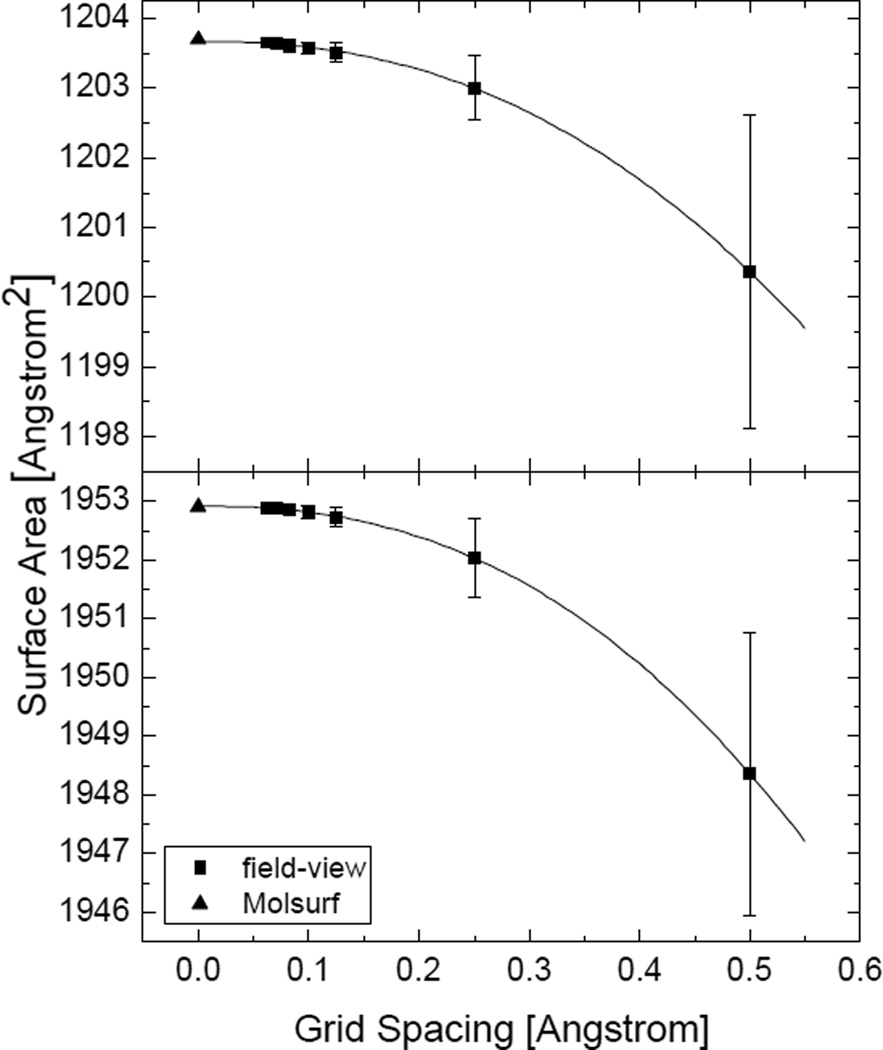
Figure 3.
Convergence of the numerical SES areas versus grid spacings for 1BRV and 1FN2, respectively. Top: 1BRV (the field-view method converges to 1203.66Å2, the power order is 2.30; the MOLSURF result is 1203.69Å2); Bottom: 1FN2 (the field-view method converges to 1952.91Å2, the power order is 2.37; the MOLSURF result is 1952.90Å2). The uncertainty bars are estimated as the standard deviations from 100 FDPB calculations with randomized grid orientations. The uncertainty bars for the finer grid spacings are too small to be seen.
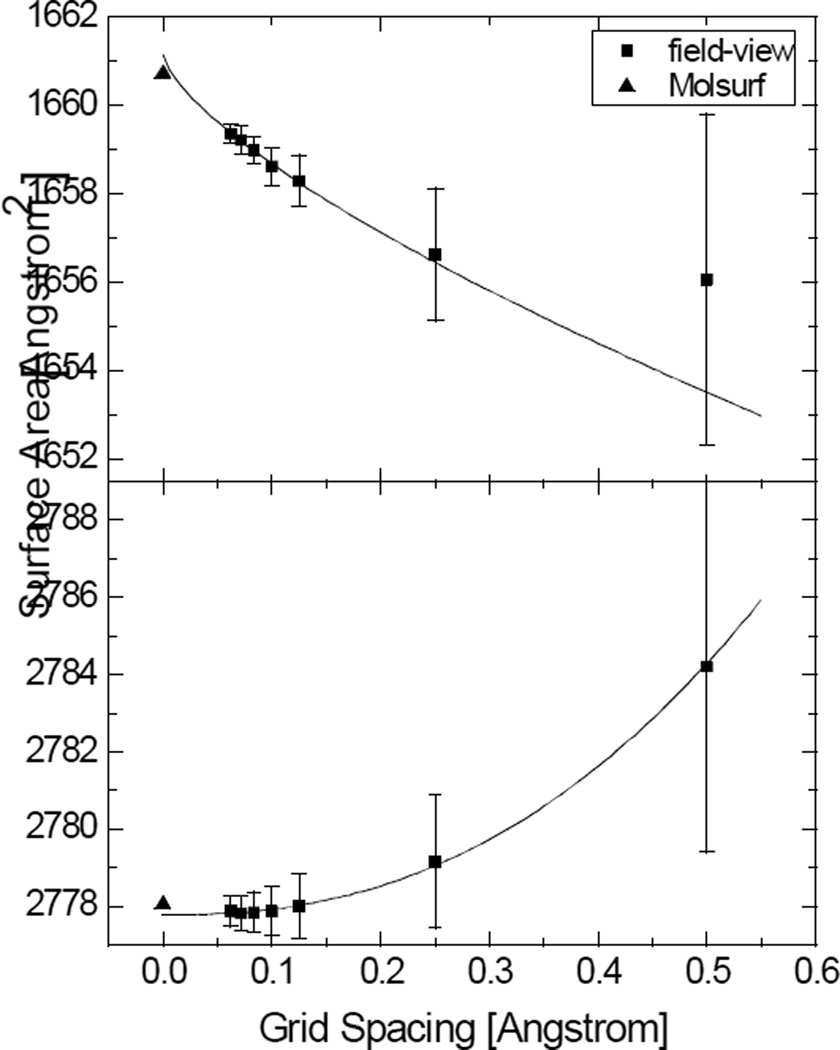
Figure 4.
Convergence of the numerical SAS areas versus grid spacings for 1BRV and 1FN2, respectively. Top: 1BRV (the field-view method converges to 1661.15Å2, the power order is 0.70; the MOLSURF result is 1660.73Å2); Bottom: 1FN2 (the field-view method converges to 2777.78Å2, the power order is 2.36; the MOLSURF result is 2778.05Å2). Note that for 1BRV, only the data at fine grid spacings can be used in the extrapolation of the surface area.
As shown in Figure 3, the performance of the field-view method in the calculation of SES areas of realistic molecules is promising. The unsigned relative error is around 0.2% at the grid spacing of 1/2Å often used in FDPB calculations of biomolecules. We also extrapolated the “converged” value using the nonlinear curve fitting method (with the formula y = a + bhc, where a is the predicted surface area when the grid spacing h goes to zero, and c is the convergence rate). Obviously the converged surface areas are highly consistent with the Amber/MOLSURF results. Interestingly the convergence rate is somewhat higher than quadratic. This is because the error at the grid spacing of 1/2Å is mainly due to the spherical representation of saddle surfaces, larger than the truncation error of the zeroth-order truncation, while at fine grid spacings, the truncation error dominates, which is quadratic as analyzed in the method section (at the same time the application does not reach the limitation of the finite resolution of solvent probe sites). Figure 3 also shows that the standard deviations for both molecules over 100 random grid orientations are smaller than the errors of the means at all grid spacings.
Figure 4 shows that the field-view method performs less well in the calculation of SAS areas. Although the unsigned relative error is still at the same low level, the convergence rate is no longer guaranteed to be quadratic. The reason is probably that the finite-difference-based numerical algorithm cannot resolve the cusps inside grid cells that are ubiquitous all over the molecular surface in the SAS definition. The situation can be mitigated at finer grid spacings but it still remains significant at the finest tested grid spacing of 1/16Å. The standard deviation of numerical SAS areas is also larger than that of numerical SES areas. Although the SES definition also has cusps or self-intersecting parts, they are much rarer and likely not the major source of errors in the numerical calculation. Indeed, the unsigned relative errors in SES areas computed by the field-view method are comparable between the three analytical test cases discussed above and the two realistic biomolecules (slightly larger errors are due to the rise of the proportion of the reentrant surface in realistic biomolecules as opposed to the analytical test cases).
To better appreciate the convergence quality of the new surface area integration, we obtained the numerical surface area and the numerical reaction field energy in the same context of FDPB calculations, and the comparison of their convergence behaviors is shown in Figure 5. The reaction field energy ΦRC was calculated by the product of atomic charges and polarization charges, i.e.,
| (26) |
where rmn is the distance between the two kinds of charges, is the finite-difference atomic charge, is the finite-difference polarization charge computed by a finite volume integral within a finite-difference grid cell,
| (27) |
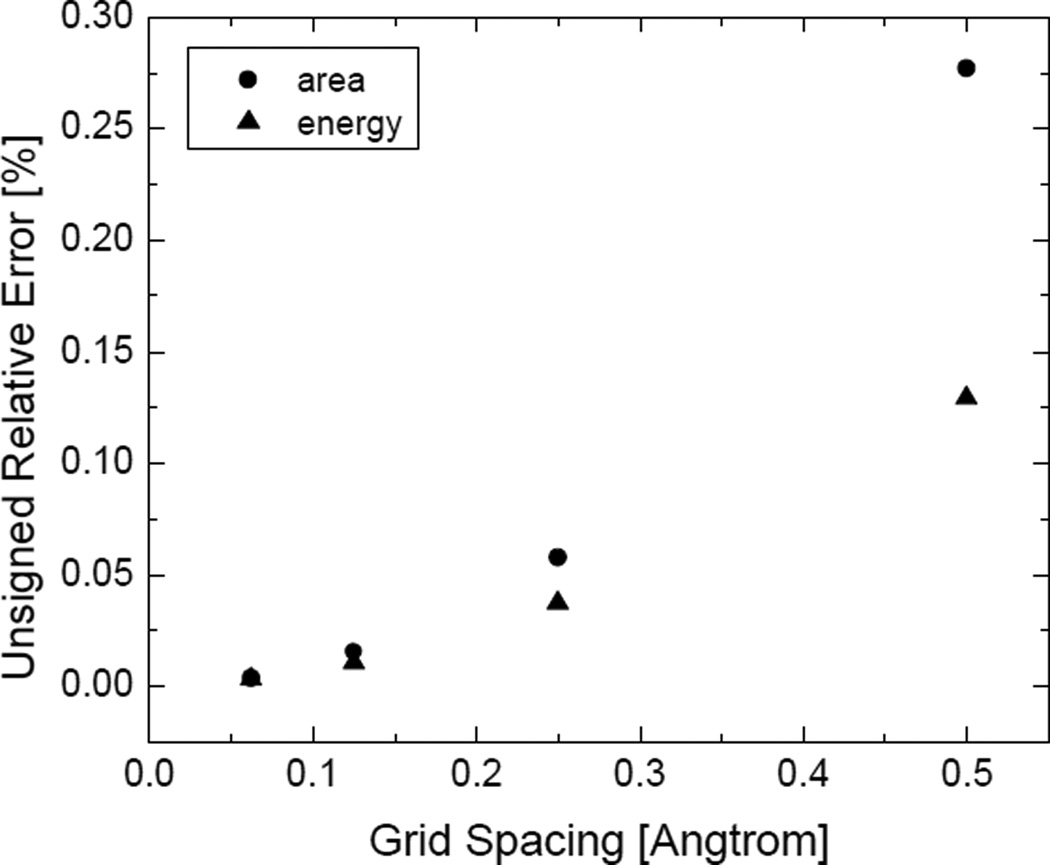
where ϕn is the potential at the center of the finite-difference grid cell, ϕn,l, l = 1,2,…,6 are the potentials at the centers of the six neighboring grid cells, and all the potentials are obtained from the finite-difference solution of the Poisson-Boltzmann equation. It has been shown that the relative error in the surface area by the field-view method is O(h2) The error in the numerical reaction field energy primarily originates from the polarization charge. Given the potential on the dielectric boundary from the FDPB method is in the first-order accuracy, the relative error of the polarization charge is O(h2) because the finite volume integration used to compute the polarization charges cancel out the leading error in the potential. To verify this analysis, we performed power curve fitting on the two curves in Figure 5. As a result, the power of the energy error curve is 1.79 and the power of the area error curve is 2.31 (the power curve here is a little different from that in Figure 3(a) due to the use of different sets of data points in the curve fitting). In addition to the common quadratic convergence rate, the relative errors of the two calculations are also in the same order of magnitude.
Figure 5.
Convergence rates of the numerical SES surface area and the numerical reaction field energy of 1BRV at successively fine grid spacings. Each result is obtained from 100 calculations with randomized grid orientations.
Consistency tests
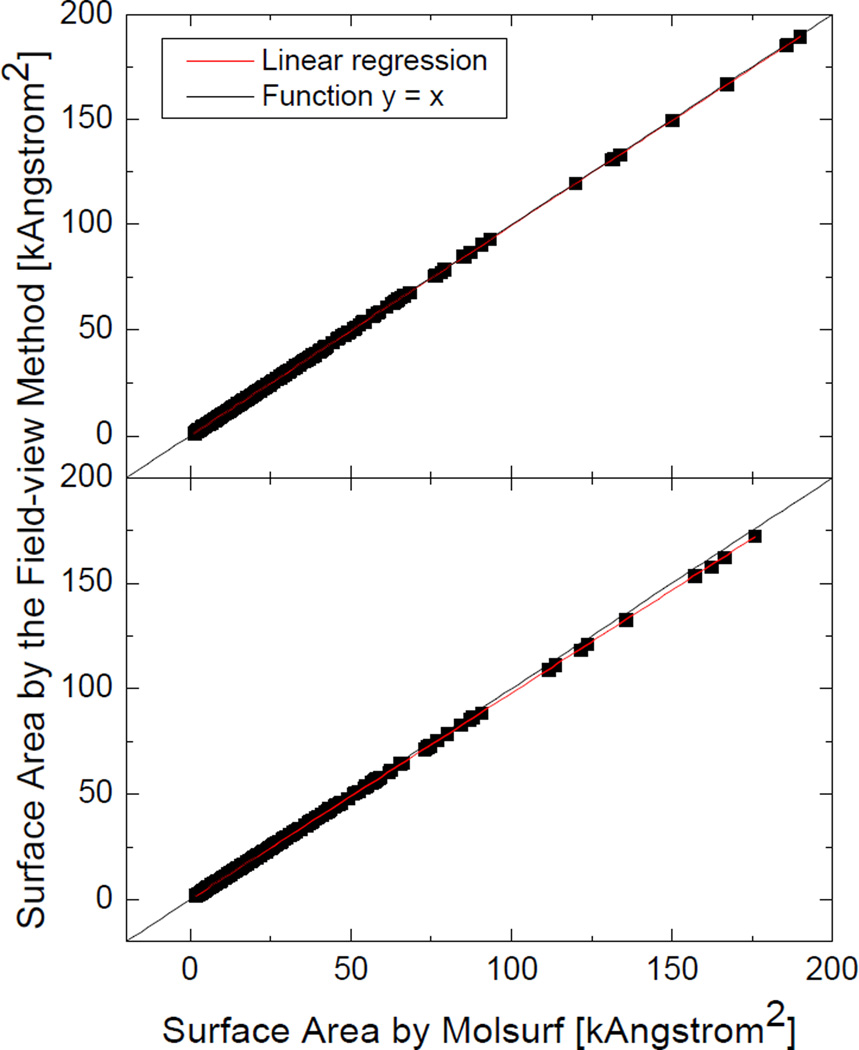
Next we tested the field-view method with a diversified set of 1,555 molecules and molecular complexes to demonstrate its applicability and robustness in realistic biomolecular applications. All test cases were run at the grid spacing of 1/2Å without random grid orientations. The correlation between the numerical molecular surface areas and the Amber/MOLSURF results is plotted in Figure 6. As in the previous tests, the numerical SES areas computed by the field-view method are overall more consistent with those by Amber/MOLSURF than the numerical SAS areas. It should be noted that the correlation coefficients are both very close to one, indicating that the numerical algorithm is consistent with the analytical algorithm regardless of the sizes or the structures of the tested molecules. The average unsigned relative error (AURE) of the numerical SES areas is 0.27% and the AURE of the numerical SAS areas is 1.05%. The analysis demonstrates that the field-view method agrees well with the analytical method at the tested coarse grid spacing often used in biomolecular applications of FDPB.
Figure 6.
Correlation between the numerical surface areas of 1,555 molecules computed at the grid spacing of 1/2Å and the analytical surface areas by MOLSURF. Top: SES areas: AURE, 0.27%, slope, 0.99696, R-square, 1.00000; Bottom: SAS areas: AURE, 1.05%, slope, 0.97753, R-square, 0.99999.
Timing analysis
It is interesting to analyze the timings for the proposed numerical algorithm. Table 1 lists the detailed timing analysis of a FDPB calculation with the algorithm turned on. The tested molecule was 2MRB (377 atoms) and the FDPB calculation was repeated 100 times with randomized grid orientations and origins. As expected, the time spent in computing the surface area is negligible compared to those used by other FDPB components in the calculation, supporting its “on-the-fly” application in FDPB calculations.
Table 1.
Timing analysis for FDPB calculations and the proposed “on-the-fly” surface area calculation of 2MRB. The timing for MOLSURF surface area calculation is also shown as reference. Note that the reported times of FDPB calculations (in second) are for 100 calculations with randomized grid orientations. The MOLSURF calculation is also repeated for 100 times.
| SES | SAS | |
|---|---|---|
| FDPB probe generation | 52.80 | N/A |
| FDPB grid labeling | 38.17 | 9.63 |
| FDPB solver | 509.11 | 506.75 |
| FDPB force calculation | 5.76 | 5.01 |
| Surface area calculation | 0.10 | 0.08 |
| MOLSURF surface area calculation | 3.38 | 3.87 |
Limitations and possible remedies
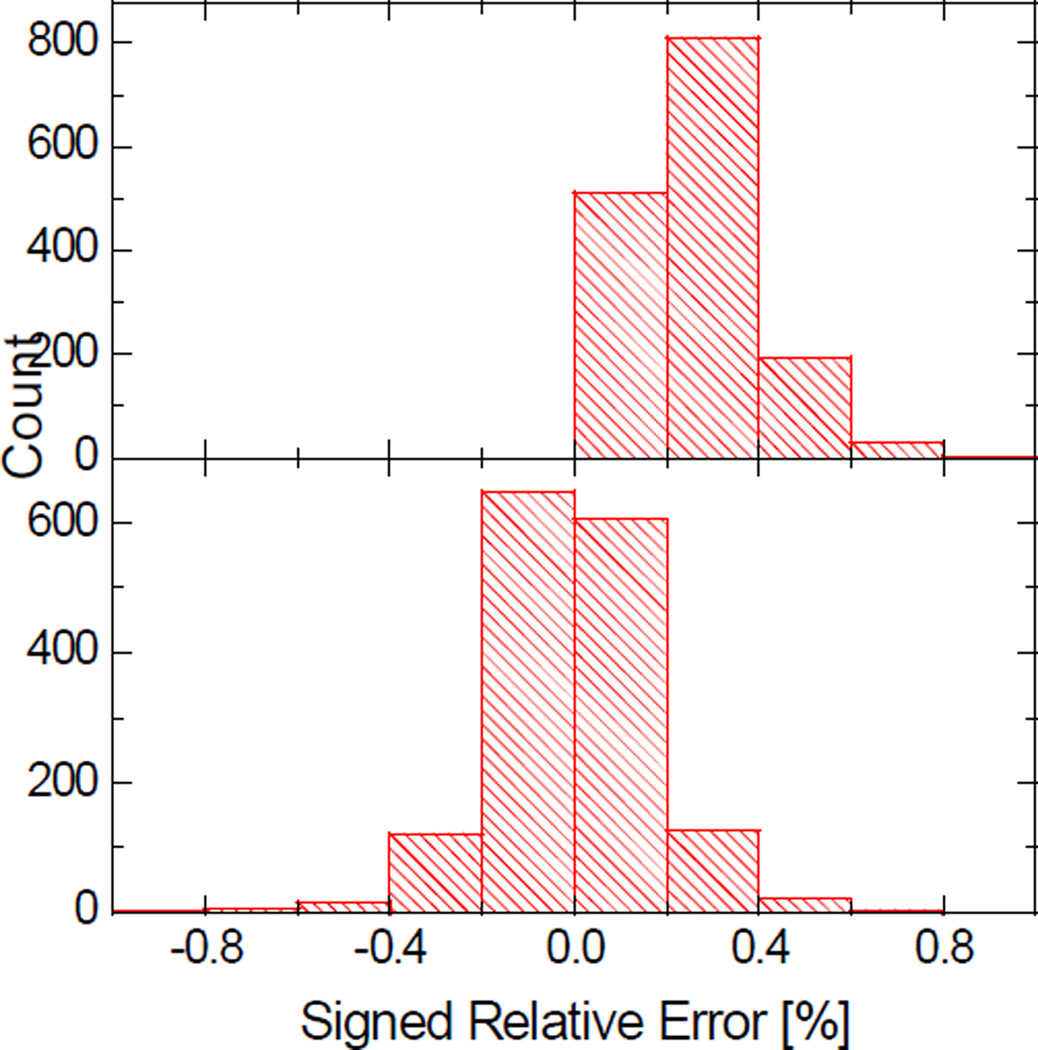
Despite the high-level consistency between the coarse-grid numerical calculations and analytical calculations, convergence errors do exist at coarse grid spacings. Interestingly the convergence errors in the numerical SES areas are systematic and can be identified with a linear regression analysis. The distributions of the signed relative errors with respect to the analytical values before and after the linear correction are shown in Figure 7. It can be seen that the AURE is reduced after the correction by half from 0.27% to 0.13%.
Figure 7.
Distributions of the signed relative errors of the numerical SES areas computed at the grid spacing of 1/2Å. Top: before correction, AURE, 0.27%; Bottom: after correction, AURE, 0.13%.
We did not apply the linear correction strategy to the numerical SAS areas based on the following observations. Figure 8 shows the trend of the signed relative errors of the SES and SAS areas. If there is a systematic error that can be corrected with a linear correction, the signed relative errors should go to a constant as the surface area increases. If the linear correction is in the form of yi = β1xi + β0 + ei, where yi is the analytical surface area, xi is the numerical surface area, β0 and β1 are the regression estimators, and ei is the residual error, the signed relative error εi of the numerical result xi with respect to the analytical result yi can be written as
| (28) |
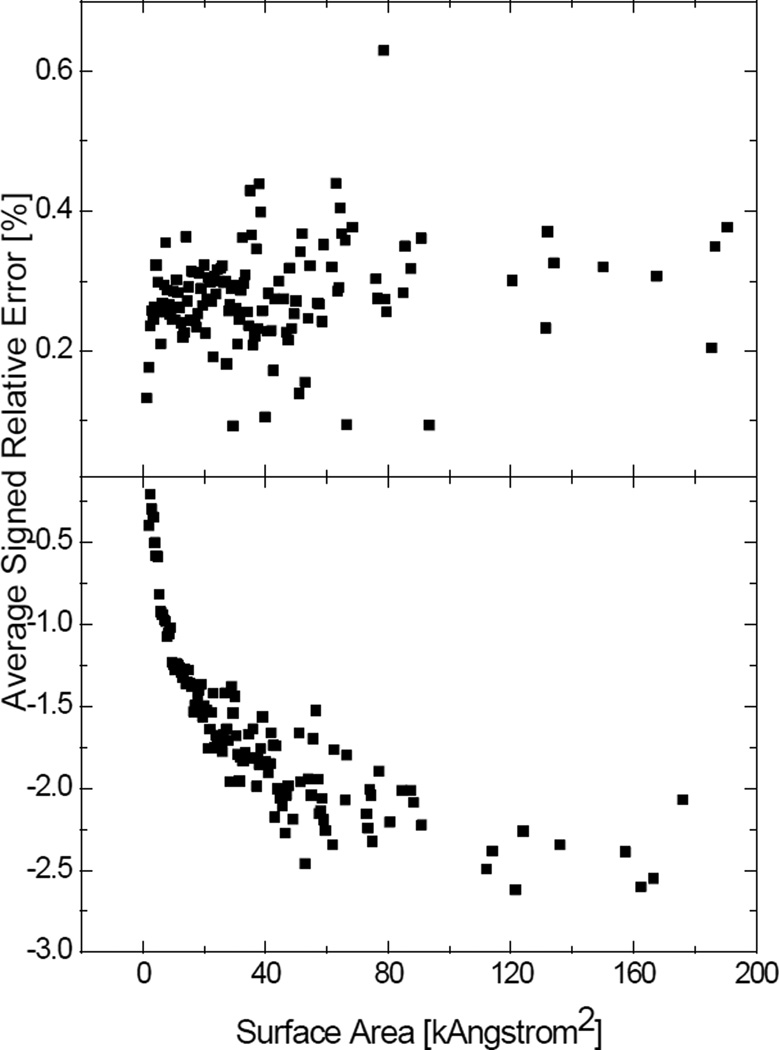
The second term is negligible and the signed relative error becomes constant if the residual error ei does not have a positive correlation with yi. Otherwise, the linear correction is unsuitable for the numerical method. It can be seen from Figure 8 that the signed relative errors of the numerical SES areas finally become stable at about 0.3%, whereas the signed relative errors of the numerical SAS areas are always negative and keep going down. This suggests that the numerical SAS areas probably need molecule-specific corrections.
Figure 8.
Correlation between the numerical surface areas and their signed relative errors. All the numerical surface areas were computed at the grid spacing of 1/2Å. Each data point represents the average signed relative error of the surface areas within a range of 0.5kÅ2. Top: SES areas; Bottom: SAS areas.
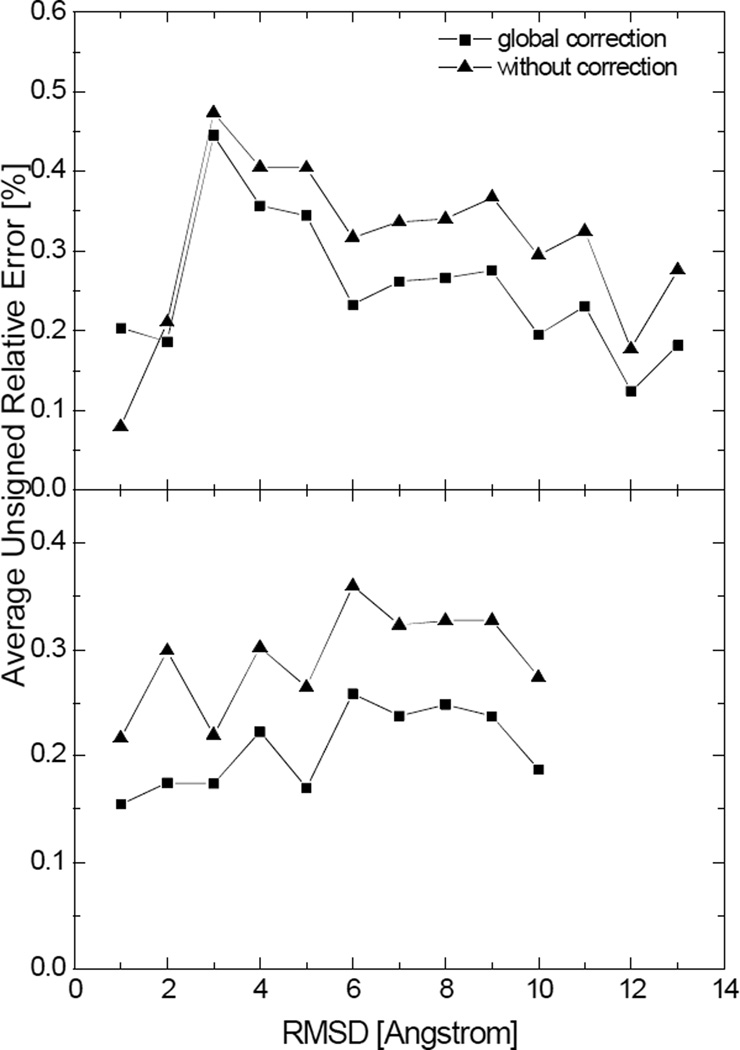
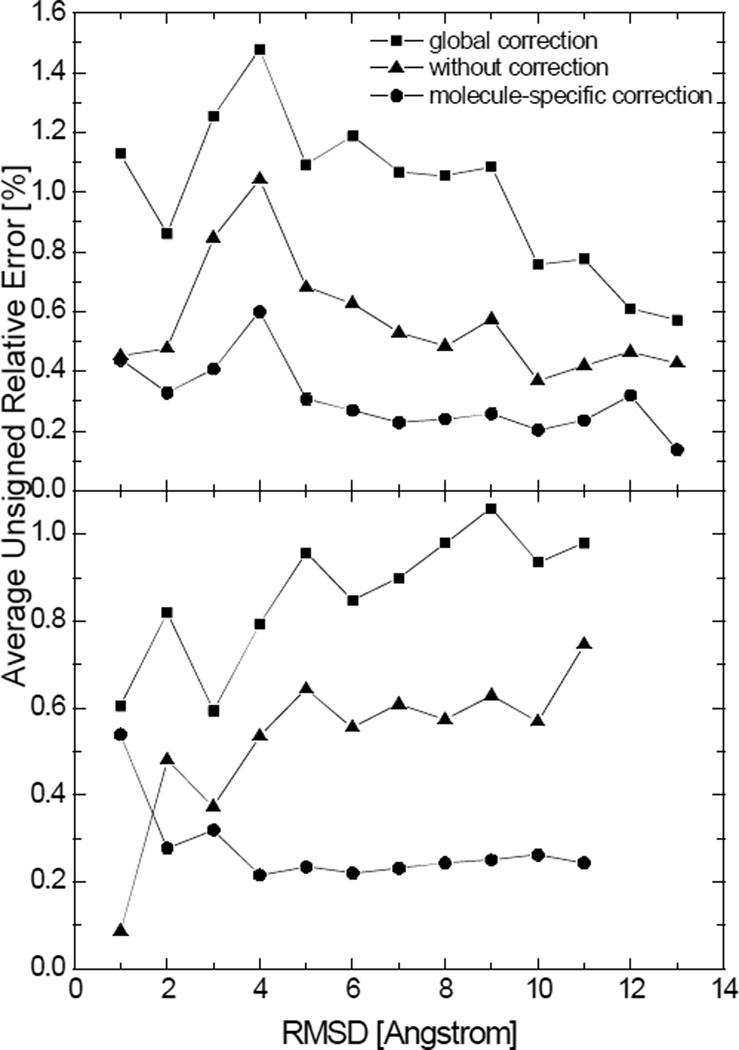
We present two examples to substantiate the above claims, each consisting of folded and unfolded structures extracted from molecular simulations of two peptides. First, the global corrections were applied to the numerical SES areas and numerical SAS areas of those structures, as shown in Figure 9 and 10, respectively. It is encouraging to note reduced errors in the numerical SES areas in both folded and unfolded structures even if these tested peptides and structures are outside the training molecules that were used to obtain the linear correction equation. In contrast, the global correction, parameterized from the numerical SAS areas of the 1,555 molecules, does not work for the numerical SAS areas of the two tested peptides. Next molecule-specific corrections were applied to the numerical SAS areas. Specifically, for each molecule, one-fifth of the structures from the trajectory were picked as the training set for parameterization of the linear correction, and the remaining structures were used as the test set to validate the linear correction. The results are also shown in Figure 10. It can be seen that the molecule-specific correction not only reduces the error but achieves more uniform performance over different conformations. The overall better applicability of the molecular-specific correction to more extended structures is mainly because the peptides unfolded shortly after the simulations started and stayed longer in the denatured status, resulting in higher population of extended structures.
Figure 9.
Average unsigned relative errors in the numerical SES areas after the global correction and without correction versus the backbone root-mean-square deviation (RMSD) for two tested peptides. Each data point represents the average unsigned relative error in the numerical surface areas for structures with the backbone RMSD within a range of 1Å with respect to the crystal structure. Top: hairpin; Bottom: helix. (grid spacing: 1/2Å)
Figure 10.
Average unsigned relative errors in the numerical SAS areas after the global correction, without correction, and after molecule-specific corrections versus the backbone RMSD for two tested peptides. Each data point represents the average unsigned relative error in the numerical surface areas for structures with the backbone RMSD within a range of 1Å with respect to the crystal structure. Top: hairpin; Bottom: helix. (grid spacing: 1/2Å)
The cusps in the SAS definition introduce singularity and numerical difficulty to the finite-difference approaches, especially at coarse grid spacings. The SES definition also has pathological self-intersecting parts that cannot be fully resolved with any finite difference method. These situations can be alleviated by using a finer grid but the computational cost grows cubically with the inverse of the grid spacing. The above linear corrections aim at reducing errors with much less computational overhead, but the final solution is to develop a new and physically reasonable molecular surface definition that is both smooth and analytical everywhere. It should be noted that the linear correction is not required as in the application of any numerical method, i.e. the FDPB solution of the Poisson Boltzmann equation, where nobody conducts any correction in biomolecular applications. Of course, no such global correction is possible for FDPB.
Conclusion
We have developed a new numerical algorithm to calculate the SES or SAS areas under the finite-difference scheme, which is based on the observation that a molecular surface, either in the SES definition or in the SAS definition, can be treated as a union of partial spheres of different centers and radii. To compute the surface area of a spherical surface element, the algorithm exploits the central symmetry of the radial field of a test point charge placed at the spherical center. Specifically, the flux through the spherical surface element is proportional to its surface area in the radial field of the point charge. The new algorithm computes the flux on the finite-difference grid surface element that subtends the same solid angle as the spherical surface element by exploiting the conservation of electric flux. Finally the summation of the surface areas of the spherical surface elements gives a good approximation for the molecular surface area. Utilization of the finite-difference data structure leads to the new algorithm’s particular suitability for the FDPB calculations. The algorithm can also be easily adapted to evaluate the surface integral of either a vector field or a scalar field defined on the SES or SAS.
Two major error sources can be identified in the new algorithm: spherical representation of saddle surfaces and truncation in the Taylor expansion used in the flux calculation. The first error is influenced by how many solvent probe sites are used to generate the reentrant surface as the probe rolls over the atoms. The second error, i.e., the truncation error, is influenced by how many terms are used in the Taylor expansion. The convergence rate of the zeroth-order is quadratic, and that of the second order is in the fourth power. We suggest using the zeroth-order truncation to compute molecular surface areas because the leading error comes from the first source at the typical coarse grid spacing of 1/2Å often used for FDPB in biomolecular applications.
The quadratic convergence of the algorithm (the zeroth-order truncation) has been demonstrated both theoretically and numerically. The proposed algorithm can achieve very good agreement with the analytical method as far as surface area calculations are concerned. The additional consistency test using a large test set of 1,555 molecules and complexes shows that the average unsigned relative error of the SES areas is 0.27% and that of the SAS areas is 1.05% at the typical coarse grid spacing of 1/2Å, indicating that the proposed algorithm can be applied to biomolecules and complexes over a broad range of sizes and structures. The timing test further shows that the field-view method takes little additional time in the context of FDPB calculations. More interestingly it was found that a systematic correction can improve the accuracy for the numerical SES areas calculated at coarse grid spacings. For example, the average unsigned relative error of the numerical SES areas by the field-view method can be reduced from 0.27% to 0.13%. In contrast, the numerical SAS areas can only be improved by molecule-specific corrections. Considering the poor numerical behavior of the SAS, we only recommend the algorithm for SES surface integrations and area calculations.
At fine grid spacings, the zeroth-order truncation may have larger error than the spherical representation of saddle surfaces. In this case, the higher-order terms generally help improve the accuracy of surface areas. Therefore, we have added the option to use higher-order terms in the algorithm so that higher-order truncations can be used at fine grid spacings for better accuracy. Apparently the computation time increases after adopting higher-order terms, but the surface area calculation uses much less time than other components in FDPB calculations. Moreover, higher-order truncations may be advantageous to computing molecular surface integrations due to lack of symmetries in an arbitrary field and little chance of significant reduction in errors by cancellation of each other.
Acknowledgements
This work is supported in part by NIH/NIGMS [GM079383 & GM093040].
Appendix
Test Set of 622 Protein-Protein Complexes
The following molecular structures, in both the Amber format and the pqr format, can be downloaded from http://rayl0.bio.uci.edu/rayl/#Database.
1A9X, 1APY, 1AQW, 1B0N, 1B5F, 1BBZ, 1BLX, 1C1Y, 1CCW, 1CG5, 1CKA, 1CLV, 1CQ4, 1CSB, 1CZQ, 1CZY, 1D2Z, 1D3B, 1D4T, 1DDV, 1DGW, 1DKZ, 1DNU, 1DOW, 1DPJ, 1DTD, 1E1H, 1E6I, 1E6Y, 1EER, 1EEX, 1EF1, 1EG4, 1EGP, 1ELR, 1ELW, 1EMU, 1EPT, 1EUV, 1EVH, 1F2T, 1F3U, 1F47, 1F60, 1FIP, 1FLT, 1FM0, 1FS1, 1FVU, 1G1S, 1G6G, 1G73, 1G8K, 1GCV, 1GJ7, 1GK9, 1GL2, 1GL4, 1GO3, 1GUX, 1GVN, 1GYB, 1H0H, 1H2S, 1H32, 1H6K, 1H6W, 1H9O, 1HBN, 1HFE, 1HLE, 1HTR, 1I7Q, 1IHJ, 1J2X, 1J34, 1JAT, 1JBO, 1JD5, 1JDH, 1JDP, 1JEK, 1JKG, 1JLT, 1JMX, 1JNR, 1JSD, 1JSM, 1JW6, 1JWI, 1JY2, 1JYO, 1K2X, 1K5N, 1K8K, 1KQF, 1KSH, 1KVE, 1KYF, 1L2W, 1L6X, 1LB6, 1LM8, 1LQV, 1LSH, 1LUC, 1LVM, 1M1N, 1M2T, 1M45, 1M93, 1MA3, 1MFG, 1MHW, 1MIZ, 1MJU, 1MSO, 1MTP, 1MTY, 1MZW, 1N0W, 1N12, 1N13, 1N1J, 1N62, 1N7F, 1N7S, 1NH0, 1NKZ, 1NQ7, 1NRJ, 1NTV, 1NVM, 1NX1, 1O6L, 1OAI, 1OAO, 1OAQ, 1OBX, 1OEY, 1OK7, 1OO0, 1OR0, 1OR7, 1OU8, 1OV3, 1P57, 1P5V, 1PBY, 1PDQ, 1PFB, 1PK1, 1PK6, 1PQ1, 1PXV, 1PYO, 1PYU, 1Q1A, 1Q3L, 1Q40, 1Q7L, 1QAV, 1QGE, 1QOP, 1QTN, 1R0R, 1R17, 1R1Q, 1R4P, 1R8O, 1R8S, 1RBD, 1RDQ, 1REQ, 1REW, 1RM6, 1RXZ, 1RYP, 1S5D, 1S5P, 1S6C, 1SB2, 1SC3, 1SCT, 1SE0, 1SEM, 1SHA, 1SR4, 1SSH, 1SVF, 1SVZ, 1T0F, 1T0H, 1T0P, 1T15, 1T3Q, 1T61, 1T6G, 1T6O, 1TA3, 1TAF, 1TQY, 1TZY, 1U00, 1U0S, 1U7B, 1U8T, 1UGH, 1UGP, 1UGX, 1UHE, 1UJ0, 1UMD, 1UPK, 1UPT, 1UTI, 1UVQ, 1UW4, 1V74, 1V7P, 1VC3, 1VLF, 1VRA, 1W2W, 1W6S, 1W70, 1W7J, 1W85, 1W9E, 1WA5, 1WDC, 1WDD, 1WHS, 1WMH, 1WQJ, 1WUI, 1WVE, 1WXC, 1XEW, 1XG0, 1XG2, 1XK4, 1XKP, 1XU1, 1Y43, 1Y5I, 1Y7L, 1YAR, 1YC5, 1YDI, 1YFN, 1YMT, 1YPH, 1YQW, 1YRO, 1YTV, 1YUC, 1YUK, 1YWO, 1Z0J, 1Z0K, 1Z3E, 1Z5Y, 1Z6O, 1Z9O, 1ZAV, 1ZGX, 1ZHH, 1ZUD, 1ZUK, 1ZV8, 2A3I, 2A50, 2A5T, 2A9K, 2AD6, 2AIJ, 2AIR, 2AKA, 2APO, 2AQ2, 2AQ9, 2ARP, 2ASU, 2B1X, 2B3G, 2B9H, 2BBA, 2BBK, 2BCG, 2BCN, 2BEQ, 2BEZ, 2BFD, 2BGR, 2BKR, 2BKY, 2BL0, 2BLF, 2BMO, 2BO9, 2BPT, 2BR9, 2BS2, 2BUR, 2BW3, 2BZ6, 2BZ8, 2C1D, 2CCH, 2CIO, 2CJS, 2CKL, 2CNZ, 2CWG, 2CZV, 2D0O, 2D1X, 2D7C, 2DE6, 2DF6, 2DG5, 2DJF, 2DKO, 2DRM, 2DS2, 2DS8, 2DYO, 2DYR, 2DZE, 2E2D, 2E4M, 2EJF, 2EKE, 2EQ7, 2EQ8, 2ES4, 2F4M, 2F69, 2F91, 2F9I, 2F9N, 2FCW, 2FF4, 2FFU, 2FGR, 2FHZ, 2FLU, 2FMM, 2FOJ, 2FOM, 2FP7, 2FTX, 2FU5, 2FYM, 2G2S, 2G2U, 2G30, 2G5L, 2GAG, 2GBW, 2GGV, 2GH0, 2GHT, 2GIA, 2GL9, 2GPH, 2GPO, 2GSM, 2GUZ, 2GW4, 2H1C, 2H4P, 2H6F, 2H7Z, 2H88, 2H9A, 2HEY, 2HMH, 2HO2, 2HPE, 2HPL, 2HQH, 2HQS, 2HT9, 2HUE, 2HY5, 2I3S, 2IG0, 2INC, 2IUH, 2IVF, 2IZX, 2J12, 2J32, 2J6F, 2J7P, 2J7Y, 2J8C, 2J9A, 2J9U, 2JDI, 2JE6, 2JGB, 2JJS, 2JK9, 2JKH, 2KIN, 2LTN, 2NL9, 2NNU, 2NPT, 2NS1, 2NW2, 2O02, 2O4J, 2O4X, 2O5G, 2O8M, 2O9V, 2OBH, 2ODE, 2OGX, 2OIZ, 2OKR, 2OMZ, 2OQ1, 2OVH, 2OX0, 2OXG, 2OZN, 2P0W, 2P1M, 2P1T, 2P45, 2P54, 2P58, 2PA8, 2PBI, 2PBK, 2PI2, 2PQR, 2PTT, 2PU9, 2PUY, 2PV2, 2Q0O, 2Q5W, 2QA9, 2QAC, 2QDY, 2QFA, 2QIY, 2QKH, 2QM6, 2QME, 2QWO, 2R25, 2R7G, 2RHI, 2RHK, 2RI7, 2RKY, 2RMC, 2UUF, 2UWJ, 2UYZ, 2V1T, 2V2F, 2V36, 2V3S, 2V3Z, 2V52, 2V6X, 2V89, 2V8C, 2V9T, 2VGO, 2VIF, 2VLQ, 2VN6, 2VNF, 2VOF, 2VOL, 2VPB, 2VR3, 2VSM, 2VT1, 2VWF, 2VZG, 2W0P, 2W3O, 2W9R, 2WJN, 2WWX, 2YVJ, 2Z30, 2Z3Q, 2Z5B, 2Z8P, 2Z9I, 2ZA4, 2ZD1, 2ZD7, 2ZFD, 2ZMI, 2ZON, 2ZS0, 2ZSI, 2ZVV, 2ZYZ, 2ZZD, 3A1G, 3B5N, 3BC1, 3BEJ, 3BFQ, 3BH7, 3BOM, 3BP6, 3BQO, 3BRL, 3BS5, 3BU3, 3BWU, 3BX4, 3BXM, 3BZY, 3C4M, 3C6W, 3C7B, 3C9A, 3CAL, 3CF4, 3CJS, 3CLS, 3CPT, 3CV0, 3CWW, 3D1K, 3D1M, 3D32, 3D3B, 3D44, 3D9N, 3D9T, 3DAC, 3DBO, 3DD7, 3DDC, 3DGP, 3DKS, 3DLQ, 3DRA, 3DS4, 3DSS, 3DWG, 3DXE, 3DY0, 3E1R, 3EBB, 3ECH, 3EGV, 3EHU, 3EJ9, 3EJB, 3EMH, 3EMW, 3EP6, 3EQS, 3ERY, 3ET3, 3EXE, 3F02, 3F1P, 3F4Y, 3F6Q, 3F75, 3F9X, 3FAP, 3FDT, 3FGR, 3FHV, 3FIV, 3FJU, 3FP2, 3FPN, 3G2S, 3G5O, 3G9A, 3G9K, 3GE3, 3GJ3, 3GL6, 3GLR, 3GV4, 3H11, 3H6P, 3H7H, 3H87, 3H8K, 3H91, 3HDS, 3HEI, 3HHS, 3HHT, 3HNA, 3HPW, 3HQR, 3HTU, 3HXI, 3JQL, 3JRV, 3JVK, 3KB3, 3KDF, 3KDJ, 3KNB, 3PCC, 4UBP, 6RLX, 6TMN
References
- 1.Lee B, Richards FM. J. Mol. Biol. 1971;55:379. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 2.Richards FM. Annu. Rev. Biophys. Bio. 1977;6:151. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 3.Im W, Beglov D, Roux B. Comput. Phys. Commun. 1998;111:59. [Google Scholar]
- 4.Grant JA, Pickup BT, Nicholls A. J. Comput. Chem. 2001;22:608. [Google Scholar]
- 5.Lu Q, Luo R. J. Chem. Phys. 2003;119:11035. [Google Scholar]
- 6.Eisenberg D, McLachlan AD. Nature. 1986;319:199. doi: 10.1038/319199a0. [DOI] [PubMed] [Google Scholar]
- 7.Wesson L, Eisenberg D. Protein Sci. 1992;1:227. doi: 10.1002/pro.5560010204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cramer CJ, Truhlar DG. Science. 1992;256:213. doi: 10.1126/science.256.5054.213. [DOI] [PubMed] [Google Scholar]
- 9.Gallicchio E, Kubo MM, Levy RM. J. Phys. Chem. B. 2000;104:6271. [Google Scholar]
- 10.Gallicchio E, Zhang LY, Levy RM. J. Comput. Chem. 2002;23:517. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 11.Levy RM, Zhang LY, Gallicchio E, Felts AK. J. Am. Chem. Soc. 2003;125:9523. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 12.Gallicchio E, Levy RM. J. Comput. Chem. 2004;25:479. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 13.Su Y, Gallicchio E. Biophys. Chem. 2004;109:251. doi: 10.1016/j.bpc.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 14.Tan C, Tan YH, Luo R. J. Phys. Chem. B. 2007;111:12263. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 15.Richmond TJ. J. Mol. Biol. 1984;178:63. doi: 10.1016/0022-2836(84)90231-6. [DOI] [PubMed] [Google Scholar]
- 16.Perrot G, Cheng B, Gibson KD, Vila J, Palmer KA, Nayeem A, Maigret B, Scheraga HA. J. Comput. Chem. 1992;13:1. [Google Scholar]
- 17.Sridharan S, Nicholls A, Sharp KA. J. Comput. Chem. 1995;16:1038. [Google Scholar]
- 18.Fraczkiewicz R, Braun W. J. Comput. Chem. 1998;19:319. [Google Scholar]
- 19.Bryant R, Edelsbrunner H, Koehl P, Levitt M. Discrete Comput. Geom. 2004;32:293. [Google Scholar]
- 20.Hayryan S, Hu CK, Skrivanek J, Hayryan E, Pokorny I. J. Comput. Chem. 2005;26:334. doi: 10.1002/jcc.20125. [DOI] [PubMed] [Google Scholar]
- 21.Yang AS, Gunner MR, Sampogna R, Sharp K, Honig B. Proteins. 1993;15:252. doi: 10.1002/prot.340150304. [DOI] [PubMed] [Google Scholar]
- 22.Yang AS, Honig B. J. Mol. Biol. 1993;231:459. doi: 10.1006/jmbi.1993.1294. [DOI] [PubMed] [Google Scholar]
- 23.You TJ, Bashford D. Biophys. J. 1995;69:1721. doi: 10.1016/S0006-3495(95)80042-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Antosiewicz J, McCammon JA, Gilson MK. Biochemistry. 1996;35:7819. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- 25.Alexov EG, Gunner MR. Biophys. J. 1997;72:2075. doi: 10.1016/S0006-3495(97)78851-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Alexov E. Proteins. 2003;50:94. doi: 10.1002/prot.10265. [DOI] [PubMed] [Google Scholar]
- 27.Vijayakumar M, Zhou HX. J. Phys. Chem. B. 2001;105:7334. [Google Scholar]
- 28.Dong F, Vijayakumar M, Zhou HX. Biophys. J. 2003;85:49. doi: 10.1016/S0006-3495(03)74453-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dong F, Zhou HX. Proteins. 2006;65:87. doi: 10.1002/prot.21070. [DOI] [PubMed] [Google Scholar]
- 30.Qin SB, Zhou HX. Biopolymers. 2007;86:112. doi: 10.1002/bip.20708. [DOI] [PubMed] [Google Scholar]
- 31.Wodak SJ, Janin J. P. Natl. Acad. Sci. USA. 1980;77:1736. doi: 10.1073/pnas.77.4.1736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Connolly ML. J. Appl. Crystallogr. 1983;16:548. [Google Scholar]
- 33.Eisenhaber F, Argos P. J. Comput. Chem. 1993;14:1272. [Google Scholar]
- 34.Edelsbrunner H. Discrete Comput. Geom. 1995;13:415. doi: 10.1007/s00454-021-00281-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gogonea V, Osawa E. J. Comput. Chem. 1995;16:817. [Google Scholar]
- 36.Augspurger JD, Scheraga HA. J. Comput. Chem. 1996;17:1549. [Google Scholar]
- 37.Gibson KD, Scheraga HA. Mol. Phys. 1988;64:641. [Google Scholar]
- 38.Liang J, Edelsbrunner H, Fu P, Sudhakar PV, Subramaniam S. Proteins. 1998;33:1. [PubMed] [Google Scholar]
- 39.Street AG, Mayo SL. Fold. Des. 1998;3:253. doi: 10.1016/S1359-0278(98)00036-4. [DOI] [PubMed] [Google Scholar]
- 40.Weiser J, Shenkin PS, Still WC. J. Comput. Chem. 1999;20:217. doi: 10.1002/(SICI)1096-987X(199905)20:7<688::AID-JCC4>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 41.Weiser J, Shenkin PS, Still WC. Biopolymers. 1999;50:373. doi: 10.1002/(SICI)1097-0282(19991005)50:4<373::AID-BIP3>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 42.Vasilyev V, Purisima EO. J. Comput. Chem. 2002;23:737. doi: 10.1002/jcc.10035. [DOI] [PubMed] [Google Scholar]
- 43.Cavallo L, Kleinjung J, Fraternali F. Nucleic Acids Res. 2003;31:3364. doi: 10.1093/nar/gkg601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guvench O, Brooks CL. J. Comput. Chem. 2004;25:1005. doi: 10.1002/jcc.20026. [DOI] [PubMed] [Google Scholar]
- 45.Rychkov G, Petukhov M. J. Comput. Chem. 2007;28:1974. doi: 10.1002/jcc.20550. [DOI] [PubMed] [Google Scholar]
- 46.Shrake A, Rupley JA. J. Mol. Biol. 1973;79:351. doi: 10.1016/0022-2836(73)90011-9. [DOI] [PubMed] [Google Scholar]
- 47.Silla E, Villar F, Nilsson O, Pascualahuir JL, Tapia O. J. Mol. Graph. 1990;8:168. doi: 10.1016/0263-7855(90)80059-o. [DOI] [PubMed] [Google Scholar]
- 48.Still WC, Tempczyk A, Hawley RC, Hendrickson T. J. Am. Chem. Soc. 1990;112:6127. [Google Scholar]
- 49.Legrand SM, Merz KM. J. Comput. Chem. 1993;14:349. [Google Scholar]
- 50.Eisenhaber F, Lijnzaad P, Argos P, Sander C, Scharf M. J. Comput. Chem. 1995;16:273. [Google Scholar]
- 51.Masuya M, Doi J. J. Mol. Graph. 1995;13:331. doi: 10.1016/0263-7855(95)00071-2. [DOI] [PubMed] [Google Scholar]
- 52.Connolly ML. J. Mol. Graph. 1993;11:139. doi: 10.1016/0263-7855(93)87010-3. [DOI] [PubMed] [Google Scholar]
- 53.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Wang B, Hayik S, Roitberg A, Seabra G, Kolossváry I, Wong KF, Paesani F, Vanicek J, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh M-J, Cui G, Roe DR, Mathews DH, Seetin MG, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. AMBER 11. San Francisco: University of California; 2010. [Google Scholar]
- 54.Sanner MF, Olson AJ, Spehner JC. Biopolymers. 1996;38:305. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 55.Edelsbrunner H, Kirkpatrick DG, Seidel R. IEEE Trans. Inf. Theory. 1983;29:551. [Google Scholar]
- 56.Edelsbrunner H, Mucke EP. ACM Trans. Graph. 1994;13:43. [Google Scholar]
- 57.Greer J, Bush BL. P. Natl. Acad. Sci. USA. 1978;75:303. doi: 10.1073/pnas.75.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Finney JL. J. Mol. Biol. 1978;119:415. doi: 10.1016/0022-2836(78)90223-1. [DOI] [PubMed] [Google Scholar]
- 59.Pearl LH, Honegger A. J. Mol. Graph. 1983;1:9. [Google Scholar]
- 60.Muller JJ. J. Appl. Crystallogr. 1983;16:74. [Google Scholar]
- 61.Pavlov MY, Fedorov BA. Biopolymers. 1983;22:1507. [Google Scholar]
- 62.Connolly ML. J. Appl. Crystallogr. 1985;18:499. [Google Scholar]
- 63.Pascualahuir JL, Silla E, Tomasi J, Bonaccorsi R. J. Comput. Chem. 1987;8:778. [Google Scholar]
- 64.Moon JB, Howe WJ. J. Mol. Graph. 1989;7:109. doi: 10.1016/s0263-7855(89)80014-1. [DOI] [PubMed] [Google Scholar]
- 65.Zauhar RJ, Morgan RS. J. Comput. Chem. 1990;11:603. [Google Scholar]
- 66.Bystroff C. Protein Eng. 2002;15:959. doi: 10.1093/protein/15.12.959. [DOI] [PubMed] [Google Scholar]
- 67.Luo R, David L, Gilson MK. J. Comput. Chem. 2002;23:1244. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 68.Cai Q, Wang J, Zhao HK, Luo R. J. Chem. Phys. 2009;130:145101. doi: 10.1063/1.3099708. [DOI] [PubMed] [Google Scholar]
- 69.Wang J, Luo R. J. Comput. Chem. 2010;31:1689. doi: 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Cai Q, Hsieh MJ, Wang J, Luo R. J. Chem. Theory Comput. 2010;6:203. doi: 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.You T, Bashford D. J. Comput. Chem. 1995;16:743. [Google Scholar]
- 72.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. J. Comput. Chem. 2002;23:128. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 73.Wang J, Luo R. in prep. [Google Scholar]
- 74.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. J. Comput. Chem. 2005;26:1668. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]