Repeatability of Quantitative MRI Measurements in Normal Breast Tissue

Abstract

PURPOSE: To evaluate the variability and repeatability of repeated magnetic resonance imaging (MRI) measurements in normal breast tissues between and within subjects. METHODS: Eighteen normal premenopausal subjects underwent two contrast-enhanced MRI scans within 72 hours or during the same menstrual phase in two consecutive months. A subset of nine women also completed diffusion-weighted imaging (DWI). Fibroglandular tissue (FGT) density and FGT enhancement were measured on the contrast-enhanced MRI. Apparent diffusion coefficient (ADC) values were computed from DWI. Between- and within-subject coefficients of variation (bCV and wCV, respectively) were assessed. Repeatability of all measurements was assessed by the coefficient of repeatability (CR) and Bland-Altman plots. RESULTS: The bCV of FGT density and FGT enhancement at visit 1 and visit 2 ranged from 47% to 63%. The wCV was 13% for FGT density, 22% for FGT enhancement, and 11% for ADC. The CRs of FGT density and FGT enhancement were 0.15 and 0.19, respectively, and for ADC, it was 6.1 x 10^-4 mm²/s. CONCLUSIONS: We present an estimate of the variability and repeatability of MR measurements in normal breasts. These estimates provide the basis for understanding the normal variation of healthy breast tissue in MRI and establishing thresholds for agreement between measurements.

Introduction

High mammographic density is well established as an independent risk factor for breast cancer [1]. However, challenges associated with mammography such as inconsistency in instrumentation calibration, variability in the extent of breast compression, and the limitations of two-dimensional (2D) X-ray image projection are potential sources of error in determining true breast density [2]. Hence, 3D quantitative image-based methods have been investigated as alternatives to mammographic density for prediction of breast cancer risk [3,4].

Magnetic resonance imaging (MRI) provides unprecedented sensitivity and resolution in evaluating breast anatomy in 3D and has been used to diagnostically evaluate and screen for breast cancer [5,6]. Breast fibroglandular tissue (FGT) can be distinguished from fatty tissue using 3D T1-weighted MRI with fat suppression, allowing a 3D assessment of breast density. The level of enhancement in FGT (also termed background parenchymal enhancement) by contrast-enhanced MRI has also been shown to be a strong independent predictor of breast cancer odds [7].

FGT enhancement can be characterized quantitatively by the percent enhancement after an injection of contrast agent. More recently, MR-based FGT density measurement has also been obtained using a semiautomatic iterative segmentation technique based on a fuzzy C-means (FCM) clustering algorithm. These quantitative measures of breast tissue have been found to correlate well with mammographic density [8]. In addition to contrast-enhanced MRI, diffusion-weighted imaging (DWI) has been investigated for characterization of normal FGT [9]. DWI provides complementary quantitative measures, such as the apparent diffusion coefficient (ADC), that reflect tissue cellularity and vascularity [10].

Despite the benefit of its use as a potential breast cancer risk factor, FGT characterization by MRI lacks specificity to differentiate malignant from benign and normal tissues [11]. In particular, the contrast enhancement profile of ductal carcinoma in situ (DCIS) may show persistent enhancement similar to normal background parenchymal enhancement. Without biopsy confirmation and experienced radiologic staff, DCIS may remain undetected [12]. Moreover, certain patient characteristics such as hormonal changes may contribute to FGT measurement variations that also lead to misdiagnoses [13,14]. These limitations underscore the need for an understanding of the expected variability of background enhancement in normal FGT. While some studies have attempted to estimate error in quantitative parameters from MRI [15–18], there is no investigation on the variability and repeatability in FGT measurements by contrast-enhanced MRI and DW-MRI. The purpose of this study was to characterize normal FGT using MR background enhancement and density parameters in repeated scans to evaluate the variability and repeatability of these measurements between and within normal subjects. In a subset of this study, DWI was also acquired in an attempt to provide complementary characterization of normal breast tissue. To control for effects of hormonal fluctuation, measurements were taken during the early follicular phase of the menstrual cycle when hormonal fluctuation is minimal.

Materials and Methods

Study Population

Nineteen healthy female volunteers were enrolled in this Health Insurance Portability and Accountability Act (HIPPA)-compliant study protocol that was reviewed by the Institutional Review Board and approved by the Committee of Human Research under the institution's Human Research Protection Program. All volunteers provided written informed consent to participate in this study. Subjects were initially scheduled for two contrast-enhanced MRI scans within a 72-hour period. To control for image fluctuations arising from elevated estrogen and progesterone levels during the luteal phase of the menstrual cycle, every attempt was made to schedule both scans during the follicular phase of the menstrual cycle. Subjects who were unable to complete both scans within 72 hours (n = 6) were scheduled to complete the second scan during the same phase of their next menstrual cycle. Other subject characteristics such as age, day of menstrual cycle, time between both scans, cycle length, and use of contraceptives were recorded. DWI was offered to all subjects and nine subjects participated in the DWI scans before contrast-enhanced MRI.

Contrast-Enhanced MRI Acquisition

MRI was performed on a 1.5-T scanner (Signa; GE Healthcare, Milwaukee, WI) using a dedicated bilateral eight-channel array breast coil [Hologic (formerly Sentinelle Medical), Toronto, Ontario]. A fat-suppressed T1-weighted 3D fast gradient-recalled echo sequence was used [repetition time/echo time (RT/TE), 8.8/4.3; flip angle, 10°; field of view (FOV) = 28–38 cm; imaging matrix = 512 x 320]. Bilateral imaging of the breasts was performed in the axial orientation with 156 slices of 2-mm thickness in a scan time of 3 minutes and 42 seconds, with the low-order phase encoding data acquired around the center of the scan. Gadopentetate dimeglumine (Magnevist; Bayer HealthCare, Berlin, Germany) was used as a contrast agent and was injected at a dose of 0.1 mmol/kg of body weight (1.2 ml/s) followed by a 10-ml saline flush. Three time points were acquired during each contrast-enhanced MRI examination: a baseline scan before contrast agent injection (t₀), followed by two time points measured in the early (t₁) and late phases (t₂) after contrast injection, yielding temporal post-contrast sampling times of 1.83 minutes and 5.67 minutes, respectively. Only the baseline and early time points were used in this study.

DWI Acquisition

DWI data were acquired bilaterally in the axial orientation using a fat-suppressed diffusion-weighted echo planar imaging sequence (TR = 6 seconds, TE = 109 milliseconds, b values = 0 and 600 s/mm², FOV = 40 cm, slice thickness = 3 mm, between slice gap = 0, imaging matrix = 128 x 128, number of averages = 6, acquisition time = 4 minutes and 24 seconds). Diffusion gradients were applied in six directions.

Contrast-Enhanced MR Image Analysis

Although images were acquired bilaterally, for the purpose of this study, all analyses were performed on the right breast. To isolate FGT from fat in the breast, a two-step process was applied: 1) delineation of the total breast volume and 2) application of an unsupervised FCM algorithm for FGT segmentation [8,19,20].

Total breast volume delineation.

A previously described graphical user interface was used to interactively delineate the contours of the breast on individual image slices [8]. As shown in Figure 1A, delineation was accomplished by placing Bézier splines [8] along the contours of the breast on individual slices. An algorithm based on the Laplacian-of-a-Gaussian filter [21] automatically attached the Bézier splines to the closest edge of the breast. Delineated regions on each of the 156 slices of the pre-contrast T1-weighted 3D series comprised the total breast volume. Given that the morphology of the breast does not change significantly between contiguous slices, Bézier splines were drawn on every four to six slices to reduce user interaction and computational time [21]. Intermediate slices were linearly interpolated, visually inspected, and adjusted whenever Bézier splines were misaligned with the contours of the breast.

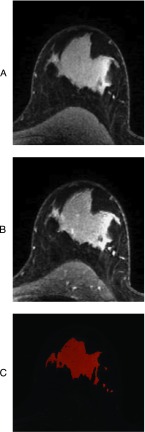
Figure 1.

Representative contrast-enhanced MR image and FGT delineation. (A) Pre-contrast enhanced image with superimposed Bézier splines. Bézier splines were used to outline the contours of the breast on pre-contrast enhanced images. These outlines over all 156 slices constituted the total breast volume. (B) Intermediate output of an FCM algorithm showing clusters of breast tissue segmented from the total breast volume based on signal intensity: Each of the five distinct shades represents a tissue cluster group. Cluster groups were visually inspected to determine which cluster groups were primarily FGT. (C) Final output of the FCM algorithm. FGT cluster groups were combined into a mask with each voxel in the mask possessing a membership from 0 to 1 representing its FGT membership. The sum of these memberships comprised the total FGT volume.

FGT segmentation.

The total breast volume was segmented into FGT and fat by a semiautomated iterative classification [8]. Before segmentation, image analysts defined the number of clusters to extract from the breast volume. Nondiseased, noncontrast T1-weighted MR images typically exhibit two broad categories of signal intensity that correspond to FGT and fat. FGT presents as hyperintense relative to suppressed fat. However, abnormalities such as cysts, benign lesions, nonuniform signal intensity in FGT, and artifacts give rise to additional categories. Hence, a total of five clusters was empirically determined to account for all signal intensity categories within the total breast volume. The algorithm assigned a membership (ratio of FGT) between “0” and “1” to each voxel, where “1” indicated a voxel that was primarily FGT and “0” indicated a voxel that was primarily fat. Such fuzzy classification has the advantage of minimizing artificial inflation or deflation of FGT quantification within voxels that demonstrate partial volume effects (i.e., possess contributions from multiple categories of signal intensity). Moreover, fuzzy classification ensures that an accurate percentage of FGT in each voxel is counted toward the FGT volume. As shown in Figure 1B, five clusters were segmented from the total breast volume. Trained image analysts decided which of the five clusters comprised FGT based on visual inspection. Selected clusters were combined into a mask (Figure 1C), and the FGT volume was computed as the sum of the memberships of all voxels within the mask.

FGT density estimation.

After total breast volume delineation and FGT segmentation, FGT density was calculated as the ratio of the FGT volume to the total breast volume.

FGT enhancement quantification.

FGT enhancement ((S₁ - S₀)/S₀) was computed on a voxel-by-voxel basis from contrast-enhanced MRI as the relative change in signal intensity from the pre-contrast (S₀) to the early post-contrast (S₁) time point. Voxels with intensity decreased between the pre-contrast and post-contrast images were excluded from the FGT enhancement analysis. Figure 2, A to C, displays a typical FGT enhancement map obtained by contrast-enhanced MRI with 1) a representative pre-contrast image, 2) a corresponding contrast-enhanced image, and 3) an illustration of all enhancing voxels within the FGT volume superimposed onto the pre-contrast enhanced image, respectively.

Figure 2.

Representative contrast-enhanced MR image and FGT enhancement illustration. (A) Pre-contrast enhanced image. (B) Early contrast-enhanced image. (C) Illustration of all enhancing voxels within the FGT volume superimposed onto the pre-contrast image.

DWI Analysis

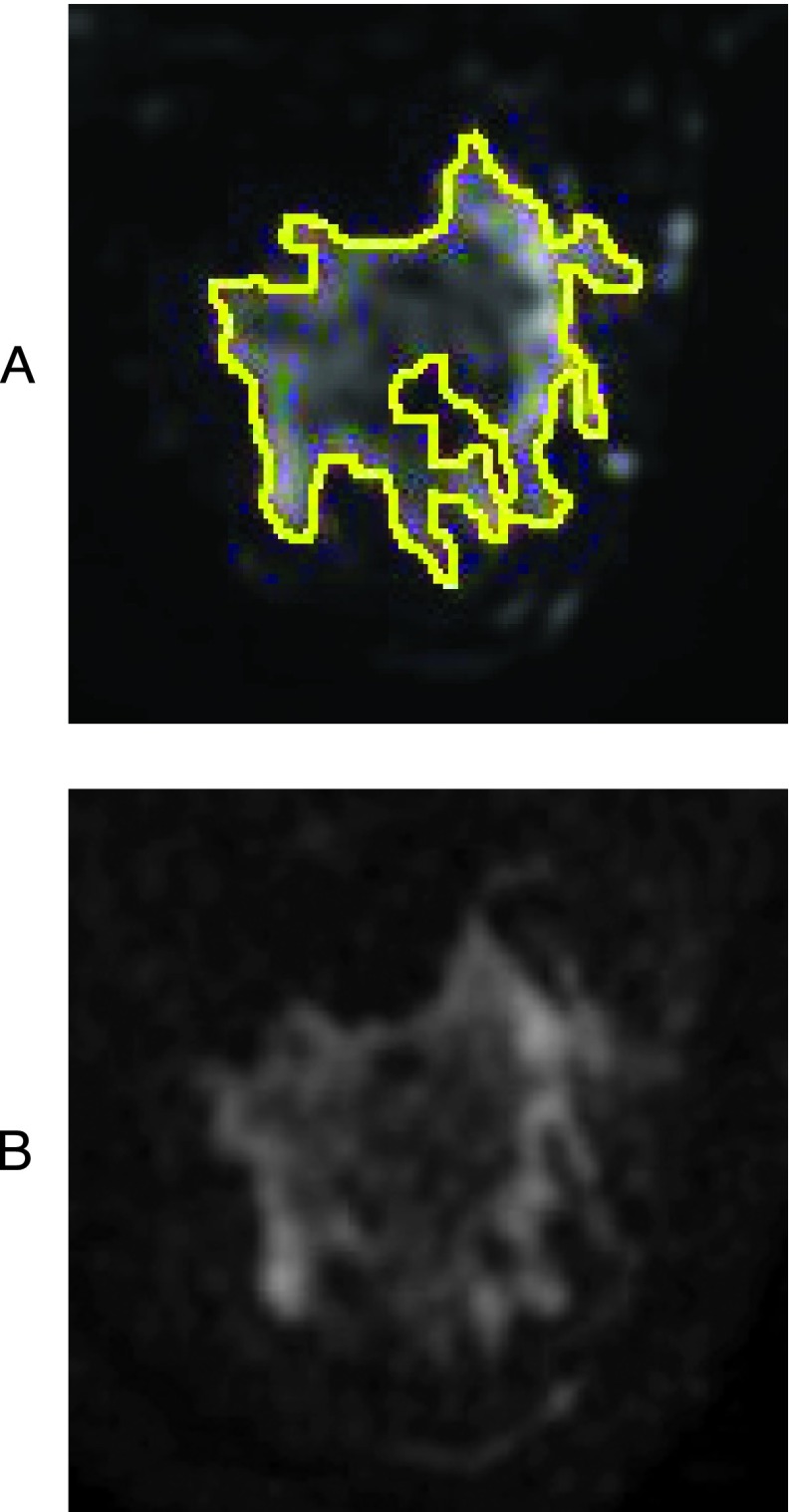
A mean FGT ADC was derived for each DWI scan. It was necessary to separately delineate FGT on the diffusion weighted images rather than applying the FGT volume derived from the contrast enhanced MR images onto the DWI images because of 1) a 2.5-fold difference in slice thickness, 2) a 3-fold difference in voxel size between the contrast-enhanced MRI and DWI images, and 3) distortions in the DWI images. FGT delineation for DWI was accomplished by drawing free-form regions of interest (ROIs) on the T2-weighted (b = 0 s/mm²) images of the DWI acquisition. Figure 3A displays a representative FGT ROI on a T2-weighted (b = 0 s/mm²) image. The mono-exponential ADC was computed on a voxel-by-voxel basis using the following equation:

$$\text{ADC}=-\ln \left(S_{600}/S_0\right)/\mathrm{\Delta b}\left({\text{mm}}^2/\text{s}\right),$$ (1)

where S₀ and S₆₀₀ are the signal intensities at b = 0 s/mm² and b = 600 s/mm², respectively, and Δb = 600 s/mm². The mean ADC of all voxels within the FGT ROI was used for statistical analysis. Figure 3B displays a representative ADC map.

Figure 3.

Representative image of DWI and FGT delineation. (A) T2-weighted image with a superimposed FGT ROI. Due to distortion present in DWI as well as mismatch in slice thickness and voxel size between both acquisitions, it was not possible to apply FGT mask generated from contrast-enhanced MRI to DWI. Hence, FGT ROIs were separately generated for DWI by drawing free-form ROIs on non-diffusion-weighted images. (B) ADC map generated from diffusion-weighted images. The mean ADC of all voxels within the FGT ROI was used for statistical analysis.

Statistical Analysis

The variability of measurements (FGT density, FGT enhancement and ADC) was assessed by the coefficient of variation (CV). The between-subject CV (bCV) for a specific visit was defined as the ratio of the standard deviation (SD) to the mean of measurements across subjects at the same visit and expressed as a percentage (Equation 2):

$$\text{bCV}=100\times \frac{\text{SD}}{\text{mean}}.$$ (2)

The within-subject CV (wCV), also expressed in percentage terms, was generated by the ratio of the within-subject SD (wSD) to the overall mean of measurements from visit 1 and visit 2 (Equation 3), for measurements Y_v1 and Y_v2 at visit 1 and visit 2, respectively:

$$\text{wSD}=\sqrt{\frac{{\displaystyle \sum {\left(Y_{\text{v}1}-Y_{\text{v2}}\right)}^2}}{2n}};\text{overall mean}=\frac{{\displaystyle \sum \left(Y_{\text{v}1}-Y_{\text{v2}}\right)}}{2n},$$

where the sums are over the n subjects in the study so that

$$\text{wCV}=100\times \frac{\text{wSD}}{\text{overall mean}}.$$ (3)

Repeatability of measurements refers to the strength of agreement between repeated measurements obtained under similar conditions [22]. Scatterplots of measurements at visit 2 versus visit 1 were evaluated. Spearman rank correlation was used to assess the agreement between visits, and results were reported with the Spearman rank correlation coefficient (ρ) and 95% confidence intervals (CIs). Residual variance from the identity line (i.e., visit 2 = visit 1) was calculated on the basis of the sum of square of deviations and degree of freedom (n - 2). Bland-Altman plots of the difference versus mean of measurements from visit 1 to visit 2 were used to assess the repeatability of measurements and its relationship to the magnitude of measurements [23]. Differences in measurements that fell within the limits of agreement (LOA = mean difference ± 1.96 x SD of the difference in measurements between visits 1 and 2 (SD_diff)) were considered clinically unimportant [24]. The coefficient of repeatability $\left(CR=1.96\times \sqrt{2}S{D}_{diff}\right)$ was used to assess the reliability of measurements. Kendall Tau test was used to assess the potential correlation between the difference and the mean of measurements between visits.

The impact of contraceptives, the nature of the subject's menstrual cycle (regular versus irregular), and the timing of repeated scans on the repeatability of measurements was investigated using a linear mixed-effects model fitted by restricted maximum likelihood [25]. Separate models were fit for each parameter (FGT density, FGT enhancement, and ADC) as a fixed effect, along with subject-specific random intercept and slope effects. All statistical analyses were performed using R statistical analysis software package (R Development Core Team (2013). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL: http://www.R-project.org/).

Results

Subject Characteristics

Detailed subject characteristics can be found in Table 1. Subjects' ages ranged from 22 to 45 (median age, 28). All subjects were premenopausal. One subject was excluded from the analysis because of poor image quality from contrast-enhanced MRI. Fifteen subjects reported regular menstrual cycles with cycle length ranging from 25 to 35 days, while three subjects reported irregular cycles. The day of menstrual cycle at the first visit ranged from 2 to 13 (median day, 9). Six of 18 subjects reported using oral contraceptives. All 18 subjects underwent contrast-enhanced MRI scans at visit 1 and visit 2, with 12 subjects completing both scans within 72 hours. A subset of nine subjects also underwent DWI scans before contrast-enhanced MRI at both visits.

Table 1.

Subject Characteristics.

ID	Age	Day of Menstrual Cycle at Visit 1	Days between Scans	Cycle Length	Contraceptive	Completed DWI
1	25.0	3	2	28	+	+
2	24.9	7	2	28	+	-
3	26.5	7	57	28	+	+
4	38.8	7	2	28	-	-
5	28.4	12	2	28	+	+
6	27.3	10	69	35	-	-
7	40.6	8	9	Irregular	-	-
8	22.4	11	2	Irregular	-	+
9	21.8	10	2	30	-	+
10	42.8	13	2	31	-	-
11	31.6	9	2	30	-	-
12	21.9	5	9	20	-	-
13	45.1	12	2	30	-	-
14	29.8	2	2	27	+	-
15	24.8	6	37	25	+	+
16	26.9	10	2	26	-	+
17	37.6	13	27	Irregular	-	+
18	42.5	8	2	28	-	+

Between-Subject Variation

There was a considerable spread in measurements between all subjects for all parameters measured. The spread of FGT density among this cohort ranged from 0.031 to 0.73 with bCV of 61%at visit 1 and 63% at visit 2. The spread of FGT enhancement values was also high, ranging from 0.080 to 0.45 with bCV of 47%and 54%at visits 1 and 2, respectively. The correlation between FGT density and FGT enhancement was not statistically significant at either visit, but the CIs are so wide that it is not possible to rule out clinically important effects (visit 1: Spearman rank correlation, ρ = -0.17; 95% CI = -0.62, 0.36; P = .5; visit 2: Spearman rank correlation, ρ = -0.42; 95% CI = -0.78, 0.07; P = .08). In the subset of nine subjects who underwent DWI, the spread of ADC ranged from 1.7 x 10^-3 to 2.8 x 10^-3 mm²/s at visit 1 and 1.4 x 10^-3 to 2.8 x 10^-3 mm²/s at visit 2. The bCV was 18% and 20% at visits 1 and 2, respectively.

Within-Subject Variation

In general, FGT density exhibited greater agreement between repeated measurements than FGT enhancement, with an interquartile range of difference of 0.079 and wCV of 13%. The interquartile range of difference between repeated FGT enhancement measurements was 0.12 with a higher wCV of 22%. For ADC, the interquartile range of difference was 0.14 x 10^-3 mm²/s and the wCV was 11%.

Repeatability Analysis

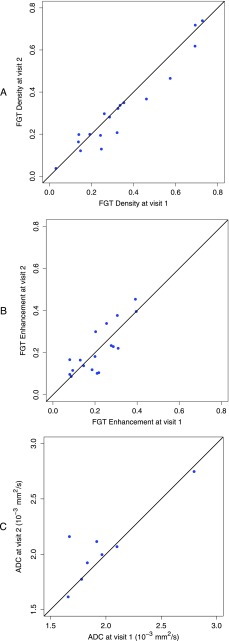
Repeatability of all measurements was first evaluated in a scatterplot of measurements at visit 2 versus visit 1. As shown in Figure 4, there was a strong agreement of FGT density between measurements with a residual variance from the identity line (i.e., visit 2 = visit 1) of 0.0039 and a Spearman rank correlation coefficient of 0.95 (95% CI = 0.80, 1.00; P < .0001). FGT enhancement, however, showed a weaker agreement with a residual variance of 0.0048 and a Spearman rank correlation coefficient of 0.75 (95% CI = 0.40, 0.92; P = .0003). Repeated measurements of ADC also showed weak agreement with a residual variance of 5.8 x 10^-8 mm⁴/s² from the identity line and a Spearman rank correlation coefficient of 0.57 (95% CI = -0.22, 1.00; P = .12).

Figure 4.

Relationships of repeated measurements from visits 1 and 2 are shown in the scatterplots with an equality line for (A) FGT density, (B) FGT enhancement, and (C) ADC.

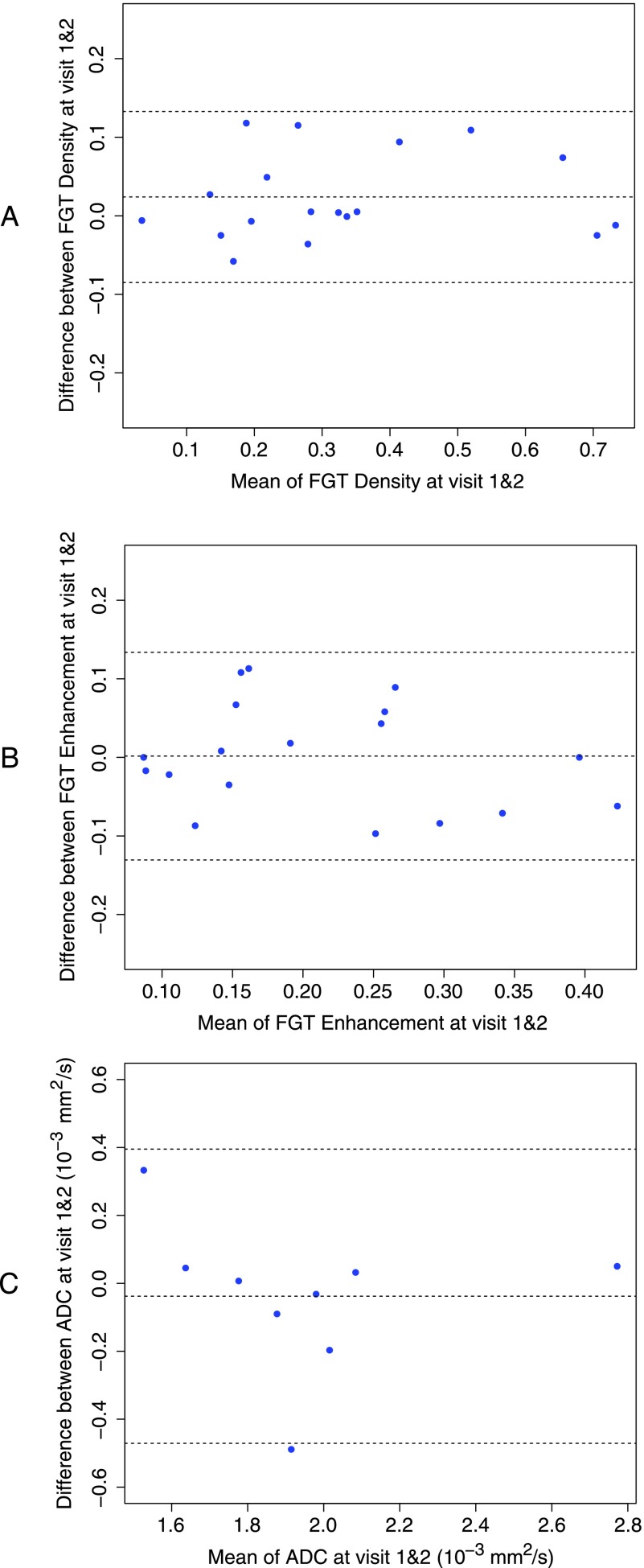
Bland-Altman plots were also used to capture the repeatability of measurements (Figure 5). Differences between measurements at visit 1 and visit 2 were plotted against the average of measurements at both visits. The mean difference between the two measurements for FGT density was 0.024 with lower/upper LOA (95% CI) of -0.085 (-0.12, -0.046)/0.13 (0.094, 0.17) and a CR of 0.15. FGT enhancement showed a weaker correlation between the measurements at both visits, but the Bland-Altman plot showed a mean difference of 0.0016 with the lower/upper LOA (95% CI) of -0.13 (-0.18, -0.084)/0.13 (0.087, 0.18) and a CR of 0.19. The mean difference between the repeated ADC measurements was -3.8 x 10^-5 mm²/s with lower/upper LOA (95% CI) of -4.7 x 10^-5 mm²/s (-7.1 x 10^-4 mm²/s, -2.3 x 10^-4 mm²/s)/4 x 10^-4 mm²/s (1.6 x 10^-4 mm²/s, 6.3 x 10^-4 mm²/s) and a CR of 6.1 x 10^-4 mm²/s. An outlier was observed in ADC measurements (Figure 5C); upon excluding it, the mean difference between the repeated ADC measurements was 1.9 x 10^-5 mm²/s with lower/upper LOA (95% CI) of -2.8 x 10^-4mm²/s (-4.6 x 10^-4mm²/s, -1 x 10^-4mm²/s)/3.2 x 10^-4mm²/s (1.4 x 10^-4mm²/s, 5 x 10^-4mm²/s) and a CR of 4.2 x 10^-4 mm²/s. Using the Kendall Tau test, the Bland-Altman plots did not reveal any clear relationships between the difference and the mean of repeated measurements for any of the parameters measured, suggesting that the observed differences were independent of the magnitude of the measurements.

Figure 5.

Bland-Altman plots of difference in measurements from visit 1 to visit 2 versus average of measurements from both visits. Upper and lower dotted lines represent the LOA; the center dotted line is the mean difference. (A) FGT density measurement with a mean difference at 0.024 and LOA (95% CI) of -0.085 (-0.12, -0.046) and 0.13 (0.094, 0.17). (B) FGT enhancement measurements with a mean difference at 0.0016 and LOA (95% CI) of -0.13 (-0.18, -0.084) and 0.13 (0.087, 0.18). (C) ADC measurements (x 10^-3) with a mean difference of -0.038 mm²/s and LOA (95% CI) of -0.47 mm²/s (-0.71 mm²/s, -0.23 mm²/s) and 0.4 mm²/s (0.16 mm²/s, 0.63 mm²/s).

Linear Mixed Effect Modeling

The effects of the covariates assessed, i.e., contraceptive use, regular menstrual cycle, and repeat scan timing, on the parameters measured are summarized in Table 3. None showed a significant effect in any of the measured parameters.

Table 3.

Summary of the Estimated Effect of Covariates on Parameters Measured.

	FGT Density Estimate/95% CI/P	FGT Enhancement Estimate/95% CI/P	ADC (mm2/s) Estimate/95% CI/P
Use of contraceptives	0.12/(-0.079, 0.33)/.21	-0.035/(-0.14, 0.072)/.5	-1 x 10-4/(-8.2 x 10-4, 6.2 x 10-4)/.75
Regularity of menstrual cycle	0.18/(-0.89, 0.44)/.18	0.036/(-0.104, 0.18)/.59	1.2 x 10-4/(-4.7 x 10-4, 7.1 x 10-4)/.64
Timing of duplicate scan	0.041/(-0.17, 0.26)/.7	0.039/(-0.071, 0.15)/.46	2.2 x 10-4/(-3.9 x 10-4, 8.2 x 10-4)/.42

The (nonstatistically significant) estimated effect of the use of contraceptives was an increase in FGT density (0.12; 95% CI = -0.079, 0.33; P = .21), a decrease in FGT enhancement (-0.035; 95% CI = -0.14, 0.072; P = .5), and a decrease in ADC (-1 x 10^-4 mm²/s; 95% CI = -8.2 x 10^-4 mm²/s, 6.2 x 10^-4 mm²/s; P = .75). Meanwhile, the estimated effect of a regular menstrual cycle was to (nonstatistically significant) increase all parameters: FGT density (0.18; 95% CI = -0.89, 0.44; P = .18), FGT enhancement (0.036; 95% CI = -0.104, 0.18; P = .59), ADC (1.2 x 10^-4 mm²/s; 95% CI = -4.7 x 10^-4 mm²/s, 7.1 x 10^-4 mm²/s; P = .64). The estimated effect of completing both scans within the same menstrual cycle was also a (nonstatistically significant) increase in all parameters: FGT density (0.041; 95% CI = -0.17, 0.26; P = .7), FGT enhancement (0.039; 95% CI = -0.071, 0.15; P = .46), ADC (2.2 x 10^-4 mm²/s; 95% CI = -3.9 x 10^-4, 8.2 x 10^-4; P = .42).

Discussion

Since the introduction of breast contrast-enhanced MRI in mid-1980s, MRI has played a key clinical role in the staging and characterization of primary and recurrent breast cancer [26]. MRI has demonstrated high sensitivity in detecting breast cancer, leading to the use of contrast-enhanced MRI for screening asymptomatic women who are at high risk for breast cancer [27]. The characteristic contrast uptake/washout kinetics in breast cancer reflects the morphologic and functional properties that discern diseased from normal breast tissues. However, the specificity of contrast-enhanced MRI is challenged by the strong FGT enhancement common in premenopausal women and is influenced by estrogen levels [7,11,28]. In these cases, strong FGT enhancement often obscures nonmass nodular malignant tissues such as those found in preinvasive DCIS [29]. In addition, misinterpretation of benign enhancement in fibroadenomas, atypical hyperplasia, and lobular carcinoma in situ may result in false positive results [26].

With the development of increasingly sophisticated techniques to improve quantitative evaluation of the breast, it is more essential than ever to gain a better understanding of normal tissue MRI characteristics [29]. Moreover, the development of quantitative imaging markers to assess breast cancer risk or response to neoadjuvant chemotherapy requires validation of the repeatability of imaging techniques. Surprisingly, despite the routine use of MRI for breast cancer diagnosis, little data exist on the repeatability of breast MRI in general, and data regarding variability and repeatability of quantitative measurements from breast contrast-enhanced MRI are even less available.

In this work, we conducted a repeated MRI study of 18 healthy female subjects to assess contrast-enhanced and diffusion imaging parameters in normal breasts. To limit bias from physiological changes that affect estrogen levels [30,31], all subjects were premenopausal, were in the follicular phase of their menstrual cycle, and were imaged either twice within a 72-hour window or at the same menstrual phase in two consecutive months. A separate analysis without the six subjects imaged in consecutive months showed that this exclusion did not substantially alter the pattern of results; hence, the data acquired were suitable for the subsequent variability and repeatability analysis.

Among the cohort of 18 subjects we examined, there was a wide spread in FGT density and FGT enhancement, with between-subject variation (bCV) ranging between 61% and 63% and 47% and 54%, respectively, suggesting that the FGT density and FGT enhancement values are highly subject dependent. While FGT density is the amount of FGT in the total breast volume, FGT enhancement is the contrast enhancement measured in the background parenchymal region. Although both FGT density and FGT enhancement may have potential as risk factors for breast cancer, they measure different characteristics of FGT in the breast. The lack of meaningful correlation between FGT density and FGT enhancement parallels similar observations that MR FGT enhancement and mammographic density are not well correlated [32,33] and that these parameters are considered independent risk factors for breast cancer [7].

In the subset of nine subjects that underwent the DWI study, the spread of mean ADC was 1.4 x 10^-3 mm²/s to 2.8 x 10^-3 mm²/s with bCV in the range of 18% and 20%. These results suggest that ADC measurements might be less subject dependent than FGT density or FGT enhancement measurements. The range of ADC values observed in this study is consistent with ADC values previously reported in healthy breast tissues [9,18,34]. While other studies have examined the variability in the ADC stemming from hormonal fluctuations during the menstrual cycle [34], no studies we encountered have studied repeatability in the ADC with hormonal effects being treated as a controlled parameter.

Between-visit measurement variations were assessed by wCV. FGT density showed higher agreement compared to FGT enhancement, with wCV of 13% versus 22%. The higher variability in FGT enhancement may be attributed to the subtle hormonal fluctuation that has less influence in the FGT density measurement. Therefore, careful study design to limit hormonal change in subjects would be prudent when using FGT enhancement to assess normal breast. The wCV for the ADC in nine subjects was 11%. Although it was lower than that of both FGT density and FGT enhancement, further study with an expanded population size is recommended to confirm this finding.

In the present study, contraceptive use, regular menstrual cycle, and repeat scan timing did not have a meaningful impact on repeated measurements. Although unlikely, variability of imaging quality because of changes in scanner performance between repeat visits and across patients cannot be ruled out. Future study design will benefit from periodic calibration scans.

One factor that could impact repeatability of FGT density estimates is subject positioning. Our estimation of FGT density assumes that the total breast volume is uncompressed. While no gross compression was evident for any patients, it is tenable, especially in larger patients, that compression of the breast between repeat visits might skew estimates of the total breast volume and, resultantly, the estimated FGT density.

Temperature and gradient nonlinearity are factors that may impact the variability and repeatability of the ADC. In the current study, we did not control for temperature. Hence, it is plausible that DWI measurements between repeat visits and across patients may have been acquired at a different temperature. Gradient nonlinearity is more pronounced at distances offset from the isocenter of the magnet, especially in breast imaging. Repositioning of patients in repeated scans may further affect the variability to the ADC values. Finally, it should also be noted that DWI analysis was only performed on a subset of nine subjects; hence, the presented ADC results are limited in scope and should be interpreted accordingly.

In summary, we presented a preliminary estimate of expected variability and repeatability of quantitative FGT density, FGT enhancement, and ADC measurements in the normal breast. We anticipate expanding this analysis with a larger population and other DWI quantifiers. These estimates form the basis for normal variation of FGT as measured by MRI and will guide the correct interpretation of cancer diagnosis and assessment of tumor treatment response.

Table 2.

Summary of Results of Variability and Repeatability.

Measurements	Bias*	bCV Visit 1	bCV Visit 2	wCV	CR	Lower LOA (95% CI)	Upper LOA (95% CI)
FGT density	0.024	61%	63%	13%	0.15	-0.085 (-0.12, -0.046)	0.13 (0.094, 0.17)
FGT enhancement	0.0016	47%	54%	22%	0.19	-0.13 (-0.18, -0.084)	0.13 (0.087, 0.18)
ADC (mm2/s)	-3.8 x 10-5	18%	20%	11%	6.1 x 10-4	-4.7 x 10-4 (-7.1 x 10-4, -2.3 x 10-4)	4 x 10-4 (1.6 x 10-4, 6.3 x 10-4)

^*Bias = mean difference between visits.