Analyzing Spatial Heterogeneity in DCE- and DW-MRI Parametric Maps to Optimize Prediction of Pathologic Response to Neoadjuvant Chemotherapy in Breast Cancer

Abstract

The purpose of this study is to investigate the ability of multivariate analysis of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) and diffusion-weighted MRI (DW-MRI) parametric maps, obtained early in the course of therapy, to predict which patients will achieve pathologic complete response (pCR) at the time of surgery. Thirty-three patients underwent DCE-MRI (to estimate K^trans, v_e, k_ep, and v_p) and DW-MRI [to estimate the apparent diffusion coefficient (ADC)] at baseline (t₁) and after the first cycle of neoadjuvant chemotherapy (t₂). Four analyses were performed and evaluated using receiver-operating characteristic (ROC) analysis to test their ability to predict pCR. First, a region of interest (ROI) level analysis input the mean K^trans, v_e, k_ep, v_p, and ADC into the logistic model. Second, a voxel-based analysis was performed in which a longitudinal registration algorithm aligned serial parameters to a common space for each patient. The voxels with an increase in k_ep, K^trans, and v_p or a decrease in ADC or v_e were then detected and input into the regression model. In the third analysis, both the ROI and voxel level data were included in the regression model. In the fourth analysis, the ROI and voxel level data were combined with selected clinical data in the regression model. The overfitting-corrected area under the ROC curve (AUC) with 95% confidence intervals (CIs) was then calculated to evaluate the performance of the four analyses. The combination of k_ep, ADC ROI, and voxel level data achieved the best AUC (95% CI) of 0.87 (0.77–0.98).

Introduction

Breast cancer is the second leading cause of cancer death among women in the United States. According to the National Cancer Institute, more than 232,000 new cases in women were diagnosed with breast cancer in 2013, and there were nearly 40,000 breast cancer deaths [1]. On the basis of incidence rates from recent years, it is currently estimated that one in eight women will be diagnosed with breast cancer during their lifetime. Although X-ray mammography and ultrasound imaging are useful in the evaluation of women with breast cancer, they do not provide adequate information for predicting tumor response to therapy to guide clinical decisions. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) and diffusion-weighted MRI (DW-MRI) have matured to the point where they are able to provide quantitative and complimentary information on tumor status [2]. DCE-MRI involves the rapid, serial acquisition of images of a region of interest (ROI) before, during, and after injection of a contrast agent (CA) into a peripheral vein of a patient. As the CA perfuses into the ROI, it changes the tissue's native relaxation times and therefore its measured signal intensity. By fitting the signal intensity time course to an appropriate pharmacokinetic model, physiological parameters that relate to tissue perfusion and permeability (K^trans), extra-vascular extracellular volume fraction (v_e), blood plasma volume (v_p), and the efflux rate constant (k_ep = K^trans/v_e) can be extracted. DW-MRI allows for the in vivo measurement of the motion of water in tissue. By applying two or more diffusion-sensitizing gradients with different amplitudes, the apparent diffusion coefficient (ADC) can be estimated from the resulting data to describe the rate of water diffusion in cellular tissues. In well-controlled studies, it has been shown that the ADC varies inversely with cell density [3].

Parameters derived from DCE-MRI and DW-MRI have been recently evaluated as surrogate biomarkers for assessing and predicting the response of breast tumors to neoadjuvant chemotherapy (NAC). Early DCE-MRI studies focused on semiquantitative analyses through obtaining changes in tumor size, volume, or morphology to evaluate treatment response [4–10]. More recent studies have focused on measuring and tracking changes in K^trans, v_e, v_p, and k_ep [11–19]. There also have been studies investigating the ability of ADC to separate responders from nonresponders after NAC [20–24]. Most of these studies have tracked changes during the course of treatment in parameters obtained from the whole-tumor ROI or histograms describing their distributions. However, these approaches cannot capture the spatial heterogeneity in tissue characteristics and therefore discard all such information. Furthermore, most previous studies reported on either DCE-MRI or DW-MRI and have not evaluated the performance of the combination of these data.

We have previously proposed and validated a longitudinal registration technique to allow registration of MRI and positron emission tomography (PET) data obtained at different time points during therapy [25–27]. In this study, we applied this registration approach to longitudinally align multiparametric MRI maps to perform a novel voxel-by-voxel analysis that incorporates spatial heterogeneity. We investigate whether this voxel-by-voxel approach outperforms the ROI-based analysis when attempting to separate pathologic complete responders (pCR) from nonresponders (non-pCR). Although others have applied multiparameter voxel level analysis [see, e.g., [28]] to predict response in patients with glioma, to the best of our knowledge, this is the first study to integrate multiparametric data analyzed at the voxel level using a multivariate regression model to optimize the prediction of the response of breast cancer to NAC.

Methods

Patient Population

Patients with stage II/III breast cancer were enrolled in a prospective, Institutional Review Board (IRB)-approved study that specified MRI examinations at the following three time points: before initiating NAC (t₁), after one cycle of treatment (t₂), and after all cycles (t₃) of NAC. Forty-one patients completed at least one of the three scans. Data from eight patients were not included for the following reasons: withdrawal from the study after the first scan (n = 6), hardware failure on the scanner (n = 1), and issues with the contrast line (n = 1). All mastectomy specimens were sliced at 5-mm intervals and examined by a breast pathologist for abnormalities. pCR was defined as the absence of any invasive cancer in breast or lymph nodes at the time of surgery following NAC. Patients with any residual invasive cancer in the breast or lymph nodes or patients who progressed before surgery were defined as non-pCR. Determination of pCR and non-pCR status was performed at the time of definitive surgery by a breast pathologist. At completion of NAC, 12 patients achieved pCR, whereas 21 patients were non-pCRs. Table 1 summarizes the salient features of the study population including receptor status, age, neoadjuvant treatment regimens, tumor grade, and the excised tumor size (as measured by a pathologist on the surgical specimen).

Table 1.

Clinical Features of the Study Population.

Patient No.	Age (yr)	Treatment Regimens	Receptor Status			Tumor Grade	Excised Tumor Size (cm)	Pathologic Response
			ER	PR	HER2
1	50	AC → Taxol*	+	+	-	3	0.5	Residual disease
2	52	Taxotere†	+	-	+	3	1.5	Residual disease
3	60	AC → Taxol + concurrent trastuzumab	+	+	+	1	2.9	Residual disease
4	36	Taxol + cisplatin ± everolimus†	-	-	-	2	2.9	Residual disease
5	48	Dose-dense AC → Taxol	+	+	-	1	1.3	Residual disease
6	43	Dose-dense AC → Taxol	+	+	-	2	2.6	Residual disease
7	59	Dose-dense AC → Taxol	+	+	-	2	4.2	Residual disease
8	53	Taxol + cisplatin ± everolimus	-	.	-	2	1.3	Residual disease
9	35	Trastuzumab + carboplatin + ixabepilone	+	+	+	3	1.4	Residual disease
10	28	Taxol + cisplatin ± everolimus	-	-	-	3	0.8	Residual disease
11	33	AC → Taxol	+	+	-	3	1.2	Residual disease
12	39	AC → Taxol	+	+	-	1	2.5	Residual disease
13	57	AC → Taxol	-	-	-	3	N/A§	Residual disease
14	67	Dose-dense AC → Taxol	-	-	+	3	1.8	Residual disease
15	45	Taxol + cisplatin ± everolimus	-	-	-	3	0.5	Residual disease
16	46	Taxotere + carboplatin + Herceptin¶	+	+	+	3	0.3	Residual disease
17	47	Taxotere → AC	+	+	-	1	8.0	Residual disease
18	36	AC → Taxol	+	+	+	2	1.0	Residual disease
19	43	Cisplatin + Taxol ± everolimus	-	-	+	3	0.7	Residual disease
20	55	AC → Taxol	+	+	-	2	3.5	Residual disease
21	58	Cisplatin + Taxol ± everolimus	-	+	-	2	1.7	Residual disease
22	53	AC → concurrent Taxol + trastuzumab	-	-	+	3	0	pCR
23	46	Taxotere → AC	-	+	-	3	0	pCR
24	46	AC → concurrent Taxol + trastuzumab	-	-	+	2	0	pCR
25	33	AC → weekly Taxol	-	-	-	3	0	pCR
26	39	Trastuzumab and Lapatinib	-	-	+	2	0	pCR
27	46	AC → Taxol	+	-	-	3	0	pCR
28	42	Taxol + cisplatin ± everolimus	-	-	-	3	0	pCR
29	34	Taxotere → AC	-	-	-	3	0	pCR
30	44	Trastuzumab + Lapatinib	-	-	+	3	0	pCR
31	37	Taxol + cisplatin ± everolimus	-	-	-	3	0	pCR
32	39	AC → Taxol	-	-	-	3	0	pCR
33	48	Taxotere + carboplatin + Herceptin	-	-	+	3	0	pCR

AC indicates adriamycin and cyclophosphamide; HER2, human epidermal growth factor receptor 2.

^*paclitaxel (Taxol; HQ SPCLT PHARMA, Paramus, NJ).

^†docetaxel (Taxotere; Sanofi-Aventis, Bridgewater, NJ).

^‡The study is ongoing, and we are blinded to the randomization.

^§This patient was transferred to another hospital, and the tumor size is not available.

^¶trastuzumab (Herceptin; Genentech Inc, San Francisco, CA).

MRI Data Acquisition

DCE-MRI was performed using a Philips 3.0T Achieva MRI scanner (Philips Healthcare, Best, The Netherlands). A 4-channel receive double-breast coil covering both breasts was used for 20 patients (Invivo Inc, Gainesville, FL), whereas a 16-channel double-breast coil was used for 13 patients. Data for constructing a T₁ map were acquired with an radio frequency (RF)-spoiled 3-dimensional (3D) gradient echo multiflip angle approach with repetition time/echo time (TR/TE) = 7.9 ms/1.3 ms and 10 flip angles from 2 to 20° in 2° increments. The acquisition matrix was 192 x 192 x 20 (full breast) over a sagittal square field of view (22 cm²) with slice thickness of 5 mm, one signal acquisition, and a sensitivity encoding factor of 2 for an acquisition time of just less than 3 minutes. The dynamic scans used identical parameters and a flip angle of 20°. Each 20-slice set was collected in 16 seconds at 25 time points for just less than 7 minutes of dynamic scanning. For the DCE study, a catheter placed within an antecubital vein delivered 0.1 mmol/kg (9–15 ml, depending on patient weight) of the CA gadopentetate dimeglumine Gadolinium diethylenetriamine pentaacetic acid (Gd-DTPA; Magnevist, Wayne, NJ) at 2 ml/s (followed by a saline flush) through a power injector (Medrad, Warrendale, PA) after the acquisition of three baseline dynamic scans.

DW-MRI was acquired with a single-shot spin-echo echo-planar imaging sequence in three orthogonal diffusion-encoding directions (x, y, and z). For 13 patients, b = 0 and 500 s/mm², TR/TE = 2500 ms/45 ms, Δ = 21.4 ms, δ = 10.3 ms, and 10 signal acquisitions were acquired. For 20 patients, b = 0 and 600 s/mm², TR/TE = “shortest” (range, 1800–3083 ms/43–60 ms), Δ = 20.7 to 29 ms, δ = 11.4 to 21 ms, and 10 signal acquisitions were acquired. The total scan time of each DW-MRI data was 4 minutes and 40 seconds. The acquisition matrix was 144 x 144 x 12 over a field of view (19.2 cm²) with a slice thickness of 5 mm.

Quantitative Image Analysis

For each patient at each time point, an ROI was drawn manually to completely surround the enhancing tumor as seen on each slice. The tumor was then defined as the voxels in each ROI displaying a percentage of enhancement larger than 80%, which was the optimal threshold enhancement level determined by a previous study [29]. The Extended Tofts-Kety model [30] was used to estimate physiological parameters from the DCE-MRI data. This pharmacokinetic model assumed a linear relationship between the time-varying longitudinal relaxation time T₁ (t), and the concentration of CA in the tissue C_t(t):

$$R_1(t)\equiv 1/T_1(t)=r_1{C}_{\text{t}}(t)+R_{10},$$ (1)

where R₁₀ is the R₁ value of the tissue before CA administration and r₁ is the relaxivity of the CA. The C_t time course was calculated as follows:

$$C_{\text{t}}(T)=K^{\text{trans}}{\int }_0^T{C}_{\text{p}}(t)\exp (-(K^{\text{trans}}/v_{\text{e}})(T-t))\mathrm{dt}+v_{\text{p}}{C}_{\text{p}}(t),$$ (2)

where K^trans is the volume transfer constant, v_e is the extravascular extracellular volume fraction, and v_p is the plasma volume fraction. The arterial input function (AIF) C_p was a population-averaged AIF constructed from 50 individual AIFs obtained from a total of 24 patients scanned at different time points. All of the 24 patients were included in the 41 patients presented in this study. Each AIF was detected through a semiautomatic AIF-tracking algorithm [31]. The efflux constant k_ep (≡ K^trans/v_e) was then computed after K^trans and v_e were obtained.

ADC maps were calculated with the following equation: ADC = ln (S₁/S₂)/(b₂ - b₁), where S₁ and S₂ denote the signal acquired with b values of b₁ and b₂, respectively.

Voxels for which either the Extended Tofts-Kety model or the ADC fitting model did not converge or converged to nonphysical values (i.e., K^trans > 5.0 min^-1, v_e > 1.0, v_p > 1.0, ADC > 3.0 x 10^-3 mm²/s or ADC < 0.01 x 10^-3 mm²/s, or any parameter below 0.0) were set equal to zero and not included in subsequent analyses.

Registration Algorithms

A tumor volume-constrained registration algorithm [25,26] was employed for alignment of breast images acquired during therapy. First, a rigid body registration algorithm [32] was used to align the averaged postcontrast images at t₁ and t₃ to the target images at t₂ to obtain a global and rough alignment. This algorithm searched the optimal rotation and translation parameters through maximizing the normalized mutual information. A nonrigid registration method [25], based on the adaptive bases algorithm [33], was then applied to the images to refine the alignment. The cost function of this method was composed of the following two terms: the negative normalized mutual information term and the tumor volume constraint term:

$$f_{\cos t}=-\frac{H(A)+H(B)}{H(A,\hspace{0.17em}B)}+\alpha {\int }_T\left|\log (J_{\text{T}}(x))\right|\mathrm{dx},$$ (3)

where H(A) and H(B) are the marginal entropy of images A and B, respectively, and H(A,B) is the joint entropy. J_T(x) is the Jacobian determinant on the tumor area, and α is the parameter to control the weight of this constraint term; α can be adjusted from 0 to 1 on the basis of individual data sets. For the patient data sets in this study, a range of 0.05 to 0.3 was (empirically) selected for the image sets. The deformation field was modeled by a linear combination of radial basis functions [34]. Through searching the optimal coefficients of radial basis functions, the cost function maximally aligns the breast volumes while minimally distorting the tumor whose volume should be kept true to what is measured at each time point. Details of the method can be found elsewhere [25,26].

As the DW- and DCE-MRI data were acquired within the same imaging session with minimal patient motion, the rigid body registration [35] mentioned above was used to transform the DW-MRI data into the DCE-MRI space at each time point. The transformations obtained from the longitudinal DCE-MRI registration were then applied to register the DW-MRI data at different time points.

Data Analysis

ROI analysis. Our previous studies [35,36] indicated that the accuracy of predicting treatment response was superior using the parameter estimates at t₂ rather than those at t₁. Thus, in the present study, we focused on the mean values for each parameter (ADC, K^trans, v_e, k_ep, and v_p) in the tumor ROIs at t₂ for each patient. The logistic regression (LR) model was then applied to seven cases: k_ep, ADC, K^trans, v_e, and v_p considered individually (five cases), the combination of k_ep and ADC, and the combination of all parameters, as follows:

$$\text{logit[pCR}=1|X\text{]}=\text{β}X,$$ (4)

where pCR is a binary outcome variable indicating whether or not a subject is a responder and X denotes covariates. For example, for the combination of k_ep and ADC, βX can be expressed as β₀ + β₁m_kep + β₂m_ADC, where m_kep and m_ADC are the mean values and β_i is the coefficient of the input variables.

Voxel-based analysis. As described above, the longitudinal registration algorithm was employed to register the averaged postcontrast images obtained at three time points to a common space. The obtained transformations were then applied to align the serial, multiparametric maps. This step allowed us to detect the subset of voxels on the data at t₂ that displayed increases in k_ep, K^trans, and v_p from t₁ to t₂ and the voxels that displayed decreases in v_e and ADC from t₁ to t₂. The corresponding percentiles of the subsets of voxels were calculated, and a redundancy analysis [37] was performed to select the most nonpredictable percentiles from the remaining percentiles for the given histograms. As described in [37], after dividing the voxels into 20 equal bins, the most predictable percentiles quantified by the coefficient of determination (equivalent to R² in linear regression) from the remaining percentiles were removed in a stepwise fashion. Those percentiles selected as the least predictable served as explanatory variables in the logistic ridge regression (LRR) model in each of the seven cases. Instead of regular LR, we employed LRR that has been widely used to handle a case with small sample size and a large number of explanatory variables; i.e., this is an example of “small n and large p” scenario [38]. The difference between the LR and LRR models is that a penalty is added in the cost function in the LRR model. The penalty is calculated as β^T β and controls the variance of the coefficients β. The contribution of the penalty to the cost function is regularized by a tuning parameter that can be chosen as described by Cule et al. [39]. For example, the selected percentiles for both k_ep and ADC were input into the model as follows:

$$\begin{array}{l}\text{logit[pCR}=1|(k_{\text{ep}},\text{ADC})\text{]}={\text{β}}_{\text{0}}+{\text{β}}_{\text{1}}{h}_{\text{kep1}}+{\text{β}}_{\text{2}}{h}_{\text{kep2}}+\dots \\ {\text{+ β}}_m{h}_{\text{ADC1}}+{\text{β}}_{m+1}{h}_{\text{ADC2}}+\dots {\text{β}}_N{h}_{\text{ADC}N},\end{array}$$ (5)

where h_kepi and h_ADCi were the ith percentiles for k_ep and ADC, respectively. These analyses were performed in R Statistical Software version 3.0.2 (http://CRAN.R-project.org; R Foundation for Statistical Computing, Vienna, Austria).

ROI and voxel analysis. In this approach, for both the single parameter and the parameter combinations, the predictor variables in the LRR model were the mean values and the selected percentiles obtained from the redundancy analysis.

ROI, voxel, and clinical data. In this approach, in addition to the mean parameters and the selected percentiles, clinical data (patient age and tumor grade) were also used as explanatory variables in the LRR model. The deviation of patient age was calculated as the measure of difference between each patient's age and the mean age of the population and input in the LRR model. Each patient's tumor was graded using the modified Nottingham method (shown in Table 1) and recorded as follows: 1 (low grade), 2 (intermediate grade), and 3 (high grade) [40]. Those scores were also input in the LRR model as predictor variables, as well as the age deviation, the mean parameters, and the percentiles.

Statistical Analysis

The regression model returned the probabilities of achieving pCRs for all patients, and receiver-operating characteristic (ROC) analysis was performed to determine the ability of each analysis to predict pCR [41]. The areas under the curve (AUCs) were estimated using the trapezoidal rule. The bootstrap method to correct for overfitting [42,43] was performed to compute the overfitting-corrected AUC and its 95% confidence intervals (CIs) with 500 replicates. At each replicate, a set of bootstrap samples was used to fit an LR (or LRR) model, and then the fitted model was validated against the original data set, which in turn resulted in the overfitting-corrected AUC estimate. This approach is known to be more reliable than the leave-one-out cross-validation that tends to inflate the variance of AUC estimates [44].

Results

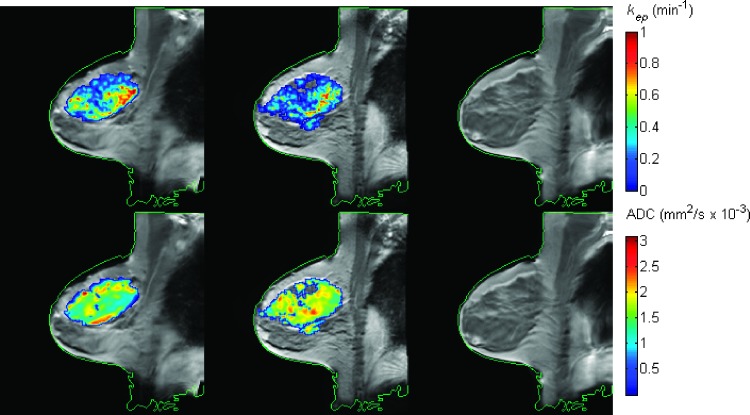
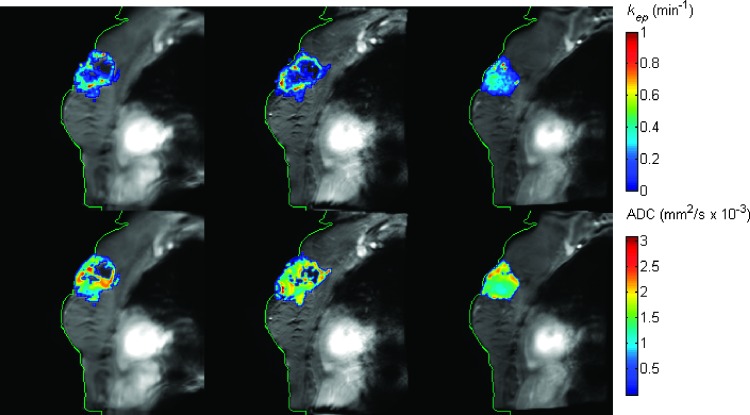
Figure 1 shows the k_ep (top row) and ADC (bottom row) maps superimposed on the postcontrast DCE-MRI data at the pre-NAC (first column), post-one cycle of NAC (second column), and post-all cycles of NAC (third column) time points for one (representative) patient achieving pCR. The parametric maps obtained at each imaging session were all registered to a common space. The green contour was drawn on the image at t₃ and copied to other panels. If the registration is accurate, the green contour at t₃ should also match the contours at t₁ and t₂ after registration. The figure demonstrates the accuracy of the alignment of the images across time (i.e., during NAC). Observe that k_ep has decreased from 0.42 min^-1 at baseline to 0.31 min^-1 after one cycle of therapy, whereas the ADC values were 1.47 mm²/s x 10^-3 and 1.75 mm²/s x 10^-3 at the first two time points, respectively. Figure 2 shows the corresponding data for one patient who is a non-pCR. In this case, the k_ep values were 0.26 min^-1, 0.32 min^-1, and 0.23 min^-1, respectively, and the ADC values were 1.59 mm²/s x 10^-3, 1.60 mm²/s x 10^-3, 1.51 mm²/s x 10^-3, respectively, at the three time points. The ROI level analysis is focused on how these averaged values changed over time to predict eventual therapeutic response. The next level of analysis is to consider the voxel level data.

Figure 1.

The k_ep (top row) and ADC (bottom row) maps superimposed on the postcontrast DCE-MRI data pre-NAC (first column), post-one cycle of NAC (second column), and post-all cycles of NAC (third column) for one patient achieving pCR. Multiparametric maps at different time points were all registered to a common space. The green contour was drawn on the images at t₃ and copied to the images at the other time points. The well-aligned contours at all three times indicate the accuracy of the temporal alignment of the images. (The area of nonspecific enhancement seen in the medial quadrant of the breast at t₃ was biopsied and found to reveal only benign fibrocystic changes.)

Figure 2.

The k_ep (top row) and ADC (bottom row) maps superimposed on the postcontrast DCE-MRI data pre-NAC (first column), post-one cycle of NAC (second column), and post-all cycles of NAC (third column) for one non-pCR. Multiparametric maps at different time points were all registered to a common space. The green contour was drawn on the images at t₃ and copied to the images at the other time points. The well-aligned contours at all three times indicate the accuracy of the temporal alignment of the images.

Using previously published methods [29], there was not a statistical difference in tumor volumes at baseline or post-one cycle of NAC between patients who went on to achieve pCR and those that did not.

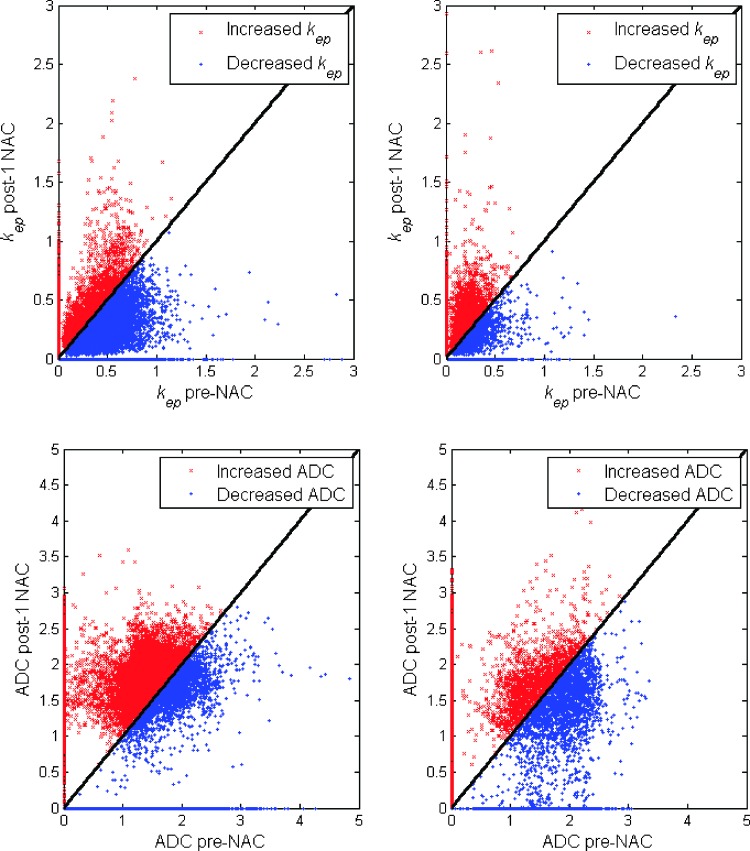
Figure 3 shows the k_ep (top row) and ADC (bottom row) values at the pre-NAC time point plotted against the k_ep and ADC values at the post-one cycle of NAC time point for one pCR (left) and one non-pCR (right); red (blue) points indicate those voxels for which there was an increase (decrease) in k_ep between the two time points. For the pCR (left), 23.7% of tumor voxels are red, and 76.3% of voxels are blue for k_ep, whereas 63.0% are red, and 37.0% are blue for ADC. For the non-pCR (right), 49.8% of tumor voxels are red, and 50.2% of voxels are blue for k_ep, whereas 48.6% of tumor voxels are red, and 51.5% of voxels are blue for ADC, respectively.

Figure 3.

The k_ep (top row) and ADC (bottom row) values at the pre-NAC time point were plotted against the k_ep and ADC values at the post-one cycle of NAC time point for one pCR (left) and one non-pCR (right); red (blue) points indicate those voxels for which there was an increase (decrease) in k_ep or ADC between the two time points. For the pCR (left), 23.7% of tumor voxels are red, and 76.3% of voxels are blue for k_ep, whereas 63.0% are red, and 37.0% are blue for ADC. For the non-pCR (right), 49.8% of tumor voxels are red, and 50.2% of voxels are blue for k_ep, whereas 48.6% of tumor voxels are red, and 51.5% of voxels are blue for ADC, respectively.

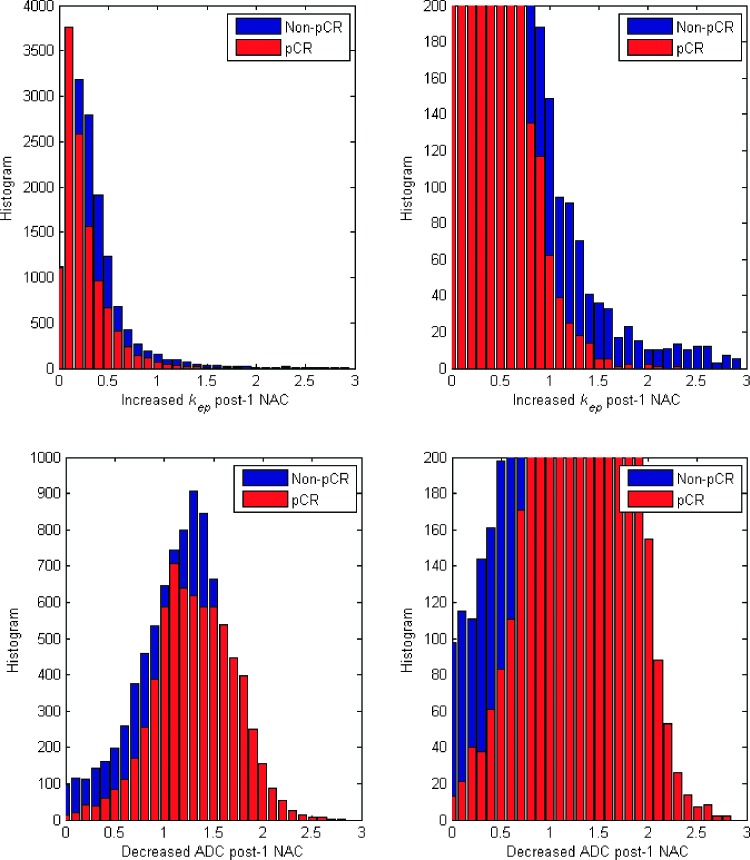
In Figure 4, the left panels show the increased k_ep histogram (top) and decreased ADC histogram (bottom) of all tumor voxels obtained from 21 patients who are non-pCRs (blue) and 12 patients who achieved pCR (red). The magnified histograms are shown in the right panel, which demonstrates that k_ep from the non-pCRs yielded a wider distribution and a longer tail than the responders. More specifically, the kurtoses, a measure of the shape of a histogram, of k_ep were 10.35 and 5.84 for the pCRs and non-pCRs, respectively, and the kurtoses of ADC were 1.92 and 2.35, respectively. The skewnesses, a measure of the extent of asymmetry of a probability distribution, of k_ep were 2.79 and 2.04 for the pCRs and non-pCRs, whereas the skewnesses of ADC were 0.73 and 0.85, respectively.

Figure 4.

The figure shows the increased k_ep histogram (top) and decreased ADC histogram (bottom) of all tumor voxels obtained from 21 non-pCRs (blue) and 12 pCRs (red). The right panels show the magnified histograms of k_ep and ADC.

Table 2 displays the AUCs, as well as the bootstrapped 95% CIs of the AUCs, for seven different parameter combinations (rows) and four different analyses (columns). Considering the first column of the table, k_ep and ADC outperformed the other individual parameters, though not significantly so as evidenced by the overlapping 95% CIs. When k_ep and ADC are combined in the regression model, the resulting AUC (0.82) and 95% CIs (0.67–0.98) indicate a substantial improvement over the single measures though, again, not significantly so. Using all five imaging parameters in the regression model (bottom row of the first column) results in a decrease in the AUC (0.73) over that achieved by combining only k_ep and ADC.

Table 2.

The AUCs of Different Parameters Using Four Different Analyses

	ROI		Voxel		ROI + Voxel		ROI + Voxel + Clinical Data
	AUC	95% CI	AUC	95% CI	AUC	95% CI	AUC	95% CI
kep	0.70	[0.49–0.96]	0.72	[0.53–0.91]	0.72	[0.52–0.91]	0.75	[0.60–0.90]
ADC	0.77	[0.40–1.00]	0.75	[0.62–0.90]	0.85	[0.71–1.00]	0.84	[0.55–1.00]
Ktrans	0.68	[0.47–0.93]	0.66	[0.47–0.85]	0.71	[0.52–0.90]	0.77	[0.62–0.93]
ve	0.49	[0.29–0.71]	0.42	[0.22–0.64]	0.70	[0.52–0.89]	0.74	[0.56–0.93]
vp	0.68	[0.39–0.96]	0.62	[0.33–0.96]	0.71	[0.52–0.90]	0.77	[0.64–0.91]
kep and ADC	0.82	[0.67–0.98]	0.75	[0.60–0.92]	0.87	[0.77–0.98]	0.81	[0.67–0.93]
kep, ADC, Ktrans, ve, and vp	0.73	[0.49–0.95]	0.72	[0.51–0.96]	0.77	[0.58–0.98]	0.81	[0.65–0.97]

The second and third columns display the AUC values when the voxel level data are used and when both the ROI and voxel level data are used to populate the logistic model, respectively. Finally, the rightmost column summarizes the results of combing the ROI level data, voxel level data, and select (available) clinical data into the regression model. Note that the combined ROI and voxel analysis yielded better AUCs for all parameters than either ROI- or voxel-based analyses. The best AUC of 0.87 was obtained when both the ROI and voxel level data were used for the combination of k_ep and ADC. In general, there is a substantial improvement in predictive ability of individual parameters as the ROI, voxel, and clinical data are used. However, as indicated by the overlapping 95% CIs, there are only a small number of entries that are statistically different. The combination of ROI, voxel level k_ep, and ADC data provides an optimal balance of model complexity and ROC performance. In addition, by further including K^trans, v_e, and v_p in the regression model, the AUC values decrease with the increased number of parameters involved in the model.

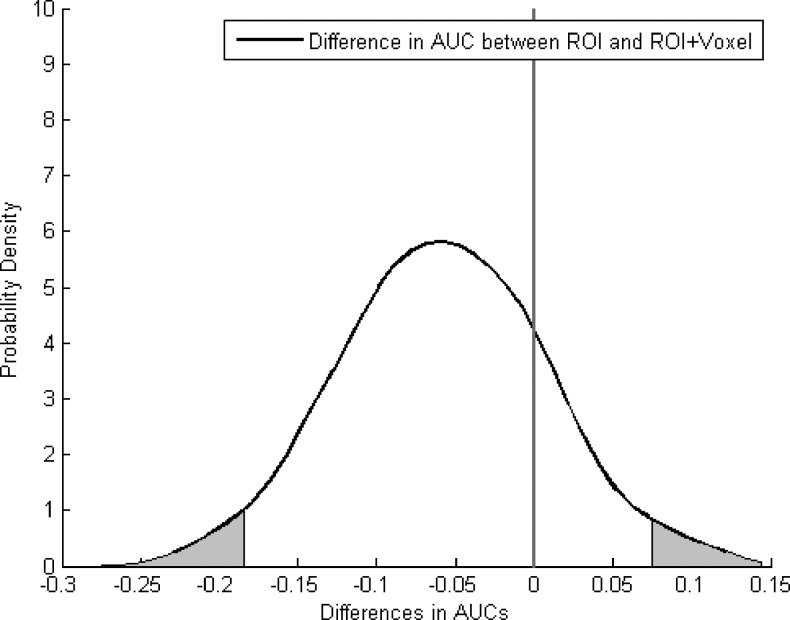
Figure 5 displays the density distributions of the AUC differences between the ROI and the combined ROI and voxel analyses for the combination of k_ep and ADC. Specifically, 500 AUCs were generated through the boot strap method for the analysis, and the AUC differences between the two analyses were calculated; the figure displays the probability density functions, which described the density distributions of the AUC differences. The 95% CIs of the AUC differences were (-0.18–0.075). For clarity, the areas outside the 95% CIs are shadowed for the distribution. Note that the shadowed areas on the right side are close to zero (the reference line), indicating a moderate trend approaching significance between the ROI and the combined ROI and voxel data analyses. [CIs (95%) that lie completely to the left or right of the zero mark would indicate a significant difference between two methods at the P < .05 level.] When these data are combined with those in Table 2, they support the selection of the logistic model that includes k_ep and ADC as the most preferable, as they combine the desirable features of being the most parsimonious approach with the greatest ROC performance.

Figure 5.

The figure displays the density distribution of the AUC differences between the ROI analysis and the combined ROI and voxel analysis for the combination of k_ep and ADC. The areas outside the 95% CIs are shadowed for the distribution. The 95% CIs of the AUC differences were (-0.18–0.075), indicating a moderate trend approaching significance.

Discussion

To the best of our knowledge, this is the first report to indicate that integrating spatial information characterizing intratumoral heterogeneity improves the ability of quantitative MRI to predict the response of breast tumors to NAC. A longitudinal registration technique was employed to spatially align parametric maps obtained at the pre-one cycle and post-one cycle of NAC time points, thereby enabling subsets of voxels to be selected on the basis of their changes in parameter values. By incorporating the ROI and voxel level data into the LRR model, the overall predictive ability was quite strong (AUC = 0.87). It is important to note that the methodology presented here is readily generalizable to include other data types including, for example, other imaging modalities or genomic data.

There are some limitations in the present study. First, although these initial results are encouraging, future work needs to investigate the proposed approach on a larger cohort of patients. Second, the temporal resolution of 16 seconds is not optimal for characterizing the AIF, and this can confound a quantitative DCE-MRI analysis. (This temporal resolution was chosen as a compromise between temporal and spatial resolution and field-of-view coverage; details on this technical point are available in [29].) Third, the NAC regimens used in this study were left to the discretion of the treating physicians and were therefore quite varied. It is certainly possible that the imaging biomarkers could vary both by the biology of the disease and by the agents used. A final limitation in the approach outlined here concerns the registration method itself. It is important to note that, although previous studies [25–27,45] have shown that longitudinal registration of the breast MRI data can be done accurately and robustly, it remains quite challenging. The improved AUCs also indicated the importance of longitudinal registration and thus warrant further investigation. One difficulty of the algorithm is that, for some data sets, it is not straightforward to find an optimal registration parameter setting (e.g., the number of radial basis functions, the number of resolution levels, or the weight of the constraint term) to deform the healthy tissues while simultaneously constraining the tumor to minimize its distortion. Once the registration is complete, the optimal approach for analyzing the aligned parametric maps has also yet to be established; in particular, the method proposed in the present study may simply not be the best. Hence, future work includes the investigation of different approaches to analyze the aligned parameter maps.

In conclusion, our study shows that tumor heterogeneity contains important information related to treatment response and should be included with ROI level data to maximize the ability of quantitative MRI to predict the response of breast tumors to NAC.