A Bayesian Approach for the Cox Proportional Hazards Model with Covariates Subject to Detection Limit

Abstract

The research on biomarkers has been limited in its effectiveness because biomarker levels can only be measured within the thresholds of assays and laboratory instruments, a challenge referred to as a detection limit (DL) problem. In this paper, we propose a Bayesian approach to the Cox proportional hazards model with explanatory variables subject to lower, upper, or interval DLs. We demonstrate that by formulating the time-to-event outcome using the Poisson density with counting process notation, implementing the proposed approach in the OpenBUGS and JAGS is straightforward. We have conducted extensive simulations to compare the proposed Bayesian approach to the other four commonly used methods and to evaluate its robustness with respect to the distribution assumption of the biomarkers. The proposed Bayesian approach and other methods were applied to an acute lung injury study, in which a panel of cytokine biomarkers was studied for the biomarkers’ association with ventilation-free survival.

INTRODUCTION

Biomarkers have been increasingly and widely used in clinical practice in recent years for disease diagnosis and prognosis based on their underlying pathological and physiologic mechanisms [1]. In these applications, biomarkers are used either to identify a subgroup of a study population or predict a disease outcome [2]. While some biomarkers are involved in the early development of a condition and thus might provide diagnoses [3, 4], others are associated more with disease outcome and are considered prognostic of patient survival [5]. For example, a nationwide cohort study revealed that a traditional serum biomarker leukotriene pathway agent was associated with the breast cancer; p53 expression in primary tumors was an independent prognostic factor that influenced relapse-free survival in stage II patients, and lack of Bcl-2 expression was independently associated with a poor prognosis among stage III patients [6]. Another large cohort study identified protein biomarker CTNNB1 to be associated with improved survival in colorectal cancer [3]. Discrepancies between studies on the same biomarkers have been observed [7], however, and a variety of problems have been cited as the cause of these discrepancies including inappropriate statistical analyses [8]. As a result, in 2005, REporting recommendations for tumor MARKer prognostic studies (RE-MARK) was published [7]. One of the goals of these guidelines was to improve the usefulness of the results from clinical prognostic studies and enhance the comparability between studies.

Detection limit (DL) is a measurement error problem with bounded error [9, 10]. In particular, DL is a measurement problem in which the actual biomarker values are immeasurable either below the lower detection limit (LDL) or above the upper detection limit (UDL) of laboratory instruments. These values are often called non-detects. The applicability of biomarkers in clinical practice has been compromised in the presence of DL as inappropriate use of statistical methods when dealing with DL may lead to biased conclusions and inconsistent results [11]. Simple methods, such as deletion and single replacement with one-half of the LDL, were often used to fill in the immeasurable values. Some sophisticated methods have been proposed to replace the missing values based on the distribution of the observed values. Regression on Order Statistic (ROS) is one such approach; however, its usage is severely limited because its goal is to estimate summary statistics [12]. More recently, vast researches have been conducted in DL and its related areas. For example, an MLE-based approach has been proposed to handle both binary [13] and continuous outcomes [14] with an independent variable subject to DL; a semiparametric Bayesian method was proposed under proportional hazards model for interval censored data with frailty effects [15]; a semiparametric imputation approach has been developed for covariates subject to DL, in which the conditional quantiles of the censored covariates are assumed to be linear in the observed variables; [16, 17] have proposed a Bayesian approach to logistic regression parameter estimation with exposure variables subject to DL; [18] discussed the full Bayesian estimation of joint models when time dependent covariates or outcomes are submitted to lower detection levels. These works have improved the usefulness of biomarkers in the development of diagnostic and prognostic models. However, in general there remain a few problems to be solved. To our knowledge, many of the medical researches involving Cox proportional hazards models with DL biomarkers still relied on simple naïve methods like deletion or single replacement to obtain the estimates of hazard ratio (HR), mainly due to the computational burden of advanced methods and lacking of user-accessible programs. Given promising prognostic value and increased clinical application of biomarkers in disease outcome prediction, a survival model that is capable of handling DL is desired. In this paper, we formulated the time-to-event outcome using the Poisson density with counting process notation, and provided straightforward JAGS/OpenBUGS programs to implement the method. In the current clinical practice, a panel of biomarkers, rather than a single biomarker, is often considered for disease diagnosis/prognosis [19], and therefore, we aim to develop a method to handle simultaneous DL issues on multiple biomarkers.

The paper is organized as follows. In the Motivating Study Section, we provide a detailed description of the motivating study which illustrates the association between biomarkers and the survival function for patients with acute lung injury (ALI). In the Methodological Development Section, we describe the proposed Bayesian method for the cases in which single or multiple explanatory variables are subject to lower, upper, and interval DLs. In the Simulation Studies Section, we present an extensive simulation study to examine the performance of the proposed method, comparing it with four existing methods. We revisit the motivating study in the section of Analysis of the Acute Lung Injury Study, followed by the Discussion Section.

MOTIVATING STUDY

With the goal of developing a prognostic model for Acute Lung Injury/Acute Respiratory Distress Syndrome (ALI/ARDS), the researcher measured 8 cytokine biomarkers that reflect the complex pathogenesis of ALI/ARDS in baseline plasma from 549 patients [20]. The patients were enrolled in the National Heart, Lung, and Blood Institute (NHLBI) ARDS Clinical Trials Network clinical trial of two different levels of positive end-expiratory pressure [20]. The collected biomarkers included markers of inflammation (IL6, IL8, and TNFR1), lung and systemic endothelial activation and injury (VWF), lung epithelial injury (SP-D), adhesion molecules (ICAM.1), and activation of coagulation and inhibition of fibrinolysis (protein C, and PAI-1). Among these biomarkers, IL8 had 35% of values that were below the DL threshold of 2.5 pg/ml of the enzyme-linked immunosorbent assay. Collected clinical data include age, cause of ALI/ARDS, severity of illness scoring (APACHE III), ventilator parameters, hemodynamic data, and alveolar-arterial O₂ difference (A-a O₂). Cox proportional hazards models were used to investigate the association between the biomarker levels and time to ventilation removal (VR).

METHODOLOGICAL DEVELOPMENT

Let T_i and C_i represent the failure and censoring times, respectively, for the ith patient, where i = 1,⋯,n. Let X_i be the transformed biomarker covariates subject to detection limit with a known transformation function g(·) and Z_i be the additional covariates. Observed times to event are denoted by Y_i = T_i ∧ C_i, and the observed event indicators are denoted by Δ_i = I(T_i ≤ C_i) where a ∧ b = min(a, b) and I(A) is an indicator function taking the value 1 when condition A holds and 0 otherwise.

In this paper, we consider the Cox proportional hazards model [21] given by

$${\lambda }_i(t|Z_i,X_i)={\lambda }_0(t)\text{exp}({\beta }^T{X}_i+{\gamma }^T{Z}_i)dt$$ (1)

where λ(t|Z,X) is the conditional hazard function of time-to-event given the covariates, λ₀(t) is an unknown baseline function, β is a q×1 vector of regression coefficients corresponding to transformed biomarker covariates X_i, and γ is a p×1 vector of regression coefficients for other additional covariates Z_i.

Single Covariate Subject to DL

We first consider the case of one covariate subject to DL (q=1) and then generalize this method to the scenario with multiple covariates subject to DL (q>1) in the next section. With q=1, we assume the lower DL for the transformed biomarker measurement x is ld. The observed data are

$$D_{\mathit{\text{obs}}}=({\gamma }_i,{\delta }_i,x_i^{*}=(x_i\text{vld}),r_i=I(x_i\le ld),z_i,i=1,2,\cdots ,n),$$

where a ∨ b = max(a, b). The likelihood function of the observed data is

$$L={\prod }_{i=1}^n{[L{y}_i(y_i|x_i,z_i,\beta ,\gamma )f(x_i^{*}|z_i,\phi )]}^{(1-r_i)}{[{\int }_{g(o)}^{ld}L{y}_i(y_i|x,z_i,\beta ,\gamma )f(x|z_i,\phi )dx]}^{r_i}$$ (2)

where Ly_i(·) is the likelihood of (y_i, δ_i) and φ is a vector of regression coefficients in the biomarker model $f(x_i^{*}|z_i,\phi )$, both will be discussed later. Note that the lower limit of the integration in (2) is g(0) because biomarker measurements have support (0,∞), and x is the transformed biomarker measurement with transformation function g(·).

Extending the proposed method to interval DL (both lower and upper DLs) is straightforward. We assume the upper DL for x is ud and denote the observations as

$$D_{\mathit{\text{obs}}}=(y_i,{\delta }_i,x_i^{*}=(x_i\vee 1\mathrm{d}\wedge \text{ud}),r_{il}=I(x_i\le ld),r_{iu}=I(x_i\ge ud),z_i,i=1,2,\cdots ,n)$$

The likelihood function of the observed data for the ith subject now becomes

$$Li=\prod _{i=1}^n{[L{y}_i(y_i|x_i,z_i,\beta ,\gamma )f(x_i^{*}|z_i,\phi )]}^{(1-r_{il})(1-r_{iu})}{[{\int }_{g(0)}^{ld}L{y}_i(y_i|x,z_i,\beta ,\gamma )f(x|z_i,\phi )dx]}^{r_{il}(1-r_{iu})}{[{\int }_{ud}^{g(\infty )}L{y}_i(y_i|x,z_i,\beta ,\gamma )f(x|z_i,\phi )dx]}^{(1-r_{il})r_{iu}}$$ (3)

Multiple Covariates Subject to DL

When there are two or more covariates subject to DL, f(x|z) in (2) becomes a multivariate density function. A simple extension may be to model f(x|z) through a multivariate Gaussian distribution; however, the normality assumption may not hold for all biomarkers subject to DL. Therefore, following [22, 23], we model the joint distribution of the biomarkers using a series of one dimensional conditional densities as

$$f(x|z,\phi )=f(x_{i1}|z_i,x_{i2},\cdots ,x_{iq},{\phi }_1)f(x_{i2}|z_i,x_{i3},\cdots ,x_{i3},\cdots ,x_{iq},{\phi }_2)\cdots f(x_{iq}|z_i,{\phi }_q),$$ (4)

where φ_k is the vector of unknown parameters in the distribution of f(x_ik|z_i, x_i,k+1,⋯,x_iq, φ_k), and φ = (φ₁, ⋯, φ_q). The advantage of (4) is that it allows for a more flexible model specification for the joint distribution of f(x|z), and it is especially useful when the biomarkers follow different distribution functions. Although the joint model depends on the order of conditioning, [22, 23], among others, have shown in the missing data literature that estimates are robust with respect to the order of conditioning; however, by no means should one discount the importance of carrying out sensitivity analysis for the order of conditioning.

When there are q biomarkers subject to lower DL, the observed data are

$$D_{\mathit{\text{obs}}}=(y_i,{\delta }_i,x_{i1}^{*}=(x_{i1}\vee l{d}_1),r_{i1}=I(x_{i1}\le l{d}_1),\cdots ,x_{iq}^{*}=(x_{iq}\vee l{d}_q),r_{iq}=I(x_{iq}\le ld),z_i,i=1,2,\cdots ,n),$$

where ld_k is the lower DL of x_k. Let x_i,−j = (x_i1, ⋯, x_i,j−1, x_i,j+1, ⋯, x_iq) denote all the biomarkers from the ith subject except the jth biomarker. The likelihood function of the ith observed value is

$$L_i={[L{y}_i(y_i|x_i=x_i^{*},z_i,\beta ,\gamma )f(x_i^{*}|z_i,\phi )]}^{(1-r_{i1})\cdots (1-r_{iq})}{\prod }_{j=1}^q{[{\int }_{g(0)}^{l{d}_j}L{y}_i(y_i|x_{i,-j},x,z_i,\beta ,\gamma )f(x_{i,j-1},x|z_i,\phi )dx]}^{(1-r_{i1})\cdots r_{ij}\cdots (1-r_{iq})}\cdots {[{\int }_{g(0)}^{l{d}_q}\cdots {\int }_{g(0)}^{l{d}_1}L{y}_i(y_i|x,z_i,\beta ,\gamma )f(x|z_i,\phi )d{x}_1\cdots d{x}_q]}^{r_{i1}\cdots r_{iq}}$$ (5)

where f(x_i|z_i, φ)is defined in (4)

Counting Process Likelihood for Posterior Computation and Inference

For purposes of computation and ease of extending the proposed method, we will formulate the likelihood of (y_i, δ_i) using the counting process in this section. In particular, for subject i, we observe counting process N_i(t), which counts the number of failures occurred up to time t. Following [24], the Cox proportional hazards model in (1) can be formulated using the counting process notation introduced by [25] and is given by

$$E\{d{N}_i(t)|{ℱ}_{t-},\mathit{Z},\mathit{X}\}={\lambda }_0(t)\text{exp}({\mathit{\beta }}^{\mathit{T}}{\mathit{X}}_{\mathit{i}}+{\mathit{\gamma }}^{\mathit{T}}{\mathit{Z}}_{\mathit{i}})dt$$ (6)

where ℱ_t− represents all the past history just before time t, and dN_i(t) is the increment of N_i(t) over the small time interval [t, t+dt]; dN_i(t) = 1 if subject i is observed to fail during the time interval [t, t+dt], and dN_i(t) = 0 otherwise. The observed data from n subjects can be rewritten using the counting process given by {N_i(t)I(t ≤ Y_i),Y_i,R_i,Z_i,C_i}, i = 1,2,⋯,n where ${\mathit{X}}_i^{*}=({\mathit{x}}_{i1}^{*},\cdots ,{\mathit{x}}_{iq}^{*})$ and R_i = (r_i1,⋯r_iq). Under the standard non-informative censoring assumption, the counting process likelihood of {N_i(t)I(t ≤ Y_i),Y_i} given (X, Z_i,C_i) is

$$L{y}_i=\left\{{\prod }_{t\le Y_i}{\lambda }_i{(t)}^{d{N}_i(t)}\right\}\text{exp}\{-{\int }_0^{Y_i}{\lambda }_i(t)dt\},$$ (7)

where λ_i (t) = λ₀ (t)exp(β^TX_i + γ^TZ_i)dt.

Following [24], we can express the counting process likelihood in (7) using Poisson density as

$$L_{yi}={\prod }_{j=1}^J\mathit{\text{Poisson}}(d{N}_{ij};V_{ij}d{\mathrm{\Lambda }}_{0J}\text{exp}({\mathit{\beta }}^{\mathit{T}}{\mathit{X}}_{\mathit{i}}+{\mathit{\gamma }}^{\mathit{T}}{\mathit{Z}}_{\mathit{i}}))$$ (8)

where the notation Poisson(x; μ) is the density of a random variable x, which follows a Poisson distribution with mean μ; t₁,⋯,t_J are the unique failure times observed in the data, V_ij = 1 if subject i is at risk at time t_i. and V_ij = 0 otherwise, dN_ij = 1 if individual i fails at time t_i and dN_ij = 0 otherwise, and d∧_0j is an increment on the cumulative baseline hazard function ${\mathrm{\Lambda }}_0(t)={\int }_0^t{\lambda }_0(\mu )d\mu$.

The joint posterior density of (β,γ,d∧₀(·),(φ) based on the observed data can be written as

$$\pi (\beta ,\gamma ,d{\mathrm{\Lambda }}_0(·),\phi |D_{\mathit{\text{obs}}})\propto L\times \pi (\beta ,\gamma ,d{\mathrm{\Lambda }}_0(·),\phi ),$$ (9)

where $L={\prod }_{i=1}^n{L}_i,L_i$ is defined in (3) or (5) for the univariate or multivariate biomarkers subject DL, respectively, L_yi. is defined in (8), and π(β, γ , d∧0(·), φ) is the joint prior for (β, γ , d∧0(·), φ). In practice, we can specify the independent prior and let π(β, γ, d∧0(·), φ) = π(β)π(β)π(d∧0(·))π(φ). We can specify the non-informative prior for β, γ, and φ to minimize the influence of the prior on the posterior distribution. For the prior of d∧(·), we consider the conjugate independent increments prior suggested by [26], namely $d{\mathrm{\Lambda }}_0(t)~\mathit{\text{Gamma}}(c\times d{\mathrm{\Lambda }}_0^{*}(t),c)$, where $d{\mathrm{\Lambda }}_0^{*}(t)$ is a prior guess for ∧₀(t) and c controls the prior precision with small values of c corresponding to weak prior beliefs.

Selection of Biomarker Density Functions

Since the distribution of cytokine biomarker measurements is often positively skewed and fits a log-normal distribution [27, 28], a logarithmic transformation of g(·) is typically used with normality assumption for f(x|z_i,φ). A QQ-plot can be used to evaluate this assumption. When the normality assumption is violated, other parametric models, such as GLMs, can be specified for the biomarkers subject to the DL and implemented easily in WinBUGS or JAGS. On the other hand, the selection of biomarker density functions can be viewed as a special case of model comparison and be investigated via Bayes factors, model diagnostics, and goodness of fit measurements [29].

Simulation Studies

We conducted extensive Monte Carlo simulations to evaluate the performance of the proposed Bayesian. We considered 18 scenarios, which included 3 distributions (normal, t₂₅, and gamma) for biomarker measurements, 3 percentages of measurements below the DL (10%, 30%, 50%), and 2 coefficients (β=0.8 for true association, and β=0 for null). In addition to a biomarker, we also simulated 2 other continuous covariates according to the motivating study. We simulated both event time and censoring time with a Weibull distribution which used pre-specified baseline hazards for event and censoring and pre-specified coefficients for the biomarker and covariates. The censoring proportions of the survival time were set to 15% throughout the simulations. For each study scenario, we considered 200 subjects and 1,000 simulations. When analyzing power change for the 9 scenarios of positive association, we used β=0.225 so that the full data analysis had 80% power to reject the null hypothesis at which the biomarker values were simulated from the log-normal distribution.

In this study, we compared the following 5 methods for their performance on the estimates of regression coefficients: (1) single replacement of non-detects with one-half of the LDL threshold; (2) case-wise deletion of non-detects; (3) regular multiple imputation (MI) method; (4) extrapolation by the ROS; and (5) the proposed Bayesian approach. Single replacement with one-half DL or $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{2}$}\right.$ is the most popular method. Deletion is simply excluding (case-wise) all the observations with values below the threshold in the analysis. MI refers to the regular multiple imputation method assuming missing at random [30]. We modified the MI procedure proposed by [31] so that the new procedure takes all aspects of uncertainty in the imputations into account [32–35]. ROS is a method which is often used in environmental science to compute summary statistics [12]. This method fits a regression line on a normal probability plot of the uncensored data, using censored values as place holders, and estimates the model parameters from the regression line, including mean and standard deviation (SD). We used the ROS-generated mean and SD to simulate values below the DL according to a truncated normal distribution. Cox regression was then used to estimate the hazard with the complete data set that combined the simulated values with the observed data. The simulation of the truncated normal distribution and the following Cox proportional hazards model were repeated C times to adjust for the uncertainty due to the simulation [36, 37]. The point estimate was the average of the C imputed data sets, and the standard error (SE) was calculated using Rubin’s rule [38]. In the simulation of the truncated data set, we used C = 10. Note that the ROS algorithm adopted here is a modified version which properly accounts for the simulation variability. The original ROS in [12] used C = 1, as the goal was to estimate summary statistics.

All computations herein were implemented using R 2.15.2, and Bayesian computation was conducted using R package R2jags. As both frequentist and Bayesian methods were considered in this paper, we evaluated the methods using bias, empirical SE, average SE, root mean square error (RMSE), and coverage probability of 95% confidence interval (CI) or Highest Posterior Density (HPD) (95% CP), as well as power for true β and type I error rate for null β.

Simulation I

This simulation evaluated the model performance model when the distribution of the biomarker measurements was correctly specified. Especially, we simulated the logarithmically transformed biomarker values from N (3.7, 1.25). All the parameter estimates were computed using a multivariable Cox proportional hazards model in which no correlation was assumed for the covariates. As in Table 1, the parameter estimates did not show much difference across the 5 methods at 10% LDL, but the difference became substantial at higher LDL fractions. The method of 1/2 DL had the largest bias and the lowest 95% CI coverage. MI and ROS also had substantial biases, large RMSEs, and poor coverage probabilities (Table 1). Although the deletion method had negligible bias, it had a larger RMSE and poorer power compared to the Bayesian method (Table 1 and Figure 1). Overall, the Bayesian method outperformed the other methods in terms of RMSE, CP, and power.

Table 1.

Estimates of log(OR) in Simulation I

P*	Method	β1 = 0.8					β1 = 0
		Bias†	ESE‡	ASE§	RMSE¶	CP(%)**	Err(%)††
0.1	Full	0.010	0.083	0.081	0.083	0.95	4.6
	Half DL	−0.037	0.080	0.078	0.088	0.92	4.6
	Deletion	0.014	0.095	0.092	0.096	0.95	4.7
	MI	0.009	0.106	0.113	0.107	0.96	3.8
	ROS	−0.031	0.084	0.087	0.089	0.93	4.6
	Bayesian	0.011	0.084	0.082	0.085	0.94	4.8
0.3	Full	0.012	0.082	0.081	0.083	0.94	6.7
	Half DL	−0.122	0.091	0.072	0.152	0.53	6.0
	Deletion	0.022	0.115	0.112	0.117	0.95	5.8
	MI	−0.025	0.167	0.158	0.169	0.93	2.7
	ROS	−0.031	0.084	0.087	0.089	0.93	4.6
	Bayesian	0.013	0.086	0.085	0.087	0.95	6.8
0.5	Full	0.010	0.082	0.081	0.083	0.95	5.3
	Half DL	−0.229	0.062	0.063	0.237	0.07	5.4
	Deletion	0.025	0.166	0.161	0.168	0.96	5.9
	MI	−0.141	0.282	0.250	0.315	0.85	3.0
	ROS	−0.152	0.078	0.096	0.171	0.64	2.3
	Bayesian	0.008	0.097	0.093	0.098	0.95	5.9

^*P is the proportion of DL

^†Bias is defined as β-β

^‡ESE is the empirical standard error

^§ASE is the average standard error

^¶RMSE is the root mean square error

^**CP is the coverage probability for 95% HPD

^††Err is the type I error rate under null hypothesis.

Figure 1.

Power Analysis for Simulation Studies.

Simulation II

We investigated the robustness of the proposed Bayesian method with respect to violation of the log-normal assumption of the biomarker measurements. We simulated the data in the same manner as in Simulation I except that the logarithmically transformed biomarker values were obtained from a heavier tailed t₂₅ distribution with mean 3.7. The study showed similar results as Simulation I. The Bayesian method still outperformed other methods for this mild misspecification of the distribution, although its coverage probability started to fall below the nominal rate with increased DL fraction (Table 2 and Figure 1).

Table 2.

Estimates of log(OR) in Simulation II

P*	Method	β1 = 0.8					β1 = 0
		Bias†	ESE‡	ASE§	RMSE¶	CP(%)**	Err(%)††
0.1	Full	0.013	0.088	0.082	0.089	0.94	5.6
	Hlf DL	−0.061	0.082	0.079	0.102	0.85	5.3
	Deletion	0.014	0.098	0.093	0.099	0.94	5.6
	MI	0.003	0.111	0.114	0.111	0.95	4.6
	ROS	−0.007	0.086	0.083	0.086	0.95	5.2
	Bayesian	0.004	0.088	0.083	0.088	0.94	5.9
0.3	Full	0.009	0.086	0.082	0.086	0.94	6.5
	Half DL	−0.193	0.067	0.068	0.205	0.20	6.0
	Deletion	0.017	0.124	0.115	0.125	0.93	5.1
	MI	−0.045	0.166	0.170	0.172	0.93	3.2
	ROS	−0.086	0.080	0.087	0.117	0.83	3.6
	Bayesian	−0.020	0.089	0.085	0.091	0.93	7.0
0.5	Full	0.010	0.083	0.082	0.084	0.95	5.5
	Half DL	−0.257	0.060	0.061	0.264	0.03	6.0
	Deletion	0.028	0.154	0.150	0.156	0.95	5.7
	MI	−0.141	0.242	0.241	0.280	0.88	2.4
	ROS	−0.214	0.072	0.091	0.225	0.32	2.2
	Bayesian	−0.039	0.090	0.090	0.098	0.91	5.8

^*P is the proportion of DL

^†Bias is defined as β-β

^‡ESE is the empirical standard error

^§ASE is the average standard error

^¶RMSE is the root mean square error

^**CP is the coverage probability for 95% HPD

^††Err is the type I error rate under null hypothesis.

Simulation III

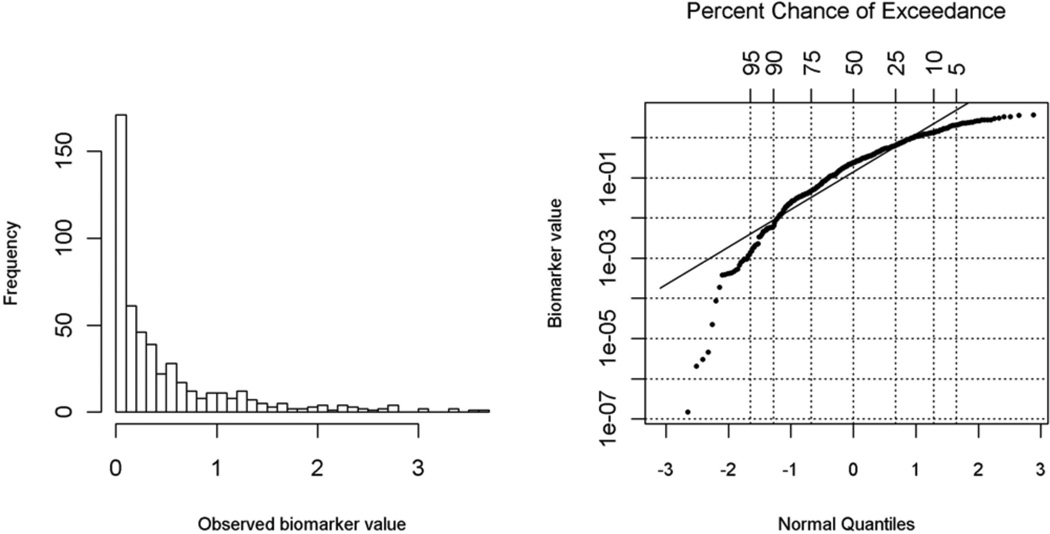
We further evaluated the proposed Bayesian method for robustness with severe misspecification of the underlying normal distribution using a highly skewed gamma distribution. We simulated the data as above, except that the logarithmically transformed biomarker was specified as a Gamma(0.5,1) distribution. For this serious misspecification, the proposed Bayesian method had increased bias and lower CP. As shown in Figure 2, the normality assumption is clearly violated judged from the QQ-plot against a normal distribution for logarithmic transformation of the DL biomarker variable in a randomly selected simulated data set. Interestingly, single replacement with the one-half DL method had very small bias, and the bias did not increase with higher DL fractions. This is because Gamma(0.5, 1) is highly positively skewed and has 10%, 30% and 50% threshold values of 0.008, 0.074, and 0.227 with corresponding half DL values of 0.004, 0.037, and 0.114, respectively. ROS, another distribution-based method, performed the worst in this setting (Table 3). Although the deletion method showed merit in this scenario, its estimates had high efficiency loss. Furthermore, as shown in Figure 3 of Section 5, the deletion method did not provide valid summary statistics, such as mean or median, which is directly related to the distribution of the DL biomarker.

Figure 2.

Histogram Plot and QQ-plot for a Randomly Selected Dataset from Simulation III.

Table 3.

Estimates of log(OR) in Simulation III

P*	Method	β1 = 0.8					β1 =0
		Bias†	ESE‡	ASE§	RMSE¶	CP(%)**	Err(%)††
0.1	Full	0.022	0.149	0.144	0.151	0.95	5.4
	Half DL	0.022	0.149	0.144	0.151	0.95	5.4
	Deletion	0.025	0.155	0.149	0.157	0.94	5.6
	MI	0.003	0.153	0.163	0.153	0.96	4.6
	ROS	−0.034	0.144	0.144	0.148	0.95	4.0
	Bayesian	−0.024	0.147	0.144	0.149	0.95	5.6
0.3	Full	0.020	0.147	0.143	0.148	0.95	4.5
	Half DL	0.023	0.147	0.143	0.149	0.95	4.6
	Deletion	0.026	0.164	0.163	0.166	0.96	4.5
	MI	−0.042	0.162	0.194	0.168	0.97	2.4
	ROS	−0.185	0.131	0.139	0.226	0.73	2.4
	Bayesian	−0.107	0.139	0.136	0.175	0.87	4.6
0.5	Full	0.021	0.143	0.143	0.144	0.95	5.2
	Half DL	0.034	0.145	0.144	0.149	0.95	4.7
	Deletion	0.034	0.197	0.188	0.200	0.95	5.3
	MI	−0.102	0.192	0.230	0.217	0.96	2.7
	ROS	−0.348	0.101	0.125	0.362	0.18	1.7
	Bayesian	−0.189	0.121	0.127	0.225	0.68	5.5

^*P is the proportion of DL

^†Bias is defined as β-β

^‡ESE is the empirical standard error

^§ASE is the average standard error

^¶RMSE is the root mean square error

^**CP is the coverage probability for 95% HPD

^††Err is the type I error rate under null hypothesis.

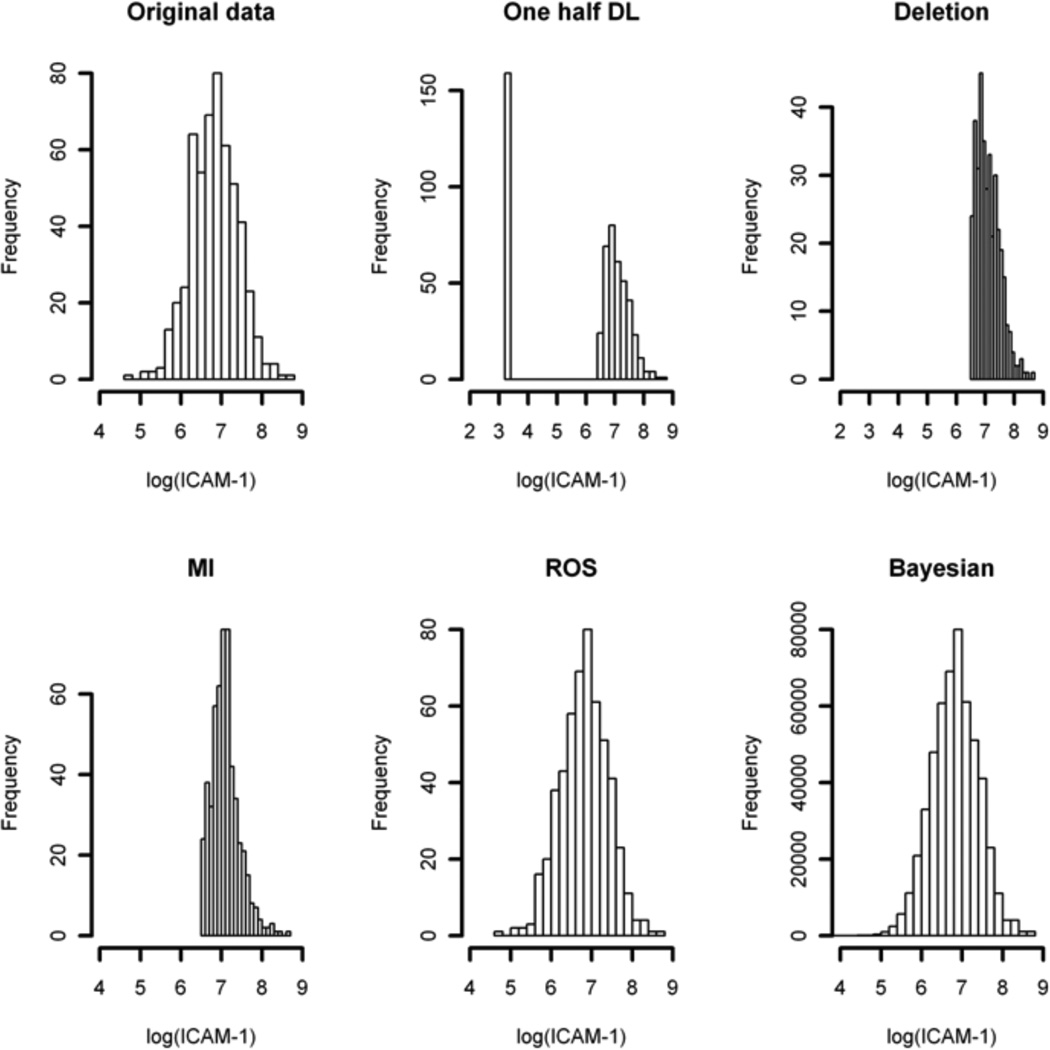
Figure 3.

Histogram Plot of log(ICAM.1) in ALI Study Completed with Imputed Values.

ANALYSIS OF THE ACUTE LUNG INJURY STUDY

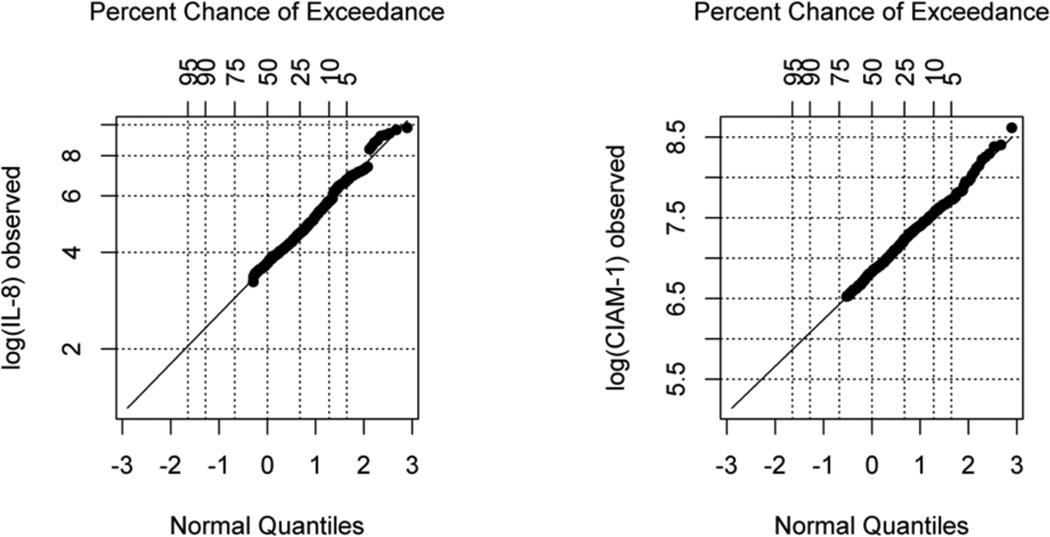
The proposed method was applied to analyze data from the acute lung injury (ALI) study introduced in the Section of motivating study. In this analysis, we are interested in the association between biomarker IL8 and time to VR, controlling for age and alveolar-arterial O₂ difference (A.a). We used the proposed Bayesian method to study the association between IL8 and VR and compared the Bayesian result with the other 4 methods. A log-normal distribution seemed reasonable based on the QQ-plot of the observed data, although 38% of the IL8 data in this study are subject to the DL (Figure 4 left panel). Trace plots were used to evaluate the convergence of the parameters (not shown due to limited number of tables and figures). Based on the Cox proportional hazards model fit with the imputed data, a moderate negative association was found in the Bayesian method for IL8 with the “hazard” of removing ventilation (HR = 0.83; 95% HPD: 0.78–0.89), suggesting the removal of ventilation was less likely for patients with higher IL8 (Single Biomarker Analysis in Table 4). The other methods yielded HR estimates ranging from 0.72 to 0.85 with larger standard error estimates compared to the Bayesian approach.

Figure 4.

QQ-plots for Logarithmic Transformation of Observed log(IL8) and log(ICAM-1) in ALI Study.

Table 4.

Log(HR) Estimate of log(IL8) (and log(ICAM.1)) in ALI Study with Sensitivity Analysis

Method	Single Biomarker Analysis* log(IL8) (α1)		Multiple Biomarkers Analysis†
			log(IL8) (β1)		log(ICAM.1) (β2)
	Estimate	SE	Estimate	SE	Estimate	SE
Half DL	−0.250	0.044	−0.241	0.044	−0.051	0.032
Deletion	−0.328	0.068	−0.322	0.073	−0.137	0.164
MI	−0.306	0.065	−0.289	0.071	−0.202	0.129
ROS	−0.158	0.033	–	–	–	–
Bayesian	−0.184	0.032	–	–	–	–
Bayesian1	–	–	−0.175	0.035	−0.160	0.100
Bayesian2	–	–	−0.173	0.033	−0.160	0.096

^*model is λ [t| log (IL8), age, A.a] = λ₀ (t) exp [α₀ + α₁ log (IL8) + α₂ age + α₃ A.a] with Bayesian method modeling f (log(IL8)|A.a, log(ICAM.1)) with linear regression model.

^†model is stated in (10) with Bayesian1 and Bayesian2 methods used the models stated in equations (11) and (12), respectively.

We also used the ALI study to demonstrate the methods in the scenario with more than one biomarker subject to DL. To this end, we truncated ICAM.1 to generate a dataset with 30% observations below DL. We also performed a sensitivity analysis to evaluate the impact of sequential conditioning of the two biomarkers subject to DL. In particular, we considered the Cox proportional hazards model

$$\lambda [t|\text{log}(IL8),\text{log}(\mathit{\text{ICAM}}.1),\mathit{\text{age}},A.a]={\lambda }_0(t)\text{exp}[{\beta }_0+{\beta }_1\text{log}(IL8)+{\beta }_2\text{log}(\mathit{\text{ICAM}}.1)+{\beta }_3\mathit{\text{age}}+{\beta }_{4}A.a]$$ (10)

and assume

$$f(\text{log}(IL8),\text{log}(\mathit{\text{ICAM}}.1)|\mathit{\text{age}},A.a)=f(\text{log}(IL8)|\mathit{\text{age}},A.a,\text{log}(\mathit{\text{ICAM}}.1))f(\text{log}(\mathit{\text{ICAM}}.1)|\mathit{\text{age}},A.a),$$ (11)

or

$$f(\text{log}(IL8),\text{log}(\mathit{\text{ICAM}}.1)|\mathit{\text{age}},A.a)=f(\text{log}(\mathit{\text{ICAM}}.1)|\mathit{\text{age}},A.a,\text{log}(IL8))f(\text{log}(IL8)|\mathit{\text{age}},A.a)$$ (12)

for the joint distribution of IL8 and ICAM.1. Figure 3 shows the histograms of log(ICAM.1) that combine the observed and imputed values of each method, as well as the full original data. Only the ROS and Bayesian methods yielded distributions that are close to the original data. Recall that the ROS method did not provide valid estimates and inferences for the regression coefficient of the DL biomarker in the previous simulation studies. This observation is not surprising as the ROS method was originally proposed to estimate summary statistics, such as the mean of the biomarker, but not to estimate the regression coefficient of the DL biomarker. The log-normal assumption for ICAM.1 was evaluated by QQ-plot of the observed data (Figure 4, right panel). Table 4 shows that the Bayesian HR estimates are robust to the order of the sequential conditioning (HR = 0.84 with 95% HPD 0.78–0.90 in Bayesian1 versus HR = 0.84 with 95% HPD 0.79–0.90 in Bayesian2, Multiple Biomarker Analysis in Table 4). ROS estimates were left in blank in Table 4 because the NADA package in R only handles single biomarker subject to DL.

DISCUSSION

This article proposes a general Bayesian approach for the Cox proportional hazards model with explanatory measurement variables subject to DL. We focused on the Cox proportional hazards model as it is the most widely-used model for survival analysis. The validity and application of the proposed approach do not rely on the proportional hazards assumption of the Cox model, thus, generalizing the method to other time-to-event models and incorporating a variety of techniques in Bayesian inference and diagnostics are straightforward [29]. With the counting process notation, we can extend our method to the Cox model with time-dependent covariates and random effect (frailty) models for multiple event time data, among others. The JAGS code in the Appendix can be easily modified to incorporate the extension.

The proposed Bayesian method performed well when biomarker measurement distribution was correctly specified or mildly misspecified as shown in the motivating example and Simulations I and II. However, the proposed Bayesian method was not robust to severe misspecification of the underlying distribution as shown in Simulation III. Our study demonstrates the importance of an appropriate specification of DL variable distribution in improving the model performance. The QQ-plot approach or model selection criteria such as deviance information criterion can be used to guide the distribution specification in this setting. When the normality assumption is violated, other parametric models can be specified for the biomarkers subject to the DL and implemented easily in JAGS or OpenBUGS by modifying the example programs given in the Appendix. If the parametric distribution assumption is reasonable, the proposed Bayesian approach can yield valid and efficient inference with joint posterior modeling for covariates with nondetects and an outcome variable. Furthermore, in order to cope with the challenges of the common practice of the multiple biomarker approach in disease outcome prediction [19], we extended the proposed Bayesian method to the case of multiple biomarkers subject to the DL through a sequence of conditional distributions. In this situation, a sensitivity analysis needs to be considered to access the effect of the order of conditioning on the biomarkers.

APPENDIX.

JAGS code is provided below. Centered values are used in continuous variables.

     data
     {
        for(i in 1:N) {
          for(j in 1:T) {
            Y[i,j] <- step(obs.t[i]-t[j]+eps)
            dN[i,j] <- Y[i,j]*step(t[j+1]-obs.t[i]-eps)*fail[i]
            }
     }
}
model
{
        for(j in 1:T) {
          for(i in 1:N) {
            dN[i,j]~ dpois(Idt[i, j])
            Idt[i,j] <- Y[i,j]*dL0[j]*exp(beta*(Z[i]-
            Z.c)+beta2*(age[i]-age.c)
                    +beta3*(il8[i]-il8.c))
            }
            dL0[j] ~ dgamma(mu[j],c)
            mu[j] <- dL0.star[j]*c
          }
          for(i in 1 :N) {
            cens.il8[i] ~ dinterval(logLDL,il8[i])
            il8[i] ~ dnorm(mu.il8[i],tau)
            mu.il8[i] <- alpha0+alpha2*(Z[i]-
            Z.c)+alpha3*(age[i]-age.c)
          }
            c <- 0.001
            r <- 0.1
            for (j in 1 :T) {
          dL0.star[j] <- r*(t[j+1]-t[j])
          }
     }