Abstract
We review the class of inverse probability weighting (IPW) approaches for the analysis of missing data under various missing data patterns and mechanisms. The IPW methods rely on the intuitive idea of creating a pseudo-population of weighted copies of the complete cases to remove selection bias introduced by the missing data. However, different weighting approaches are required depending on the missing data pattern and mechanism. We begin with a uniform missing data pattern (i.e., a scalar missing indicator indicating whether or not the full data is observed) to motivate the approach. We then generalize to more complex settings. Our goal is to provide a conceptual overview of existing IPW approaches and illustrate the connections and differences among these approaches.
Keywords: missing data, inverse probability weighting, missing at random, missing not at random, monotone missing, non-monotone missing
1. Introduction
Interest in the use of secondary healthcare databases (e.g., administrative claims, electronic health records, EHR, cancer registries) for medical research is increasing, partially because these data are readily available, relatively inexpensive to access, and cover large representative populations. However, these databases are collected for non-research purposes. For example, administrative and medical claims databases are assembled for the purposes of administering, billing, and reimbursing healthcare services. Moreover, patients in clinical practice settings are not monitored as closely as those in clinical trials. In consequence, a substantial fraction of the needed data is missing for some subjects. These data issues pose analytic challenges and raise validity concerns.
By design, each of these secondary databases may contain only a subset of the variables of interest. For example, administrative claims data contain information on healthcare insurance membership, drug coverage, healthcare utilizations (i.e., diagnosis and procedure codes), and medication dispensing records. But more detailed clinical information (e.g., BMI, vital signs, laboratory tests results) are recorded in EHR. For cancer patients, the cancer stage and histology information are recorded in cancer registries. As a consequence, systematic missing data occurs for some study participants for whom the data in certain databases are unavailable. Even for those with linked databases, missing data may still occur for reasons such as missed office visits, loss to follow-up, switch of healthcare systems, and coding errors. Thus, failure to appropriately handle missing data may lead to inefficient or even invalid use of available data sources.
The simplest and most commonly used method to deal with missing data is the complete case approach in which standard analyses are applied to subjects with complete data on relevant variables. However, this analysis is biased unless the complete cases are representative of the study population (i.e., the data is missing complete at random, MCAR). This MCAR assumption rarely holds in medical applications.1
More advanced statistical methods have been developed in the past decades to deal with missing data under less restrictive missing data mechanisms 2, i.e., missing at random (MAR) and missing not at random (MNAR). MAR means the probability of missingness does not depend on unobserved elements conditional on observed data.3 MNAR indicates settings in which neither MCAR nor MAR holds. In this paper, we review a class of approaches for missing data - the inverse probability weighting (IPW) approaches. The intuitive idea is to create weighted copies of the complete cases to remove selection bias introduced by missing data processes. The weighting idea originates in the survey sampling literature.4 It has been further generalized by Robins, Rotnitzky, and others to address a variety of important issues such as confounding bias in observational studies and bias due to missing data.5–8 Alternatives to IPW include parametric likelihood inference 9–11, parametric Bayesian inference 12–14, and parametric multiple imputation 15–17 inference.
We introduce and illustrate the class of IPW approaches for three missing data patterns, uniform missingness, monotone missingness, and non-monotone missingness. For each pattern, we consider both MAR and MNAR mechanisms. We begin with relatively simple scenarios, and then generalize to more complex settings. Due to space limitations, we do not dwell on mathematical detail but refer the interested readers to the original journal articles or to the books by Tsiatis or van der Laan and Robins.18,19
The paper is organized as follows. In Section 2, we introduce the notation and models needed to formalize the missing data patterns and mechanisms we consider. We also introduce four motivating examples. In Section 3, we motivate the weighting approaches by demonstrating the bias in the complete case approach when MCAR does not hold. In Sections 4, 5, 6, we introduce weighting approaches for our three missing data patterns. We conclude with a discussion.
2. Models and notations
We let denote the full data on the n study subjects, where the p-dimensional vector Wi = (W1,i,…,Wp,i)T denotes the variables that are always observed for each subject i and the q-dimensional vector Vi = (V1,i,…,Vq,i)T denotes the variables that are subject to missingness. We let Ri = (R1,i,…,Rq,i)T denote the vector of missing indicators for subject i where the sth element Rs,i (1 ≤ s ≤ q) equals 1 if Vs,i is observed, and 0 otherwise. Let V(Ri),i denote the observed components of Vi. Let denote the observed data for subject i and let Lmis,i = V(1−Ri),i denote the unobserved components of Vi. Here 1 denotes a vector of 1’s. This notation can be used to represent a wide class of missing data patterns. For example, in a missing outcome model, W represents a vector of covariates and V is the outcome of interest Y. The parameter of interest might be the marginal outcome mean E[Y] or the coefficients β in an outcome regression model E[Y | W; β]. In missing data models with missing outcome and covariates, W would represent the covariates that are always observed and V would include both the outcome of interest and the covariates that are subject to missingness.
Throughout we assume that (Wi, Vi, Ri), i = 1,…,n are independent and identically distributed random vectors. We assume the parameter of interest β* is the unique solution to the equation E[M(Wi, Vi; β*)] = 0, where M(Wi, Vi; β) is a known m-dimensional function of the full data (Wi, Vi) and a parameter β, β* is the true value of β, and the expectation is under the distribution of (Wi, Vi). Thus M(Wi, Vi; β) is an unbiased estimating function for β*. Here β* is a functional of the distribution of the full data (Wi, Vi).
We consider the following three missing data patterns: uniform missingness, monotone missingness, and non-monotone missingness. The weighting approach applies equally to all. However, its implementation is much more complicated for non-monotone missing data patterns. We will start with a simple uniform missing pattern to illustrate and motivate the basic idea.
Missing pattern 1: uniform missing data, i.e., R1 = ··· = Rq = R. Under uniform missingness, either the entire vector Vi is observed for subject i or it is completely missing. This pattern often occurs when information is extracted from multiple data sources. For example, administrative claims data contain information on basic demographics (age, gender), healthcare utilizations, and medication dispensing records. However, more detailed clinical information such as vital signs and lab test results would be available only for a subset of the study participants with linked EHR data.
Motivating example 1: Consider a hypothetical study evaluating the 1-year incidence rate of heart disease among new users of non-steroidal anti-inflammatory drugs. Data are extracted from a health insurance administrative claims database which contains information on medication dispensing records and disease diagnosis history. The indicator variable V = Y indicates whether heart disease occurred during the 1-year follow-up period after drug initiation. Let β* = E[Y]. Then M(Y ; β) is Y − β. The outcome will be missing in participants who dis-enroll from the insurance plan during the follow-up period. The vector of covariates W includes demographics (age, gender), geographic region, geographically derived socioeconomic status, and comorbidity conditions.
Missing pattern 2: monotone missing data. Under monotone missingness, if the sth element (Rs = 0) of Vi is missing then all subsequent elements are missing (Rt = 0 for any s < t ≤ q). This pattern occurs frequently in longitudinal studies with repeated measurements in which subjects who drop out of the study never re-enter. Then Vs might denote the data that were to be collected at the sth planned clinic visit. Even if some subjects return after missing one or more visits, one can choose to make the data “monotone” for purposes of data analysis by choosing to ignore in the analysis any data recorded subsequent to a missing visit. Note uniform missing data is actually a special case of monotone missing data.
Motivating example 2: Consider an observational study to compare the effects of two anti-hypertensive agents (e.g., angiotensin-converting enzyme inhibitors and beta-blockers) on reducing blood pressure (BP) level among incident users. The study participants were identified using claims and EHR data. Then W contains the treatment indicator and some baseline covariates (e.g., age, sex, and comorbidity conditions). The vector V contains two elements; V1 records the baseline BP and V2 = Y records the BP at the end of a 12-month follow-up period. The baseline BP V1 is incomplete as some patients do not have EHR data available or did not have their BP measured during the baseline period. Similarly, some subjects have V2 = Y missing. We decide to make the data “monotone” by ignoring the data on V2 for subjects missing V1. Suppose we are interested in the coefficient β in the regression model E[Y | W, V1; β] = b(W, V1; β) = (WT, V1)β. We would take .
Missing pattern 3: non-monotone missing data; non-monotone missingness refers to any missing data pattern that is not monotone. Thus we may have Rt =1 but Rs = 0 for some subjects and Rt = 0 but Rs =1 for others. This is the most complicated missing data pattern. We consider two motivating examples for this pattern.
Motivating example 3: Consider a regression analysis with missing covariates. Suppose we are interested in identifying predictors of episodes of exacerbation for children with persistent asthma. The study cohort of children with persistent asthma was identified using healthcare claims data. The vector W, ascertained from claims data, includes data on demographic characteristics and a binary outcome encoding 2 or more ER visits for asthma during a 12-month study period. Surveys were mailed to parents to obtain data on a baseline asthma severity score (V1), household income (V2), and a measure of the parents’ expectation on child functioning with asthma (V3). Parents may answer none, one, two, or three of the three questions. This missing pattern is non-monotone. We are interested in the regression parameter β* in a logistic regression model regressing the outcome on potential predictors. The estimating equation M(W, V; β) is the score function for β.
Motivating example 4: Consider a longitudinal follow-up study with repeated measurements of BP at three time points, s =1,2,3. As before, W contains the treatment indicator and baseline covariates (e.g., age, sex). Let Vs,i indicate the BP measured at the sth time point and Vi = (V1,i, V2,i, V3,i)T. Unlike in example 2, we do not ignore subsequent data on subjects missing V1 or V2. Thus this missing pattern is non-monotone. We are interested in the mean of Vi, β* = E[Vi]. Thus M(W, V; β) = V − β.
For each missing pattern, we consider both MAR and MNAR data generating processes.3 Data are said to be MAR if the conditional missing probabilities given the full data do not depend on the unobserved components of V, i.e.,
| (1) |
In the special case of MCAR, P(Ri = r | Wi, Vi) is constant. Let γ denote the parameters governing the missing data process and θ denote the parameters governing the distribution of the full data L = (W, V), and assume they are variation independent. Then under MAR, the likelihood f(Oi, γ, θ) of the observed data factors into a component Pr(Ri = r | Lobs,i; γ) depending on γ alone and a component f(Lobs,i; θ) depending on θ alone. Thus MAR is referred to as ignorable missingness because the missing data process can be “ignored” in likelihood-based inference on a parameter β* that are functions of the parameters θ governing the marginal distribution of the full data L. The IPW approach takes a different perspective than likelihood-based approaches by using estimates of the missing data process to derive valid inferences on the parameter of interest β*.
When MAR fails to hold, the missing data mechanism is said to be MNAR or nonignorable, i.e., the missing probabilities depend on unobserved components of V conditional on observed data. In this setting, the parameter of interest is typically unidentifiable unless additional assumptions on the missing data process are imposed. These assumptions usually are investigator specified and cannot be empirically tested when the full data model is nonparametric. Therefore, it is a common practice to conduct a sensitivity analysis in which we vary these additional assumptions over a plausible range and examine how inferences on β* change. As we will show next, weighting approaches in MAR settings can be naturally extended to MNAR settings by specifying a selection bias function to quantify the residual association of the missing probabilities and unobserved components of V after adjusting for observed data. Sensitivity analysis can then be conducted by varying the parameters in the selection bias function and/or the functional form.
We let πi(Wi, Vi, r) denote the conditional missing probability P(Ri = r | Wi, Vi). Throughout we assume that P(Ri =1 | Wi, Vi) > 0 with probability 1.
3. Why the complete case approach may be biased?
We first illustrate why the complete case approach may be biased when MCAR does not hold.10 If the full data were observed, β* could be estimated by solving
| (2) |
the empirical version of E[M(Wi, Vi; β)]. Unfortunately, when missing data exist, the solution to eq. (2) depends on unobserved components of V. Suppose E[M(Wi, Vi; β*)] = 0, but E[M(Wi, Vi; β*) | Ri = 1] ≠ 0, then if we use complete cases only and estimate β* by solving the estimating equation , it is obvious that the solution to the equation above, β̃cc, may be biased unless E[P(Ri = 1 | Wi, Vi)M(Wi, Vi; β*)] = 0, e.g., P(Ri =1 | Wi, Vi) is constant.
Heuristically, when MCAR fails to hold, the complete cases are a selected, non-random subsample of the study population. Thus inference obtained by applying standard approaches to the complete cases may be biased for β*. The IPW approach restores unbiasedness by creating a pseudo-population in which selection bias due to the missing data is removed. We next introduce the IPW methods for the three missing data patterns respectively.
4. Uniform missing pattern
A uniform missing data pattern is a pattern in which the missing indicator vector R takes only two possible values 1 = (1,1,…,1,…1)T or 0 = (0,0,…0,…0)T. Noted above, unless MCAR holds, the complete case approach is likely biased. To remove selection bias due to missing data, the IPW approach weights each subject i with complete data (Ri = 1) by the inverse of the conditional probability of observing the full data πi(Wi, Vi, 1). For illustration, we temporarily assume πi(Wi, Vi, 1) is a known function of (Wi, Vi) as is the case in studies with missingness by design (e.g., studies with two-stage sampling). Then, the simple IPW estimator β̂0 solves the following estimating equation20
| (3) |
Under regularity conditions, β̂0 is a consistent estimator of β* since
Note that the above equalities hold regardless of whether or not the missingness is ignorable (i.e., MAR or MNAR). In addition, a fully parametric model for the full data is not required. Under mild conditions, the solution to eq. (3) is a consistent and asymptotically normal (CAN) estimator of β*.20
This IPW estimator β̂0 demonstrates the fundamental principle of the weighting approach; weighted copies of complete cases remove the selection bias introduced by the missing data process. However, note eq. (3) depends only on data from complete cases. Then β̂0 is not fully efficient. To increase efficiency, we can add to the estimating equation augmentation terms. These terms depend on data from both complete and incomplete cases.
From the definition of πi(Wi, Vi, 1), it is clear that an augmentation term Ai(φ) that takes the form (I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)φ(Wi) has mean zero, where φ(Wi) is an m-dimensional vector of arbitrary functions of the always observed variables Wi. Let Di(β, φ) be . Then Di(β, φ) is mean zero at β* and the solution β̂φ to is a consistent estimator of β* under regularity conditions.21 Moreover, the asymptotic variance of β̂φ equals Γ−1 var[Di(β*, φ)]Γ−1,T where . This implies that the choice of φ affects the efficiency of β̂φ only through the term var[Di(β, φ)]. By simple algebra, one can easily show that
and
as the two terms in the above representation of Di(β, φ) are uncorrelated. We want to select φ so that var[Di(β, φ)] ≤ var[Di(β, φ = 0)] for any M(Wi, Vi; β). Since the first term in var[Di(β, φ)] does not depend on φ, we need to select φ such that var[(I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)M(Wi, Vi; β) − Ai(φi)] ≤ var[(I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)M(Wi, Vi; β)]. The inequality above is satisfied when Ai(φ) = (I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)φ(Wi) is the projection of (I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)M(Wi, Vi; β) onto a subspace Λsub of Λ1 ≡ {(I(Ri = 1)πi(Wi, Vi, 1)−1 − 1)h(Wi) : h ∈ L2(f(W))}, as the norm of the residual from a projection is smaller than or equal to the norm of the original vector. For a given M(Wi, Vi; β), the most efficient augmentation term, φeff, is obtained by projecting [I(Ri = 1)πi(Wi, Vi, 1)−1 − 1]M(Wi, Vi; β) onto the entire space Λ1. With uniform missing patterns, when MAR holds, φeff equals E[M | R = 1, W]. For example, in our motivating example 1, M = Y − β and thus φeff = E[Y | R = 1, W] − β. See references for technical details.6,19–30
So far we have assumed that πi(Wi, Vi, 1) is known, i.e., missingness by design, which occurs infrequently in medical applications. Therefore, we need to estimate πi(Wi, Vi, 1) using the observed data. We next discuss strategies to obtain estimated missing probabilities π̂i(Wi, Vi, 1) under MAR and MNAR mechanisms respectively.
4.1. MAR
Under MAR, by eq. (1), πi(Wi, Vi, 0) depends on Wi only since V(0),i is an empty set. Thus πi(Wi, Vi, 1) also depends only on Wi since πi(Wi, Vi, 1) = 1 − πi(Wi, Vi, 0). In other words, for r ∈ {1,0}, P(Ri = r | Wi, Vi ) = P(Ri = r | Wi). Since (Ri, Wi) is observed for each subject i, then the estimated conditional missing probability π̂i(Wi, r) can be obtained by regressing the missing indicator Ri on the always observed covariates Wi via either a parametric regression model (e.g., logistic regression) or nonparametric, data-adaptive algorithms (e.g., tree-based methods).31–35
In many studies that obtain data from electronic medical databases, the number of covariates that need to be adjusted for to make the MAR assumption plausible is quite large.36 Then it will be difficult to impose a correct parametric model for P(Ri = 1 | Wi) due to the curse of dimensionality. A misspecified parametric model may result in significantly biased results. Data-adaptive, tree-based methods provide promising alternatives.32,33,35 They are designed to minimize the mean squared prediction error, no matter how many covariates need to be adjusted for. The methods are easy to implement with minimum analyst input. Trees have many advantages including being robust to outliers, insensitive to covariate transformation, and the ability to capture complex interactions and highly correlated variables. See Hastie, Tibshrani, and Friedman35 and Therneau & Atkinsoon37 for a comprehensive review of the method and software programs.
After {π̂i(Wi,1), i =1,…,n} are obtained, the IPW estimator β̂0 is obtained by solving eq. (3), with π̂i(Wi,1) substituted for πi(Wi,1). To obtain the efficient augmented IPW estimators β̂φeff, additional modeling and estimation are needed since φeff depends on the unknown outcome regression function E[M | R = 1, W]. In example 1, φeff = E[Y | R = 1, W] − β. We use the complete cases to estimate E[Y | R = 1, W]. As before, we can use either a parametric working model E[Y | R = 1, W; ξ] or data-adaptive, tree-based regression techniques. After all the unknown functions and parameters are estimated, the augmented estimator β̂φeff is obtained by solving the augmented estimating equation . In this example 1,
It is worth noting that β̂φeff is doubly robust (DR) in the sense that it is consistent for β* if either the working model for the missing data process π(Wi, 1) or the working model for the outcome regression function E[Y | R = 1, W] is correctly specified, but not necessarily both.38 This nice property offers analysts two chances of making correct inference. Furthermore, the specified working models are practically certain to be incorrect especially in the presence of high-dimensional covariates. But as long as at least one model is nearly correct, the bias of β̂φeff will be small by theory and simulation results.38 The variance estimates of β̂φeff can be obtained using either the asymptotic theory and delta methods or bootstrap re-sampling approaches.
4.2. MNAR
The MAR assumption cannot be empirically tested using observed data except under limited scenarios.39 Subject matter expertise is usually required to judge its plausibility. When MAR does not appear to be reasonable, then additional assumptions on the missing data process need to be imposed to make the parameters of interest identifiable. Since these additional assumptions are not verifiable under a nonparametric full data model for (W, V), a sensitivity analysis is recommended. There are different ways of conducting a sensitivity analysis for MNAR (i.e., nonignorable) data. We focus on the selection bias function approach for IPW estimators.27,30 This approach decomposes the nonignorable missing data process in a natural and straightforward manner, and thus makes it relatively easy to impose sensitivity assumptions using background information and substance knowledge.
Under MNAR, πi(Wi, Vi, 0) depends on both Wi and Vi. The selection bias function approach uses a user-specified function to quantify the residual association between the missingness probability and the possibly unobserved components of V conditioning on observed data. Specifically, we assume that
| (4) |
where h(Wi) is an unrestricted function of Wi and q(Wi, Vi) is the selection bias function. In other words, the “odds” of having missing data depends on the possibly unobserved components Vi through the selection bias function q(Wi, Vi). Note that q(Wi, Vi) needs to be specified by investigators, e.g., q(Wi, Vi; c) = cTVi where c is a given constant vector. When the model for the full data is nonparametric, the functional form chosen for q(Wi, Vi) and the value of the parameter c are not empirically testable. In this paper, we do not dwell on the choice of the selection bias function q(Wi, Vi) as it depends heavily on the study setting and existing substance knowledge about the missing mechanism. 27,30
Assuming eq. (4) holds and q(Wi, Vi) has been specified, we still need to estimate h(Wi) to obtain an estimated missing probability π̂i(Wi, Vi, 1). To do so, we usually impose a parametric working model h(Wi; α) indexed by a unknown parameter α, e.g., h(Wi; α) = αTWi. If W is categorical and the sample size is large, then we can use a saturated model to avoid model misspecification. The parameter estimate α̂ is obtained by solving the unbiased estimating equation
where πi(Wi, Vi, 1; α, q) = [1 + exp{h(Wi; α) + q(Wi, Vi)}]−1 and ψ is a vector of selected functions of Wi (e.g., ψ(Wi) = Wi). Note that the dimension of ψ needs to be equal to the dimension of α. Under regularity conditions, the corresponding α̂ is consistent for the true value α* as long as the parametric working model is correct and eq. (4) holds. However, the variance of α̂ depends on ψ.
As with MAR settings, the IPW estimator β̂0 can be obtained as the solution to eq. (3) using the estimated missing probability π̂i(Wi, Vi, 1) = πi(Wi, Vi, 1; α̂, q). See references27,28,40 for details on doubly-robust estimators and other, more efficient augmented estimators.
5. Monotone missing pattern
We now introduce the weighting approach for monotone missing patterns. Without loss of generality, we assume Rs,i ≥ Rt,i for any 1 ≤ s < t ≤ q. Equivalently, for each subject i, if the sth element Vs,i is missing, then all subsequent elements {Vt,i: t > s} are missing.
We first focus on example 2 and then present general results. Specially, we consider the setting in which Wi contains the treatment indicator and a vector of baseline covariates that are recorded for each subject (e.g., age, sex, comorbidity conditions); while Vi = (V1,i, Yi)T denotes the BP measured at baseline and at 12 months. We make the data “monotone” by ignoring Y = V2 on subjects missing V1 (R2,i = 0 if R1,i = 0). We will estimate the coefficients β in the outcome regression model
Monotone missing data can be analyzed by applying the weighting approach for a uniform missing pattern in a nested fashion; that is, a monotone missing pattern can be decomposed into multiple uniform missing data models. For example, in example 2, since we have two missing components, we derive our estimators in two steps. In the first step, we derive estimators under an artificial missing data model in which the full data is but the observed data is . That is, both V1,i and Yi are observed whenever the missing indicator R1,i is 1. In the second step, we consider a second artificial missing data model with now the full data and Oi = Wi, R1,i, R2,i, R1,iV1,i, R2,iYi the observed data. Our final estimator will only depend on the actual data {Oi, i =1,…,n}.
Specifically, let E1,i = e1,i(Wi, V1,i, Y) ≡ P(R1,i = 1 | Wi, V1,i, Yi) and E2,i = e2,i(Wi, V1,i, Yi) ≡ P(R2,i = 1 | R1,i = 1, Wi, V1,i, Yi). Then, under monotone missingness, πi (Wi,V1,i,Y,1)= P(Ri =1 | Wi,V1,i,Yi)= E1,i E2,i, πi (Wi,V1,i,Y,(1,0)T)= P(Ri = (1,0)T | Wi,V1,i,Yi)= E1,i(1−E2,i) and πi (Wi,V1,i,Y,0)= P(Ri = 0 | Wi,V1,i,Yi)=1−E1,i. As above, suppose e1,i and e2,i are known functions. Later we relax this assumption.
The first step of our estimation procedure is to apply the IPW approach to the first artificial missing data model. In Section 4, we obtain a first-stage class of estimators {β̃φ1: φ1} by solving the estimating equation where
Here φ1 is a vector of selected functions of the observed components Wi. However, the first term in D̃i (β,φ1)depends on the outcome Yi which might still be missing in the actual data even if R1,i =1. To obtain unbiased estimating equations that depend only on the observed data Oi, in the second stage of our estimation procedure, we apply the IPW approach to the second artificial missingness model, where is now the full data and Oi is the observed data. Note that in this artificial missingness model, the missing indicator does not equal R2,i. Rather, the missing indicator equals one when the “full” data and the observed data are the same. Since if R1,i = 0 or R1,i = R2,i =1, we define a new missing indicator
with . Thus, our second-stage IPW estimators {β̂(φ1φ2): φ1,φ2)} are solutions to the estimating equation where
By definition, and . Thus, (R̃i Ẽi−1−1)φ2(Wi, R1,i, R1,iV1,i)= R1,i (R2,i E2,i−1−1) φ2 (Wi, R1,i =1,V1,i). For simplicity, we denote φ2 (Wi, R1,i =1,V1,i) as φ2 (Wi,V1,i). After some algebra, one has
| (5) |
Under regularity conditions, it can be proved that β̂(φ1,φ2) is a CAN estimator of β*.21 Let and . We can rewrite Di (β,φ1, φ2) as
To maximize efficiency under MAR, we select to be E[M(Wi,V1,i,Yi;β)| Ri=1, Wi,V1,i] and to be . See Robins, Rotnitzky, and others for further discussions of efficiency.5,6,20–22,24,25,40
Next we consider how to estimate E1,i and E2,i under MAR and MNAR mechanisms respectively.
5.1. MAR
If MAR holds, then for r = (r1, r2)T ∈ {1,0,(1,0)T},
Thus E1,i =1−P(Ri = 0 | Wi)= P(R1,i =1| Wi) is a function of Wi only, whereas
depends on (Wi,V1,i). That is, E2,i = P(R2,i =1| R1,i =1, Wi,V1,i). Therefore, E1,i can be estimated using the observed data {(R1,i, Wi): i =1,…,n} by regressing R1,i on Wi using either a parametric working model or data-adaptive nonparametric techniques. Similarly, E2,i can be estimated using the observed data {(R2,i, Wi,V1,i): i ∈ {1,…,n} and R1,i =1} by regressing R2,i on (Wi,V1,i) among those with R1,i =1.
5.2. MNAR
When the missing data process depends on possibly unobserved data and the full data model is nonparametric, we must impose additional assumptions to make the parameters of interest identifiable. We extend the sensitivity analysis approach for the uniform missing pattern and assume that
Here q1 (Wi,V1,i,Yi) and q2 (Wi,V1,i,Yi) are investigator-specified selection bias functions. To estimate h1 (Wi) and h2 (Wi,V1,i), we impose parametric working models h1 (Wi;α) and h2 (Wi, V1,i;α), and obtain the estimated parameter α̂ by solving the unbiased estimating equation where
Here
πi(Wi, Vi,1;α̂, q1, q2)= Ê1,i Ê2,i, πi(Wi, Vi,(1,0)T;α̂, q1, q2)= Ê1,i(1−Ê2,i), and πi (Wi, Vi,0;α̂, q1, q2)=1−Ê 1,i. Moreover, ψr (Wi,r(V1,i,Yi)T) is a vector of functions of the variables that are observed when Ri = r.
5.3. General monotone results
The results we introduced above for example 2 can be extended to multiple-occasion monotone missing data models. In such models, Vi consists q ≥ 2 elements and Ri indicates the corresponding vector of missing indicators. If the s th component (1 ≤ s ≤ q) Vs,i is missing (Rs,i = 0), all subsequent components of Vi are missing (Rt,i = 0 for any s < t ≤q). Let indicate a q-dimensional vector with the first q − s elements being 1 and the remaining s elements being 0 (i.e., the first q − s elements of Vi are observed while the remaining s elements are missing). The class of IPW estimators β̂ is constructed based on the estimating equations where
where φs (Wi,V(rs)i) is a vector of selected functions of the variables Wi and (V1,i,…,Vq−s,i)T, which are observed when Ri = rs. For any 1 ≤ s ≤ q, let Es,i ≡ P(Rs,i=1|Rs−1,i =1, Wi, Vi) denote subject i’s conditional probability of observing the sth element Vs,i given the full data (Wi,Vi) and the event that all previous elements (V1,i,…,Vs−1,i) are observed. Due to monotone missingness, .
Under MAR, Es,i depends on (Wi,V1,i,…,Vs−1,i) only, i.e., P(Rs,i=1|Rs−1,i=1, Wi,Vi)=P(Rs,i=1|Rs−1,i =1, Wi,V1,i,…,Vs−1,i). Then Es,i can be estimated from the observed data {Rs,i, Wi,V1,i,…,Vs−1,i: i =1,…,n and Rs−1,i =1} by regressing Rs,i on (Wi,V1,i,…,Vs−1,i) among those with Rs−1,i =1.
The estimation of the missing data process under MNAR is much more complicated. As before, selection bias functions need to be specified for the “odds” of having missing data. Specifically, for any 1 ≤ s ≤ q,
Then, and . The estimated α̂ solves the estimating equation where
and ψs(Wi,V1,i,…,Vq−s,i) is a vector of functions of (Wi,V1,i,…,Vq−s,i).
6. Non-monotone missing pattern
In non-monotone missing data models, the q-dimensional vector of missing indicators Ri can take 2q possible values as each element can be either 0 or 1. For example, when q = 2, Ri = r ∈ {(0,0)T,(0,1)T,(1,0)T,(1,1)T }. In such models, the estimation of the missing data process is substantially more challenging.
The estimation of the parameter of interest β when the missing probabilities {πi (Wi, Vi,r): r} are known is similar to the estimation in monotone missing data models. Specifically, the IPW estimator β̂ is obtained by solving the estimating equation where
and φr (Wi, V(r),i) is a selected m × 1 vector of functions of the observed components (Wi, V(r),i) when Ri = r. Unlike in Section 5.3, r is no longer restricted to .
In most applications, πi (Wi, Vi, r) is unknown and must be estimated from the observed data. Robins and colleagues proposed the randomized monotone missingness (RMM) processes41 to analyze non-monotone ignorable missing data, and the selection bias permutation missingness (PM) models42,43 to analyze non-monotone nonignorable missing data. These approaches are sometimes plausible. However, they are quite complex and computationally intensive. There currently exists no user-friendly software program to facilitate their implementation. These limitations likely contribute to lack of wide adoption. Through introducing the heuristic ideas behind these approaches, we hope to encourage researchers to develop user-friendly software tools for these methods.
We use two motivating examples for MAR and MNAR mechanisms respectively; PM models are best explained in the context of a longitudinal study. In contrast, RMM models do not apply to longitudinal data. Both examples share common notation. The full data is denoted by Li = {(WiT, V1,i, V2,i, V3,i)T, i = 1, …, n}, and the observed data is denoted by {Oi = (WiT, R1,i, R2,i, R3,i, R1,iV1,i, R2,iV2,i, R3,iV3,i)T, i = 1, …, n} where Ri = (R1,i, R2,i, R3,i)T is the vector of missing indicators. The parameter of interest β* is the unique solution to E[M(W, V; β*)] = 0
6.1. MAR
We consider example 3. Under MAR, for any r = (r1, r2, r3)T,
If (Wi, Vi) is discrete with few levels, the estimated missing probabilities π̂i (Wi, Vi, r) can be obtained as the empirical proportions within each covariate level. In practice, we need to impose parametric working models for πi (Wi, Vi, r) to reduce dimension and borrow information across different covariate levels. To simultaneously satisfy the restrictions imposed by MAR, the inequalities 0 ≤ πi (r) ≤ 1, and the equality , it will be difficult, if not impossible, to directly model {πi (Wi, Vi, r): r}.
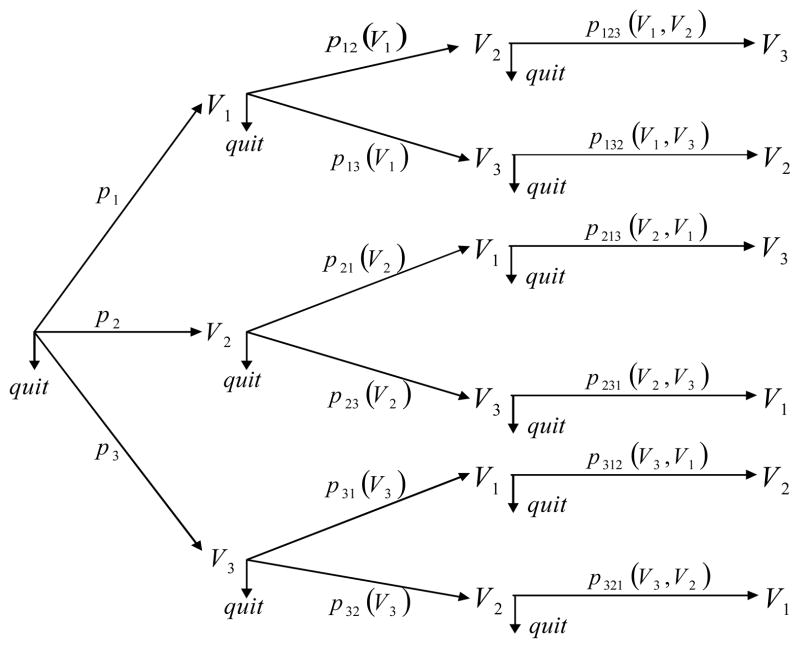
Robins & Gill 41 proposed an algorithm to estimate πi (Wi, Vi, r) under a sub-model of MAR models, which they referred to as a RMM model. This model is assumed to be generated as follows. For each subject i, Wi is observed. Then one of the three elements of Vi, Vs,i, 1 ≤ s ≤ 3 is observed with probability ps = ps (Wi), or one quits without observing any element of Vi with probability . If, for example, V1,i is observed, then in a second step, we observe V2,i with a conditional probability p12 (V1,i), or observe V3,i with a conditional probability p13 (V1,i), or quit with probability 1 − p12 (V1,i) − p13 (V1,i). Note that the conditional probabilities p12 (V1,i) and p13 (V1,i) depend both on Wi and the value of V1,i observed at the first step. For simplicity, we suppress the dependence on Wi when no ambiguity arises. Suppose V2,i is observed at the second step, then in the third step, we observe the third component V3,i with a conditional probability p123 (V1,i, V2,i) or quit with probability 1 − p123 (V1,i, V2,i). The following figure is similar to Figure 1 in Robins & Gill41 to help understanding.
An RMM process satisfies MAR. For example, the overall probability of observing (V1,i, V2,i), πi (r = (1,1,0)T), equals p1 p12 (V1,i)(1 − p123 (V1,i, V2,i)) + p2 p21 (V2,i)(1 − p213 (V2,i, V1,i)), since we either observe V1,i at the first step and then V2,i at the second step and then quit without observing V3,i, or observe V2,i at the first step and then V1,i at the second step and then quit without observing V3,i. This overall probability depends on (Wi, V1,i, V2,i) which are observed when Ri = (1,1,0)T. It can be shown that the probabilities sum to 1.
Gill & Robins44 showed that there do exist ignorable (i.e., MAR) missing data processes that are not RMM. However, such processes are often unrealistic “due to the subtle and precise manner in which the data must be ‘hidden’ to insure that the process is MAR”.
The estimation of πi (Wi, Vi, r) is non-trivial for RMM processes. To reduce the dimension, the authors considered Markov RMM processes in which the conditional probabilities do not depend on the order in which the variables were observed. For example, p123 (V1,i, V2,i) = p213 (V1,i, V2,i) and will be denoted as . Parametric working models are imposed for these conditional probabilities. For example, for any k ∈ {1,2,3}, we model the first-step probabilities with a multinomial logistic regression model
The second step probabilities are modeled by
Finally, the third step probabilities are modeled by,
where V(−k),i indicates the two elements other than Vk,i (e.g., V(−1),i = (V2,i, V3,i)T). When appropriate, we can further decrease the dimension of the parameter space by assuming, for example, (γ0,k, ) does not depend on k.
The maximum likelihood estimates (MLEs) of the unknown parameters cannot be directly obtained as the order in which variables were observed is missing. For example, there are two paths in the figure above by which V1,i and V2,i could be observed: V1,i − V2,i − quit, or V2,i − V1,i − quit. The authors suggest treating the path information as missing and to obtain the MLE with the Expectation-Maximization (EM) algorithm. See 41 for details.
6.2. MNAR
For non-monotone nonignorable missing data processes, Robins et al.43 propose selection bias PM models. Consider our motivating example 4, a longitudinal study with three BP measurements. In longitudinal studies, the PM order is the reverse of the temporal order. Under a PM model, we assume that the conditional probability of observing Vs,i at the sth visit depends (i) on the observed components from previous visits (i.e., Ls,i ≡ (Wi, R1,i, …Rs−1,i, R1,iV1,i, …, Rs−1,iVs−1,i)) but not on the unobserved components of (V1,i, …, Vs−1,i); (ii) on the value of Vs,i through a specified selection bias function; and (iii) on both observed and unobserved components in future visits ((Vs+1,i, …, Vq,i)). In our motivating example 4, we consider a simplified PM model in which the conditional probability of observing Vs,i does not depend on any future data. Thus,
| (6) |
Here qs (Vs,i, Ls,i) is an investigator specified selection bias function and hs(Ls,i) is an unrestricted function to be estimated. By eq. (6), the conditional probability Es,i (rs) depends on the possibly unobserved value of Vs,i through qs (Vs,i, Ls,i).
In most applications, we impose parametric working models hs (Ls,i; δs) for hs (Ls,i) to overcome the curse of dimensionality. The parameter δs can be estimated by solving
| (7) |
where φs (Wi) is a vector of selected known functions of Wi and has the same dimension as δs. See Vansteelandt et al.30 for an extension of this approach to estimate the mean vector of repeated outcomes in a nonignorable, non-monotone missing data model.
Although a subject’s decision to miss the sth visit cannot directly depend on future data. But Rs, the indicator variable indicating whether Vs was observed, might be statistically associated with future data, when some factors that affect the decision are not recorded in (Ls, Vs) but are associated with (Vs+1, …, Vq). See Robins, Rotnitzky, and Scharfstein43 for further discussions.
7. Discussion
We have introduced the IPW approaches in a wide range of settings with different missing data patterns and mechanisms. These weighting approaches share the same basic idea. However, different strategies are needed to estimate the missing probabilities depending on the missing data pattern and mechanism. Our goal in this review paper was to provide a conceptual overview of existing weighting approaches.
Our review began with a simple uniform missing data model; for each subject i, either the entire vector Vi is observed or it is completely missing. We then discussed monotone missing data patterns. We show these models can be decomposed into multiple “artificial” uniform missing data models and estimators are obtained by applying weighting approaches for uniform missing data models in a nested fashion. In Section 6, we discussed non-monotone missing patterns and notice the estimation of the missingness probabilities is substantially more challenging and complex. We then introduced the RMM processes for non-monotone MAR data and the selection bias PM approach for non-monotone MNAR data. User-friendly software programs need to be developed to make these methods useful for practice.
We considered both MAR and MNAR mechanisms. IPW estimators for MNAR are natural extensions of IPW estimators for MAR in which selection bias functions quantify the residual association of the missing probabilities and unobserved data conditional on observed data. The MAR assumption cannot be empirically tested when the model of the full data is nonparametric. Subject matter expertise and prior information are typically required to judge its plausibility. In uniform and monotone missing patterns, MAR sometimes is reasonable if data on a large set of variables are collected. The MAR assumption is less likely to hold with non-monotone missingness.30 Unless strong prior information is available, we recommend analysts consider the possibility that the missingness mechanism is nonignorable and conduct a sensitivity analysis.
Figure 1.
Missing data process in a RMM process
Contributor Information
Lingling Li, Department of Population Medicine, Harvard Medical School and Harvard Pilgrim Health Care Institute, US.
Changyu Shen, Division of Biostatistics, Indiana University School of Medicine, US.
Xiaochun Li, Division of Biostatistics, Indiana University School of Medicine, US.
James M. Robins, Departments of Biostatistics and Epidemiology, Harvard School of Public Health, US
References
- 1.Little R, Rubin D. Statistical Analysis with Missing Data. New York: John Wiley & Sons; 1987. [Google Scholar]
- 2.Raghunathan TE. What do we do with missing data? Some options for analysis of incomplete data. Annual Review of Public Health. 2004;25:99–117. doi: 10.1146/annurev.publhealth.25.102802.124410. [DOI] [PubMed] [Google Scholar]
- 3.Rubin D. Inference and missing data (with discussion) Biometrika. 1976;63:581–592. [Google Scholar]
- 4.Horvitz DG, Thompson DJ. A Generalization of Sampling Without Replacement from A Finite Universe. Journal of the American Statistical Association. 1952;47:663–685. [Google Scholar]
- 5.Robins J, Rotnitzky A, Zhao L. Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association. 1994;89:846–866. [Google Scholar]
- 6.Robins J, Rotnitzky A, Zhao L. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- 7.Robins J, Hernan M, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 8.Hernan M, Brumback B, Robins J. Marginal structural models to estimate the causal effect of Zidovudine on the survival of HIV-positive men. Epidemiology. 2000;11:561–570. doi: 10.1097/00001648-200009000-00012. [DOI] [PubMed] [Google Scholar]
- 9.Horton NJ, Laird NM. Maximum likelihood analysis of generalized linear models with missing covariates. Statistical Methods in Medical Research. 1999;8:37–50. doi: 10.1177/096228029900800104. [DOI] [PubMed] [Google Scholar]
- 10.Ibrahim JG, Chen MH, Lipsitz SR, Herring AH. Missing-data methods for generalized linear models: A comparative review. Journal of the American Statistical Association. 2005;100:332–346. [Google Scholar]
- 11.Ibrahim JG, Molenberghs G. Missing data methods in longitudinal studies: a review. Test. 2009;18:1–43. doi: 10.1007/s11749-009-0138-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ibrahim JG, Chen MH. Power prior distributions for regression models. Statistical Science. 2000;15:46–60. [Google Scholar]
- 13.Chen MH, Ibrahim JG, Lipsitz SR. Bayesian methods for missing covariates in cure rate models. Lifetime Data Analysis. 2002;8:117–146. doi: 10.1023/a:1014835522957. [DOI] [PubMed] [Google Scholar]
- 14.Ibrahim JG, Chen MH, Lipsitz SR. Bayesian methods for generalized linear models with covariates missing at random. Canadian Journal of Statistics-Revue Canadienne de Statistique. 2002;30:55–78. [Google Scholar]
- 15.Harel O, Zhou XH. Multiple imputation: Review of theory, implementation and software. Statistics in Medicine. 2007;26:3057–3077. doi: 10.1002/sim.2787. [DOI] [PubMed] [Google Scholar]
- 16.Rubin DB. Multiple Imputation for Nonresponse in Surveys. New York: Wiley; 1987. [Google Scholar]
- 17.Schafer JL. Multiple imputation: a primer. Statistical Methods in Medical Research. 1999;8:3–15. doi: 10.1177/096228029900800102. [DOI] [PubMed] [Google Scholar]
- 18.Tsiatis A. Semiparametric theory and missing data. New York: Springer; 2006. [Google Scholar]
- 19.van der Laan M, Robins J. Unified methods for censored longitudinal data and causality. New York: Springer; 2003. [Google Scholar]
- 20.Robins JM, Rotnitzky A. Semiparametric Efficiency in Multivariate Regression-Models with Missing Data. Journal of the American Statistical Association. 1995;90:122–129. [Google Scholar]
- 21.Rotnitzky A, Robins JM, Scharfstein DO. Semiparametric regression for repeated outcomes with nonignorable nonresponse. Journal of the American Statistical Association. 1998;93:1321–1339. [Google Scholar]
- 22.Robins JM, Rotnitzky A, Zhao LP. Analysis of Semiparametric Regression-Models for Repeated Outcomes in the Presence of Missing Data. Journal of the American Statistical Association. 1995;90:106–121. [Google Scholar]
- 23.Rotnitzky A, Robins JM. Semiparametric regression estimation in the presence of dependent censoring. Biometrika. 1995;82:805–820. [Google Scholar]
- 24.Rotnitzky A, Robins JM. Semiparametric Estimation of Models for Means and Covariances in the Presence of Missing Data. Scandinavian Journal of Statistics. 1995;22:323–333. [Google Scholar]
- 25.Rotnitzky A, Holcroft CA, Robins JM. Efficiency comparisons in multivariate multiple regression with missing outcomes. Journal of Multivariate Analysis. 1997;61:102–128. [Google Scholar]
- 26.Bickel PJ, Klaassen CA, Ritov Y, Wellner JA. Efficient and adaptive estimation for semiparametric models. New York: Springer Verlag; 1998. [Google Scholar]
- 27.Scharfstein DO, Rotnitzky A, Robins JM. Adjusting for nonignorable drop-out using semiparametric nonresponse models. Journal of the American Statistical Association. 1999;94:1096–1120. [Google Scholar]
- 28.Scharfstein DO, Rotnitzky A, Robins JM. Adjusting for nonignorable drop-out using semiparametric nonresponse models - Rejoinder. Journal of the American Statistical Association. 1999;94:1135–1146. [Google Scholar]
- 29.Robins JM, Rotnitzky A. Inference for semiparametric models: Some questions and an answer - Comments. Statistica Sinica. 2001;11:920–936. [Google Scholar]
- 30.Vansteelandt S, Rotnitzky A, Robins J. Estimation of regression models for the mean of repeated outcomes under nonignorable nonmonotone nonresponse. Biometrika. 2007;94:841–860. doi: 10.1093/biomet/asm070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. Belmont, CA: Wadsworth International Group; 1984. [Google Scholar]
- 32.Friedman J, Hastie T, Tibshirani R. Additive logistic regression: A statistical view of boosting. Annals of Statistics. 2000;28:337–374. [Google Scholar]
- 33.Friedman J, Hastie T, Tibshirani R. Additive logistic regression: A statistical view of boosting - Rejoinder. Annals of Statistics. 2000;28:400–407. [Google Scholar]
- 34.Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- 35.Hastie T, Tibshirani R, Friedman J. The elements of statistical learning: data mining, inference, and prediction. 2. New York: Springer; 2009. [Google Scholar]
- 36.Schneeweiss S, Rassen JA, Glynn RJ, Avorn J, Mogun H, Brookhart MA. High-dimensional Propensity Score Adjustment in Studies of Treatment Effects Using Health Care Claims Data. Epidemiology. 2009;20:512–522. doi: 10.1097/EDE.0b013e3181a663cc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Therneau TM, Atkinsoon EJ. An introduction to recursive partitioning using the RPART routines. 1997. [Google Scholar]
- 38.Bang H, Robins J. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61:962–972. doi: 10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- 39.Potthoff RF, Tudor GE, Pieper KS, Hasselblad V. Can one assess whether missing data are missing at random in medical studies? Statistical Methods in Medical Research. 2006;15:213–234. doi: 10.1191/0962280206sm448oa. [DOI] [PubMed] [Google Scholar]
- 40.Rotnitzky A, Robins J. Analysis of semi-parametric regression models with non-ignorable non-response. Statistics in Medicine. 1997;16:81–102. doi: 10.1002/(sici)1097-0258(19970115)16:1<81::aid-sim473>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 41.Robins JM, Gill RD. Non-response models for the analysis of non-monotone ignorable missing data. Statistics in Medicine. 1997;16:39–56. doi: 10.1002/(sici)1097-0258(19970115)16:1<39::aid-sim535>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 42.Robins JM. Non-response models for the analysis of non-monotone non-ignorable missing data. Statistics in Medicine. 1997;16:21–37. doi: 10.1002/(sici)1097-0258(19970115)16:1<21::aid-sim470>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 43.Robins JM, Rotnitzky A, Scharfstein D. Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models. In: Halloran M, Berry D, editors. Statistical Models in Epidemiology: The Environment and Clinical Trials. New York: Springer-Verlag; 1999. pp. 1–92. [Google Scholar]
- 44.Gill RD, van der Laan M, Robins JM. Coarsening at random: characterizations, conjectures and counterexamples. In: Lin DY, editor. Proceedings of the First Seattle Symposium on Biostatistics: Survival Analysis. New York: Springer Verlag; 1997. pp. 255–94. [Google Scholar]