A class of covariate-dependent spatiotemporal covariance functions

Abstract

In geostatistics, it is common to model spatially distributed phenomena through an underlying stationary and isotropic spatial process. However, these assumptions are often untenable in practice because of the influence of local effects in the correlation structure. Therefore, it has been of prolonged interest in the literature to provide flexible and effective ways to model non-stationarity in the spatial effects. Arguably, due to the local nature of the problem, we might envision that the correlation structure would be highly dependent on local characteristics of the domain of study, namely the latitude, longitude and altitude of the observation sites, as well as other locally defined covariate information. In this work, we provide a flexible and computationally feasible way for allowing the correlation structure of the underlying processes to depend on local covariate information. We discuss the properties of the induced covariance functions and discuss methods to assess its dependence on local covariate information by means of a simulation study and the analysis of data observed at ozone-monitoring stations in the Southeast United States.

1 Introduction

The advance of technology has allowed for the storage and analysis of complex datasets. In particular, environmental phenomena are usually observed at fixed locations over a region of interest at several time points. The literature on modeling spatio-temporal processes has been experiencing a significant growth in the recent years. The main objective of this research is to define flexible and realistic spatiotemporal covariance structures, since predictions for unobserved locations and future time points are highly-dependent on the covariance structure of the process. An important challenge is to specify a flexible covariance structure, while retaining model simplicity.

In this paper we are concerned with modeling ozone levels observed in the Southeast USA. We explore models for ozone which allow the covariance structure to be non-separable and non-stationary. Many spatiotemporal models have been proposed for ambient ozone data for various purposes. Guttorp et al. (1994) and Meiring et al. (1998) generate predictions using independent spatial deformation models for each time period to evaluate deterministic models. Carroll et al. (1997) combine ozone predictions with population data to calculate exposure indices. Huerta et al. (2004) and Dou et al. (2010) use a dynamic linear model to perform short-term forecasting over a small region, while Sahu et al. (2007) use a dynamic linear model to predict temporal summaries of ozone and examine meteorologically-adjusted trends over space. Gilleland and Nychka (2005) seek a method for drawing attainment boundaries. McMillan et al. (2005) present a mixture model that allows heavy-ozone-production and normal regimes; the probability of each depends on atmospheric pressure. Berrocal et al. (2010) combine deterministic model output with observations via a computationally efficient hierarchical Bayesian approach. Nail et al. (2010) explicitly model ozone chemistry and transport with additional goals of decomposition into global background, local creation, and regional transport components, and of long-term prediction under hypothetical emission controls.

A challenging aspect of modeling ozone is its complex relationship with meteorology. Most tropospheric ozone is not emitted directly, but rather it is formed from a complex series of photochemical reactions of the primary precursors: nitrogen oxides (NOx), volatile organic compounds (VOCs), and to a smaller extent other pollutants. Since the reactions that form ozone are driven by sunlight, ambient concentrations are highest in hot and sunny conditions. Because of this complicated relationship with meteorology, it is natural to wonder whether meteorological variables affect not only the mean concentration, but also its variance and spatio-temporal correlation. Of the studies mentioned, Guttorp et al. (1994), Meiring et al. (1998), Huang and Hsu (2004), and Nail et al. (2010) model the dependence of the covariance on covariates in some form. Guttorp et al. (1994) and Meiring et al. (1998) allow the spatial covariance to vary by hour of the day. Huang and Hsu (2004) and Nail et al. (2010) model the transport of ozone using wind speed and direction.

We present a class of spatio-temporal covariance functions that allow the meteorological covariates to affect the covariance function (Schmidt et al., 2010; Schmidt and Rodríguez, 2010). This produces a non-stationary covariance, since the correlation between pairs of points separated by the same distance may have different covariance depending on local meteorological conditions. There are many models for non-stationary spatial covariance functions, for example, Higdon et al. (1999), Fuentes (2002), Schmidt and O'Hagan (2003), and Paciorek and Schervish (2006), to mention just a few. On the other hand, Cressie and Huang (1999), Gneiting (2002), and Stein (2005) present examples of non-separable stationary covariance functions for space-time processes. Although these models provide flexible covariance structures they usually have many parameters, which may be challenging to estimate.

Schmidt et al. (2010), Schmidt and Rodríguez (2010), and Cooley et al. (2007) use a covariance model that defines the distance between two observations not only in terms of the spatial distance, but also distance in covariate space. In this paper we provide a more flexible covariance model that allows not only the distance between covariates, but also the covariate values themselves to affect the spatial covariance. For example, the spatial covariance is allowed to be different for a pair of observations with same temperature on a cold day than for a pair of observations with same temperature on a warm day. Following Fuentes (2002), we model spatial process at location s, μ(s), as a linear combination of stationary processes with different covariances,

$$\mu (\mathbf{s})=\sum _{j=1}^M{w}_j(\mathbf{s}){\theta }_j(\mathbf{s}),$$ (1)

where w_j(s) are the weights and θ_j are independent zero-mean Gaussian processes with covariance K_j. Fuentes (2002) models the weights as kernel functions of space centered at pre-defined knots ϕ_j so that K_j represents the local covariance for sites near ϕ_j. In contrast, we specify the weights in terms of spatial covariates, so that K_j represents the covariance under environmental conditions described by the covariates.

The paper proceeds as follows. Section 2 introduces the model and Section 3 discusses its properties. Model-fitting issues and computational details are discussed in Sections 4 and 5, respectively. In Section 6, we present a brief simulation study to illustrate the effectiveness of the proposed model. We analyze ozone data in Section 7. We find that the spatial correlation is stronger on windy days, and that temporal correlation depends on temperature and cloud cover. Section 8 concludes.

2 Covariate-dependent covariance functions

Let y(s, t) be the observation taken at spatial location s ∈ ℛ² and time t ∈ ℛ. The response is modeled as a function of p covariates x(s, t) = [x₁(s, t),⋯, x_p(s, t)]^T where x₁(s, t) = 1 for the intercept. We assume that

$$y(\mathbf{s},t)=\mathbf{x}{(\mathbf{s},t)}^T\beta +\mu (\mathbf{s},t)+\epsilon (\mathbf{s},t),$$ (2)

where β is the p-vector of regression coefficients, μ(s, t) is a spatiotemporal effect, and $\epsilon (\mathbf{s},t)\stackrel{iid}{~}\mathrm{N}(0,{\sigma }^2)$ is pure error.

The spatiotemporal process μ is taken to be a Gaussian process with mean zero and covariance that may depend on (perhaps a subset of) the covariates, x. As described in Section 1, we model μ as a linear combination of stationary processes,

$$\mu (\mathbf{s},t)=\sum _{j=1}^M{w}_j[\mathbf{x}(\mathbf{s},t)]{\theta }_j(\mathbf{s},t),$$ (3)

where the θ_j are independent Gaussian processes with mean zero and covariance K_j and w_j[x(s, t)] is the weight on process j. The motivation for this model is that different environmental conditions, described by the covariates, may favor different covariance functions. The weight w_j [x(s, t)] determines the spatiotemporal locations where the covariance function K_j is the most relevant.

Integrating over the latent processes θ_j, the covariance becomes

$$\text{Cov}[\mu (\mathbf{s},t),\mu (\mathbf{s}\prime ,t\prime )|\mathbf{x}]=\sum _{j=1}^M{w}_j[\mathbf{x}(\mathbf{s},t)]w_j[\mathbf{x}(\mathbf{s}\prime ,t\prime )]K_j(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ).$$ (4)

With M = 1, only the variance of the process depends on the covariates, and the correlation, K_j(s − s′, t − t′)/K_j(0, 0), is stationary. With M > 1, both the variance and the correlation depend on the covariates. This covariance is clearly positive definite as long as the K_j are positive definite. To see this, for any (s₁, t₁), …, (s_n, t_n), denote the covariance matrix of [μ(s₁, t₁), …, μ(s_n, t_n)]^T as Σ. Then for any a ∈ ℛⁿ with a ≠ 0,

$${\mathbf{a}}^T\mathrm{\Sigma }\mathbf{a}={\mathbf{a}}^T\left(\sum _{j=1}^M{W}_j{S}_j{W}_j\right)\mathbf{a}=\sum _{j=1}^M{\mathbf{a}}^T{W}_j{S}_j{W}_j\mathbf{a}=\sum _{j=1}^M{\mathbf{ã}}^T{S}_j\mathbf{ã}>0,$$ (5)

where $\mathrm{\Sigma }={\sum }_{j=1}^M{W}_j{S}_j{W}_j$, W_j is diagonal with diagonal elements w_j [x(s_i, t_i)], the (l, k) element of S_j is K_j(s_l − s_k, t_l − t_k), and ã = W_ja ≠ 0.

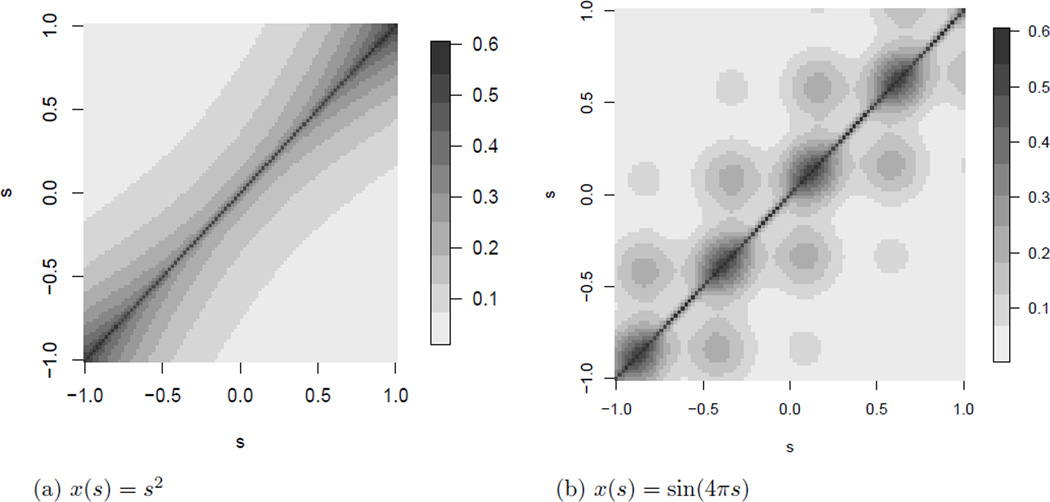
As an illustration of the flexible spatial patterns allowed by our specification, Figure 1 plots the spatial covariance for two simple examples. In both cases we assume a one-dimensional spatial grid with s ∈ ℛ, a single covariate x(s), and that the spatial correlation is high in areas with large x(s). Both examples have M = 2, logit(w₂(s)) = x(s), w₁(s) = 1 − w₂(s), K₁(s − s′) = exp(−|s − s′|/0.02), and K₂(s − s′) = exp(−|s − s′|/0.50). Figure 1 shows the covariance for x(s) = s² and x(s) = sin(4πs). For the quadratic covariate, the second term has higher spatial correlation and the weight on the second process is high for locations with large x(s), therefore the spatial correlation is stronger for s near −1 and 1 where x(s) is high. The spatial covariance is not a monotonic function of spatial distance for the periodic covariate. This may be reasonable if, say, x(s) is elevation and a site with high elevation shares more common features with other high-elevation sites than nearby low-elevation sites.

Figure 1.

Covariance functions for a one-dimensional spatial process with M = 2, logit(w₂(s)) = x(s), w₁(s) = 1 − w₂(s), K₁(s − s′) = exp(−|s − s′|/0.02), and K₂(s − s′) = exp(−|s − s′|/0.50).

This covariance model has interesting connections with other commonly-used spatial models. For example, if we consider purely spatial data, as mentioned in Section 1, taking the weights to be kernel functions of the spatial location alone, i.e., w_j [x(s)] = w_j(s), gives the nonstationary spatial model of Fuentes (2002). By modeling the weights as functions of the covariates, it may be possible to explain non-stationarity with fewer terms giving a more concise and interpretable model. Also, with M = p and w_j [x(s)] = x_j(s) for j = 1, …, p, we obtain the spatially-varying coefficient model of Gelfand et al. (2003). In this model θ_j(s) represents the effect of the j^th covariate at location s. The motivation for the spatially-varying coefficients model is to study local effects of covariates on the mean response. In contrast, our objective is to model the covariance. For example, in a situation with p = 20 covariates it may be sufficient to describe the spatial covariance using M = 2 stationary processes where conditions that favor the two covariance functions are described by weights w₁ and w₂ that depend on all p covariates. Therefore, to provide an adequate description of the covariance, we assume the weights are random functions of unknown parameters that describe environmental conditions (see Section 4) rather than taking the weights to be the covariates themselves. Finally, setting the weights w_j to be constant in time and the latent processes θ_j to be constant over space gives the spatial dynamic factor model of Lopes et al. (2008). Our model differs from this approach since our weights (loadings) are functions of spatial covariates rather than purely stochastic spatial processes.

3 Properties of the covariance model

In this section, we discuss some properties of the proposed model in (3) and the spatiotemporal covariance function. For example, it is clear that even if the individual covariances K_j are separable, stationary, and isotropic, the resulting covariance (4) is in general non-separable, non-stationary, and anisotropic. Below we discuss other properties of the covariance model.

3.1 Monotonicity of the spatial covariance function

As shown in Figure 1, the covariance function can be a non-monotonic function of spatial distance, even if the underlying covariances K_j are decreasing. Intuitively, this occurs only if the spatial variability of the covariates is large relative to the spatial range of the covariance functions K_j. More formally, assuming s ∈ ℛ and the w_j and each component of x are differentiable. Then for any h > 0

$$\frac{\partial \text{Cov}(\mu (\mathbf{s}),\mu (\mathbf{s}+h)|\mathbf{x})}{\partial h}=\sum _{j=1}^M{w}_j(\mathbf{x}[s])w_j(\mathbf{x}[s+h])K_j(h)[\frac{w_j^{\prime }(\mathbf{x}[s+h])}{w_j(\mathbf{x}[s+h])}+\frac{K_j^{\prime }(h)}{K_j(h)}].$$ (6)

Therefore, if the weights w_j(x[s]) are positive, a sufficient but not necessary condition for a monotonic covariance is that $w_j^{\prime }(\mathbf{x}[s+h])/w_j(\mathbf{x}[s+h])+K_j^{\prime }(h)/K_j(h)<0$ for all j. The ratios $w_j^{\prime }(\mathbf{x}[s])/w_j(\mathbf{x}[s])\text{and}-K_j^{\prime }(h)/K_j(h)$ can be interpreted as the elasticity of the weight function and covariance function, respectively. This condition makes the initial statement more precise, in that (6) is negative if the elasticity of the weight function is less than the elasticity of the spatial covariance.

In the special case of a powered-exponential covariance model $K_j(\mathbf{s},\mathbf{s}+h)={\tau }_j^2\text{exp}(-{\rho }_j{h}^{{\kappa }_j})$ and exponential weights w_j(x) = exp(x^Tα_j), where α_j is a vector of coefficients, (6) becomes

$$\frac{\partial \text{Cov}(\mu (\mathbf{s}),\mu (\mathbf{s}+h)|\mathbf{x})}{\partial h}=\sum _{j=1}^M{w}_j(\mathbf{x}[s])w_j(\mathbf{x}[s+h])K_j(h)[{\mathrm{\Delta }}_x{(\mathbf{s}+h)}^T{\alpha }_j-{\kappa }_j{\rho }_j{h}^{{\kappa }_j-1}].$$ (7)

where Δ_x(s + h) denotes the vector of derivatives of x(s + h) with respect to h. The covariance is decreasing in h if Δ_x(s+h)α_j < κ_j ρ_jh^κ_j−1 for all j and h. This shows that it is possible to allow the spatial covariance to depend on covariates but retain monotonicity by restricting the parameters α_j, κ_j, and ρ_j based on bounds the covariate process derivatives.

3.2 Smoothness properties of the spatial process

The smoothness properties of a Gaussian process are often quantified in terms of the mean squared continuity of its derivatives. For many spatial processes, including the non-stationary model of Fuentes (2002), the smoothness of their process realizations is well-studied (see Banerjee and Gelfand, 2003; Banerjee et al., 2003). However, our model postulates a more general dependence of the covariance on spatial covariates. Hence, in this section we explore the effect of that dependence on the smoothness properties of the realizations. For notational convenience, we assume a one-dimensional spatial process with s ∈ ℛ; the results naturally extend to more general direction derivatives by taking s = u^T s for any unit vector u. We start by assuming the covariates x are fixed; this assumption will be later relaxed.

Following the arguments of Banerjee and Gelfand (2003), we say that the k^th derivative (with respect to s) of the process μ (if it exists) is mean square continuous at s if

$$\underset{h\to 0}{\text{lim}}\mathrm{E}{[{\mu }^{(k)}(s)-{\mu }^{(k)}(s+h)|\mathbf{x}]}^2=0.$$ (8)

For k = 0, we can substitute (3) in (8) and get

$$\underset{h\to 0}{\text{lim}}\mathrm{E}{[\mu (s)-\mu (s+h)|\mathbf{x}]}^2=\sum _{j=1}^M\underset{h\to 0}{\text{lim}}{K}_j(0){(w_j[\mathbf{x}(s+h)]-w_j[\mathbf{x}(s)])}^2+\sum _{j=1}^M\underset{h\to 0}{\text{lim}}2w_j[\mathbf{x}(s)]w_j[\mathbf{x}(s+h)](K_j(0)-K_j(h)),$$ (9)

which shows that μ is mean square continuous if each latent process is mean square continuous (lim_h→0K_j(h) = K_j(0)) and the weights are smooth enough to satisfy lim_h→0(w_j [x(s + h)] − w_j [x(s)])² = 0 for all j, e.g., they are continuous functions of the continuous spatial covariates.

In some settings, it may be reasonable to consider x to be a random process. We extend the discussion of Banerjee and Gelfand (2003) to the case when the weights are functions of stochastic covariates. In this case, to study the smoothness of μ requires considering variability in both the latent θ_j as well as the covariates x. The covariates enter the covariance model only through the stochastic weights W_j(s) = w_j [x(s)]. Taking the expectation with respect to both θ_j and W_j(s) gives

$$\underset{h\to 0}{\text{lim}}\mathrm{E}{[\mu (s)-\mu (s+h)]}^2=\sum _{j=1}^M\underset{h\to 0}{\text{lim}}{K}_j(0)E_{W_j}{[W_j(s)-W_j(s+h)]}^2+2\sum _{j=1}^M\underset{h\to 0}{\text{lim}}(K_j(0)-K_j(h)){\mathrm{E}}_{W_j}[W_j(s)W_j(s+h)].$$ (10)

Therefore, under stochastic covariates, the process μ is mean square continuous if and only if the latent processes θ_j and the weight processes W_j are both mean square continuous. It is well known from probability theory that the weight function W_j is mean-square continuous, for example, if it is bounded and the covariate processes are almost surely continuous. Mean square continuity also follows when w_j is Lipschitz continuous of order 1 and the covariate processes are mean square continuous. For example, the logistic weights w_j(x) = exp(x^Tα_j)/[1+exp(x^Tα_j)] are both bounded and Lipschitz continuous of order 1, whereas exponential weights w_j(x) = exp(x^Tα_j) are not.

These results naturally extend from mean squared continuity to mean square differentiability, and higher-order derivatives. Since μ(s) is the sum of stochastic processes Z_j(s) = W_j(s)θ_j(s), then ${\mu }^{(k)}(s)={\sum }_{j=1}^M{Z}_j^{(k)}(s)$. In particular, for k = 1 the derivative process at s is

$${\mu }^{(1)}(s)=\sum _{j=1}^M{\theta }_j^{(1)}(s)W_j(s)+{\theta }_j(s)W_j^{(1)}(s).$$ (11)

So the process μ is mean square differentiable if bothW_j(s) and θ_j(s) are mean square differentiable. Conditions analogous to those outlined above for mean square continuity will assure that the weights are mean square differentiable. More precisely, if the covariate processes x₁(s), …, x_p(s) are mean square differentiable and the function w_j(·) is Lipschitz continuous of order 1, then the resulting process W_j(s) is mean square differentiable, and so is μ(s).

3.3 Span of the covariance function

The covariance (4) is quite flexible. For example, consider a partition of covariate space with N partitions, 𝒜₁, …, 𝒜_N. Now, with a slight abuse of notation, letting M = N² the covariance (4) can be written

$$\text{Cov}[\mu (\mathbf{s},t),\mu (\mathbf{s}\prime ,t\prime )|\mathbf{x}]=\sum _{j=1}^N\sum _{l=1}^N{w}_{jl}[\mathbf{x}(\mathbf{s},t)]w_{jl}[\mathbf{x}(\mathbf{s}\prime ,t\prime )]K_{jl}(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ),$$ (12)

where K_jl(s − s′, t − t′) = K_lj(s − s′, t − t′). If $w_{jl}(\mathbf{x})=a[I(\mathbf{x}\in {𝒜}_j)+I(\mathbf{x}\in {𝒜}_l)]/\sqrt{2}$ for terms with j ≠ l and w_jj(x) = bI(x ∈ 𝒜_j), then

$$\text{Cov}[\mu (\mathbf{s},t),\mu (\mathbf{s}\prime ,t)|\mathbf{x}]=\{\begin{array}{cc}{a}^2{K}_{kk\prime }(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ),\hfill & k\ne k\prime \hfill \\ b^2{K}_{kk}(\mathbf{s}-\mathbf{s}\prime ,t-t\prime )+a^2{\sum }_{l\ne k}{K}_{kl}(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ),\hfill & k=k\prime \hfill \end{array}$$ (13)

where x(s, t) ∈ 𝒜_k and x(s′, t′) = 𝒜_k′. If b² >> a²

$$\text{Cov}[\mu (\mathbf{s},t),\mu (\mathbf{s}\prime ,t\prime )|\mathbf{x}]\approx \{\begin{array}{cc}{a}^2{K}_{kk\prime }(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ),\hfill & k\ne k\prime \hfill \\ b^2{K}_{kk}(\mathbf{s}-\mathbf{s}\prime ,t-t\prime ),\hfill & k=k\prime \hfill \end{array}$$ (14)

Therefore, the model can essentially have a separate spatiotemporal covariance function for pairs of observations with each combination of covariates. Letting N → ∞ gives an arbitrarily flexible covariance model. Although of limited practical applications, the previous arguments show how the covariate-dependent weights can be used to describe specific spatial behaviors depending on the values assumed by the covariates.

4 Priors and model-fitting

In this section we describe a convenient specification of the model. For notational convenience, we assume that at each time point observations are taken at spatial locations s₁, …, s_N ∈ ℛ². We assume an autoregressive spatiotemporal model for the latent processes θ_j,

$${\theta }_j(\mathbf{s},t)={\gamma }_j{\theta }_j(\mathbf{s},t-1)+e_j(s,t)$$ (15)

where γ_j ∈ (0, 1) controls the temporal correlation and e_jt = [e_j(s₁, t), …, e_j(s_N, t)] are independent (over j and t) spatial processes with mean zero and spatial covariance $K_j^s$. The spatial covariances are taken to be the Matérn spatial covariance

$$K_j^s(\Vert h_s\Vert )=\frac{{\tau }_j^2}{2^{{\nu }_j-1}\mathrm{\Gamma }({\nu }_j)}{\left(\frac{2{\nu }_j^{1/2}\Vert h_s\Vert }{{\rho }_j}\right)}^{{\nu }_j}{𝒦}_{{\nu }_j}\left(\frac{2{\nu }_j^{1/2}\Vert h_s\Vert }{{\rho }_j}\right),$$ (16)

where 𝒦 is the modified Bessel function. The Matérn has three parameters: ${\tau }_j^2$ is the variance, ρ_j controls the spatial range, and ν_j controls the smoothness. The Matérn has several popular special cases, including the exponential $K_j^s(\Vert h_s\Vert )={\tau }_j^2\text{exp}(-\Vert h_s\Vert /{\rho }_j)$ with ν_j = 1/2 and the Gaussian $K_j^s(\Vert h_s\Vert )={\tau }_j^2\text{exp}(-{\Vert h_s\Vert }^2/{\rho }_j^2)$ with ν_j = ∞.

In (4) there is confounding between the scale of the weights w_j and covariances K_j, since multiplying the weights by constant c > 0 and dividing the standard deviation of K_j by c give the same covariance. Therefore, for identification purposes we restrict the weights for each observation sum to one, ${\sum }_{j=1}^M{w}_j[\mathbf{x}({\mathbf{s}}_2,t_2)]=1$. Although there are other possibilities, we assume the weights have the multinomial logistic form

$$w_j[\mathbf{x}(\mathbf{s},t)]=\frac{\text{exp}(\mathbf{x}{(\mathbf{s},t)}^T{\alpha }_j)}{{\sum }_{l=1}^M\text{exp}(\mathbf{x}{(\mathbf{s},t)}^T{\alpha }_l)},$$ (17)

where α₁, …, α_M are vectors of regression coeffcients that control the effects of the covariates on the covariance. For these weights setting M = 1 gives w₁[x(s, t)] = 1 and the model is stationary with covariance K₁. The choice of logistic weights also ensures mean square continuity of the process realizations, as outlined in Section 3. For identification purposes, we fix α₁ = 0 as is customary in logistic regression.

The effect of an individual covariate on the covariance in (4) is rather obscure. A simple way to summarize the effect of the k^th covariate in terms of the posterior of the ratio of the covariance of two observations with x_k = 1 compared to the covariance of two observations with x_k = 0, assuming all other covariates are fixed at zero. That is,

$${\mathrm{\Delta }}_k(h_s,h_t)=\frac{{\sum }_{j=1}^M\frac{\text{exp}({\alpha }_{j1}+{\alpha }_{jk})}{{\sum }_{l=1}^M\text{exp}({\alpha }_{l1}+{\alpha }_{lk})}{K}_j(h_s,h_t)}{{\sum }_{j=1}^M\frac{\text{exp}({\alpha }_{j1})}{{\sum }_{l=1}^M\text{exp}({\alpha }_{l1})}{K}_j(h_s,h_t)}$$ (18)

where α_jk is the k^th element of α_j and $K_j(h_s,h_t)=K_j^s(\Vert h_s\Vert ){\gamma }_j^{|h_t|}$, with $K_j^s$ as in (16). We also inspect the ratio of correlations Δ̃_k(h_s, h_t) = Δ_k(h_s, h_t)/Δ_k(0, 0). We consider a covariate to have a significant effect on the variance if the posterior interval for Δ_k(0, 0) excludes one. Similarly, we consider a covariate to have a significant effect on the spatial (temporal) correlation if the posterior interval for Δ̃_k(h_s, 0) (Δ̃_k(0, h_t)) excludes one.

Finally, we discuss how to select the number of terms, M. One approach would be to model M as unknown and average over model space using reversible jump MCMC. Lopes et al. (2008) and Salazar et al. (2009) use reversible jump MCMC to select the number of factors in a latent spatial factor model. However, this approach is likely to pose computational challenges for large spatiotemporal data sets. Therefore, we select the number of terms using the deviance information criteria (DIC; Spiegelhalter et al. (2002)) and assume M is fixed in the final analysis. DIC is defined as

$$DIC=\mathrm{D̄}+p_D$$

where D̄ is the posterior mean of the deviance, pD = D̄ − D̂ is the effective number of parameters, and D̂ is the deviance evaluated at the posterior mean of the parameters in the likelihood, (2). The model’s fit is measured by D̄, while the model’s complexity is captured by p_D. We prefer models with small DIC.

5 Computational details

We perform MCMC sampling using R (http://www.r-project.org/), although it would be straight-forward to code the model using WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs/). We use Gibbs sampling to update θ_jt = [θ_j(s₁, t), …, θ_j(s_N, t)], β, σ², and γ_j, which have conjugate full conditionals. Metropolis sampling using a Gaussian candidate distribution is used to update α_jk, ρ_j and ν_j. We tune the Metropolis candidate distribution of give acceptance probability around 0.4. R code is available from the first author upon request.

Convergence is monitored using trace plots and autocorrelation plots for several representative parameters. We note that monitoring convergence is challenging for this model since the labels of the latent terms may switch during MCMC sampling. For example, exchanging α₁, ρ₁, ν₁ and γ₁ with α₂, ρ₂, ν₂ and γ₂ does not affect the covariance in (4). Therefore, rather than monitoring convergence for these parameters individually, we monitor convergence of the covariance (4) at several lags and of the spatiotemporal effect μ(s, t) for several spatiotemporal locations. For the simulation study in Section 6, we generate 10,000 samples and discard the first 2,000 samples as burn-in.

6 Simulation study

In this section we conduct a simulation study to compare our model with competing approaches. We generate all data from (2). Data are generated for 5 time points. For simplicity the data are independent over time (γ_j = 0). The data are generated on a 15 × 15 square grid covering [0, 1]²; 200 of the sites are analyzed as the training set, and 25 randomly-selected sites are withheld as the test set (125 total observations). Each data design has a single covariate which, for comparison with the convolution approach described below, is constant over time. We consider two cases for the covariate as functions of the first spatial coordinate:

• Linear: x_i = 2s_1i − 1

• Periodic: x_i = sin(10πs_1i).

We set β = 0 and σ = 0.1 and use either M = 1 or M = 2. We generate data using two spatial covariances:

• Exponential: τ₁ = τ₂ = 1, ν₁ = ν₂ = 0.5, ρ₁ = 0.02, and ρ₂ = 0.25

• Matérn: τ₁ = τ₂ = 1, ν₁ = ν₂ = 10, ρ₁ = 0.01, and ρ₂ = 0.03.

For the M = 2 case we take the weights to be logit(w₁(x_i)) = −1 + 2x_i and w₂(x_i) = 1 − w₁(x_i).

We compare our model with the kernel-convolution approach of Higdon et al. (1999). This model allows for non-stationarity, but does not explicitly model non-stationarity as a function of the spatial covariates. The kernel convolution model is

$$\mu (\mathbf{s},t)=\sum _{k=1}^R{w}_k(\Vert \mathbf{s}-{\psi }_k\Vert ){\theta }_{kt},$$ (19)

where ${\theta }_{kt}\stackrel{iid}{~}\mathrm{N}(0,{\tau }^2)$ is a kernel function, and ψ_k ∈ ℛ² are fixed spatial knots. We pick the kernel function to approximate the Matérn covariance with a spatially-varying range, i.e.,

$$w_k(\mathbf{u})=\frac{\gamma {(\nu +1)}^{1/2}{\nu }^{\nu /4+1/4}{|\mathbf{u}|}^{\nu /2-1/2}}{{\pi }^{1/2}\mathrm{\Gamma }(\nu /2+1/2)\mathrm{\Gamma }{(\nu )}^{1/2}{\rho }_k^{\nu /2+1/2}}{𝒦}_{\nu /2+1/2}\left(\frac{2{\nu }^{1/2}|\mathbf{u}|}{{\rho }_k}\right).$$ (20)

We take log(ρ_k) to be Gaussian with mean ρ̄ and Cov(log(ρ_k), log(ρ_l)) = δ² exp (−||ψ_k − ψ_l||/η). For priors we assume τ⁻², δ, η ~ Gamma(0.1,0.1) and ρ̄ ~ N(0,10²). The knots ψ_k are taken to be the 15 × 15 grid of locations for the data points (testing and training sites). Convergence was slow assuming the smoothness parameter ν was unknown, therefore it was fixed at the true value for this, and all other, models.

We fit our model with M = 1 and M = 2. The model with M = 1 is a stationary Matérn covariance, the model with M = 2 is the non-stationary model with covariance depending on the covariate. For priors we use $\beta ,{\alpha }_{jk}\stackrel{iid}{~}\mathrm{N}(0,{10}^2),{\sigma }^{-2},{\tau }_j^{-2}\stackrel{iid}{~}\text{Gamma}(0.1,0.1)$, and ρ_j ~ Unif(0,2).

We generate S = 25 data sets from each design. We compare the three models using mean squared error for the μ(s, t), separately for the training and testing observations, as well as coverage probabilities of the 90% posterior predictive intervals for μ(s, t) for the training observations. The results are reported in Table 1.

Table 1.

Simulation study results. Values reported as the mean (standard error) over the S = 25 data sets. The three models fit to each data set are the stationary model (“Stationary”), covariate dependent covariance model (“CDC”), and the non-stationary kernel convolution model (“Kernel Con.”).

(a) MSE for the training observations
True M	x model	Cov model	Stationary	CDC	Kernel Con.
1	Linear	Expo	0.102 (0.001)	0.102 (0.001)	0.100 (0.001)
1	Linear	Matérn	0.118 (0.005)	0.107 (0.003)	0.149 (0.006)
2	Linear	Expo	0.501 (0.010)	0.106 (0.002)	0.124 (0.002)
2	Linear	Matérn	0.172 (0.007)	0.087 (0.001)	0.091 (0.001)
2	Periodic	Expo	0.698 (0.018)	0.106 (0.002)	0.682 (0.014)
2	Periodic	Matérn	0.101 (0.001)	0.087 (0.001)	0.105 (0.003)

(b) MSE for the testing observations
True M	x model	Cov model	Stationary	CDC	Kernel Con.
1	Linear	Expo	0.495 (0.007)	0.494 (0.007)	0.506 (0.008)
1	Linear	Matérn	0.638 (0.007)	0.638 (0.007)	0.642 (0.008)
2	Linear	Expo	0.753 (0.013)	0.721 (0.013)	0.765 (0.013)
2	Linear	Matérn	0.437 (0.012)	0.424 (0.013)	0.433 (0.012)
2	Periodic	Expo	0.835 (0.012)	0.738 (0.011)	0.835 (0.013)
2	Periodic	Matérn	0.620 (0.015)	0.469 (0.015)	0.727 (0.023)

(c) Coverage probabilities of 90% intervals for the testing observations
True M	x model	Cov model	Stationary	CDC	Kernel Con.
1	Linear	Expo	0.89 (0.01)	0.89 (0.01)	0.91 (0.01)
1	Linear	Matérn	0.89 (0.01)	0.90 (0.01)	0.88 (0.01)
2	Linear	Expo	0.68 (0.01)	0.88 (0.01)	0.86 (0.01)
2	Linear	Matérn	0.83 (0.01)	0.92 (0.01)	0.85 (0.01)
2	Periodic	Expo	0.51 (0.02)	0.89 (0.01)	0.52 (0.02)
2	Periodic	Matérn	0.91 (0.01)	0.91 (0.01)	0.78 (0.01)

When the data are generated from the stationary model with M = 1 the three models per-form similarly, showing that the nonstationary models can reduce to the stationary model when appropriate. In the nonstationary case with M = 2 and a linear covariate, the stationary model has large mean squared error and coverage probability below the nominal level. In this case, the kernel convolution model performs well. Although the kernel convolution model does not directly use the covariate in covariance, it assumes that the spatial range varies smoothly over space and thus is able to approximate the nonstationary spatial covariance induced by the smoothly-varying covariate. In contrast, for the more complicated periodic covariate the kernel convolution model is not able to capture the nonstationarity and has high mean squared error and low coverage, similar to the stationary model. In this case, incorporating the covariate into the spatial covariance gives a dramatic improvement in mean squared error.

7 Data analysis

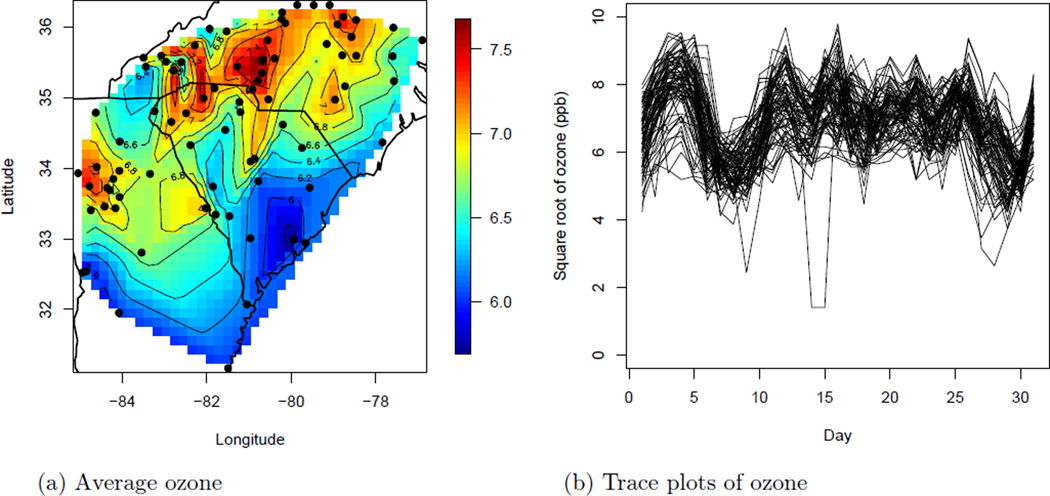
As an illustration of how our proposed spatiotemporal covariance model can be fit to real data, we analyze maximum daily ozone data in the Southeast US. The data were obtained from the US EPA’s Air Explorer Data Base (http://www.epa.gov/airexplorer/index.htm). The primary ozone standard says that the three-year average of the annual fourth-highest daily maximum 8-hour average concentration (EPA, 2004, p.3) must fall beneath 75 parts per billion. Our response variable is thus the maximum of the 8-hour rolling averages of ozone (ppb) in a given day. The data are plotted in Figure 2. We analyze data for the 31 days in August, 2005 for 79 monitoring stations in North Carolina, South Carolina, and Georgia (9/2440<1% missing). To justify a Gaussian model we use a square root transformation of the raw data.

Figure 2.

Plots of square root ozone (pbb). Panel (a) plots the average for each station (the stations are marked with points) and Panel (b) gives trace plots for each station (Day 1 is August 1, 2005).

We obtained daily average temperature and daily maximum wind speed from the NCDC’s Global Summary of the Day Data Base, and daily average cloud cover from the NCDC’s National Solar Radiation Data Base. Meteorological and ozone data are not observed at the same locations. Therefore we imputed meteorological variables at the ozone locations using spatial Kriging. Spatial imputation was performed using SAS version 9.1 and the MIXED procedure with spatial exponential covariance function, separately for each day and each variable. We treat these predictors as fixed. Li, Tang, and Lin (2009) discuss the implications of ignoring uncertainty in spatial predictors. Temperature and cloud cover are fairly smooth across space and thus have small interpolation errors, however there is more uncertainty in the wind speed interpolation. Accounting for uncertainty in the predictors using a spatial model for the meteorological variables warrants further consideration.

We transform the spatial locations to a two-dimensional surface using the Mercator projection, and then scale them to the unit square. We include as predictors in the mean, x(s, t)^T β, temperature, wind speed, cloud cover, log elevation, longitude, latitude, day of the year, and indicators of whether the station is in an urban or rural location (suburban is the baseline). All variables are standardized to have mean zero and variance one. We also include all two-way interactions between the three meteorological variables and quadratic effects for the meteorological variables. The covariance is modeled as a function of temperature, wind speed, and cloud cover.

We begin studying the data by analyzing the variogram. The spatial variogram is defined as γ(h) = E ([r(s) − r(s + hu)]²), where r(s) is the residual after accounting for the mean trend and u is a unit vector. This is often estimated as the sample mean squared difference between all pairs of observations in a bin D_h, i.e.,

$$\mathrm{\gamma ̂}(h)=\frac{1}{|D_h|}\sum _{(\mathbf{s},\mathbf{s}\prime )\in D_h}{[r(\mathbf{s})-r(\mathbf{s}\prime )]}^2$$ (21)

where D_h is the set of pairs of points on the same day with ||s−s′|| ∈ (h − ε, h + ε) and |D_h| is the cardinality of D_h. To explore the effects on covariates on the spatial covariance, we compute the variogram separately for different combinations of covariates. We estimate the variogram for pairs of observations with similar average covariates,

$$\mathrm{\gamma ̂}(h,{\mathrm{x̄}}_j)=\frac{1}{|D_{h{\mathrm{x̄}}_j}|}\sum _{(\mathbf{s},\mathbf{s}\prime )\in D_{h{\mathrm{x̄}}_j}}{[r(\mathbf{s})-r(\mathbf{s}\prime )]}^2$$ (22)

where D_hx̄j is the set of pairs of observations on the same day with ||s − s′|| ∈ (h − ε₁, h + ε₁) and [x_j(s) + x_j(s′)]/2 ∈ (x̄_j − ε₂, x̄_j + ε₂).

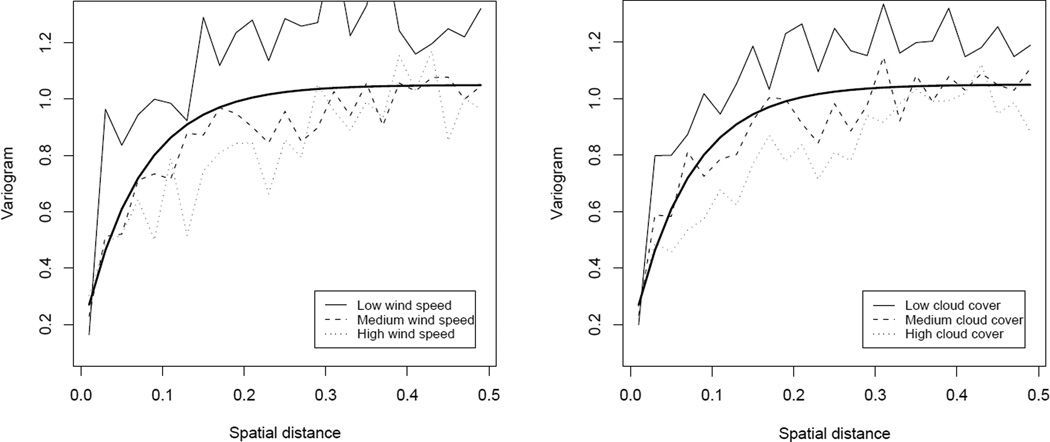
Figure 3 plots the sample variogram with 25 bins of standardized spatial distances separately for pairs of observations with covariate mean, [x_j(s) − x_j(s′)]/2, in three bins defined by the 25^th and 75^th percentiles of the covariate. There is evidence that the spatial covariance depends on the covariates. The variogram is high for pairs of observations with low wind speed and low cloud cover, especially at moderate spatial lag near 0.2. For all combinations of covariates considered, the variogram resembles an exponential variogram, therefore we assume ν_j = 0.5 for all analyses. We note that this does not imply that the non-stationary covariance is exponential, but rather a mixture of exponentials.

Figure 3.

Sample variogram for the ozone data, plotted for different values of wind speed (left) and cloud cover (right). The thick curves are the exponential variogram 0.15 + 0.9[1 − exp(−h/.07)].

We use the same priors as in Section 6, except now that we are accounting for temporal correlation we also assume γ_j in (15) has prior γ_j ~ Unif(0,1). We fit the model with M varying from M = 1 to M = 6. DIC (p_D) was 2573 (1079), 1997 (1413), 1328 (1681), 1253 (1691), 952 (1780), and 1098 (1737) for M = 1 to M = 6. The results are similar for M = 3 to M = 6; we present results with M = 5 since this value minimized DIC.

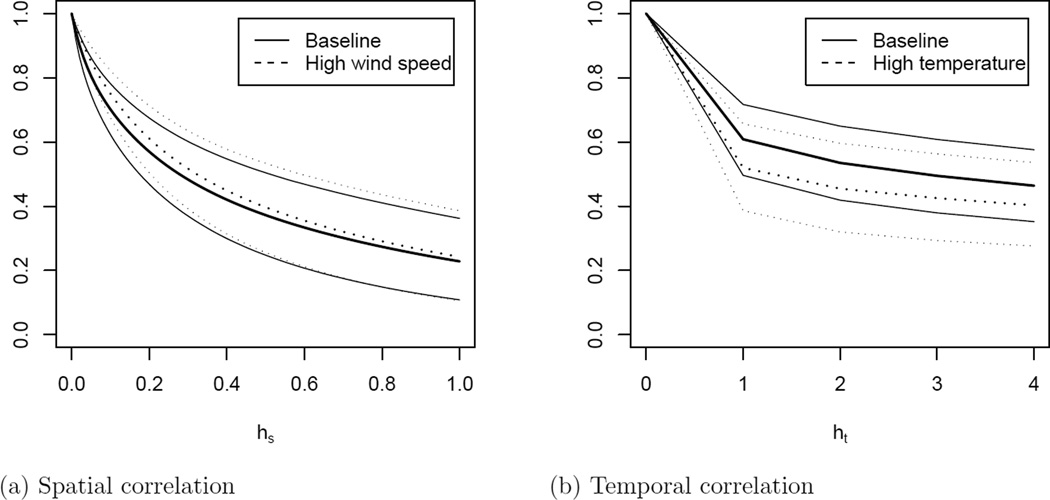
Table 2 and Figure 4 summarize the covariate effects on the mean and spatiotemporal correlation. As expected, the strongest mean effects are those for temperature and cloud cover. There are also significant effects for elevation, day, longitude, latitude, squared temperature, and squared wind speed. As suggested by Figure 3, spatial correlation is higher for days with high wind speed. It may be that in windy conditions more ozone is transported from location to location. Temperature and cloud cover do not appear to affect the spatial correlation for these data. However, there is evidence of weaker temporal correlation on hot and cloudy days.

Table 2.

Summary of the CDC model with M = 5 components. “Sample” gives the sample mean (sd) for the predictors. The remaining columns gives the posterior means (95% intervals) from for the mean effects β_k, the relative spatial correlation at lag 0.2 (Δ̃_k(0.2, 0)), and the relative temporal correlation at lag 3 (Δ̃_k(0, 3)). β_k, Δ̃_k(0.2, 0), and Δ̃_k(0, 3) are scaled to represent the effect of a one standard deviation increase in the predictor.

	Sample	βk	Δ̃k(0.2, 0)	Δ̃k(0, 3)
Temperature (F)	78.2 (3.64)	0.31 (0.19, 0.42)	0.97 (0.89, 1.03)	0.85 (0.72, 0.94)
Wind speed (m/s)	9.42 (2.48)	0.00 (−0.07, 0.05)	1.07 (1.02, 1.12)	1.02 (0.97, 1.07)
Cloud cover (%)	0.46 (0.23)	−0.18 (−0.28, −0.09)	1.01 (0.94, 1.07)	0.91 (0.81, 0.99)
Log elevation (ft)	4.77 (1.75)	0.08 (0.02, 0.14)	–	–
Urban	0.08 (0.27)	0.00 (−0.04, 0.05)	–	–
Rural	0.58 (0.49)	−0.02 (−0.07, 0.02)	–	–
Day	16.0 (9.09)	−0.03 (−0.05, −0.02)	–	–
Longitude	0.43 (0.25)	−0.26 (−0.48, −0.05)	–	–
Latitude	0.67 (0.23)	0.55 (0.32, 0.86)	–	–
Temp2	-	−0.05 (−0.11, 0.00)	–	–
WS2	-	0.01 (0.00, 0.02)	–	–
CC2	-	−0.02 (−0.07, 0.03)	–	–
Temp × WS	-	−0.03 (−0.07, 0.01)	–	–
Temp × CC	-	0.00 (−0.06, 0.08)	–	–
WS × CC	-	0.02 (−0.02, 0.06)	–	–

Figure 4.

Posterior mean (thick) and 95% intervals (thin) of the spatiotemporal correlation (4) for various combinations of the covariates. “Baseline” assumes that all covariates are zero (the mean after standardization) for both observations. The other plots assume that all covariates are zero with the exception of one covariate, which equals one standard deviation unit above the mean. The spatial correlation is plotted as a function of spatial distance h_s with temporal distance h_t = 0, and vice versa.

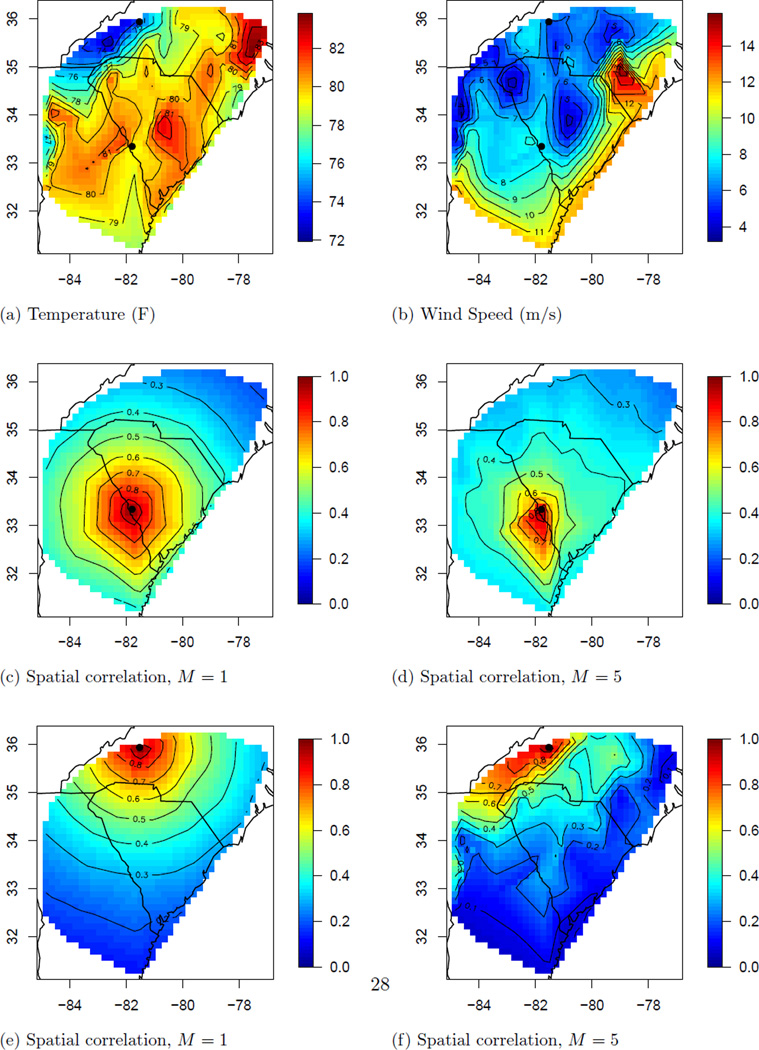
Figure 5 plots the posterior mean of the spatial correlation for two sites on August 3 for the stationary model with M = 1 and the non-stationary model with M = 5. The first site on the Georgia/South Carolina border (Figure 5d) has stronger correlation with sites to its southwest than its northeast for the non-stationary model. This is due to the strong winds to the southwest (Figure 5b). The second site in western North Carolina (Figure 5f) also has stronger correlation with sites to its southwest for the non-stationary model due to the moderate winds and low temperature to the southwest.

Figure 5.

Data and spatial covariance estimate for August 3, 2005 for stationary (M = 1) and non-stationary (M = 5) models. Panels (a) and (b) plot the observed temperature and wind speed. The remaining panels plot the posterior mean of the correlation between the point marked with a dot and the remaining sites.

8 Discussion

In this paper we present a class of spatiotemporal covariance functions that allows the covariance to depend on environmental conditions described by known covariates. Our simulation study shows that using covariates to explain non-stationarity can be more efficient than other commonly-used non-stationary models. For the Southeastern US ozone data, we find that spatial covariance is higher in the presence of high wind, and temporal correlation is higher in cool and sunny conditions.

Our analysis of the effect of covariates on the spatiotemporal covariance is limited because we only analyzed data for one month. Exploratory analyses using variograms for data throughout the year suggest that temperature also affects spatial covariance, but this is not apparent in the current analysis that only used days in August. We also included other variables, such as elevation and urban/rural indicators in the covariance model but these parameters had large posterior variance which led to slow MCMC convergence. Longer temporal coverage may allow these covariates to be included in the covariance model.

Finally, our covariance model assumes that all nonstationarity can be explained by the spatial covariates. However, in some cases a more flexible model would be useful. One approach would be to add pure functions of space and time as covariates in the covariance to capture non-stationarity. An even more flexible model would take the weights to be Gaussian processes, possibly with means that depend on the covariates, to allow the weights to vary smoothly through the spatial domain while still making use of the covariate information.