Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2013 Dec 18;112(5):552–561. doi: 10.1038/hdy.2013.139

Relatedness severely impacts accuracy of marker-assisted selection for disease resistance in hybrid wheat

M Gowda 1, Y Zhao 2, T Würschum 1, C FH Longin 1, T Miedaner 1, E Ebmeyer 3, R Schachschneider 4, E Kazman 5, J Schacht 6, J-P Martinant 6, M F Mette 2, J C Reif 2,*
PMCID: PMC3998782  PMID: 24346498

Abstract

The accuracy of genomic selection depends on the relatedness between the members of the set in which marker effects are estimated based on evaluation data and the types for which performance is predicted. Here, we investigate the impact of relatedness on the performance of marker-assisted selection for fungal disease resistance in hybrid wheat. A large and diverse mapping population of 1739 elite European winter wheat inbred lines and hybrids was evaluated for powdery mildew, leaf rust and stripe rust resistance in multi-location field trials and fingerprinted with 9 k and 90 k SNP arrays. Comparison of the accuracies of prediction achieved with data sets from the two marker arrays revealed a crucial role for a sufficiently high marker density in genome-wide association mapping. Cross-validation studies using test sets with varying degrees of relationship to the corresponding estimation sets revealed that close relatedness leads to a substantial increase in the proportion of total genotypic variance explained by the identified QTL and consequently to an overoptimistic judgment of the precision of marker-assisted selection.

Keywords: disease resistance, marker density, relatedness, marker-assisted selection, hybrid wheat

Introduction

Genome-wide association mapping is a powerful tool to dissect the genetic architecture of complex traits (Yu et al., 2006). It was originally developed in human genetics, later extensively used in animal genetic studies (McCarthy et al., 2008) and nowadays is also widely applied in numerous crop plants (Thornsberry et al., 2001; Breseghello and Sorrels, 2006; Cockram et al., 2010; Würschum et al., 2011). The power of QTL detection and the mapping resolution of genome-wide association mapping are largely determined by the extent and pattern of linkage disequilibrium in the germplasm under study (Myles et al., 2009; Reif et al., 2011). Especially in mapping populations containing diverse genotypes with a low extent of linkage disequilibrium, dense marker information is needed for genome-wide association mapping.

Association mapping is becoming increasingly popular as a first step in marker-assisted selection because it allows exploiting existing phenotypic and genomic data routinely collected in applied plant breeding programmes (Würschum, 2012). After having estimated effects of the detected functional markers, genotypic values are predicted based on the genomic profiles of the untested individuals (Guo et al., 2013). However, the accuracy of marker-assisted selection greatly depends on the precise assessment of QTL effects. Estimated marker effects can be unreliable and the proportion of genotypic variance explained by the detected QTL grossly overestimated, as has been uncovered by simulation studies (Beavis, 1994) and cross-validation surveys based on bi-parental (Utz et al., 2000; Schön et al., 2004) as well as multiple-line crosses (Liu et al., 2013). The potential bias in the estimation of the explained proportion of genotypic variance by detected QTL in association mapping was recently reported using a mapping population of 1739 winter wheat inbred lines and hybrids (Zhao et al., 2013).

Wheat (Triticum aestivum L.) is one of the most important crops grown on 200 million hectares of farmland worldwide (Ortiz et al., 2008). Biotic stress resistance is of central importance for a sustainable wheat production. Fungal diseases like powdery mildew caused by Blumeria graminis f. sp. tritici, leaf rust caused by Puccinia triticina and stripe rust (also known as yellow rust) caused by Puccinia striiformis f. sp. tritici adversely affect grain yield and quality in winter wheat. Resistance to the causative pathogens can be based on major, race-specific, host–pathogen recognition genes that are effective at all plant stages or on multiple additive minor genes conferring resistance to seedlings or adult plants in a more stage-specific manner (Singh et al., 2012). This expected mix of small and large effect genes makes stripe rust, leaf rust and powdery mildew resistance promising target traits to investigate the prospects of marker-assisted selection based on genome-wide association mapping (Miedaner and Korzun, 2012).

In order to elucidate the genetic architecture underlying fungal pathogen resistances in wheat, we performed an association mapping and a genomic selection study based on a large and diverse mapping population of 135 elite winter wheat lines and 1604 factorial F1 hybrids derived from them. Adult plants were evaluated for powdery mildew, leaf rust and stripe rust disease severity in multi-location field trials and fingerprinted with a 9 k and 90 k SNP array. The objectives of our study were to (1) examine the impact of the marker density on the power of QTL detection, (2) investigate the influence of genetic relatedness and significance threshold on the explained proportion of the total genotypic variance using cross-validation approaches and (3) propose a strategy to manage fungal disease resistances in wheat hybrid breeding based on the estimated dominance effects.

Materials and methods

Plant material and field experiments

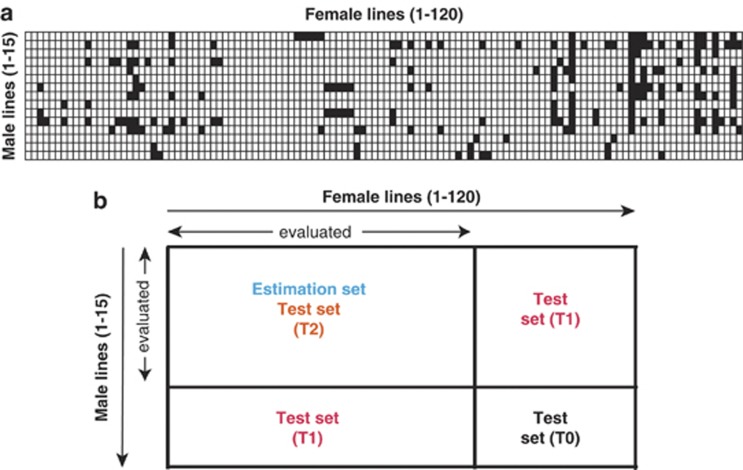
The present study was based on 135 elite winter wheat lines adapted to Central Europe and 1604 F1 hybrids derived from them (Longin et al., 2013; Miedaner et al., 2013; Zhao et al., 2013). The hybrids were generated in a facultative crossing scheme with 120 inbred lines serving as female and 15 inbred lines serving as male parents with the aid of chemical hybridization agents (Figure 1a). All of the above 1739 genotypes and in addition 10 commercial wheat lines as common checks were evaluated in unreplicated trials in three to four environments in Germany in the year 2012. The environments were Böhnshausen (latitude 51°51′N, longitude 10°57′E, 146 m above sea level (asl), sandy loam texture), Hadmersleben (latitude 51°59′N, longitude 11°18′E, 88 m asl, silt loam soil texture), Harzhof (latitude 54°24′N, longitude 9°51′E, 25 m asl, sandy loam soil texture) and Rosenthal (latitude 52°18′N, longitude 10°10′E, 73 m asl, loam soil texture). The experimental design was an alpha design where environments were treated as replications (for details, see Longin et al., 2013). Sowing density ranged from 230 to 250 seeds per m2 and plot sizes from 0.56 to 1.50 m2. In each environment, susceptible spreader cultivars were planted along one side of the plots and additionally around the experiments. Deliberate inoculation was done for leaf rust tests in Hadmersleben and Böhnshausen, whereas leaf rust disease severities in Rosenthal and Harzhof were scored based on natural infection. Stripe rust inoculation was applied in Rosenthal, Hadmersleben and Böhnshausen, but not in Harzhof. Puccinia triticina and Puccinia striiformis f. sp. tritici inoculates containing a broad variety of strains of each pathogen were sprayed on spreader lines only in Hadmersleben and Böhnshausen, while only a variety of strains of Puccinia striiformis f. sp. tritici was applied to whole testing plots in Rosenthal. Powdery mildew disease severity was recorded in Rosenthal, Hadmersleben and Harzhof based on natural infection only. Disease severity caused by the three pathogens was monitored on the same plots and visually scored on a scale from 1 (fully resistant) to 9 (fully susceptible) referring to the guidelines of the German Federal Plant Variety Office (Bundessortenamt, 2000). Data were recorded in the last week of June 2012 in all environments.

Figure 1.

Figure 1

Open in a new tab

(a) Factorial crossing scheme with 120 wheat inbred lines used as female and 15 lines used as male parents. Non-filled boxes indicate the presence and filled boxes indicate the absence of a particular hybrid. (b) Scheme for the allocation of hybrids to an estimation set and test sets T2, T1 and T0 with successively decreasing degrees of relatedness to the estimation set. Estimation sets comprised random selections of 80 (out of 120) female (F) and 10 (out of 15) male (M) ‘evaluated' parental inbred lines as well as 610 hybrids derived from them. Test sets included only hybrids not assigned so far that had both parents (T2), one parent (T1) or no parent (T0) in common with the hybrids in the corresponding estimation set.

Genotypic data generation

DNA was extracted according to standard procedures from all genotypes and fingerprinting was performed with a 9 k (Cavanagh et al., 2013; Würschum et al., 2013) and a 90 k (J-P Martinant, personal communication) SNP array based on the Illumina Infinium assay (Supplementary Tables S1, S2). All markers that were either monomorphic, had missing values of >5%, heterozygosity of >5% in inbred lines or had a minor allele frequency of <5% were discarded from analysis (Zhao et al., 2013). After this filtering, 1280 and 17 372 high-quality SNP markers were retained in the data set for the 9 k and 90 k SNP array, respectively. In total 87% of the markers present after filtering on the 9 k SNP array (Cavanagh et al., 2013) were also included in the 90 k SNP array.

Details on the 9 k SNP array data have been presented previously (Würschum et al., 2013). The 90 k SNP array data was based on 35 856 evaluable markers. For this set of SNPs, 23 159 were polymorphic. Among the 23 159 polymorphic markers, 17 687 SNPs had minor allele frequencies of >5%. From these SNPs, 315 markers were further discarded as they had missing values of >5%.

Associations among the 135 inbred lines were analyzed by estimating the Rogers' distances among the individuals (Rogers, 1972). The extent of linkage disequilibrium between pairs of loci was determined by estimating r2 as described by Hill and Robertson (1968) using the software Plabsoft (Maurer et al., 2008).

Phenotypic data analyses

All quantitative genetic parameters were estimated based on the performance of the 1739 inbred lines and hybrids. Residuals for all traits were normally distributed except for stripe rust, where data was skewed more towards resistance. Therefore, stripe rust data were transformed by applying an arcsin(sqrt(x/10)) transformation. We performed analyses of variance according to Payne (2006). The variance of hybrids was further split into variance due to general and variance due to specific combining ability effects (Hallauer and Miranda, 1981). Significance of variance components was tested by model comparison with likelihood ratio tests in which the halved P-values were used as an approximation (Stram and Lee, 1994). Heritability on an entry-mean basis was estimated as the ratio of the genotypic (σ2G) versus the phenotypic variance (σ2P), that is, σ2G/σ2P. The phenotypic variance σ2P comprises σ2G and the masking variances divided by the number of locations. In addition, we assumed fixed genetic effects and estimated the best linear unbiased estimates for the 1739 genotypes involved.

Genome-wide association mapping

SNP marker data from the 9 k and the 90 k arrays were analyzed independently. Design matrices for additive and dominance effects were specified for the hybrids and their parental lines according to the F∞ metric (Falconer and Mackay, 1996). As a consequence of the F∞ metric, SNP frequency has no influence on the estimated genetic effects under the assumption of absence of epistasis. Data from each environment were used in association mapping scans with correcting for population stratification with a kinship matrix (Zhao et al., 2013). The kinship matrices for the inbred lines and hybrids were modeled as described previously (Reif et al., 2011; Zhao et al., 2013). Briefly, we estimated the coancestry coefficients θij between inbreds i and j on the basis of marker data as θij=1+(Sij –1)/(1–T), where Sij is the proportion of marker loci with shared variants between inbreds i and j and T is the average probability that a variant from one parent of inbred i and a variant from one parent of inbred j are alike in state, given that they are not identical by descent. T was set as minimum of (1–Sij) values. The kinship matrix for the parental lines was modeled using twice the estimated coancestry coefficients θij between inbreds i and j on the basis of marker data. The general combining ability effects reflect the additive effects of the hybrids (Hallauer and Miranda, 1981). Therefore, the kinship matrix for the hybrids modeled the covariance among general combining ability effects (Zhao et al., 2013).

Genome-wide scans for marker–trait associations were conducted to detect main-effect QTL. The Bonferroni–Holm procedure (Holm, 1979) was applied to correct for multiple testing at different significance levels (P<0.10, P<0.05, P<0.01, P<0.001 and P<0.0001). The total proportion of phenotypic variance explained by the detected QTL was calculated by fitting all QTL simultaneously in a linear model to obtain R2adj. The proportion of the genotypic variance explained by all QTL was calculated as the ratio of pG=R2adj/h2, with h2 referring to the heritability on an entry-mean basis. All statistical analyses were performed using the software ASReml-R 3.0 (Butler et al., 2009).

Cross-validation

The accuracy of the prediction of genotypic values from marker effects was checked by cross-validation tests based on splitting the total data set into estimation and test sets. As in factorial mating designs relatedness between estimation and test set influences prediction accuracy, we followed the suggestion of Schrag et al. (2009) and sampled estimation sets consisting of 10 (out of 15) male and 80 (out of 120) female parental lines as well as 610 hybrids derived from them (Figure 1b). The sampling of the male and female lines was performed at random and the sampling scheme is available upon request. From the remaining hybrids, test sets with three successively decreasing degrees of relatedness to the estimation set were formed. Test set T2 most closely related to the estimation set included only hybrids derived from the same parents as the hybrids that had been evaluated, while the less related test set T1 included hybrids sharing one parent (either female or male parental line) with the hybrids in the estimation set and the least related test set T0 included only hybrids having no parents in common with the estimation set.

For each test set, we used 100 cross-validations and estimated marker effects of the QTL identified in the genome-wide association mapping scan in each cross-validation run. We applied the association mapping model outlined above correcting for population stratification with a kinship matrix. The obtained marker effects were then used to predict the performance of the hybrids in the T2, T1 and T0 test sets. The prediction accuracy for each test set was estimated as the Pearson correlation coefficient (r) between the predicted and the observed hybrid performance. The explained proportion of the total genotypic variance was computed for each test set (pG TS) as the ratio of r2/h2, with h2 referring to the heritability on an entry-mean basis. The difference between the on-average explained proportion of the total genotypic variance (pG) in the estimation set (pG ES) and a particular test set (pG TS) was denoted as bias.

Genomic selection

In addition to the association mapping, ridge regression best linear unbiased prediction (RR-BLUP; Whittaker et al., 2000; Zhao et al., 2013) was applied based on the adjusted entry means. SNP marker data from the 9 k and the 90 k arrays were analyzed independently. Design matrices for additive and dominance effects were again specified for the hybrids and their parental lines according to the F∞ metric (Falconer and Mackay, 1996). Details of the implementation of the RR-BLUP model have been described in Zhao et al. (2013). The prediction accuracy of the genomic selection approach was evaluated using the cross-validation scenarios outlined above. The explained proportion of the total genotypic variance was computed as the ratio of r2/h2, with h2 referring to the heritability on an entry-mean basis.

Results

High disease pressure across all environments permitted excellent genetic differentiation

Disease severity scores for all three fungal pathogens indicated comparable disease pressures across test locations (Supplementary Figure S1), which resulted in significant (P<0.01) Pearson correlation coefficients among phenotypic values determined at different environments (Supplementary Table S3). This suggested that a combined analysis across environments should not be severely biased by race-specific stress responses. The three diseases were scored on the same plots, which could cause an interaction among diseases and consequently a bias. We estimated the pairwise Pearson moment correlations between the adjusted entry means of the three diseases separately for the inbred and hybrids and observed low absolute values with a maximum of r=−0.21 between leaf and stripe rust resistance. This finding suggests that interactions between diseases are most likely not leading to a bias in the estimation of the level of resistance of the genotypes.

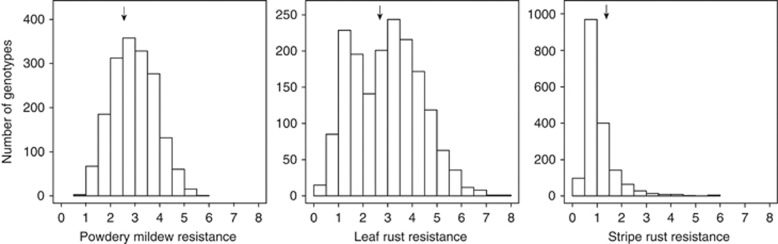
The distribution of the phenotypic values for powdery mildew resistance across environments followed approximately a normal distribution (Figure 2). In contrast, that for stripe rust was skewed towards resistant genotypes and the distribution of residuals did not follow a normal distribution. As a consequence, phenotypic values for stripe rust resistance were transformed for the analyses of variance. For leaf rust resistance, the phenotypic values tended towards a bimodal distribution, which can be interpreted as an indicator for the presence of resistance genes exhibiting large effects.

Figure 2.

Figure 2

Open in a new tab

Distributions of phenotypic values for resistance against powdery mildew, leaf rust and stripe rust based on an evaluation of 1739 genotypes (1604 hybrids and 135 parental lines) in three to four environments. Arrows indicate mean resistance of genotypes.

Means and ranges of evaluated disease severities hardly differed between parental inbred lines and hybrids (Table 1). However, wide genetic variation in disease resistances resulted in genotypic variances significantly (P<0.01) larger than zero for the parental lines and hybrids for all three disease resistance traits. Further decomposition of the genotypic variance of the hybrids revealed prevalence of additive gene actions as indicated by σ2GCA for powdery mildew and leaf rust disease severity. In contrast, non-additive genetic variance as indicated by σ2SCA was substantial for stripe rust and amounted to 28% of the total genotypic variance of the hybrids for disease severity. Heritability estimates for lines and hybrids were high for powdery mildew (0.79 and 0.77) and leaf rust resistance (0.85 and 0.75), and moderate to high for stripe rust resistance (0.76 and 0.58, respectively).

Table 1. First and second degree statistics for 135 inbred lines and 1604 hybrids derived from them for resistance against powdery mildew, leaf rust and stripe rust evaluated in field trials at three to four environments.

Source of variation Powdery mildew (1–9) Leaf rust (1–9) Stripe rust (1–9)
Means (ranges)
 Lines 2.74 (1.07–5.44) 2.88 (0.40–6.90) 1.66 (0.88–6.00)
 Hybrids 2.97 (0.92–5.97) 2.97 (0.13–7.54) 1.66 (0.76–6.01)
       
Variances
 σ2Lines 0.52a 1.40a 0.0073a
 σ2Hybrids 0.57a 1.36a 0.0045a
 σ2GCA—Female 0.48a 1.05a 0.0019a
 σ2GCA—Male 0.06a 0.07a 0.0012a
 σ2SCA 0.04a 0.08a 0.0012a
 σ2GCA—Female × Environment 0.08a 0.59a 0.0019a
 σ2GCA—Male × Environment 0.01a 0.02a 0.0011a
 σ2e 0.43 0.99 0.0093
       
HeritabilityLines 0.79 0.85 0.76
HeritabilityHybrids 0.77 0.75 0.58
Open in a new tab

Abbreviations: GCA, general combining ability; SCA, specific combining ability.

Disease resistance was scored from 1 (no damage) to 9 (no plant survived).

a

significantly different from zero at 0.001 level of probability.

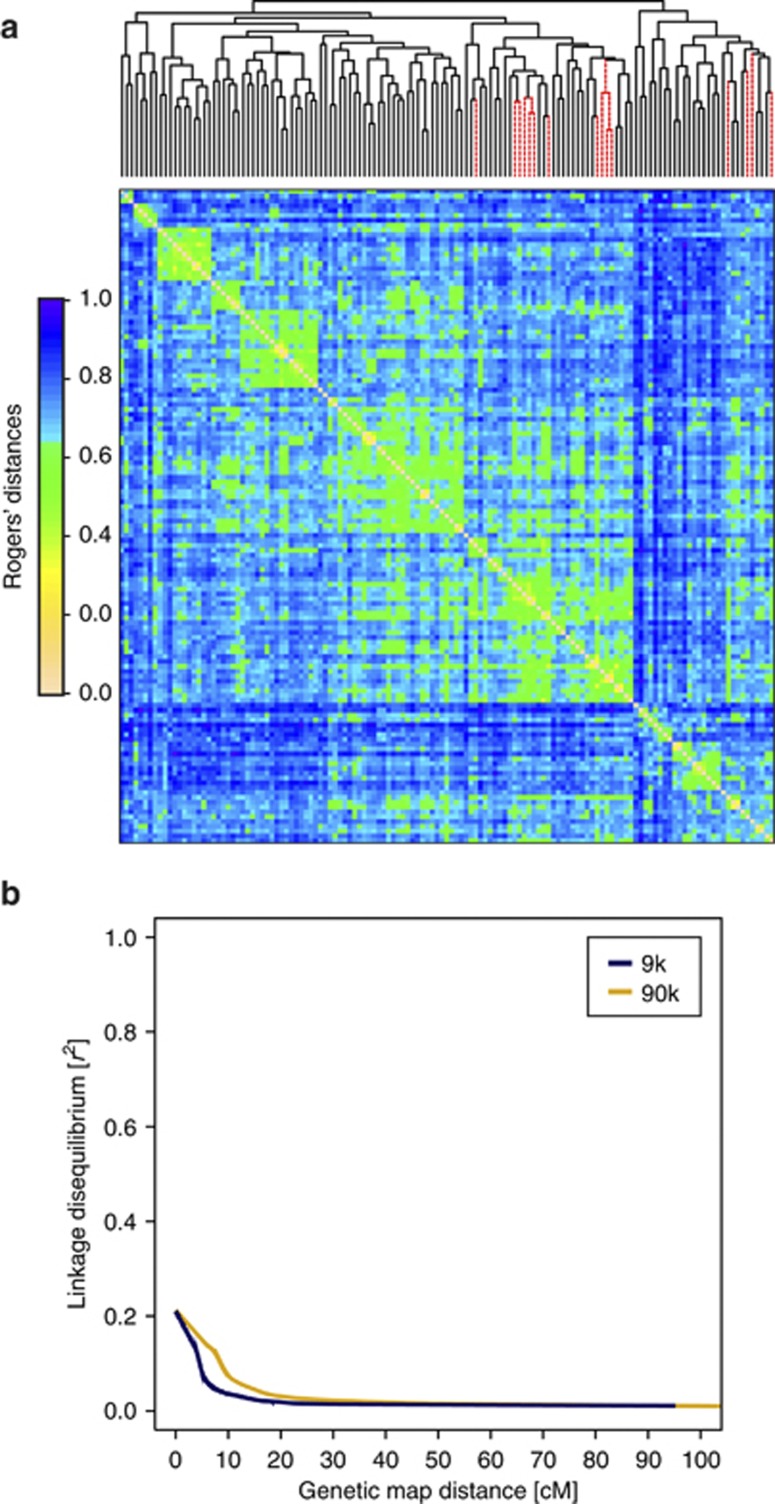
Family but not population structure was detected with 9 k and 90 k SNP arrays

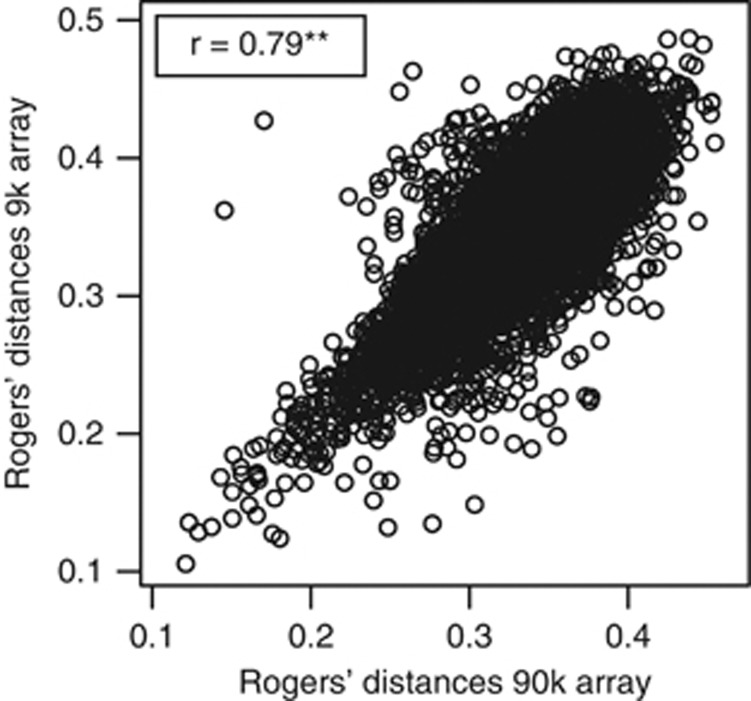
Previous analysis of 172 European winter wheat inbred lines including the 135 parental lines used in this study with the 9 k SNP array had not revealed major population structure, but showed the presence of family structures (Würschum et al., 2013). Population structure was defined following Würschum (2012) as the presence of major subpopulations such as heterotic groups in maize (Reif et al., 2005). In contrast, family structure refers to finer-scale degrees of relatedness among the lines. The genetic distance matrix based on the 90 k SNP array data was highly correlated (r=0.79) with that of the 9 k SNP data (Figure 3) and, consequently, the analysis of the 90 k SNP array data revealed also the presence of family structures (Figure 4a). Therefore, in the following association mapping analyses we corrected for family structures using kinship matrices for the parental lines and hybrids. In the data sets from the 9 k and the 90 k array, a comparable decline of linkage disequilibrium with genetic map distance was detected (Figure 4b).

Figure 3.

Figure 3

Open in a new tab

Associations between Rogers' distances among the 135 parental inbred lines estimated using a 9 k and a 90 k SNP array.

Figure 4.

Figure 4

Open in a new tab

(a) Pairwise Rogers' distances estimated for the winter wheat inbred lines based on the 90 k SNP array. Average linkage clustering was used for ordering the individual lines. The 15 lines used as male parents are marked as dashed line and the 120 used as female parents as solid lines. (b) Linkage disequilibrium as a function of genetic map distance for analysis based on 9 k SNP array (blue) or 90 k SNP array (red) data. Curves were fitted by robust locally fitted regression. A full color version of this figure is available at the Heredity journal online.

Marker–trait associations were detected for all three disease resistances based on the full data set

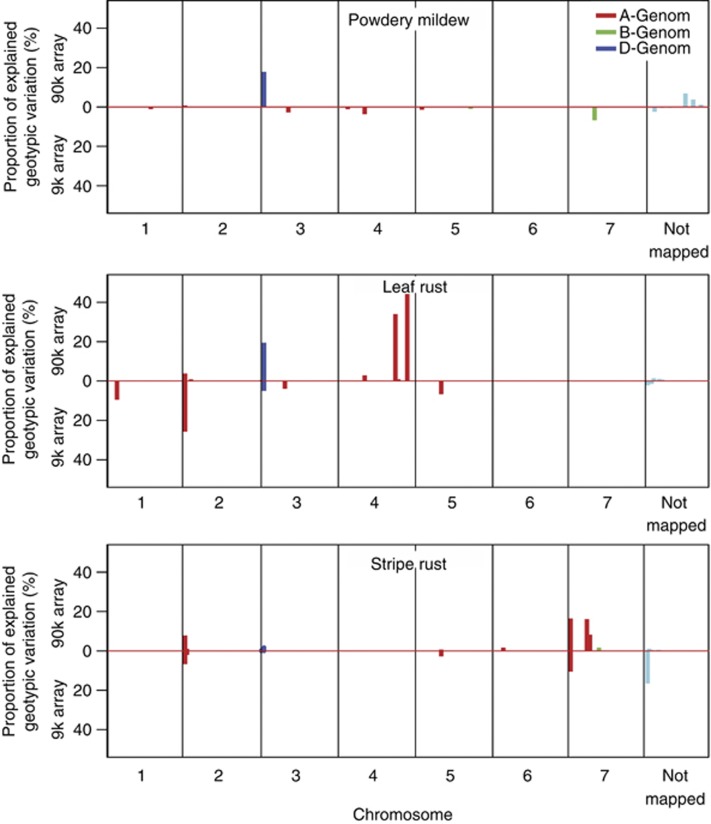
The genome-wide association mapping study exploited data of both the parents and the hybrids. The genome-wide scan based on the data from the 9 k SNP array revealed 11, 9 and 10 significant (P<0.05 and Bonferroni–Holm correction) marker–trait associations for powdery mildew, leaf rust and stripe rust resistances, respectively (Supplementary Tables S4, S5). With the data from the 90 k SNP array, 9, 44 and 62 significant (P<0.05 and Bonferroni–Holm correction) marker–trait associations were detected for powdery mildew, leaf rust and stripe rust resistances, respectively (Supplementary Tables S6, S7). The overlap of regions with significant (P<0.05 and Bonferroni–Holm correction) marker–trait associations identified based on data from 9 k and 90 k SNP arrays was moderate (Figure 5). Several regions with SNPs that exhibited a large contribution to the genotypic variance were detected based on the 90 k SNP array data but not with data from the 9 k SNP array. In line with this observation, the explained proportion of genotypic variance by all significant (P<0.05 and Bonferroni–Holm correction) markers increased by ∼50–70% from the analysis based on 9 k to analysis based on 90 k SNP array data.

Figure 5.

Figure 5

Open in a new tab

Explained proportion of genotypic variation for significant (P<0.05 and Bonferroni–Holm correction) marker–trait associations observed based on data from a 9 k and a 90 k SNP array for resistance against powdery mildew, leaf rust and stripe rust.

The SNPs explaining >15% of the genotypic variation for the three resistance traits were compared with previously described QTL using available consensus maps (Huang et al., 2012; Cavanagh et al., 2013). SNP IWA1512 associated with leaf rust resistance was located on chromosome 2A adjacent to the seedling resistance gene locus Lr37. Interestingly, the Lr37 locus is clustered with the stripe rust resistance gene Yr17 (Helguera et al., 2003) and SNP IWA6922 exhibiting an r2 value of 0.36 to IWA1512 explained a large proportion of the genotypic variance for stripe rust resistance. LG_Wsnp12474 on chromosome 4A and LG_Wsnp409 on chromosome 3D were positioned adjacent to the seedling resistance genes Lr28 and Lr32, respectively.

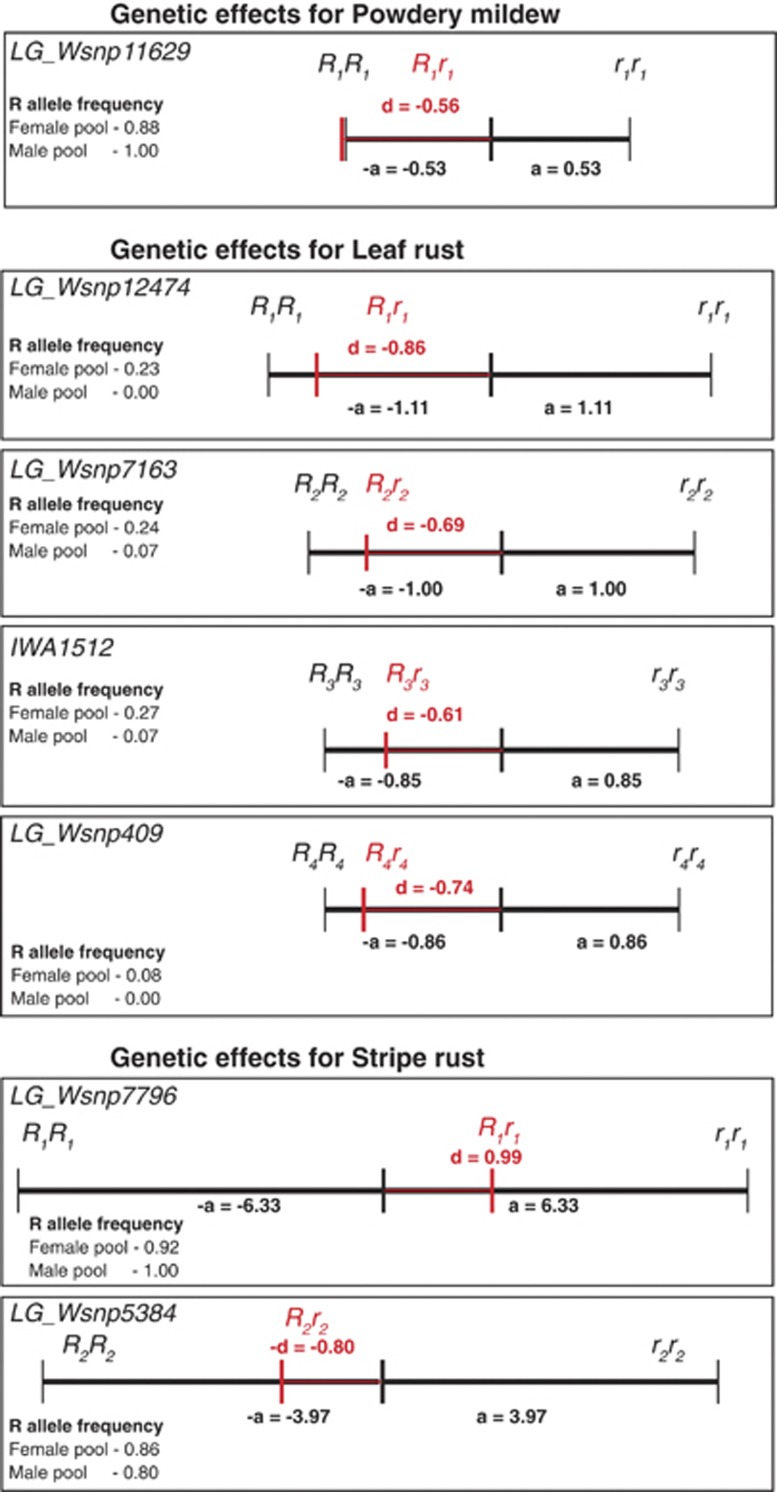
Except for powdery mildew resistance, we observed the presence of significant dominance effects (Supplementary Tables S4 and S6). Interestingly, only a few marker–trait associations showed combined significant (P<0.05 and Bonferroni–Holm correction) additive and dominance effects. For the SNPs with a large contribution to the genotypic variance (pG>15%), we estimated the degrees of dominance (Figure 6). All analyzed SNP markers except for LG_Wsnp7796 associated with stripe rust resistance were in the range of partial dominance in the direction of the more resistant genotype. Comparing the allele setup of the parental inbred lines and hybrids derived from them at these SNPs, we found resistance-promoting alleles of markers LG_Wsnp11629 (R1) concerning powdery mildew, LG_Wsnp12474 (R1) and LG-Wsnp409 (R4) concerning leaf rust and LG_Wsnp7796 (R1) and LG_Wsnp5384 (R2) concerning stripe rust resistance to be in particular relevant for low disease severity scores (Figure 7). In almost all parental inbred lines at least one SNP-allele associated with low stripe rust disease severity was fixed, whereas only approximately one quarter of the lines contained SNP-alleles associated with low leaf rust and one tenth of the lines had SNP-allele associated with low powdery mildew disease severity. In hybrids, the heterozygous presence of only one allele promoting resistance to powdery mildew and leaf rust was already associated with low disease severity, while for stripe rust, consistent low disease severity was only seen if alleles promoting resistance were present in the homozygous state.

Figure 6.

Figure 6

Open in a new tab

Additive and dominance effects of markers explaining >15% of the genotypic variance for resistance to powdery mildew, leaf rust and stripe rust in winter wheat populations. R represents alleles promoting resistance, r alleles promoting susceptibility. Marker abbreviations starting with IWA refer to markers on the 9 k SNP array, and LG_W refers to the markers on the 90 k SNP array.

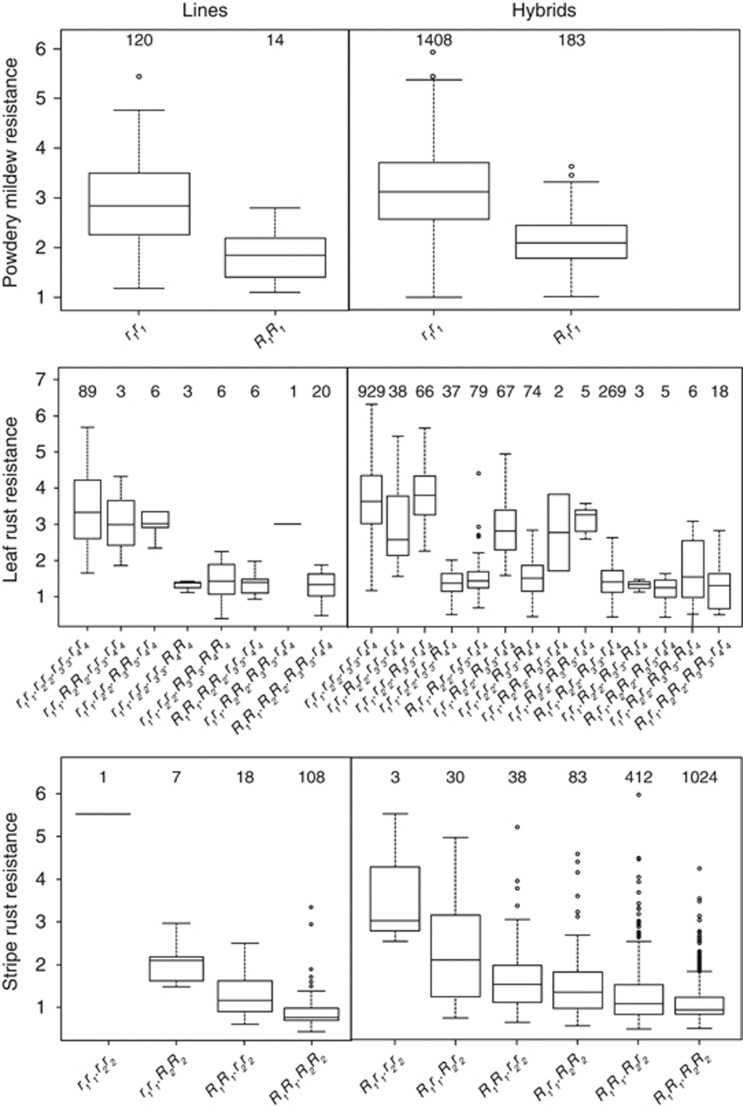
Figure 7.

Figure 7

Open in a new tab

Disease resistance in dependence on genotypes as determined by associated SNP markers. Box-whisker plots display disease severities determined in adult plants for different allele combinations at resistance gene loci explaining >15% of the genotypic variation for powdery mildew, leaf rust and stripe rust resistance as determined by associated SNP markers. The numbers at the top of each box refers to the observed numbers of parental inbred lines (left) and hybrids (right) with the indicated genotypes. Parental lines heterozygous at a gene locus of interest and all hybrids derived from them were excluded from analysis.

Cross-validation-based determination of the accuracy of prediction of marker-assisted selection revealed dependency on marker density and test set relatedness

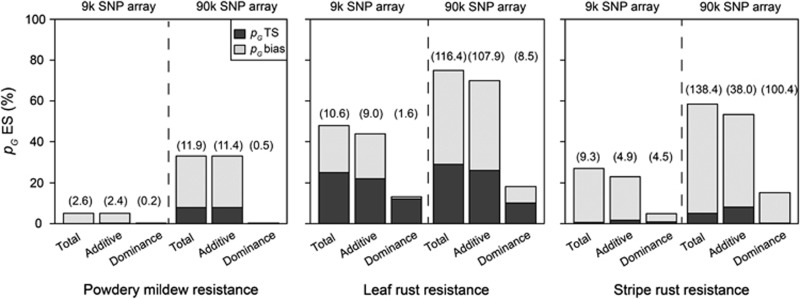
The test set of the cross-validation study comprises only hybrids and not the parental lines to avoid confounding effects of the differences in the mean performance of both germplasm groups on the prediction accuracy. The cross-validation analysis for the T0 scenario revealed a severe overestimation of the explained proportion of genotypic variance pG for all three resistance traits with both marker densities in association mapping (Figure 8). The bias in the estimation of the explained proportion of genotypic variance pG was substantial for powdery mildew and stripe rust resistance and slightly less pronounced for leaf rust resistance.

Figure 8.

Figure 8

Open in a new tab

Average proportion of cross-validated explained genotypic variance in the T0 test sets (pG TS; filled basis of columns) and estimation sets (pG ES; open top of columns) by all QTL (P<0.05 and Bonferroni–Holm correction) detected through genome-wide association mapping for resistance against powdery mildew, leaf rust and stripe rust with a 9 k and a 90 k SNP array. The difference in the explained proportion of genotypic variance between estimation set (pG ES) and test set (pG TS) is denoted as the bias (pG bias). The numbers in brackets indicate the average number of significant marker–trait associations in the estimation set based on 100 cross-validation runs.

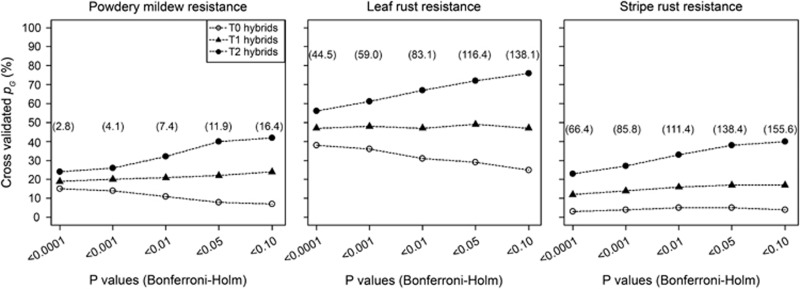
Trends and levels for pG at varying significance threshold differed largely for the three test sets T0, T1 and T2 as illustrated for the 90 k SNP array data (Figure 9). For the T0 test sets least related to the estimation set, we observed a decrease in pG with more liberal significance thresholds. In contrast, for T2 test sets closest related to the estimation set, we observed a decrease in pG with more stringent significance thresholds, while the intermediate test set T1 was not severely impacted by the different thresholds. The magnitude of pG was highest for T2 and lowest for T0 across all significance thresholds.

Figure 9.

Figure 9

Open in a new tab

Proportion of cross-validated genotypic variance explained in the test sets (pG TS) based on marker–trait associations detected in estimation set for resistance against powdery mildew, leaf rust and stripe rust with 90 k SNP array data at different levels of significance. T2 test sets included hybrids sharing both parents, T1 test sets hybrids sharing one parent and T0 test sets hybrids having no parents in common with the hybrids in the related estimation set. Numbers in brackets indicate the average number of significant marker–trait associations in the estimation set based on 100 cross-validations.

Cross-validated accuracy of genomic selection

Trends for pG for the three test sets T0, T1 and T2 was similar for genomic as compared with marker-assisted selection approach (Table 2). For the T0 test sets least related to the estimation set, we observed low values in pG often not substantially higher compared with those for marker-assisted selection. The only exception was the pG value for leaf rust resistance based on the 90 k SNP array data. For the T1 and T2 test sets, we observed a substantial increase in pG compared with T0.

Table 2. Average proportion of cross-validated explained genotypic variance in the test sets of ridge regression best linear unbiased prediction for resistance against powdery mildew, leaf rust and stripe rust based on data from a 9 k and a 90 k SNP array.

  Powdery mildew Leaf rust Stripe rust
9 k SNP array
 T0 0.06 0.26 0.07
 T1 0.42 0.57 0.35
 T2 0.81 0.92 0.65
       
90 k SNP array
 T0 0.06 0.43 0.11
 T1 0.43 0.69 0.39
 T2 0.81 0.92 0.68
Open in a new tab

T2 test sets included hybrids sharing both parents, T1 test sets hybrids sharing one parent and T0 test sets hybrids having no parents in common with the hybrids in the related estimation set.

Discussion

Increased marker density leads to higher power to detect QTL

The power to detect QTL in genome-wide association mapping greatly depends on the number of genotypes included, the heritability of the traits under consideration and the applied marker density. Our study based on a large population of 1739 elite wheat genotypes comprising 135 inbred lines and 1604 hybrids derived from them allowed an estimation of genotypic effects for fungal pathogen resistance with high accuracies (Table 1). Therefore, the population size and quality of phenotyping provides a solid basis for genome-wide association mapping for powdery mildew, as well as leaf and stripe rust resistances.

We observed a comparable decline of linkage disequilibrium with genetic map distance in the data sets of the parental lines from the 9 k and the 90 k array (Figure 4b), suggesting that genome-wide association mapping in wheat can be expected to profit from an increased marker density. In accordance with this expectation, we observed in the analysis of the full data set (Figure 5) and also in our cross-validation studies (Figure 7) an increased explained proportion of genotypic variance for 90 k compared with 9 k SNP array-based data. Therefore, we will in the following focus on the results of the 90 k SNP data if not mentioned otherwise.

The genome-wide scan revealed only a moderate overlap of regions with significant (P<0.05 and Bonferroni–Holm correction) marker–trait associations identified based on data from 9 k and 90 k SNP arrays (Figure 5). Astonishingly, markers which were significant at the 9 k SNP array were often not significant at the 90 k SNP array even when applying the same Bonferroni–Holm corrected significance threshold (Supplementary Table S4). These discrepancies can be explained by differences in the kinship matrices, which displayed a Pearson moment correlation of 0.79 (P<0.01) (Figure 3).

The impact of dominance on marker-assisted selection in wheat hybrid breeding is trait-dependent

The decomposition of the genetic variance suggested that dominance effects should mainly influence stripe rust resistance, with the contribution of dominance effects amounting to 28% of the total genetic variance, in contrast to only 7% for powdery mildew and leaf rust resistance (Table 1). Accordingly, no SNPs exhibiting significant (P<0.05 and Bonferroni–Holm correction) dominance effects (Supplementary Tables S4 and S6) were detected for powdery mildew resistance and cross-validation did not indicate the involvement of dominance effects (Figure 8). In contrast, for leaf rust resistance, a number of SNPs exhibiting significant dominance effects was detected (Supplementary Tables S4 and S6) and including dominance effects in marker-assisted selection increased the explained proportion of genotypic variance for leaf rust resistance (Figure 8). In accordance to the phenotypic data analysis for stripe rust resistance, we also detected a large number of SNPs exhibiting significant dominance effects (Supplementary Tables S4 and S6). However, our cross-validation studies revealed that adding dominance effects into the prediction model hardly increased the explained proportion of genotypic variation in comparison to prediction solely based on additive effects (Figure 8). This might be due to the presence of multiple dominance effects, each with only a small contribution to the total genotypic variation of stripe rust resistance.

The estimated degrees of dominance for all markers explaining >15% of the genotypic variation were in the range of partial dominance except for powdery mildew (Figure 6), indicating that ideally superior genotypes should carry the resistance genes in a homozygous state. A closer examination of the distribution of hybrid genotypes grouped according to their allele status however revealed that hybrids showing low disease severity for powdery mildew and leaf rust can also be achieved by the presence of particular resistance loci in a heterozygous state (Figure 7). This finding abolishes the need to fix all resistance loci as in inbred lines and opens new options unique to hybrid breeding to manage disease resistances in wheat via the combination of male and female parental lines carrying diverse resistance loci (Longin et al., 2013).

Cross-validation reveals a large bias in genotypic variation explained by detected QTL

To judge possible options for a further refinement of association mapping in hybrid wheat breeding, cross-validation and simulation studies were applied to investigate the bias in estimating the explained proportion of the genotypic variation. Cross-validations allow distinguishing between the goodness of fit of the final list of detected QTL in the total data set and the prediction accuracy in independent data sets. Such cross-validation studies have been reported previously in the context of bi-parental QTL mapping (Beavis, 1998; Schön et al., 2004). Schön et al. (2004), for instance, used an extended mapping population in maize of ∼1000 individuals phenotyped for grain yield and grain moisture in 19 locations to show that splitting their data set into smaller subsets led to gross overestimation of the explained proportion of the genotypic variation, particularly in small mapping populations. According to their conclusion, increasing the number of genotypes analyzed added more to the reliability than increasing the number of environments. Liu et al. (2013) extended these findings for QTL mapping in multiple crosses with ∼1000 maize lines evaluated for grain yield and grain moisture and also observed that QTL results were unreliable and hampered by a large overestimation of the explained proportion of genotypic variance based on the detected QTL. Our association mapping study in winter wheat was also based on a large set of 135 wheat inbred lines and their 1604 factorial hybrids evaluated for three fungal disease resistance traits. The genetic architecture of these traits can be expected to be less complex compared with grain yield and grain moisture in maize. Nevertheless, we observed that marker-assisted selection even for these three disease resistance traits is afflicted with a large overestimation of the explained proportion of genotypic variance of the detected QTL (Figure 8). This underlines the necessity for validation of prediction results also for association mapping employing large populations.

The observed bimodal distribution for genotypic values for leaf rust resistance pointed toward the presence of QTL with large effects (Figure 2). In accordance with this expectation, we observed SNPs on chromosome 2A, 3D and 4A, each explaining >15% of the genotypic variation in the full data set (Figure 5, Supplementary Tables S4 and S6). Moreover, cross-validated genotypic variation explained by all SNPs for the 9 k as well as for the 90 k SNP array was >20% (Figure 8), supporting the view that a substantial proportion of the estimated effects are stable. This clearly suggests that marker-assisted selection based on the 90 k SNP array is valuable for leaf rust resistance in European wheat. In contrast, the further potential of marker-assisted selection for powdery mildew and stripe rust resistance based on the 9 k and 90 k SNP array seems limited due to the high bias and the low proportion of cross-validated genotypic variance explained by the detected marker–trait associations (Figure 8).

Choice of the optimal significance threshold in marker-assisted selection is affected by genetic relatedness

Knapp (1998) suggested application of a conservative significance threshold to decrease the rate of false positives and hence to improve the accuracy of marker-assisted selection. This was in contrast to the results of a simulation study (Moreau et al., 1998) and of a cross-validation study in maize (Schön et al., 2004) reporting that increasing the type I error rate led to a higher relative efficiency of marker-assisted selection because the power of QTL detection increased more than the risk of detecting false positives. Our results revealed that for the unrelated test set T0, the explained genotypic variance increased with application of more stringent significance thresholds for powdery mildew and leaf rust resistance and stayed the same for stripe rust (Figure 9). In contrast, for test set T2 most related to the estimation set, application of more stringent significance thresholds resulted in a reduction of the explained genotypic variance for all three traits. This observed discrepancy in the trends clearly suggests that the optimal choice of significance thresholds in marker-assisted selection is not only determined by a balance between power of QTL detection and rate of false positives but also by the possibility to exploit relatedness to predict genotypic values.

An increase in the accuracy of the prediction of genotypic values with an enhanced relatedness among the estimation and test sets is well known from genomic selection studies (Habier et al., 2007). We confirmed the impact of relatedness in genomic selection using our data set and applying RR-BLUP, which exploits the information of all marker data (Table 2). Interestingly, we observed for the T0 scenario only slight differences between prediction accuracy for the marker-assisted (Figure 8) and the genomic selection approach (Table 2). In contrast, for the T1 and T2 scenario, where relatedness is exploited in a more pronounced manner, genomic selection was substantially more accurate than marker-assisted selection.

Our cross-validation study for marker-assisted selection revealed also a severe impact of relatedness between estimation and test set on the explained genotypic variance. The explained proportion of genotypic variance was up to 2–7 times higher if estimation and test populations were highly related (T2) compared with an unrelated test population (T0; Figure 9). These findings suggest that evaluation of the prospects of marker-assisted selection based on cross-validation studies relying on closely related estimation and test sets—as for instance in bi-parental QTL mapping studies—yields a too optimistic picture if the aim is to evaluate the long-term validity of functional markers. Therefore, robustness and potential of marker-assisted selection on a long-term should be evaluated using estimation and test populations exhibiting a low degree of relatedness.

Data archiving

Relevant data sets have been added as supplementary Tables and also available from the Dryad Digital Repository: 10.5061/dryad.461nc.

Acknowledgments

We thank Patrick Schweizer from IPK Gatersleben for valuable comments on the manuscript. This research was conducted within the HYWHEAT project funded by BMBF (Grant ID: FKZ0315945D).

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Figure S1
Click here for additional data file. (2MB, tif)
Supplementary Tables
Click here for additional data file. (34.4MB, xls)
Supplementary Information
Click here for additional data file. (205KB, doc)

References

  1. Beavis WD. 49th Annual Corn and Sorghum Industry Research Conference. ASTA: Washington DC, USA; 1994. The power and deceit of QTL experiments: lessons from comparative QTL studies; pp. 250–266. [Google Scholar]
  2. Beavis WD.1998QTL analyses: power, precision and accuracyIn: Paterson AH, (ed)Molecular Dissection of Complex Traits AHCRC Press: Boca Raton, FL, USA; 145–162. [Google Scholar]
  3. Breseghello F, Sorrels ME. Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics. 2006;172:1165–1177. doi: 10.1534/genetics.105.044586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bundessortenamt . Richtlinien für die Durchführung von landwirtschaftlichen Wertprüfungen und Sortenversuchen. Landbuch Verlagsgesellschaft mbH: Hannover, Germany; 2000. [Google Scholar]
  5. Butler D, Cullis BR, Gilmour AR, Gogel BJ. ASREML-R, Reference Manual. Version 3. Queensland Department of Primary Industries and Fisheries: Brisbane, Australia; 2009. [Google Scholar]
  6. Cavanagh CR, Chao S, Wang S, Huang BE, Stephen S, Kiani S, et al. Genome-wide comparative diversity uncovers multiple targets of selection for improvement in hexaploid wheat landraces and cultivars. Proc Natl Acad Sci USA. 2013;110:8057–8062. doi: 10.1073/pnas.1217133110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cockram J, White J, Zuluaga DL, Smith D, Comadran J, Macaulay M, et al. Genome-wide association mapping to candidate polymorphism resolution in the unsequenced barley genome. Proc Natl Acad Sci USA. 2010;107:21611–21616. doi: 10.1073/pnas.1010179107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Falconer DS, Mackay TFC.1996Introduction to Quantitative Genetics4th ednLongman House: London, UK [Google Scholar]
  9. Guo Z, Tucker DM, Wang D, Basten CJ, Ersoz E, Briggs WH, et al. Accuracy of across-environment genome-wide prediction in maize nested association mapping populations. G3 (Bethesda) 2013;3:263–272. doi: 10.1534/g3.112.005066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Habier D, Fernando RL, Dekkers JCM. The impact of genetic relationship information on genome-assisted breeding values. Genetics. 2007;177:2389–2397. doi: 10.1534/genetics.107.081190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hallauer AR, Miranda JB. Quantitative Genetics in Maize Breeding. Iowa State University Press: Ames, IA, USA; 1981. [Google Scholar]
  12. Helguera M, Khan IA, Kolmer J, Lijavetzky D, Zhong-qi L, Dubcovsky J. PCR assays for the Lr37-Yr17-Sr38 cluster of rust resistance genes and their use to develop isogenic hard red spring wheat lines. Crop Sci. 2003;43:1839–1847. [Google Scholar]
  13. Hill WG, Robertson A. Linkage disequilibrium in finite populations. Theor Appl Genet. 1968;38:226–231. doi: 10.1007/BF01245622. [DOI] [PubMed] [Google Scholar]
  14. Holm S. A simple sequentially rejective Bonferroni test procedure. Scand J Stat. 1979;6:65–70. [Google Scholar]
  15. Huang BE, George AW, Forrest KL, Kilian A, Hayden MJ, Morell MK, et al. A multiparent advanced generation inter-cross population for genetic analysis in wheat. J Plant Biotechnol. 2012;10:826–839. doi: 10.1111/j.1467-7652.2012.00702.x. [DOI] [PubMed] [Google Scholar]
  16. Knapp SJ. Marker-assisted selection as a strategy for increasing the probability of selecting superior genotypes. Crop Sci. 1998;38:1164–1174. [Google Scholar]
  17. Liu W, Maurer HP, Reif JC, Melchinger AE, Utz HF, Tucker MR, et al. Optimum design of family structure and allocation of resources in association mapping with lines from multiple crosses. Heredity. 2013;110:71–79. doi: 10.1038/hdy.2012.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Longin CFH, Gowda M, Mühleisen J, Ebmeyer E, Kazman E, Schachschneider R, et al. Hybrid wheat: quantitative genetic parameters and consequences for the design of breeding programs. Theor Appl Genet. 2013;126:2791–2801. doi: 10.1007/s00122-013-2172-z. [DOI] [PubMed] [Google Scholar]
  19. Maurer HP, Melchinger AE, Frisch M. Population genetic simulation and data analysis with Plabsoft. Euphytica. 2008;161:133–139. [Google Scholar]
  20. McCarthy MI, Abecasis GR, Cardon LR, Goldstein DB, Little J, Ioannidis JP, et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9:356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
  21. Miedaner T, Korzun V. Marker-assisted selection for disease resistance in wheat and barley breeding. Phytopathology. 2012;102:560–566. doi: 10.1094/PHYTO-05-11-0157. [DOI] [PubMed] [Google Scholar]
  22. Miedaner T, Zhao Y, Gowda M, Longin CFH, Korzun V, Ebmeyer E, et al. Genetic architecture of resistance to Septoria tritici blotch in European wheat. BMC Genomics. 2013;14:858. doi: 10.1186/1471-2164-14-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Moreau L, Charcosset A, Hospital F, Gallais A. Marker-assisted selection efficiency in populations of finite size. Genetics. 1998;148:1353–1365. doi: 10.1093/genetics/148.3.1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Myles S, Peiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, et al. Association mapping: critical considerations shift from genotyping to experimental design. Plant Cell. 2009;21:2194–2202. doi: 10.1105/tpc.109.068437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ortiz R, Sayre KD, Govaerts B, Gupta R, Subbarao GV, Ban T, et al. Climate change: can wheat beat the heat? Agriculture. Ecosystem Environ. 2008;126:46–58. [Google Scholar]
  26. Payne RW. New and traditional methods for the analysis of unreplicated experiments. Crop Sci. 2006;46:2476–2481. [Google Scholar]
  27. Reif JC, Hallauer AR, Melchinger AE. Heterosis and heterotic pattern in maize. Maydica. 2005;50:215–223. [Google Scholar]
  28. Reif JC, Maurer HP, Korzun V, Ebmeyer E, Miedaner T, Würschum T. Mapping QTLs with main and epistatic effects underlying grain yield and heading time in soft winter wheat. Theor Appl Genet. 2011;123:283–292. doi: 10.1007/s00122-011-1583-y. [DOI] [PubMed] [Google Scholar]
  29. Rogers JS. Measures of Genetic Similarity and Genetic Distance. University of Texas Publications 7213: Austin, TX, USA; 1972. pp. 145–153. [Google Scholar]
  30. Schrag TA, Frisch M, Dhillon BS, Melchinger AE. Marker-based prediction of hybrid performance in maize single-crosses involving doubled haploids. Maydica. 2009;54:353–362. [Google Scholar]
  31. Schön CC, Utz HF, Groh S, Truberg B, Openshaw S, Melchinger AE. Quantitative trait locus mapping based on resampling in a vast maize testcross experiment and its relevance to quantitative genetics for complex traits. Genetics. 2004;167:485–498. doi: 10.1534/genetics.167.1.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Singh S, Hernandez MV, Crossa J, Singh PK, Bains NS, Singj K, et al. Multi-trait and multi-environment QTL analyses for resistance to wheat diseases. PLoS One. 2012;7:e38008. doi: 10.1371/journal.pone.0038008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Stram DO, Lee JW. Variance components testing in longitudinal mixed effects model. Biometrics. 1994;50:1171–1177. [PubMed] [Google Scholar]
  34. Thornsberry JM, Goodman MM, Doebley J, Kresovich S, Nielsen D, Buckler ES. Dwarf8 polymorphisms associate with variation in flowering time. Nat Genet. 2001;28:286–289. doi: 10.1038/90135. [DOI] [PubMed] [Google Scholar]
  35. Utz HF, Melchinger AE, Schön CC. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics. 2000;154:1839–1849. [PMC free article] [PubMed] [Google Scholar]
  36. Whittaker JC, Thompson R, Denham MC. Marker-assisted selection using ridge regression. Genet Res. 2000;75:249–252. doi: 10.1017/s0016672399004462. [DOI] [PubMed] [Google Scholar]
  37. Würschum T. Mapping QTL for agronomic traits in breeding populations. Theor Appl Genet. 2012;125:201–210. doi: 10.1007/s00122-012-1887-6. [DOI] [PubMed] [Google Scholar]
  38. Würschum T, Langer SM, Longin CFH, Korzun V, Akhunov E, Ebmeyer E, et al. Population structure, genetic diversity and linkage disequilibrium in elite winter wheat assessed with SNP and SSR marker. Theor Appl Genet. 2013;126:1477–1486. doi: 10.1007/s00122-013-2065-1. [DOI] [PubMed] [Google Scholar]
  39. Würschum T, Maurer HP, Schulz B, Möhring J, Reif JC. Genome-wide association mapping reveals epistasis and genetic interaction networks in sugar beet. Theor Appl Genet. 2011;123:109–118. doi: 10.1007/s00122-011-1570-3. [DOI] [PubMed] [Google Scholar]
  40. Yu J, Pressoir G, Briggs WH, Bi IV, Yamasaki M, Doebley J, et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 2006;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]
  41. Zhao Y, Gowda M, Würschum T, Longin CFH, Korzun V, et al. Dissecting the genetic architecture of frost tolerance in wheat adapted to Central Europe with genome-wide mapping approaches. J Exp Bot. 2013;64:4453–4460. doi: 10.1093/jxb/ert259. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure S1
Click here for additional data file. (2MB, tif)
Supplementary Tables
Click here for additional data file. (34.4MB, xls)
Supplementary Information
Click here for additional data file. (205KB, doc)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES