Stacked Predictive Sparse Coding for Classification of Distinct Regions of Tumor Histopathology

Abstract

Image-based classification of tissue histology, in terms of distinct histopathology (e.g., tumor or necrosis regions), provides a series of indices for tumor composition. Furthermore, aggregation of these indices from each whole slide image (WSI) in a large cohort can provide predictive models of clinical outcome. However, the performance of the existing techniques is hindered as a result of large technical variations (e.g., fixation, staining) and biological heterogeneities (e.g., cell type, cell state) that are always present in a large cohort. We suggest that, compared with human engineered features widely adopted in existing systems, unsupervised feature learning is more tolerant to batch effect (e.g., technical variations associated with sample preparation) and pertinent features can be learned without user intervention. This leads to a novel approach for classification of tissue histology based on unsupervised feature learning and spatial pyramid matching (SPM), which utilize sparse tissue morphometric signatures at various locations and scales. This approach has been evaluated on two distinct datasets consisting of different tumor types collected from The Cancer Genome Atlas (TCGA), and the experimental results indicate that the proposed approach is (i) extensible to different tumor types; (ii) robust in the presence of wide technical variations and biological heterogeneities; and (iii) scalable with varying training sample sizes.

1. Introduction

Tumor histology provides a detailed insight into cellular morphology, organization, and heterogeneity. For example, tumor histological sections can be used to identify mitotic cells, cellular aneuploidy, and autoimmune responses. More importantly, if tumor morphology and architecture can be quantified on large histological datasets, then it will pave the way for constructing histological databases that are prognostic, the same way that genome analysis techniques have identified molecular subtypes and predictive markers. Genome wide analysis techniques (e.g., microarray analysis) have the advantages of standardized tools for data analysis and pathway enrichment, which enables hypothesis generation for the underlying mechanism. On the other hand, histological signatures are hard to compute because of the technical variations and biological heterogeneities in the stained histological sections; however, they offer insights into tissue composition as well as heterogeneity (e.g., mixed populations) and rare events.

Histological sections are often stained with hematoxylin and eosin stains (H&E), which label DNA and protein contents, respectively. Traditional histological analysis is performed by a trained pathologist through the characterization of phenotypic content, such as various cell types, cellular organization, cell state and health, and cellular secretion. While, such manual analysis may incur inter- and intra-observer variations [10]. The value of the quantitative histological image analysis originates from its capability in capturing detailed morphometric features on a cell-by-cell basis and the organization of cells. Such rich descriptions can then be linked with genomic information and survival distribution as an improved basis for diagnosis and therapy. Additionally, in the presence of large datasets, quantitative histological signatures can be used to identify intrinsic subtypes of a specific tumor type, which is supplementary to histological tumor grading.

One of the main technical barriers for processing a large collection of histological data is that the color composition is subject to technical variations (e.g., fixation, staining) and biological heterogeneities (e.g., cell type, cell state) across histological tissue sections, especially when these tissue sections are processed and scanned at different laboratories. Here, a histological tissue section refers to an image of a thin slice of tissue applied to a microscopic slide and scanned from a light microscope. From an image analysis perspective, color variations can occur both within and across tissue sections. For example, within a tissue section, some nuclei may have low chromatin content (e.g., light blue signals), while others may have higher signals (e.g., dark blue); nuclear intensity in one tissue section may be very close to the background intensity (e.g., cytoplasmic, macromolecular components) in another tissue section.

In this paper, we aim to quantify composition of each tissue section in terms of distinct histopathology, such as tumor or necrosis regions. We suggest that, compared with human engineered features, unsupervised feature learning is more tolerant to batch effect (e.g., technical variations associated with sample preparation) and can learn pertinent features without user intervention. Here, we propose a tissue classification method based on unsupervised feature learning and spatial pyramid matching (SPM) [24], which utilize sparse tissue morphometric signatures at various locations and scales.

Due to the robustness of unsupervised feature learning and the effectiveness of the spatial pyramid matching framework, our approach achieves excellent performance even with a small number of training samples across independent datasets of vastly different tumor types.

Organization of this paper is as follows: Section 2 reviews related works. Section 3 describes the details of our proposed approach. Section 4 elaborates the details of our experimental setup, followed by detailed discussion on the experimental results. Lastly, section 5 concludes the paper.

2. Related Work

Several outstanding reviews for the analysis of histology sections can be found in [12, 18]. From our perspective, four distinct works have defined the trends in tissue histology analysis: (i) one group of researchers proposed nuclear segmentation and organization for tumor grading and/or the prediction of tumor recurrence [2, 11, 3, 13]. (ii) A second group of researchers focused on patch level analysis (e.g., small regions) [4, 22, 19], using color and texture features, for tumor representation. (iii) A third group focused on block-level analysis to distinguish different states of tissue development using cell-graph representation [1, 5]. (iv) Finally, a fourth group has suggested detection and representation of the auto-immune response as a prognostic tool for cancer [17].

The major challenge for tissue classification is the large amounts of technical variations and biological heterogeneities in the data [23], which typically results in techniques that are tumor type specific. To overcome this problem, recent studies have focused on either fine tuning human engineered features [4, 22, 23], or applying automatic feature learning [20], for robust representation.

In the context of image categorization research, the traditional bag of features (BoF) model has been widely studied and improved through different variations, i.e., modeling of co-occurrence of descriptors based on generative methods [8, 7, 27, 31], improving dictionary construction through discriminative learning [14, 29], modeling the spatial layout of local descriptors based on SPM kernel [24]. It is clear that SPM has become the major component of the state-of-art systems [15] for its effectiveness in practice.

Pathologists often use “context” to assess the disease state, and SPM partially captures context as a result of its hierarchical nature. Motivated by the works of [24, 21], we have therefore encoded sparse tissue morphometric signatures, at different locations and scales within the SPM framework. The end results are highly robust and effective systems across multiple tumor types utilizing a limited number of training samples.

3. Approach

In this work (PSDⁿSPM), we employ the predictive sparse decomposition (PSD) [21] as the building block for the purpose of constructing hierarchical learning framework, which can capture higher-level sparse tissue morphometric features. Unlike many unsupervised feature learning algorithms [25, 26, 30, 36], the feed-forward feature inference of PSD is very efficient, as it involves only element-wise nonlinearity and matrix multiplication. For classification, the predicted sparse features are used in a similar fashion as SIFT features in the traditional framework of SPM, as shown in Figure 1.

Figure 1.

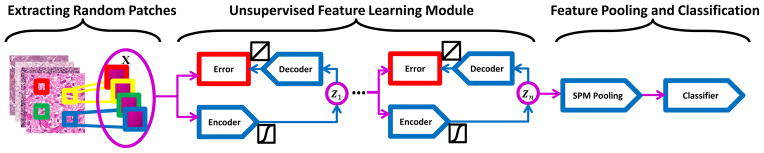
Computational workflow of our approach (PSDⁿSPM).

3.1. Unsupervised Feature Learning

Given X = [x₁, …, x_N ] ∈ ℝ^m×N as a set of vectorized image patches, we formulate the PSD optimization problem as:

$$\begin{array}{ll}\hfill \underset{\mathbf{B},\mathbf{Z},\mathbf{G},\mathbf{W}}{min}\hfill & {\Vert \mathbf{X}-\mathbf{BZ}\Vert }_F^2+\lambda {\Vert \mathbf{Z}\Vert }_1+{\Vert \mathbf{Z}-\mathbf{G}\sigma (\mathbf{WX})\Vert }_F^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\hfill & {\Vert {\mathbf{b}}_i\Vert }_2^2=1,\forall i=1,\dots ,h\hfill \end{array}$$ (1)

where B = [b₁, …, b_h] ∈ ℝ^m×h is a set of the basis functions; Z = [z₁, …, z_N ] ∈ ℝ^h×N is the sparse feature matrix; W ∈ ℝ^h×m is the auto-encoder; G = diag(g₁, …, g_h) ∈ ℝ^h×h is a scaling matrix with diag being an operator aligning vector [g₁, …, g_h] along the diagonal, σ(·) is the element-wise sigmoid function and λ is a regularization constant. The goal of jointly minimizing Eq. (1) with respect to the quadruple 〈B, Z, G, W〉 is to enforce the inference of the nonlinear regressor Gσ(WX) to be resemble to the optimal sparse codes Z that can reconstruct X over B [21].

An iterative process is employed for optimizing Eq. (1), as detailed below. The algorithm is terminated once either the objective function is below a preset threshold or a maximum number of iterations is reached.

1. Randomly initialize B, W, and G.

2. Fixing B, W and G, minimize Eq. (1) with respect to Z, where Z can be either solved as a ℓ₁-minimization problem [25] or equivalently solved by greedy algorithms, e.g., Orthogonal Matching Pursuit (OMP) [32].

3. Fixing B, W and Z, solve for G, which is a simple least-square problem with analytic solution.

4. Fixing Z and G, update B and W respectively using the stochastic gradient descent algorithm.

5. Repeat [2]–[4] until stopping condition is satisfied.

In large-scale feature learning problems, involving ~ 10⁵ image patches, it is computationally intensive to evaluate the sum-gradient over the entire training set. Therefore, to improve the scalability of our approach, we use both stochastic gradient descent algorithm and GPU parallel computing (based on an Nvidia GTX 580 graphics card). The former approximates the true gradient of the objective function by the gradient evaluated over mini-batches, and the latter further accelerates the process up to 5X with our Matlab implementation. Figure 2 illustrates 1024 basis functions computed from the GBM dataset, which capture both color and texture information from the data and is generally difficult to realize using hand-engineered features.

Figure 2.

Basis functions (B) computed from the GBM dataset.

3.2. Spatial Pyramid Matching (SPM)

Now suppose we have obtained the sparse features Z ∈ ℝ^h×N, i.e., predictions by the nonlinear regressor Gσ(WX). We first construct a codebook D = [d₁, …, d_K] ∈ ℝ^h×K, which consists of K sparse tissue morphometric types, by solving the the following optimization problem:

$$\begin{array}{ll}\underset{\mathbf{D},\mathbf{C}}{min}\hfill & \sum _{i=1}^N{\Vert {\mathbf{z}}_i-{\mathbf{D}\mathbf{c}}_i\Vert }^2\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & \mathit{card}({\mathbf{c}}_i)=1,{\Vert {\mathbf{c}}_i\Vert }_{1}1,{\mathbf{c}}_i\underset{\_}{\succ }0,\forall i\hfill \end{array}$$ (2)

where C = [c₁, …, c_N ] ∈ ℝ^K×N is the code matrix assigning each z_i to its closest sparse tissue morphometric type in D, card(c_i) is a cardinality constraint enforcing only one nonzero element in c_i, c_i ≥ 0 is a non-negative constraint on all vector elements. Eq. (2) is optimized by alternating between the two variables, i.e., minimizing one while keeping the other fixed. After training, D is fixed and the query signal set Z is encoded by solving Eq. (2) with respect to C only.

The second step is to construct spatial histogram for SPM [24]. By repeatedly subdividing an image, we compute the histograms of different sparse tissue morphometric types over the resulting subregions. Then, the spatial histogram, H, is formed by concatenating the appropriately weighted histograms of sparse tissue morphometric types at all resolutions, i.e.,

$$\begin{array}{lll}{H}_0\hfill & =\hfill & H_0^0\hfill \\ H_l\hfill & =\hfill & (H_l^1,\dots ,H_1^{4^l}),1\le l\le L\hfill \\ H\hfill & =\hfill & (\frac{1}{2^L}{H}_0,\frac{1}{2^L}{H}_1,\dots ,\frac{1}{2^{L-l+1}}{H}_l,\dots ,\frac{1}{2}{H}_L)\hfill \end{array}$$ (3)

where (·) denotes the vector concatenation operator, l ∈ {0, …, L} is the resolution level of the image pyramid, and H_l represents the concatenation of histograms for all image subregions at pyramid level l. Instead of using kernel SVM, we employ the homogeneous kernel map [33] and linear SVM [16] for improved efficiency.

4. Experiments And Discussion

In this section, we give the details of the datasets and methods involved in our experiments, which are followed by a thorough discussion on the experimental results.

4.1. Experimental Setup

We have evaluated five classification methods on two distinct datasets, curated from (i) Glioblastoma Multiforme (GBM) and (ii) Kidney Renal Clear Cell Carcinoma (KIRC) from The Cancer Genome Atlas (TCGA), which are publicly available from the NIH (National Institute of Health) repository. The five methods and detailed implementations are:

1. PSDⁿSPM^NR: the nonlinear kernel SPM that uses spatial-pyramid histograms of sparse tissue morphometric types. In the implementation,

   1. n = 1, 2;

   2. nonlinear regressor (Z = Gσ(WX)) is trained for the inference of Z;

   3. the image patch size was fixed to be 20 × 20 and the number of basis functions in the top layer was fixed to be 1024. We adopt the SPAMS optimization toolbox [28] for efficient implementation of OMP to compute the sparse code Z, with sparsity prior set to 30.

   4. standard K-means clustering was used for the construction of the dictionary;

   5. the level of pyramid was fixed to be 3;

   6. homogeneous kernel map was applied, followed by linear SVM for classification.

2. PSD¹SPM^LR [9]: the nonlinear kernel SPM that uses spatial-pyramid histograms of sparse tissue morphometric types. In the implementation,

   1. linear regressor (Z = WX) is trained for the inference of Z;

   2. for fair comparison, the image patch size was fixed to be 20×20, and the number of basis functions was fixed to be 1024. To achieve the best performance, the sparse constraint parameter λ was fixed to be 0.3.

   3. standard K-means clustering was used for the construction of the dictionary;

   4. the level of pyramid was fixed to be 3;

   5. homogeneous kernel map was applied, followed by linear SVM for classification.

3. ScSPM [34]: the linear SPM that uses linear kernel on spatial-pyramid pooling of SIFT sparse codes. In the implementation,

   1. the dense SIFT features was extracted on 16×16 patches sampled from each image on a grid with stepsize 8 pixels;

   2. the sparse constraint parameter λ was fixed to be 0.15, empirically, to achieve the best performance;

   3. the level of pyramid was fixed to be 3;

   4. linear SVM was used for classification.

4. KSPM [24]: the nonlinear kernel SPM that uses spatial-pyramid histograms of SIFT features; In the implementation,

   1. the dense SIFT features was extracted on 16×16 patches sampled from each image on a grid with stepsize 8 pixels;

   2. standard K-means clustering was used for the construction of the dictionary;

   3. the level of pyramid was fixed to be 3;

   4. homogeneous kernel map was applied, followed by linear SVM for classification.

5. CTSPM: the nonlinear kernel SPM that uses spatial-pyramid histograms of color and texture features; In the implementation,

   1. color features were extracted from the RGB color space;

   2. texture features were extracted via steerable filters [35] with 4 directions ( $\theta \in \{0,\frac{\pi }{4},\frac{\pi }{2},\frac{3\pi }{2}\}$) and 5 scales (σ ∈ {1, 2, 3, 4, 5}) from the grayscale image;

   3. the feature vector was constructed by concatenating texture and mean color on 20 × 20 patches, empirically, to achieve the best performance;

   4. standard K-means clustering was used for the construction of the dictionary;

   5. the level of pyramid was fixed to be 3;

   6. homogeneous kernel map was applied, followed by linear SVM for classification.

All experimental processes were repeated 10 times with randomly selected training and testing images, and the final results were reported as the mean and standard deviation of the classification rates on the following two distinct datasets, which included vastly different tumor types:

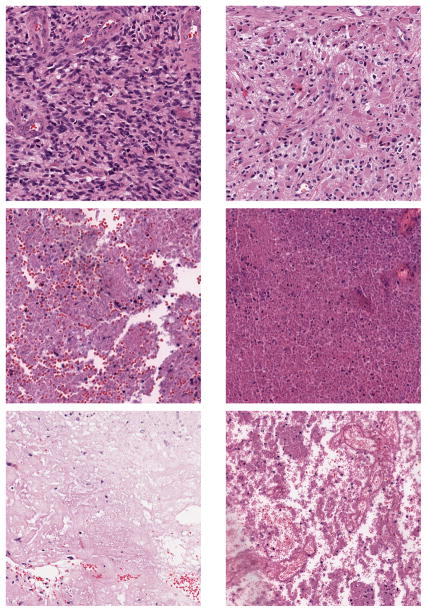
1. GBM Dataset. The GBM dataset contains 3 classes: Tumor, Necrosis, and Transition to Necrosis, which were curated from whole slide images (WSI) scanned with a 20X objective (0.502 micron/pixel). Examples can be found in Figure 3. The number of images per category are 628, 428 and 324, respectively. Most images are 1000 × 1000 pixels. In this experiment, we trained on 40, 80 and 160 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024. Detailed comparisons are shown in Table 1.

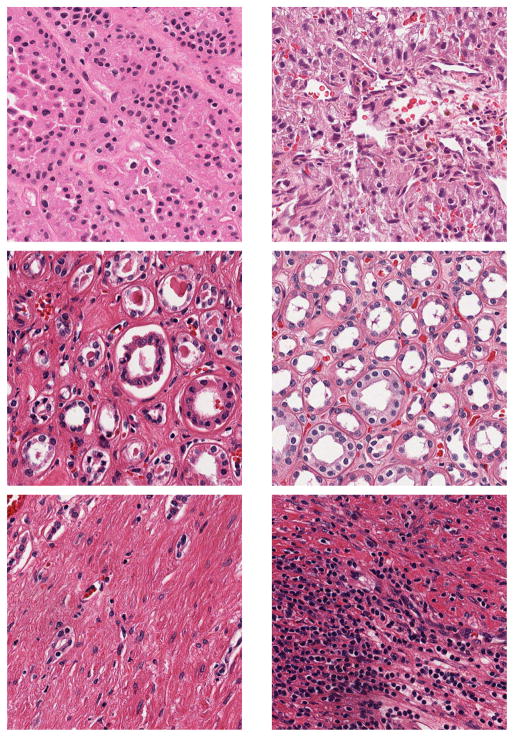
2. KIRC Dataset. The KIRC dataset contains 3 classes: Tumor, Normal, and Stromal, which were curated from whole slide images (WSI) scanned with a 40X objective (0.252 micron/pixel). Examples can be found in Figure 4. The number of images per category are 568, 796 and 784, respectively. Most images are 1000 × 1000 pixels. In this experiment, we trained on 70, 140 and 280 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024. Detailed comparisons are shown in Table 2.

Figure 3.

GBM Examples. First row: Tumor; Second row: Transition to necrosis; Third row: Necrosis.

Table 1.

Performance of different methods on the GBM dataset.

	Method	Dictionary Size=256	Dictionary Size=512	Dictionary Size=1024
160 training	PSD2SPMNR	91.85 ± 1.03	91.86 ± 0.78	92.07 ± 0.65
	PSD1SPMNR	91.85 ± 0.69	91.89 ± 0.99	91.74 ± 0.85
	PSD1SPMLR [9]	91.02 ± 1.89	91.41 ± 0.95	91.20 ± 1.29
	ScSPM [34]	79.58 ± 0.61	81.29 ± 0.86	82.36 ± 1.10
	KSPM [24]	85.00 ± 0.79	86.47 ± 0.55	86.81 ± 0.45
	CTSPM	78.61 ± 1.33	78.71 ± 1.18	78.69 ± 0.81
80 training	PSD2SPMNR	90.51 ± 1.06	90.88 ± 0.66	90.51 ± 1.06
	PSD1SPMNR	90.74 ± 0.95	90.42 ± 0.94	89.70 ± 1.20
	PSD1SPMLR [9]	88.63 ± 0.91	88.91 ± 1.18	88.64 ± 1.08
	ScSPM [34]	77.65 ± 1.43	78.31 ± 1.13	81.00 ± 0.98
	KSPM [24]	83.81 ± 1.22	84.32 ± 0.67	84.49 ± 0.34
	CTSPM	75.93 ± 1.18	76.06 ± 1.52	76.19 ± 1.33
40 training	PSD2SPMNR	87.90 ± 0.91	88.21 ± 0.90	87.71 ± 0.81
	PSD1SPMNR	87.72 ± 1.21	86.99 ± 1.76	86.33 ± 1.32
	PSD1SPMLR [9]	84.06 ± 1.16	83.72 ± 1.46	83.40 ± 1.14
	ScSPM [34]	73.60 ± 1.68	75.58 ± 1.29	76.24 ± 3.05
	KSPM [24]	80.54 ± 1.21	80.56 ± 1.24	80.46 ± 0.56
	CTSPM	73.10 ± 1.51	72.90 ± 1.09	72.65 ± 1.41

Figure 4.

KIRC Examples. First row: Tumor; Second row: Normal; Third row: Stromal.

Table 2.

Performance of different methods on the KIRC dataset.

	Method	Dictionary Size=256	Dictionary Size=512	Dictionary Size=1024
280 training	PSD2SPMNR	99.03 ± 0.20	98.89 ± 0.19	98.92 ± 0.21
	PSD1SPMNR	98.98 ± 0.35	98.81 ± 0.45	98.69 ± 0.41
	PSD1SPMLR [9]	97.19 ± 0.49	97.27 ± 0.44	97.08 ± 0.45
	ScSPM [34]	94.52 ± 0.44	96.37 ± 0.45	96.81 ± 0.50
	KSPM [24]	93.55 ± 0.31	93.76 ± 0.27	93.90 ± 0.19
	CTSPM	87.45 ± 0.59	87.95 ± 0.49	88.53 ± 0.49
140 training	PSD2SPMNR	98.26 ± 0.34	98.07 ± 0.46	97.85 ± 0.56
	PSD1SPMNR	98.17 ± 0.72	98.05 ± 0.71	97.99 ± 0.82
	PSD1SPMLR [9]	96.80 ± 0.75	96.52 ± 0.76	96.55 ± 0.84
	ScSPM [34]	93.46 ± 0.55	95.68 ± 0.36	96.76 ± 0.63
	KSPM [24]	92.50 ± 1.12	93.06 ± 0.82	93.26 ± 0.68
	CTSPM	86.55 ± 0.99	86.40 ± 0.54	86.49 ± 0.58
70 training	PSD2SPMNR	96.67 ± 0.53	96.20 ± 0.54	95.57 ± 0.66
	PSD1SPMNR	96.42 ± 0.68	96.41 ± 0.59	96.03 ± 0.69
	PSD1SPMLR [9]	95.12 ± 0.54	95.13 ± 0.51	95.09 ± 0.40
	ScSPM [34]	91.93 ± 1.00	93.67 ± 0.72	94.86 ± 0.86
	KSPM [24]	90.78 ± 0.98	91.34 ± 1.13	91.59 ± 0.97
	CTSPM	84.76 ± 1.32	84.29 ± 1.53	83.71 ± 1.42

4.2. Discussion

The experiments, conducted above, indicate that,

1. Features from unsupervised feature learning are more tolerant to batch effect than human engineered features for tissue classification. In our experiments, we show that (see Tables 1 and 2), PSDⁿSPM consistently outperforms KSPM and CTSPM on the two distinct datasets, which suggest that, given the large amounts of technical variations and biological heterogeneities in the TCGA datsets, features from unsupervised feature learning are more tolerant to batch effect than human engineered features for tissue classification.

2. PSD with nonlinear regressor outperforms PSD with linear regressor in terms of both reconstruction and classification, as shown in Figure 5 and Tables 1 and 2.

3. Stacking multiple layers of PSD enables learning higher level features, thus further improves the performance.

Figure 5.

Comparison of PSD with linear and nonlinear regressor in terms of reconstruction. (a) Original image; (b) Reconstruction by PSD with linear regressor (SNR=14.9429); (c) Reconstruction by PSD with nonlinear regressor (SNR=19.3436).

As a result, the proposed approach has the following merits,

1. Extensibility to different tumor types. Tables 1 and 2 confirm the superiority and consistency in performance of the proposed approach on two vastly different tumor types, which is due to the improved generalization ability of features from unsupervised feature learning, compared with human engineered features (e.g., SIFT), and ensures the extensibility of proposed approach to different tumor types.

2. Robustness in the presence of large amounts of technical variations and biological heterogeneities. Tables 1 and 2 indicate that the performance of our approach based on small number of training samples is either better than or comparable to the performance of Sc-SPM, KSPM and CTSPM based on large number of training samples. Given the fact that TCGA datasets contain large amount of technical variations and biological heterogeneities, these results clearly indicate the robustness of our approach, which improves the scalability with varying training sample sizes, and the reliability of further analysis on large cohort of whole mount tissue sections.

4.3. Extensibility to Different Cell Culture Model

As a further validation, we also applied our approach for the task of 3D cell culture differentiation, where the 3D cell cultures were grown in Matrigel using on-top method for one non-transformed line (MCF10A) and one malignant line (MDA-MB-231), both of which are breast epithelial lines that have been obtained from ATCC [6]. 5 samples per cell line were collected on day 5 with pixel size of 0.25 micron in X,Y and 1 micron in Z dimensions. An example of middle slices of two different cell cultures are demonstrated in Figure 6. All images were scaled isotropically with image patch size fixed to be 20×20×20 in the isotropic space for unsupervised feature learning, and the performance is reported as the mean classification rate, as shown in Table 3, which indicates the extensibility of our method to different cell culture models.

Figure 6.

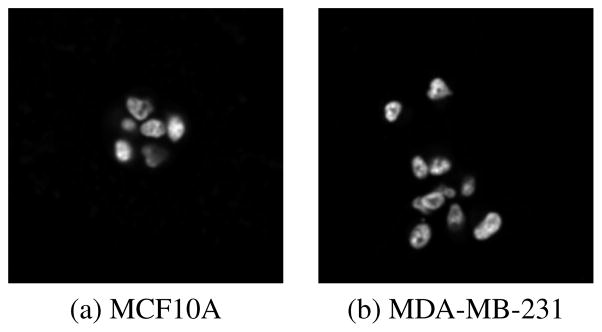
Example of middle slices from two different 3D cell cultures on day 5.

Table 3.

Performance of proposed method on 3D cell culture differentiation.

	Method	Dictionary Size=256	Dictionary Size=512	Dictionary Size=1024
2 training	PSD1SPMNR	61.67	81.67	88.33

5. Conclusion and Future Work

In this paper, we proposed a multi-layer PSD framework for classification of distinct regions of tumor histopathology, which outperforms traditional methods that are typically based on pixel- or patch-level features. The most encouraging results of this paper are that our approach is i) extensible to different tumor types; ii) robust in the presence of large amounts of technical variations and biological heterogeneities; iii) scalable with varying training sample sizes; and iv) extensible to different cell culture models. Future work will be focused on further validating our approach on other tissue types and different cell culture models.

6. Disclaimer

This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California.