Abstract
Repeated x-ray computed tomography (CT) scans are often required in several specific applications such as perfusion imaging, image-guided biopsy needle, image-guided intervention, and radiotherapy with noticeable benefits. However, the associated cumulative radiation dose significantly increases as comparison with that used in the conventional CT scan, which has raised major concerns in patients. In this study, to realize radiation dose reduction by reducing the x-ray tube current and exposure time (mAs) in repeated CT scans, we propose a prior-image induced nonlocal (PINL) regularization for statistical iterative reconstruction via the penalized weighted least-squares (PWLS) criteria, which we refer to as “PWLS-PINL”. Specifically, the PINL regularization utilizes the redundant information in the prior image and the weighted least-squares term considers a data-dependent variance estimation, aiming to improve current low-dose image quality. Subsequently, a modified iterative successive over-relaxation algorithm is adopted to optimize the associative objective function. Experimental results on both phantom and patient data show that the present PWLS-PINL method can achieve promising gains over the other existing methods in terms of the noise reduction, low-contrast object detection and edge detail preservation.
Keywords: X-ray computed tomography, prior image, statistical iterative reconstruction, penalized weighted least-squares, regularization
I. Introduction
X-RAY computed tomography (CT) techniques have been widely explored for specific applications in clinic including perfusion imaging, image-guided biopsy needle, image-guided intervention, and radiotherapy with noticeable benefits [1], [2], [3], [4]. Under these situations, repeated tomographic acquisitions are often prescribed. For instance, in the case of interventional imaging, a patient may undergo one or more imaging studies prior to the current image acquisition, whereas in other cases such as in daily CBCT examinations for target localization in image-guided radiation therapy (IGRT), repeated scans have become routine procedures. Despite the achievements of the repeated CT scans, the cumulative radiation dose still significantly increases as comparison with that used in the conventional CT scans [5], which has raised major concerns in patients. Reducing the radiation exposure is one of the major efforts in the CT fields [6], [7], [8], [9]. It is known that lowering the X-ray tube current and /or shortening the exposure time (mAs) in CT scan would be a simple and cost-effective method to reduce radiation exposure. However, the associated image usually suffers from serious noise induced artifacts due to the excessive quantum noise if adequate treatment on the noisy measurement is not applied.
Up to now, various techniques have been investigated, including optimal scan protocols [7], [8], [9] and advanced image reconstruction algorithms [10], [11], [12], [13], [14], to reduce radiation dose in CT scans. Among them, the statistical iterative reconstruction (SIR) methods [12], [13], which take into account the statistical noise properties of the measurement and accommodate the imaging geometry, have shown great potential to reduce the quantum noise and artifacts as comparison with the filtered back-projection (FBP) reconstruction method [15]. A major drawback of the SIR methods is the computational burden associated with the multiple re-projection and back-projection operation cycles through the image domain. However, with the development of fast computers and dedicated hardware [16], [17], the modified SIR methods have been used recently in advanced CT equipments [13], [18].
Generally, the SIR methods can be derived from the maximum a posteriori (MAP) estimator given the observed-data or measurement, which usually consist of two terms in the associative objective function. Specifically, the first term, named as the “data-fidelity term”, models the statistical measurement; and the second term, named as the “image prior” or “regularization term”, penalizes the solution. The data-fidelity term incorporating an accurate statistical modelling of the measurement is a prerequisite of the SIR algorithms [11], [12], [13], [18] and the edge-preserving regularization term plays an important role in the successful image reconstruction. Usually, the regularization term is chosen as a shift-invariant function that penalizes the differences among local neighboring pixels. These regularizations through equally smoothing both the noise and edge details often tend to produce an unfavorable over-smoothing effect [12]. In contrast to the smooth regularization, many edge-preserving regularizations/priors were proposed in the literature [11], [22]. A typical example is the Huber prior [19], [20], [21], which replaces the quadratic penalty function with a non-quadratic penalty function that increases less rapidly compared with the quadratic penalty function for sufficiently large arguments. However, these edge-preserving regularizations/priors mostly rely on the properties of the local smoothness or edges and do not consider the basic affinity structure information of the desired image, such as the gray levels, edge indicator, dominant direction, and dominant frequency. To address the aforementioned issues of the conventional regularizations/priors, an edge-preserving nonlocal (NL) prior was proposed for CT and positron emission tomography (PET) image reconstructions with encouraging results [22], [23], [24] by fully exploiting the density difference information and the nonlocal connectivity and continuity information of the desired image.
With regard to the repeated CT scans, a previously scanned high-quality diagnostic CT image volume usually contains same anatomical information with the current scan except for some anatomical changes due to internal motion or patient weight change. Generally, the CT scans at different times are often dealt independently and no systematic attempt has been made to integrate the valuable patient-specific prior knowledge, i.e., the previous scanned data that hold a wealth of prior information on the patient-specific anatomy, to promote the subsequent imaging process. Undoubtedly, performing a low-dose protocol in the follow-up CT scan by fully using the previous image into the current image reconstruction framework, is a promising and interesting research topic [25], [28], [29], [31], [34]. For instance, Chen et al proposed a prior image constrained compressed sensing (PICCS) algorithm [29] to enable view angle under-sampling by integrating a prior image into the reconstruction procedure. Lauzier extended the PICCS algorithm to the DR-PICCS algorithm [30] for CT radiation dose reduction using a statistical model. A weakness of PICCS is that the prior and current images are taken at the same global geometrical coordinates. This assumption, however, does not necessarily translate into practical settings like in the IGRT applications. Accurate registration and voxel consistency may limit the wide use of the PICCS algorithm. To address this issue, Ma et al [10] proposed a low-dose CT image filtering method (named as “ndiNLM” algorithm) by utilizing a high-quality normal-dose scan as priori information to perform current low-dose CT image restoration based on nonlocal means criteria [26]. The ndiNLM algorithm performed well in noise reduction, but actually it is a post-processing approach without considering the statistical property of the CT projection data. Another strategy that relaxes image registration was the dictionary learning based approach proposed by Xu et al, which was derived with the consideration of sparse representation theory via a sparse linear combination of the patch-based atoms in the dictionary.
In the present work, we aim to lower mAs for radiation reduction in the case of repeated CT scans and propose a prior-image induced nonlocal (PINL) regularization for statistical iterative reconstruction via the penalized weighted least-squares (PWLS) criteria, which we refer to as “PWLS-PINL”. Specifically, the present PINL regularization utilizes the redundant information in the prior-image and the weighted least-squares term considers a data-dependent variance estimation, aiming to improve current low-dose image quality. Subsequently, a modified iterative successive over-relation algorithm is adopted to optimize the associative objective function.
II. METHODS AND MATERIALS
A. PWLS Criteria for CT Image Reconstruction
Mathematically, the X-ray CT measurement can be approximately expressed as a discrete linear system:
| (1) |
where μ denotes the vector of attenuation coefficients, i.e., μ = (μ1, μ2, …, μN)′, and y represents the obtained sinogram data (projections after system calibration and logarithm transformation), i.e., y = (y1, y2, …, yM)′, where “′” denotes the matrix transpose. The operator H represents the system or projection matrix with a M × N size. The element of Hij denotes the length of intersection of projection ray i with pixel j. In our implementation, the associated element was pre-calculated by a fast ray-tracing technique [32] and stored as a file. The goal of CT image reconstruction is to estimate the attenuation coefficients μ from the measurement y.
According to the measurement model (1) and the MAP estimation criterion [12], [33], the mathematical formula for PWLS image reconstruction with a regularization term R(μ) can be expressed as:
| (2) |
where Σ is a diagonal matrix with the ith element of which is the variance of sinogram data y. β is a hype-parameter that controls the strength of regularization.
To determine the parameter in Eq. (2), several methods can be used [12], [34]. In this study, the variance of was determined by the mean-variance relationship proposed by Ma et al [27], which is written as:
| (3) |
where I0 denotes the incident x-ray intensity, is the mean of sinogram data y at bin i and is the background electronic noise variance.
B. Overview of the PINL regularization
Traditionally, R(μ) in Eq. (2) is designed by a simple weighted sum of the potential function on the different values of the neighboring pixels in the image domain [12], and can be described as:
| (4) |
where index j runs over all image elements in the image domain. Sj represents the local neighborhood of the jth image pixel in two dimensions. φ denotes a convex and positive potential function satisfying φ(0) = 0. Weight w(k, j) is positive and symmetric, i.e., w(k, j) ≥ 0 and w(k, j) = w(j, k), which are usually designed as an inverse proportion of the distance between the pixels k and j in Sj. These regularizations are inherently local because they lack global connectivity or continuity.
In the repeated CT scans, a previously scanned normal-dose CT image has lower noise level and higher resolution than the current low-dose CT image, and majority of the anatomical information are same between the two scans. Thus, in this work, to utilize fully the redundancy of information in the prior image, we propose a prior-image induced nonlocal (PINL) regularization with quadratic potential function, which can be written as:
| (5) |
where denotes the registered prior image between the prior image μprior and the current low-dose image μ. Nj denotes the search-window in the image . The non-local weight w(k, j) between the prior image and the current objective image is defined as:
| (6) |
| (7) |
| (8) |
Here, weight w(k, j) is a decreasing function of the similarity between two local neighborhoods nk and nj (named patch-window) centered at the pixel k in the image domain of and the pixel j in the image domain of μ, respectively. represents the 2D Euclidean distance between two similarity patch-windows. μ(nj) and denote the vector of neighborhood pixel values restricted in the patch-windows nj and nk, respectively. h is a parameter that controls the decay of the exponential function.
In summary, the objective function of the PWLS with the present PINL regularization (i.e., PWLS-PINL) for CT image reconstruction can be rewritten as:
| (9) |
C. Implementation of the PWLS-PINL Method
In the implementation of the present PWLS-PINL method, the current CT images and the initial high-dose CT images are first reconstructed by the FBP method, and then a B-spline based image registration technique [37] is adopted to generate the registered prior image from the initial high-dose CT image. The effectiveness of the B-spline based image registration algorithm has been extensively validated by many registration experiments. Based on the transformation matrix, all voxels of the prior CT images are then transformed into the current CT images to obtain globally aligned prior images. Similar to our previous studies in low-dose CT image restoration [10], through two roughly aligned images, the rich redundant information in the prior image can be effectively used to induce the PINL regularization for low-dose image reconstruction. Further evaluation of image registration in our study is presented in Section III-A5.
After we obtained the registered prior image , weight w(k, j) in Eq. (6) can be regarded as a function of the current estimation μ and the registered prior image . Because of the nonlinearity in calculating weight w(k, j), minimizing the objective function of Eq. (9) is difficult for a closed solution. To address this problem, based on our previous studies [23], [28], a binary optimal scheme can be used to minimize the objective function of Eq. (9). Specifically, weight w(k, j) is automatically adjusted according to the similarity between the patch-windows in the current estimation μn (n is the iterative index) and the registered prior image during each iteration.
In this study, we modified the iterative successive over-relaxation algorithm described in [12], [38] to calculate the solution of Eq. (9). In the implementation, the variance , i.e., the element of weight matrix in Eq. (9), is updated in each iteration according to Eq. (3) for a more accurate estimation of the sinogram variance. For simplicity, we call our implementation as the PWLS-PINL algorithm, and similar to [12], [38], it can be summarized as follows:
-
1
Initialization
-
2
μ= FBP{y}
-
3
-
4
-
5
Sj = H′jΣ−1Hj, ∀ j.
-
6
For n = 1, 2, 3, …, IterMax,
-
7
Update {w(k, j)} according to Eq. (6).
-
8
For each voxel,
-
9
-
10
-
11
-
12
-
13
.
-
14
End
-
16
.
-
17
End
where IterMax denotes the total iterative number, the parameter ω should satisfy 0 ≤ ω ≤1. The iterative process is terminated if certain convergence criteria is satisfied for a relatively stable solution [12], [22]. In this study, the 200th iterated image was selected as the result which corresponds to a stable estimation without visually changing for further iterations.
D. Data Acquisition
1) Anthropomorphic Torso Phantom
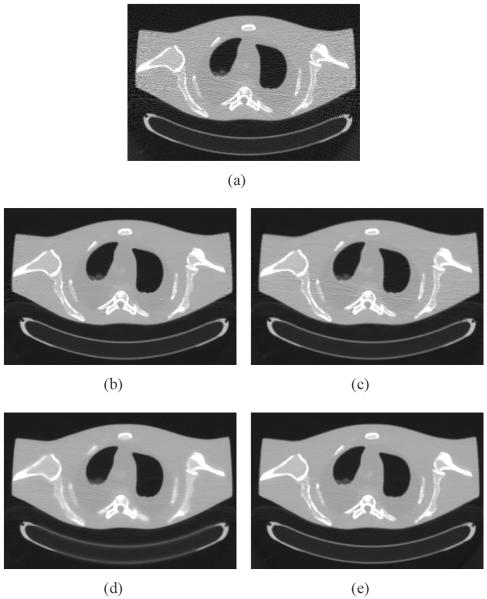
An anthropomorphic torso phantom (Radiology Support Devices, Inc., Long Beach, CA) was used for the experimental data acquisition, as shown in Fig. 1(a). The phantom was scanned by a clinical CT scanner (Siemens SOMATOM Sensation 16 CT) at three exposure levels, i.e., 17, 40, 100 mAs. For each exposure level, the tube voltage was set at 120 kVp and the phantom was scanned in a cine mode at a fixed bed position. Fig. 1(b) shows the CT image reconstructed by the FBP method with an optimized Hamming filter from the sinogram data acquired at 100 mAs, 120 kVp. The deformed images were simulated by mechanically performing a cosine transform warped distortion on the images reconstructed by the FBP method from the sinogram data acquired at 100 mAs, 120 kVp. To obtain the registered prior images, the deformed images were registered to the images reconstructed by the FBP method from the sinogram data acquired at 17 and 40 mAs, respectively.
Fig. 1.

Illustration of an anthropomorphic torso phantom (a), and (b) a CT image reconstructed by the FBP method with an optimized Hamming filter from the sinogram data acquired with 100 mAs, 120 kVp.
2) Numerical XCAT Phantom
To evaluate the influence of mismatch between the prior and current images on the performance of the PWLS-PINL and PICCS methods, the XCAT phantom [39] was used to simulate the normal-dose and low-dose CT image volumes with the same anatomical structures. The associated projection data were simulated using a CT simulator [39] at two exposure levels, i.e, 232 and 23.2 mAs. For each exposure level, the tube voltage was set at 120 kVp, the time per gantry rotation was 1.0 s, the slice thickness was 3.0 mm. The system geometry represented a system with 1800 mm source-to-detector distance, 1510.4 mm center-to-source distance, and 0.8448 mm detector pixels (672 radial bins). Reconstructions were made onto an image volume with the size of 512 × 512 × 100.
3) Patient Data
The patient data were obtained with a patient consent for a chest CT study for medical reasons. The experimental data were acquired by the Siemens SOMATOM Sensation 16 CT scanner. The scanning parameters were as follows: the pitch was 1.0 mm, the time per gantry rotation was 0.5 s, the slice thickness was 5.0 mm, the tube voltage was 120 kVp, the tube currents are 40 and 400 mA.
E. Evaluation Merits
1) Evaluation by Noise Reduction
The following metrics were utilized to evaluate the noise reduction on the reconstructed image from the low-dose sinogram data: (1) signal to noise ratio (SNR); (2) local signal to noise ratio (lSNR); and (3) relative root mean square error (rRMSE):
| (10) |
| (11) |
| (12) |
where μ represents the reconstructed image from the low-dose sinogram data, and μGS denotes a golden standard image. m indicates the voxel index in the region of interest (ROI), and Q is the number of voxels in the ROI. denotes the mean voxel value in the ROI. In this study, the golden standard image is reconstructed by the FBP method with ramp filter from the averaged sinogram data of 150 times repeated scans at 100 mAs, 120 kVp.
2) Evaluation by Image Similarity
To explore the performance of the various algorithms at the local detail level, the universal quality index (UQI) [40] was utilized to conduct an ROI based analysis by evaluating the degree of similarity between the reconstructed and golden standard images. Given a selected ROI at the corresponding locations in the two images, the mean, variance and covariance of intensities in the ROI can be respectively calculated as:
| (13) |
| (14) |
| (15) |
where μGS denotes a golden standard image, m is the voxel index, and Q denotes the number of voxels within the ROI. Then, the UQI can be calculated as follows:
| (16) |
UQI measures the intensity similarity between the two images, and its value ranges from zero to one. A UQI value closer to one suggests better similarity to the golden standard image.
3) Evaluation by Contrast-to-Noise Ratio
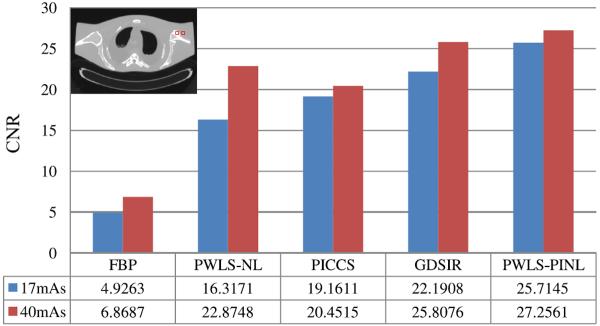
For quantitative evaluation of the reconstructed images, we selected two different ROIs as indicated by the red squares in Table III for the calculation of the contrast-to-noise ratio (CNR). The CNR is defined as:
| (17) |
where is the mean of the voxels inside the ROI, and the mean of the voxels in the background. σROI and σBG are the standard deviations of the voxel values inside the ROI and the background region, respectively.
TABLE III.
CNR measures of the images reconstructed by the four different methods from the sinogram data at 17 and 40 mAs.
|
F. Comparison Methods
To validate and evaluate the performance of the present PWLS-PINL method, the FBP method using ramp filter, the NL-prior based PWLS (PWLS-NL) method [23], [24], the PICCS method [29], [30] and a global dictionary based statistical iterative reconstruction (GDSIR) approach [34] were adopted for comparison. The NL-prior term in the PWLS-NL approach is expressed as:
| (18) |
wherein weight w(k; j) is defined as
| (19) |
| (20) |
where nj and nk represent the patch-windows, and Nj denotes the search-window in the current low-dose CT image domain.
The PICCS algorithm under the PWLS framework can be formulated as [30]:
| (21) |
where μprior is the prior image, Ψ1 and Ψ2 are the sparsifying transforms, and α ∈ [0, 1] is a scalar that controls the relative weights to be allocated to the prior image and compressing sensing (CS) terms. ∥x∥1 represents the l1-norm defined as ∥x∥1 = Σi|xi|. In the implementation, the sparsifying transform used for both ψ1 and ψ2 is the image spatial gradient norm, which is also equivalent to the total variation (TV).
The GDSIR is a patch based approach by extracting the prior information via a global dictionary trained from a high-quality image [34], and the associative image reconstruction is equivalent to solve the following minimization problem:
| (22) |
where D ∈ RN×K represents the trained dictionary whose column dk ∈ RN×1 (k = 1,…, K) is a N dimensional vector, αs ∈ RK×1 is the representation vector with few nonzero entries and ∥ · ∥0 denotes the l0-norm. Es ∈ RK × K is the matrix to extract a patch from the image μ. vs is the Lagrange multiplier and γ is a hyper-parameter. In this study, the global dictionary with the size of 64 × 256, (N = 8 × 8, K = 256) was generated from a normal-dose prior image by using a KSVD algorithm [35] wherein an orthogonal matching pursuit (OMP) technique [36] was used for sparse representation. Additionally, an alternating minimization scheme described in [34] was adapted to find the solution of (22).
III. RESULTS
A. Anthropomorphic Torso Phantom Study
1) Noise and Artifacts Suppression
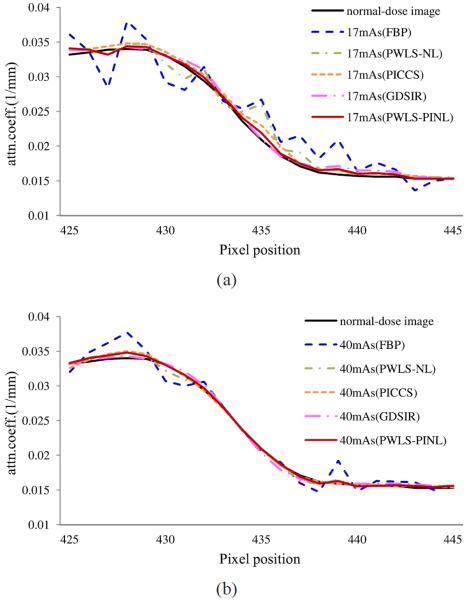
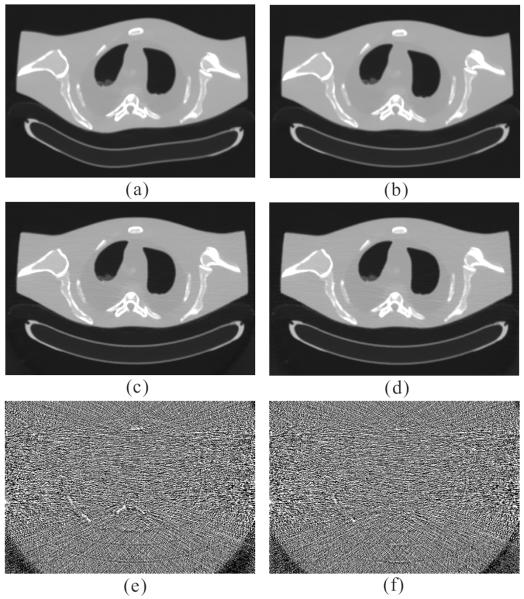
Figs. 2 and 3 show the results reconstructed by five different methods from the sinogram data acquired at 17 and 40 mAs, respectively. Figs. 2(a) and 3(a) show the images reconstructed by the FBP method with ramp filter. Serious noise-induced streak artifacts can be observed. Figs. 2(b) and 3(b) show the images reconstructed by the PWLS-NL method. The noise was mostly suppressed, but undesired streak artifacts can still be observed in the highly attenuated regions, partially because the properties of nonlocal weight calculations for structuring preserving. Figs. 2(c) and 3(c) show the images reconstructed by the PICCS method using Fig. 1(b) as the prior image. The PICCS method can yield reasonable images with sharp edges. Further, the smooth regions are plagued by some streak artifacts, which may have resulted from the TV processing. In the context of medical imaging, this noise might result in some deceptive structures. Figs. 2(d) and 3(d) show the images reconstructed by the GDSIR method wherein the global dictionary was trained from the normal-dose image Fig. 1(b). It can be seen that some distortions occurred in the case of 17 mAs while satisfactory result appeared with noticeable noise reduction in the case of 40 mAs. Figs. 2(e) and 3(e) show the images reconstructed by the present PWLS-PINL method wherein the prior image is the same as that used in the PICCS and GDSIR methods. The PWLS-PINL method achieves more gains over the PICCS and GDSIR methods in terms of successful noise-induced artifacts suppression and edges detail preservation. Fig. 4 depicts the associated horizontal profiles located at the voxel position y = 277 and x from 425 to 445 as indicated by the red line in Fig. 1(b). The profiles from the present PWLS-PINL method agree much better with those from the normal-dose scan compared with those from the other methods.
Fig. 2.
The anthropomorphic torso phantom reconstructions by using different methods from the sinogram dataset acquired with 17 mAs, 120 kVp. (a) the FBP reconstruction with ramp filter; (b) the PWLS-NL reconstruction (N = 21 × 21, n = 5 × 5, h = 2.0 × 10−3, β = 2.5 × 104); (c) the PICCS reconstruction (α = 0.6, λ = 0.1); (d) the image reconstructed by the GDSIR method (λ = 4 × 10−2) with a global dictionary trained from the prior image of Fig. 1(b); and (e) the PWLS-PINL reconstruction using Fig. 1(b) as the prior image (N = 21 × 21, n = 5 × 5, h = 2.0 × 10−3, β = 2.0 × 104). All the images are displayed in a same window.
Fig. 3.
The anthropomorphic torso phantom reconstructions by the four methods from the sinogram data set acquired at 40 mAs, 120 kVp. (a) the FBP reconstruction with ramp filter; (b) the PWLS-NL reconstruction (N = 21 × 21, n = 5 × 5, h = 2.0 × 10−3, β = 2.5 × 104); (c) the PICCS reconstruction using Fig. 1(b) as the prior image (α = 0.6, λ = 0.12); (d) the image reconstructed by the GDSIR method (λ = 3 × 10−2); and (e) the PWLS-PINL reconstruction using Fig. 1(b) as the prior image (N = 21 × 21, n = 5 × 5, h = 2.0 × 10−3, β = 2.0 × 104). All the images are displayed in a same window.
Fig. 4.
Horizontal profiles located at the voxel position y = 227 and x from 425 to 445 as indicated by the red line in Fig. 1(b). (a) are from the different reconstructions in Fig. 2 in the case of 17 mAs, 120 kVp; (b) are from the different reconstructions in Fig. 3 in the case of 40 mAs, 120 kVp.
To further evaluate quantitatively the present PWLS-PINL method, the lSNR and rRMSE of the three different ROIs, as indicated by the squares in Fig. 1(b), were measured in the two cases of 17 and 40 mAs, and are listed in Tables I and II. All statistical model based methods, i.e., the PWLS-NL, PICCS, GDSIR and PWLS-PINL, yielded more gains over the FBP reconstructions from the same sinogram data in terms of the lSNR and rRMSE measures in the three different ROIs. The results partially demonstrate that the present PWLS-PINL method can achieve noticeable gains over the other methods in terms of noise and artifacts suppression. However, the PICCS method is superior to the present PWLS-PINL algorithm in terms of the lSNR and rRMSE measures in the matched region of ROIA due to the strong same information from the prior image incorporated into the reconstructed image.
TABLE I.
Image quality metrics on the three ROIs as indicated by the squares in Fig. 1(b) in the case of 17 mAs.
| ROI A | ROI B | ROI C | ||||
|---|---|---|---|---|---|---|
| Methods | lSNR | rRMSE | lSNR | rRMSE | lSNR | rRMSE |
| FBP | 8.66 | 0.1158 | 5.64 | 0.1783 | 4.94 | 0.2078 |
| PWLS-NL | 76.56 | 0.0157 | 62.25 | 0.0181 | 36.61 | 0.0310 |
| PICCS | 96.80 | 0.0116 | 50.74 | 0.0213 | 15.87 | 0.0674 |
| GDSIR | 48.83 | 0.0224 | 38.75 | 0.0272 | 27.49 | 0.0407 |
| PWLS-PINL | 76.72 | 0.0156 | 62.19 | 0.0181 | 44.31 | 0.0266 |
TABLE II.
Image quality metrics on the three ROIs as indicated by the squares in Fig. 1(b) in the case of 40 mAs.
| ROI A | ROI B | ROI C | ||||
|---|---|---|---|---|---|---|
| Methods | lSNR | rRMSE | lSNR | rRMSE | lSNR | rRMSE |
| FBP | 15.05 | 0.0654 | 9.15 | 0.1090 | 9.05 | 0.1100 |
| PWLS-NL | 89.25 | 0.0126 | 59.77 | 0.0179 | 52.84 | 0.0205 |
| PICCS | 106.18 | 0.0043 | 91.55 | 0.0138 | 54.99 | 0.0177 |
| GDSIR | 98.45 | 0.0115 | 74.11 | 0.0153 | 59.10 | 0.0190 |
| PWLS-PINL | 101.54 | 0.0114 | 72.96 | 0.0155 | 61.20 | 0.0183 |
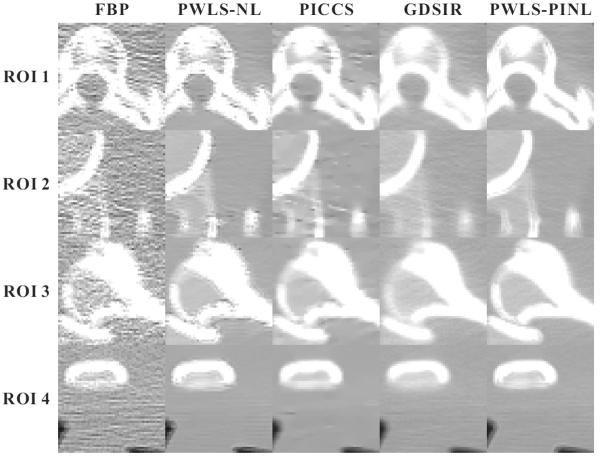
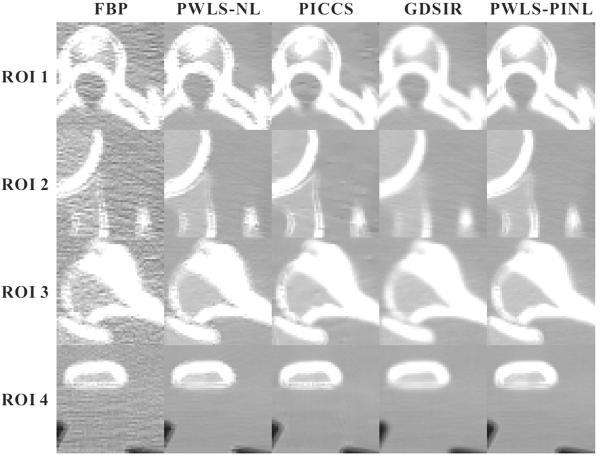
2) UQI Measure
Figs. 5 and 7 show the zoomed details of the four ROIs in Figs. 2 and 3, respectively. The PWLS-PINL method achieves significant gains over the other methods in terms of the resolution preservation. The corresponding UQI scores are shown in Figs. 6 and 8, respectively. The PWLS-PINL method yields higher UQI scores (more than 0.98) than the other methods in both the cases of 17 and 40 mAs.
Fig. 5.
Zoomed details of the four ROIs in Fig. 2.
Fig. 7.
Zoomed details of the four ROIs in Fig. 3.
Fig. 6.
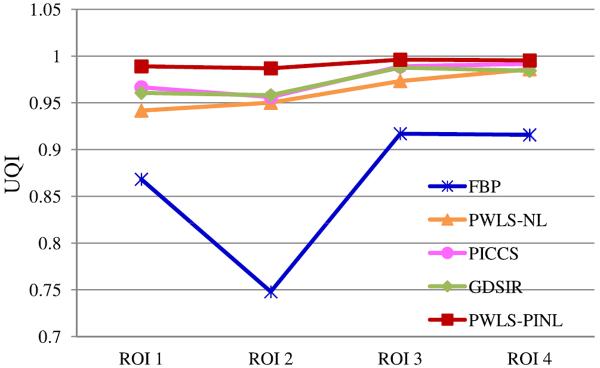
UQI measures on the four ROIs in Fig. 5.
Fig. 8.

UQI measures on the four ROIs in Fig. 7.
3) CNR Measure
Table III shows the CNRs of the images reconstructed by the four different methods from the sinogram data at 17 and 40 mAs. The ROIs for the CNR measure are marked by two squares in the figure located at the top left corner of Table III. Evidently, the present PWLS-PINL method can achieve significant ability for region contrast identification, which is very important for low-dose CT image reconstruction.
4) Convergence Analysis of the PWLS-PINL Algorithm
To validate and analyze the convergence of the present PWLS-PINL method, global rRMSE and SNR measures on the entire to-be-reconstructed anthropomorphic torso phantom image were performed. Fig. 9 shows the rRMSE and SNR measures with respect to the number of iterations in the two cases of 17 and 40 mAs. The results show that the present PWLS-PINL algorithm can yield a steadily convergence solution in terms of the global rRMSE and SNR measurements.
Fig. 9.

Global rRMSE and SNR measures of the present PWLS-PINL method with respect to the number of iterations from the anthropomorphic torso phantom reconstructions in the two cases of 17 mAs and 40 mAs. (a) rRMSE versus the number of iterations; (b) SNR versus the number of iterations.
5) Influence of Image Registration Accuracy on the PWLS-PINL Method
To evaluate the influence of the image registration accuracy on the performance of the PWLS-PINL method, we used an elastically deformed FBP image from the original one reconstructed from the sinogram data acquired at 100 mAs, 120 kVp and the corresponding registered image by the B-spline based registration algorithm as the prior images to induce image reconstruction by the PWLS-PINL method. Fig. 10 shows the influence of the registration accuracy on the PWLS-PINL method in the low-dose image reconstruction from the sinogram data acquired at 17 mAs, 120 kVp. Figs. 10(a) and (b) show the elastic deformed FBP image and the corresponding registered FBP image, respectively. The deformation between the two images is significant. Fig. 10(c) shows the image reconstructed by the PWLS-PINL method using Fig. 10(a) as the prior-image. Fig. 10(d) shows the image reconstructed by the PWLS-PINL method using Fig. 10(b) as the prior-image. For both the reconstructions of Figs. 10(c) and (d), h was 2.0×10−3 and β was 2.0 × 104. Fig. 10(e) shows the corresponding difference image between Fig. 10(c) and Fig. 2(a). Fig. 10(f) shows the corresponding difference image between Fig. 10(d) and Fig. 2(a). These difference images indicate that the performance of the PWLS-PINL method is not sensitive to the deformed prior image when a large search-window N is used to minimize the influence of the mis-registration. In other words, the present PWLS-PINL method does not heavily depend on the prior image registration accuracy. In practice, a rough registration may be sufficient.
Fig. 10.
Influence of registration accuracy on the performance of the PWLS-PINL method. (a) an elastic deformed FBP image from the original one reconstructed from the sinogram data acquired at 100 mAs, 120 kVp; (b) the corresponding registered image by using the B-spline based registration algorithm; (c) the image reconstructed by the PWLS-PINL method from the sinogram data acquired at 17 mAs, 120 kVp using (a) as the prior-image; (d) the image reconstructed by the PWLS-PINL method using (b) as the prior-image from the sinogram data acquired at 17 mAs, 120 kVp; (e) the difference image between (c) and Fig. 2(a); and (f) the difference image between (d) and Fig. 2(a). All the images are displayed in a same window.
B. Numerical XCAT Phantom Study
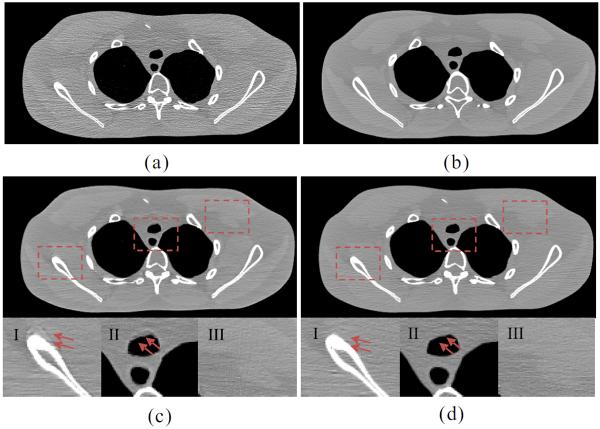
The adjacent slices of the normal-dose images were used as the prior image to induce the desired-image reconstruction by the PICCS and PWLS-PINL methods from the low-dose sinogram data. Figs. 11 and 12 show the resultant influence of mismatch between the two different prior images and the desired images on the PWLS-PINL and PICCS methods, respectively. Figs. 11(a) and 12(a) show the FBP images reconstructed with ramp filter from the low-dose sinogram data; Figs. 11(b) and 12(b) show the unregistered prior images reconstructed from the normal-dose sinogram data by the FBP method with ramp filter. The bone structure at the top of Fig. 11(a) does not appear in Fig. 11(b), but appears large in Fig. 12(b) due to the different slice selections. These kinds of features were used to analyze the influence of prior information on the desired-image reconstruction. Figs. 11(c) and 12(c) show the images reconstructed by the PICCS method from the low-dose sinogram data using Figs. 11(b) and 12(b) as the prior-image, respectively. The zoomed ROIs at the bottom of each sub-figure show the pseudo boundaries from the PICCS method. The results suggest that some local mismatches between the prior and current images may propagate into the desired-image. However, Figs. 11(d) and 12(d) show that the PWLS-PINL method with the same prior-image can deal with the mismatches between the prior and current images. These results indicate that the performance of the PWLSPINL method is not sensitive to the mismatched prior images when a relatively large search-window is used to minimize the influence of the mismatch regions. In other words, the present PWLS-PINL method does not heavily depend on the prior-image mismatch accuracy, and a rough registration may be sufficient in practice.
Fig. 11.
Influence of the mismatch between the first prior image and the desired image on the performance of the PWLS-PINL and PICCS methods. (a) the FBP image reconstructed with ramp filter from the low-dose sinogram data; (b) the unregistered prior image reconstructed from the normal dose sinogram data using the FBP method with ramp filter; (c) the image reconstructed by the PICCS method from the low-dose sinogram data using (b) as the prior-image (α = 0.7, λ = 8.0 × 10−3); and (d) the image reconstructed by the PWLS-PINL method from the low-dose sinogram data using (b) as the prior-image (N = 35 × 35, n = 5 × 5, h = 1.0 × 10−3, β = 5.0 × 105). The zoomed ROIs indicated by three squares in (c) and (d) are displayed at the bottom, respectively. All the images are displayed in a same window.
Fig. 12.
Influence of the mismatch between the second prior image and the desired images on the PWLS-PINL and PICCS methods. (a) the FBP image reconstructed with ramp filter from from the low-dose sinogram data; (b) the unregistered prior- image reconstructed from the normal dose sinogram data using the FBP method with ramp filter; (c) the image reconstructed by the PICCS method from the low-dose sinogram data using (b) as the prior-image (α=0.7, λ=8.0×10−3); and (d) the image reconstructed by the PWLS-PINL method from the low-dose sinogram data using (b) as the prior-image(N = 35 × 35, n = 5 × 5, h = 1.0 × 10−3, β = 5.0 × 105). The zoomed ROIs indicated by three squares in (c) and (d) are displayed at the bottom, respectively. All the images are displayed in a same window.
For the low-contrast detectability, as shown in Figs. 11(c)-III and 11(d)-III, the PICCS method appears to perform better than the PWLS-PINL method in the matched regions. However, as shown in the zoomed ROI of Figs. 11(c) and 12(c), the PWLS-PINL method outperforms the PICCS method when the low contrast features in the desired-image are different from those in the prior image.
C. Patient Study
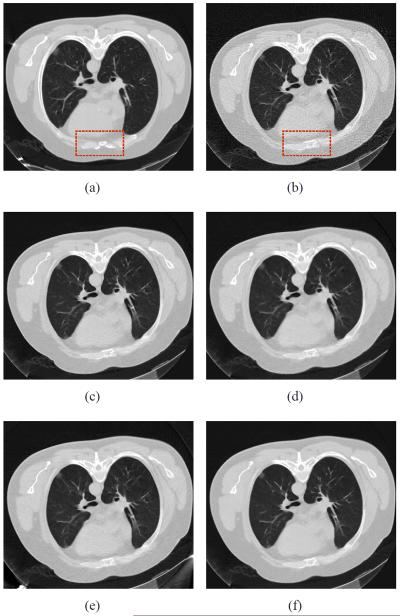
Fig. 13 shows the chest CT images reconstructed by five different methods from two different sinogram data. Fig. 13(a) shows the image reconstructed by the FBP method with ramp filter from the sinogram data acquired at 200 mAs, 120 kVp, which was used as the prior image for the PWLSPINL, PICCS and GDSIR methods. Fig. 13(b) shows the image reconstructed by the FBP with ramp filter from the sinogram data acquired at 20 mAs, 120 kVp. The anatomical structures between two FBP images are mostly similar except some noticeable organ elastic deformation as indicated by the rectangles in Figs. 13(a) and 13(b) because of the heteronomous breathing or heartbeat. The noise-induced streak artifacts can be observed in Fig. 13(b). Fig. 13(c) shows the image reconstructed by the PWLS-NL method from the sinogram data acquired at 20 mAs, 120 kVp. Fig. 13(d) shows the image reconstructed by the PICCS method using Fig. 13(a) as the prior image. Most of the noise is mitigated by the TV term of the PICCS objective function, whereas some deceptive structures appear in the mismatched areas. This phenomenon suggests that the edge structure in the prior images may have been passed to the current images. Fig. 13(e) shows the image reconstructed by the GDSIR method from the sinogram data acquired at 20 mAs, 120 kVp. The global dictionary was learned from patches extracted from Fig. 13(a). It can be seen most of the noise is removed without introducing new fake structure, but noticeable streak artifacts still exist. Fig. 13(f) shows the image reconstructed by the PWLS-PINL method from the sinogram data acquired at 20 mAs, 120 kVp. To illustrate further the performance of the PWLS-based methods, the zoomed ROIs are shown in Fig. 14. The results show that the present PWLS-PINL method can achieve significant gains over the other methods in terms of reconstruction accuracy by visual inspection. In the implementation of the four PWLS-based methods, the FBP image reconstructed with ramp filter, i.e., Fig. 13(b), was used as the initial image. All the parameters were selected by visual inspection for eye-appealing results, together with the normal-dose FBP image (i.e., Fig. 13(a)) for comparison.
Fig. 13.
Clinical chest CT image reconstructions. (a) the image reconstructed by the FBP method with ramp filter from the sinogram data acquired at 200 mAs, 120 kVp, which is used as the prior image for the PWLS-PINL and PICCS methods; (b) image reconstructed by the FBP with ramp filter from the sinogram data acquired at 20 mAs, 120 kVp; (c) image reconstructed by the PWLS-NL method from the sinogram data acquired at 20 mAs, 120 kVp (N = 21 × 21, n = 5 × 5, h = 0.6 × 10−3, β = 1.0 × 104); (d) image reconstructed by the PICCS method from the sinogram data acquired at 20 mAs, 120 kVp (α = 0.5, λ = 0.1); (e) the image reconstructed by the GDSIR method from the sinogram data acquired at 20 mAs, 120 kVp (γ = 4×10−2); and (f) image reconstructed by the PWLS-PINL method from the sinogram data acquired at 20 mAs, 120 kVp (N = 41×41, n = 5×5, h = 0.6×10−3, β = 1.0×104). All the images are displayed in the window [0 0.02] mm−1.
Fig. 14.
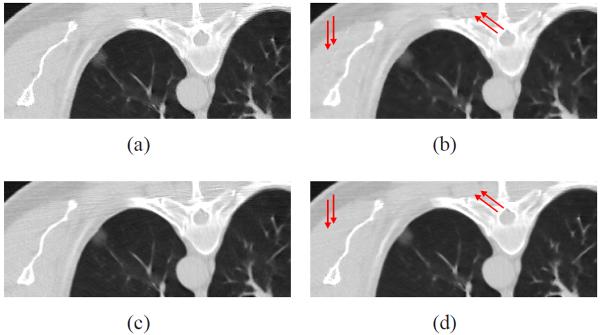
The zoomed ROIs in Fig. 12. (a) image reconstructed by the PWLS-NL method from the sinogram data acquired at 20 mAs, 120 kVp (N = 21×21, n = 5×5, h = 0.6×10−3, β = 1.0×104); (b) image reconstructed by the PICCS method from the sinogram data×acquired at 20 mAs, 120 kVp (α = 0.5, λ = 0.1); (c) the image reconstructed by the GDSIR method from the sinogram data acquired at 20 mAs, 120 kVp (γ = 4 × 10−2); and (d) image reconstructed by the PWLS-PINL method from the × sinogram data acquired at 20 mAs, 120 kVp (N = 41 × 41, n = 5 × 5, h = 0.6 × 10−3, β = 1.0×104). All the images are displayed in the window [0 0.02] mm−1.
IV. Discussion and Conclusion
Prior information is useful for successful PWLS-based image reconstruction [11], [22], [23], [24], [28]. In the medical clinic, several situations exist where repeated tomographic acquisitions are prescribed. In these cases, substantial similarity exists among images in the acquisition sequence. As a result, a previously scanned normal-dose CT image may provide strong prior information for subsequent iterative image reconstruction from the projection data with a low-dose protocol. For example, Chen et al [29] proposed the PICCS method for CT iterative image reconstruction from the spare-view measurements using a high-quality reference image. Ma et al [10] proposed the ndiNLM filter for low-dose CT image restoration using the previously scanned CT image without requiring the accurate image registration processing due to its patch-based search mechanism. In the present work, we have proposed a prior-image induced nonlocal regularization term for PWLS image reconstruction, which was named as the “PWLS-PINL”. Preliminary results using both phantom and patient data suggested that the present algorithm can robustly incorporate redundant information from previously acquired images without requiring accurate image registration, as discussed in Section III-A5. Moreover, a substantial improvement in image quality was observed compared with the traditional methods if the prior images were not incorporated. The present algorithm can be applied to the scenario where sequences of tomographic data are acquired, such as lung nodule surveillance, image-guided biopsy needle and volumetric CBCT imaging during a radiation therapy course. Because the prior image may be offset or rotated with respect to the anatomy at the time of imaging, a coarse registration should be applied in the implementation of the present PWLS-PINL method aiming to reduce the computational burden with a selected median size search window. Practically, due to the registration accuracy depending on the dose in CT scan [42], some robust registration techniques should be adopted to improve the registration accuracy with a low-dose CT imaging.
In this study, two prior image based methods were explored for comparison, i.e., the PICCS and GDSIR. The PICCS and PWLS-PINL methods can be regarded as a voxel updating technique while the GDSIR method is a patch updating technique. As shown in Section-III, the PICCS method cannot achieve satisfactory performance in suppressing noise-induced artifacts as the misalignments between the prior- and desired-images are significant. And, the GDSIR method cannot also effectively deal with the noise-induced artifacts in the case of ultra-low-dose scan. Meanwhile, the present PWLS-PINL method can relax the tradeoff of fake structures introduction and noise-induced streak artifacts reduction based on the nature of non-local means processing in image restoration. In addition, it is worth to note that the nonlocal mean algorithm as a post-processing technique for low-dose CT image restoration can also work well in some cases. But, when the projection data was seriously corrupted by excessive x-ray photon noise, the associative FBP image will suffer from serious noise-induced streak artifacts and then the nonlocal means algorithm cannot yield any possible satisfactory results due to its ability in preserving structural information. Meanwhile, the present PWLS-PINL method, by modelling several important physical and statistical factors including detector geometry, photon statistics and electronic background noise, can yield more accurate results than the nonlocal means algorithm from the noisy projection measurements.
For the implementation of the PWLS-PINL method, four parameters, i.e., search-window N, patch-window n, control parameter h, and hyper-parameter β, were selected by visual inspection for eye-appealing result, together with the normal-dose image as comparison. In practice, to reduce the computing burden, the size of the search-window should be limited to an appropriate size. However, the search-window should be large enough to obtain more similar information while minimizing the influence of the mismatched tissues. Hence, search-window N should be optimally determined by fully considering both the registration accuracy and the degree of the overall structure changes between the to-be-reconstructed and prior images. For the selection of the patch-window, extensive experiments showed that a 5 × 5 patch-window is adequate for effective noise and artifacts suppression while retaining computational efficiency. As for the selection of h and β in this study, we briefly fixed the sizes of the search- and patch-windows and did not consider the methods that adaptively optimized them, but we studied the results obtained using a broad range of parameter values by hand in term of visual inspection and quantitative measurements. This scheme can also be considered as a trial and error process. Theoretical studies in optimizing the non-local relevant parameters have already been conducted using the SURE approach [43], [44], which provided a useful technique to determine the parameters in the present algorithm. This is an interesting topic for future research.
For the modified iterative successive over-relaxation algorithm in this study, we would like to make the following discussions. As a version of the widely-used one-step-late (OSL) iteration scheme, the present PWLS-PINL algorithm can be feasibly and effectively implemented using the present joint optimal reconstruction strategy presented in Section II-C. However, due to the fact that weight w(k, j) in Eq. (6) depends on the unknown image intensity, the present PINL regularization in Eq. (5) is nonconvex for a global optimization. Similar to many existing OSL algorithms where global convergence is an open issue, the present algorithm also suffered from the lack of strict global convergence proof. Despite the lack of guarantee of global convergence, the present algorithm is still effective in practice together using the joint optimization scheme.
Another major drawback of the present PWLS-PINL algorithm is that the update of the non-local weights matrix unavoidably increases the computational burden as described in [28]. To address this issue, one possible strategy is to use infrequent update of the parameters (non-local weights matrix) interleaved with more frequent OSL steps; and another one is to use fast computers and dedicated hardware [45] to develop parallel iterative image reconstruction algorithm. We believe that in the future, most iterative based image reconstruction algorithms including the present PWLS-PINL may be widely used in medical clinic.
Acknowledgment
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions that greatly improve the quality of the manuscript.
This work was partially supported by the National Natural Science Foundation of China under grand (No. 81000613, No. 81101046, No. 81371544), the National Key Technology Research and Development Program of the Ministry of Science and Technology of China under grant (No. 2011BAI12B03), the Science and Technology Program of Guangdong Province of China under grant (No. 2011A030300005), and the 973 Program of China under grant (No. 2010CB732503). Z. Liang was partially supported by the NIH/NCI under grant #CA143111 and grant #CA082402.
References
- [1].Schubert T, Jacob AL, Takes M, Menter T, Gutzeit A, Kos S. CT-guided percutaneous biopsy of a mass lesion in the upper presacral space: a sacral transneuroforaminal approach. Cardiovasc. Intervent. Radiol. 2012 Oct.35(5):1255–1257. doi: 10.1007/s00270-011-0232-9. [DOI] [PubMed] [Google Scholar]
- [2].Siewerdsen JH. Cone-beam CT with a flat-panel detector: From image science to image-guided surgery. Nucl. Instrum. Methods Phys. Res. A. 2011 Aug.648(S1):S241–S250. doi: 10.1016/j.nima.2010.11.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Dharap SB, Khandkar AA, Pandey A, Sharma AK. Repeat CT scan in closed head injury. Injury. 2005 Mar.36(3):412–416. doi: 10.1016/j.injury.2004.06.020. [DOI] [PubMed] [Google Scholar]
- [4].Zhao B, James LP, Moskowitz CS, Guo P, Ginsberg MS, Lefkowitz RA, Qin Y, Riely GJ, Kris MG, Schwartz LH. Evaluating variability in tumor measurements from same-day repeat CT scans of patients with non-small cell lung cancer. Radiology. 2009 Jul.252(1):263–272. doi: 10.1148/radiol.2522081593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Kuo YC, Wu TH, Chung TS, Huang KW, Chao KS, Su WC, Chiou JF. Effect of regression of enlarged neck lymph nodes on radiation doses received by parotid glands during intensity-modulated radiotherapy for head and neck cancer. Am. J. Clin. Oncol. 2006 Dec.29(6):600–605. doi: 10.1097/01.coc.0000239093.95769.b3. [DOI] [PubMed] [Google Scholar]
- [6].Yu L, Liu X, Leng S, Kofler JM, Ramirez-Giraldo JC, Qu M, Christner J, Fletcher JG, McCollough CH. Radiation dose reduction in computed tomography: techniques and future perspective. Imaging Med. 2009 Oct.1(1):65–84. doi: 10.2217/iim.09.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].McCollough CH, Bruesewitz MR, Kofler JM., Jr CT dose reduction and dose management tools: overview of available options. Radiographics. 2006 Mar-Apr;26(2):503–512. doi: 10.1148/rg.262055138. [DOI] [PubMed] [Google Scholar]
- [8].Kalra MK, Maher MM, Toth TL, Schmidt B, Westerman BL, Morgan HT, Saini S. Techniques and applications of automatic tube current modulation for CT. Radiology. 2004 Dec.233(3):649–657. doi: 10.1148/radiol.2333031150. [DOI] [PubMed] [Google Scholar]
- [9].Yu L, Bruesewitz MR, Thomas KB, Fletcher JG, Kofler JM, McCollough CH. Optimal tube potential for radiation dose reduction in pediatric CT: principles, clinical implementations, and pitfalls. Radiographics. 2011 May-Jun;31(3):835–848. doi: 10.1148/rg.313105079. [DOI] [PubMed] [Google Scholar]
- [10].Ma J, Huang J, Feng Q, Zhang H, Lu H, Liang Z, Chen W. Low-dose computed tomography image restoration using previous normal-dose scan. Med. Phys. 2011 Oct.38(10):5713–5731. doi: 10.1118/1.3638125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wang J, Li T, Xing L. Iterative image reconstruction for CBCT using edge-preserving prior. Med. Phys. 2009 Jan.36(1):252–260. doi: 10.1118/1.3036112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Wang J, Li T, Lu H, Liang Z. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography. IEEE Trans. Med. Imaging. 2006 Oct.25(10):1272–1283. doi: 10.1109/42.896783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Singh S, Kalra MK, Gilman MD, Hsieh J, Pien HH, Digumarthy SR, Shepard JA. Adaptive statistical iterative reconstruction technique for radiation dose reduction in chest CT: a pilot study. Radiology. 2011 May;259(2):565–573. doi: 10.1148/radiol.11101450. [DOI] [PubMed] [Google Scholar]
- [14].Ouyang L, Solberg T, Wang J. Effects of the penalty on the penalized weighted least-squares image reconstruction for low-dose CBCT. Phys. Med. Biol. 2011 Sep.56(17):5535–5552. doi: 10.1088/0031-9155/56/17/006. [DOI] [PubMed] [Google Scholar]
- [15].Guedon JP, Bizais Y. Bandlimited and Haar filtered back-projection reconstructions. IEEE Trans. Med. Imaging. 1994;13(3):430–440. doi: 10.1109/42.310874. [DOI] [PubMed] [Google Scholar]
- [16].Hofmann HG, Keck B, Rohkohl C, Hornegger J. Comparing performance of many-core CPUs and GPUs for static and motion compensated reconstruction of C-arm CT data. Med. Phys. 2011 Jan.38(1):468–473. doi: 10.1118/1.3525838. [DOI] [PubMed] [Google Scholar]
- [17].Jia X, Dong B, Lou Y, Jiang SB. GPU-based iterative cone-beam CT reconstruction using tight frame regularization. Phys. Med. Biol. 2011 Jul.56(13):3787–3807. doi: 10.1088/0031-9155/56/13/004. [DOI] [PubMed] [Google Scholar]
- [18].Mitsumori LM, Shuman WP, Busey JM, Kolokythas O, Koprowicz KM. Adaptive statistical iterative reconstruction versus filtered back projection in the same patient: 64 channel liver CT image quality and patient radiation dose. Eur. Radiol. 2012 Jan.22(1):138–143. doi: 10.1007/s00330-011-2186-3. [DOI] [PubMed] [Google Scholar]
- [19].Li SZ. Markov Random Field Modeling in Image Analysis. Springer-Verlag; Japan: 2001. [Google Scholar]
- [20].Shulman D, Herve J. Regularization of discontinuous flow fields. Proc. Workshop on Visual Motion; Irvine, CA. 1989. pp. 81–86. [Google Scholar]
- [21].Black M, Sapiro G. Edges as outliers: anisotropic smoothing using local image statistics. Proc. Scale-Space Theories in Computer Vision; Corfu, GREECE. 1999. pp. 259–270. [Google Scholar]
- [22].Yu DF, Fessler JA. Edge-preserving tomographic reconstruction with nonlocal regularization. IEEE Trans. Med. Imaging. 2002 Feb.21(2):159–173. doi: 10.1109/42.993134. [DOI] [PubMed] [Google Scholar]
- [23].Ma J, Feng Q, Feng Y, Huang J, Chen W. Generalized Gibbs priors based positron emission tomography reconstruction. Comput. Biol. Med. 2010 Jun.40(6):565–571. doi: 10.1016/j.compbiomed.2010.03.012. [DOI] [PubMed] [Google Scholar]
- [24].Chen Y, Gao D, Nie C, Luo L, Chen W, Yin X, Lin Y. Bayesian statistical reconstruction for low-dose X-ray computed tomography using an adaptive-weighting nonlocal prior. Comput. Med. Imaging Graph. 2009 Oct.33(7):495–500. doi: 10.1016/j.compmedimag.2008.12.007. [DOI] [PubMed] [Google Scholar]
- [25].Yu H, Zhao S, Hoffman EA, Wang G. Ultra-low dose lung CT perfusion regularized by a previous scan. Acad. Radiol. 2009 Mar.16(3):363–373. doi: 10.1016/j.acra.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Buades A, Coll B, Morel JM. A nonlocal algorithm for image denoising. Proc. IEEE Computer Vision and Pattern Reconization. 2005;2:60–65. [Google Scholar]
- [27].Ma J, Liang Z, Fan Y, Liu Y, Huang J, Chen W, Lu H. Variance analysis of x-ray CT sinograms in the presence of electronic noise background. Med. Phys. 2012 Jul.39(7):4051–4065. doi: 10.1118/1.4722751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Ma J, Zhang H, Gao Y, Huang J, Liang Z, Feng Q, Chen W. Iterative image reconstruction for cerebral perfusion CT using a pre-contrast scan induced edge-preserving prior. Phys. Med. Biol. 2012 Nov.57(22):7519–7542. doi: 10.1088/0031-9155/57/22/7519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Chen GH, Theriault-Lauzier P, Tang J, Nett B, Leng S, Zambelli J, Qi Z, Bevins N, Raval A, Reeder S, Rowley H. Time-resolved interventional cardiac C-arm cone-beam CT: an application of the PICCS algorithm. IEEE Trans. Med. Imaging. 2012 Apr.31(4):907–923. doi: 10.1109/TMI.2011.2172951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Thriault Lauzier P, Chen GH. Characterization of statistical prior image constrained compressed sensing (PICCS): II. Application to dose reduction. Med. Phys. 2013 Feb.40(2):021902:1–14. doi: 10.1118/1.4773866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ouyang L, Solberg T, Wang J. Noise reduction in low-dose cone beam CT by incorporating prior volumetric image information. Med. Phys. 2012 May;39(5):2569–2577. doi: 10.1118/1.3702592. [DOI] [PubMed] [Google Scholar]
- [32].Han G, Liang Z, You J. A fast ray-tracing technique for TCT and ECT studies. Proc. IEEE NSS-MIC; Seattle, WA. 1999. pp. 1515–1518. [Google Scholar]
- [33].Li T, Li X, Wang J, Wen J, Lu H, Hsieh J, Liang Z. Nonlinear sinogram smoothing for low-dose X-ray CT. IEEE Trans. Nucl. Sci. 2004 Oct.51(5):2505–2513. [Google Scholar]
- [34].Xu Q, Yu H, Mou X, Zhang L, Hsieh J, Wang G. Low-dose X-ray CT reconstruction via dictionary learning. IEEE Trans. Med. Imaging. 2012 Sep.31(9):1682–1697. doi: 10.1109/TMI.2012.2195669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006 Dec.15(12):3736–3745. doi: 10.1109/tip.2006.881969. [DOI] [PubMed] [Google Scholar]
- [36].Pati YC, Rezaiifar R, Krishnaprasad P. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. Proc. 27th Asilomar Conf. Signals Syst. Comput.; Pacific Grove, CA. 1993. pp. 40–44. [Google Scholar]
- [37].Szeliski R, Coughlan J. Spline-Based Image Registration. International Journal of Computer Vision. 1997 Mar-Apr;22(3):199–218. [Google Scholar]
- [38].Fessler JA. Penalized weighted least-squares image reconstruction for positron emission tomography. IEEE Trans. Med. Imaging. 1994;13(2):290–300. doi: 10.1109/42.293921. [DOI] [PubMed] [Google Scholar]
- [39].Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Med. Phys. 2010 Sep.37(9):4902–4915. doi: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004 Apr.13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- [41].Black MJ, Sapiro G, Marimont DH, Heeger D. Robust anisotropic diffusion. IEEE Trans. Image Process. 1998;7(3):421–432. doi: 10.1109/83.661192. [DOI] [PubMed] [Google Scholar]
- [42].Dandekar O, Siddiqui K, Walimbe V, Shekhar R. Image registration accuracy with low-dose CT: how low can we go?. Proc. IEEE ISBI; Arlington, VA. 2006. pp. 502–505. [Google Scholar]
- [43].De Ville DV, Kocher M. SURE-based non-local means. IEEE Signal Processing Letters. 2009 Nov.16(11):973–976. [Google Scholar]
- [44].Duval V, Aujol JF, Gousseau Y. On the parameter choice for the Non-Local Means. Tech. Rep. hal-00468856, HAL. 2010 [Google Scholar]
- [45].Xu F, Mueller K. Accelerating popular tomographic reconstruction algorithms on commodity PC graphics hardware. IEEE Trans. Nucl. Sci. 2005 Jun.52(3):654–663. [Google Scholar]